Institute of Astronomy, School of Sciences, The University of Tokyo, Mitaka, Tokyo 181-0015, Japan

Abstract
Aims. We determine carbon, oxygen, and their isotopic abundances based on CO and OH spectra in 23 red giant stars, and identify possible origin of difficulty in abundance analysis of cool luminous stars.
Methods. We apply the line-by-line analysis based on the classical micro-turbulent model and 1D model photospheres.
Results. We found empirically that there is a critical value of log ${W/\nu} \approx -4.75$ (W is the equivalent width and $\nu$ the wavenumber) above which the observed lines do not follow the classical line formation theory based on the micro-turbulent model and that the classical abundance analysis can be applied only to the weak lines of log ${W/\nu} \la -4.75$ . The carbon, oxygen, and their isotopic abundances in 23 K-M giant stars obtained from such weak lines are approximately consistent with evolutionary models, although the ¹²C/¹³C puzzle (observed ¹²C/¹³C ratios are too small compared with theoretical predictions) remains unsolved. It is already known that the strong lines of log ${W/\nu} > -4.4$ are contaminated by the contribution from outer molecular layers. The less strong but saturated lines of $-4.75 < {\rm log}~{W/\nu} \la -4.4$ (intermediate-strength lines) cannot be understood at all with the abundance and turbulent velocity based on the weak lines. By studying the behavior of these lines and considering other observations such as the detection of H₂O lines, not only in the late M giants but also in the early M and K giants, we show that the intermediate-strength lines are essentially identical to the strong lines in that they also include contamination from the extra molecular layers. Thus, the behavior of the intermediate-strength lines, including those with LEP as high as 2 eV, appears to be nothing but a manifestation of the warm molecular envelope or MOLsphere.
Conclusions. The infrared spectra of K-M giant stars are a hybrid of at least two components originating in the photosphere and MOLsphere. Only the weak lines, mostly high excitation, are relatively free from the effect of MOLsphere and can be used to extract photospheric abundances. The strong lines and the intermediate-strength lines, which dominate the observed infrared spectra, are affected badly by contamination from the MOLsphere. For this reason, they provide little information about the photosphere, but instead can be important proves of the warm molecular envelope for which little is known yet. In the interpretation and analysis of the infrared spectra of K-M giant stars, it is essential to consider their hybrid nature.

Key words: stars: abundances - stars: atmospheres - stars: mass-loss - stars: late-type - line: formation - infrared: stars

The basic principle of stellar abundance determination was established almost half a century ago (e.g. Unsöld 1955), but high quality spectroscopic data have become available to complete accurate abundance analyses only from a far later date. Abundance determinations have been done primarily using classical methods based on grids of model photospheres (e.g. Gustafsson et al. 1975; Tsuji 1978; Kurucz 1979; Plez et al. 1992). Local thermodynamical equilibrium (LTE) was assumed to hold in many applications (e.g. Unsöld 1955) and favored for its simplicity in abundance determinations. The next major step was to treat line formation without the restriction of the LTE assumption (e.g. Mihalas 1978). Classical photosphere models study only the structure in the radial direction, that is are one-dimensional; the limitations of these models have been challenged by authors who considered the hydrodynamics of convection in 3 dimensions, that is three-dimensional models (e.g. Asplund 2005). In the regime of the coolest stars such as red giant and supergiant stars, however, the situation may be a bit different and there may be another problem.

In cool giant stars representing evolution from the red giant branch (RGB) to the asymptotic giant branch (AGB), CNO and their isotopic abundances experience drastic changes and accurate abundance determination should be vital not only to testing the stellar evolutionary models but also to understanding the chemistry of interstellar matter, which is enriched by the mass-loss from red giant stars. Despite their importance, few abundance analyses of high resolution spectra have been carried out for cool giant stars, in contrast to studies of other stellar types. It should be remembered that high quality infrared spectra needed for this purpose have been available, thanks to the Fourier transform spectroscopy (FTS) pioneered by P. & J. Connes (e.g. Connes 1970) and developed further in the 1970's (e.g. Maillard 1974; Hall et al. 1979; Ridgway & Brault 1984), even before highly efficient detectors such as CCD innovated optical spectroscopy. Our obstacles were therefore not in the quality of the observational data but difficulties that are inherent in the spectral analysis of very cool stars. Some efforts were made to determine the CNO and their isotopic abundances for the oxygen-rich case (e.g. Harris & Lambert 1984; Smith & Lambert 1985, 1986, 1990; Harris et al. 1985; Tsuji 1986, 1991; Aoki & Tsuji 1997) as well as the carbon-rich case (e.g. Lambert et al. 1984; Harris et al. 1987; Ohnaka & Tsuji 1996, 1999; Abia & Isern 1997; Ohnaka et al. 2000; Wahlin et al. 2006; Abia et al. 2008). Although many interesting results were shown by these works, we were not convinced entirely that the stellar abundance analysis could be completed for cool giant stars.

In our previous analysis of the CO first overtone bands in M giant stars, we found that most lines could be interpreted consistently with the classical model in terms of the micro-turbulent velocity and carbon abundance (Tsuji 1986, hereafter Paper I). The strong lines of low excitation could not be included in this scheme, but it was demonstrated that these strong lines were contaminated by the contributions of outer molecular layers (Tsuji 1988, hereafter Paper II). We then analyzed the CO second overtone bands of the same sample of M giant stars and found that the resulting carbon abundances appear to be higher by about a factor of 2 compared with those based on the CO first overtone bands (Tsuji 1991, hereafter Paper III). The origin of these discrepant results remains unsolved. The difficulty in abundance analysis of very cool stars was also noticed by Smith & Lambert (1990), who found that the strong OH 1-0 and 2-0 bands correspond to unreasonably high oxygen abundances compared with those based on the weaker bands and that strong CO lines cannot be used for abundance analysis.

The carbon and oxygen abundances in other stars are by no means well established. Even for the Sun, the classical values widely adopted (e.g. Anders & Grevesse 1989) were challenged by a new approach based on 3D models; a reduction in carbon and oxygen abundances by more than 50% from the classical values was proposed (Allende Pietro et al. 2002). The classical values, however, were defended by a detailed analysis of CO lines with semi-empirical model solar photospheres by Ayres et al. (2006). These results imply that the accurate modeling of photospheric structure is a critical issue in abundance determinations. It is unknown whether the difficulties in abundance analyses in M giant stars described above are due to limitations in the classical 1D model photospheres for cool giant stars or to other problems. For example, spectra of red giant stars have unexpected features such as H₂O lines, not only for the early M giants and K5 giant $\alpha$ Tau (Tsuji 2001) but also the earlier K giant star $\alpha$ Boo (Ryde et al. 2002). These features cannot be reproduced by our present models of the photospheres of red giant stars, and imply that we have a lack of understanding of the photosphere and/or the atmosphere extending beyond the photosphere. For this reason, we analyze the nature of the difficulty in interpreting the spectra of cool giant stars in some detail in this paper.

2 Input data

2.1 Observed spectra

Our sample consists of one K giant and 22 M giant stars listed in Table 1 and shown in Fig. 1. We use high resolution infrared spectra observed with the FTS of KPNO (Hall et al. 1979). Spectra of the H and K band regions are taken from the KPNO archive, and we also observed some spectra of the H and K band regions and most spectra of the L band region. Most of these spectra were also used in our previous analyses of CO (Papers I-III), SiO (Tsuji et al. 1994), and NH & CN (Aoki & Tsuji 1997). Some details of the spectra including the resolution, S/N ratio, and observing dates are summarized in Table 2. We measured equivalent widths (EWs) of isolated lines of ¹²C¹⁶O, ¹³C¹⁶O, and ¹²C¹⁷O in the H and K band regions, and those of ¹⁶OH in the H and L band regions. The logarithms of $W/\nu$ (W is the measured equivalent width and $\nu$ is the wavenumber of a line) are given in Tables 3a-3w.

Table 1: Program stars and their basic stellar parameters.
Obj(BS/HD) Sp. type $T_{\rm eff}^{a}$ $M_{\rm bol}^{b}$ ${\rm Mass}^{c}$

K mag $M_{\odot }$

$\alpha$ Tau (1457) K5+III 3874 -1.7 $\pm$ 0.2 1.5 $\pm$ 0.3

$\delta$ Oph (6056) M0.5III 3790 -2.2 $\pm$ 0.3 1.6 $\pm$ 0.3

$\nu$ Vir (4517) M1III 3812 -2.2 $\pm$ 0.4 1.7 $\pm$ 0.4

$\alpha$ Cet (911) M1.5IIIa 3909 -3.2 $\pm$ 0.3 3.6 $\pm$ 0.4

$\sigma$ Lib (5603) M2.5III 3596 -3.4 $\pm$ 0.5 2.2 $\pm$ 0.5

$\lambda$ Aqr (8698) M2.5III 3852 -3.4 $\pm$ 0.7 3.7 $\pm$ 1.2

$\beta$ Peg (8775) M2.5II-III 3603 -3.3 $\pm$ 0.2 2.2 $\pm$ 0.3

$\tau ^4$ Eri (1003) M3+IIIa 3712 -2.9 $\pm$ 0.4 2.0 $\pm$ 0.4

$\mu$ Gem (2286) M3III 3643 -3.3 $\pm$ 0.3 2.3 $\pm$ 0.5

$\delta$ Vir (4910) M3III 3643 -2.4 $\pm$ 0.3 1.4 $\pm$ 0.3

10 Dra (5226) M3.5III 3730 -2.9 $\pm$ 0.3 2.1 $\pm$ 0.4

$\rho$ Per (921) M4II 3523 -4.1 $\pm$ 0.4 3.2 $\pm$ 0.5

BS6861 (6861) M4 3600 -5.2 $\pm$ 2.0 6.3 $\pm$ 4.0

$\delta ^{2}$ Lyr (7139) M4II 3420 -5.5 $\pm$ 0.8 5.5 $\pm$ 2.0

RR UMi (5589) M4.5III 3397 -3.4 $\pm$ 0.3 1.6 $\pm$ 0.3

$\alpha$ Her (6406) M5Ib-II 3293 -5.8 $\pm$ 1.6 5.0 $\pm$ 2.0

OP Her (6702) M5II 3325 -4.4 $\pm$ 0.8 2.3 $\pm$ 1.0

XY Lyr (7009) M5II 3300 -5.1 $\pm$ 1.1 3.7 $\pm$ 1.5

R Lyr (7157) M5III 3313 -4.3 $\pm$ 0.3 2.1 $\pm$ 0.5

RZ Ari (867) M6III 3341 -3.5 $\pm$ 0.6 1.5 $\pm$ 0.4

30g Her (6146) M6-III 3298 -4.2 $\pm$ 0.4 2.0 $\pm$ 0.6

SW Vir (114961) M7-III: 2886 -4.4 $\pm$ 0.9 1.3 $\pm$ 0.3

RX Boo (126327) M7.5-8 2850 -4.6 $\pm$ 0.8 1.3 $\pm$ 0.3

^a Based on the infrared flux method. The uncertainty in $T_{\rm eff}$ for individual objects is estimated to be $\pm$ 100 K; ^b based on the Hipparcos trigonometric parallaxes and measured bolometric fluxes; ^c based on the evolutionary tracks of Fig. 1.

**Table 1:** Program stars and their basic stellar parameters.
Obj(BS/HD)	Sp. type	$T_{\rm eff}^{a}$	$M_{\rm bol}^{b}$	${\rm Mass}^{c}$
		K	mag	$M_{\odot }$
$\alpha$ Tau (1457)	K5+III	3874	-1.7 $\pm$ 0.2	1.5 $\pm$ 0.3
$\delta$ Oph (6056)	M0.5III	3790	-2.2 $\pm$ 0.3	1.6 $\pm$ 0.3
$\nu$ Vir (4517)	M1III	3812	-2.2 $\pm$ 0.4	1.7 $\pm$ 0.4
$\alpha$ Cet (911)	M1.5IIIa	3909	-3.2 $\pm$ 0.3	3.6 $\pm$ 0.4
$\sigma$ Lib (5603)	M2.5III	3596	-3.4 $\pm$ 0.5	2.2 $\pm$ 0.5
$\lambda$ Aqr (8698)	M2.5III	3852	-3.4 $\pm$ 0.7	3.7 $\pm$ 1.2
$\beta$ Peg (8775)	M2.5II-III	3603	-3.3 $\pm$ 0.2	2.2 $\pm$ 0.3
$\tau ^4$ Eri (1003)	M3+IIIa	3712	-2.9 $\pm$ 0.4	2.0 $\pm$ 0.4
$\mu$ Gem (2286)	M3III	3643	-3.3 $\pm$ 0.3	2.3 $\pm$ 0.5
$\delta$ Vir (4910)	M3III	3643	-2.4 $\pm$ 0.3	1.4 $\pm$ 0.3
10 Dra (5226)	M3.5III	3730	-2.9 $\pm$ 0.3	2.1 $\pm$ 0.4
$\rho$ Per (921)	M4II	3523	-4.1 $\pm$ 0.4	3.2 $\pm$ 0.5
BS6861 (6861)	M4	3600	-5.2 $\pm$ 2.0	6.3 $\pm$ 4.0
$\delta ^{2}$ Lyr (7139)	M4II	3420	-5.5 $\pm$ 0.8	5.5 $\pm$ 2.0
RR UMi (5589)	M4.5III	3397	-3.4 $\pm$ 0.3	1.6 $\pm$ 0.3
$\alpha$ Her (6406)	M5Ib-II	3293	-5.8 $\pm$ 1.6	5.0 $\pm$ 2.0
OP Her (6702)	M5II	3325	-4.4 $\pm$ 0.8	2.3 $\pm$ 1.0
XY Lyr (7009)	M5II	3300	-5.1 $\pm$ 1.1	3.7 $\pm$ 1.5
R Lyr (7157)	M5III	3313	-4.3 $\pm$ 0.3	2.1 $\pm$ 0.5
RZ Ari (867)	M6III	3341	-3.5 $\pm$ 0.6	1.5 $\pm$ 0.4
30g Her (6146)	M6-III	3298	-4.2 $\pm$ 0.4	2.0 $\pm$ 0.6
SW Vir (114961)	M7-III:	2886	-4.4 $\pm$ 0.9	1.3 $\pm$ 0.3
RX Boo (126327)	M7.5-8	2850	-4.6 $\pm$ 0.8	1.3 $\pm$ 0.3

2.2 Model photospheres

We apply classical 1D model photospheres that are almost identical to those adopted in our previous works (Tsuji 1978; Papers I-III), apart from the fact that we now assume that the photosphere is spherically symmetric (SS) rather than plane-parallel (PP) and some molecular opacity data were updated (Tsuji 2002). We include 34 elements in the solar composition (Table 1 of Tsuji 2002) except for C, N, and O for which we assume two cases a and b listed in Table 4. Case a represents the mean C and N abundances of early M giants and case b of late M giants based on our previous analyses (Paper III; Aoki & Tsuji 1997). The masses, radii, effective temperatures, and log g of our model photospheres are listed in Table 5. We consider masses of one and two solar masses to study the effects of mass. However, we use the models with $M = 2 ~M_{\odot}$ in the following analyses, since this appears to be closer to the masses of most of the red giant stars we study (Table 1). Also, the changes in the photospheric structure are rather minor if the masses are increased beyond 2 $M_{\odot }$ , since the differences between the SS and PP models tend to be reduced for larger masses. We assume that the micro-turbulent velocity of the models is 3 km s^-1 at all times.

Some characteristics of the resulting models are given in Table 5, that is the surface temperature T₀ at $\tau_0 = 10^{-6}$ ( $\tau_0$ is the optical depth defined by the continuous opacity at $\lambda = 0.81~\mu$ m) and extension parameter defined by $d = r(\tau_0 = 10^{-6})/R$ . Some of our models are compared with those by Plez (1992) in Fig. 2. These models are based on similar assumptions apart from that Plez et al. (1992) applied the opacity sampling method while we used the band model method in taking the blanketing effect of molecular lines into account. The agreements are in general good apart from at the very surface of the coolest model. In evaluating the flux, we calculate spectra at a sampling interval of 0.05 cm^-1 using a detailed line list including CO (Guelachivili et al. 1983; Chackerian & Tipping 1983), OH (Jacquinet-Husson et al. 1999), CN (Cerny et al. 1978; Bausclicher et al. 1988), H₂O (Partridge & Schwenke 1997), and SiO (Lavas et al. 1981; Tipping & Chackerian 1981). Based on the resulting spectra, the flux in the L band of the wide-band photometry, F_L, and log R_L, where $R_{L} = F_{\rm bol}/F_{L}$ with the bolometric flux $F_{\rm bol} = \sigma~T_{\rm eff}^4/\pi$ ( $\sigma$ : Stefan-Boltzmann constant), are obtained (Table 5).

**Table 4:** CNO abundances used in model photospheres.
	Case a	Case b
log $A_{\rm C}^{a}$	8.35	8.08
log $A_{\rm N}^{b}$	8.11	8.45
log $A_{\rm O}^{c}$	8.69	8.69

Table 5: Model photospheres.
Case R $T_{\rm eff}$ log g T₀^a d^b log F_L^c log R_L^d

$R_{\odot}$ K K

M = $M_{\odot }$

a 50 4000 1.04 2196 1.06 12.206 -2.542

a 50 3900 1.04 2185 1.08 12.193 -2.572

a 75 3800 0.69 2117 1.13 12.185 -2.609

a 75 3700 0.69 2094 1.13 12.171 -2.641

a 100 3600 0.44 2023 1.18 12.160 -2.679

b 100 3600 0.44 2074 1.18 12.159 -2.677

b 100 3500 0.44 2037 1.18 12.144 -2.711

b 150 3400 0.09 1857 1.30 12.137 -2.755

b 150 3300 0.09 1628 1.29 12.118 -2.787

b 200 3200 -0.16 1396 1.40 12.102 -2.825

b 200 3100 -0.16 1291 1.38 12.064 -2.842

b 250 3000 -0.36 1079 1.51 12.031 -2.866

b 250 2900 -0.36 1021 1.47 11.974 -2.868

b 300 2800 -0.52 895 1.58 11.931 -2.886

M = $2~M_{\odot}$

a 50 4000 1.34 2251 1.04 12.200 -2.536

a 50 3900 1.34 2234 1.04 12.187 -2.566

a 75 3800 0.99 2172 1.06 12.178 -2.602

a 75 3700 0.99 2152 1.06 12.163 -2.634

a 100 3600 0.74 2089 1.08 12.152 -2.670

b 100 3600 0.74 2142 1.08 12.151 -2.668

b 100 3500 0.74 2107 1.08 12.135 -2.702

b 150 3400 0.39 2003 1.13 12.124 -2.742

b 150 3300 0.39 1884 1.12 12.104 -2.773

b 200 3200 0.14 1652 1.17 12.083 -2.806

b 200 3100 0.14 1525 1.16 12.041 -2.819

b 250 3000 -0.06 1342 1.20 11.998 -2.833

b 250 2900 -0.06 1234 1.19 11.936 -2.830

b 300 2800 -0.22 1102 1.22 11.882 -2.837

^a Temperature at $\tau_0 = 10^{-6}$ where $\tau_0$ is the optical depth defined by the continuous opacity at $\lambda = 0.81~\mu$ m; ^b $d = r(\tau_0 = 10^{-6})/R$ is a measure of the extension of the photosphere; ^c F_L is the flux in the L band in unit of erg cm^-2 s^-1 per $\Delta~\lambda = 1$ cm; ^d $R_{L} = F_{\rm bol}/F_{L}$ where $F_{\rm bol}$ is the bolometric flux.

**Table 5:** Model photospheres.
Case	R	$T_{\rm eff}$	log g	T₀^a	d^b	log F_L^c	log R_L^d
	$R_{\odot}$	K		K
M =	$M_{\odot }$
a	50	4000	1.04	2196	1.06	12.206	-2.542
a	50	3900	1.04	2185	1.08	12.193	-2.572
a	75	3800	0.69	2117	1.13	12.185	-2.609
a	75	3700	0.69	2094	1.13	12.171	-2.641
a	100	3600	0.44	2023	1.18	12.160	-2.679
b	100	3600	0.44	2074	1.18	12.159	-2.677
b	100	3500	0.44	2037	1.18	12.144	-2.711
b	150	3400	0.09	1857	1.30	12.137	-2.755
b	150	3300	0.09	1628	1.29	12.118	-2.787
b	200	3200	-0.16	1396	1.40	12.102	-2.825
b	200	3100	-0.16	1291	1.38	12.064	-2.842
b	250	3000	-0.36	1079	1.51	12.031	-2.866
b	250	2900	-0.36	1021	1.47	11.974	-2.868
b	300	2800	-0.52	895	1.58	11.931	-2.886
M =	$2~M_{\odot}$
a	50	4000	1.34	2251	1.04	12.200	-2.536
a	50	3900	1.34	2234	1.04	12.187	-2.566
a	75	3800	0.99	2172	1.06	12.178	-2.602
a	75	3700	0.99	2152	1.06	12.163	-2.634
a	100	3600	0.74	2089	1.08	12.152	-2.670
b	100	3600	0.74	2142	1.08	12.151	-2.668
b	100	3500	0.74	2107	1.08	12.135	-2.702
b	150	3400	0.39	2003	1.13	12.124	-2.742
b	150	3300	0.39	1884	1.12	12.104	-2.773
b	200	3200	0.14	1652	1.17	12.083	-2.806
b	200	3100	0.14	1525	1.16	12.041	-2.819
b	250	3000	-0.06	1342	1.20	11.998	-2.833
b	250	2900	-0.06	1234	1.19	11.936	-2.830
b	300	2800	-0.22	1102	1.22	11.882	-2.837

The stellar mass has a significant effect on the surface temperature T₀ and the extension parameter d especially at low values of $T_{\rm eff}$ , and we examine its effects on abundance determinations (Sects. 4.3 and 5.3). The calculated values of log R_L differ only slightly, however, from our previous values (Tsuji 1981), which would be expected because the L band region is relatively free from the heavy line-blanketing effect. For $T_{\rm eff} = 3600$ K, we compare the results for cases a and b, but the differences are rather minor (Table 5).

2.3 Basic stellar parameters

For our sample of 23 red giant stars, the effective temperatures are determined by applying the infrared flux method (Blackwell et al. 1980) using the log R_L values from Table 5 and observed values of log R_L (Tsuji 1981). The resulting values of $T_{\rm eff}$ agree with our previous results (Tsuji 1981) in general to within 50 K. Our $T_{\rm eff}$ scale is also consistent with the empirical ones based on the measured angular diameters by Ridgway et al. (1980) and more recent results (e.g. Dyck et al. 1998; Perrin et al. 1998; van Belle et al. 1999; Mondal & Chandrasekhar 2005). We found that our individual values of effective temperature agree with the empirical values of these authors, in most cases, to within about 100 K; we therefore assume an error bar of 100 K for our estimations of $T_{\rm eff}$ . With the Hipparcos parallaxes (ESA 1997) and the bolometric luminosities obtained by the integration of the SEDs (Tsuji 1981), the absolute bolometric magnitudes are determined. The uncertainty in $M_{\rm bol}$ is dominated by errors in the parallaxes. The errors in the photometric data are estimated to be about $\pm$ 0.1 mag, including absolute calibration errors of a few percent (Bersaneli et al. 1991).

Our sample is shown on the HR diagram (Fig. 1) and an evolutionary mass is estimated by comparison with the evolutionary tracks by Claret (2004). Unfortunately, nearly half of our sample cannot be accounted for by the models of Claret, and we have to extrapolate the evolutionary tracks to be able to derive the stellar masses given in Table 1. The error bars of the masses are derived from the errors in $M_{\rm bol}$ and $T_{\rm eff}$ . For objects with $T_{\rm eff}$ lower than $\approx$ 3000 K, the extrapolations needed are so significant that the uncertainties should be much larger, and we hope that theoretical evolutionary tracks can be extended to describe these objects.

3 Method of analysis

Given a model photosphere characterized by a set of mass, radius, and luminosity (or reduced to $T_{\rm eff}$ and log g in PP models), a given EW can be interpreted in terms of abundance and micro-turbulent velocity within the framework of the classical theory of line formation. Abundances of 34 elements are assumed in our model photosphere, and we in fact determine corrections to the abundances assumed. In our analysis, we apply the line-by-line analysis based on the classical micro-turbulent model. In this method, we plot the abundance correction $\Delta$ log Aobtained for an assumed value of $\xi_{\rm micro}$ against the log $W/\nu$ of the line. We expect that larger (smaller) abundance corrections are needed if lower (higher) values of the micro-turbulent velocity are assumed especially for more saturated lines, while abundance corrections are independent of the assumed $\xi_{\rm micro}$ value for very weak lines free from saturation effect. The micro-turbulent velocity $\xi_{\rm micro}$ is determined so that abundance corrections for individual lines show the least dependence on EWs (as for detail, see Paper I, Sect. 5.1).

The probable errors (PEs) in the resulting abundance (correction) and micro-turbulent velocity are determined from the scatter in the data points plotted on the $\Delta$ log A-log $W/\nu$ plane, as described in Paper I (see its Fig. 2 and related explanation). Accordingly, the probable errors are robust assessments of the internal errors in our analysis and any result that has a large PE should be assumed as to have a large uncertainty (e.g. some values of the micro-turbulent velocity with large PEs in Table 6). Apart from the internal error, we notice that there should be a systematic error due to a selection of the lines. The analysis, which is based on the classical micro-turbulent model outlined above, should be applied only to lines weaker than a critical value, since otherwise a large systematic error will be introduced, as will be shown in Sects. 4 and 5.

4 Reanalysis of CO

We analyzed the lines of the CO first and second overtone bands separately in Papers I and III, respectively, and we summarize briefly the difficulties in these analyses. We then reanalyze the CO lines using the same observed and spectroscopic data as before, but consider the first and second overtone bands together.

4.1 Previous analysis of CO

The method outlined in Sect. 3 was applied to the lines of the ¹²C¹⁶O first overtone bands (see Figs. 1a-g of Paper I). The analysis in Paper I was done using PP model photospheres, but we confirm that the results are similar for SS model photospheres of the same $T_{\rm eff}$ . As an example, we repeat the line-by-line analysis of $\alpha$ Her in Fig. 3a; for assumed values of $\xi _{\rm micro} = 3.0$ , 3.5, and 4.0 km s^-1, the CO lines of ${\rm log}~W/\nu \la -4.5$ (those shown by filled circles) show behavior expected from the classical micro-turbulent model outlined in Sect. 3, and it is possible to find a $\xi_{\rm micro}$ value for which the abundance corrections do not depend on ${\rm log}~W/\nu$ values. The resulting values of $\xi_{\rm micro} = 3.81 \pm 0.43$ km s^-1 and log $A_{\rm C} = 8.08 \pm 0.27$ provide a null mean logarithmic abundance correction as confirmed in Fig. 3b.

Although it appeared to be possible that a self-consistent abundance analysis could be done for the lines of log $W/\nu \la -4.5$ , it was found that the lines of log $W/\nu > -4.5$ could not be described by the above scheme, but behave quite differently (also see Figs. 1 and 2 of Paper II). From a detailed analysis of the line profiles, strengths, and velocity shifts of these strong lines, we suggested that these lines should be contaminated by the contributions of extra molecular layers above the photosphere as detailed in Paper II and hence these lines cannot be used for abundance analysis.

We then analyzed the lines of the CO second overtone bands by the same method as for the CO first overtone bands (Paper III). In this case, many weak lines were available and the abundances determined were relatively insensitive to the value of $\xi_{\rm micro}$ . At the same time, the value of $\xi_{\rm micro}$ could not be specified well in some cases (Fig. 2 of Paper III). The resulting carbon abundances based on the CO second overtone bands, however, appeared to be about twice as high of those based on the CO first overtone bands. The origin of such a systematic difference between the carbon abundances based on the CO first and second overtone bands is difficult to understand, since both the analyses of the first and second overtone bands were internally self-consistent.

Since weak lines are preferred in abundance analysis, it may be possible to adopt the carbon abundances based on the CO second overtone bands and abandon the results based on the first overtone bands. However, the CO first overtone bands are useful for investigating isotopic abundances, since ¹³C¹⁶O and ¹²C¹⁷O lines of the first overtone bands are good indicators of ¹³C and ¹⁷O abundances, respectively (Sect. 6). We should then investigate in some detail the problems with the first overtone bands if we are to use them for investigating isotopic abundances. We assumed that the isotopic ratios can be determined even if the elemental abundances themselves cannot be determined accurately in our preliminary analysis of the isotopic ratios (Tsuji 2007), but we believe that it is necessary to reconsider such an assumption.

4.2 The first and second overtone bands

Although the OH analysis detailed in Sect. 5 suggests that lines stronger than a critical value of ${\rm log} W/\nu \approx -4.75$ behave differently from the weaker lines, we are unable to observe this effect in the CO lines of Fig. 3, since only a few lines of the CO first overtone bands with ${\rm log}~W/\nu \la -4.75$ could be measured especially in the later M giant stars (e.g. only 3 lines could be measured in $\alpha$ Her shown in Fig. 3). To include more weak lines, we tried to analyze together the first and second overtone bands of CO. The results for $\xi _{\rm micro} = 2.4$ , 3.0, and 3.6 km s^-1 are shown in Fig. 4a, where the lines of the first and second overtone bands of CO are shown by circles and triangles, respectively. All these lines are analyzed together, regardless of whether they are of the first or the second overtone bands. Unlike Fig. 3a based on the CO lines of the first overtone bands alone, it now appears that there is a clear distinction between the lines of ${\rm log}~W/\nu > -4.75$ (shown by the open symbols) and those of ${\rm log}~W/\nu \la -4.75$ (shown by the filled symbols). Only the lines of ${\rm log}~W/\nu \la -4.75$ show the behavior expected from the classical micro-turbulent model of line formation theory noted in Sect. 3.

It is evident in Fig. 4a that it is impossible to find a turbulent velocity that provides a consistent abundance correction to all lines measured covering $-5.0 < {\rm log}~W/\nu < -4.2$ . Thus, the critical value of ${\rm log} W/\nu \approx -4.75$ found for the CO lines is purely empirical as for OH to be discussed in Sect. 5.1. Unfortunately, we thought previously (Paper I) that such a critical value is ${\rm log} W/\nu \approx -4.5$ rather than -4.75. In this paper, we confirm that this new critical value of ${\rm log} W/\nu \approx -4.75$ should apply to all red giant stars that we are to study.

From the weak lines which behave as expected for different values of $\xi_{\rm micro}$ in Fig. 4a, we can determine $\xi_{\rm micro}$ value using the method described in Sect. 3. The solution is found to be $\xi_{\rm micro} = 2.82 \pm 0.23$ km s^-1 and log $A_{\rm C} = 8.40 \pm 0.13$ , for which the mean abundance correction is null as confirmed in Fig. 4b. On the other hand, the intermediate-strength lines remain unexplained. We previously concluded that lines with ${\rm log} W/\nu > -4.5$ , most of which originate in the low excitation levels, should include excess absorption originating in the outer molecular layers. It is, however, unclear if this interpretation can be extended to the intermediate-strength lines and we return to this subject in Sect. 7.2 after we examine more cases.

The results of the same analysis on other late M giants show similar patterns as shown for $\delta ^{2}$ Lyr and 30g Her in Figs. 5a,b. It appears that the abundance corrections for the second overtones (filled triangles) are often larger than those for the first overtones (filled circles), but we assume that such a difference may be within the margins of error of the measurements, including the difference in the assumed continuum levels. The case of RX Boo shown in Fig. 5c is the most difficult case with only 3 weak lines, but nevertheless we could find a solution in this case. The PEs of both $\xi_{\rm micro}$ and log $A_{\rm C}$ , estimated by the method noted in Sect. 3 are, however, large, which reflects the poor quality of the data available for this latest M giant in our sample.

We then examine earlier M giants and apply the same analysis to the lines of the CO first and second overtone bands of $\beta$ Peg, as shown in Fig. 6a. We applied the same method of the line-by-line analysis to the first and second overtone bands separately in Fig. 1c of Paper I and Fig. 2 of Paper III, respectively. The lines of the second overtone bands are all weak and our results were $\xi_{\rm micro} = 4.1 \pm 2.8$ km s^-1 and log $A_{\rm C} = 8.24 \pm 0.08$ (Paper III). Although the lines of the first overtone bands cover the range of $-5.1 < {\rm log}~W/\nu < -4.5$ , these lines could also be analyzed consistently, and the results were found to be $\xi_{\rm micro} = 3.12$ km s^-1 and log $A_{\rm C} = 7.89$ (Paper I). We now analyze precisely the same lines of the first and second overtone bands together, and our results for $\xi_{\rm micro}$ = 1.6, 2.0 and 2.4 km s^-1 are shown in Fig. 6a. It appears again that no consistent solution can be obtained for all these lines covering $-5.3 < {\rm log}~W/\nu < -4.4$ . Instead the lines are divided into two groups separated at ${\rm log} W/\nu \approx -4.75$ , and a consistent abundance correction is derived for only the weak lines. The resulting values of $\xi_{\rm micro} = 2.04 \pm 0.07$ km s^-1 and log $A_{\rm C} = 8.27 \pm 0.05$ are confirmed to provide null abundance corrections as shown in Fig. 6b. The resulting carbon abundance agrees well with that of Paper III but differs substantially from that of Paper I. It is now clear that the analysis of Paper I included the lines of ${\rm log} W/\nu >-4.75$ , which were inappropriate for abundance analyses.

The results of the same analysis on other early M giants (including a K giant) show similar patterns. Some examples are shown for $\alpha$ Tau, $\nu$ Vir, and $\alpha$ Cet in Figs. 7a-c. It is noted that the anomalous behavior of the lines stronger than the critical value already appears in the K5 giant $\alpha$ Tau, and in all the early M giants that we have examined. The nature of the intermediate-strength lines, however, is quite difficult to understand. We have previously suggested that the lines with ${\rm log}~W/\nu > -4.5$ may be contaminated by the contribution of the warm molecular layers above the photosphere, but this interpretation has been accepted only for low excitation lines observed in late M giants (Paper II). It is noted, however, that the anomalous behaviors of the intermediate-strength lines shown on the $\Delta$ log A - log $W/\nu$ diagram are similar between the late (Figs. 4 and 5) and early (Figs. 6 and 7) M giants.

Finally, we noticed that the case of $\rho$ Per is somewhat different. We again apply the line-by-line analysis with $\xi _{\rm micro} = 3.0$ , 3.5, and 4.0 km s^-1 as shown in Fig. 8a. The resulting $\xi_{\rm micro} = 3.59 \pm 0.64$ km s^-1 and log $A_{\rm C} = 8.27 \pm 0.07$ based on the weak lines are confirmed in Fig. 8b. It is to be remembered that exactly the same lines of the first overtone bands alone (omitting lines with ${\rm log} W/\nu > -4.5$ ) resulted $\xi_{\rm micro} = 2.68 \pm 0.30$ km s^-1 and log $A_{\rm C} = 8.00 \pm 0.22$ (see Fig. 1e of Paper I), although it now appears that almost all lines used in Paper I were intermediate-strength lines, which may be inappropriate for abundance analysis. Although the weak lines behave as expected, the intermediate-strength lines do not at all in that the abundance corrections are now mostly negative, while they were mostly positive in the cases examined so far (see Figs. 4-7).

We found more or less similar patterns in other objects such as $\tau ^4$ Eri, R Lyr, and SW Vir shown in Figs. 9a-c. We note that the presence of the warm molecular layers is already known in late M giants including $\rho$ Per, R Lyr, and SW Vir (Paper II) and the strong low excitation lines in Figs. 8 and 9 show positive abundance corrections consistent with the excess absorption in the outer molecular layers, even though weaker intermediate-strength lines show negative abundance corrections. Thus, the presence of the extra molecular layers in these objects can still be considered, but we return to this subject after we also analyze OH lines (Sect. 7.2).

We conclude that the weak lines of CO behave quite well as expected from the classical micro-turbulent model described in Sect. 3 and hence photospheric abundances can be determined with reasonable accuracy from these lines, although the behaviors of the intermediate-strength lines cannot yet be understood. Thus, our initial purpose to determine carbon abundance could be achieved, and we summarize the resulting carbon abundances based on the lines of the CO first and second overtone bands for 23 objects in the 6th column of Table 6. We found that the results do not agree at all with those of Paper I but agree rather well with those of Paper III except for a few cases. We conclude that the carbon abundances of Paper I cannot be correct because they were based on the lines that we found to be inappropriate for abundance analysis on a purely empirical basis.

Although our new ${\rm log}~A_{\rm C}$ values agree rather well with those of Paper III, we notice for a few objects that there are differences as large as 0.3 dex, which have a direct effect on the determination of the nitrogen abundances based on CN lines (Aoki & Tsuji 1997). Roughly speaking, if $P_{\rm C}$ and $P_{\rm N}$ are determined by CO and N₂ formations, respectively,

4.3 Uncertainties

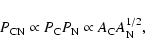
We have only considered internal errors (PEs) in our results shown in Table 6, but the PEs are useful indicators of the reliability of the results, as noted in Sect. 3. For example, inspection of Table 6 reveals that the PEs for $\xi_{\rm micro}$ are larger than 1 km s^-1 for BS6861, SW Vir, and RX Boo, and this may be because the numbers of weak lines available in these cases are only a few. A large systematic error due to an improper selection of lines in Paper I is corrected with the recognition of the possibly true critical value of log $W/\nu = -4.75$ in this paper. Other possible uncertainties are due to errors in the input parameters such as $T_{\rm eff}$ , M, R, and to our modeling of the photospheres. We previously examined the effect of uncertainties in $T_{\rm eff}$ and ${\rm log}~g$ within the framework of PP models. The results (Fig. 14 of Paper III) indicate that the uncertainties are $\Delta~{\rm log}~A_{\rm C} \la 0.1$ for $\Delta T_{\rm eff} = 100$ K and $\Delta~{\rm log}~A_{\rm C} \approx 0.2$ for $\Delta {\rm log}~g = 0.5$ .

The use of SS models, however, introduces another problem; inspection of Table 5 reveals that the photospheric extensions and hence surface temperatures show considerable differences between models of one and two solar masses especially at low $T_{\rm eff}$ . In the model photospheres of $T_{\rm eff} = 3000$ K, for example, the photospheric extension increases from 0.20 R to 0.51 R and the surface temperature decreases from 1342 K to 1079 K if mass is reduced from $2.0~M_{\odot}$ to $1~M_{\odot}$ (Table 5). We assume 2 $M_{\odot }$ in our analysis at all times, but mass is the most uncertain parameter. For this reason, we examined the effect of mass for the typical example of $\alpha$ Her. We derived the results shown in Table 6 ( ${\rm log}~A_{\rm C} = 8.40$ and $\xi _{\rm micro} = 2.82$ km s^-1) with a model of $M = 2 ~M_{\odot}$ (b/2.0/150/3300). We repeat the same analysis with a model of $M = 1.0~M_{\odot}$ (b/1.0/150/3300). The result is ${\rm log}~A_{\rm C} = 8.29 \pm 0.13$ and $\xi_{\rm micro} = 3.05 \pm 0.24$ km s^-1. The difference in derived carbon abundance is 0.11 dex and turbulent velocities differ by less than 10%. Thus the conclusion obtained with PP models remains almost unchanged if we use SS models. The reason for this may be due to the use of only the weak lines which are formed rather deep in the photosphere. Also CO is quite stable at low temperatures because of its high dissociation energy; its abundance may be hardly affected by some changes in the physical conditions. This is in marked contrast to the case of the Sun in which CO is just forming at temperatures considerably higher than in M giants and its abundance is highly sensitive to temperature.

4.4 Comparisons with other author's results

We compare our carbon abundances with those by Smith & Lambert (1990) for objects analyzed in both analyses presented in Table 8. Some significant differences are found for $\nu$ Vir, $\beta$ Peg, and $\rho$ Per, which show differences of 0.38, 0.15, and 0.19 dex, respectively. The agreements for other objects, however, are generally within the internal errors of both analyses. Unfortunately, we are unaware of other high resolution studies of photospheric abundances of cool giant stars.

We note, however, an interesting intermediate-resolution analysis for a large sample of 70 M giant stars (Lazaro et al. 1991). Their result implied rather low carbon abundances consistent with our previous result of Paper I, which we just discarded. Since their intermediate-resolution analysis necessarily included the intermediate-strength lines as we also did in our previous analysis in Paper I, their result demonstrates that low and high resolution analyses provide similar results if applied to the same types of lines. Certainly, intermediate-resolution analyses should be useful for applications to faint objects in remote stellar systems. However, the problem of how to treat the stronger lines that have not been well modeled by the classical line formation theory must be settled before lower resolution spectra can be used successfully in abundance analyses.

Another interesting attempt of medium resolution spectroscopy was reported by Decin et al. (2003), who analyzed infrared spectra observed with ISO SWS. They carefully compared the observed and synthetic spectra and estimated basic stellar parameters, including the CNO and their isotopic abundances. For synthetic spectra of medium resolution, it may again be difficult to avoid the use of the intermediate-strength and strong lines inappropriate for abundance analysis. Nevertheless, the resulting carbon abundances agree rather well with the other results except for $\alpha$ Cet, for which our result shows unusually high C abundance.

5 The case of OH

Hydroxyl radical OH shows rich spectra due to ro-vibrational transitions in the infrared region. The fundamental and first overtone bands are observed well in the L and H band regions, respectively, in cool oxygen-rich stars. Spectroscopic data such as the line positions and intensities of OH are taken from the GEISA databank (Jacquinet-Husson et al. 1999), which covers well the high excitation transitions of OH observed in stellar spectra.

5.1 The OH fundamental bands

First, we applied the same method as used for CO to the lines of the OH fundamentals. We included the carbon abundance determined in the previous section as an input abundance for each star. Since OH formation depends on $A_{\rm O} - A_{\rm C}$ rather than on $A_{\rm O}$ , determination of the carbon abundance is a prerequisite for OH analysis to determine the oxygen abundance. An example is shown for $\alpha$ Her in Fig. 10a, in which the results of the analysis with $\xi _{\rm micro} = 2.0$ , 3.0, and 4.0 km s^-1are shown. We again encountered the same difficulty as for the case of the CO first overtone bands in that the stronger lines do not follow the pattern expected from the weaker lines. Furthermore, it appears very clearly that these weaker and stronger lines are divided at log ${W/\nu} \approx -4.75$ and not at log $W/\nu \approx -4.5$ suggested from our previous analysis of the CO first overtone bands alone (Paper I). In fact, we first noticed that log ${W/\nu} \approx -4.75$ should be an important value for dividing the lines into two groups by this analysis of OH fundamental bands. With this result in mind, we also confirmed that this value is similarly important for the CO lines, but clearly seen only if the first and second overtone bands are analyzed together (Sect. 4.2).

As for CO, the weaker lines show the behavior expected from the classical micro-turbulent model noted in Sect. 3. However, the stronger lines, which should suffer heavier saturation effect, do not show the behavior expected for the saturated lines. Thus, we apply the same grouping of lines as defined for CO (see footnote 5) to OH. From the weak lines, we found that the abundance corrections from different lines show a consistent value for $\xi _{\rm micro} = 2.92$ km s^-1 as shown in Fig. 10b. We found again that it is impossible to smooth out the reflection at log ${W/\nu} \approx -4.75$ by any choice of the micro-turbulent velocity, and thus the critical value of log ${W/\nu} \approx -4.75$ can be deemed as well defined empirically. This result is consistent with Smith & Lambert (1990), who found that OH lines of 1-0 and 2-1 bands (mostly stronger than the lines of 3-2, 4-3, 5-4 bands) provide unreasonably large values of the oxygen abundance and cannot be used for abundance determinations.

It is unclear if the same problem exists for the OH lines of K giant $\alpha$ Tau, since almost all lines measured are the weak lines. We recall that the anomalous behavior of the intermediate-strength lines of CO was already noticed in the K giant $\alpha$ Tau (Sect. 4.2). We are able to use almost all OH lines detected for $\alpha$ Tau in the abundance analysis because they are the weak lines and the result is shown in Fig. 11a. However, all the other late M giants show similar patterns as for $\alpha$ Her. As examples, the results for R Lyr and SW Vir are shown in Figs. 11b and 11c, respectively (30g Her, RZ Ari, and RX Boo also show similar patterns).

We assumed that the photospheric abundances of oxygen could be obtained exclusively from the weak lines, and summarize the resulting oxygen abundances and turbulent velocities obtained from the OH fundamentals in Table 6 for 7 objects for which the L band spectra are available (those objects with non-zero $N_{L}^{\rm wk}$ in the 11th column).

Again, a problem is why the intermediate strength lines cannot be used for abundance analysis. We suggest that some contributions from the outer molecular layers will disturb the strongest lines in the case of CO. To examine if this may also be the case for OH, we plotted the lower excitation potentials (LEPs) of all the lines in Fig. 10a against log $W/\nu$ in Fig. 12b. For comparison, we made a similar plot in Fig. 12a for CO lines of $\alpha$ Her analyzed in Fig. 3. Unlike the case of the strong CO lines originating in the levels of very low LEP less than 0.5 eV, the intermediate strength lines of OH do not necessarily originate in the very low LEP, but rather from the levels with LEP $\approx$ 0.5-1.5 eV. However, the intermediate strength lines of CO do not originate in levels of very low excitation as well, and the intermediate strength lines of CO and OH may have the same origin as discussed in Sect. 7.2.

5.2 The OH first overtone bands

Unfortunately, we have only 7 spectra of the L band region, and we analyze the OH first overtone bands observed in the H band region to extend our sample. Unlike the most molecules for which the overtone bands are weaker than the fundamental bands, the case of OH is rather special in that the first overtone bands are as strong as the fundamental bands or even stronger. As a result, it is more difficult to measure weak lines in the first overtone than in the fundamental bands especially in cooler objects, and we cannot analyze the first overtones of OH in some cool objects. Fortunately, most of these objects are those for which we have the L band spectra and oxygen abundances have already been determined from the OH lines of the fundamental bands (Sect. 5.1).

We apply the same method as used for the fundamental bands and an example is shown in Fig. 13a for $\rho$ Per. For this case of the overtone bands, compared to the case of the fundamental bands discussed in Sect. 5.1, it is shown more clearly that the OH lines are divided into two groups that behave quite differently. Although abundances can be determined rather well from the weak lines, it is hopeless to determine abundances from the intermediate-strength lines. It is also interesting to note that the abundance corrections for the intermediate-strength lines show a similar behavior to those for the intermediate-strength lines of CO in $\rho$ Per (Figs. 8a, b).

In the K giant $\alpha$ Tau, most lines measured are the weak lines as in the fundamental bands, and we use most of these lines for our abundance determination (Fig. 14a). In the M3 giant $\sigma$ Lib, the abundance corrections for the intermediate-strength lines show large positive deviations compared with those for the weak lines, for which the abundance corrections converge to null values for log $A_{\rm C} = 8.82$ and $\xi _{\rm micro} = 2.03$ km s^-1 (Fig. 14b). The M5 giant R Lyr shows similar patterns as for $\rho$ Per (Fig. 14c). The resulting micro-turbulent velocity is unreasonably large, but the large PE implies that such a result cannot be realistic. This is because small errors in the measured equivalent widths seriously affect the determination of $\xi_{\rm micro}$ value when only a few weak lines are available, and this is a difficulty of our line-by-line analysis. Nevertheless, the abundance can be determined rather well because of the use of the weak lines, which depend little on the value of $\xi_{\rm micro}$ . The difficulty of measuring weak lines in the first overtones of OH is more significant for some late M giants including $\delta ^{2}$ Lyr, 30g Her, $\alpha$ Her, SW Vir, RX Boo, and we were unable to analyze the H band spectra of these stars.

We confirm both in the CO and OH lines that the behaviors of the intermediate-strength lines are quite complicated and show different patterns for different objects. For example, the intermediate-strength lines, both of OH and CO, do not necessarily show positive abundance corrections compared with those for the weak lines in $\rho$ Per and R Lyr. It is interesting to note that CO and OH lines show similar patterns on $\Delta$ log A-log $W/\nu$ diagram if these OH and CO lines are measured from the same spectra as are the cases of $\rho$ Per and R Lyr.

We summarize the resulting oxygen abundances based on the weak lines of the OH first overtone bands for 15 objects in Table 6 (those with non-zero $N_{H}^{\rm wk}$ in the 9th column). The oxygen abundances could be determined independently from the fundamental and first overtone bands for three objects, $\alpha$ Tau, R Lyr, and RZ Ari. The resulting oxygen abundances, compared directly in the 12th column of Table 6, agree well within the internal errors of both analyses. The micro-turbulent velocities also agree well except for R Lyr, for which the reason for the difficulty was discussed already (see Fig. 14c). The micro-turbulent velocities of $\alpha$ Tau based on the fundamental and overtone bands agree quite well ( $\xi_{\rm micro} \approx 3.8$ km s^-1), but disagree with the result obtained from the CO lines ( $\xi_{\rm micro} \approx 2.2$ km s^-1). This result again prompts the question of what the micro-turbulent velocity represents.

5.3 Uncertainties and comparison with other authors

We notice in Table 6 that the values of micro-turbulent velocity are sometimes unexpectedly large both for CO and OH, and that most cases of $\xi_{\rm micro} \ga 4$ km s^-1 are found when the numbers of weak lines used are below 10. The $\xi_{\rm micro}$ value by our analysis based on the method outlined in Sect. 3 is susceptible to small errors in the measured EWs especially if only a small number of lines can be used. The poor quality of the data is reflected in the large PE of the derived $\xi_{\rm micro}$ in Table 6, and the resulting $\xi_{\rm micro}$ value is therefore unreliable. For example, $\xi_{\rm micro}$ values as large as 6 km s^-1 for $\lambda$ Aqr and R Lyr are almost unusable because they have very large PEs.

Unlike CO, OH may be more susceptible to a change in the physical conditions. To compare with the case of CO (Sect. 4.3), we again examined the case of the cool giant $\alpha$ Her. We repeated the same analysis of the OH lines of $\alpha$ Her done for a model of $M = 2.0 ~M_{\odot}$ (b/2.0/150/3300) giving the results shown in Table 6 ( ${\rm log}~A_{\rm O} = 8.85$ and $\xi _{\rm micro} = 2.92$ km s^-1). Now, for a model of $M = 1.0~M_{\odot}$ (b/1.0/150/3300), the results are ${\rm log}~A_{\rm O} = 8.91 \pm 0.13$ and $\xi_{\rm micro} = 3.30 \pm 0.08$ km s^-1. The differences are again unexpectedly small. The reason for this may again be due to the use of only the weak lines, which originate deep in the photosphere.

Finally, we compare our results with those by Smith & Lambert (1990) and by Decin et al. (2003) in Table 8. For most cases of oxygen abundances, the results agree reasonably well within the error bars of these analyses. It is interesting that the agreements are reasonably good despite possible differences in the model photospheres used.

$\begin{figure} \par\includegraphics[width=16.0cm,clip]{9869fg16.eps} \end{figure}$

Figure 16: Observed spectra are shown by dots. Some ¹²C¹⁶O and ¹²C¹⁷O features are indicated by open and filled triangles, respectively. Synthetic spectra with assumed ¹⁶O/¹⁷O ratios are shown by heavy solid lines while those with null ¹⁷O value by light solid lines. a) Observed spectrum of 10 Dra compared with the synthetic one with ¹⁶O/¹⁷O = 151. b) Observed spectrum of RZ Ari compared with the synthetic one with ¹⁶O/¹⁷O = 607. c) Observed spectrum of $\lambda$ Aqr compared with the synthetic one with ¹⁶O/¹⁷O = 1000. d) Observed spectrum of RR UMi compared with the synthetic one with ¹⁶O/¹⁷O = 2000.

Table 6: Carbon and oxygen abundances and micro-turbulent velocities (with probable errors(PEs) in 23 red giant stars.
Star N_H^a $N_{H}^{\rm wk}$ N_K^b $N_{K}^{\rm wk}$ log $A_{\rm C}$ $\xi_{\rm micro}$ N_H^c $N_{H}^{\rm wk}$ N_L^d $N_{L}^{\rm wk}$ log $A_{\rm O}$ $\xi_{\rm micro}$ log $A_{\rm N}^{f}$

km s^-1 km s^-1

$\alpha$ Tau 13 13 25 9 8.38 $\pm$ 0.04 2.20 $\pm$ 0.09 ... ... 28 25 8.79 $\pm$ 0.04 3.85 $\pm$ 0.13 8.05

23 21 ... ... 8.76 $\pm$ 0.09 3.81 $\pm$ 0.94

$\delta$ Oph 5 5 21 6 8.27 $\pm$ 0.08 2.46 $\pm$ 0.16 42 27 ... ... 8.83 $\pm$ 0.14 2.84 $\pm$ 0.54 8.58

$\nu$ Vir 6 6 22 10 8.13 $\pm$ 0.08 2.14 $\pm$ 0.15 55 20 ... ... 8.84 $\pm$ 0.05 2.67 $\pm$ 0.24 8.11

$\alpha$ Cet 6 6 11 3 8.64 $\pm$ 0.05 1.95 $\pm$ 0.08 38 18 ... ... 8.98 $\pm$ 0.14 4.25 $\pm$ 1.03 7.73

$\sigma$ Lib 12 12 14 2 8.23 $\pm$ 0.03 2.09 $\pm$ 0.13 51 19 ... ... 8.82 $\pm$ 0.10 2.03 $\pm$ 0.20 8.15

$\lambda$ Aqr 5 5 13 4 8.56 $\pm$ 0.11 1.97 $\pm$ 0.15 30 7 ... ... 8.92 $\pm$ 0.15 6.24 $\pm$ 6.01 7.88

$\beta$ Peg 12 12 29 7 8.27 $\pm$ 0.05 2.04 $\pm$ 0.07 53 16 ... ... 8.77 $\pm$ 0.12 3.12 $\pm$ 0.72 8.11

$\tau ^4$ Eri 6 5 20 1 8.41 $\pm$ 0.04 3.57 $\pm$ 0.46 25 9 ... ... 8.87 $\pm$ 0.19 3.38 $\pm$ 1.32 7.94

$\mu$ Gem 19 19 34 9 8.32 $\pm$ 0.06 2.00 $\pm$ 0.11 36 16 ... ... 8.81 $\pm$ 0.13 2.58 $\pm$ 0.33 ...

$\delta$ Vir 16 16 19 4 8.50 $\pm$ 0.06 2.20 $\pm$ 0.11 36 11 ... ... 8.84 $\pm$ 0.15 2.47 $\pm$ 0.45 7.90

10 Dra 5 5 15 3 8.43 $\pm$ 0.14 2.69 $\pm$ 0.26 30 15 ... ... 8.92 $\pm$ 0.18 2.44 $\pm$ 0.41 8.11

$\rho$ Per 13 13 22 2 8.27 $\pm$ 0.07 3.59 $\pm$ 0.64 43 7 ... ... 8.87 $\pm$ 0.07 3.11 $\pm$ 0.98 8.15

BS6861 5 4 12 2 8.38 $\pm$ 0.13 4.91 $\pm$ 1.29 ... ... ... ... ... ... ...

$\delta ^{2}$ Lyr 5 5 13 1 8.22 $\pm$ 0.18 2.86 $\pm$ 0.40 19 3^e ... ... ... ... 8.41

RR UMi 15 15 15 4 8.26 $\pm$ 0.12 2.48 $\pm$ 0.23 34 5 ... ... 8.76 $\pm$ 1.05 2.66 $\pm$ 2.60 8.07

$\alpha$ Her 11 10 17 3 8.40 $\pm$ 0.13 2.82 $\pm$ 0.23 22 0 42 16 8.85 $\pm$ 0.05 2.92 $\pm$ 0.09 8.14

OP Her ... ... 21 4 8.27 $\pm$ 0.60 2.53 $\pm$ 0.72 ... ... ... ... ... ... ...

XY Lyr ... ... 14 4 8.15 $\pm$ 0.15 2.96 $\pm$ 0.24 ... ... ... ... ... ... ...

R Lyr 14 14 17 2 8.26 $\pm$ 0.08 2.95 $\pm$ 0.24 ... ... 52 31 8.61 $\pm$ 0.04 2.99 $\pm$ 0.10 8.06

25 4 ... ... 8.62 $\pm$ 0.05 6.53 $\pm$ 3.20

RZ Ari 12 12 26 7 8.10 $\pm$ 0.09 2.54 $\pm$ 0.15 ... ... 28 15 8.57 $\pm$ 0.14 3.35 $\pm$ 0.28 8.44

52 21 ... ... 8.67 $\pm$ 0.07 3.49 $\pm$ 0.50

30g Her 6 5 24 3 8.35 $\pm$ 0.11 2.61 $\pm$ 0.26 23 0 38 26 8.75 $\pm$ 0.09 2.49 $\pm$ 0.16 7.92

SW Vir 11 6 15 1 8.26 $\pm$ 0.20 4.21 $\pm$ 2.38 ... ... 29 16 8.54 $\pm$ 0.11 1.83 $\pm$ 0.71 8.46

RX Boo 6 2 13 1 8.32 $\pm$ 1.62 3.41 $\pm$ 2.38 ... ... 13 12 8.55 $\pm$ 0.10 2.04 $\pm$ 0.18 8.26

^a The number of CO lines measured in the H band region, of which the number of weak lines (log ${W/\nu} \la -4.75$ ) is given in the next column; ^b the same as ^a but in the K band region; ^c the same as ^a but for OH lines in the H band region; ^d the same as ^a but for OH lines in the L band region; ^e with only 3 weak lines of similar intensities, the micro-turbulent velocity cannot be fixed by our line-by-line analysis; ^f N abundances based on CN (Aoki & Tsuji 1997) corrected for the effect of the revised C abundances.

**Table 6:** Carbon and oxygen abundances and micro-turbulent velocities (with probable errors(PEs) in 23 red giant stars.
Star	N_H^a	$N_{H}^{\rm wk}$	N_K^b	$N_{K}^{\rm wk}$	log $A_{\rm C}$	$\xi_{\rm micro}$	N_H^c	$N_{H}^{\rm wk}$	N_L^d	$N_{L}^{\rm wk}$	log $A_{\rm O}$	$\xi_{\rm micro}$	log $A_{\rm N}^{f}$
						km s^-1						km s^-1
$\alpha$ Tau	13	13	25	9	8.38 $\pm$ 0.04	2.20 $\pm$ 0.09	...	...	28	25	8.79 $\pm$ 0.04	3.85 $\pm$ 0.13	8.05
							23	21	...	...	8.76 $\pm$ 0.09	3.81 $\pm$ 0.94
$\delta$ Oph	5	5	21	6	8.27 $\pm$ 0.08	2.46 $\pm$ 0.16	42	27	...	...	8.83 $\pm$ 0.14	2.84 $\pm$ 0.54	8.58
$\nu$ Vir	6	6	22	10	8.13 $\pm$ 0.08	2.14 $\pm$ 0.15	55	20	...	...	8.84 $\pm$ 0.05	2.67 $\pm$ 0.24	8.11
$\alpha$ Cet	6	6	11	3	8.64 $\pm$ 0.05	1.95 $\pm$ 0.08	38	18	...	...	8.98 $\pm$ 0.14	4.25 $\pm$ 1.03	7.73
$\sigma$ Lib	12	12	14	2	8.23 $\pm$ 0.03	2.09 $\pm$ 0.13	51	19	...	...	8.82 $\pm$ 0.10	2.03 $\pm$ 0.20	8.15
$\lambda$ Aqr	5	5	13	4	8.56 $\pm$ 0.11	1.97 $\pm$ 0.15	30	7	...	...	8.92 $\pm$ 0.15	6.24 $\pm$ 6.01	7.88
$\beta$ Peg	12	12	29	7	8.27 $\pm$ 0.05	2.04 $\pm$ 0.07	53	16	...	...	8.77 $\pm$ 0.12	3.12 $\pm$ 0.72	8.11
$\tau ^4$ Eri	6	5	20	1	8.41 $\pm$ 0.04	3.57 $\pm$ 0.46	25	9	...	...	8.87 $\pm$ 0.19	3.38 $\pm$ 1.32	7.94
$\mu$ Gem	19	19	34	9	8.32 $\pm$ 0.06	2.00 $\pm$ 0.11	36	16	...	...	8.81 $\pm$ 0.13	2.58 $\pm$ 0.33	...
$\delta$ Vir	16	16	19	4	8.50 $\pm$ 0.06	2.20 $\pm$ 0.11	36	11	...	...	8.84 $\pm$ 0.15	2.47 $\pm$ 0.45	7.90
10 Dra	5	5	15	3	8.43 $\pm$ 0.14	2.69 $\pm$ 0.26	30	15	...	...	8.92 $\pm$ 0.18	2.44 $\pm$ 0.41	8.11
$\rho$ Per	13	13	22	2	8.27 $\pm$ 0.07	3.59 $\pm$ 0.64	43	7	...	...	8.87 $\pm$ 0.07	3.11 $\pm$ 0.98	8.15
BS6861	5	4	12	2	8.38 $\pm$ 0.13	4.91 $\pm$ 1.29	...	...	...	...	...	...	...
$\delta ^{2}$ Lyr	5	5	13	1	8.22 $\pm$ 0.18	2.86 $\pm$ 0.40	19	3^e	...	...	...	...	8.41
RR UMi	15	15	15	4	8.26 $\pm$ 0.12	2.48 $\pm$ 0.23	34	5	...	...	8.76 $\pm$ 1.05	2.66 $\pm$ 2.60	8.07
$\alpha$ Her	11	10	17	3	8.40 $\pm$ 0.13	2.82 $\pm$ 0.23	22	0	42	16	8.85 $\pm$ 0.05	2.92 $\pm$ 0.09	8.14
OP Her	...	...	21	4	8.27 $\pm$ 0.60	2.53 $\pm$ 0.72	...	...	...	...	...	...	...
XY Lyr	...	...	14	4	8.15 $\pm$ 0.15	2.96 $\pm$ 0.24	...	...	...	...	...	...	...
R Lyr	14	14	17	2	8.26 $\pm$ 0.08	2.95 $\pm$ 0.24	...	...	52	31	8.61 $\pm$ 0.04	2.99 $\pm$ 0.10	8.06
							25	4	...	...	8.62 $\pm$ 0.05	6.53 $\pm$ 3.20
RZ Ari	12	12	26	7	8.10 $\pm$ 0.09	2.54 $\pm$ 0.15	...	...	28	15	8.57 $\pm$ 0.14	3.35 $\pm$ 0.28	8.44
							52	21	...	...	8.67 $\pm$ 0.07	3.49 $\pm$ 0.50
30g Her	6	5	24	3	8.35 $\pm$ 0.11	2.61 $\pm$ 0.26	23	0	38	26	8.75 $\pm$ 0.09	2.49 $\pm$ 0.16	7.92
SW Vir	11	6	15	1	8.26 $\pm$ 0.20	4.21 $\pm$ 2.38	...	...	29	16	8.54 $\pm$ 0.11	1.83 $\pm$ 0.71	8.46
RX Boo	6	2	13	1	8.32 $\pm$ 1.62	3.41 $\pm$ 2.38	...	...	13	12	8.55 $\pm$ 0.10	2.04 $\pm$ 0.18	8.26

6 Carbon and oxygen isotopic ratios

6.1 Line-by-line analysis

We applied the line-by-line analysis to the isolated lines of ¹²C¹⁶O, ¹³C¹⁶O, and ¹²C¹⁷O. We used only the weak lines but included ¹²C¹⁶O lines of both the first and second overtone bands. The $\xi_{\rm micro}$ values determined from the ¹²C¹⁶O lines of the first and second overtone bands in Sect. 4.2 were used to determine abundances of ¹³C¹⁶O and ¹²C¹⁷O. Given a $\xi_{\rm micro}$ value, abundance can be determined directly for each line. Some examples of the results are shown in Figs. 15a-d for 10 Dra, RZ Ari, $\delta$ Oph, and $\mu$ Gem. Unfortunately, the number of lines of the isotopic species measured is rather small and the weak lines could not be measured at all for some cases especially for ¹²C¹⁷O.

For example, the lines measured for 10 Dra are ¹²C¹⁷O (2, 0) R 25, R 27, and R 32 in the spectrum shown in Fig. 16a. This is a favorable case for which three ¹²C¹⁷O lines could be measured, and these lines are used for the analysis of Fig. 15a. In the case of RZ Ari shown in Fig. 16b, the ¹²C¹⁷O lines are weaker and we could measure only two lines (R 25 and R 32) for the line-by-line analysis of Fig 15b. The ¹²C¹⁷O lines are still weaker in $\lambda$ Aqr and RR UMi shown in Figs. 16c and d, respectively, and no line could be measured in these cases. The difficulty of measuring weak lines for ¹³C¹⁶O is more or less the same, although at least one line could be measured in most objects except for RX Boo.

The ¹²C/¹³C and ¹⁶O/¹⁷O ratios based on the resulting ¹²C¹⁶O, ¹³C¹⁶O, and ¹²C¹⁷O abundances are given in the 4 and 5th columns, respectively, of Table 7 with their probable errors (PEs). The resulting ¹²C/¹³C ratios are mostly larger compared with our previous result (Tsuji 2007), and this is because ¹²C¹⁶O abundances are increased due to the use of lines of both the first and second overtones.

6.2 Synthetic spectra

We applied the spectral synthesis method as a check of our results given in Sect. 6.1. With the carbon abundance and micro-turbulent velocity from Table 6 and with the isotopic ratios from Table 7, we generated synthetic spectra between 4279 and 4294 cm^-1, where ¹²C¹⁷O (2-0) R 25 - 33 lines are found. Before we compare the synthetic spectra with observed ones, we corrected for the effects of the instrument broadening with the Norton-Beer's apodization function 2 (Norton & Beer 1976), which was used in the apodization of the observed spectra (see Paper I), and also of the macro-turbulent broadening based on the measured intrinsic line widths (see Table 4 of Paper III). As an example, we compared the observed spectrum of 10 Dra (dots) with the synthetic one (heavy solid line) in Fig. 16a. In this region, the weak line of ¹²C¹⁶O (2-0) R 92 can clearly be seen at 4292 cm^-1, which serves as a check of the carbon abundance. The lines of ¹²C¹⁷O (2-0) R 25, 27, and 32 used to determine ¹²C¹⁷O abundance in Sect. 6.1 can be reproduced well by the synthetic spectrum. Some other lines of ¹²C¹⁷O such as (2-0) R 26 and 29 should include extra components, since the synthetic spectrum computed without ¹²C¹⁷O at all (light solid line) shows some absorption features. Also some ¹²C¹⁷O lines are blended significantly with other lines, but all lines of ¹²C¹⁷O are not in disagreement with the synthetic spectrum computed for ¹⁶O/¹⁷O ratio of 151 (Table 7). As another example, the case of RZ Ari is shown in Fig. 16b. Although the ¹²C¹⁷O lines are weaker than in the case of 10 Dra, some unblended features such as (2-0) R 25 and 32 and all other lines of ¹²C¹⁷O are approximately similar to those in the synthetic spectrum computed for ¹⁶O/¹⁷O ratio of 607 (Table 7).

**Table 7:** Isotopic ratios (with PEs) in 23 red giant stars.
Obj.	$N_{\rm wk}$ (13)^a	$N_{\rm wk}$ (17)^b	¹²C/¹³C	¹⁶O/¹⁷O
$\alpha$ Tau	2	0	10.6 $\pm$ 1.0	>1000
$\delta$ Oph	3	2	11.1 $\pm$ 0.9	387 $\pm$ 68
$\nu$ Vir	5	0	8.7 $\pm$ 1.3	>2000
$\alpha$ Cet	2	2	11.1 $\pm$ 0.8	586 $\pm$ 47
$\sigma$ Lib	2	0	7.5 $\pm$ 0.3	>1500
$\lambda$ Aqr	2	0	7.9 $\pm$ 1.4	>1000
$\beta$ Peg	3	0	7.7 $\pm$ 0.5	>2500
$\tau ^4$ Eri	1	1	12.4 $\pm$ 0.3	687 $\pm$ 14
$\mu$ Gem	6	1	10.5 $\pm$ 1.2	798 $\pm$ 73
$\delta$ Vir	4	0	12.3 $\pm$ 1.2	>2500
10 Dra	3	3	14.8 $\pm$ 1.6	151 $\pm$ 11
$\rho$ Per	2	0	9.7 $\pm$ 1.0	>1000
BS6861	1	0	48.5 $\pm$ 2.9	>1000
$\delta ^{2}$ Lyr	2	2	16.2 $\pm$ 1.5	465 $\pm$ 41
RR UMi	1	0	10.0 $\pm$ 0.8	>2000
$\alpha$ Her	2	4	11.1 $\pm$ 0.7	102 $\pm$ 8
OP Her	2	1	11.3 $\pm$ 1.2	329 $\pm$ 31
XY Lyr	1	3	15.0 $\pm$ 0.4	223 $\pm$ 16
R Lyr	1	3	6.4 $\pm$ 0.3	368 $\pm$ 44
RZ Ari	3	2	7.9 $\pm$ 0.8	607 $\pm$ 48
30g Her	2	3	12.5 $\pm$ 1.1	211 $\pm$ 42
SW Vir	2	2	22.0 $\pm$ 4.7	432 $\pm$ 37
RX Boo	0	3	...	233 $\pm$ 20

^a Number of weak lines of ¹³C¹⁶O; ^b number of weak lines of ¹²C¹⁷O.

The major purpose of computing the synthetic spectra, however, is to estimate the ¹⁶O/¹⁷O ratio for the cases in which the ¹²C¹⁷O lines are too weak for EWs to be measured accurately. For example, all ¹²C¹⁷O features are too weak for their EWs to be measured in the case of $\lambda$ Aqr shown in Fig. 16c and these features, including relatively undisturbed ones such as (2-0) R 32 and 33, do not contradict with the synthetic spectrum computed for ¹⁶O/¹⁷O ratio of 1000. As another example, the observed spectrum of RR UMi shown in Fig. 16d should be in approximate agreement with the synthetic spectrum computed for ¹⁶O/¹⁷O ratio of 2000. This conclusion depends largely on subtle depressions in (2-0) R 25 and 32. On the other hand, definite absorption seen at the position of R 26 and 29 also appear in the synthetic spectrum computed without ¹²C¹⁷O at all (light solid line) and are not due to ¹²C¹⁷O. However, it is possible that the features assumed to be due to ¹²C¹⁷O may still include unknown impurities, and the ¹⁶O/¹⁷O ratio estimated on such subtle features should at best be regarded as a lower estimate to the ¹⁶O/¹⁷O ratio. The ¹⁶O/¹⁷O ratios estimated this way are given in the 5th column of Table 7 without error bars.

6.3 Uncertainties and comparisons with other authors

The most significant uncertainties in the analysis of such faint lines as ¹²C¹⁷O in cool stars are the location of the continuum level and the effect of the blending by many weak lines. As a guide to examining these problems, we computed synthetic spectra similar to those shown in Fig. 16 for the regions with rich lines of ¹²C¹⁷O (4264-4295 cm^-1) and ¹³C¹⁶O (4235-4266 cm^-1) for all spectra analyzed. This aided the rejection of blended lines in our line list. Furthermore, we examined the correlations between line intensities, line-widths, line-depths, and radial velocities, and rejected those lines that had large deviations. The continuum level was estimated by connecting the highest peaks with a smooth curve and the consistency of the resulting continuum can also be checked by comparison with the synthetic spectra. However, we need to analyze spectra of yet higher resolution to check the accuracy of the continuum used. By comparing results of different authors (see below), the errors in the final isotopic ratios due to these uncertainties are estimated to be as large as 100% (or a factor of two).

The carbon isotopic ratios were studied relatively well; we compare our ¹²C/¹³C ratios with those by Smith & Lambert (1990) and other authors in Table 8. In addition to those cited in Table 8, Wallerstein & Morell (1994) reported the ¹²C/¹³C ratios for 8 early M giants to be in the range 7-12, although no object common to our sample is included. Our results for ¹²C/¹³C ratios appear to agree well with the results of other authors in general.

The determination of the oxygen isotopic ratios is more difficult but a detailed identification of ¹²C¹⁷O features was completed for high resolution FTS spectra by Maillard (1974), who estimated ¹⁶O/¹⁷O ratio in $\alpha$ Her for the first time. We compare our ¹⁶O/¹⁷O ratios with those by Harris & Lambert (1984) and by other authors in Table 8. Wallerstein & Morell (1994) reported lower limits to ¹⁶O/¹⁷O ratio in 8 early M giant stars to be 85-295. Inspection of Table 8 reveals that ¹⁶O/¹⁷O ratios by different authors differ by factors of 2-4. This may largely be due to difficulty to locating the continuum levels and measuring weak features; more accurate results could be achieved by using spectroscopic data of higher quality.

7 Discussion

7.1 Abundance analysis and photospheric structure

The abundance analysis of very cool stars is associated with many difficulties. In particular, absorption lines tend to be strong due to the low continuous opacity at low temperatures in the photospheres of cool giant stars. The consequences are severe blending and uncertainties in the continuum level, which are obvious difficulties by themselves and, in addition, increase the difficulty in measuring other weak lines that are essential in abundance determination. If a sufficient number of weak lines, which are linearly proportional to the effective column densities of a species under consideration, can be measured, abundance determination become straightforward. This ideal case is seldom realized especially for cool stars. However, it was understood to be possible to carry out an abundance analysis by using the micro-turbulent model (or curve-of-growth method) even if saturated lines had to be used. With reasonable success, this model was in fact applied to abundance analyses in general.

The real difficulty in the abundance analysis of cool stars is that the classical method based on the micro-turbulent model can no longer be applied for lines of equivalent width higher than a certain critical value, which we found to be log ${W/\nu} \approx -4.75$ for the case of M giant stars (Sects. 4 and 5). Since stronger lines are formed in the upper photospheric layers where modeling may be increasingly uncertain, this difficulty can be related to the problem of the model photospheres. Smith & Lambert (1990) noted that the CO lines stronger than about log $W/\nu \approx -4.8 \sim -4.7$ should not be used for abundance analysis, since these lines are formed in the layers above the continuous optical depth of $\tau_{\rm c} \approx 10^{-3}$ , where the photospheric structure cannot be described accurately by the usual model photospheres. We arrive at a similar conclusion that the lines stronger than log ${W/\nu} \approx -4.75$ cannot be used for abundance analysis, although by a different argument based on purely empirical evidence shown most clearly for the OH lines of the fundamental bands (Fig. 10).

An unanswered question remains why do the intermediate-strength lines show abundance corrections as large as 1.0 dex or more when the weak lines show null corrections? It is unlikely that the uncertain in the thermal structure of the upper layers could produce such a large effect on the intermediate-strength lines, since differences in the model photospheres have only modest effects on abundances as we have seen before (Sects. 4.3 and 5.3). Also, no model of the upper photosphere is known to explain the difficulty of the intermediate-strength lines or the stronger lines. However, the dynamical structure represented by stellar turbulence may have a more dramatic effect on the intermediate-strength lines heavily saturated. Taking advantage of the fact that the line positions and profiles accurately can be measured with FTS, we showed that the line asymmetries and differential line shifts of CO lines are quite large and that a simple model of the depth-independent and isotropic Gaussian micro-turbulence cannot be justified (Paper III).

Even if we know that a simple model of micro-turbulence is not sufficiently realistic, it is unknown how the behavior of the intermediate-strength lines (Figs. 4-11 and 13, 14) can be reproduced by a more accurate description of stellar turbulence. It is interesting if a more consistent treatment of the dynamical structure of stellar photosphere by a 3D model can resolve the present difficulty. A detailed numerical simulation of surface convection in red giant stars is reported by Collet et al. (2007). Although their simulations were not extended to the regime of M giants, their result for the coolest model of $T_{\rm eff} = 4697$ K and [Fe/H] = 0.0 indicated that the difference between 3D and 1D oxygen abundances derived from OH lines (not ro-vibrational lines but of A-X system at 3150 Å) is about 0.1 dex. This appears to be due to the difference in thermal structures of the 3D and 1D models, but possible effects of the dynamical structure of the 3D models on the saturated lines are still unknown. Their results indicated that the effect of the 3D structure should be more important in stars of lower mentallicities, but it is unclear if such a large difference in abundances derived from the weaker and stronger lines in our population I sample can be relaxed by considering the dynamical effect of convection in the 3D models. Thus, we conclude that the difficulty we encountered may not be resolved by considering variation in models of the photospheric structure.

7.2 Abundance analysis and outer molecular envelope

We know that the strong lines of CO in late M giant stars are affected significantly by the contributions of the extra molecular layers (Paper II). Since the intermediate-strength lines and the strong lines behave similarly on $\Delta$ log A-log $W/\nu$ diagram (e.g. Figs. 4, 5), a natural question to ask is; can the intermediate-strength lines be understood in a similar way to the strong lines? For the late M giants, the intermediate-strength lines do not necessarily originate in the levels of low LEP (see Fig. 12a), but increasingly reduced contributions from higher excitation lines can be possible for modest kinetic temperatures in the warm molecular layers, and the trend of intermediate-strength lines together with the strong lines in these giants (Figs. 4, 5) can be explained consistently. Given that the presence of the MOLsphere was demonstrated in the late M giants (Paper II), it should at the same time produce excess absorption in the intermediate-strength lines as it does for the strong lines. It is then natural to assume the same origin for the intermediate-strength lines and the strong lines in the late M giants.

Interestingly, the intermediate-strength lines of CO in the early M giants (including a K giant) provide, in general, larger abundance corrections compared with those from the weak lines (e.g. $\beta$ Peg, $\alpha$ Tau, $\nu$ Vir, $\alpha$ Cet in Figs. 6, 7). We have not previously considered the effects of outer molecular layers in these early M giant stars. But why not? The behavior of the intermediate-strength lines on the $\Delta$ log A-log $W/\nu$ diagram, in particular, are so similar for the late M (Figs. 4, 5) and early M (Figs. 6, 7) giants that it is natural to assume the same origin for the intermediate-strength lines in the early and late M giants. Furthermore, we identified H₂O bands on the ISO spectra of the K-early M giants included in our present sample (e.g. $\alpha$ Tau, $\beta$ Peg, and $\alpha$ Cet) and one possibility is that these H₂O bands are originating in the outer molecular layers as for the late M giants (Tsuji 2001). However, this is not a unique interpretation. For example, Ryde et al. (2002) detected H₂O lines in the high resolution spectrum of the K giant $\alpha$ Boo and suggested that its origin can be due to the anomalous structure of the photosphere. We note, however, that the anomalous behavior of the intermediate-strength lines and the presence of H₂O bands in the K-early M giant stars can consistently be understood by assuming the presence of the outer molecular layers.

In the case of CO lines in late M giants such as $\rho$ Per, R Lyr, and SW Vir, and also in the M3 giant $\tau ^4$ Eri, the intermediate-strength lines and the strong lines show quite different behaviors as shown in Figs. 8, 9; the strong lines show positive abundance corrections, while the intermediate-strength lines show mostly negative corrections for the carbon abundances derived from the weak lines. We first thought that this difference should be a reason for considering alternative explanations for the intermediate-strength lines and the strong lines. However, we reach the opposite conclusion that this provides evidence that the intermediate-strength and strong lines have identical origins. In fact, a possible contribution from the outer molecular layers can be either absorption or emission depending on the extension, temperature, and optical thickness of the outer molecular layers for a particular line. For the intermediate-strength lines, we can therefore explain the negative abundance corrections as reductions in their EWs due to infilling by emission from the outer molecular layers. At present, however, the negative abundance corrections for the intermediate-strength lines cannot be explained if they are assumed to originate in the photosphere.

**Table 8:** Comparisons with the results by other authors.
Obj.	log $A_{\rm C}^{a}$	log $A_{\rm C}$	log $A_{\rm O}^{a}$	log $A_{\rm O}$	¹²C/¹³C^a	¹²C/¹³C	¹⁶O/¹⁷O^a	¹⁶O/¹⁷O
$\alpha$ Tau	8.38 $\pm$ 0.04	8.40 $\pm$ 0.07^b	8.78 $\pm$ 0.07	8.78 $\pm$ 0.08^b	11 $\pm$ 1	10 $\pm$ 2^b	>1000	560 $\pm$ 180^f
		8.35 $\pm$ 0.20^c		8.93 $\pm$ 0.20^c		10 $\pm$ 2^c
$\nu$ Vir	8.13 $\pm$ 0.08	8.51 $\pm$ 0.08^b	8.84 $\pm$ 0.05	8.91 $\pm$ 0.06^b	9 $\pm$ 1	12 $\pm$ 2^b
$\alpha$ Cet	8.64 $\pm$ 0.05	8.20 $\pm$ 0.30^c	8.98 $\pm$ 0.14	8.93 $\pm$ 0.30^c	11 $\pm$ 1	10 $\pm$ 2^c
$\beta$ Peg	8.27 $\pm$ 0.05	8.42 $\pm$ 0.07^b	8.77 $\pm$ 0.12	8.81 $\pm$ 0.06^b	8 $\pm$ 1	8 $\pm$ 2^b	>2500	1050 $\pm$ 375^f
		8.20 $\pm$ 0.40^c		8.93 $\pm$ 0.40^c		5 $\pm$ 3^c
$\mu$ Gem	8.32 $\pm$ 0.06	8.43 $\pm$ 0.04^b	8.81 $\pm$ 0.13	8.82 $\pm$ 0.12^b	11 $\pm$ 1	13 $\pm$ 2^b	798 $\pm$ 73	325 $\pm$ 112^f
$\delta$ Vir	8.50 $\pm$ 0.06	8.61 $\pm$ 0.10^b	8.84 $\pm$ 0.15	8.82 $\pm$ 0.06^b	12 $\pm$ 1	16 $\pm$ 4^b
10 Dra	8.43 $\pm$ 0.14	8.59 $\pm$ 0.08^b	8.92 $\pm$ 0.18	9.04 $\pm$ 0.09^b	15 $\pm$ 2	12 $\pm$ 3^b
$\rho$ Per	8.27 $\pm$ 0.07	8.46 $\pm$ 0.04^b	8.87 $\pm$ 0.07	8.92 $\pm$ 0.15^b	10 $\pm$ 1	15 $\pm$ 2^b
$\alpha$ Her					11 $\pm$ 1	17 $\pm$ 4^d	102 $\pm$ 8	190 $\pm$ 40^f
						5 $\pm$ 1^e		450 $\pm$ 50^e
30g Her	8.35 $\pm$ 0.11	8.25 $\pm$ 0.07^b	8.75 $\pm$ 0.09	8.73 $\pm$ 0.08^b	13 $\pm$ 1	10 $\pm$ 2^b	211 $\pm$ 42	675 $\pm$ 175^g

^a Present results; ^b Smith & Lambert (1990); ^c Decin et al. (2003); ^d Hinkle et al. (1976);
^e Maillard (1974); ^f Harris & Lambert (1984); ^g Harris et al. (1985).

Finally, an additional problem is if the intermediate-strength lines of OH can be understood in the same way as for the CO lines. Unlike CO, OH may not be so abundant in the outer molecular layers, since oxygen may be mostly in H₂O within cooler environments expected for the MOLsphere. For this reason, we first believed that the anomalous strengths of the intermediate-strength lines of OH may not be due to contamination from the outer molecular envelope, but may instead originate in the photosphere itself. However, the infrared OH lines show behavior quite similar to the CO lines (e.g. Figs. 4 and 10), and it is again natural to assume the same interpretation for the OH and CO lines. Given that OH has been detected even in the cooler circumstellar envelopes of red giant stars by OH masers, it may be possible that OH can be abundant in the warmer MOLsphere. Furthermore, the assumption of chemical equilibrium should probably not be applied to the outer layers and we should instead use the OH lines as probes of non-equilibrium processes in the outer layers. Then, we conclude that the intermediate-strength lines of OH observed in the late M giants such as $\alpha$ Her, R Lyr, and SW vir (Figs. 10, 11) as well as in the earlier M giant such as $\sigma$ Lib (Fig. 14b) also include contributions from the outer molecular layers.

$\begin{figure} \par\includegraphics[width=16.0cm,clip]{9869fg17.eps} \end{figure}$

Figure 17: Observed abundances of a) carbon (Table 6), b) nitrogen (Aoki & Tsuji 1997; Table 6), c) oxygen (Table 6; if the results derived from the H and L band spectra are available, mean values are used), and d) C + N + O, compared with the predictions of evolutionary models (Claret 2004). The results of FDU and SDU for the case of Z = 0.02 are shown by solid and dash-dotted lines, respectively, in each panel. The observed C + N + O abundances are smaller by about 0.16 dex compared with the predictions based on Z = 0.02 as can be seen in panel d). This initial metallicity correction of -0.16 dex is applied to the predicted C, N, and O abundances in panels a), b), and c), respectively, and the corrected results are shown by dashed lines. In each panel, the solar abundances are shown by open square (Anders & Grevesse 1989; Ayres et al. 2006) and by open diamond (Allende Prieto et al. 2002).

The possible presence of the outer molecular layers in red giant stars is supported by direct measurements of the angular extensions. For example, angular diameters of normal K and M giant stars, including several objects common to our sample, were measured in the strong TiO bands at 712 nm and in the nearby pseudo-continuum at 754 nm (Quirrenbach et al. 1993). The observed 712 nm/754 nm diameter ratios appeared to be larger than predicted by model photospheres, suggesting that the photospheric models cannot describe adequately the outer layers of these red giant stars, and the result may lend support for the presence of the extra molecular envelopes (Quirrenbach 2001). Interferometric observations in the infrared bands provided direct support for the presence of extended warm molecular gas layers not only in Mira variables but also in late M giants (e.g. Mennesson et al. 2002; Perrin et al. 2004). On the other hand, the apparent angular diameter of $\alpha$ Her in the mid infrared was found to be larger by 30% than its near infrared size, but the high resolution 11 $\mu$ m spectrum does not show any substantial spectral lines in $\alpha$ Her (Weiner et al. 2003). This result was explained by a balance of absorption and emission in a spherically extended envelope, and the mid infrared spectra and visibilities could be consistent with the warm molecular envelope model (Ohnaka 2004).

We should remember that the possibility of a warm molecular envelope in the early M giant stars was noticed previously when we first identified H₂O bands in the spectrum of the M2 giant $\beta$ Peg observed with ISO SWS (Tsuji et al. 1997). Also, H₂O bands were found in several M giants earlier than M6 by Matsuura et al. (1999) with IRTS (Infrared Telescope in Space) launched in March 1995 by ISAS. These results were further extended to several K-M giant stars (Tsuji 2001) and also confirmed by other authors (e.g. Decin et al. 2003). The implications of this finding, however, were not fully recognized even by ourselves, and some time elapsed before this finding was finally related to the difficulty in the abundance analysis of red giant stars. Since the temperatures and radial velocities of the MOLsphere differ only slightly from those of the upper photosphere, it was difficult to recognize the presence of the MOLsphere using the spectroscopic method. However, we finally recognize the effect of the overlaying warm molecular layers on the high resolution infrared spectra of dozens of red giant stars.

Considering several lines of reasonings outlined above, we conclude that the presence of a warm and quasi-static molecular envelope above the photosphere is a common feature in K and M giant stars. It is unexpected and surprising if that both CO and OH lines of intermediate-strength with LEP as high as 2.0 eV (Fig. 12) include the absorption and/or emission originating in the outer molecular layers. We previously noted this possibility mainly for the late M giants (Paper II), but now we find that the presence of the extra molecular envelope is a general phenomenon not only in the late M giants but also in the early M and K giants as well. Also, the fact that the rather high excitation lines are included in these intermediate-strength lines implies that the extra molecular envelope is indeed ``warm'' and should be even warmer than we imagined before from the analysis of the strong lines (Paper II). Yet we know little about this new feature consisting of warm gaseous molecules such as CO, OH, and H₂O. We hope to extend our analysis done for the strong lines (Paper II) to the intermediate-strength lines and clarify the nature of the warm molecular envelope in more detail.

We conclude that the observed infrared spectra should actually be a hybrid of multiple components originating in the photosphere and overlaying warm molecular layers. The hybrid nature of the infrared spectra of red giant stars is now confirmed both in the low resolution ISO spectra and high resolution FTS spectra. We must then abandon the traditional idea that the stellar spectra are primary defined by the stellar photospheric structure, at least for the infrared spectra of K-M giant stars.

7.3 CNO abundances

Even if the photosphere of a cool giant star is veiled by the warm molecular envelope, the weak lines of high excitation may remain almost undisturbed. The weak lines are clearly distinguished from the intermediate-strength lines on the $\Delta$ log A-log $W/\nu$ diagram (Figs. 4-11, 13-14), and we confirmed that the weak lines behaved as expected from the classical micro-turbulent model (Sects. 4 and 5). Thus, we are convinced that abundance determination could be possible using the weak lines of log ${W/\nu} \la -4.75$ . With this caution, our results agreed well with those by Smith & Lambert (1990), who have already used only weak lines in their abundance analyses. We therefore continue to compare our results with the predictions of evolutionary models.

We plotted the resulting C and O abundances in Figs. 17a and c, respectively. We plotted N abundances based on our previous analysis of the same sample (Aoki & Tsuji 1997), corrected for the effect of the revised C abundances (14th column of Table 6), in Fig. 17b. For 5 late M giants for which the N abundances based on the ro-vibrational lines of NH are available, we plotted the mean log $A_{\rm N}$ values based on the lines of CN and NH. Given the C, N, and O abundances, we obtained the sum of the C, N, and O abundances as plotted in Fig. 17d. The results are compared with the predictions of the standard evolutionary models by Claret (2004); the results of the first dredge-up (FDU) are shown by solid lines and those of the second dredge-up (SDU) by dash-dotted lines in Figs. 17a-d.

We first examined the sum of the C, N, and O abundances in Fig. 17d. The model prediction confirmed that the CNO processing conserved the sum of the C, N, and O abundances corresponding to Z = 0.02, as assumed by the evolutionary models. The observed values are generally smaller than the values of the models, which are log $(A_{\rm C} + A_{\rm N} + A_{\rm O}) \approx 9.16$ . The mean of the observed values in low mass stars $(M < 2.5~ M_{\odot})$ is log $(A_{\rm C} + A_{\rm N} + A_{\rm O}) \approx 9.00$ as shown by the dashed line in Fig. 17d, and thus the mean metalliciy of the low mass stars that we have analyzed is smaller than the value assumed in the evolutionary models by Claret (2004). This metallicity difference should be kept in mind when comparing the observed and predicted C, N, and O abundances. A solar value of the C + N + O abundances based on the C and O abundances by Alende Prieto et al. (2002) is shown by the open diamond and a classical value (e.g. Anders Grevesse 1989), supported by Ayres et al. (2006), is indicated by the open squares in Fig. 17d; the N abundance is taken from Anders & Grevesse (1989).

The observed carbon abundances are generally smaller than those of the model predictions, but may be consistent with the predictions after the metallicity difference between the evolutionary models and actual stars is corrected as shown by the dashed line in Fig. 17a. The scatters about the dashed line may be due to those of the metallicity in our sample, except for a few objects. For example, two stars appear above the predicted FDU curve; the object showing the largest deviation is $\alpha$ Cet and the other one is $\lambda$ Aqr. It is interesting to notice that these two stars also show the largest under-abundances of N at $M \approx 3.6 ~M_{\odot}$ in Fig. 17b .

The nitrogen abundances may roughly be consistent with the FDU curve with and/or without metallicity correction in general. However, the deviations from the predictions appear to be larger in a few objects, and it is as if some extra mixing may be needed as in the case of the ¹²C/¹³C ratios discussed in Sect. 7.4. Most lines of both CN and NH used are weak lines that satisfy the condition of log ${W/\nu} \la -4.75$ , and N abundances may be free from the difficulty encountered in the analysis of the CO first overtone bands in Paper I (also Sect. 4.1).

Finally, the oxygen abundances in Fig. 17c show a similar pattern as the C + N + O abundances in Fig. 17d, and the scatters may represent those of the metallicity in our sample. There is a tendency for the oxygen abundances to be higher in higher mass objects. The resulting oxygen and carbon abundances correlate rather well and the mean $A_{\rm C}/A_{\rm O}$ ratio for 19 objects for which C and O abundances are determined is 0.37 (with the standard deviation of $\pm$ 0.10).

7.4 Carbon and oxygen isotopic ratios

The resulting ¹⁶O/¹⁷O ratios (Table 7) are plotted versus stellar mass in Fig. 18a by filled circles or by filled triangles if only lower limits could be estimated. For comparison, predicted results of FDU and SDU by Claret (2004) are shown by solid and dash-dotted lines, respectively. The large variation in ¹⁶O/¹⁷O of low mass stars is consistent with the predictions of the evolutionary models, confirming the previous analysis by Dearborn (1992) using the observed data known at that time. In the higher mass stars, some objects have very low ¹⁶O/¹⁷O ratios, but the general trend that the ¹⁶O/¹⁷O ratios are confined to lower values is consistent with the predicted ones. Considering the possible uncertainties in the stellar masses, the observed and predicted ¹⁶O/¹⁷O ratios can be regarded to be not in serious contradiction.

The observed ¹²C/¹³C ratios (Table 7) are shown by filled circles and compared with the predicted ones (Claret 2004) in Fig. 18b. The observed ¹²C/¹³C ratios are now around 10 in contrast to our previous ¹²C/¹³C ratios, which were mostly below 10 (Tsuji 2007), but yet too small compared with ¹²C/¹³C $\approx$ 20 predicted by the standard evolutionary models. This contradiction has been known for a long time and we simply confirm this long-standing puzzle. To resolve this dilemma, extra mixing of the CN-cycle processed material had to be assumed. For example, a deep circulation below the bottom of the convective zone, referred to as ``cool bottom processing'', was proposed (Boothroyd & Sackmann 1999). It was shown recently by Eggleton et al. (2008) that a deep mixing mechanism should operate in all low mass giants due to a molecular weight inversion resulting from ³He (³He, 2p) ⁴He reaction in the layers just above the H-burning shell. The predicted ¹²C/¹³C ratios by this ``Compulsory Deep Mixing (CDM)'' are shown by the dashed line in Fig. 18b. The more modern prediction appears close to the upper boundary of the observed results, and discrepancies between observations and predictions are relaxed if not perfectly.

7.5 The warm molecular envelope and mass loss from red giants

Given that the presence of the warm molecular envelope or MOLsphere is a general phenomenon in normal red giant stars, the next problem is to clarify the nature of the MOLsphere in detail, and to understand the structure of the entire atmosphere extending beyond the photosphere. An initial step towards this goal was achieved by a detailed MHD simulation of the red giant wind by Suzuki (2007), who showed that nearly static regions of $T \approx 10^3 {-} 10^4$ K are formed at several stellar radii above the photosphere. It is interesting that the mass loss from red giant stars with wind velocities far smaller than the surface escape velocity can be understood consistently with his simulation in which the stellar winds are accelerated from the quasi-static region at several stellar radii above the photosphere.

The quasi-static region predicted by Suzuki's simulation can be identified with the warm molecular envelope that we confirmed in several observational studies as discussed in Sect. 7.2; we hope that the simulation of Suzuki can be extended to include spectral modeling so that more detailed confrontation between theory and observations can be achieved. We include the measured data on the stronger lines in Tables 3a-3w, in addition to those on the weaker lines used in the abundance analysis, and we hope that these data can be interpreted correctly with more sophisticated models in the future. With this detailed confrontation between theory and observations, we expect to find a consistent solution to the long-standing problem of the origin of mass-loss from red giant stars for the first time.

8 Concluding remarks

We initiated our study hoping to clarify the nature of the difficulty encountered in our previous analysis of CO (Papers I and III ), since we felt that something is still not understood well in abundance analyses of cool giant stars. At first, we had to recognize that line spectra of cool giant stars are highly complicated and may consist of at least three different groups of lines of different origins; the weak lines of log ${W/\nu} \la -4.75$ , the intermediate-strength lines of $-4.75 < {\rm log} W/\nu \la -4.4$ , and the strong lines of log ${W/\nu} > -4.4$ . Of these three groups, only the weak lines could be understood well on the basis of the classical micro-turbulent model of line formation. On the other hand, it was known that the strong lines could not be understood as being of photospheric origin alone but should include an extra component originating in the outer molecular layers (Paper II).

The most difficult case was the intermediate-strength lines. However, we finally concluded that the intermediate-strength lines are essentially the same as the strong lines. This means that not only the low excitation strong lines but also medium strong lines with LEP as high as 2 eV (Fig. 12) are disturbed by the contaminations originating in the outer molecular envelope, which we refer to as MOLsphere for simplicity. This in turn means that most of the dominant molecular lines observed in the infrared spectra of K-M giant stars should be badly disturbed by the contaminations from the extra component beyond the photosphere. At the same time, however, this finding provides further support for the presence of the warm molecular envelope on the basis of the high resolution spectra of dozens of red giant stars.

We found that the largest fault in our previous analysis (Paper I) was to have assumed that the critical value discriminating the weak and the intermediate-strength lines was log $W/\nu \approx -4.5$ rather than -4.75. For this reason, many lines which are disturbed by the contaminations from the outer molecular envelope were included in the abundance analysis of Paper I. It is certainly difficult to attempt abundance analyses with such lines, and the reason why abundance analysis of cool giant stars often encountered difficulties appeared to be simple, at least partly. This result also implies that it should be difficult in principle to apply low resolution infrared spectra to abundance analyses of cool luminous stars, and the hybrid nature of the infrared spectra reinforces the reason why high resolution spectroscopy is indispensable in abundance analyses.

On the other hand, it is fortunate that the weak lines are relatively free from disturbance by extra component of non-photospheric origin and we are convinced that the abundance analysis of cool giant stars is possible with these lines. With a limited number of the weak lines, we could determine the C, O, and their isotopic abundances with reasonable accuracy. The resulting CNO and their isotopic abundances are roughly consistent with the predictions of the first and second dredges-up during the red giant phase. We noticed, however, that there are some deviations from the evolutionary models especially for the ¹²C, ¹³C, and ¹⁴N abundances of some stars, and it seems that some additional episodic events may be needed to explain them. Since the CNO isotopes in the universe, especially ¹³C, ¹⁴N, and ¹⁷O, are largely supplied by red giant stars, further refinements of both abundance analyses and evolutionary models are required.

In conclusion, high resolution infrared spectra provide a wealth of information about not only photospheric abundances but also the structure of the entire atmosphere extending beyond the photosphere. For this reason, infrared spectra must be of hybrid nature with contributions from multiple components. It is essential to keep the hybrid nature in mind in the interpretation and analysis of the infrared spectra of cool luminous stars.

References

9 Online Material

Table 2: Observed spectra.
Obj. Filter Res. (mK) S/N Date of obs. EW data in

alf Tau H 46.19 60 Aug. 17, 1976 Table 3a

alf Tau K 46.19 76 Sep. 28, 1976 Table 3a

alf Tau L 49.90 159 Oct. 21, 1977 Table 3a

del Oph H, K 49.70 75 Jun. 24, 1977 table3b

nu Vir H 41.21 51 Apr. 08, 1982 Table 3c

nu Vir K 41.20 115 Apr. 09, 1982 Table 3c

alf Cet H, K 46.19 69 Sep. 28, 1976 Table 3d

sig Lib H, K 46.19 89 Aug. 18, 1976 Table 3e

lam Aqr H, K 46.19 61 Jul. 06, 1976 Table 3f

bet Peg H, K 48.76 103 May 12, 1976 Table 3g

tau4 Eri H, K 46.19 59 Sep. 29, 1976 Table 3h

mu Gem H 46.19 - Nov. 07, 1976 Table 3i

mu Gem K 16.53 80 Jan. 27, 1988 Table 3i

del Vir H 46.19 54 Jun. 18, 1976 Table 3j

del Vir H, K 49.70 86 Jun. 24, 1977 Table 3j

10 Dra H, K 49.82 61 Jun. 28, 1977 Table 3k

rho Per H 29.70 44 Apr. 07, 1982 Table 3l

rho Per K 22.28 66 Apr. 08, 1982 Table 3l

BS6861 H, K 46.19 42 Sep. 29, 1976 Table 3m

del2 Lyr H, K 46.19 78 Apr. 11, 1976 Table 3n

RR UMi H, K 46.19 61 Aug. 18, 1976 Table 3o

alf Her H, K 49.70 106 Jun. 24, 1977 Table 3p

alf Her L 16.53 45 Jul. 09, 1987 Table 3p

OP Her K 16.53 142 Jul. 01, 1988 Table 3q

XY Lyr K 16.53 86 Jul. 08, 1987 Table 3r

R Lyr H 29.70 70 Apr. 08, 1982 Table 3s

R Lyr K 16.53 65 Jul. 07, 1987 Table 3s

R Lyr L 16.53 107 Jul. 09, 1987 Table 3s

RZ Ari H, K 46.19 88 Aug. 17, 1976 Table 3t

RZ Ari L 16.53 65 Oct. 02, 1987 Table 3t

30g Her H, K 49.10 102 Jun. 30, 1977 Table 3u

30g Her L 16.53 - Jul. 09, 1987 Table 3u

SW Vir H, K 46.19 65 Jun. 18, 1976 Table 3v

SW Vir L 16.53 88 Jul. 09, 1987 Table 3v

RX Boo H, K 48.10 62 Jan. 14, 1976 Table 3w

RX Boo L 16.53 108 Jul. 09, 1987 Table 3w

**Table 2:** Observed spectra.
Obj.	Filter	Res. (mK)	S/N	Date of obs.	EW data in
alf Tau	H	46.19	60	Aug. 17, 1976	Table 3a
alf Tau	K	46.19	76	Sep. 28, 1976	Table 3a
alf Tau	L	49.90	159	Oct. 21, 1977	Table 3a
del Oph	H, K	49.70	75	Jun. 24, 1977	table3b
nu Vir	H	41.21	51	Apr. 08, 1982	Table 3c
nu Vir	K	41.20	115	Apr. 09, 1982	Table 3c
alf Cet	H, K	46.19	69	Sep. 28, 1976	Table 3d
sig Lib	H, K	46.19	89	Aug. 18, 1976	Table 3e
lam Aqr	H, K	46.19	61	Jul. 06, 1976	Table 3f
bet Peg	H, K	48.76	103	May 12, 1976	Table 3g
tau4 Eri	H, K	46.19	59	Sep. 29, 1976	Table 3h
mu Gem	H	46.19	-	Nov. 07, 1976	Table 3i
mu Gem	K	16.53	80	Jan. 27, 1988	Table 3i
del Vir	H	46.19	54	Jun. 18, 1976	Table 3j
del Vir	H, K	49.70	86	Jun. 24, 1977	Table 3j
10 Dra	H, K	49.82	61	Jun. 28, 1977	Table 3k
rho Per	H	29.70	44	Apr. 07, 1982	Table 3l
rho Per	K	22.28	66	Apr. 08, 1982	Table 3l
BS6861	H, K	46.19	42	Sep. 29, 1976	Table 3m
del2 Lyr	H, K	46.19	78	Apr. 11, 1976	Table 3n
RR UMi	H, K	46.19	61	Aug. 18, 1976	Table 3o
alf Her	H, K	49.70	106	Jun. 24, 1977	Table 3p
alf Her	L	16.53	45	Jul. 09, 1987	Table 3p
OP Her	K	16.53	142	Jul. 01, 1988	Table 3q
XY Lyr	K	16.53	86	Jul. 08, 1987	Table 3r
R Lyr	H	29.70	70	Apr. 08, 1982	Table 3s
R Lyr	K	16.53	65	Jul. 07, 1987	Table 3s
R Lyr	L	16.53	107	Jul. 09, 1987	Table 3s
RZ Ari	H, K	46.19	88	Aug. 17, 1976	Table 3t
RZ Ari	L	16.53	65	Oct. 02, 1987	Table 3t
30g Her	H, K	49.10	102	Jun. 30, 1977	Table 3u
30g Her	L	16.53	-	Jul. 09, 1987	Table 3u
SW Vir	H, K	46.19	65	Jun. 18, 1976	Table 3v
SW Vir	L	16.53	88	Jul. 09, 1987	Table 3v
RX Boo	H, K	48.10	62	Jan. 14, 1976	Table 3w
RX Boo	L	16.53	108	Jul. 09, 1987	Table 3w

Table 3: Measured data (Only a few lines at the beginning of Table 3a, as examples).
alf Tau

----

Isotope v $^\prime$ v $^{\prime\prime}$ Rot. tr. nu(cm-1) log gf L.E.P.(cm^-1) log EW/nu

C12O16 3 1 P 2 4199.480 -6.282 2154.701 -4.739

C12O16 2 0 P 9 4222.953 -6.128 172.978 -4.585

C12O16 4 2 R 68 4237.805 -4.241 12982.145 -4.721

C12O16 3 1 R 8 4238.289 -5.600 2280.402 -4.611

C12O16 4 2 R 36 4243.637 -4.604 6763.398 -4.608

C12O16 3 1 R 18 4266.090 -5.248 2794.075 -4.572

C12O16 3 1 R 22 4275.180 -5.154 3105.648 -4.553

C12O16 2 0 R 92 4292.047 -4.817 16004.551 -5.067

C12O16 3 1 R 32 4292.750 -4.969 4148.160 -4.563

C12O16 3 1 R 35 4296.566 -4.923 4533.898 -4.595

Contents

Cool luminous stars: the hybrid nature of their infrared spectra^,

1 Introduction

2 Input data

2.1 Observed spectra

2.2 Model photospheres

2.3 Basic stellar parameters

3 Method of analysis

4 Reanalysis of CO

4.1 Previous analysis of CO

4.2 The first and second overtone bands

4.3 Uncertainties

4.4 Comparisons with other author's results

5 The case of OH

5.1 The OH fundamental bands

5.2 The OH first overtone bands

5.3 Uncertainties and comparison with other authors

6 Carbon and oxygen isotopic ratios

6.1 Line-by-line analysis

6.2 Synthetic spectra

6.3 Uncertainties and comparisons with other authors

7 Discussion

7.1 Abundance analysis and photospheric structure

7.2 Abundance analysis and outer molecular envelope

7.3 CNO abundances

7.4 Carbon and oxygen isotopic ratios

7.5 The warm molecular envelope and mass loss from red giants

8 Concluding remarks

References

9 Online Material

alf Tau
----
Isotope	v $^\prime$ v $^{\prime\prime}$	Rot. tr.	nu(cm-1)	log gf	L.E.P.(cm^-1)	log EW/nu
C12O16	3 1	P 2	4199.480	-6.282	2154.701	-4.739
C12O16	2 0	P 9	4222.953	-6.128	172.978	-4.585
C12O16	4 2	R 68	4237.805	-4.241	12982.145	-4.721
C12O16	3 1	R 8	4238.289	-5.600	2280.402	-4.611
C12O16	4 2	R 36	4243.637	-4.604	6763.398	-4.608
C12O16	3 1	R 18	4266.090	-5.248	2794.075	-4.572
C12O16	3 1	R 22	4275.180	-5.154	3105.648	-4.553
C12O16	2 0	R 92	4292.047	-4.817	16004.551	-5.067
C12O16	3 1	R 32	4292.750	-4.969	4148.160	-4.563
C12O16	3 1	R 35	4296.566	-4.923	4533.898	-4.595

Cool luminous stars: the hybrid nature of their infrared spectra,

9 Online Material

Cool luminous stars: the hybrid nature of their infrared spectra^,