- ... CIAO
![[*]](/icons/foot_motif.gif)
- Chandra Interactive Analysis of Observations.
http://cxc.harvard.edu/ciao/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... data
![[*]](/icons/foot_motif.gif)
- And from XMM2, we only make use of the EPIC pn data, since it has
a better calibration below 0.8 keV than the EPIC MOS
(see http://xmm.vilspa.esa.es/docs/documents/CAL-TN-0018-2-4.pdf). No significant
differences are seen between MOS and pn data, and the conclusions of the analysis
can be easily applied to the MOS data as well.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dB.
![[*]](/icons/foot_motif.gif)
- Decibans (tenths of a power of 10), is a common unit to
represent weights of evidence.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... XSTAR
![[*]](/icons/foot_motif.gif)
- Version 2.1kn6.
See http://heasarc.gsfc.nasa.gov/docs/software/xstar/xstar.html.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... abundance
![[*]](/icons/foot_motif.gif)
- Atomic abundances are entered relative to solar abundances asdefined in
Grevesse et al. (1996), with 1.0 being defined as the solar.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... unacceptable
![[*]](/icons/foot_motif.gif)
-
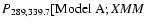 -
-
![${\it Newton}]=2 \times 10^{-2}$](/articles/aa/full/2008/37/aa10264-08/img235.gif) and
and
![$P_{183,241.3}[{\rm Model~A};{\it Chandra}]=2 \times 10^{-3}$](/articles/aa/full/2008/37/aa10264-08/img236.gif) ,
where
,
where
 is the probability of exceeding
is the probability of exceeding  for
for
 degrees of freedom.
degrees of freedom.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spectra
![[*]](/icons/foot_motif.gif)
- i.e., not taking into account radiative transfer effects.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... data
![[*]](/icons/foot_motif.gif)
- We made the analysis of best-fit velocity by inspecting the evaluation of
 at every outflow velocity point of our grid of velocities, while the other parameters
of interest are varied as usual. Then, we proceed to adopt the velocity-model
with the minimum
at every outflow velocity point of our grid of velocities, while the other parameters
of interest are varied as usual. Then, we proceed to adopt the velocity-model
with the minimum  .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... component)
![[*]](/icons/foot_motif.gif)
- This is the best high-velocity component we found able to fit both sets of data with high
 -probability.
-probability.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fluxes
![[*]](/icons/foot_motif.gif)
- For completeness we have computed the observed flux of the
 16 ks XMM-Newton observation (XMM1) and the result is:
16 ks XMM-Newton observation (XMM1) and the result is:
![$F_{(0.2-10~{\rm keV})}[{\rm XMM1}]=9.6\pm 0.6 \times 10^{-13}$](/articles/aa/full/2008/37/aa10264-08/img295.gif) erg cm-2
erg cm-2
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... band
![[*]](/icons/foot_motif.gif)
- We verified that the data is sensitive to an increase of oxygen abundance.
We take the best-fit two-absorbers model and compute models with the oxygen abundance
at 1.5, 3 and 5
 solar oxygen abundance. The fit get worse with
solar oxygen abundance. The fit get worse with
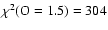 ,
,
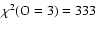 and
and
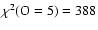 .
The conclusions are: 1) the data is sensitive to the Fe/O ratio. 2) This ratio must
be
.
The conclusions are: 1) the data is sensitive to the Fe/O ratio. 2) This ratio must
be 
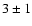 ,
in order to produce acceptable fits
(and produce good description of the low-energy band).
,
in order to produce acceptable fits
(and produce good description of the low-energy band).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... luminosity
![[*]](/icons/foot_motif.gif)
- This is the unabsorbed intrinsic (1-50) keV rest-frame luminosity
of the source. From the XMM-Newton data
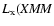 -
-
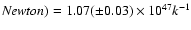 erg
erg
 ,
from the Chandra data
,
from the Chandra data
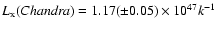 erg
erg
 .
We are taking the average of both.
.
We are taking the average of both.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.