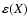 = =
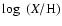 + 12.
Error estimates consist of statistical 1 + 12.
Error estimates consist of statistical 1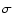 -uncertainties
derived from line-to-line scatter (# lines) plus 0.1 dex for continuum
placement uncertainty (added in quadrature);
realistic uncertainties, including systematic effects e.g. if a magnetic
field were present, are expected to be larger.
NLTE model atoms: 1 Przybilla (2005);
2 Nieva & Przybilla (2008,2006); 3 Przybilla & Butler (2001); 4 Przy-billa et al. (2000); 5 Przybilla et al. (2001);
6 Becker & Butler (1990), extended and updated; 7 Vrancken et al. (1996), updated;
8 Becker (1998). -uncertainties
derived from line-to-line scatter (# lines) plus 0.1 dex for continuum
placement uncertainty (added in quadrature);
realistic uncertainties, including systematic effects e.g. if a magnetic
field were present, are expected to be larger.
NLTE model atoms: 1 Przybilla (2005);
2 Nieva & Przybilla (2008,2006); 3 Przybilla & Butler (2001); 4 Przy-billa et al. (2000); 5 Przybilla et al. (2001);
6 Becker & Butler (1990), extended and updated; 7 Vrancken et al. (1996), updated;
8 Becker (1998).
|