A&A 488, 653-666 (2008)
DOI: 10.1051/0004-6361:200810031
G. F. Porto de Mello - W. Lyra![]() -
G. R. Keller
-
G. R. Keller![]()
Universidade Federal do Rio de Janeiro, Observatório do Valongo, Ladeira do Pedro Antônio, 43, CEP: 20080-090, Rio de Janeiro, RJ, Brazil
Received 23 April 2008 / Accepted 20 June 2008
Abstract
Context. The ![]() Centauri binary system, owing to its duplicity, proximity and brightness, and its components' likeness to the Sun, is a fundamental calibrating object for the theory of stellar structure and evolution and the determination of stellar atmospheric parameters. This role, however, is hindered by a considerable disagreement in the published analyses of its atmospheric parameters and abundances.
Centauri binary system, owing to its duplicity, proximity and brightness, and its components' likeness to the Sun, is a fundamental calibrating object for the theory of stellar structure and evolution and the determination of stellar atmospheric parameters. This role, however, is hindered by a considerable disagreement in the published analyses of its atmospheric parameters and abundances.
Aims. We report a new spectroscopic analysis of both components of the ![]() Centauri system, compare published analyses of the system, and attempt to quantify the discrepancies still extant in the determinations of the atmospheric parameters and abundances of these stars.
Centauri system, compare published analyses of the system, and attempt to quantify the discrepancies still extant in the determinations of the atmospheric parameters and abundances of these stars.
Methods. The analysis is differential with respect to the Sun, based on spectra with
R = 35 000 and signal-to-noise ratio ![]() 1000, and employed spectroscopic and photometric methods to obtain as many independent
1000, and employed spectroscopic and photometric methods to obtain as many independent
![]() determinations as possible. We also check the atmospheric parameters for consistency against the results of the dynamical analysis and the positions of the components in a theoretical HR diagram.
determinations as possible. We also check the atmospheric parameters for consistency against the results of the dynamical analysis and the positions of the components in a theoretical HR diagram.
Results. The spectroscopic atmospheric parameters of the system are found to be
![]() = (
= (
![]() ) K, [Fe/H
) K, [Fe/H
![]() ,
,
![]() ,
and
,
and
![]() km s-1, for
km s-1, for ![]() Cen A, and
Cen A, and
![]() = (5316
= (5316 ![]() 28) K, [Fe/H
28) K, [Fe/H
![]() ,
,
![]() ,
and
,
and
![]() km s
km s![]() for
for ![]() Cen B. The parameters were derived from the simultaneous excitation & ionization equilibria of Fe I and Fe II lines.
Cen B. The parameters were derived from the simultaneous excitation & ionization equilibria of Fe I and Fe II lines.
![]() s were also obtained by fitting theoretical profiles to the H
s were also obtained by fitting theoretical profiles to the H![]() line and from photometric calibrations.
line and from photometric calibrations.
Conclusions. We reached good agreement between the three criteria for ![]() Cen A. For
Cen A. For ![]() Cen B the spectroscopic
Cen B the spectroscopic
![]() is
is ![]() 140 K higher than the other two determinations. We discuss possible origins of this inconsistency, concluding that the presence of non-local thermodynamic equilibrium effects is a probable candidate, but we note that there is as yet no consensus on the existence and cause of an offset between the spectroscopic and photometric
140 K higher than the other two determinations. We discuss possible origins of this inconsistency, concluding that the presence of non-local thermodynamic equilibrium effects is a probable candidate, but we note that there is as yet no consensus on the existence and cause of an offset between the spectroscopic and photometric
![]() scales of cool dwarfs. The spectroscopic surface gravities also agree with those derived from directly measured masses and radii. An average of three independent
scales of cool dwarfs. The spectroscopic surface gravities also agree with those derived from directly measured masses and radii. An average of three independent
![]() criteria leads to
criteria leads to
![]() (A
(A
![]() K and
K and
![]() (B) = (5223
(B) = (5223 ![]() 62) K. The abundances of Na, Mg, Si, Mn, Co, and Ni and, possibly, Cu are significantly enriched in the system, which also seems to be deficient in Y and Ba. This abundance pattern can be deemed normal in the context of recent data on metal-rich stars. The position of
62) K. The abundances of Na, Mg, Si, Mn, Co, and Ni and, possibly, Cu are significantly enriched in the system, which also seems to be deficient in Y and Ba. This abundance pattern can be deemed normal in the context of recent data on metal-rich stars. The position of ![]() Cen A in an up-to-date theoretical evolutionary diagram yields a good match of the evolutionary mass and age (in the 4.5 to 5.3 Gyr range) with those from the dynamical solution and seismology, but only marginal agreement for
Cen A in an up-to-date theoretical evolutionary diagram yields a good match of the evolutionary mass and age (in the 4.5 to 5.3 Gyr range) with those from the dynamical solution and seismology, but only marginal agreement for ![]() Cen B, taking into account its more uncertain
Cen B, taking into account its more uncertain
![]() .
.
Key words: stars: abundances - stars: fundamental parameters - stars: late-type - techniques: spectroscopic - stars: individual: ![]() Centauri
Centauri
The ![]() Centauri binary system, composed of two solar-type
stars (HD 128620 and 128621), is one of the brightest in the sky
and figures as our second closest galactic neighbor, 1.34 parsec
away. The star closest to the Sun is the M5.5 dwarf Proxima
Centauri (Gliese & Jahreiss 1991),
Centauri binary system, composed of two solar-type
stars (HD 128620 and 128621), is one of the brightest in the sky
and figures as our second closest galactic neighbor, 1.34 parsec
away. The star closest to the Sun is the M5.5 dwarf Proxima
Centauri (Gliese & Jahreiss 1991), ![]() 15 000 AU away from
the
15 000 AU away from
the ![]() Centauri binary, and its gravitational connection to
the system is still a topic of controversy. Anosova et al. (1994)
proposed that Proxima has a hyperbolic orbit around the inner
pair, and that the three stars might form part of a more extended
kinematical group. Wertheimer & Laughlin (2006), however, found
the distance between Proxima and the pair to be comparable to the
Hill radius of the latter, whereby the Galactic potential becomes
dominant over that of the inner pair and the system becomes
unbound. These authors favor the existence of a physically-bound
triple system, suggesting that Proxima is presently at the
apoastron of its orbit. Highly precise monitoring of radial
velocity variations of the system by Endl et al. (2001) constrains
the upper limit of the mass of putative planetary or substellar
companions of the system at less than 3.5 Jupiter masses (actually
less than one Saturn mass if coplanar orbits are assumed).
Centauri binary, and its gravitational connection to
the system is still a topic of controversy. Anosova et al. (1994)
proposed that Proxima has a hyperbolic orbit around the inner
pair, and that the three stars might form part of a more extended
kinematical group. Wertheimer & Laughlin (2006), however, found
the distance between Proxima and the pair to be comparable to the
Hill radius of the latter, whereby the Galactic potential becomes
dominant over that of the inner pair and the system becomes
unbound. These authors favor the existence of a physically-bound
triple system, suggesting that Proxima is presently at the
apoastron of its orbit. Highly precise monitoring of radial
velocity variations of the system by Endl et al. (2001) constrains
the upper limit of the mass of putative planetary or substellar
companions of the system at less than 3.5 Jupiter masses (actually
less than one Saturn mass if coplanar orbits are assumed).
| |
|||||||
| Reference | Atmospheric parameter | Method used | |||||
|
|
|
|
|||||
| French & Powell (1971) | 5770 | - | - | +0.22 | a | - | |
| Soderblom (1986) | 5770 | - | - | - | b | - | |
| England (1980) | 5750 | 4.38 | 1.0 | +0.28 | b,c,d | c,d | |
| Bessell (1981) | 5820 | 4.25 | 1.7 | -0.01 | a,e | e | |
| Smith et al. (1986) | 5820 | 4.40 | 1.54 | +0.20 | a,e | d | |
| Gratton & Sneden (1987) | 5750 | 4.38 | 1.2 | +0.11 | f | c,e | |
| Abia et al. (1988) | 5770 | 4.5 | 1.0 | +0.22 | b | f | |
| Edvardsson (1988) | - | 4.42 | - | +0.28 | - | d | |
| Furenlid & Meylan (1990) | 5710 | 4.27 | 1.0 | +0.12 | a,e | e | |
| Chmielewski et al. (1992) | 5800 | 4.31 | - | +0.22 | b | c | |
| Neuforge-Verheecke & Magain (1997) | 5830 | 4.34 | 1.09 | +0.25 | a | ce | |
| Allende-Prieto et al. (2004) | 5519 | 4.26 | 1.04 | +0.12 | f | c | |
| Doyle et al. (2005) | 5784 | 4.28 | 1.08 | +0.12 | direct | direct | |
| Santos et al. (2005) | 5844 | 4.30 | 1.18 | +0.28 | a | a | |
| del Peloso et al. (2005a) | 5813 | 4.30 | 1.23 | +0.26 | b,f | c | |
| Valenti & Fischer (2005) | 5802 | 4.33 | - | +0.23 | a | e | |
| This work | 5824 | 4.34 | 1.46 | +0.24 | a,b,e,f | c,e | |
| |
|||||||
| Reference | Atmospheric parameter | Method used | |||||
|
|
|
|
|||||
| French & Powell (1971) | 5340 | - | - | +0.12 | a | - | |
| Soderblom (1986) | 5350 | - | - | - | b | - | |
| England (1980) | 5260 | 4.73 | 1.1 | +0.38 | b,c,e | c,e | |
| Bessell (1981) | 5350 | 4.5 | 1.0 | -0.05 | a,e | e | |
| Smith et al. (1986) | 5280 | 4.65 | 1.35 | +0.20 | a,e | d | |
| Gratton & Sneden (1987) | 5250 | 4.50 | 1.0 | +0.08 | f | c,e | |
| Abia et al. (1988) | 5300 | 4.5 | 1.5 | +0.14 | b | f | |
| Edvardsson (1988) | - | 4.65 | - | +0.32 | - | d | |
| Chmielewski et al. (1992) | 5325 | 4.58 | - | +0.26 | b | c | |
| Neuforge-Verheecke & Magain (1997) | 5255 | 4.51 | 1.00 | +0.24 | a | c,e | |
| Allende-Prieto et al. (2004) | 4970 | 4.59 | 0.81 | +0.18 | f | c | |
| Santos et al. (2005) | 5199 | 4.37 | 1.05 | +0.19 | a | a | |
| Valenti & Fischer (2005) | 5178 | 4.56 | - | +0.22 | a | e | |
| This work | 5223 | 4.44 | 1.28 | +0.25 | a,b,e,f | c,e | |
|
The notation used from Cols. 6 to 7
stands for: a excitation equilibrium; b wings of Balmer
lines; c trigonometric parallax; d wings of strong lines;
e ionization equilibrium; f photometric color indexes;
direct directly-measured luminosity, mass and radius. Note
that, generally, the microturbulence velocities have not the same
zero point and cannot be directly compared. Typical errors,
respectively, in
|
The proximity of the ![]() Centauri system provides a
well-determined parallax, and its brightness allows for the
acquisition of extremely high-quality spectra. Moreover, its
binary nature and relatively short period of 80 years enables the
hypothesis-free accurate determination of masses (Pourbaix et al.
1999, 2002). If we couple to these facts their being very
solar-like, the
Centauri system provides a
well-determined parallax, and its brightness allows for the
acquisition of extremely high-quality spectra. Moreover, its
binary nature and relatively short period of 80 years enables the
hypothesis-free accurate determination of masses (Pourbaix et al.
1999, 2002). If we couple to these facts their being very
solar-like, the ![]() Centauri stars thus appear as objects of
fundamental importance in the calibration of evolutionary tracks,
theoretical isochrones, and model atmospheres, hence the great
interest in the precise determination of their atmospheric
parameters, evolutionary state, and chemical composition.
Centauri stars thus appear as objects of
fundamental importance in the calibration of evolutionary tracks,
theoretical isochrones, and model atmospheres, hence the great
interest in the precise determination of their atmospheric
parameters, evolutionary state, and chemical composition.
The brightness of the system's components also favor the
determination of internal structure and state of evolution by
seismological observations. The analysis of the frequency spectrum
and amplitudes of both photometric and spectroscopic oscillations
in the outer layers of solar-type stars, driven by convection, can
yield otherwise unobtainable information on internal structure,
such as the depth of the convection zone and the density and
temperature profiles. They can also provide independent checks on
stellar masses, ages, and chemical composition. Yildiz (2007),
Eggenberger et al. (2004), and Thoul et al. (2003) have agreed on
an age for the system between 5.6 and 6.5 Gyr. Miglio &
Montalbán (2005) propose model-dependent ages in the 5.2 to 7.1 Gyr interval. However, they also note that fixing the non-seismic
observables, namely masses and radii, leads to an age as large as
8.9 Gyr, proposing that further seismological observations may be
needed to clarify this apparent discrepancy between the
independent observation of the oscillation spectra and the
directly-measured masses and radii. The previous analysis of
Guenther & Demarque (2000) favors a slightly higher age of ![]() 7.6 Gyr. The masses are very well constrained at
7.6 Gyr. The masses are very well constrained at
![]() and
and
![]() in solar
masses (Pourbaix et al. 2002), which, along with
interferometrically measured (in solar units) radii of
in solar
masses (Pourbaix et al. 2002), which, along with
interferometrically measured (in solar units) radii of
![]() and
and
![]() (Kervella
et al. 2003) yield surface gravities (in c.g.s. units) of
(Kervella
et al. 2003) yield surface gravities (in c.g.s. units) of
![]() and
and
![]() ,
an accuracy seldom enjoyed by stellar spectroscopists.
Altogether these data pose very tight constrains on the modelling
of fundamental quantities of internal structure, such as
mixing-length parameters and convection zone depths.
,
an accuracy seldom enjoyed by stellar spectroscopists.
Altogether these data pose very tight constrains on the modelling
of fundamental quantities of internal structure, such as
mixing-length parameters and convection zone depths.
Nevertheless, the state of our current understanding of this
system still lags behind its importance, since published
spectroscopic analyses reveal considerable disagreement in the
determination of atmospheric parameters and chemical abundances,
particularly for component B, though most authors agree that the
system is significantly metal-rich with respect to the Sun. A
non-exhaustive review is given in Table 1. This
fact is embarrassing, even in our modern era of massive surveys,
since the individual study of key objects is necessary to quantify
systematic errors that might be lurking inside huge databases and
cannot be reduced with large number statistics. Indeed,
considering only those analyses since the 90 s, eight performed a
detailed analysis of the atmospheric parameters and chemical
composition of ![]() Cen A: Furenlid & Meylan (1990),
hereafter FM90; Chmielewski et al. (1992), Neuforge-Verheecke &
Magain (1997), Allende-Prieto et al (2004), hereafter ABLC04; del
Peloso et al. (2005a), Santos et al. (2005), Valenti & Fisher
(2005), and Doyle et al. (2005). Five of them also performed this
analysis for the cooler and fainter component
Cen A: Furenlid & Meylan (1990),
hereafter FM90; Chmielewski et al. (1992), Neuforge-Verheecke &
Magain (1997), Allende-Prieto et al (2004), hereafter ABLC04; del
Peloso et al. (2005a), Santos et al. (2005), Valenti & Fisher
(2005), and Doyle et al. (2005). Five of them also performed this
analysis for the cooler and fainter component ![]() Cen B:
Chmielewski et al. (1992), Neuforge-Verheecke & Magain (1997),
ABLC04; Valenti & Fisher (2005) and Santos et al. (2005). All
these authors, but Chmielewski et al. (1992) and Santos et al.
(2005), obtained abundances for many chemical elements other than
iron.
Cen B:
Chmielewski et al. (1992), Neuforge-Verheecke & Magain (1997),
ABLC04; Valenti & Fisher (2005) and Santos et al. (2005). All
these authors, but Chmielewski et al. (1992) and Santos et al.
(2005), obtained abundances for many chemical elements other than
iron.
The analysis of FM90 for ![]() Cen A is noteworthy in that it
was the first to imply an abundance pattern considerably different
from solar, with excesses relative to Fe in Na, V, Mn, Co, Cu, and
deficits in Zn and the heavy neutron capture elements. The authors
also proposed a low
Cen A is noteworthy in that it
was the first to imply an abundance pattern considerably different
from solar, with excesses relative to Fe in Na, V, Mn, Co, Cu, and
deficits in Zn and the heavy neutron capture elements. The authors
also proposed a low
![]() and a near solar metallicity for
component A, in contrast with most previously published figures.
These authors invoked a supernova to explain the peculiar chemical
features of the system. The next analysis (Chmielewski et al.
1992) sustained a high
and a near solar metallicity for
component A, in contrast with most previously published figures.
These authors invoked a supernova to explain the peculiar chemical
features of the system. The next analysis (Chmielewski et al.
1992) sustained a high
![]() and appreciably higher metallicity
for the system, which was also obtained by Neuforge-Verheecke &
Magain (1997). The latter authors, moreover, found an abundance
pattern not diverging significantly from that of the Sun, though
supporting the deficiency of heavy elements found by FM90.
and appreciably higher metallicity
for the system, which was also obtained by Neuforge-Verheecke &
Magain (1997). The latter authors, moreover, found an abundance
pattern not diverging significantly from that of the Sun, though
supporting the deficiency of heavy elements found by FM90.
The papers of del Peloso et al. (2005a) and Santos et al. (2005)
both derived a high metallicity for the system. Doyle et al.
(2005) added to the controversy by proposing both a low
![]() and
a metallicity not appreciably above solar for component A, as did
FM90. Their abundance pattern is, however, solar. ABLC04 propose
for both components much lower
and
a metallicity not appreciably above solar for component A, as did
FM90. Their abundance pattern is, however, solar. ABLC04 propose
for both components much lower
![]() s than previously found by
any author. Even though their metallicity agrees reasonably with
that of Chmielewski et al. (1992) and Neuforge-Verheecke & Magain
(1997), their detailed abundance pattern is highly non-solar and
also very different from any thus far, with high excesses of Mg,
Si, Ca, Sc, Ti, Zn and Y. Their low metallicity is a result of a
lower adopted
s than previously found by
any author. Even though their metallicity agrees reasonably with
that of Chmielewski et al. (1992) and Neuforge-Verheecke & Magain
(1997), their detailed abundance pattern is highly non-solar and
also very different from any thus far, with high excesses of Mg,
Si, Ca, Sc, Ti, Zn and Y. Their low metallicity is a result of a
lower adopted
![]() ,
as also is the case for the FM90 analysis.
,
as also is the case for the FM90 analysis.
Doyle et al. (2005) presented the most recent abundance analysis
of ![]() Cen A and obtained abundances for six elements. They
made use of the Anstee, Barklem, and O'Mara (ABO) line damping
theory (Barklem et al. 1998, and references therein), which allowed
them to fit accurate damping constants to the profile of strong
lines, turning these into reliable abundances indicators, an
approach normally avoided in abundance analyses. They found
[Fe/H
Cen A and obtained abundances for six elements. They
made use of the Anstee, Barklem, and O'Mara (ABO) line damping
theory (Barklem et al. 1998, and references therein), which allowed
them to fit accurate damping constants to the profile of strong
lines, turning these into reliable abundances indicators, an
approach normally avoided in abundance analyses. They found
[Fe/H
![]() for the iron abundance, which is in
disagreement with most authors using the standard method, although
in line with FM90. To bring home the point of the existing large
disagreement between the various published results, one needs look
no further than at the last entries of Table 1,
all based on very high-quality data and state of the art methods.
These disagreements in chemical composition lie beyond the
confidence levels usually quoted by the authors. Moreover, the
dispersion of the
for the iron abundance, which is in
disagreement with most authors using the standard method, although
in line with FM90. To bring home the point of the existing large
disagreement between the various published results, one needs look
no further than at the last entries of Table 1,
all based on very high-quality data and state of the art methods.
These disagreements in chemical composition lie beyond the
confidence levels usually quoted by the authors. Moreover, the
dispersion of the
![]() values found range between 300 K and 400 K,
respectively, for component A and B.
values found range between 300 K and 400 K,
respectively, for component A and B.
Pourbaix et al. (1999) finish their paper thus: ``we urge southern
spectroscopists to put a high priority on ![]() Centauri''.
Clearly, this very important stellar system is entitled to
additional attention, fulfilling its utility as a reliable
calibrator for theories of stellar structure and evolution, and
taking full advantage of its tight observational constraints
towards our understanding of our second closest neighbor and the
atmospheres of cool stars. The widely differing results of the
chemical analysis also cast doubt about the place of
Centauri''.
Clearly, this very important stellar system is entitled to
additional attention, fulfilling its utility as a reliable
calibrator for theories of stellar structure and evolution, and
taking full advantage of its tight observational constraints
towards our understanding of our second closest neighbor and the
atmospheres of cool stars. The widely differing results of the
chemical analysis also cast doubt about the place of ![]() Centauri in the galactic chemical evolution scenario. The goal of
the present study is a simultaneous analysis of the two components
of the system, obtaining their atmospheric parameters and detailed
abundance pattern, providing an up-to-date comparative analysis of
the different determinations, the methods used and their results.
Centauri in the galactic chemical evolution scenario. The goal of
the present study is a simultaneous analysis of the two components
of the system, obtaining their atmospheric parameters and detailed
abundance pattern, providing an up-to-date comparative analysis of
the different determinations, the methods used and their results.
This paper is organized as follows. In Sect. 2, we describe the data acquisition and reduction. In Sect. 3, we describe the spectroscopic derivation of the atmospheric parameters and Fe abundance, and compare them to other recent results from other techniques, discussing possible sources of discrepancies. The chemical composition pattern and its comparison to those of other authors, is outlined in Sect. 4. Section 5 is devoted to the analysis of the evolutionary state of the system, and Sect. 6 summarizes the conclusions.
We performed observations, in 2001, with the coudé
spectrograph, coupled to the 1.60 m telescope of Observatório
do Pico dos Dias (OPD, Brasópolis, Brazil), operated by
Laboratório Nacional de Astrofisica (LNA/CNPq). As both
![]() Cen A and B are solar-type stars, the Sun is the
natural choice as the standard star of a differential analysis.
The expectation of this approach is that systematic errors in the
measurement of line strengths, the representation of model
atmospheres, and the possible presence of non-local thermodynamic
Equilibrium (NLTE) effects, will be eliminated or at least greatly
lessened if the standard and the analyzed object are sufficiently
similar. We chose the moon as a sunlight surrogate to secure a
solar flux spectrum. The slit width was adjusted to give a
two-pixel resolving power
R = 35 000. A 1800 l/mm diffraction
grating was employed in the first direct order, projecting onto a
24
Cen A and B are solar-type stars, the Sun is the
natural choice as the standard star of a differential analysis.
The expectation of this approach is that systematic errors in the
measurement of line strengths, the representation of model
atmospheres, and the possible presence of non-local thermodynamic
Equilibrium (NLTE) effects, will be eliminated or at least greatly
lessened if the standard and the analyzed object are sufficiently
similar. We chose the moon as a sunlight surrogate to secure a
solar flux spectrum. The slit width was adjusted to give a
two-pixel resolving power
R = 35 000. A 1800 l/mm diffraction
grating was employed in the first direct order, projecting onto a
24 ![]() m, 1024 pixels CCD. The exposure times were chosen to allow
for a S/N ratio in excess of 1000. A decker was used to block
one star of the binary system while exposing the other, and we
ascertained that there was no significant contamination. The moon
image, also exposed to very high S/N, was stopped orthogonally to
the slit width to a size comparable to the seeing disks of the
stars.
m, 1024 pixels CCD. The exposure times were chosen to allow
for a S/N ratio in excess of 1000. A decker was used to block
one star of the binary system while exposing the other, and we
ascertained that there was no significant contamination. The moon
image, also exposed to very high S/N, was stopped orthogonally to
the slit width to a size comparable to the seeing disks of the
stars.
Nine spectral regions were observed, centered at
![]()
![]() 5100, 5245, 5342, 5411, 5528, 5691, 5825, 6128,
and 6242 Å, with spectral coverage of 90 Å each. The
chemical species represented by spectral lines reasonably free
from blending are Na I, Si I, Ca I,
Sc I, Sc II, Ti I, Ti II,V I,
Cr I, Cr II, Mn I, Fe I, Fe II,
Co I, Ni I, Cu I, Y II, and
Ba II. Additional data centered on the H
5100, 5245, 5342, 5411, 5528, 5691, 5825, 6128,
and 6242 Å, with spectral coverage of 90 Å each. The
chemical species represented by spectral lines reasonably free
from blending are Na I, Si I, Ca I,
Sc I, Sc II, Ti I, Ti II,V I,
Cr I, Cr II, Mn I, Fe I, Fe II,
Co I, Ni I, Cu I, Y II, and
Ba II. Additional data centered on the H![]() spectral
region, for the
spectral
region, for the ![]() Cen stars and moonlight, were secured in 2004, using a 13.5
Cen stars and moonlight, were secured in 2004, using a 13.5 ![]() m, 4608 pixels CCD, integrated to
m, 4608 pixels CCD, integrated to
![]() and with
R = 43 000.
and with
R = 43 000.
Data reduction was carried out by the standard procedure using
IRAF![]() . After usual bias and flat-field
correction, we subtracted the background and scattered light and
extracted one-dimensional spectra. No fringing was present in our
spectra. The pixel-to-wavelength calibration was obtained from the
stellar spectra themselves by selecting isolated spectral lines in
the object spectra and checking for the absence of blends, the
main screen for blends being the Solar Flux Atlas (Kurucz et al.
1984) and the Utrecht spectral line compilation (Moore et al.
1966). Gaussian fits were applied to the cores of the selected
lines, and pixel-
. After usual bias and flat-field
correction, we subtracted the background and scattered light and
extracted one-dimensional spectra. No fringing was present in our
spectra. The pixel-to-wavelength calibration was obtained from the
stellar spectra themselves by selecting isolated spectral lines in
the object spectra and checking for the absence of blends, the
main screen for blends being the Solar Flux Atlas (Kurucz et al.
1984) and the Utrecht spectral line compilation (Moore et al.
1966). Gaussian fits were applied to the cores of the selected
lines, and pixel-![]() polynomial fits determined. For the
short spectral selections individually reduced, a 2nd-order
polynomial always sufficed, the average r.m.s. of the residuals
being 0.005
polynomial fits determined. For the
short spectral selections individually reduced, a 2nd-order
polynomial always sufficed, the average r.m.s. of the residuals
being 0.005 ![]() or better. There followed the Doppler
correction of all spectra to a rest reference frame.
or better. There followed the Doppler
correction of all spectra to a rest reference frame.
Normalization of the continuum is a very delicate and relevant
step in the analysis procedure, since the accuracy of line
equivalent width (hereafter
![]() )
measurements is very sensitive
to a faulty determination of the continuum level. We selected
continuum windows in the Solar Flux Atlas, apparently free from
telluric or photospheric lines. We took great care in constantly
comparing the spectra of the two
)
measurements is very sensitive
to a faulty determination of the continuum level. We selected
continuum windows in the Solar Flux Atlas, apparently free from
telluric or photospheric lines. We took great care in constantly
comparing the spectra of the two ![]() Cen components and the
Sun, to ensure that a consistent choice of continuum windows was
achieved in all three objects since the very strong-lined spectra
of the
Cen components and the
Sun, to ensure that a consistent choice of continuum windows was
achieved in all three objects since the very strong-lined spectra
of the ![]() Cen stars caused continuum depressions
systematically larger than in the Sun. A number of pixels was
chosen in the selected continuum windows, followed by the
determination of a low order polynomial fitting these points. The
wavelength coverage of each single spectrum was in all cases
sufficient to ensure an appropriate number of windows, with
special attention given to the edge of the spectra. Sample spectra
are shown in Fig. 1. As will be seen below, the
errors of the atmospheric parameters derived directly from the
spectra, and the element abundances of
Cen stars caused continuum depressions
systematically larger than in the Sun. A number of pixels was
chosen in the selected continuum windows, followed by the
determination of a low order polynomial fitting these points. The
wavelength coverage of each single spectrum was in all cases
sufficient to ensure an appropriate number of windows, with
special attention given to the edge of the spectra. Sample spectra
are shown in Fig. 1. As will be seen below, the
errors of the atmospheric parameters derived directly from the
spectra, and the element abundances of ![]() Cen B, are
greater than in
Cen B, are
greater than in ![]() Cen A, probably due to a less
trouble-free normalization of its strongly line-blocked spectrum,
and to a better cancellation of uncertainties in the differential
analysis.
Cen A, probably due to a less
trouble-free normalization of its strongly line-blocked spectrum,
and to a better cancellation of uncertainties in the differential
analysis.
For the determination of element abundances, we chose lines of
moderate intensity with profiles that indicate little or no
blending. To avoid contamination of telluric lines we computed for
each spectrum, using cross-correlation techniques, the
displacement
![]() the telluric lines would show
relative to their rest position
the telluric lines would show
relative to their rest position ![]() ,
as given by the Solar
Flux Atlas. We discarded photospheric lines closer than
2
,
as given by the Solar
Flux Atlas. We discarded photospheric lines closer than
2
![]() from a telluric line.
from a telluric line.
The equivalent widths were measured by fitting single or multiple
(the latter when de-blending closely spaced lines) Gaussian
profiles to the selected lines, using IRAF. The moderately high
spectral resolution we chose was designed to guarantee that the
instrumental profile dominates the observed profile, and therefore
that purely Gaussian fits would adequately represent the observed
line profiles. To test the representation of the solar flux
spectrum by the moon, we also observed, with exactly the same
setup, spectra of daylight, and the asteroid Ceres. A direct
comparison of the moon, daylight, and asteroid
![]() s showed
perfect agreement between the three sets of measurements to better
than 1% even for moderately strong lines. This lends confidence
to our determination of solar gf-values based on
s showed
perfect agreement between the three sets of measurements to better
than 1% even for moderately strong lines. This lends confidence
to our determination of solar gf-values based on
![]() measured
off the moon spectra. The moonlight spectra was actually preferred
due to its higher S/N ratio as compared to Ceres, for which no
high-quality spectrum could be obtained in a reasonable exposure
time. Also, daylight spectra may show
measured
off the moon spectra. The moonlight spectra was actually preferred
due to its higher S/N ratio as compared to Ceres, for which no
high-quality spectrum could be obtained in a reasonable exposure
time. Also, daylight spectra may show
![]() systematic fill-in
effects by up to 4%, as a combination of aerosol and
Rayleigh-Brillouin effects (this effect depends on the observing
angle and can be eliminated or minimized if care is applied, see
Gray et al. 2000, for details). Even though no difference could be
measured in our spectra, we considered it more prudent to use the
moonlight spectrum as the solar proxy: it should be an accurate
representation of the solar flux spectrum in the visible.
systematic fill-in
effects by up to 4%, as a combination of aerosol and
Rayleigh-Brillouin effects (this effect depends on the observing
angle and can be eliminated or minimized if care is applied, see
Gray et al. 2000, for details). Even though no difference could be
measured in our spectra, we considered it more prudent to use the
moonlight spectrum as the solar proxy: it should be an accurate
representation of the solar flux spectrum in the visible.
Even at our not-so-high resolution, lines stronger than ![]() 50 mÅ begin to develop visible Voigt wings. To account for this
effect, we performed a linear regression of our Gaussian moon
50 mÅ begin to develop visible Voigt wings. To account for this
effect, we performed a linear regression of our Gaussian moon
![]() s against the
s against the
![]() s measured off the Solar Flux Atlas by
Meylan et al. (1993). These authors fitted Voigt profiles to a set
of lines deemed sufficiently unblended to warrant the measurement
of their true
s measured off the Solar Flux Atlas by
Meylan et al. (1993). These authors fitted Voigt profiles to a set
of lines deemed sufficiently unblended to warrant the measurement
of their true
![]() s, and they should be a homogeneous and
high-precision representation of the true line intensities. We
then determined the correction necessary to convert our
measurements to a scale compatible with the Voigt-fitted
s, and they should be a homogeneous and
high-precision representation of the true line intensities. We
then determined the correction necessary to convert our
measurements to a scale compatible with the Voigt-fitted
![]() s. A
linear regression defines the correction to be applied to our
measured
s. A
linear regression defines the correction to be applied to our
measured
![]() s to lessen systematic errors due to inadequate
Gaussian profile fitting. As expected for non-saturated lines, we
ascertained that a linear relationship suffices to describe the
correction. The result is shown in Fig. 2, where
the excellent correlation, with very small dispersion, is seen.
The correction derived is
s to lessen systematic errors due to inadequate
Gaussian profile fitting. As expected for non-saturated lines, we
ascertained that a linear relationship suffices to describe the
correction. The result is shown in Fig. 2, where
the excellent correlation, with very small dispersion, is seen.
The correction derived is
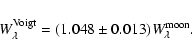 |
(1) |
A solar gf-value for each spectral line was calculated from a LTE,
1D, homogeneous and plane-parallel solar model atmosphere from
the NMARCS grid, as described by Edvardsson et al. (1993, see
http://marcs.astro.uu.se; Gustafsson et al. 2008). The adopted
parameters for the Sun were
![]() = 5780 K,
= 5780 K,
![]() ,
[Fe/H] = +0.00 and
,
[Fe/H] = +0.00 and
![]() km s
km s![]() ,
and we
employed the
,
and we
employed the
![]() s measured off the moon spectra, corrected to
the Voigt scale. The adopted solar absolute abundances are those
of Grevesse & Noels (1993). In a purely differential analysis
such as ours, the absolute abundance scale is inconsequential. We
provide in Table 2 (where A and B stand,
respectively, for
s measured off the moon spectra, corrected to
the Voigt scale. The adopted solar absolute abundances are those
of Grevesse & Noels (1993). In a purely differential analysis
such as ours, the absolute abundance scale is inconsequential. We
provide in Table 2 (where A and B stand,
respectively, for ![]() Cen A and B) the details of all lines
used. They include wavelength
Cen A and B) the details of all lines
used. They include wavelength ![]() ,
excitation potential
,
excitation potential
![]() ,
the calculated solar
,
the calculated solar ![]() values, and the raw measured
values, and the raw measured
![]() s in the moon's,
s in the moon's, ![]() Cen A and
Cen A and ![]() Cen B
spectra, prior to the correction to the Voigt system
(Fig. 2). Hyperfine structure (HFS) corrections
for the lines of Mg I, Sc I, Sc II,
V I, Mn I, Co I, Cu I, and
Ba II were adopted from Steffen (1985). del Peloso et al.
(2005b) discuss the influence of adopting different HFS scales on
abundance analyses of Mn and Co, concluding that it is small,
particularly for metallicities not too far from the solar one, as
compared to not using any HFS data. Therefore, the source of the
HFS corrections is not an important issue on the error budget of
our analysis, at least for Mn and Co. The other elements of our
analysis requiring HFS have usually simpler structures (excepting
Cu), and it is safe to conclude that the use of HFS has not
introduced any important error.
Cen B
spectra, prior to the correction to the Voigt system
(Fig. 2). Hyperfine structure (HFS) corrections
for the lines of Mg I, Sc I, Sc II,
V I, Mn I, Co I, Cu I, and
Ba II were adopted from Steffen (1985). del Peloso et al.
(2005b) discuss the influence of adopting different HFS scales on
abundance analyses of Mn and Co, concluding that it is small,
particularly for metallicities not too far from the solar one, as
compared to not using any HFS data. Therefore, the source of the
HFS corrections is not an important issue on the error budget of
our analysis, at least for Mn and Co. The other elements of our
analysis requiring HFS have usually simpler structures (excepting
Cu), and it is safe to conclude that the use of HFS has not
introduced any important error.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0031fig2.eps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg41.gif) |
Figure 2:
A plot of Voigt-fitted
|
![\begin{figure}
\par\includegraphics[angle=270,width=14.3cm,clip]{0031fig4.ps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg43.gif) |
Figure 4:
Effective temperature determination by fitting
theoretical profiles to the wings of H |
The atmospheric parameters of the ![]() Cen stars were
determined by simultaneously realizing the excitation &
ionization equilibria of Fe I and Fe II. For each
star, we obtained the
Cen stars were
determined by simultaneously realizing the excitation &
ionization equilibria of Fe I and Fe II. For each
star, we obtained the
![]() by forcing the Fe I line
abundances to be independent of their excitation potential. We
determined the surface gravity by forcing the lines of Fe I
and Fe II to yield the same abundance. Lastly, we derived
the microturbulence velocities
by forcing the Fe I line
abundances to be independent of their excitation potential. We
determined the surface gravity by forcing the lines of Fe I
and Fe II to yield the same abundance. Lastly, we derived
the microturbulence velocities ![]() by forcing the lines of
Fe I to be independent of their
by forcing the lines of
Fe I to be independent of their
![]() s. The Fe abundance
[Fe/H] (we use throughout the notation [A/B
s. The Fe abundance
[Fe/H] (we use throughout the notation [A/B
![]() (A)/N(B)
(A)/N(B)
![]() (A)/N(B)
(A)/N(B)
![]() ,
where Ndenotes the number abundance) is automatically obtained as a
byproduct of this method. The solution thus obtained is unique for
a given set of gf values,
,
where Ndenotes the number abundance) is automatically obtained as a
byproduct of this method. The solution thus obtained is unique for
a given set of gf values,
![]() s, and model atmospheres, being
independent of the starting point and the iteration path. The
spectrum synthesis code is originally due to Spite (1967), having
been continuously up-dated in the last 40 years.
s, and model atmospheres, being
independent of the starting point and the iteration path. The
spectrum synthesis code is originally due to Spite (1967), having
been continuously up-dated in the last 40 years.
![\begin{figure}
\par\includegraphics[angle=270,width=15cm,clip]{0031fig5.ps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg47.gif) |
Figure 5:
The same as in Fig. 4 for
|
Formal errors are estimated as follows: for
![]() ,
the 1
,
the 1![]() uncertainty of the slope of the linear regression in the [Fe/H] vs.
uncertainty of the slope of the linear regression in the [Fe/H] vs. ![]() diagram yields the
diagram yields the
![]() variation, which could still
be accepted at the 1
variation, which could still
be accepted at the 1![]() level. For the microturbulence
velocity, the same procedure provides the 1
level. For the microturbulence
velocity, the same procedure provides the 1![]() microturbulence uncertainty in the [Fe/H] vs.
microturbulence uncertainty in the [Fe/H] vs.
![]() diagram. For
the metallicity [Fe/H], we adopt the standard deviation of the
distribution of abundances derived from the Fe I lines. The
error in
diagram. For
the metallicity [Fe/H], we adopt the standard deviation of the
distribution of abundances derived from the Fe I lines. The
error in ![]() is estimated by evaluating the variation in this
parameter, which produces a disagreement of 1
is estimated by evaluating the variation in this
parameter, which produces a disagreement of 1![]() between the
abundances of Fe I and Fe II, where we regarded the
abundance offset as 1
between the
abundances of Fe I and Fe II, where we regarded the
abundance offset as 1![]() when its value was equal to the
largest dispersion of the Fe abundances (usually that of
Fe II). The results of this procedure are shown in
Fig. 3, where we plot the iron abundances of
when its value was equal to the
largest dispersion of the Fe abundances (usually that of
Fe II). The results of this procedure are shown in
Fig. 3, where we plot the iron abundances of
![]() Cen A derived from lines of both Fe I and
Fe II against the excitation potential and
Cen A derived from lines of both Fe I and
Fe II against the excitation potential and
![]() s. The
baseline of the Fe I lines is seen to be large both in
s. The
baseline of the Fe I lines is seen to be large both in
![]() and
and ![]() .
.
Additional effective temperatures were determined by fitting the
observed wings of H![]() ,
using the automated procedure
described in detail in Lyra & Porto de Mello (2005). We have
employed for the
,
using the automated procedure
described in detail in Lyra & Porto de Mello (2005). We have
employed for the ![]() Cen stars new spectroscopic data from
the Observatório do Pico dos Dias, with the same resolution but
greater signal-to-noise ratio than used by Lyra & Porto de Mello
(2005). This procedure is shown in Figs. 4 and 5. We found
Cen stars new spectroscopic data from
the Observatório do Pico dos Dias, with the same resolution but
greater signal-to-noise ratio than used by Lyra & Porto de Mello
(2005). This procedure is shown in Figs. 4 and 5. We found
![]() =
=
![]() K (
K (![]() Cen A) and
Cen A) and
![]() =
=
![]() K
(
K
(![]() Cen B). The moon spectrum is very well fitted by the
parameters adopted for the NMARCS solar atmosphere model. The
quoted standard errors refer exclusively to the dispersion of
temperature values attributed to the fitted profile data points.
This makes the uncertainty of the
Cen B). The moon spectrum is very well fitted by the
parameters adopted for the NMARCS solar atmosphere model. The
quoted standard errors refer exclusively to the dispersion of
temperature values attributed to the fitted profile data points.
This makes the uncertainty of the
![]() of
of ![]() Cen B
artificially very low, due to the high number of rejected points.
An analysis of errors incurred by the atmospheric parameters
assumed in the fitting procedure, plus the photon statistics (not
including possible systematic effects produced by the modelling,
see Lyra & Porto de Mello 2005, for a full discussion), points to
an average error of
Cen B
artificially very low, due to the high number of rejected points.
An analysis of errors incurred by the atmospheric parameters
assumed in the fitting procedure, plus the photon statistics (not
including possible systematic effects produced by the modelling,
see Lyra & Porto de Mello 2005, for a full discussion), points to
an average error of ![]() 50 K in the
50 K in the
![]() s determined from the
H
s determined from the
H![]() line. For the very low-noise spectra of these two stars,
the expected errors would be slightly less, but the greater
difficulty in finding line-free sections in the H
line. For the very low-noise spectra of these two stars,
the expected errors would be slightly less, but the greater
difficulty in finding line-free sections in the H![]() profile
of the severely blended spectrum of
profile
of the severely blended spectrum of ![]() Cen B offsets this
advantage. For the latter, thus, the probable uncertainty should
be closer to
Cen B offsets this
advantage. For the latter, thus, the probable uncertainty should
be closer to ![]() 100 K. The normalization procedure is a a
relevant source of error for
100 K. The normalization procedure is a a
relevant source of error for
![]() s derived from H
s derived from H![]() ,
as
discussed by Lyra & Porto de Mello (2005): they found that a
0.2% error in the continuum level translates to
,
as
discussed by Lyra & Porto de Mello (2005): they found that a
0.2% error in the continuum level translates to ![]() 25 K in
25 K in
![]() .
.
As an external check on our normalization procedure, we compared
H![]() spectra of the Sun (moon) obtained from eight
independent observing runs of Lyra & Porto de Mello (2005) and
reduced independently, with the data of ABLC04, who performed a
careful two-dimensional continuum normalization of the echelle
spectra. Due to normalization problems in the FEROS/ESO (La Silla)
spectra, these authors employed H
spectra of the Sun (moon) obtained from eight
independent observing runs of Lyra & Porto de Mello (2005) and
reduced independently, with the data of ABLC04, who performed a
careful two-dimensional continuum normalization of the echelle
spectra. Due to normalization problems in the FEROS/ESO (La Silla)
spectra, these authors employed H![]() spectra as a
spectra as a
![]() criterion only for the northern stars of their sample, which could
be observed with the McDonald 2dcoudé spectrograph. So a direct
comparison between the two sets of H
criterion only for the northern stars of their sample, which could
be observed with the McDonald 2dcoudé spectrograph. So a direct
comparison between the two sets of H![]() spectra is not
possible for the
spectra is not
possible for the ![]() Cen stars. We found, for the solar
spectra, an average difference of only (
Cen stars. We found, for the solar
spectra, an average difference of only (
![]() )%, as
measured in those regions relevant to the
)%, as
measured in those regions relevant to the
![]() determination.
This assures us of the absence of important systematic errors in
this respect. A comparison of the H
determination.
This assures us of the absence of important systematic errors in
this respect. A comparison of the H![]() normalized spectra is
shown in Fig. 6. In the example shown, the mean
difference between the two spectra (computed only for the line
wing regions actually fitted) is
normalized spectra is
shown in Fig. 6. In the example shown, the mean
difference between the two spectra (computed only for the line
wing regions actually fitted) is
![]() %, and it is the
worst case of our comparison of the eight spectra.
%, and it is the
worst case of our comparison of the eight spectra.
Another check on the
![]() values of the two stars may be
obtained from the IRFM scale of Ramírez & Meléndez
(2005a). Ramírez & Meléndez (2005b) compare, for the two
values of the two stars may be
obtained from the IRFM scale of Ramírez & Meléndez
(2005a). Ramírez & Meléndez (2005b) compare, for the two
![]() Cen stars, direct
Cen stars, direct
![]() s, obtained from measured
bolometric fluxes and angular diameters, with those determined
from the IRFM method, as well those obtained from the application
of their own
s, obtained from measured
bolometric fluxes and angular diameters, with those determined
from the IRFM method, as well those obtained from the application
of their own
![]() (IRFM) scale to color indices and an adopted
metallicity of [Fe/H] = +0.20, for both stars. Respectively,
they find, for
(IRFM) scale to color indices and an adopted
metallicity of [Fe/H] = +0.20, for both stars. Respectively,
they find, for ![]() Cen A,
Cen A,
![]() (direct) = 5771,
(direct) = 5771,
![]() (IRFM) = 5759 K and
(IRFM) = 5759 K and
![]() (calibration) = 5736 K; the
corresponding values for
(calibration) = 5736 K; the
corresponding values for ![]() Cen B are, respectively,
Cen B are, respectively,
![]() (direct) = 5178 K,
(direct) = 5178 K,
![]() (IRFM) = 5221 K and
(IRFM) = 5221 K and
![]() (calibration) =
5103 K. They adopt as weighted averages
(calibration) =
5103 K. They adopt as weighted averages
![]() (
(![]() Cen A) =
Cen A) =
![]() K and
K and
![]() (
(![]() Cen B) =
Cen B) =
![]() K.
For
K.
For ![]() Cen A, a good agreement is found between this
Cen A, a good agreement is found between this
![]() and our H
and our H![]() one. Formally, there is also a reasonable
agreement between this
one. Formally, there is also a reasonable
agreement between this
![]() and our spectroscopic one. For
and our spectroscopic one. For
![]() Cen B, however, the spectroscopic
Cen B, however, the spectroscopic
![]() is
significantly higher than those derived from H
is
significantly higher than those derived from H![]() and the
IRFM method.
and the
IRFM method.
Yildiz (2007) drew attention to often neglected BVRI (Cousins
system) measurements of the system's components by Bessell (1990).
It has long been considered risky to use color indices for the
![]() determination of very bright stars in which a variety of
systematic effects are expected as compared to standard stars of
photometric systems, among which non-linearity, detector
dead-time, and, in the case of
determination of very bright stars in which a variety of
systematic effects are expected as compared to standard stars of
photometric systems, among which non-linearity, detector
dead-time, and, in the case of ![]() Cen, possible
contamination by the companion (see Chmielewski et al. 1992, for a
full discussion). Introducing Bessell's color indices into the
Ramírez & Meléndez (2005b) calibrations, along with our
metallicities (Table 3), we derive
Cen, possible
contamination by the companion (see Chmielewski et al. 1992, for a
full discussion). Introducing Bessell's color indices into the
Ramírez & Meléndez (2005b) calibrations, along with our
metallicities (Table 3), we derive
![]() (
(![]() Cen A) =
Cen A) =
![]() K and
K and
![]() (
(![]() Cen B)
=
Cen B)
=
![]() K, as a weighted average of the (B-V), (V-R) and
(V-I) color indices, the latter two in the Cousins system. These
new photometric
K, as a weighted average of the (B-V), (V-R) and
(V-I) color indices, the latter two in the Cousins system. These
new photometric
![]() determinations, directly from the
calibrations, agree well, for
determinations, directly from the
calibrations, agree well, for ![]() Cen A, with both the
H
Cen A, with both the
H![]() and the spectroscopic one. On the other hand, for
and the spectroscopic one. On the other hand, for
![]() Cen B this determination lessens slightly, but does not
eliminate, the disagreement between the spectroscopic
Cen B this determination lessens slightly, but does not
eliminate, the disagreement between the spectroscopic
![]() and
the other two. We must therefore state clearly that there is an
offset between the spectroscopic
and
the other two. We must therefore state clearly that there is an
offset between the spectroscopic
![]() of
of ![]() Cen B and the
other two
Cen B and the
other two
![]() determinations. These last figures, in a classical
spectroscopic analysis of solar-type stars, would be regarded as
``photometric''
determinations. These last figures, in a classical
spectroscopic analysis of solar-type stars, would be regarded as
``photometric''
![]() s, to be compared to those obtained from
other methods. Our results are all displayed in
Table 3, where we also list the direct surface
gravities resulting from the directly-observed radii and dynamical
masses.
s, to be compared to those obtained from
other methods. Our results are all displayed in
Table 3, where we also list the direct surface
gravities resulting from the directly-observed radii and dynamical
masses.
Valenti & Fischer (2005) have derived the atmospheric parameters
of ![]() Cen A and B by means of a different technique. They
have directly fitted large sections of the observed spectra to
synthetic ones, obtaining the atmospheric parameters (this
technique also relies on the excitation & ionization equilibria
of atomic species). Their analysis is differential with respect to
the Sun, for which they adopted
Cen A and B by means of a different technique. They
have directly fitted large sections of the observed spectra to
synthetic ones, obtaining the atmospheric parameters (this
technique also relies on the excitation & ionization equilibria
of atomic species). Their analysis is differential with respect to
the Sun, for which they adopted
![]() = 5770, [Fe/H] = +0.00 and
= 5770, [Fe/H] = +0.00 and
![]() .
They quote uncertainties of 44 K, 0.03 dex and 0.06 dex, respectively, for
.
They quote uncertainties of 44 K, 0.03 dex and 0.06 dex, respectively, for
![]() ,
log g and [Fe/H]. Their results are
,
log g and [Fe/H]. Their results are
![]() = 5802 K,
= 5802 K,
![]() and [Fe/H] = +0.23, for
and [Fe/H] = +0.23, for
![]() Cen A, and
Cen A, and
![]() = 5178 K,
= 5178 K,
![]() and [Fe/H] =
+0.21, for
and [Fe/H] =
+0.21, for ![]() Cen B. These figures are in good agreement,
even within their very small claimed uncertainties, with our
spectroscopic parameters, again, with the exception of the
spectroscopic
Cen B. These figures are in good agreement,
even within their very small claimed uncertainties, with our
spectroscopic parameters, again, with the exception of the
spectroscopic
![]() of
of ![]() Cen B. Particularly, their
Cen B. Particularly, their ![]() values are in excellent agreement with the direct
values are in excellent agreement with the direct ![]() values of
Table 3.
values of
Table 3.
Frutiger et al. (2005) have also analyzed the spectra of
![]() Cen A and B with a fundamentally different and
promising technique. They have inverted high-resolution (
Cen A and B with a fundamentally different and
promising technique. They have inverted high-resolution (
![]() ), moderately high S/N (
), moderately high S/N (![]() 250) spectra of the
stars by means of a multi-component model photosphere. The
components take into account rotational broadening, center-to-limb
variations and vertical and horizontal flows of surface elements,
such as granules and inter-granular areas. In this approach, the
full line profile is used to constrain the temperature
stratification of the atmosphere, as well as the velocity fields
(Allende-Prieto et al. 1998). The technique is rather
model-dependent, however, and should be compared with classical
spectroscopic analyses with caution. For the 3-component models,
the ones they favor,
250) spectra of the
stars by means of a multi-component model photosphere. The
components take into account rotational broadening, center-to-limb
variations and vertical and horizontal flows of surface elements,
such as granules and inter-granular areas. In this approach, the
full line profile is used to constrain the temperature
stratification of the atmosphere, as well as the velocity fields
(Allende-Prieto et al. 1998). The technique is rather
model-dependent, however, and should be compared with classical
spectroscopic analyses with caution. For the 3-component models,
the ones they favor,
![]() s and [Fe/H] substantially lower than
those found by us are obtained (their Table 4). For
s and [Fe/H] substantially lower than
those found by us are obtained (their Table 4). For
![]() Cen A, they favor
Cen A, they favor
![]() = 5705 K,
= 5705 K,
![]() and [Fe/H
and [Fe/H
![]() (we have converted their
abundances from absolute to relative values with respect to the
Sun, which they also analyzed with the same techniques. Their
analysis, in this sense, may also be considered as differential).
For
(we have converted their
abundances from absolute to relative values with respect to the
Sun, which they also analyzed with the same techniques. Their
analysis, in this sense, may also be considered as differential).
For ![]() Cen B, the results are
Cen B, the results are
![]() = 5310 K,
= 5310 K,
![]() and [Fe/H
and [Fe/H
![]() .
.
|
|
|
|
|
|
||||
| excitation | H |
photometric | weighted mean | ionization | direct | |||
| 5847 |
5793 |
5794 |
5824 |
4.34 |
4.307 |
+0.24 |
1.46 |
|
| 5316 |
5155 |
5182 |
5223 |
4.44 |
4.538 |
+0.25 |
1.28 |
It is not straightforward to determine the uncertainties of their
![]() values, since they only quote the uncertainty of this
parameter as derived by a weighted average of the
values, since they only quote the uncertainty of this
parameter as derived by a weighted average of the
![]() fluxes of each atmospheric component, weighted by the
filling-factors, by means of the Eddington-Barbier relation
applied to a grey atmosphere. The
fluxes of each atmospheric component, weighted by the
filling-factors, by means of the Eddington-Barbier relation
applied to a grey atmosphere. The
![]() s we quoted are the ones
they computed from the flux spectra obtained from their
temperature stratifications fed into an ATLAS9 model, for which
they provided no formal uncertainty. The uncertainties of their
s we quoted are the ones
they computed from the flux spectra obtained from their
temperature stratifications fed into an ATLAS9 model, for which
they provided no formal uncertainty. The uncertainties of their
![]() s within the Eddington-Barbier approximation, are,
respectively, 130 K and 67 K for
s within the Eddington-Barbier approximation, are,
respectively, 130 K and 67 K for ![]() Cen A and B. Within
these error bars, then, their
Cen A and B. Within
these error bars, then, their
![]() s resulting purely from the
inversion procedure (letting all parameters free) may be regarded
as compatible with ours. Their metallicities, however, are
significantly lower. They also found a very high
s resulting purely from the
inversion procedure (letting all parameters free) may be regarded
as compatible with ours. Their metallicities, however, are
significantly lower. They also found a very high ![]() for
for
![]() Cen B, prompting them to attempt a larger number of
inversions this for component, first fixing
Cen B, prompting them to attempt a larger number of
inversions this for component, first fixing
![]() dex,
which led to a reduced
dex,
which led to a reduced
![]() = 5154 K with no appreciable change
in metallicity, and then fixing the rotational velocity, which
produced
= 5154 K with no appreciable change
in metallicity, and then fixing the rotational velocity, which
produced
![]() = 5260 K, again with no significant impact on
metallicity, and a new
= 5260 K, again with no significant impact on
metallicity, and a new
![]() .
.
The
![]() s favored by the inversion method of Frutiger et al.
(2005) add to a complex situation. They seem to be in good
agreement with our spectroscopic
s favored by the inversion method of Frutiger et al.
(2005) add to a complex situation. They seem to be in good
agreement with our spectroscopic
![]() for
for ![]() Cen B when
all parameters are independently derived from the inversion
method, but the agreement switches to one with the H
Cen B when
all parameters are independently derived from the inversion
method, but the agreement switches to one with the H![]() and
photometric
and
photometric
![]() s, when the surface gravity is fixed. All [Fe/H]
values they obtain are lower than ours. For
s, when the surface gravity is fixed. All [Fe/H]
values they obtain are lower than ours. For ![]() Cen A,
their surface gravity is in good agreement with ours and the
direct one. It is difficult, however, to reconcile their surface
gravity for
Cen A,
their surface gravity is in good agreement with ours and the
direct one. It is difficult, however, to reconcile their surface
gravity for ![]() Cen B with our spectroscopic one, and the
direct one given in Table 3. It is not clear whether
their results can be directly compared to ours, given the
difference in approach. These authors discuss the possibility of
improving their technique by higher resolution spectra: they
remark on the difficulty of disentangling effects of rotation,
macro-turbulence, granulation, and instrumental profile. This
sophisticated approach can lead to substantially improved
constraints in the derivation of the atmospheric parameters of
solar-type stars, leading to increased physical insight on the
shortcomings of 1D, static atmospheric models.
Cen B with our spectroscopic one, and the
direct one given in Table 3. It is not clear whether
their results can be directly compared to ours, given the
difference in approach. These authors discuss the possibility of
improving their technique by higher resolution spectra: they
remark on the difficulty of disentangling effects of rotation,
macro-turbulence, granulation, and instrumental profile. This
sophisticated approach can lead to substantially improved
constraints in the derivation of the atmospheric parameters of
solar-type stars, leading to increased physical insight on the
shortcomings of 1D, static atmospheric models.
| element | ||||||||
| [X/Fe] | [X/Fe] | |||||||
| Na | +0.14 | - | +0.25 | - | 0.03 | |||
| Mg | +0.00 | - | +0.04 | - | 0.03 | |||
| Si | +0.00 | 0.06 | +0.00 | 0.05 | 0.05 | |||
| Ca | +0.03 | 0.03 | +0.09 | 0.08 | 0.03 | |||
| Sc | +0.00 | 0.02 | +0.01 | 0.07 | 0.06 | |||
| Ti | -0.01 | 0.04 | +0.19 | 0.14 | 0.06 | |||
| V | +0.02 | 0.05 | +0.21 | 0.09 | 0.07 | |||
| Cr | +0.00 | 0.06 | +0.06 | 0.09 | 0.06 | |||
| Mn | +0.07 | 0.01 | +0.19 | 0.06 | 0.04 | |||
| Co | +0.00 | 0.06 | +0.06 | 0.07 | 0.07 | |||
| Ni | +0.10 | 0.07 | +0.11 | 0.05 | 0.04 | |||
| Cu | +0.10 | - | +0.10 | - | 0.04 | |||
| Y | -0.09 | 0.05 | -0.09 | 0.08 | 0.07 | |||
| Ba | -0.13 | 0.05 | -0.16 | 0.08 | 0.06 | |||
A disagreement between photometric and spectroscopic
![]() scales
has been recently pointed out by a number of authors. Ramírez
et al. (2007) discussed how the Fe I/Fe II
ionization equilibrium is not realized in cool stars when an IRFM
scales
has been recently pointed out by a number of authors. Ramírez
et al. (2007) discussed how the Fe I/Fe II
ionization equilibrium is not realized in cool stars when an IRFM
![]() scale is applied, in the derivation of oxygen abundances
from the
scale is applied, in the derivation of oxygen abundances
from the ![]() 7774 triplet lines. Their sample is large, and
they convincingly show (their Fig. 5) that the
7774 triplet lines. Their sample is large, and
they convincingly show (their Fig. 5) that the
![]() offset
between the IRFM and the spectroscopic scales is significant for
offset
between the IRFM and the spectroscopic scales is significant for
![]()
![]() 5000 K (a reasonable agreement was found for
5000 K (a reasonable agreement was found for
![]()
![]() 6000 K). They note that Ramírez & Meléndez (2004)
found the same offset, as did Santos et al. (2004), Yong et al.
(2004) and Heiter & Luck (2003). Yong et al. (2004) suggested
that non-LTE effects, shortcomings of the model atmosphere
representation for cool stars, or as yet unidentified effects,
might be responsible for the discrepancy. Ramírez et al.
(2007), however, note that Santos et al. (2005) reported good
agreement between IRFM and spectroscopic
6000 K). They note that Ramírez & Meléndez (2004)
found the same offset, as did Santos et al. (2004), Yong et al.
(2004) and Heiter & Luck (2003). Yong et al. (2004) suggested
that non-LTE effects, shortcomings of the model atmosphere
representation for cool stars, or as yet unidentified effects,
might be responsible for the discrepancy. Ramírez et al.
(2007), however, note that Santos et al. (2005) reported good
agreement between IRFM and spectroscopic
![]() scales. Adding to
this complex picture, Casagrande et al. (2006), in the derivation
of their own IRFM
scales. Adding to
this complex picture, Casagrande et al. (2006), in the derivation
of their own IRFM
![]() scale, also found good agreement between
spectroscopic and IRFM
scale, also found good agreement between
spectroscopic and IRFM
![]() s. They argue that the disagreement
reported by other authors might be due, at least in part, to
uncertainties in the different absolute flux calibrations adopted,
and suggest that additional direct angular diameter measurements
for a well-chosen sample of G and K dwarfs might go a long way
towards clarifying the disagreement of the
s. They argue that the disagreement
reported by other authors might be due, at least in part, to
uncertainties in the different absolute flux calibrations adopted,
and suggest that additional direct angular diameter measurements
for a well-chosen sample of G and K dwarfs might go a long way
towards clarifying the disagreement of the
![]() scales.
scales.
The results of Casagrande et al. (2006) were essentially backed by
the
![]() scale of Masana et al. (2006). The latter employed a
variation of the IRFM method, in which the stellar energy
distributions were fitted, from the optical to the IR, to
synthetic photometry computed from stellar atmosphere models. They
found their results only slightly offset from the IRFM results.
The offset, at
scale of Masana et al. (2006). The latter employed a
variation of the IRFM method, in which the stellar energy
distributions were fitted, from the optical to the IR, to
synthetic photometry computed from stellar atmosphere models. They
found their results only slightly offset from the IRFM results.
The offset, at ![]() 30 K, was deemed to be small, and these
authors optimistically assert that their
30 K, was deemed to be small, and these
authors optimistically assert that their
![]() scale agrees with
the spectroscopic one for FGK dwarfs and subgiants, such that
scale agrees with
the spectroscopic one for FGK dwarfs and subgiants, such that
![]() s for this class of stars may be regarded as accurate within
s for this class of stars may be regarded as accurate within
![]() 1% or better.
1% or better.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0031fig7a.eps}\hspace*{4mm}
\includegraphics[width=8.2cm,clip]{0031fig7b.eps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg69.gif) |
Figure 7:
The abundance pattern of |
The consistency of the different
![]() scales is sought as an
important confirmation that 1D, plane-parallel, static and LTE
model atmospheres adequately represent cool stars, if not in the
absolute, at least in the relative sense, provided that the Sun
can be accurately placed in the stellar context. The solar
placement in the Fe I/Fe II excitation & ionization
equilibria and Balmer line
scales is sought as an
important confirmation that 1D, plane-parallel, static and LTE
model atmospheres adequately represent cool stars, if not in the
absolute, at least in the relative sense, provided that the Sun
can be accurately placed in the stellar context. The solar
placement in the Fe I/Fe II excitation & ionization
equilibria and Balmer line
![]() scale is obtained by the
observation of solar flux spectra. An accurate photometric
placement of the Sun in the corresponding
scale is obtained by the
observation of solar flux spectra. An accurate photometric
placement of the Sun in the corresponding
![]() scale, however, is
a difficult task still beset with large uncertainties (see, e.g.,
Holmberg et al. 2006, for an up-to-date discussion). These three
scale, however, is
a difficult task still beset with large uncertainties (see, e.g.,
Holmberg et al. 2006, for an up-to-date discussion). These three
![]() scales actually gauge rather dissimilar physical quantities.
The excitation & ionization
scales actually gauge rather dissimilar physical quantities.
The excitation & ionization
![]() is obtained by matching models
to observed spectral line intensities. The Balmer line
is obtained by matching models
to observed spectral line intensities. The Balmer line
![]() measures the temperature stratification of the atmosphere, which
is mapped onto the line wings by the depth-dependence of the
source-function. The photometric
measures the temperature stratification of the atmosphere, which
is mapped onto the line wings by the depth-dependence of the
source-function. The photometric
![]() must reproduce the stellar
flux distribution in a large wavelength regime, and is the one
most directly tied to the fundamental definition of effective
temperature (Böhm-Vitense 1981). As long as the consistency
between these scales is realized no better than within
must reproduce the stellar
flux distribution in a large wavelength regime, and is the one
most directly tied to the fundamental definition of effective
temperature (Böhm-Vitense 1981). As long as the consistency
between these scales is realized no better than within ![]() 150 K, the
150 K, the
![]() of cool dwarfs and subgiants will remain uncertain by
this amount at the very least.
of cool dwarfs and subgiants will remain uncertain by
this amount at the very least.
Non-LTE and other possibly more complex effects have repeatedly
been blamed for offsets between spectroscopically- and
photometrically-derived atmospheric parameters in cool stars.
Schuler et al. (2006), in their analysis of Hyades dwarfs,
reported a systematic offset of the oxygen abundances derived from
the ![]() 7774 triplet lines, for
7774 triplet lines, for
![]() < 5450 K, in the
opposite sense of the NLTE expectations. They tentatively suggest
that chromospheric activity might be at least partially
responsible for the offset, an explanation also concurred by Morel
& Micela (2004), though the latter propose that model atmosphere
pitfalls might be also present. Schuler et al. (2006) reinforce
this interpretation in an analysis of the
< 5450 K, in the
opposite sense of the NLTE expectations. They tentatively suggest
that chromospheric activity might be at least partially
responsible for the offset, an explanation also concurred by Morel
& Micela (2004), though the latter propose that model atmosphere
pitfalls might be also present. Schuler et al. (2006) reinforce
this interpretation in an analysis of the ![]() 6300 [OI] line
in the very active Hyades stars, reporting offsets between
Fe I/Fe II abundances which increase as
6300 [OI] line
in the very active Hyades stars, reporting offsets between
Fe I/Fe II abundances which increase as
![]()
![]() 5000 K. It should be emphasized that high chromospheric activity
is unlikely to be a source of the
5000 K. It should be emphasized that high chromospheric activity
is unlikely to be a source of the
![]() discrepancy of
discrepancy of
![]() Cen B, since both components of the system are inactive
stars, which probably implies that the problem is more complex. We
also draw attention to the result of Shchukina & Trujillo-Bueno
(2001), who found an offset of the Fe I/Fe II
abundances of the Sun. They interpret this offset as well
explained by NLTE effects amounting to 0.07 dex for Fe I,
the best fit Fe abundance for a LTE analysis being the lower by
this amount. They assert that a full 3D, NLTE model atmosphere
formulation is able to bring the solar photospheric Fe abundance
in line with the meteoritic one, at
Cen B, since both components of the system are inactive
stars, which probably implies that the problem is more complex. We
also draw attention to the result of Shchukina & Trujillo-Bueno
(2001), who found an offset of the Fe I/Fe II
abundances of the Sun. They interpret this offset as well
explained by NLTE effects amounting to 0.07 dex for Fe I,
the best fit Fe abundance for a LTE analysis being the lower by
this amount. They assert that a full 3D, NLTE model atmosphere
formulation is able to bring the solar photospheric Fe abundance
in line with the meteoritic one, at ![]() (Fe) = 7.50 (in the usual
scale where
(Fe) = 7.50 (in the usual
scale where ![]() (H) = 12.00). The main cause of the offset is the
overionization of Fe I, and the larger errors are seen in
the
(H) = 12.00). The main cause of the offset is the
overionization of Fe I, and the larger errors are seen in
the
![]() s of low excitation lines, which are weaker in the NLTE
case.
s of low excitation lines, which are weaker in the NLTE
case.
It is interesting to note that this effect, in a classical LTE
model atmosphere analysis, would result in the overabundance of
the high excitation Fe I lines, an effect naturally
interpreted as too low a
![]() being attributed to the model. This
is exactly the condition necessary for a 1D, LTE analysis to lead
to the high spectroscopic
being attributed to the model. This
is exactly the condition necessary for a 1D, LTE analysis to lead
to the high spectroscopic
![]() that we obtained. Forcing the
Fe I/Fe II abundances into agreement in a LTE
analysis would indeed call for a higher
that we obtained. Forcing the
Fe I/Fe II abundances into agreement in a LTE
analysis would indeed call for a higher
![]() ,
to a first
approximation, by
,
to a first
approximation, by ![]() 100 K, a value similar to the difference
between our spectroscopic and H
100 K, a value similar to the difference
between our spectroscopic and H![]() /photometric
/photometric
![]() s of
s of
![]() Cen B. We suggest that the similarity in atmospheric
parameters between
Cen B. We suggest that the similarity in atmospheric
parameters between ![]() Cen A and the Sun, in the context of
a differential analysis, led to a good agreement between the three
Cen A and the Sun, in the context of
a differential analysis, led to a good agreement between the three
![]() criteria for the former. For
criteria for the former. For ![]() Cen B, a much cooler
object, an imperfect cancellation of the presence of NLTE effects
is probably the reason why the three different
Cen B, a much cooler
object, an imperfect cancellation of the presence of NLTE effects
is probably the reason why the three different
![]() criteria do
not agree.
criteria do
not agree.
Even if the presence of NLTE effects and other problems can be
established, one must keep in mind that other uncertainties are
present in the photometric and H![]()
![]() scales, as
discussed above. It would be very valuable to extend the novel
approaches of Valenti & Fischer (2005) and Frutiger et al. (2005)
to additional stars for which stringent observational constraints
are available, to quantify how discrepancies of the type discussed
here occur for objects with atmospheric parameters increasingly
different from the Sun's. At present, we can state that it is
likely that our spectroscopic
scales, as
discussed above. It would be very valuable to extend the novel
approaches of Valenti & Fischer (2005) and Frutiger et al. (2005)
to additional stars for which stringent observational constraints
are available, to quantify how discrepancies of the type discussed
here occur for objects with atmospheric parameters increasingly
different from the Sun's. At present, we can state that it is
likely that our spectroscopic
![]() for
for ![]() Cen B is more
uncertain, and systematically higher, that the other two
determinations. This conclusion is, however, drawn in the context
of a confusing picture. Additional work is clearly necessary
before a definitive judgment can be passed on the consistency
between the excitation & ionization, Balmer line, and
photometric
Cen B is more
uncertain, and systematically higher, that the other two
determinations. This conclusion is, however, drawn in the context
of a confusing picture. Additional work is clearly necessary
before a definitive judgment can be passed on the consistency
between the excitation & ionization, Balmer line, and
photometric
![]() scales can be reached.
scales can be reached.
Notwithstanding the discrepancies, if we follow an usual practice
in spectroscopic abundance analysis, which obtain atmospheric
parameters with more than one criterion, mean
![]() s for the
s for the
![]() Cen stars can be calculated from the values of
Table 3, averaged by their inverse variances. The
results are
Cen stars can be calculated from the values of
Table 3, averaged by their inverse variances. The
results are
![]() (
(![]() Cen A) =
Cen A) =
![]() K and
K and
![]() (
(![]() Cen B) =
Cen B) =
![]() K, where the quoted
uncertainties are the standard deviations of the average, and do
not reflect external and systematic errors. Good agreement between
our ionization surface gravities, and those directly determined
from measured masses and radii, within the errors, for both stars,
is realized.
K, where the quoted
uncertainties are the standard deviations of the average, and do
not reflect external and systematic errors. Good agreement between
our ionization surface gravities, and those directly determined
from measured masses and radii, within the errors, for both stars,
is realized.
![\begin{figure}
\par\includegraphics[width=13.4cm,clip]{0031fig9.ps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg74.gif) |
Figure 9: The same as Fig. 9, but averaging the [X/Fe] abundances of the elements with published data from at least three authors. The boxes comprise 50% of the data points, and are centered at the mean. The horizontal dashes inside the boxes mark the median. The whiskers mark the maximum and minimum values. In this more stringent statistical analysis of the available data, Na, Mg, Si, Mn, Co, and Ni are enhanced; Ca, Sc, Ti, V, and Cr are normal; Y and Ba are under-abundant. |
The abundances of the other elements were obtained with the
adopted atmospheric model of each star, corresponding to the
spectroscopic
![]() s, and the
s, and the ![]() ,
[Fe/H] and
,
[Fe/H] and ![]() values
as given in Table 3. Average abundances were
calculated by the straight mean of the individual line abundances.
For Sc, Ti, and Cr, good agreement, within the errors, was
obtained for the abundances of the neutral and singly ionized
species, and thus these species confirm the
Fe I/Fe II ionization equilibria. The results are
given in Table 4 and Fig. 7 as [X/Fe]
relative to the Sun. In Table 4, the first two columns
give the [X/Fe] ratios with the corresponding observed dispersions
of the line abundances, for those elements with three or more
available lines, for
values
as given in Table 3. Average abundances were
calculated by the straight mean of the individual line abundances.
For Sc, Ti, and Cr, good agreement, within the errors, was
obtained for the abundances of the neutral and singly ionized
species, and thus these species confirm the
Fe I/Fe II ionization equilibria. The results are
given in Table 4 and Fig. 7 as [X/Fe]
relative to the Sun. In Table 4, the first two columns
give the [X/Fe] ratios with the corresponding observed dispersions
of the line abundances, for those elements with three or more
available lines, for ![]() Cen A. The next two columns give the
corresponding data for
Cen A. The next two columns give the
corresponding data for ![]() Cen B. The fifth column provides
the total uncertainty of the [X/Fe] ratios corresponding to errors
in
Cen B. The fifth column provides
the total uncertainty of the [X/Fe] ratios corresponding to errors
in
![]() ,
,
![]() ,
[Fe/H],
,
[Fe/H], ![]() and
and
![]() ,
respectively, of 30 K, 0.12 dex, 0.04 dex, 0.03 km s-1 and 2.9 mÅ, composed in
quadrature (the latter enters twice, see Sect. 3).
,
respectively, of 30 K, 0.12 dex, 0.04 dex, 0.03 km s-1 and 2.9 mÅ, composed in
quadrature (the latter enters twice, see Sect. 3).
In Fig. 7, the error bars are merely the internal
dispersion of the individual line abundances. For Na I,
Mg I, Cu I, and Ba II, the dispersions refer
to the difference between the abundances of the two available
lines for each element. Na is seen to be overabundant, while a
solar pattern is seen from Mg to Co, but for an excess of Mn. Ni
and Cu are also overabundant. Some doubt can be cast about Ti and V, since they seem overabundant in ![]() Cen B although solar in
Cen B although solar in ![]() Cen A. The slow neutron capture elements Y and Ba
are in clear deficit. The bigger uncertainty bars seen in
Cen A. The slow neutron capture elements Y and Ba
are in clear deficit. The bigger uncertainty bars seen in
![]() Cen B are probably a result of a less accurate
normalization of the spectra of a cooler star, and may also be due
to its less accurate atmospheric parameters. We may conclude that
there is a good consistency between the abundance patterns of the
two stars, except for the Ti I and V I abundances,
but these can still be accomodated by the larger error bars for
Cen B are probably a result of a less accurate
normalization of the spectra of a cooler star, and may also be due
to its less accurate atmospheric parameters. We may conclude that
there is a good consistency between the abundance patterns of the
two stars, except for the Ti I and V I abundances,
but these can still be accomodated by the larger error bars for
![]() Cen B at the 2
Cen B at the 2![]() level.
level.
In Fig. 7, the vertical dark grey bars besides the
data points of the abundance pattern of ![]() Cen A are the
composed rms uncertainties, for each element, calculated
by varying the spectroscopic atmospheric parameters of
Cen A are the
composed rms uncertainties, for each element, calculated
by varying the spectroscopic atmospheric parameters of
![]() Cen A by the corresponding uncertainties of
Table 3. To this calculation, we added the abundance
variations caused by summing to all
Cen A by the corresponding uncertainties of
Table 3. To this calculation, we added the abundance
variations caused by summing to all
![]() s the 2.9 mÅ
uncertainty of the correction of Fig. 2. This
s the 2.9 mÅ
uncertainty of the correction of Fig. 2. This
![]() uncertainty enters twice: once for the uncertainty in the
corrected moon
uncertainty enters twice: once for the uncertainty in the
corrected moon
![]() s, reflecting onto the solar
s, reflecting onto the solar ![]() s, and
another one due to stellar
s, and
another one due to stellar
![]() themselves. In
Fig. 7, it is apparent that the abundance variations
due to the uncertainties in the atmospheric parameters and
themselves. In
Fig. 7, it is apparent that the abundance variations
due to the uncertainties in the atmospheric parameters and
![]() s
are comparable to the observed dispersions of the line abundances
for
s
are comparable to the observed dispersions of the line abundances
for ![]() Cen A. For
Cen A. For ![]() Cen B, the line abundance
dispersions are generally larger, probably due to its more
uncertain
Cen B, the line abundance
dispersions are generally larger, probably due to its more
uncertain
![]() s, but also, as discussed above, possibly owing to
its larger
s, but also, as discussed above, possibly owing to
its larger
![]() difference from the standard object (the Sun) and
its more uncertain atmospheric parameters.
difference from the standard object (the Sun) and
its more uncertain atmospheric parameters.
Our abundance pattern for ![]() Cen A is clearly the most
reliable of the pair, and is directly compared to those of other
authors in Fig. 8. Only abundances represented by
more than one spectral line are shown. The observed dispersion is
comparable to the uncertainties normally quoted in a
spectroscopic analysis. Only for the light elements between Mg and
Ti is a larger disagreement observed, in this case due to the
analysis of ABLC04, in which abundances are higher than in the
bulk of other data by
Cen A is clearly the most
reliable of the pair, and is directly compared to those of other
authors in Fig. 8. Only abundances represented by
more than one spectral line are shown. The observed dispersion is
comparable to the uncertainties normally quoted in a
spectroscopic analysis. Only for the light elements between Mg and
Ti is a larger disagreement observed, in this case due to the
analysis of ABLC04, in which abundances are higher than in the
bulk of other data by ![]() 0.2 dex. For the elements heavier than
V, essentially all data agree that V and Cr have normal abundance
ratios, that Mn, Co, Ni, and Cu are enhanced, and all heavy
elements from Y to Eu are deficient in the abundance pattern of
0.2 dex. For the elements heavier than
V, essentially all data agree that V and Cr have normal abundance
ratios, that Mn, Co, Ni, and Cu are enhanced, and all heavy
elements from Y to Eu are deficient in the abundance pattern of
![]() Cen A with respect to the Sun, with the sole exception
of Ba, for which ABLC04 found a normal abundance. The available
literature data also suggests that the C, N, and O abundance
ratios of
Cen A with respect to the Sun, with the sole exception
of Ba, for which ABLC04 found a normal abundance. The available
literature data also suggests that the C, N, and O abundance
ratios of ![]() Cen A are solar.
Cen A are solar.
This statistical analysis can be extended if we regard only the
elements for which at least three independent studies provided
data. This is shown in Fig. 9, for a more select
sample of elements. We may conclude, with somewhat greater
robustness, considering the number of abundance results, that Na,
Mg, Si, Mn, Co, and Ni are over-abundant; that Ca, Sc, Ti, V, and
Cr have solar abundance ratios; and that Y and Ba are
over-deficient in the abundance pattern of ![]() Cen with
respect to the Sun.
Cen with
respect to the Sun.
The high metallicity of the ![]() Cen system, and its space
velocity components (U,V,W) (km s
Cen system, and its space
velocity components (U,V,W) (km s
![]() ,
+10, +8)
(Porto de Mello et al. 2006, all with respect to the Sun) place it
unambiguously as a thin disk star. We next analyze its abundance
ratios, for the elements with more reliable data, as compared to
recent literature results for metal-rich stars. Bensby et al.
(2003, hereafter BFL) analyzed 66 stars belonging to the thin and
thick disks of the Milky Way, deriving abundances of Na, Mg, Al,
Si, Ca, Ti, Cr, Fe, Ni, and Zn. Bodaghee et al. (2003, hereafter
BSIM) studied a sample of 119 stars, of which 77 are known to
harbor planetary companions, deriving abundances of Si, Ca, Sc,
Ti, V, Cr, Mn, Fe, Co, and Ni. The data of the latter study comes
from the Geneva observatory planet-search campaign (e.g., Santos
et al. 2005). Since they concluded that planet-bearing stars
merely represent the high metallicity extension of the abundance
distribution of nearby stars, their full sample can be used to
adequately represent the abundance ratios of metal rich stars,
without distinction to the presence or absence of low mass
companions. These two works have in common the important fact that
they sample well the metallicity interval +0.20 < [Fe/H]
< +0.40, an essential feature for our aim.
,
+10, +8)
(Porto de Mello et al. 2006, all with respect to the Sun) place it
unambiguously as a thin disk star. We next analyze its abundance
ratios, for the elements with more reliable data, as compared to
recent literature results for metal-rich stars. Bensby et al.
(2003, hereafter BFL) analyzed 66 stars belonging to the thin and
thick disks of the Milky Way, deriving abundances of Na, Mg, Al,
Si, Ca, Ti, Cr, Fe, Ni, and Zn. Bodaghee et al. (2003, hereafter
BSIM) studied a sample of 119 stars, of which 77 are known to
harbor planetary companions, deriving abundances of Si, Ca, Sc,
Ti, V, Cr, Mn, Fe, Co, and Ni. The data of the latter study comes
from the Geneva observatory planet-search campaign (e.g., Santos
et al. 2005). Since they concluded that planet-bearing stars
merely represent the high metallicity extension of the abundance
distribution of nearby stars, their full sample can be used to
adequately represent the abundance ratios of metal rich stars,
without distinction to the presence or absence of low mass
companions. These two works have in common the important fact that
they sample well the metallicity interval +0.20 < [Fe/H]
< +0.40, an essential feature for our aim.
The elements in common between the two abundance sets are Si, Ca,
Ti, Cr, and Ni. It can be concluded (Fig. 13 of BFL, Fig. 2 of
BSIM) that, in [Fe/H
![]() stars, Ca is
under-abundant, Ti is normal and Ni is enhanced. For Si, BFL
suggest abundance ratios higher than solar, while BSIM found a
normal abundance. For Cr, the data of BSIM suggests abundance
ratios lower than solar, while BFL found solar ratios. For the
elements not in common in the two studies, Na, Mg, Al, Sc, V, Mn,
and Co are found to be enhanced in [Fe/H
stars, Ca is
under-abundant, Ti is normal and Ni is enhanced. For Si, BFL
suggest abundance ratios higher than solar, while BSIM found a
normal abundance. For Cr, the data of BSIM suggests abundance
ratios lower than solar, while BFL found solar ratios. For the
elements not in common in the two studies, Na, Mg, Al, Sc, V, Mn,
and Co are found to be enhanced in [Fe/H
![]() stars, while Zn has normal abundance ratios.
stars, while Zn has normal abundance ratios.
An interesting feature of the ![]() Cen abundance pattern is
the under-abundance in the elements heavier than Y, which could be
reliably established for Y and Ba (Fig. 9). This
result is confirmed by Bensby et al. (2005), who found both for Y and Ba lower than solar abundance ratios for metal rich thin disk
stars. Another interesting feature, the excess of Cu (found by us
and FM90), can be checked with the recent results of Ecuvillon et al. (2004), who also obtain for [Fe/H
Cen abundance pattern is
the under-abundance in the elements heavier than Y, which could be
reliably established for Y and Ba (Fig. 9). This
result is confirmed by Bensby et al. (2005), who found both for Y and Ba lower than solar abundance ratios for metal rich thin disk
stars. Another interesting feature, the excess of Cu (found by us
and FM90), can be checked with the recent results of Ecuvillon et al. (2004), who also obtain for [Fe/H![]() 0.20 stars an
average [Cu/Fe
0.20 stars an
average [Cu/Fe![]() dex.
dex.
Merging our evaluation of the abundance pattern of
![]() Cen A, from the available independent analyses, with
the previous discussion, we conclude that
Cen A, from the available independent analyses, with
the previous discussion, we conclude that ![]() Cen A is a
normal metal-rich star in its Na, Mg, Si, Ti, V, Cr, Mn, Co, and
Ni abundances. The result for Ca is inconclusive, and only for Sc
does its abundance diverge from the BFL/BSIM data in that its
normal abundance ratio contrasts with the overabundance found for
[Fe/H]
Cen A is a
normal metal-rich star in its Na, Mg, Si, Ti, V, Cr, Mn, Co, and
Ni abundances. The result for Ca is inconclusive, and only for Sc
does its abundance diverge from the BFL/BSIM data in that its
normal abundance ratio contrasts with the overabundance found for
[Fe/H] ![]() +0.20 stars by BSIM. It seems reasonably well
established then that the
+0.20 stars by BSIM. It seems reasonably well
established then that the ![]() Cen system is composed of two
normal metal rich stars when regarded in the local disk
population.
Cen system is composed of two
normal metal rich stars when regarded in the local disk
population.
An important outcome of the present analysis is to establish if
the derived atmospheric parameters, coupled to high-quality
parallaxes, allow a consistent determination of the masses and
ages of the ![]() Cen system in a traditional HR diagram
analysis, matching the stringent constraints posed by the orbital
solution and seismological data. In Fig. 10, we plot the
position of the
Cen system in a traditional HR diagram
analysis, matching the stringent constraints posed by the orbital
solution and seismological data. In Fig. 10, we plot the
position of the ![]() Cen components in the theoretical HR
diagram of Kim et al. (2002) and Yi et al. (2003), corresponding
to its exact metallicity and a solar abundance pattern. The
bolometric corrections were taken from Flower (1996), and in
calculating the luminosities the Hipparcos (ESA 1997) parallaxes
and visual magnitudes were used. Evolutionary tracks and
isochrones from different authors (e.g., Girardi et al. 2000;
Charbonnel et al. 1999; Schaller et al. 1992) were also tested,
and good agreement between the different tracks was found, to
better than
Cen components in the theoretical HR
diagram of Kim et al. (2002) and Yi et al. (2003), corresponding
to its exact metallicity and a solar abundance pattern. The
bolometric corrections were taken from Flower (1996), and in
calculating the luminosities the Hipparcos (ESA 1997) parallaxes
and visual magnitudes were used. Evolutionary tracks and
isochrones from different authors (e.g., Girardi et al. 2000;
Charbonnel et al. 1999; Schaller et al. 1992) were also tested,
and good agreement between the different tracks was found, to
better than ![]() 50 K, for the position of both
50 K, for the position of both ![]() Cen
components. This is an expected result, given that the Sun is
generally used to calibrate these models. The solar mass, radius,
and age provide a zero point to the models and allow for a
solution as a function of the adopted mixing-length of the
convection theory (still a free parameter) and the initial helium
abundance. Thus, differences between the models can be substantial
in the treatment of stars that are very different from the Sun
(e.g., Lyra et al. 2006), but good agreement for solar-type stars
is a natural outcome of this procedure. The conclusions drawn
below, then, are essentially model-independent, at least for the
Cen
components. This is an expected result, given that the Sun is
generally used to calibrate these models. The solar mass, radius,
and age provide a zero point to the models and allow for a
solution as a function of the adopted mixing-length of the
convection theory (still a free parameter) and the initial helium
abundance. Thus, differences between the models can be substantial
in the treatment of stars that are very different from the Sun
(e.g., Lyra et al. 2006), but good agreement for solar-type stars
is a natural outcome of this procedure. The conclusions drawn
below, then, are essentially model-independent, at least for the
![]() and luminosity intervals involved here.
and luminosity intervals involved here.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0031fig10.eps}\end{figure}](/articles/aa/full/2008/35/aa10031-08/Timg80.gif) |
Figure 10:
The evolutionary state of the |
The
![]() values and error bars in the diagram are those of the
weighted mean of Table 3. From the diagram, masses of
values and error bars in the diagram are those of the
weighted mean of Table 3. From the diagram, masses of
![]() and
and
![]() can be derived, and agree well with the orbital solution of
Pourbaix et al. (2002). The age of
can be derived, and agree well with the orbital solution of
Pourbaix et al. (2002). The age of ![]() Cen A can be
relatively well constrained to the interval of 4.5 to 5.3 Gyr
(1
Cen A can be
relatively well constrained to the interval of 4.5 to 5.3 Gyr
(1![]() ), again, in good agreement with the seismological
results of Yildiz (2007), Eggenberger et al. (2004), Miglio &
Montalbán (2005) and Thoul et al. (2003), within the quoted
uncertainties. We conclude that, adopting the average
), again, in good agreement with the seismological
results of Yildiz (2007), Eggenberger et al. (2004), Miglio &
Montalbán (2005) and Thoul et al. (2003), within the quoted
uncertainties. We conclude that, adopting the average
![]() s and
[Fe/H] found in this work, the position of
s and
[Fe/H] found in this work, the position of ![]() Cen A in
up-to-date theoretical HR diagrams can be reconciled both with
seismological and dynamical data. Despite its higher mass and its
being (probably) older than the Sun, the higher metallicity slows
the evolution to the point that the star has not yet reached the
``hook'' zone of the HR diagram, thus enabling a unique age
solution through this type of analysis.
Cen A in
up-to-date theoretical HR diagrams can be reconciled both with
seismological and dynamical data. Despite its higher mass and its
being (probably) older than the Sun, the higher metallicity slows
the evolution to the point that the star has not yet reached the
``hook'' zone of the HR diagram, thus enabling a unique age
solution through this type of analysis.
Concerning ![]() Cen B, it is also apparent in Fig. 10
that its position cannot be reconciled, within 1
Cen B, it is also apparent in Fig. 10
that its position cannot be reconciled, within 1![]() ,
with an
age near 5 Gyr, as was possible for
,
with an
age near 5 Gyr, as was possible for ![]() Cen A. However, an
upward revision of only
Cen A. However, an
upward revision of only ![]() 60 K would bring its position in
agreement with a track of 0.93 solar mass (the dynamical value),
and an age of
60 K would bring its position in
agreement with a track of 0.93 solar mass (the dynamical value),
and an age of ![]() 5-8 Gyr. Given the uncertainties discussed in
Sect. 3, along with the probable effect of systematic errors in
the
5-8 Gyr. Given the uncertainties discussed in
Sect. 3, along with the probable effect of systematic errors in
the
![]() determination of
determination of ![]() Cen B, this is not outside
the 2
Cen B, this is not outside
the 2![]() confidence interval of the results. We conclude that
confidence interval of the results. We conclude that
![]() Cen A has its position in the theoretical HR diagram
well matched by up-to-date models, within the uncertainties of the
determination of its atmospheric parameters, and also within the
small differences, in this
Cen A has its position in the theoretical HR diagram
well matched by up-to-date models, within the uncertainties of the
determination of its atmospheric parameters, and also within the
small differences, in this
![]() and luminosity regime, between
different grids of evolutionary models. For
and luminosity regime, between
different grids of evolutionary models. For ![]() Cen B,
however, the larger
Cen B,
however, the larger
![]() uncertainty precludes a more stringent
assessment of a match between its evolutionary mass and age and
the results from the dynamical solution and asteroseismology.
Further data are still necessary to allow for a more definitive
conclusion on this issue. If indeed its spectroscopic
uncertainty precludes a more stringent
assessment of a match between its evolutionary mass and age and
the results from the dynamical solution and asteroseismology.
Further data are still necessary to allow for a more definitive
conclusion on this issue. If indeed its spectroscopic
![]() is
systematically offset, the mean
is
systematically offset, the mean
![]() we derived would decrease
and displace its position on the HR diagram to the right,
forestalling a match with the age of
we derived would decrease
and displace its position on the HR diagram to the right,
forestalling a match with the age of ![]() Cen A. For a
better understanding of the onset of possible NLTE effects in
cool stars, and the hindrance thus incurred in the determination
of their atmospheric parameters, it would be interesting to
perform further analyses of such objects for which high-quality
spectra could be secured, and the relevant observational
constraints made at least partially available. Interesting bright,
nearby K-dwarf candidates for such an enterprise are
Cen A. For a
better understanding of the onset of possible NLTE effects in
cool stars, and the hindrance thus incurred in the determination
of their atmospheric parameters, it would be interesting to
perform further analyses of such objects for which high-quality
spectra could be secured, and the relevant observational
constraints made at least partially available. Interesting bright,
nearby K-dwarf candidates for such an enterprise are
![]() Eri, 36 and 70 Oph, o
Eri, 36 and 70 Oph, o![]() Eri and
Eri and ![]() Dra.
Dra.
We have undertaken a new detailed spectroscopic analysis of the
two components of the ![]() Centauri binary system, and have
attempted an appraisal of the many discordant determinations of
its atmospheric parameters and abundance pattern, and of the
sources of errors in their determination. We derived purely
spectroscopic atmospheric parameters, from
R = 35 000 and
S/N >
1000 spectra, in a strictly differential analysis with the Sun
as the standard. We obtained
Centauri binary system, and have
attempted an appraisal of the many discordant determinations of
its atmospheric parameters and abundance pattern, and of the
sources of errors in their determination. We derived purely
spectroscopic atmospheric parameters, from
R = 35 000 and
S/N >
1000 spectra, in a strictly differential analysis with the Sun
as the standard. We obtained
![]()
![]() K and
K and
![]()
![]() K from the spectroscopic analysis,
and
K from the spectroscopic analysis,
and
![]()
![]() K and
K and
![]()
![]() K from the average of spectroscopic, H
K from the average of spectroscopic, H![]() and
photometric
and
photometric
![]() s. We derived [Fe/H
s. We derived [Fe/H
![]() dex
for the system. The spectroscopic surface gravities,
dex
for the system. The spectroscopic surface gravities,
![]() and
and
![]() ,
are
a good match to those determined from directly measured masses and
radii. Good agreement, in both components, is found between the
photometric
,
are
a good match to those determined from directly measured masses and
radii. Good agreement, in both components, is found between the
photometric
![]() and the one resulting from the fitting of the
wings of H
and the one resulting from the fitting of the
wings of H![]() .
For
.
For ![]() Cen A, these two
Cen A, these two
![]() s also
agree with the spectroscopic one. However, for
s also
agree with the spectroscopic one. However, for ![]() Cen B,
the spectroscopic
Cen B,
the spectroscopic
![]() was found to be significantly higher, by
was found to be significantly higher, by ![]() 140 K, than the other two. A comparison of the published
140 K, than the other two. A comparison of the published
![]() s for the system in the last 20 years roughly support a
spectroscopic
s for the system in the last 20 years roughly support a
spectroscopic
![]() scale hotter than the ones owed to photometric
methods or the fitting of Balmer lines.
scale hotter than the ones owed to photometric
methods or the fitting of Balmer lines.
A comparison with recent results from other techniques revealed an
unclear picture. Atmospheric parameters for the ![]() Cen
stars derived by Valenti & Fisher (2005) by fitting directly
synthetic spectra to a large spectral coverage, agree well with
our determinations, but for the spectroscopic
Cen
stars derived by Valenti & Fisher (2005) by fitting directly
synthetic spectra to a large spectral coverage, agree well with
our determinations, but for the spectroscopic
![]() of
of
![]() Cen B. Their surface gravities and metallicities are
also in line with our figures. Frutiger et al. (2005), inverting
high-resolution line profiles, found a substantially lower [Fe/H],
and their model-dependent
Cen B. Their surface gravities and metallicities are
also in line with our figures. Frutiger et al. (2005), inverting
high-resolution line profiles, found a substantially lower [Fe/H],
and their model-dependent
![]() s agree either with our
spectroscopic or with the photometric/H
s agree either with our
spectroscopic or with the photometric/H![]()
![]() ,
depending
on assumptions. Their
,
depending
on assumptions. Their ![]() for
for ![]() Cen B is also higher
than all other recent determinations.
Cen B is also higher
than all other recent determinations.
We discuss possible origins of the offset between the
![]() scales, concluding that the presence of NLTE effects, and also a
possible inconsistency between spectroscopic and photometric
scales, concluding that the presence of NLTE effects, and also a
possible inconsistency between spectroscopic and photometric
![]() scales, are probable explanations. Recent results reporting
offsets between spectroscopic and photometric
scales, are probable explanations. Recent results reporting
offsets between spectroscopic and photometric
![]() scales in cool
stars, of similar magnitude, lend some credence to this
interpretation. But we note that some authors claim consistency
between the two scales, and that other sources of errors may be at
play, such as uncertainties in the absolute flux calibration of
photometric
scales in cool
stars, of similar magnitude, lend some credence to this
interpretation. But we note that some authors claim consistency
between the two scales, and that other sources of errors may be at
play, such as uncertainties in the absolute flux calibration of
photometric
![]() s. We also note that recent claims of such
s. We also note that recent claims of such
![]() offsets as caused by chromospheric activity cannot explain the
present discrepancy given that both
offsets as caused by chromospheric activity cannot explain the
present discrepancy given that both ![]() Cen stars are
considerably inactive stars. These discordant data still preclude
a clear evaluation of the problem. For both
Cen stars are
considerably inactive stars. These discordant data still preclude
a clear evaluation of the problem. For both ![]() Cen A and
B, the spectroscopic surface gravities agree well, within the
uncertainties, with direct values derived from the dynamical
masses of Pourbaix et al. (2002) and the radii of Kervella et al.
(2003). The atmospheric parameters resulting from our analysis are
collected in Table 3.
Cen A and
B, the spectroscopic surface gravities agree well, within the
uncertainties, with direct values derived from the dynamical
masses of Pourbaix et al. (2002) and the radii of Kervella et al.
(2003). The atmospheric parameters resulting from our analysis are
collected in Table 3.
The abundance pattern of the system, when the various authors's data are considered for those elements for which at least three independent analyses are available, is found to be enriched in Na, Mg, Si, Mn, Co, Ni, and (with less reliability) Cu, and deficient in Y and Ba (Fig. 9). This abundance pattern is found to be in very good agreement with recent results on the abundance ratios of metal-rich stars. Thus, the system may be considered as a normal pair of middle-aged, metal-rich, thin disk stars.
An analysis of the evolutionary state of the system in the
theoretical tracks of Kim et al. (2002) and Yi et al. (2003)
yields a very good agreement of the evolutionary mass (
![]() )
and age (4.5-5.3 Gyr) of
)
and age (4.5-5.3 Gyr) of ![]() Cen A with
the results of recent seismological and dynamical data
(Fig. 10). For
Cen A with
the results of recent seismological and dynamical data
(Fig. 10). For ![]() Cen B, a 1
Cen B, a 1![]() upward
revision of its
upward
revision of its
![]() would bring its position in the HR diagram
within reasonable agreement with the age found for
would bring its position in the HR diagram
within reasonable agreement with the age found for
![]() Cen A, and an evolutionary mass (
Cen A, and an evolutionary mass (
![]() )
in good agreement with the dynamical one would result. This
merely marginal compatibility suggests that to fulfill the
privileged situation of the
)
in good agreement with the dynamical one would result. This
merely marginal compatibility suggests that to fulfill the
privileged situation of the ![]() Cen system as a fundamental
calibrator of the modelling of stellar structure and atmosphere
models, additional analyses of component B seem to be necessary to
quantify the onset and magnitude of possible NLTE in cool stars,
as well as to allow for a more precise evaluation of possible
offsets between spectroscopic and photometric
Cen system as a fundamental
calibrator of the modelling of stellar structure and atmosphere
models, additional analyses of component B seem to be necessary to
quantify the onset and magnitude of possible NLTE in cool stars,
as well as to allow for a more precise evaluation of possible
offsets between spectroscopic and photometric
![]() scales in this
class of objects.
scales in this
class of objects.
Acknowledgements
We acknowledge fruitful discussions with Bengt Edvardsson. W.L. and G.R.K. wish to thank CNPq-Brazil for the award of a scholarship. G.F.P.M. acknowledges financial support by CNPq grant n
476909/2006-6, FAPERJ grant n
APQ1/26/170.687/2004, and a CAPES post-doctoral fellowship n
BEX 4261/07-0. We thank the staff of the OPD/LNA for considerable support in the observing runs necessary for this project. Use was made of the Simbad database, operated at CDS, Strasbourg, France, and of NASA's Astrophysics Data System Bibliographic Services. We thank Dr. Monique Spite (Observatoire de Paris-Meudon) for use of the spectral line synthesis code. Criticism and suggestions from the anonymous referee have considerably improved the manuscript.
|
|
|
|
|
|
|
||||||||||||||
(Å) |
(eV) | Moon | A | B | (Å) |
(eV) | Moon | A | B | (Å) |
(eV) | Moon | A | B | |||||
Na I |
5381.020 | 1.57 | -1.855 | 65.9 | 79.0 | 80.9 | 5701.557 | 2.56 | -2.116 | 89.2 | 99.5 | 127.9 | |||||||
6154.230 |
2.10 | -1.532 | 40.6 | 62.5 | 92.3 | 5418.756 | 1.58 | -2.116 | 52.8 | 66.9 | 55.8 | 5705.473 | 4.30 | -1.427 | 42.1 | 53.0 | 66.8 | ||
6160.753 |
2.10 | -1.224 | 60.5 | 86.3 | 120.4 | 5731.761 | 4.26 | -1.115 | 60.9 | 71.1 | 85.9 | ||||||||
| V I | 5784.666 | 3.40 | -2.487 | 33.0 | 42.8 | 61.0 | |||||||||||||
Mg I |
5657.436 | 1.06 | -0.889 | 8.5 | 10.4 | 40.4 | 5811.916 | 4.14 | -2.383 | 11.3 | 17.6 | 26.3 | |||||||
5711.095 |
4.34 | -1.658 | 112.2 | 124.3 | ... | 5668.362 | 1.08 | -0.940 | 7.3 | 11.7 | 38.2 | 5814.805 | 4.28 | -1.851 | 23.7 | 33.6 | 44.7 | ||
5785.285 |
5.11 | -1.826 | 59.0 | 68.3 | 88.7 | 5670.851 | 1.08 | -0.396 | 21.6 | 31.4 | 82.1 | 5835.098 | 4.26 | -2.085 | 16.2 | 22.8 | 35.0 | ||
| 5727.661 | 1.05 | -0.835 | 9.8 | 14.6 | 56.8 | 5849.681 | 3.69 | -2.963 | 8.3 | 13.5 | 22.9 | ||||||||
Si I |
6135.370 | 1.05 | -0.674 | 14.1 | 20.6 | 59.6 | 5852.222 | 4.55 | -1.180 | 43.2 | 54.3 | 71.3 | |||||||
5517.533 |
5.08 | -2.454 | 14.5 | 25.5 | 21.8 | 6150.154 | 0.30 | -1.478 | 12.9 | 20.4 | 65.5 | 5855.086 | 4.61 | -1.521 | 24.5 | 34.8 | 42.8 | ||
5665.563 |
4.92 | -1.957 | 43.0 | 57.0 | 62.3 | 6274.658 | 0.27 | -1.570 | 11.1 | 15.0 | 60.6 | 5856.096 | 4.29 | -1.553 | 36.6 | 48.1 | 61.2 | ||
5684.484 |
4.95 | -1.581 | 65.1 | 79.4 | 78.6 | 6285.165 | 0.28 | -1.543 | 11.5 | 25.1 | 66.3 | 5859.596 | 4.55 | -0.579 | 77.4 | 88.4 | 105.6 | ||
5690.433 |
4.93 | -1.627 | 63.2 | 67.4 | 64.6 | 6098.250 | 4.56 | -1.760 | 17.7 | 25.7 | 35.4 | ||||||||
5701.108 |
4.93 | -1.967 | 41.9 | 57.3 | 58.2 | Cr I | 6120.249 | 0.92 | -5.733 | 7.5 | 11.8 | 29.1 | |||||||
5708.405 |
4.95 | -1.326 | 78.7 | 93.1 | 95.9 | 5214.144 | 3.37 | -0.739 | 18.2 | 27.2 | 39.9 | 6137.002 | 2.20 | -2.830 | 72.9 | 83.4 | 104.9 | ||
5793.080 |
4.93 | -1.896 | 46.1 | 62.4 | 60.3 | 5238.964 | 2.71 | -1.312 | 19.9 | 33.8 | 55.2 | 6151.616 | 2.18 | -3.308 | 51.1 | 60.7 | 80.5 | ||
6125.021 |
5.61 | -1.496 | 34.7 | 51.3 | 51.4 | 5272.007 | 3.45 | -0.311 | 32.9 | 42.9 | 88.0 | 6173.340 | 2.22 | -2.871 | 70.2 | 83.7 | 100.9 | ||
6142.494 |
5.62 | -1.422 | 38.5 | 52.5 | 49.8 | 5287.183 | 3.44 | -0.822 | 13.8 | 16.6 | 34.9 | 6219.287 | 2.20 | -2.412 | 93.6 | 102.9 | 134.6 | ||
6145.020 |
5.61 | -1.397 | 40.5 | 55.1 | 55.3 | 5296.691 | 0.98 | -1.343 | 96.5 | 107.0 | 153.1 | 6226.730 | 3.88 | -2.068 | 31.2 | 40.1 | 56.8 | ||
6243.823 |
5.61 | -1.220 | 51.8 | 67.5 | 64.1 | 5300.751 | 0.98 | -2.020 | 64.7 | 76.6 | 103.7 | 6240.645 | 2.22 | -3.295 | 50.0 | 60.0 | 80.4 | ||
6244.476 |
5.61 | -1.264 | 48.8 | 66.5 | 66.3 | 5304.183 | 3.46 | -0.701 | 16.8 | 25.1 | 16.8 | 6265.131 | 2.18 | -2.537 | 88.3 | 99.9 | 135.0 | ||
| 5318.810 | 3.44 | -0.647 | 19.2 | 27.9 | 53.4 | 6271.283 | 3.33 | -2.703 | 26.5 | 36.7 | 54.9 | ||||||||
Ca I |
5784.976 | 3.32 | -0.360 | 34.0 | 48.0 | 72.9 | |||||||||||||
5261.708 |
2.52 | -0.564 | 126.9 | 123.0 | 182.1 | 5787.965 | 3.32 | -0.129 | 49.4 | 59.8 | 83.8 | Fe II | |||||||
5867.572 |
2.93 | -1.566 | 26.7 | 35.8 | 58.6 | 5234.630 | 3.22 | -2.199 | 90.4 | 110.9 | 92.7 | ||||||||
6161.295 |
2.52 | -1.131 | 135.5 | 85.7 | 128.7 | Cr II | 5264.812 | 3.33 | -2.930 | 53.1 | 67.2 | 64.8 | |||||||
6163.754 |
2.52 | -1.079 | 126.6 | 87.7 | 93.8 | 5305.855 | 3.83 | -2.042 | 27.1 | 37.8 | 24.1 | 5325.560 | 3.22 | -3.082 | 51.1 | 66.3 | 52.7 | ||
6166.440 |
2.52 | -1.116 | 72.6 | 88.9 | 114.0 | 5313.526 | 4.07 | -1.539 | 38.7 | 49.3 | 43.4 | 5414.075 | 3.22 | -3.485 | 33.7 | 46.0 | 32.1 | ||
6169.044 |
2.52 | -0.718 | 97.7 | 113.4 | 158.0 | 5425.257 | 3.20 | -3.229 | 45.5 | 58.1 | 46.3 | ||||||||
6169.564 |
2.52 | -0.448 | 118.5 | 137.5 | 185.8 | Mn I | 6149.249 | 3.89 | -2.761 | 37.8 | 48.4 | 30.0 | |||||||
| 5394.670 | 0.00 | -2.916 | 83.4 | 103.8 | 165.0 | 6247.562 | 3.89 | -2.325 | 57.1 | 69.6 | 48.3 | ||||||||
Sc I |
5399.479 | 3.85 | -0.045 | 42.9 | 63.4 | 96.6 | |||||||||||||
5671.826 |
1.45 | 0.538 | 16.1 | 24.2 | 64.1 | 5413.684 | 3.86 | -0.343 | 28.0 | 45.8 | 73.1 | Co I | |||||||
6239.408 |
0.00 | -1.270 | 7.8 | 12.3 | 12.9 | 5420.350 | 2.14 | -0.720 | 88.6 | 116.4 | 177.5 | 5212.691 | 3.51 | -0.180 | 20.0 | 34.8 | 50.6 | ||
| 5432.548 | 0.00 | -3.540 | 54.9 | 73.3 | 141.0 | 5301.047 | 1.71 | -1.864 | 22.5 | 33.8 | 57.9 | ||||||||
Sc II |
5537.765 | 2.19 | -1.748 | 37.3 | 57.4 | 113.3 | 5342.708 | 4.02 | 0.661 | 35.1 | 48.5 | 80.5 | |||||||
5318.346 |
1.36 | -1.712 | 16.0 | 23.3 | 28.7 | 5359.192 | 4.15 | 0.147 | 11.9 | 20.1 | 37.3 | ||||||||
5526.815 |
1.77 | 0.099 | 80.2 | 97.8 | 86.5 | Fe I | 5381.772 | 4.24 | 0.000 | 8.2 | 15.6 | 20.0 | |||||||
5657.874 |
1.51 | -0.353 | 71.2 | 85.9 | 76.5 | 5054.647 | 3.64 | -1.806 | 53.0 | 67.6 | 97.6 | 5454.572 | 4.07 | 0.319 | 18.9 | 26.8 | 42.8 | ||
5684.189 |
1.51 | -0.984 | 40.4 | 55.6 | 48.9 | 5067.162 | 4.22 | -0.709 | 85.4 | 90.3 | 123.1 | ||||||||
6245.660 |
1.51 | -1.063 | 37.6 | 51.1 | 51.0 | 5109.649 | 4.30 | -0.609 | 87.9 | 100.1 | 143.0 | Ni I | |||||||
| 5127.359 | 0.93 | -3.186 | 109.6 | 117.7 | 164.8 | 5094.406 | 3.83 | -1.088 | 32.4 | 45.0 | 62.2 | ||||||||
Ti I |
5151.971 | 1.01 | -3.128 | 108.9 | 120.8 | 177.5 | 5220.300 | 3.74 | -1.263 | 28.5 | 40.6 | 52.1 | |||||||
5071.472 |
1.46 | -0.683 | 36.1 | 45.7 | 99.0 | 5213.818 | 3.94 | -2.752 | 7.5 | 13.0 | 20.2 | 5435.866 | 1.99 | -2.340 | 57.4 | 73.8 | 88.9 | ||
5113.448 |
1.44 | -0.815 | 30.9 | 36.4 | 98.3 | 5223.188 | 3.63 | -2.244 | 32.3 | 41.6 | 56.5 | 5452.860 | 3.84 | -1.420 | 19.0 | 29.1 | 37.3 | ||
5145.464 |
1.46 | -0.615 | 39.6 | 50.8 | 90.6 | 5225.525 | 0.11 | -4.577 | 83.2 | 92.7 | 128.8 | 5846.986 | 1.68 | -3.380 | 24.2 | 35.8 | 56.9 | ||
5147.479 |
0.00 | -1.973 | 43.7 | 66.8 | 102.7 | 5242.491 | 3.63 | -1.083 | 92.3 | 107.5 | 132.2 | 6176.807 | 4.09 | -0.315 | 61.2 | 86.8 | 90.1 | ||
5152.185 |
0.02 | -2.130 | 34.9 | 43.5 | 79.1 | 5243.773 | 4.26 | -0.947 | 69.6 | 84.3 | 91.5 | 6177.236 | 1.83 | -3.476 | 16.4 | 29.4 | 41.2 | ||
5211.206 |
0.84 | -2.063 | 9.3 | 13.7 | ... | 5250.216 | 0.12 | -4.668 | 78.1 | 96.1 | 136.0 | ||||||||
5219.700 |
0.02 | -2.264 | 28.9 | 39.0 | 82.9 | 5321.109 | 4.43 | -1.191 | 48.0 | 59.5 | 76.8 | Cu I | |||||||
5295.780 |
1.07 | -1.633 | 14.2 | 18.6 | 49.8 | 5332.908 | 1.56 | -2.751 | 102.8 | 118.6 | 139.8 | 5218.209 | 3.82 | 0.293 | 55.9 | 71.8 | 82.5 | ||
5426.236 |
0.02 | -2.903 | 9.0 | 12.1 | 48.2 | 5379.574 | 3.69 | -1.542 | 64.8 | 76.5 | 94.4 | 5220.086 | 3.82 | -0.630 | 15.5 | 25.0 | 32.5 | ||
5679.937 |
2.47 | -0.535 | 8.6 | 10.1 | 28.8 | 5389.486 | 4.41 | -0.533 | 87.3 | 102.2 | 123.0 | ||||||||
5866.452 |
1.07 | -0.842 | 49.6 | 64.8 | 107.5 | 5395.222 | 4.44 | -1.653 | 25.2 | 33.7 | 52.1 | Y II | |||||||
6098.694 |
3.06 | -0.095 | 6.9 | 10.1 | 27.6 | 5432.946 | 4.44 | -0.682 | 76.4 | 90.2 | 106.7 | 5087.426 | 1.08 | -0.329 | 49.3 | 53.7 | 54.2 | ||
6126.224 |
1.07 | -1.358 | 25.3 | 31.9 | 68.3 | 5491.845 | 4.19 | -2.209 | 14.3 | 25.4 | 32.9 | 5289.820 | 1.03 | -1.847 | 4.5 | 5.6 | 7.7 | ||
6258.104 |
1.44 | -0.410 | 54.2 | 65.5 | 102.5 | 5522.454 | 4.21 | -1.418 | 46.8 | 59.9 | 70.4 | 5402.780 | 1.84 | -0.510 | 14.7 | 22.2 | 22.1 | ||
| 5560.207 | 4.43 | -1.064 | 55.1 | 66.7 | 75.6 | ||||||||||||||
Ti II |
5577.013 | 5.03 | -1.415 | 14.5 | 20.3 | 26.3 | Ba II | ||||||||||||
5211.544 |
2.59 | -1.551 | 33.5 | 46.1 | 35.2 | 5661.348 | 4.28 | -1.802 | 25.5 | 33.6 | 48.6 | 5853.688 | 0.60 | -0.828 | 67.5 | 73.4 | 68.6 | ||
5336.783 |
1.58 | -1.592 | 76.7 | 90.0 | 89.7 | 5680.240 | 4.19 | -2.255 | 13.2 | 19.1 | 27.8 | 6141.727 | 0.70 | 0.244 | 124.4 | 127.4 | 140.1 | ||