A&A 482, 883-905 (2008)
DOI: 10.1051/0004-6361:20078467
P. Marigo1 - L. Girardi2 - A. Bressan2,3 - M. A. T. Groenewegen4 - L. Silva5 - G. L. Granato2
1 - Dipartimento di Astronomia, Università di Padova,
Vicolo dell'Osservatorio 2, 35122 Padova, Italy
2 -
Osservatorio Astronomico di Padova - INAF,
Vicolo dell'Osservatorio 5, 35122 Padova, Italy
3 -
INAOE, Luis Enrique Erro 1, 72840 Tonantzintla, Puebla, Mexico
4 -
Instituut voor Sterrenkunde, Katholieke Universiteit Leuven,
Celestijnenlaan 200 D, 3001 Leuven, Belgium
5 -
Osservatorio Astronomico di Trieste - INAF,
via Tiepolo 11, 34131 Trieste, Italy
Received 10 August 2007 / Accepted 29 January 2008
Abstract
We present a large set of theoretical isochrones, whose distinctive
features mostly reside on the greatly-improved treatment of the
thermally-pulsing asymptotic giant branch (TP-AGB) phase. Essentially,
we have coupled the TP-AGB tracks described in Paper I, at their
stages of pre-flash quiescent H-shell burning, with the evolutionary
tracks for the previous evolutionary phases from Girardi et al. (2000, A&AS, 141, 371). Theoretical isochrones for any intermediate value of age
and metallicity are then derived by interpolation in the grids. We
take care that the isochrones keep, to a good level of detail, the
several peculiarities present in these TP-AGB tracks -
e.g., the cool tails of C-type stars owing to the use of
proper molecular opacities as convective dredge-up occurs
along the TP-AGB; the bell-shaped
sequences in the Hertzsprung-Russell (HR) diagram for stars with
hot-bottom burning; the changes of pulsation mode between fundamental
and first overtone; the sudden changes of mean mass-loss rates as the
surface chemistry changes from M- to C-type; etc. Theoretical
isochrones are then converted to about 20 different photometric
systems - including traditional ground-based systems, and those of
recent major wide-field surveys such as SDSS, OGLE, DENIS, 2MASS,
UKIDSS, etc., - by means of synthetic photometry applied to an
updated library of stellar spectra, suitably extended to include
C-type stars. Finally, we correct the predicted photometry for the
effect of circumstellar dust during the mass-losing stages of
the AGB evolution, which allows us to improve the results for the
optical-to-infrared systems, and to simulate mid- and far-IR systems
such as those of Spitzer and AKARI. We illustrate the most striking
properties of these isochrones by means of basic comparisons with
observational data for the Milky Way disc and the Magellanic
Clouds. Access to the data is provided both via a web repository of
static tables (http://stev.oapd.inaf.it/dustyAGB07 and
CDS), and via an interactive web interface (http://stev.oapd.inaf.it/cmd), which provides tables for any intermediate value of age and metallicity, for several photometric
systems, and for different choices of dust properties.
Key words: astronomical data bases: miscellaneous - stars: AGB and post-AGB - stars: carbon - stars: evolution - galaxies: Magellanic Clouds - stars: Hertzsprung-Russell (HR) and C-M diagrams
Theoretical isochrones find a wide range of applications in modern astrophysics, going from the simple age-dating of star clusters, to more complex problems like the derivation of star formation histories of resolved galaxies, and, since Charlot & Bruzual (1991), the modelling of their spectrophotometric evolution across the Hubble time.
In fact, many different groups are publishing large grids of stellar isochrones, covering a wide enough range of stellar parameters (age, mass, metal content, alpha-enhancement, etc.) to become useful in the stellar population synthesis of galaxies. These isochrones normally comprehend a detailed description of all evolutionary phases, from the zero-age main sequence (ZAMS), up to either carbon ignition, or to the onset of the thermally-pulsing asymptotic giant branch phase (TP-AGB). The coverage of the TP-AGB evolution, however, has always been far from detailed and physically accurate, as we will illustrate below. The poor modelling of this phase greatly contrasts with its importance to the integrated light of stellar populations with ages from a few 108 yr up to the Hubble time. According to Frogel et al. (1990), the TP-AGB contribution to the total luminosity of single-burst stellar populations reaches a maximum of about 40 percent at ages from 1 to 3 Gyr, falling to less than 10 percent at 10 Gyr. Obviously, TP-AGB stars have a great impact on the rest-frame near-infrared spectra of galaxies. Moreover, TP-AGB stars account for most of the bright-infrared (IR) objects in resolved galaxies, as clearly demonstrated by DENIS, 2MASS, SAGE and S3MC data for the Magellanic Clouds (Cioni et al. 1999; Nikolaev & Weinberg 2000; Blum et al. 2006; Bolatto et al. 2007).
Table 1: Available stellar isochrones including the TP-AGB phase.
The situation regarding the TP-AGB phase in published sets of
isochrones is the following: Whereas early isochrones sets do not even
include the TP-AGB phase, more recent ones include it, but in a very
approximate way, ignoring crucial aspects of the TP-AGB evolution. A
summary table of available isochrones is provided
in Marigo (2007) and updated in Table 1 herewith. In short, Bertelli et al. (1994) and
Girardi et al. (2000, hereafter Gi00) adopt a very simple TP-AGB synthetic model that does not include the third dredge-up and the
over-luminosity above the core mass-luminosity relation caused by hot
bottom burning (HBB). A luminosity correction for stars undergoing HBB is instead included by Cordier et al. (2007), but in this case the
third dredge-up - together with its most remarkable consequence,
i.e. the formation of C stars - and the HBB nucleosynthesis are
completely missing. Marigo & Girardi (2001) present the first
isochrones based on tracks (Marigo et al. 1999) with the third
dredge-up included, and moreover, its efficiency is calibrated to reproduce
the C-star luminosity functions in both Magellanic Clouds
(MC)![]() . Another distinctive aspect of Marigo et al. (1999) tracks,
is that the HBB efficiency, together with the model effective
temperatures, are derived from numerical integrations of
the envelope structure.
. Another distinctive aspect of Marigo et al. (1999) tracks,
is that the HBB efficiency, together with the model effective
temperatures, are derived from numerical integrations of
the envelope structure.
Besides the above mentioned works, the literature abounds in descriptions of evolutionary population synthesis models which have included the complete TP-AGB evolution (e.g. Charlot & Bruzual 2003; Raimondo et al. 2005; Vázquez & Leitherer 2005; only to mention a few). However, in all these cases, critical processes of TP-AGB evolution - again the third dredge-up, HBB, or superwind-like mass loss - are missing in the models. In some cases (e.g. Vázquez & Leitherer 2005; Charlot & Bruzual 2003), the tracks for the TP-AGB and previous evolutionary phases come from different sources; this implies that basic stellar properties like the core mass and envelope chemical composition are discontinuous along the composite tracks. As demonstrated by Marigo & Girardi (2001), discontinuities in these quantities also produce an energetic inconsistency in the sense that they violate the strict coupling between stellar integrated light and chemical yields implied by the condition of energy conservation.
A few authors have computed isochrones aimed at modelling spectral evolution of galaxies, which consider the effect of circumstellar dust around AGB stars (Bressan et al. 1998; Mouhcine 2002; Piovan et al. 2003), but without improving the treatment of the underlying TP-AGB evolution, with respect to those already mentioned.
In all the previously-mentioned cases, moreover, the effect of
variable opacities along the TP-AGB evolution is completely ignored:
the basic stellar properties, and in particular, the effective
temperature
![]() ,
are derived using opacities valid for scaled-solar
compositions, which are highly inadequate to describe the
chemically-evolved envelopes of TP-AGB stars. The proper consideration of
variable opacities is now known to be crucial (see Marigo 2002; Marigo
et al. 2003a), especially for stars undergoing the transition to the
C-rich phase - i.e., comprising, for MC metallicities, all stars with
initial masses between about 1.5 and 3.5
,
are derived using opacities valid for scaled-solar
compositions, which are highly inadequate to describe the
chemically-evolved envelopes of TP-AGB stars. The proper consideration of
variable opacities is now known to be crucial (see Marigo 2002; Marigo
et al. 2003a), especially for stars undergoing the transition to the
C-rich phase - i.e., comprising, for MC metallicities, all stars with
initial masses between about 1.5 and 3.5 ![]() ,
and all isochrones
with ages between about 0.5 and 5 Gyr. This situation is partially
remedied by Cioni et al. (2006), who has made publicly available the
first isochrone sets in which variable molecular opacities were
considered along the TP-AGB evolution
,
and all isochrones
with ages between about 0.5 and 5 Gyr. This situation is partially
remedied by Cioni et al. (2006), who has made publicly available the
first isochrone sets in which variable molecular opacities were
considered along the TP-AGB evolution![]() . In fact, the C-star phase in these isochrones is
characterized by much lower temperatures (reaching
. In fact, the C-star phase in these isochrones is
characterized by much lower temperatures (reaching
![]() as low as 2300 K) than previously published isochrones.
Those specific TP-AGB models, however, preceded the extensive calibration of dredge-up
efficiency performed in Marigo & Girardi (2007, hereafter
Paper I). In this latter work, the dredge up-parameters are
tuned so that the models reproduce the observed C-star luminosity
functions in the Magellanic Clouds, and the TP-AGB lifetimes of M and
C stars in Magellanic Cloud star clusters (Girardi & Marigo 2007a).
as low as 2300 K) than previously published isochrones.
Those specific TP-AGB models, however, preceded the extensive calibration of dredge-up
efficiency performed in Marigo & Girardi (2007, hereafter
Paper I). In this latter work, the dredge up-parameters are
tuned so that the models reproduce the observed C-star luminosity
functions in the Magellanic Clouds, and the TP-AGB lifetimes of M and
C stars in Magellanic Cloud star clusters (Girardi & Marigo 2007a).
The goal of the present paper is to remedy this highly unsatisfactory situation, providing the first set of isochrones in which the TP-AGB evolution is treated with a satisfactory level of completeness and detail - i.e. considering the crucial effects of third dredge-up, hot bottom burning, and variable molecular opacities - and calibrated at the same time, i.e., able to reproduce the basic observables of AGB stars in the MCs. Moreover, we wish to provide these results in many photometric systems and including the reprocessing of radiation by circumstellar dust in mass-losing stars, which is crucial for modelling of infrared photometry.
The properties of our stellar evolutionary tracks are briefly recalled in Sect. 2, which discusses the basic aspects of constructing isochrones with the new TP-AGB tracks of Paper I - including new variables like the C/O ratio, pulsation periods, pulsation modes, etc. Section 3 deals with the transformation of the isochrones to many photometric systems, which require updating and extending the libraries of stellar spectra previously in use. The inclusion of dust reprocessing in the predicted photometry is illustrated in Sect. 4. A preliminary comparison with observational data is done in Sect. 5. Section 6 describes how to access the data tables - containing isochrones, bolometric corrections, dust attenuation curves, integrated magnitudes of single-burst populations, etc. - and summarizes both the main novelties and caveats of our new isochrones.
The evolutionary tracks used in this work have already been thoroughly
presented in previous papers. The evolution from the ZAMS up to the
first thermal pulse on the AGB is taken from Gi00 for the initial
metallicities Z=0.0004, 0.001, 0.004, 0.008, 0.019 (the
solar value), 0.03, and from Girardi (2001, unpublished; see http://pleiadi.oapd.inaf.it) for Z=0.0001. The range of initial
masses of these tracks goes from
![]() to 7
to 7 ![]() ,
out of which
all models between
,
out of which
all models between
![]() and 5
and 5 ![]() are considered to
undergo the TP-AGB phase.
are considered to
undergo the TP-AGB phase.
The TP-AGB phase is then computed via a synthetic code as described in
Paper I, starting from the physical conditions at the first thermal
pulse, and up to the complete loss of the envelope via
stellar winds. The model takes into account many critical aspects of the
TP-AGB evolution, suh as the third dredge-up events; HBB over-luminosity
and nucleosynthesis; pulse cycle luminosity and
![]() variations;
opacity variations driven by the changing chemical composition in the
envelope; long-period variability (LPV) in both first overtone and
fundamental modes; and their modulation of the mass-loss rates
variations;
opacity variations driven by the changing chemical composition in the
envelope; long-period variability (LPV) in both first overtone and
fundamental modes; and their modulation of the mass-loss rates ![]() via changes in the pulsation period P.
via changes in the pulsation period P.
Especially relevant for this paper are the formalisms
adopted for the mass loss: besides affecting the AGB lifetimes, high mass-loss rates determine the formation of circumstellar dust and hence the obscuration of AGB stars in the
optical and their brightening in the mid- and far-IR (see
Sect. 4). As detailed in Paper I, for O-rich AGB stars we
use the results of dynamical atmospheres including dust for
long-period variables calculated by Bowen (1988) and Bowen & Willson
(1991), taking into account whether pulsation occurs on the first
overtone or on the fundamental mode. For C-rich stars, we assume two
different regimes of mass loss: initially stars follow the
semi-empirical relation from Schröder et al. (2003), then switching,
above a critical luminosity, to the ![]() values derived from the
pulsating dust-driven wind models by Winters et al. (2000, 2003). In
both cases, mass-loss rates depend on the pulsation period, which is
predicted along the evolutionary tracks according to the
period-mass-radius relations derived
by Ostlie & Cox (1986), Fox & Wood (1982), Wood et al. (1983).
values derived from the
pulsating dust-driven wind models by Winters et al. (2000, 2003). In
both cases, mass-loss rates depend on the pulsation period, which is
predicted along the evolutionary tracks according to the
period-mass-radius relations derived
by Ostlie & Cox (1986), Fox & Wood (1982), Wood et al. (1983).
We replace the most massive TP-AGB tracks (
![]()
![]() )
of
Paper I by new calculations, accounting for a better description of the
transition luminosity between the first-overtone and the fundamental-mode
pulsation. This aspect is thoroughly described in the Appendix.
)
of
Paper I by new calculations, accounting for a better description of the
transition luminosity between the first-overtone and the fundamental-mode
pulsation. This aspect is thoroughly described in the Appendix.
The synthetic TP-AGB evolution of Paper I has been followed up to
the complete ejection of the stellar envelopes, hence including
a good fraction of the post-AGB phase prior to the planetary nebula
regime, i.e. the fast terminal stages
during which the star evolves at almost constant luminosity,
while
![]() rapidly increases due to the combined effect
of the outward displacement of the H-burning shell, and stripping of the residual
envelope by stellar winds. These final parts
of the tracks may not be reliable since some relations used in
the synthetic TP-AGB code become inaccurate. Moreover, the mass-loss
rates are critical in determining the duration of this post-AGB transition phase, but the rates are still poorly known.
rapidly increases due to the combined effect
of the outward displacement of the H-burning shell, and stripping of the residual
envelope by stellar winds. These final parts
of the tracks may not be reliable since some relations used in
the synthetic TP-AGB code become inaccurate. Moreover, the mass-loss
rates are critical in determining the duration of this post-AGB transition phase, but the rates are still poorly known.
Anyway, this transition phase turns out to be
very short-lived (![]() 104 yr for low-mass stars, and even shorter
for intermediate-mass ones) if compared to the previous TP-AGB evolution. Therefore, although we mostly include this post-AGB phase in the new isochrones, its overall impact on them is
almost negligible.
104 yr for low-mass stars, and even shorter
for intermediate-mass ones) if compared to the previous TP-AGB evolution. Therefore, although we mostly include this post-AGB phase in the new isochrones, its overall impact on them is
almost negligible.
Another important detail is that before building the isochrones,
TP-AGB tracks are ``cleaned'' of their luminosity and
![]() variations caused by thermal pulse cycles. We only keep the stages of
quiescent H-shell burning previous to He-shell flashes, along with the
stage of coolest
variations caused by thermal pulse cycles. We only keep the stages of
quiescent H-shell burning previous to He-shell flashes, along with the
stage of coolest
![]() ,
are kept for the isochrone
interpolation. This is a necessary approximation since the large
luminosity and
,
are kept for the isochrone
interpolation. This is a necessary approximation since the large
luminosity and
![]() variations between confining tracks would lead
to wild variations in the interpolated isochrones. Anyway,
we can easily introduce the
detailed evolution of luminosity and
variations between confining tracks would lead
to wild variations in the interpolated isochrones. Anyway,
we can easily introduce the
detailed evolution of luminosity and
![]() over the
thermal pulse cycles in the tabulated isochrones a posteriori,
since the shape of thermal pulse cycles is a
known function of other quantities that are also interpolated and
stored along the isochrones, like the core mass and surface chemical
composition (see, e.g., Wagenhuber & Groenewegen 1998).
over the
thermal pulse cycles in the tabulated isochrones a posteriori,
since the shape of thermal pulse cycles is a
known function of other quantities that are also interpolated and
stored along the isochrones, like the core mass and surface chemical
composition (see, e.g., Wagenhuber & Groenewegen 1998).
The Gi00 and Paper I sets of evolutionary tracks differ in their
source of low-temperature (![]() K) opacities: while Gi00 uses
tables for scaled-solar chemical compositions taken from Alexander &
Ferguson (1994), in Paper I the opacities are computed ``on-the-fly''
with the proper chemical mixture of the evolving TP-AGB envelopes, by
means of the methods and approximations described in Marigo (2002).
There is no dramatic change in opacities, however, in passing from the
scaled-solar tables of Alexander & Ferguson (1994) to Marigo's (2002)
formalism, provided that the passage occurs at C/O ratios much smaller
than 1, as indeed is the case at the first thermal pulse of all TP-AGB tracks. The molecular opacities depart from those in Alexander &
Ferguson (1994) only later in the TP-AGB evolution, when the third
dredge-up sets in and the C/O ratio increases above 1. Therefore, the
concatenation of both sets of tracks at the stage of first thermal
pulse produces only modest discontinuities in the tracks, i.e. small
jumps in
K) opacities: while Gi00 uses
tables for scaled-solar chemical compositions taken from Alexander &
Ferguson (1994), in Paper I the opacities are computed ``on-the-fly''
with the proper chemical mixture of the evolving TP-AGB envelopes, by
means of the methods and approximations described in Marigo (2002).
There is no dramatic change in opacities, however, in passing from the
scaled-solar tables of Alexander & Ferguson (1994) to Marigo's (2002)
formalism, provided that the passage occurs at C/O ratios much smaller
than 1, as indeed is the case at the first thermal pulse of all TP-AGB tracks. The molecular opacities depart from those in Alexander &
Ferguson (1994) only later in the TP-AGB evolution, when the third
dredge-up sets in and the C/O ratio increases above 1. Therefore, the
concatenation of both sets of tracks at the stage of first thermal
pulse produces only modest discontinuities in the tracks, i.e. small
jumps in
![]() that are caused by the small differences in opacities
for O-rich mixtures
that are caused by the small differences in opacities
for O-rich mixtures![]() . For other quantities,
like the luminosity, core mass, and surface chemical composition, the
inspection of isochrones does not reveal any discontinuity.
. For other quantities,
like the luminosity, core mass, and surface chemical composition, the
inspection of isochrones does not reveal any discontinuity.
Although the reader may feel uncomfortable with the small
discontinuities in
![]() at the stage of first thermal pulse in the
isochrones, we remark that they are dramatically less important
than any discontinuity that one may find when amalgamating tracks from
completely different sources. The simple fact that the core mass and
envelope chemical composition vary in a smooth and continuous way, for
instance, ensures that the total emitted light derived from a given
set of isochrones will be fully consistent with the chemical yields
and total remnant masses derived from the same sets of tracks. As
illustrated by Marigo & Girardi (2001), this is an important,
although largely ignored, consistency requirement to evolutionary
population synthesis models of galaxies.
at the stage of first thermal pulse in the
isochrones, we remark that they are dramatically less important
than any discontinuity that one may find when amalgamating tracks from
completely different sources. The simple fact that the core mass and
envelope chemical composition vary in a smooth and continuous way, for
instance, ensures that the total emitted light derived from a given
set of isochrones will be fully consistent with the chemical yields
and total remnant masses derived from the same sets of tracks. As
illustrated by Marigo & Girardi (2001), this is an important,
although largely ignored, consistency requirement to evolutionary
population synthesis models of galaxies.
Theoretical isochrones are built via simple linear interpolations inside the grids of evolutionary tracks, performed between ``equivalent evolutionary points''. The final isochrone, for a given age t, is made of a sample of such points conveniently distributed on the HR diagram. For each point, several stellar parameters are stored. In fact, the newest TP-AGB tracks take into account various aspects of evolution that have been ignored while making the Gi00 isochrones, but that are essential components of the TP-AGB models of Paper I, namely: surface chemical composition (especially the C/O ratio), stellar core and envelope mass, mass-loss rates, pulsation modes and periods. These parameters can, for instance, allow easy identification of C-type and dust-obscured stars, and are essential to the simulation of variations in stellar properties due to thermal pulse cycles and long-period variability. Therefore, our isochrone-making routines have been extended to take explicit care of these properties.
When an isochrone is built out of our tabulated tracks,
mass loss and LPV pulsation are taken into detailed
account only after the transition from the early-AGB to the TP-AGB
regime. Variables, such as mass-loss rates, pulsation periods, and
circumstellar dust emission, pass from ``non-defined'' to
well-defined values, corresponding to the occurrence of
the first thermal pulse. In order to avoid
discontinuities in these variables, we have a posteriori evaluated the
mass-loss rates and pulsation properties of stars in earlier phases,
even if these have been computed at constant mass.
The procedure is straightforward: for each star in the pre-TP-AGB section of the isochrones, the basic stellar properties (L,
![]() ,
,
![]() )
are used to determine pulsation periods and mass-loss rates in the same way as for O-rich AGB stars. Notice that in most cases mass
loss prior to the TP-AGB phase is expected to be very modest and not
have evolutionary implications, so that this procedure is well
justified. The only exception is for low-mass models close to the tip
of the red giant branch (TRGB), where the use of Reimers (1975)
mass-loss formula with a multiplicative factor of
)
are used to determine pulsation periods and mass-loss rates in the same way as for O-rich AGB stars. Notice that in most cases mass
loss prior to the TP-AGB phase is expected to be very modest and not
have evolutionary implications, so that this procedure is well
justified. The only exception is for low-mass models close to the tip
of the red giant branch (TRGB), where the use of Reimers (1975)
mass-loss formula with a multiplicative factor of ![]() ,
leads to
the loss of
,
leads to
the loss of
![]()
![]() for low-mass
stars
for low-mass
stars![]() . This amount of mass lost is necessary to explain the HB morphologies observed in galactic globular clusters (see Renzini & Fusi Pecci 1988). The use of the Reimers mass-loss formula for the RGB is seen as a ``conservative choice'' since,
although alternative formulas exist (see Catelan 2000, 2007),
currently none can be clearly favoured over the others.
We take the RGB mass loss into consideration during the construction of stellar isochrones
by simply jumping from a TRGB track of given mass M to a ZAHB track
of mass
. This amount of mass lost is necessary to explain the HB morphologies observed in galactic globular clusters (see Renzini & Fusi Pecci 1988). The use of the Reimers mass-loss formula for the RGB is seen as a ``conservative choice'' since,
although alternative formulas exist (see Catelan 2000, 2007),
currently none can be clearly favoured over the others.
We take the RGB mass loss into consideration during the construction of stellar isochrones
by simply jumping from a TRGB track of given mass M to a ZAHB track
of mass
![]() .
The procedure is somewhat detailed in
Bertelli et al. (1994) and in Gi00.
.
The procedure is somewhat detailed in
Bertelli et al. (1994) and in Gi00.
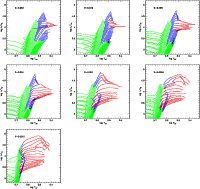 |
Figure 1:
Isochrones in the H-R diagram, zooming in the region of the AGB for the 7 metallicity values of the original tracks. The isochrones are plotted with ages
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{8467f2a.ps}\hspace*{3.5mm}...
...2b.ps}\hspace*{3.5mm}
\includegraphics[width=5.8cm,clip]{8467f2c.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg40.gif) |
Figure 2: The same as in Fig. 1, but for a sequence that illustrates the evolution of the TP-AGB phase since the release of Gi00 isochrones. From left to right, isochrones are from Gi00, Marigo & Girardi (2001), and Cioni et al. (2006). This sequence would be completed with the third panel of Fig. 1. |
| Open with DEXTER | |
Extended sets of isochrones are depicted in the HR diagrams of Fig. 1. Since the main novelty of the present paper is in the detailed description of the TP-AGB phase, the HR diagrams are zoomed on this phase. In other parts of the HR, isochrones are simply identical to those previously computed by Gi00.
It is evident from the figure that our new isochrones reflect all of the peculiar behaviours of the TP-AGB tracks they derive from (see Fig. 20 in Paper I). In particular, we notice the following:
These stars usually have C/O < 1, although a late transition to the C-rich phase may take place due to final dredge-up events when HBB has already ceased (see Frost et al. 1998) in agreement with observations (e.g. van Loon et al. 1998, 1999).
The C-star phase is completely developed in isochrones of intermediate
ages, and it happens at very low
![]() (reaching
(reaching
![]() K), in a sort of ``red tail'' which is neatly separated from the
sequences of O-rich stars. This separation naturally results from
the very different low-temperature opacities of C-rich envelopes
(Marigo 2002).
K), in a sort of ``red tail'' which is neatly separated from the
sequences of O-rich stars. This separation naturally results from
the very different low-temperature opacities of C-rich envelopes
(Marigo 2002).
In the oldest isochrones, dredge-up is not operating and the TP-AGB sections of the isochrones simply align above the previous early-AGB phase. They steadily increase in luminosity and slightly bend to the left at their upper end, as a result of the progressive thinning of stellar envelopes.
A more detailed discussion of the above-mentioned behaviors is presented in Paper I.
In order to better illustrate the peculiarities of the TP-AGB models presently available, Fig. 2 presents a series of Z=0.008 isochrones derived from Gi00 tracks connected with different extensions of the TP-AGB phase. In the first isochrones (Gi00), the TP-AGB phase is simplified and merely extends the previous evolution straight above the RGB and early-AGB phases, without any C-star sequence and without any signature of HBB. Then, the Marigo & Girardi (2001) isochrones introduce dredge-up and HBB in the TP-AGB, and present a well-defined C-star region, which is still aligned on top of the RGB and early-AGB, as expected from models with opacities for scaled-solar compositions. Cioni et al. (2006) introduce variable molecular opacities and then the C-star sequence clearly changes its shape on the HR diagram (as explained by Marigo 2002). Finally, the sequence of Fig. 2 could be completed with the third panel of Fig. 1, which represents the present state of the Z=0.008 isochrones, differing from the Cioni et al. (2006) in that the C-star luminosities and lifetimes are now calibrated (see Paper I).
The new isochrones are transformed to several photometric systems, following the formalism described in Girardi et al. (2002) to derive bolometric corrections from a library of stellar spectra. Although this argument will be more thoroughly discussed in a forthcoming paper (Girardi et al. 2007, in preparation), it is worth recalling the main steps we follow to deal with the novelties of the present release.
Given the spectral flux at the stellar surface, ![]() ,
bolometric corrections for any set of filter transmission curves
,
bolometric corrections for any set of filter transmission curves ![]() are given by (see Girardi et al. 2002, for details):
are given by (see Girardi et al. 2002, for details):
Notice that Eq. (1) uses photon count integration instead of energy integration, as adequate to most modern photometric systems which use photon-counting devices instead of energy-amplifiers.
The equation also includes the interstellar extinction curve ![]() ,
which we set to
,
which we set to
![]() .
For the optical and near-IR, we provide the extinction coefficients
.
For the optical and near-IR, we provide the extinction coefficients
![]() as computed for a yellow dwarf of solar metallicity (the Sun) using the
Cardelli et al. (1989)
as computed for a yellow dwarf of solar metallicity (the Sun) using the
Cardelli et al. (1989)
![]() extinction curve. The small
variations of such coefficients with spectral type and extinction (see
Grebel & Roberts 1995) will be discussed in a separate paper (Girardi
et al., in prep.) that will detail the transformations to WFPC2 and
ACS systems, and describe a way to include consistently the
interstellar extinction into the isochrones.
extinction curve. The small
variations of such coefficients with spectral type and extinction (see
Grebel & Roberts 1995) will be discussed in a separate paper (Girardi
et al., in prep.) that will detail the transformations to WFPC2 and
ACS systems, and describe a way to include consistently the
interstellar extinction into the isochrones.
Girardi et al. (2002) describes the assembly of a large library of
spectral fluxes, covering wide ranges of initial metallicities ([M/H],
from -2.5 to +0.5),
![]() (from 600 to 50 000 K), and
(from 600 to 50 000 K), and ![]() (from -2 to 5)
(from -2 to 5)![]() . This grid is wide enough to include most
of the spectral types that constitute the bulk of observed samples. It
is composed of ATLAS9 ``NOVER'' spectra from Castelli et al. (1997;
see also Bessell et al. 1998) for most of the stellar types; Allard et al. (2000; see also Chabrier et al. 2000) for M, L, and T dwarfs
. This grid is wide enough to include most
of the spectral types that constitute the bulk of observed samples. It
is composed of ATLAS9 ``NOVER'' spectra from Castelli et al. (1997;
see also Bessell et al. 1998) for most of the stellar types; Allard et al. (2000; see also Chabrier et al. 2000) for M, L, and T dwarfs![]() ; Fluks et al. (1994) empirical spectra for M giants; and,
finally, pure black-body spectra for stars exceeding 50 000 K.
; Fluks et al. (1994) empirical spectra for M giants; and,
finally, pure black-body spectra for stars exceeding 50 000 K.
Since then this library been revised. We have replaced the ATLAS9
spectra by the newest ``ODFNEW'' ones from Castelli & Kurucz (2003),
which incorporate several corrections to the atomic and molecular
data, especially regarding the molecular line lists of CN, OH, SiO,
H2O and TiO, and the inclusion of H I-H+ and H I-H+
quasi-molecular absorption in the UV. These new models are
considerably better than previous ones in the UV region of the
spectrum, and over most of the wavelength range for
![]() between
between
![]() 4500 and 3500 K (see Figs. 1 to 3 in Castelli & Kurucz 2003).
4500 and 3500 K (see Figs. 1 to 3 in Castelli & Kurucz 2003).
Moreover, the library has been extended with the Loidl et al. (2001)
synthetic C-star spectra for
![]() ,
derived
from hydrostatic model atmospheres computed with MARCS (see also
Höfner et al. 2003, for more details). For C-stars cooler than
2600 K, we simply adopt the BC values derived from 2600 K
spectra. These Loidl et al. (2001) spectra are computed for C/O = 1.1
for all
,
derived
from hydrostatic model atmospheres computed with MARCS (see also
Höfner et al. 2003, for more details). For C-stars cooler than
2600 K, we simply adopt the BC values derived from 2600 K
spectra. These Loidl et al. (2001) spectra are computed for C/O = 1.1
for all
![]() ,
and for both C/O = 1.1 and 1.4 for
,
and for both C/O = 1.1 and 1.4 for
![]() K. We
have verified that bolometric corrections for all broadbands redder
than V are quite insensitive to the C/O ratio, varying by less than
0.1 mag between the C/O = 1.1 and 1.4 cases. These differences become
K. We
have verified that bolometric corrections for all broadbands redder
than V are quite insensitive to the C/O ratio, varying by less than
0.1 mag between the C/O = 1.1 and 1.4 cases. These differences become
![]() 0.01 mag in the J-band. For the bluest optical pass-bands
the choice between these two C/O values causes significant differences
in the bolometric corrections, amounting for instance to
0.01 mag in the J-band. For the bluest optical pass-bands
the choice between these two C/O values causes significant differences
in the bolometric corrections, amounting for instance to ![]() 0.4 mag in
B. The
0.4 mag in
B. The
![]() K C-stars are much fainter (more than
4 mag in a Vega system) at these blue wavelengths than at the
I-band, and therefore these cases are of little practical
interest. Hence, we adopt by default the C/O = 1.1 C-star spectra, for
all
K C-stars are much fainter (more than
4 mag in a Vega system) at these blue wavelengths than at the
I-band, and therefore these cases are of little practical
interest. Hence, we adopt by default the C/O = 1.1 C-star spectra, for
all
![]() .
We will folllow a more elaborate approach when spectra
for a wider range of C/O values become available (Aringer et al., in preparation).
.
We will folllow a more elaborate approach when spectra
for a wider range of C/O values become available (Aringer et al., in preparation).
Finally, as part of the TRILEGAL project (Girardi et al. 2005), we
have included spectra for DA white dwarfs from Finley et al. (1997)
and Homeier et al. (1998) for
![]() between 100 000 and 5000 K,
and
between 100 000 and 5000 K,
and ![]() between 7 and 9.
between 7 and 9.
The Castelli & Kurucz (2003) and Allard et al. (2000) tabulated
spectra extend well into the far-IR, until 160 and 971 ![]() m
respectively. In the other cases, the available spectra were only tabulated
to the mid-IR, namely until 12.5
m
respectively. In the other cases, the available spectra were only tabulated
to the mid-IR, namely until 12.5 ![]() m for Fluks et al. (1994) and 2.5
m for Fluks et al. (1994) and 2.5 ![]() m for Loidl et al. (2001). In all cases, we have extended the flux to the very far-IR with a scaled
Rayleigh-Jeans law starting from the point of maximum tabulated
m for Loidl et al. (2001). In all cases, we have extended the flux to the very far-IR with a scaled
Rayleigh-Jeans law starting from the point of maximum tabulated
![]() .
This is clearly a crude approximation. For instance,
van der Bliek et al. (1996) find that blackbody fluxes in the far-IR
present discrepancies of the order of 20 per cent with respect to the
solar flux. Decin & Eriksson (2007) recently discussed in detail the status of
the predicted spectral energy distributions in the IR. In light of their
results, our predicted BC for the mid- and far-IR will be uncertain
by up to a few tenths of a magnitude for the coolest M and C stars. However, we expect that the errors in colours will be somewhat smaller, and they will become irrelevant in stars with
significant mass-loss, which are exactly those with the most
prominent fluxes in the mid- and far-IR. In fact, in these cases, the
emission at mid- and far-IR wavelengths is dominated by the circumstellar dust
shells and not by the stellar photosphere (see Sect. 4).
.
This is clearly a crude approximation. For instance,
van der Bliek et al. (1996) find that blackbody fluxes in the far-IR
present discrepancies of the order of 20 per cent with respect to the
solar flux. Decin & Eriksson (2007) recently discussed in detail the status of
the predicted spectral energy distributions in the IR. In light of their
results, our predicted BC for the mid- and far-IR will be uncertain
by up to a few tenths of a magnitude for the coolest M and C stars. However, we expect that the errors in colours will be somewhat smaller, and they will become irrelevant in stars with
significant mass-loss, which are exactly those with the most
prominent fluxes in the mid- and far-IR. In fact, in these cases, the
emission at mid- and far-IR wavelengths is dominated by the circumstellar dust
shells and not by the stellar photosphere (see Sect. 4).
Table 2 presents all the photometric systems we have considered so far. They include several traditional ground-based photometric systems (Johnson-Cousins-Glass, Strömgren-Crawford, Washington, BATC), systems belonging to some influential wide-field surveys (DENIS, 2MASS, OGLE-II, SDSS) and cameras (WFI, UKIDSS), and then to some of the most successful satellite-based cameras of the recent past (Tycho, ACS) or still in operation (WFPC2, NICMOS, Spitzer, AKARI). Other systems are presently being added to the list.
Note that the transformations to some of these photometric systems are described in other papers (e.g., Girardi et al. 2007, for WFPC2 and ACS; Vanhollebeke et al. 2007, for OGLE-II); they are listed in Table 2, and no further detail on these systems will be provided here. All systems in the Table are already available at the web interface (see Sect. 6.1).
Table 2: Photometric systems for which our new isochrones are made available (updated to November 2007).
Circumstellar dust reprocesses a substantial fraction of the photons
emitted by the coolest evolved stars. Since, on one hand, the efficiency
of dust extinction decreases quickly above ![]()
![]() m and, on the
other hand, dust does not survive at temperatures above 1000-2000 K,
the general effect of the presence of dust in an astrophysical source
is to shift part of the intrinsic emitted power from the
optical-ultraviolet to the mid- and far-infrared region.
m and, on the
other hand, dust does not survive at temperatures above 1000-2000 K,
the general effect of the presence of dust in an astrophysical source
is to shift part of the intrinsic emitted power from the
optical-ultraviolet to the mid- and far-infrared region.
A serious difficulty in taking into account in detail the effects of dust is that the optical properties (i.e., the efficiency of absorption and scattering as a function of wavelength) differ significantly in different environments. This is particularly true for the envelopes of AGB stars, which are believed to be one of the two main producers of interstellar grains, the other being the supernovae blast waves (e.g., Dwek 1998; Todini & Ferrara 2001; Morgan & Edmunds 2003; Calura et al. 2007). As for the dust composition, the general wisdom is that the envelopes of C-type stars are composed of carbonaceous grains while those of M-type stars are dominated by silicates, however several recent detailed studies, mainly based on Spitzer data (e.g., Lebzelter et al. 2006; Verhoelst et al. 2006) and in more detailed modelling (e.g., Ireland & Scholz 2006; Woitke 2006; Ferrarotti & Gail 2006) demonstrated that the situation may be more complex. Moreover, the grain size distribution, which together with the composition determines the optical properties, is expected to be significantly different from that inferred in the general interstellar medium.
A further big difficulty in the understanding of AGB envelopes is
the occurrence of strong mass loss and the possible relation with
the type of dust that can condensate in their outflows. The massive
winds in AGB stars are commonly ascribed to the coupled effect between
large amplitude pulsations and radiation pressure on dust
grains. According to detailed dynamical studies, in C-rich stars the
radiation pressure on dust can in fact be strong enough to explain the
observed outflows (see e.g., Winters et al. 2000; Höfner et al. 2003). Instead in O-rich stars the possible type of grains are
either not stable or opaque enough near ![]()
![]() m to explain the
outflows (e.g., Ireland & Scholz 2006; Woitke 2006).
m to explain the
outflows (e.g., Ireland & Scholz 2006; Woitke 2006).
Furthermore, recent spectroscopic analyses of oxygen-rich AGB stars based on ISO data for the LMC (Dijkstra et al. 2005) and the Galactic Bulge (Blommaert et al. 2006) have shown a clear correlation
between the dust composition and the mass-loss rates. For instance,
the dust features displayed by oxygen-rich stars are mainly ascribed
to Al2O3 for low ![]() ,
while going to higher
,
while going to higher ![]() they
are interpreted with an increasing amount of silicates. These findings
are consistent with the latest results from Spitzer data of AGB stars
belonging to the globular cluster 47 Tuc (Lebzelter et al. 2006). The
dust mineralogy actually changes as the star evolves at increasing
luminosities and pulsation periods. On the other hand, for C stars
unveiling the dust-condensation sequence is more problematic due to
its complex dependence on a number of factors (Speck et al. 2006;
Thompson et al. 2006).
they
are interpreted with an increasing amount of silicates. These findings
are consistent with the latest results from Spitzer data of AGB stars
belonging to the globular cluster 47 Tuc (Lebzelter et al. 2006). The
dust mineralogy actually changes as the star evolves at increasing
luminosities and pulsation periods. On the other hand, for C stars
unveiling the dust-condensation sequence is more problematic due to
its complex dependence on a number of factors (Speck et al. 2006;
Thompson et al. 2006).
What emerges is that, despite conspicuous progress in both observational and theoretical grounds, the issue of dust formation and evolution in AGB stars is still affected by large uncertainties. For these reasons in this paper we will explore a few kinds of circumstellar dust, essentially following the prescriptions by Groenewegen (2006, G06) and Bressan et al. (1998, B98). Alternative and more complex descriptions will be examined in subsequent papers.
This section outlines the adopted procedure to include the effect
of dust in our isochrones.
In general, for a given star of
![]() ,
losing
mass at a rate
,
losing
mass at a rate ![]() ,
with dust expansion velocity
,
with dust expansion velocity
![]() and dust-to-gas ratio
and dust-to-gas ratio ![]() ,
radiation transfer (RT) calculations
provide the dust optical depth
,
radiation transfer (RT) calculations
provide the dust optical depth ![]() and its corresponding
attenuation/emission spectrum. The optical depth
and its corresponding
attenuation/emission spectrum. The optical depth ![]() scales with
the other quantities via the approximated relation
scales with
the other quantities via the approximated relation
For convenience, we have pre-computed a number of reference R models
parametrized as a function of a basic set of parameters, namely:
![]() ,
,
![]() ,
L, dust condensation temperature
,
L, dust condensation temperature ![]() ,
and for different dust mixtures, as specified in Sects. 4.4.1 and 4.4.2
for G06 and B98 models, respectively. Then, each star along the isochrone is assigned its proper dusty envelope by using Eq. (4), with the corresponding values of
,
and for different dust mixtures, as specified in Sects. 4.4.1 and 4.4.2
for G06 and B98 models, respectively. Then, each star along the isochrone is assigned its proper dusty envelope by using Eq. (4), with the corresponding values of
![]() ,
,
![]() ,
,
![]() ,
L,
,
L,
![]() ,
and
,
and ![]() .
.
Each determination of
![]() corresponds to specific dust
attenuation and emission functions, which in turn fix the ratio
between the flux derived from RT calculations
and the dust-free intrinsic flux, i.e.,
corresponds to specific dust
attenuation and emission functions, which in turn fix the ratio
between the flux derived from RT calculations
and the dust-free intrinsic flux, i.e.,
![]() .
Finally, bolometric corrections are derived, i.e.
.
Finally, bolometric corrections are derived, i.e.
![]() .
.
In summary, for each AGB star along the isochrone, the general scheme proceeds through the following steps:
The wind terminal velocity or expansion velocity,
![]() ,
is calculated according to the formalism presented by Elitzur
& Ivezic (2001), to which the reader should refer for the
details of the underlying theoretical analysis. In brief, following
Elitzur & Ivezic (2001) the dust-wind problem is solved by means of
a suitable scaling approach, so as it is possible to express
,
is calculated according to the formalism presented by Elitzur
& Ivezic (2001), to which the reader should refer for the
details of the underlying theoretical analysis. In brief, following
Elitzur & Ivezic (2001) the dust-wind problem is solved by means of
a suitable scaling approach, so as it is possible to express
![]() as a function of mass-loss rate, stellar luminosity, and
various dust parameters (dust-to-gas ratio, chemical composition,
condensation temperature, etc.) in the form,
as a function of mass-loss rate, stellar luminosity, and
various dust parameters (dust-to-gas ratio, chemical composition,
condensation temperature, etc.) in the form,
The dependence of
![]() on the dust-to-gas ratio is included
in the definition of the parameters A and B (through the quantity
on the dust-to-gas ratio is included
in the definition of the parameters A and B (through the quantity
![]() ,
see below):
,
see below):
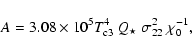 |
(6) |
![\begin{displaymath}%
B=\left[2.28\frac{Q_{\star}^{1/2}~\chi_{0}^{1/4}}{Q_V^{3/4}~
\sigma_{22}^{1/2}~T_{\rm c3}}\right]^{-4/3}
\end{displaymath}](/articles/aa/full/2008/18/aa8467-07/img104.gif) |
(7) |
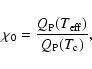 |
(8) |
We define
![]() ,
where
,
where
![]() (in cm2) is the dust cross-sectional area per gas particle
at condensation
(in cm2) is the dust cross-sectional area per gas particle
at condensation
The dust-to-gas mass ratio is defined as
Assuming that the dust grains have a specific density
![]() (in g cm-3),
the explicit form of the dust density reads
(in g cm-3),
the explicit form of the dust density reads
Finally, inserting Eqs. (11) and (12) into
Eq. (10), we can re-write Eq. (9) to show
the dependence on the dust-to-gas ratio
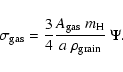 |
(13) |
Moreover, given the dust chemical type (either amorphous carbon or
silicates) in Elitzur & Ivezic (2001) the quantities ![]() and
and ![]() are assigned fixed values corresponding to a
particular choice of the dust condensation temperature (
are assigned fixed values corresponding to a
particular choice of the dust condensation temperature (
![]() K) and the stellar effective temperature (
K) and the stellar effective temperature (
![]() K). We have carried out additional runs of DUSTY (Ivezic et al. 1999) to evaluate
K). We have carried out additional runs of DUSTY (Ivezic et al. 1999) to evaluate ![]() and
and ![]() for various values of
for various values of ![]() and
and
![]() ,
and for different dust
compositions. The results are presented in Table 3
and are used in our calculations, by interpolating in
,
and for different dust
compositions. The results are presented in Table 3
and are used in our calculations, by interpolating in
![]() and
and ![]() and allowing for different dust mixtures. In the
present paper, we adopt
and allowing for different dust mixtures. In the
present paper, we adopt
![]() K when C/O < 1 and
K when C/O < 1 and
![]() K when C/O > 1. The grain size is set
K when C/O > 1. The grain size is set ![]() m in all cases.
The other input parameters, i.e.,
effective temperature and dust chemical type, are just those
predicted by our stellar isochrones.
m in all cases.
The other input parameters, i.e.,
effective temperature and dust chemical type, are just those
predicted by our stellar isochrones.
It should be also mentioned that Eq.( 5) is valid as long
as dust condensation is efficient enough to drive an
outflow. As discussed in Elitzur & Ivezic (2001)
this condition corresponds to the minimum mass-loss rate:
For
![]() ,
while dust is not a driving mechanism
to produce a wind, it may be still formed passively
in the circumstellar ejecta.
To handle this case we have simply evaluated
the expansion velocity setting
,
while dust is not a driving mechanism
to produce a wind, it may be still formed passively
in the circumstellar ejecta.
To handle this case we have simply evaluated
the expansion velocity setting
![]() in the
corresponding Eq. (5). In this way
in the
corresponding Eq. (5). In this way
![]() is seen to
decline smoothly with the luminosity to the lowest measured values and,
perhaps more importantly, by using
is seen to
decline smoothly with the luminosity to the lowest measured values and,
perhaps more importantly, by using
![]() together with the actual
together with the actual ![]() in Eq. (4),
we can deal with the very optically-thin circumstellar envelopes
(
in Eq. (4),
we can deal with the very optically-thin circumstellar envelopes
(
![]() )
expected at low
)
expected at low ![]() .
.
One important feature of Eq.( 5) is that it naturally
predicts a maximum value for the expansion velocity, which is attained
at large ![]() as a consequence of the weakening of radiative
coupling in optically-thick winds:
as a consequence of the weakening of radiative
coupling in optically-thick winds:
![]() .
This aspect may bring along significant
implications for the interpretation of the observed data
(Sect. 5.1; see Fig. 4).
.
This aspect may bring along significant
implications for the interpretation of the observed data
(Sect. 5.1; see Fig. 4).
Table 3: Characteristic quantities used in the dust models, following the formalism developed by Elitzur & Ivezic (2001). They are defined in Sect. 4.2.
Under the assumptions of steady-state,
spherically symmetric, radial outflow with complete coupling
between dust and gas (i.e. both components sharing the same velocity),
from the mass-conservation law
![]() ,
the dust-to-gas mass ratio
,
the dust-to-gas mass ratio ![]() - defined by Eq. (10) - can be expressed:
- defined by Eq. (10) - can be expressed:
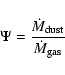 |
(15) |
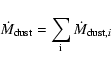 |
(16) |
The types of dust species that may condensate in the AGB circumstellar envelopes depend critically on the available abundances of the main dust forming elements, i.e., C, O, Mg, Si, S, and Fe. We recall that in the present calculations the chemical mixture of metals at the ZAMS is assumed to be scaled solar, according to the Grevesse & Noels (1993) compilation. While the surface abundances of C and O may change in the course of the stellar evolution (mainly due to dredge-up episodes and HBB), those of Mg, Si, S, and Fe remain practically unaltered.
Following the results of non-equilibrium dust-formation calculations
carried out by Ferrarotti & Gail (2006), it is useful to define two
critical carbon abundances, namely
![]() and
and
![]() ,
where Y=X/Ais the abundance in mol
,
where Y=X/Ais the abundance in mol
![]() .
They define sharp boundaries
between three different domains of dust compounds, as described in the
following.
.
They define sharp boundaries
between three different domains of dust compounds, as described in the
following.
Adopting the solar O abundance of Grevesse & Noels (1993), and under
the assumption that the surface abundance of O is not affected during
the evolution, then
![]() and
and
![]() define two
critical C/O ratios, namely (C/O)1=0.90 and (C/O)2=0.97.
The invariance of O is a common assumption, since
standard predictions of detailed AGB nucleosynthesis indicate that the
material dredged up at thermal pulses comprises only a small amount of
oxygen, i.e.,
define two
critical C/O ratios, namely (C/O)1=0.90 and (C/O)2=0.97.
The invariance of O is a common assumption, since
standard predictions of detailed AGB nucleosynthesis indicate that the
material dredged up at thermal pulses comprises only a small amount of
oxygen, i.e.,
![]() (Boothroyd & Sackmann 1988;
Izzard et al. 2004). However, one should consider that this result is
highly dependent on the treatment of convective boundaries (see
e.g., Herwig 2000, for high O inter-shell abundances); in addition the
surface abundance of O may be even depleted as a consequence of
efficient HBB in low-metallicity high-mass AGB stars (Ventura et al. 2002).
(Boothroyd & Sackmann 1988;
Izzard et al. 2004). However, one should consider that this result is
highly dependent on the treatment of convective boundaries (see
e.g., Herwig 2000, for high O inter-shell abundances); in addition the
surface abundance of O may be even depleted as a consequence of
efficient HBB in low-metallicity high-mass AGB stars (Ventura et al. 2002).
Since in our calculations the oxygen variations are negligible in most cases, we adopt the initial O abundance to define three main regimes of dust composition as a function of (C/O)1 and (C/O)2, which broadly correspond to the three main spectral classes of AGB stars (M, S, C). Details are given in Sects. 4.3.1 to 4.3.3.
When applied to our isochrones, the formalism outlined above produces
![]() values typically up to 0.004, 0.002, 0.0001 for O-rich stars,
and up to 0.01, 0.02, 0.02 for C-rich stars,
with
Z=0.019, 0.008, 0.001, respectively. These are
maximum predicted values, and they are not meant to be representative of
AGB stars at varying Z. Detailed population synthesis models are
needed to explore this issue, which is postponed to future analysis.
values typically up to 0.004, 0.002, 0.0001 for O-rich stars,
and up to 0.01, 0.02, 0.02 for C-rich stars,
with
Z=0.019, 0.008, 0.001, respectively. These are
maximum predicted values, and they are not meant to be representative of
AGB stars at varying Z. Detailed population synthesis models are
needed to explore this issue, which is postponed to future analysis.
Regardless, from comparing the upper values given above we derive
some interesting trends. While for O-rich stars
we find a direct proportionality between ![]() and Z, for
C-rich stars the relation becomes more complex and non-monotonic.
In the case of O-rich envelopes the relation
and Z, for
C-rich stars the relation becomes more complex and non-monotonic.
In the case of O-rich envelopes the relation
![]() is
explained by considering that the maximum amount of dust
that can be formed is controlled by the abundances of
the seed elements (i.e., Si, Fe), which scale with the initial
metallicity.
is
explained by considering that the maximum amount of dust
that can be formed is controlled by the abundances of
the seed elements (i.e., Si, Fe), which scale with the initial
metallicity.
In the case of C-rich envelopes one key parameter in the formation of dust
is the excess of carbon with respect to oxygen, and this quantity
does not trace the initial metallicity as it is crucially affected by
the third dredge-up and HBB during the TP-AGB phase.
It follows that the large ![]() values predicted for C-rich stars even at
low Z reflect their relatively high C/O ratios as predicted by our TP-AGB models at decreasing metallicity.
values predicted for C-rich stars even at
low Z reflect their relatively high C/O ratios as predicted by our TP-AGB models at decreasing metallicity.
It is worth noticing that these theoretical expectations are in line with the observational evidence presented in van Loon (2000) and Marshall et al. (2004) for the proportionality of the dust-to-gas ratio on Z in oxygen-rich stars; and van Loon et al. (1999) for the enhanced abundance of free carbon available for molecule and dust formation in metal-poor carbon stars. More observational data on this issue has been recently provided by e.g., Speck et al. 2006; Thompson et al. 2006; Sloan et al. 2006; Zijlstra et al. 2006; Lagadec et al. 2007; Matsuura et al. 2007.
In this interval, there are sufficient oxygen atoms to allow the
formation of the silicate-type dust. These conditions roughly
correspond to the domain of M stars. Two main dust
contributions are considered:
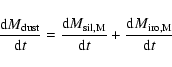 |
(18) |
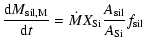 |
(19) | ||
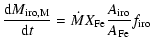 |
(20) |
The condensation degree of silicate dust,
![]() accounts for
the possible contributions of olivine-type dust, pyroxene-type dust,
and quartz-type dust:
accounts for
the possible contributions of olivine-type dust, pyroxene-type dust,
and quartz-type dust:
| (21) |
| (22) |
Finally,
![]() and
and
![]() are evaluated with the
analytic fits provided by Ferrarotti (2003):
are evaluated with the
analytic fits provided by Ferrarotti (2003):
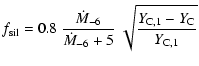 |
(23) | ||
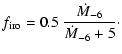 |
(24) |
In this interval a small amount of silicates can be produced because of
the deficit in O and the dust composition is iron-dominated. These
conditions may roughly include the class of S stars.
Two main dust contributions are considered:
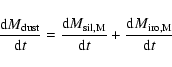 |
(25) |
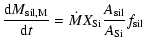 |
(26) | ||
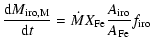 |
(27) |
Following Ferrarotti (2003) the condensation degrees are approximated with
| |
= | 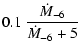 |
(28) |
| = | 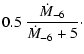 |
(29) |
In this interval, the dust mixture becomes carbon-dominated.
These conditions apply to the class of C stars. Two dust
contributions are included:
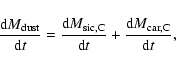 |
(30) |
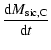 |
= | (31) | |
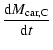 |
= | (32) |
Finally,
![]() ,
and
,
and
![]() denote the degree of
condensation of the elements Si and C in the corresponding dust
species. Following Ferrarotti (2003) they are evaluated with
denote the degree of
condensation of the elements Si and C in the corresponding dust
species. Following Ferrarotti (2003) they are evaluated with
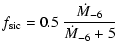 |
(33) | ||
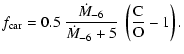 |
(34) |
We provide bolometric corrections from two independent RT calculations, which are updates and extensions of those originally described by B98 and G06. In both cases the models have been calculated with 1-dimensional codes that solve the RT equation and the thermal balance equation in a self-consistent way (see Granato & Danese 1994; Groenewegen 1993; and Groenewegen 1995).
Although they differ in several minor details related to the
structure of the original codes - as described in Sects. 4.4.1
and 4.4.2 - B98 and G06 calculations produce very similar results, proving
the robustness of both RT models. For instance, whereas B98 tabulate
the complete output ![]() spectra with a regular spacing in
spectra with a regular spacing in
![]() (here set to be
(here set to be
![]() dex), G06 code
directly provides the integrated
dex), G06 code
directly provides the integrated
![]() for a given
set of input pass-bands. In fact, we
have estimated that the differences in
for a given
set of input pass-bands. In fact, we
have estimated that the differences in
![]() coming from these two different
approaches, for the broadband filters we are using, are of the order
of just
coming from these two different
approaches, for the broadband filters we are using, are of the order
of just ![]() 0.05 mag for
0.05 mag for
![]() .
Considering the
overall uncertainties, these differences are small enough to be
safely ignored.
.
Considering the
overall uncertainties, these differences are small enough to be
safely ignored.
Instead, much more important are the differences associated with the assumed dust compositions, and the coverage of stellar parameters, as detailed below.
The dust models that are incorporated in the isochrones are an
extension of the work described in G06.
We have calculated the models for (arbitrary) values
of
![]() ,
d = 8.5 kpc,
,
d = 8.5 kpc,
![]() ,
,
![]() .
In G06,
only few effective temperatures were considered. Here we calculated
models for spectral types M0, 1,
.
In G06,
only few effective temperatures were considered. Here we calculated
models for spectral types M0, 1, ![]() ,
10 (
,
10 (
![]() = 3850,
3750, 3650, 3550, 3490, 3397, 3297, 3129, 2890, 2667, 2500 K) from
Fluks et al. (1994) for O-rich stars, and
= 3850,
3750, 3650, 3550, 3490, 3397, 3297, 3129, 2890, 2667, 2500 K) from
Fluks et al. (1994) for O-rich stars, and
![]() = 3400, 3200,
3000, 2800, 2650 K from Loidl et al. (2001) for C-rich stars (with a
C/O ratio of 1.1). The O- and C-stellar input spectra are for solar
metallicities.
= 3400, 3200,
3000, 2800, 2650 K from Loidl et al. (2001) for C-rich stars (with a
C/O ratio of 1.1). The O- and C-stellar input spectra are for solar
metallicities.
Several types of dust are considered (see G06 for a discussion). For
O-rich stars, (1) 100% Aluminium Oxide (AlOx; amorphous porous
Al2O3), with optical constants from Begemann et al. (1997), (2) a
combination of 60% AlOx and 40% Silicate (optical constants from
David & Pégourié 1995), (3) 100% silicate.
A condensation temperature of
![]() K was assumed in the
first two cases, 1000 K for the pure silicate dust.
K was assumed in the
first two cases, 1000 K for the pure silicate dust.
For C-stars, we consider either a combination of 85% Amorphous Carbon
(AMC) and 15% Silicon Carbide (SiC) with optical constants from,
respectively, Rouleau & Martin (1991) for the AC1 species and
![]() -SiC from Pégourié (1988), and assuming a
-SiC from Pégourié (1988), and assuming a ![]() of 1200 K, or 100% AMC with a
of 1200 K, or 100% AMC with a ![]() of 1000 K.
of 1000 K.
The results of such computations consist in the apparent stellar
magnitudes for several values of ![]() (and hence
(and hence ![]() ), ranging
from 10-10 to 4
), ranging
from 10-10 to 4 ![]()
![]() ,
and for
each spectral type and filter under consideration. Over this range of
mass loss
,
and for
each spectral type and filter under consideration. Over this range of
mass loss ![]() increases up to
increases up to ![]() 3 for AMC (at 11.33
3 for AMC (at 11.33 ![]() m)
and
m)
and ![]() 45 for AlOx (at 11.75
45 for AlOx (at 11.75 ![]() m). We considred a total of 90 filters in these specific computations. We converted these magnitude
tables into
m). We considred a total of 90 filters in these specific computations. We converted these magnitude
tables into
![]() values that directly give the
difference between the magnitudes of non-dusty (
values that directly give the
difference between the magnitudes of non-dusty (![]() )
and dusty
stars
)
and dusty
stars![]() .
.
In B98 for each dust type (either O-rich or C-rich)
the reference grid of AGB dusty envelopes consists of
models calculated for L=10 000,
![]() K,
while varying the optical depth
K,
while varying the optical depth
![]() from 5
from 5 ![]() 10-4 to 200in 50 equal logarithmic steps. The condensation temperature is assumed
10-4 to 200in 50 equal logarithmic steps. The condensation temperature is assumed
![]() K for O-rich envelopes, and
K for O-rich envelopes, and
![]() K for C-rich envelopes.
Additional tests have shown that, for the adopted dust mixtures, the resulting spectral shapes
are little affected by changes in L and
K for C-rich envelopes.
Additional tests have shown that, for the adopted dust mixtures, the resulting spectral shapes
are little affected by changes in L and
![]() within the
typical ranges for AGB stars, for fixed values of
within the
typical ranges for AGB stars, for fixed values of
![]() .
.
The radiative transfer of the photospheric stellar spectrum
through the dust is computed with the Granato & Danese (1994) code
(originally built for AGN tori), assuming spherical symmetry and the
radial dust density distribution decreasing as r-2. The adopted
dust grain model is that of Rowan-Robinson et al. (1986)![]() ,
which considers six different kinds of grains: AMC of radius
,
which considers six different kinds of grains: AMC of radius
![]() and graphites of 0.03 and
and graphites of 0.03 and
![]() for C-rich mixtures,
and amorphous silicate of
for C-rich mixtures,
and amorphous silicate of
![]() and silicates of 0.03and
and silicates of 0.03and
![]() for O-rich mixtures.
for O-rich mixtures.
Although we updated in several aspects the B98 model, in particular in the dust grain properties, the detailed exploration with Spitzer data of these updates is still underway and will be presented in a forthcoming paper. Therefore here we adopt the already well-established B98 model in its original form. The dust composition we consider is carbon for C-type mass-losing stars, and silicates for M-type ones.
The relation between
![]() and the mass loss is given by Eq. (4)
with
and the mass loss is given by Eq. (4)
with
![]()
![]() 1011 for silicates and
1011 for silicates and
![]()
![]() 1011 for the carbonaceous mix (with
1011 for the carbonaceous mix (with
![]() in
in
![]() ,
L in solar units). The quantity
,
L in solar units). The quantity ![]() is slightly affected by the spectrum of the
illuminating star. However, B98 have checked that the errors in
is slightly affected by the spectrum of the
illuminating star. However, B98 have checked that the errors in
![]() estimated from Eq. (4)
with the above values of
estimated from Eq. (4)
with the above values of ![]() are kept within 5% for spectra with
are kept within 5% for spectra with
![]() in the range 2500-4000 K. This is a fair approximation because
models with
in the range 2500-4000 K. This is a fair approximation because
models with
![]() differing by less than 5-10% produce almost
identical spectra.
differing by less than 5-10% produce almost
identical spectra.
Figure 3 illustrates the behaviour of
![]() as a function of wavelength, for the dust compositions considered
in this work, and for the specific case of
as a function of wavelength, for the dust compositions considered
in this work, and for the specific case of
![]() and
and
![]() K. We note that all curves agree very well in
the case of O-rich mixtures, and differ significantly only for the
C-rich mixtures at
K. We note that all curves agree very well in
the case of O-rich mixtures, and differ significantly only for the
C-rich mixtures at
![]() .
These differences become
higher for higher values of
.
These differences become
higher for higher values of ![]() ,
and can be ascribed to the use of
different dust mixtures and spectral libraries.
,
and can be ascribed to the use of
different dust mixtures and spectral libraries.
In summary, we consider several possible choices of dust
composition, namely: four for O-rich envelopes and
three for C-rich envelopes. Alternatively,
we can ignore dust setting ![]() .
All these cases are allowed in
our isochrone calculations.
.
All these cases are allowed in
our isochrone calculations.
Gi00 isochrones have been used extensively in the literature for the study of resolved stellar populations. Most of their use has regarded the optical photometry of stars in the most populated evolutionary phases like the main sequence, sub-giant branch, RGB, red clump and early-AGB. Now the addition of the detailed TP-AGB evolution together with the infrared photometry open new perspectives for the application of these new stellar models, which we briefly illustrate in the following via comparisons with Galactic Disc and Magellanic Cloud data.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{8467f3.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg222.gif) |
Figure 3:
The absorption/emission properties of the dust mixtures
considered in this work, in the form of
|
| Open with DEXTER | |
Most of the comparisons are intended to illustrate the locus of our new isochrones in different diagrams, and do not consider crucial aspects of the host galaxies, such as their age-metallicity relations and star formation histories. A detailed comparison, between present models and the observed star counts in several parts of these diagrams, is left to future papers.
As a first check of our models, we compare the predicted expansion velocities (Sect. 4.2) as a function of pulsation periods with observations of variable AGB stars in the Galactic Disc and Magellanic Clouds. The results, displayed in Fig. 4, are consistent with the empirical estimates.
A relevant remark should be made in respect to the O-rich stars. While
for
P < 500-600 days a positive correlation between periods and
expansion velocities seems to exist in the observed data, this trend
does not proceed at longer periods, where a considerable scatter of
![]() is detected. It should be noticed that while reproducing
the mean observed trend at shorter periods, the widely-used relation
of Vassiliadis & Wood (1993; solid line) fails to describe the data
at longer periods, where
is detected. It should be noticed that while reproducing
the mean observed trend at shorter periods, the widely-used relation
of Vassiliadis & Wood (1993; solid line) fails to describe the data
at longer periods, where
![]() is assumed to be constant (15 km s-1).
is assumed to be constant (15 km s-1).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{8467f4.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg223.gif) |
Figure 4: Expansion velocities of circumstellar flows against pulsation periods of variable AGB stars, for both O-rich ( left panels) and C-rich objects ( right panels). Upper panels: galactic observations (empty circles) are taken from the compilations assembled by Groenewegen et al. (1998) for O-rich stars and Groenewegen et al. (2002) for C-rich stars. Observed data for LMC variables (Marshall et al. 2004) is also plotted (empty squares). The fit relation proposed by Vassiliadis & Wood (1993) is shown by the solid line. Bottom panels: predicted expansion velocities for a few selected isochrones with Z=0.019 and Z=0.008. Ages are indicated in the figure. See the text for more details. |
| Open with DEXTER | |
In the bottom panels of Fig. 4 we show the results of our
calculations for a few selected isochrones with Z=0.019 and
Z=0.008. Regardless of age all isochrones describe a similar non-monotonic evolution on
the
![]() diagram. At increasing periods, first the
expansion velocity increases, reaches a maximum and eventually
declines. This bell-shaped behaviour is particularly well developed
for the youngest isochrones (with ages of
diagram. At increasing periods, first the
expansion velocity increases, reaches a maximum and eventually
declines. This bell-shaped behaviour is particularly well developed
for the youngest isochrones (with ages of ![]() 1.6
1.6 ![]() 108 yr and
108 yr and
![]() 2
2 ![]() 108 yr), which correspond to massive AGB stars (with
initial masses of
108 yr), which correspond to massive AGB stars (with
initial masses of
![]() and
and
![]() )
and it
appears to explain the existence of variables with high periods and
relatively low expansion velocities.
)
and it
appears to explain the existence of variables with high periods and
relatively low expansion velocities.
With respect to this, it is also interesting to compare
the two isochrones with
![]() and different
metallicities (Z=0.019 and Z=0.008). The one with
Z=0.008 reaches, on average, lower
and different
metallicities (Z=0.019 and Z=0.008). The one with
Z=0.008 reaches, on average, lower
![]() .
Moreover,
the few OH/IR stars in the LMC for which
.
Moreover,
the few OH/IR stars in the LMC for which
![]() has been measured (empty squares; Marshall et al. 2004)
fall in correspondence with the declining branches of the
has been measured (empty squares; Marshall et al. 2004)
fall in correspondence with the declining branches of the
![]() curves. This fact suggests that the low expansion velocities of
LMC OH/IR stars compared to those of Galactic OH/IR stars with the
same P, may not reflect a pure effect of metallicity (i.e., a linear
Z-dependence of the dust-to-gas ratio
curves. This fact suggests that the low expansion velocities of
LMC OH/IR stars compared to those of Galactic OH/IR stars with the
same P, may not reflect a pure effect of metallicity (i.e., a linear
Z-dependence of the dust-to-gas ratio ![]() such that the lower Z,
the lower
such that the lower Z,
the lower
![]() ), as commonly invoked (see the discussion in
Marshall et al. 2004); rather it may be the result of a more complex dependence
of
), as commonly invoked (see the discussion in
Marshall et al. 2004); rather it may be the result of a more complex dependence
of
![]() as a function of stellar and dust parameters (
as a function of stellar and dust parameters (
![]() ). We will perform a deep investigation of this
issue in future work.
). We will perform a deep investigation of this
issue in future work.
TP-AGB stars become striking objects in galactic surveys conducted at pass-bands redder than I. The best available data for the AGB population in galaxies is likely the data obtained from the extensive near- and mid-infrared surveys of the Magellanic Clouds.
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{8467f5a.ps}\hspace*{1.1cm}
\includegraphics[width=8.15cm,clip]{8467f5b.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg232.gif) |
Figure 5:
The 2MASS |
| Open with DEXTER | |
In Fig. 5, we plot the 2MASS ![]() vs.
vs.
![]() diagram of the
inner LMC and SMC. The data are taken directly from the SAGE and
S3MC catalogs (Blum et al. 2006; and Bolatto et al. 2007,
respectively), and hence correspond to objects that have counterparts
in the Spitzer pass-bands.
diagram of the
inner LMC and SMC. The data are taken directly from the SAGE and
S3MC catalogs (Blum et al. 2006; and Bolatto et al. 2007,
respectively), and hence correspond to objects that have counterparts
in the Spitzer pass-bands.
We start discussing the LMC case depicted in the left panel. The
circular area of ![]() sqrdeg centered on the LMC bar at
sqrdeg centered on the LMC bar at
![]() ,
,
![]() ,
is
large enough to include thousands of AGB stars brighter than the TRGB,
and small enough to somewhat limit the presence of features that are
not due to the LMC. These latter features are, however, still evident in
the plot, and consist of (1) the vertical fingers in the top left part
of the CMD, at
,
is
large enough to include thousands of AGB stars brighter than the TRGB,
and small enough to somewhat limit the presence of features that are
not due to the LMC. These latter features are, however, still evident in
the plot, and consist of (1) the vertical fingers in the top left part
of the CMD, at
![]() mag and
mag and
![]() mag, caused by foreground
stars in the Milky Way disc and halo, and (2) the plume of objects at
the bottom right part of the CMD, roughly at
mag, caused by foreground
stars in the Milky Way disc and halo, and (2) the plume of objects at
the bottom right part of the CMD, roughly at
![]() mag vs.
mag vs.
![]() mag, which largely consists of background galaxies (see Nikolaev & Weinberg 2000, his Region L). Outside of these two CMD regions, the bulk of objects indeed consists of stars located in the LMC.
mag, which largely consists of background galaxies (see Nikolaev & Weinberg 2000, his Region L). Outside of these two CMD regions, the bulk of objects indeed consists of stars located in the LMC.
On this diagram, we over-plot our isochrones for the initial metallicity Z=0.008 (which are adequate to describe the youngest LMC populations) and at four selected ages:
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{8467f6a.ps}\hspace*{1.2cm}
\includegraphics[width=8.1cm,clip]{8467f6b.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg248.gif) |
Figure 6:
Left panel: the 2MASS |
| Open with DEXTER | |
The left panel of Fig. 6 details the region of the
![]() vs.
vs.
![]() diagram that includes the bulk of the TP-AGB stars. In addition to the 2MASS data for the inner LMC, we plot the Groenewegen (2004) database of LMC stars spectroscopically classified
as being of types M and C. The latter are LPVs selected from the OGLE database for the entire LMC. Although they are not distributed evenly
over the CMD, they clearly illustrate that the bulk of M- (dark-green)
and C-type (orange) stars are well separated in the CMD; in particular,
they show the striking red tail of C stars extending from
diagram that includes the bulk of the TP-AGB stars. In addition to the 2MASS data for the inner LMC, we plot the Groenewegen (2004) database of LMC stars spectroscopically classified
as being of types M and C. The latter are LPVs selected from the OGLE database for the entire LMC. Although they are not distributed evenly
over the CMD, they clearly illustrate that the bulk of M- (dark-green)
and C-type (orange) stars are well separated in the CMD; in particular,
they show the striking red tail of C stars extending from
![]() mag up to
mag up to
![]() mag, and the confinement of M stars at the bluest colours (
mag, and the confinement of M stars at the bluest colours (
![]() mag).
mag).
Then, the figure evidences how the new isochrones reproduce the
general appearance of the data, and in particular the red tail of C stars which is well described by the
![]() isochrone. It is also remarkable how well the isochrones predict the
neat separation between O-rich (M-type) and C-rich (C-type) stars in
the diagram. In the
isochrone. It is also remarkable how well the isochrones predict the
neat separation between O-rich (M-type) and C-rich (C-type) stars in
the diagram. In the
![]() isochrone, the red tail
reaches
isochrone, the red tail
reaches
![]() even in absence of circumstellar dust. Dust
obscuration in stars with
even in absence of circumstellar dust. Dust
obscuration in stars with
![]() provides an additional
provides an additional
![]() mag that improves the
comparison at the reddest part of the red tail, at
mag that improves the
comparison at the reddest part of the red tail, at
![]() between 1.6
and 2.0 mag. As thoroughly discussed in Marigo et al. (2003a), the main
physical effect driving the appearance of the red tail of C stars are
the cool
between 1.6
and 2.0 mag. As thoroughly discussed in Marigo et al. (2003a), the main
physical effect driving the appearance of the red tail of C stars are
the cool
![]() caused by changes in molecular opacities as the third
dredge-up events increase the photospheric C/O ratio.
caused by changes in molecular opacities as the third
dredge-up events increase the photospheric C/O ratio.
The right panel of Fig. 6 over-plots isochrones from
Gi00 and Cordier et al. (2007) over the same data. These isochrone sets
contain the complete TP-AGB phase, but computed in a rather crude way,
i.e. without considering the third dredge-up events and HBB nucleosynthesis, and using
![]() relations derived from scaled-solar mixtures. These isochrones fail to reproduce the basic features indicated by 2MASS and spectroscopic data, although in
different ways:
relations derived from scaled-solar mixtures. These isochrones fail to reproduce the basic features indicated by 2MASS and spectroscopic data, although in
different ways:
![\begin{figure}
\par\mbox{\includegraphics[width=8.1cm,clip]{8467f7a.ps}\hspace*{...
...ps}\hspace*{1.2cm}
\includegraphics[width=8.1cm,clip]{8467f7d.ps} }
\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg257.gif) |
Figure 7: A comparison between the new isochrones and the near- to mid-infrared data for the LMC. The isochrones are the same as plotted in the left panel of Fig. 5. The data (dots) come from the SAGE epoch 1 point source catalog (Blum et al. 2006) and combine IRAC+MIPS with 2MASS data inside a circle of 1 degree radius in the inner LMC. The panels show the 2MASS+IRAC [3.6] vs. J-[3.6], 2MASS+IRAC [8.0] vs. J-[8.0], IRAC [8.0] vs. [3.6]-[8.0], and IRAC+MIPS [24] vs. [8.0]-[24] diagrams. The gray dots correspond to objects not detected by 2MASS, most of which are expected to correspond to background galaxies and young pre-main sequence stars, which are not discussed in this paper. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8.1cm,clip]{8467f8a.ps}\hspace*{...
...ps}\hspace*{1.2cm}
\includegraphics[width=8.1cm,clip]{8467f8d.ps} }
\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg258.gif) |
Figure 8: As Fig. 7 but for the SMC. The data (dots) come from the S3MC catalog (Bolatto et al. 2007). The isochrones are the same as in the right panel of Fig. 5. |
| Open with DEXTER | |
From the failure of both the G00 and Cordier et al. (2007) isochrone sets in describing a red tail made of C stars, it follows that such models are not suitable for the interpretation of near-infrared photometry in the age interval in which C stars form. For LMC metallicities, this interval is quite ample, going from a few 108 yr up to about 5 Gyr (see also Frogel et al. 1990).
Finally, the 2MASS ![]() vs.
vs.
![]() diagram for the area within the SMC covered by the S3MC survey (right panel of Fig. 5) can be described in a similar way to the LMC diagram. The most obvious difference between the two panels is in the
diagram for the area within the SMC covered by the S3MC survey (right panel of Fig. 5) can be described in a similar way to the LMC diagram. The most obvious difference between the two panels is in the ![]() 0.5 mag shift of all
features coming from the LMC-SMC difference in distance, which we also
took in consideration when plotting the isochrones. Also, due to the
particular selection of data the SMC plot presents less contamination
from background galaxies than the LMC plot.
0.5 mag shift of all
features coming from the LMC-SMC difference in distance, which we also
took in consideration when plotting the isochrones. Also, due to the
particular selection of data the SMC plot presents less contamination
from background galaxies than the LMC plot.
![\begin{figure}
\par\mbox{\includegraphics[width=6.1cm,clip]{8467f9a.ps}\hspace*{3.1cm}
\includegraphics[width=6.4cm,clip]{8467f9b.ps} }
\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg263.gif) |
Figure 9:
Broad-band V-K and J-K colours of LMC clusters as a function of cluster age. Top panels: observed photometric data taken from various compilations: Persson et al. (1983,
filled circles); Kyeong et al. (2003, empty squares); and the V-band
photometry by Goudfrooij et al. (2006) adopting an aperture radius of
50 arcsec, combined to the
|
| Open with DEXTER | |
Figures 7 and 8 show a series of CMDs
involving the near- and mid-IR photometry of the Magellanic Clouds,
comparing the new isochrones with 2MASS+SAGE data for the inner LMC
(Blum et al. 2006) and with 2MASS+S3MC data for the SMC
(Bolatto et al. 2007)![]() . In all these plots, the effect of
circumstellar dust becomes crucial in describing the observed
photometry. The features present in these CMDs (except for the
IRAC+MIPS [24] vs.
[8.0]-[24] diagram, for which the data is poorer)
are essentially the same as those present in the
. In all these plots, the effect of
circumstellar dust becomes crucial in describing the observed
photometry. The features present in these CMDs (except for the
IRAC+MIPS [24] vs.
[8.0]-[24] diagram, for which the data is poorer)
are essentially the same as those present in the ![]() vs.
vs.
![]() diagram. In particular, all of them show contamination from foreground
Milky Way stars in the form of a narrow vertical finger confined to
the left part of the CMDs, and contamination from background galaxies
at their bottom-right corner. The gray dots correspond to objects not
detected by 2MASS, most of which are expected to correspond to
background galaxies and young pre-main sequence stars, which are not
of interest in this paper.
diagram. In particular, all of them show contamination from foreground
Milky Way stars in the form of a narrow vertical finger confined to
the left part of the CMDs, and contamination from background galaxies
at their bottom-right corner. The gray dots correspond to objects not
detected by 2MASS, most of which are expected to correspond to
background galaxies and young pre-main sequence stars, which are not
of interest in this paper.
The LMC population in these plots again shows O-rich sequences (core
He burning red super-giants plus O-rich TP-AGBs) that progressively
merge into an almost-vertical blue sequence when colours involving
redder pass-bands are considered; plus an inclined C-rich sequence that
can be identified as the main body of the
![]() mag red
tail. From the extremity of this more populated red tail, a very
extended and less populated plume departs, which corresponds to
the stars with high mass-loss rates. Our isochrones reproduce well the
position of these plumes in the several CMDs considered here,
and moreover predict
that they are populated by both O- and C-rich stars.
mag red
tail. From the extremity of this more populated red tail, a very
extended and less populated plume departs, which corresponds to
the stars with high mass-loss rates. Our isochrones reproduce well the
position of these plumes in the several CMDs considered here,
and moreover predict
that they are populated by both O- and C-rich stars.
Broadband colours of Magellanic Cloud clusters represent the basic
observable against which any population synthesis model should be
compared for testing its predicting performance.
Figure 9 displays the results for two integrated
colours, V-K and J-K, which are expected to be significantly
affected by the existence of TP-AGB stars. By looking at
Fig. 9 (top panels), we actually see that the observed
data for both V-K and J-K colours show a rising trend starting
from
![]() yr toward older ages, which is currently well
explained by our current single-burst stellar populations (SSP) models
(solid line) as due to the development of the TP-AGB phase.
We refer the reader to Appendix A for a discussion on
the behaviour of V-K at ages
yr toward older ages, which is currently well
explained by our current single-burst stellar populations (SSP) models
(solid line) as due to the development of the TP-AGB phase.
We refer the reader to Appendix A for a discussion on
the behaviour of V-K at ages
![]() yr and its relation to the
evolution of the most massive AGB stars. Integrated magnitudes are
calculated accounting for the luminosity variations (i.e. the
long-lived luminosity dips in low-mass stars) driven by thermal
pulses, and the effect on the emitted spectrum by circumstellar dust.
yr and its relation to the
evolution of the most massive AGB stars. Integrated magnitudes are
calculated accounting for the luminosity variations (i.e. the
long-lived luminosity dips in low-mass stars) driven by thermal
pulses, and the effect on the emitted spectrum by circumstellar dust.
For comparison we also show the results of other two widely-used SSP
models, namely Charlot & Bruzual (2003; dot-dashed line) and Maraston
(2005; dashed line). A few points should be noticed in respect to the
age interval
![]() yr, when AGB stars are present. While
Charlot & Bruzual (2003) colours tend to be bluer than the observations
because of their likely underestimation of the TP-AGB phase (see
Bruzual 2007, for a recent revision of this aspect in their models),
Maraston (2005) tends to form an upper envelope to the data,
especially in V-K. Our results are intermediate between the two.
yr, when AGB stars are present. While
Charlot & Bruzual (2003) colours tend to be bluer than the observations
because of their likely underestimation of the TP-AGB phase (see
Bruzual 2007, for a recent revision of this aspect in their models),
Maraston (2005) tends to form an upper envelope to the data,
especially in V-K. Our results are intermediate between the two.
The bottom panels of Fig. 9 illustrate the same
colour evolution, by means of simulated clusters. The cluster
simulations are performed by randomly adding stars to the isochrones,
with the probability of a given initial stellar mass given by
the Chabrier (2001) log-normal initial mass function. The addition of
stars to a simulated cluster is stopped when its initial total mass
reaches a given value ![]() .
The entire cluster sample is
assumed to follow a
.
The entire cluster sample is
assumed to follow a
![]() distribution, which is derived
from the luminosity function of LMC clusters (Elson & Fall 1985; see
also Girardi et al. 1995, Sect. 8.2). The cluster metallicities follow
the LMC age-metallicity relation from Pagel & Tautvaisienè's (1998)
bursting model, which has been shown to reproduce the observed
trend. The distribution of cluster ages is assumed to be constant;
although this is not a realistic assumption (see Girardi et al. 1995),
it allows us a good illustration of the colour evolution over the
complete age range. A posteriori, we impose a limiting magnitude of
distribution, which is derived
from the luminosity function of LMC clusters (Elson & Fall 1985; see
also Girardi et al. 1995, Sect. 8.2). The cluster metallicities follow
the LMC age-metallicity relation from Pagel & Tautvaisienè's (1998)
bursting model, which has been shown to reproduce the observed
trend. The distribution of cluster ages is assumed to be constant;
although this is not a realistic assumption (see Girardi et al. 1995),
it allows us a good illustration of the colour evolution over the
complete age range. A posteriori, we impose a limiting magnitude of
![]() mag to the simulated sample, which roughly
corresponds to that of the observed samples in the top panels of
Fig. 9. The results present the intrinsic colour
dispersion expected for the cluster data due to their small numbers of
evolved stars (stochastic fluctuations), and in this aspect they look
clearly more similar to the observations than the continuous narrow
SSP lines depicted in the top panel. The main discrepancy between
models and simulations is at ages younger than 108 yr, where a
bunch of very blue clusters is predicted, but absent from the
observed sample
mag to the simulated sample, which roughly
corresponds to that of the observed samples in the top panels of
Fig. 9. The results present the intrinsic colour
dispersion expected for the cluster data due to their small numbers of
evolved stars (stochastic fluctuations), and in this aspect they look
clearly more similar to the observations than the continuous narrow
SSP lines depicted in the top panel. The main discrepancy between
models and simulations is at ages younger than 108 yr, where a
bunch of very blue clusters is predicted, but absent from the
observed sample![]() . The blue clusters are essentially those for which no red super-giant was
predicted, and derive naturally from the fact that the red super-giant
phase is short-lived. In order to recover the observed colours of the youngest
clusters, the red super-giant phase has to be significantly
longer and cooler than in the Bertelli et al. (1994) isochrones.
On one hand, a longer duration could be
attained, for instance, by invoking a larger efficiency of overshoot,
but this may in turn inhibit the development of the blue loops
of massive stars (see the discussion in Alongi et al. 1991).
On the other hand, the effective temperatures of
red super-giants depend very much on the
treatment of the density inversion that is predicted to take
place in the outermost atmospheric layers. A deeper analysis of this issue
is beyond the scope of the paper and it is postponed to future work.
. The blue clusters are essentially those for which no red super-giant was
predicted, and derive naturally from the fact that the red super-giant
phase is short-lived. In order to recover the observed colours of the youngest
clusters, the red super-giant phase has to be significantly
longer and cooler than in the Bertelli et al. (1994) isochrones.
On one hand, a longer duration could be
attained, for instance, by invoking a larger efficiency of overshoot,
but this may in turn inhibit the development of the blue loops
of massive stars (see the discussion in Alongi et al. 1991).
On the other hand, the effective temperatures of
red super-giants depend very much on the
treatment of the density inversion that is predicted to take
place in the outermost atmospheric layers. A deeper analysis of this issue
is beyond the scope of the paper and it is postponed to future work.
Another questionable point involves the ages between 108 yr and
![]() 4
4 ![]() 108 yr, after the AGB phase develops: in this age
interval, our models become on the mean redder than the data. As
mentioned in the Appendix, removing this feature from the models
poses a theoretical difficulty as it would as well prevent the significant
enrichment of helium and nitrogen in the most massive AGB stars,
which is instead required to explain the observed abundances
in planetary nebulae of type I. Finally, at older ages
the adoption of an age-metallicity relation allows us to reproduce the colours of the oldest LMC clusters, which have ages and metallicities typical of old Galactic
globular clusters.
108 yr, after the AGB phase develops: in this age
interval, our models become on the mean redder than the data. As
mentioned in the Appendix, removing this feature from the models
poses a theoretical difficulty as it would as well prevent the significant
enrichment of helium and nitrogen in the most massive AGB stars,
which is instead required to explain the observed abundances
in planetary nebulae of type I. Finally, at older ages
the adoption of an age-metallicity relation allows us to reproduce the colours of the oldest LMC clusters, which have ages and metallicities typical of old Galactic
globular clusters.
In short, these isochrones offer a valid alternative for the modelling of the integrated light of star clusters and galaxies, since they pass the LMC cluster test performing similarly well as the widely-used Charlot & Bruzual (2003) and Maraston (2005) SSP models, when we look at the mean colour evolution (top panels of Fig. 9). Moreover, the isochrones we provide allow the simulation of resolved stellar populations, which is essential for their further testing - as illustrated by the simulations in the bottom panels of Fig. 9. The isochrones are based on internally consistent sets of tracks, which naturally obey the fuel consumption theorem, and provide other quantities necessary for a consistent modelling of galaxies - namely the chemical yields and remnant masses (see Marigo & Girardi 2001, for a discussion on this latter point). Having all these components together allows us the simultaneous comparison of the model results with many different observables, indicating hidden problems (like the young blue clusters predicted in Fig. 9) and hopefully pointing the way to future improvements in the models.
The data presented in this paper are provided in two different ways:
Moreover, the http://stev.oapd.inaf.it/cmd URL allows the mass
range to be extended from 7 to 100 ![]() ,
using the tracks from
Bertelli et al. (1994) isochrones. This allows the age range to be
extended down to about 4 Myr for complete isochrones - or even down
to t=0 in case one is interested in obtaining an extended
zero-age main sequence. The only problem is that the tracks
for massive stars are not available for
,
using the tracks from
Bertelli et al. (1994) isochrones. This allows the age range to be
extended down to about 4 Myr for complete isochrones - or even down
to t=0 in case one is interested in obtaining an extended
zero-age main sequence. The only problem is that the tracks
for massive stars are not available for
![]() ,
and in
such a case have to be taken from the Z=0.02 set of Bertelli et al. (1994).
,
and in
such a case have to be taken from the Z=0.02 set of Bertelli et al. (1994).
The basic information provided along isochrones consists of the
luminosity, effective temperature, surface gravity, and absolute
magnitudes in the photometric system under consideration. For the
TP-AGB phase, this information is complemented with the core mass,
surface C/O ratio, pulsation mode and period, and mass-loss rate. The
TP-AGB section of an isochrone can be easily identified by the
information about the core mass, whereas the C-star phase is
identified by
![]() .
These latter variables are also useful to
simulate, a posteriori, the luminosity and
.
These latter variables are also useful to
simulate, a posteriori, the luminosity and
![]() variations caused by
pulse cycles on the TP-AGB, as we have done in a series of papers
(e.g., Marigo et al. 2003; Cioni et al. 2006; Girardi & Marigo 2007b).
variations caused by
pulse cycles on the TP-AGB, as we have done in a series of papers
(e.g., Marigo et al. 2003; Cioni et al. 2006; Girardi & Marigo 2007b).
Finally, we remark that the http://stev.oapd.inaf.it/cmd web interface is going to be continuously expanded, either with new extensions to the tracks (e.g., with the planetary nebulae and white dwarf sequences), new photometric systems, new spectra from which to derive bolometric corrections, and different dust compositions. Interstellar extinction will be included in the isochrones in a consistent way (Girardi et al. 2007, in prep.). In any case, the original database, as here described, will remain available as well.
Users of the new isochrones should be aware that:
Despite the caveats, we believe that our new isochrones constitute significant progress. We recall that the simple discussion of the above mentioned points would have been meaningless in the context of the more crude TP-AGB isochrones listed in Table 1.
In fact, we believe this is the first extended set of isochrones that
includes the TP-AGB evolutionary phase with the level of completeness
and detail it deserves. Crucial effects such as the third dredge-up
(which makes C-type stars), hot bottom burning (which largely prevents
the most massive AGB stars from becoming C-type), and variable
molecular opacities (which causes the cool red tail of C stars in
near- and mid-IR CMDs), have been considered. Mass-loss rates are
described with a formalism that discriminates between C- and M-type
stars, and leads to the attainment of the super-wind regime during the
latest stages of the TP-AGB evolution. The transition from the first
overtone to the fundamental mode is predicted, which helps trigger
higher mass-loss rates. Parameters associated with the third dredge-up
are calibrated so as to reproduce the C-star luminosity functions
observed in the Magellanic Clouds, and the lifetimes of C- and M-type
stars derived from star counts in Magellanic Cloud clusters. Many
photometric systems are considered, properly taking into account the
different spectra of O-rich and C-rich stars, including the stellar
obscuration by circumstellar dust at optical to near-IR wavelengths,
and its dust emission in the mid- and far-IR. We vary the expansion velocity
of the wind and the dust-to-gas ratio consistently as
a function of stellar parameters (![]() ,
,
![]() ,
L, C/O,
Z), in place of simpler parametrizations often used in the
literature. Dust reprocessing of radiation makes the most evolved AGB stars disappear in optical pass-bands, and appear at a very
extended red tail in near- and mid-IR CMDs. All these features make
the new isochrones potentially very useful in the study of systems
containing AGB stars, both resolved and unresolved.
,
L, C/O,
Z), in place of simpler parametrizations often used in the
literature. Dust reprocessing of radiation makes the most evolved AGB stars disappear in optical pass-bands, and appear at a very
extended red tail in near- and mid-IR CMDs. All these features make
the new isochrones potentially very useful in the study of systems
containing AGB stars, both resolved and unresolved.
The new models have been included in the TRILEGAL code (Girardi et al. 2005; Girardi & Marigo 2007b)![]() for the simulation of resolved
stellar populations in the Milky Way and in external galaxies, and in
the GRASIL code (GRAphite and SILicate; Silva et al. 1998; Panuzzo et al. 2005)
for the simulation of resolved
stellar populations in the Milky Way and in external galaxies, and in
the GRASIL code (GRAphite and SILicate; Silva et al. 1998; Panuzzo et al. 2005)![]() for computing the
integrated spectrum of galaxies from the X-ray to the radio
domain taking into account the effects of dust. Forthcoming papers will present applications of both codes, including the extensive testing of our TP-AGB tracks and dust models
against observational data.
for computing the
integrated spectrum of galaxies from the X-ray to the radio
domain taking into account the effects of dust. Forthcoming papers will present applications of both codes, including the extensive testing of our TP-AGB tracks and dust models
against observational data.
Acknowledgements
This study was supported by the University of Padova (Progetto di Ricerca di Ateneo CPDA052212), COFIN INAF 2005, and contract ASI-INAF I/016/07/0. We acknowledge Rita Gautschy-Loidl for providing us the C-star spectra, and Bernhard Aringer for the help in implementing them. We thank Anil Seth, Ben Williams, Enrico Held, Marco Gullieuszik, Leandro Kerber, and Mauro Barbieri for pointing out some bugs and problems in preliminary versions of these isochrones, and Jacco van Loon for his very useful suggestions.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{8467fA1.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg276.gif) |
Figure A.1:
Integrated V-K colours as a function of SSP age, derived
from the original Paper I TP-AGB tracks (dashed line), and after the
revision applied to the TP-AGB models with initial masses
|
| Open with DEXTER | |
The TP-AGB evolution of more massive stars, with initial masses
![]() ,
has been modified as follows.
The starting point that has stimulated the revision is the behaviour
of the integrated colours (e.g. V-K, J-K, H-K) as a function of
age as displayed by the Magellanic Clouds' clusters of age
,
has been modified as follows.
The starting point that has stimulated the revision is the behaviour
of the integrated colours (e.g. V-K, J-K, H-K) as a function of
age as displayed by the Magellanic Clouds' clusters of age
![]() yr. As shown in Fig. A.1, the comparison with
SSP colours, derived from the isochrones including the original TP-AGB tracks from Paper I, would indicate a sizable excess in the predicted
V-K colours at ages around 1-4
yr. As shown in Fig. A.1, the comparison with
SSP colours, derived from the isochrones including the original TP-AGB tracks from Paper I, would indicate a sizable excess in the predicted
V-K colours at ages around 1-4 ![]() 108 yr. The sudden jump to
108 yr. The sudden jump to
![]() at
at
![]() yr is due to the occurrence of the AGB phase in models with
yr is due to the occurrence of the AGB phase in models with
![]()
![]() ,
which corresponds to the
maximum initial mass (for our set of models) required to develop an
electron-degenerate C-O core. In the 1-4
,
which corresponds to the
maximum initial mass (for our set of models) required to develop an
electron-degenerate C-O core. In the 1-4 ![]() 108 yr age
range, while the integrated V-band luminosity is essentially
produced by less-evolved stars still populating the region close to
the main-sequence turn-off (see e.g., Charlot & Bruzual 1991), a
significant contribution in the K-band comes from the most massive
AGB stars, with initial masses in the range
108 yr age
range, while the integrated V-band luminosity is essentially
produced by less-evolved stars still populating the region close to
the main-sequence turn-off (see e.g., Charlot & Bruzual 1991), a
significant contribution in the K-band comes from the most massive
AGB stars, with initial masses in the range
![]() .
.
It follows that the V-K colour jump at
![]() yr should be
ascribed to an overestimation of the TP-AGB phase of more massive AGB models, which translates into either a) too high luminosities and/or b) too long lifetimes. Of course these aspects are interrelated as they are both highly sensitive to model details dealing with two crucial
processes that affect the evolution of these stars, namely HBB and
mass loss by stellar winds.
yr should be
ascribed to an overestimation of the TP-AGB phase of more massive AGB models, which translates into either a) too high luminosities and/or b) too long lifetimes. Of course these aspects are interrelated as they are both highly sensitive to model details dealing with two crucial
processes that affect the evolution of these stars, namely HBB and
mass loss by stellar winds.
Given the high degree of uncertainty that affects the theoretical
predictions for ![]() along the AGB phase,
the theoretical discrepancy is likely attributed to an
underestimation of the mass-loss efficiency in massive AGB stars.
A simple remedy could be obtained artificially just introducing a
multiplicative factor in front of our mass-loss law (similar to
the
along the AGB phase,
the theoretical discrepancy is likely attributed to an
underestimation of the mass-loss efficiency in massive AGB stars.
A simple remedy could be obtained artificially just introducing a
multiplicative factor in front of our mass-loss law (similar to
the ![]() parameter of the Reimers law) for
parameter of the Reimers law) for
![]() ,
but in this case we would introduce a discontinuity in our adopted formalism for
,
but in this case we would introduce a discontinuity in our adopted formalism for ![]() ,
as
the correction factor should then vanish at lower
,
as
the correction factor should then vanish at lower ![]() .
.
After a general re-consideration of the many prescriptions of our synthetic TP-AGB model, we have found that a more physically-sound way to obtain higher mass-loss rates may come from an improved treatment of the pulsation properties of the most massive AGB stars, compared to the original description given in Paper I.
Specifically, following the results of non-adiabatic pulsation models
of Fox & Wood (1982) for stellar masses
![]() ,
it seems
likely that in Paper I the switching of the pulsation mode from the
first overtone to the fundamental one has been assumed to occur at too
high luminosities in the most massive TP-AGB models.
,
it seems
likely that in Paper I the switching of the pulsation mode from the
first overtone to the fundamental one has been assumed to occur at too
high luminosities in the most massive TP-AGB models.
We recall that the critical luminosity, L1-0, is defined as the luminosity at
which the growth rates of the first overtone mode and the fundamental
mode are equal. In Paper I the critical luminosity has been derived from the
pulsation models calculated by Ostlie & Cox (1986) in the mass range
![]() ,
and the fitting relation is given by
,
and the fitting relation is given by
| (A.3) |
![\begin{figure}
\par\includegraphics[width=8.55cm,clip]{8467fA2.ps}\end{figure}](/articles/aa/full/2008/18/aa8467-07/Timg299.gif) |
Figure A.2:
Transition luminosity defining the switching from fundamental
mode to first-overtone pulsation mode, as a function of the current
stellar mass, assuming Z=0.008 and
|
| Open with DEXTER | |
The new formula for the critical luminosity L1-0 is used to
re-calculate the TP-AGB evolution of models with initial masses
![]() for all choices of the metallicity.
Massive models start to pulsate in the fundamental mode at lower
luminosities than assumed in Paper I, which favours the attainment of
larger mass-loss rates with consequent earlier termination of the AGB phase. This effect is more pronounced at larger masses (
for all choices of the metallicity.
Massive models start to pulsate in the fundamental mode at lower
luminosities than assumed in Paper I, which favours the attainment of
larger mass-loss rates with consequent earlier termination of the AGB phase. This effect is more pronounced at larger masses (
![]() )
shortening the TP-AGB lifetimes by a factor of 2-5. The impact on the integrated V-K colours is good as we see in
Fig. A.1. The jump at
)
shortening the TP-AGB lifetimes by a factor of 2-5. The impact on the integrated V-K colours is good as we see in
Fig. A.1. The jump at
![]() yr is reduced and a
more gradual increase of the colour proceeds at larger ages, allowing
for the seeked consistency with the observations. Similar results are
obtained for other integrated colours, like J-K, and H-K.
yr is reduced and a
more gradual increase of the colour proceeds at larger ages, allowing
for the seeked consistency with the observations. Similar results are
obtained for other integrated colours, like J-K, and H-K.
It should also be emphasized that the TP-AGB fuel at ages
![]() yr cannot be arbitrarily cut down since otherwise we would
run into other problems related to the observed properties of the
most luminous AGB stars and their progeny. For instance, we have
verified that even invoking an extreme shortening of the TP-AGB phase
for these stars, the predicted integrated V-K and J-K colours are
still consistent with the observed ones, but in this case we cannot
fulfill the nucleosynthesis constraint set by type I planetary
nebulae. Such objects are characterized by high He and N abundances,
which are currently interpreted as the result of hot-bottom burning in
more massive AGB stars (e.g., Marigo et al. 2003b; Pottasch &
Bernard-Salas 2006). An overly-short activation of the CNO cycle at the
base of the convective envelope would not allow the massive AGB progenitors to reach the He and N surface enrichment measured in type I planetary nebulae. In other
words, the nuclear fuel burnt during the TP-AGB phase cannot be
constrained only on the basis of the integrated luminosities, but it
should also be checked against indications provided by abundance
analyses in the stellar ejecta. In fact, as extensively discussed by
Marigo & Girardi (2001) a precise fraction of the nuclear fuel
consumption (emitted light) in post-main sequence stars ends in the
form of chemical (mainly He, N, O) yields. One cannot produce large
amounts of He and N in the most massive AGB stars (as observed in
their PN descendants), without adding a marked contribution of these same stars to the
integrated light.
yr cannot be arbitrarily cut down since otherwise we would
run into other problems related to the observed properties of the
most luminous AGB stars and their progeny. For instance, we have
verified that even invoking an extreme shortening of the TP-AGB phase
for these stars, the predicted integrated V-K and J-K colours are
still consistent with the observed ones, but in this case we cannot
fulfill the nucleosynthesis constraint set by type I planetary
nebulae. Such objects are characterized by high He and N abundances,
which are currently interpreted as the result of hot-bottom burning in
more massive AGB stars (e.g., Marigo et al. 2003b; Pottasch &
Bernard-Salas 2006). An overly-short activation of the CNO cycle at the
base of the convective envelope would not allow the massive AGB progenitors to reach the He and N surface enrichment measured in type I planetary nebulae. In other
words, the nuclear fuel burnt during the TP-AGB phase cannot be
constrained only on the basis of the integrated luminosities, but it
should also be checked against indications provided by abundance
analyses in the stellar ejecta. In fact, as extensively discussed by
Marigo & Girardi (2001) a precise fraction of the nuclear fuel
consumption (emitted light) in post-main sequence stars ends in the
form of chemical (mainly He, N, O) yields. One cannot produce large
amounts of He and N in the most massive AGB stars (as observed in
their PN descendants), without adding a marked contribution of these same stars to the
integrated light.