All Figures

$\begin{figure} \par\includegraphics[width=6.7cm,clip]{5295f1.eps} \end{figure}$ Figure 1: Schematic illustration of the cosmic ray momentum spectrum in our two parameter model. We adopt a simple power-law description, where the slope of the cosmic ray spectrum is given by a spectral index $\alpha$ , kept constant throughout our simulation. The normalization of the spectrum is given by the variable C, and the low-momentum cut-off is expressed in terms of a dimensionless variable q, in units of $m_{\rm p} c$ where $m_{\rm p}$ is the proton rest mass.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{5295f2.eps} \end{figure}$ Figure 2: The function $\beta _\alpha (q)$ introduced in Eq. (5), for several different values of the spectral slope $\alpha$ .
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{5295f3.eps} \end{figure}$ Figure 3: The distribution of cosmic ray energy per unit logarithmic interval of proton momentum, for several different values of the spectral slope $\alpha$ . The distributions have been normalized to $\tilde{\varepsilon}(0)$ in each case.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{5295f4.eps} \end{figure}$ Figure 4: Cosmic ray pressure in units of the cosmic ray energy density, as a function of the spectral cut-off q. Except in the transition region from non-relativistic to relativistic behaviour, the cosmic ray pressure depends only weakly on q. In the ultra-relativistic regime, the ratio approaches $P_{\rm CR}/({\rho ~ \tilde\varepsilon}) \simeq (4/3-1)$ , which is shown as the lower dotted line. The upper dotted line gives the expected value of (5/3-1) for an ideal gas. For the same energy content, cosmic rays always contribute less pressure than thermal gas.
Open with DEXTER

In the text

$\begin{figure} \par\hspace*{-2mm}\includegraphics[width=7cm,clip]{5295f5a.eps}\vspace*{3mm} \includegraphics[width=6.55cm,clip]{5295f5b.eps} \end{figure}$ Figure 5: The top panel shows the cooling times due to Coulomb losses (rising solid line) and hadronic dissipation (nearly horizontal line) as a function of the spectral cut-off. The dot-dashed line gives the total cooling time, while the vertical dashed lines marks the asymptotic equilibrium cut-off reached by the CR spectrum when no sources are present. The bottom panel shows the cooling time of ordinary thermal gas due to radiative cooling (for primordial metallicity), as a function of temperature. The horizontal dashed line marks the cooling time of CRs with a high momentum cut-off ( $q\gg 1$ ), for comparison. In both panels, the times have been computed for a gas density of $\rho = 2.386$ $\times$ $10^{-25}~{\rm g~cm^{-3}}$ , which corresponds to the density threshold for star formation that we usually adopt. Note however that the cooling times all scale as $\tau \propto 1/\rho$ , i.e. for different densities only the vertical scale would change but the relative position of the lines would remain unaltered.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7cm,clip]{5295f6.eps} \end{figure}$ Figure 6: The total cooling time due to Coulomb losses and hadronic dissipation as a function of the spectral cut-off, for different assumptions about the slope of the spectrum ( $\alpha =2.01$ , 2.1, 2.5 and 2.99, as labelled). For low values of the cut-off, in the regime dominated by Coulomb cooling, the cooling time depends quite sensitively on $\alpha$ . However, after a relatively short time, the cut-off of a cooling population moves to $q\sim 1$ and beyond, at which point the cooling shifts into the hadronically dominated regime, where it does not depend strongly on $\alpha$ any more.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{5295f7.eps} \end{figure}$ Figure 7: Pressure of the cosmic ray population predicted for equilibrium between supernova injection on one hand, and Coulomb cooling and catastrophic losses on the other hand. The solid lines mark the pressure as a function of overdensity for two values of the injection efficiency $\zeta _{\rm SN}$ . The assumed threshold density for star formation, $\rho _0 =2.4$ $\times$ $10^{-25}~{\rm g~cm^{-3}}$ , is derived from the multiphase model of Springel & Hernquist (2003a). The latter also predicts an effective equation of state for the star forming phase, shown as a dot-dashed line. The part below the threshold is an isothermal equation of state with temperature $10^4~{\rm K}$ .
Open with DEXTER

In the text

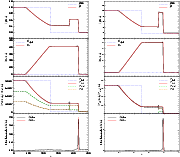$\begin{figure} \par\resizebox{!}{14cm}{\includegraphics{5295f8a.eps}}\resizebox{!}{14cm}{\includegraphics{5295f8b.eps}}\end{figure}$ Figure 8: Shock-tube tests for a gas with thermal and cosmic ray pressure components. The simulations are carried out in a three-dimensional periodic box which is longer in the x-direction than in the other two dimensions. The numerical result of the averaged hydrodynamical quantities of all SPH particles within bins with a spacing equal to the interparticle separation of the denser medium is shown in black and compared with the analytic result in colour. The typical rms-scatter in each bin among the particles is $\sim$ $10\%$ , reflecting the typical level of SPH noise for irregular particle distributions. The particle mass was constant and chosen such that the mean particle spacing was 1 length unit in the high-density regime (meaning that there were initially 250 particles along the x-axis in the left half and 146 in the right half of the tube). In the test shown on the left, the relative CR pressure is $X_{\rm CR} = P_{\rm CR} / P_{\rm th} = 2$ in the left half-space (x<250), while we assume pressure equilibrium between CRs and thermal gas for x>250. The evolution then produces a Mach number ${\mathcal M}=3$ shock wave. In this test, CR acceleration was disregarded at the shock front, so the cosmic ray component is merely adiabatically compressed by the shock. In the test shown on the right, the shock-tube was initially filled with purely thermal gas ( $\gamma = 5/3$ ), and with a higher pressure ratio of 4625 at the initial interface. A shock with Mach number ${\mathcal M}=30$ develops and propagates to the right, and here we include cosmic ray acceleration at the shock front. We see that our numerical method correctly captures the production of cosmic rays by the shock, as the good agreement with the analytic solution of the Riemann problem demonstrates. To derive the latter (see Pfrommer et al. 2007, in preparation), we assumed a sufficiently strong shock that injects a hard population of CRs for which their ultra-relativistic equation of state holds.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=4.5cm,clip]{5295f9a.eps}\hspace*{5mm} ... ...e.eps}\hspace*{5mm} \includegraphics[width=4.5cm,clip]{5295f9f.eps} \end{figure}$ Figure 9: Time evolution of a step function in cosmic ray energy density due to diffusion, for a gas that is at rest. The times shown in the different panels are ( from top left to bottom right): t = 0, 0.1, 0.2, 0.5, 1.0 and $2.0~{{\rm Gyr}}$ . Black dots give particle values at the corresponding time, while the red line shows the analytical solution. The initial distribution is indicated by a thin dashed line. The diffusivity $\tilde \kappa$ is constant at $1~{\rm kpc^2~Gyr^{-1}}$ on the left hand side, and four times higher on the right hand side. A ``glass'' like particle distribution was used with a mean particle separation of $1~{\rm kpc}$ . A constant spectral cut-off and slope was assumed throughout the volume. The maximum deviation of SPH particles from the analytic results drops from $L_\infty = 0.33$ at $t= 0.1 ~{{\rm Gyr}}$ to $L_\infty = 0.039$ at $t= 2.0 ~{{\rm Gyr}}$ , while the mean relative error per particle in the range $-10 ~{{\rm kpc}}\le x \le 10~{{\rm kpc}}$ is always below $L_1 \le 0.01$ .
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[height=6.7cm,width=6.8cm,clip]{5295f10a.eps}... ...6mm} \includegraphics[height=6.7cm,width=6.55cm,clip]{5295f10d.eps} \end{figure}$ Figure 10: Time evolution of the star formation rate in isolated halos of different mass which are initially in virial equilibrium. In each panel, we compare the star formation rate in simulations without cosmic ray physics (solid red line) to two runs with different injection efficiency of cosmic rays by supernovae, $\zeta _{\rm SN}=0.1$ (blue lines) and $\zeta _{\rm SN}=0.3$ (green lines), respectively. From top left to bottom right, results for halos of virial mass $10^{9}~h^{-1}~{M}_\odot$ to $10^{12}~h^{-1}~{M}_\odot$ are shown, as indicated in the panels. Efficient production of cosmic rays can significantly reduce the star formation rate in very small galaxies, but it has no effect in massive systems.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{5295f11a.eps}\hspace*{3mm} \includegraphics[width=7.2cm,clip]{5295f11b.eps} \end{figure}$ Figure 11: Phase-space diagram of the star-forming phase in two simulations with halos of different mass. In these fiducial simulations, we included cosmic ray physics but ignored the cosmic ray pressure in the equations of motion, i.e. there is no dynamical feedback by cosmic rays. However, a comparison of the cosmic ray pressure and the thermal pressure allows us to clearly identify regions where the cosmic rays should have had an effect. For graphical clarity, we plot the pressures in terms of a corresponding effective temperature, $T_{\rm eff}= (\mu /k) P / \rho$ . Above the star formation threshold, the small galaxy of mass $10^{9}~h^{-1}~{M}_\odot$ shown in the left panel has a lot of gas in the low-density arm of the effective equation of state, shown by the curved dashed line. On the other hand, the massive $10^{12}~h^{-1}~{M}_\odot$ galaxy shown on the right has characteristically higher densities in the ISM. As a result, the cosmic ray pressure is insufficient to affect this galaxy significantly. Note that the falling dashed line marks the expected location where cosmic ray loss processes balance the production of cosmic rays by supernovae. We show the systems at time $t= 2.0 ~{{\rm Gyr}}$ after the start of the evolution.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{5295f12.eps} \end{figure}$ Figure 12: Efficiency of star formation as a function of halo mass in our isolated disk formation simulations. We show the ratio of the stellar mass formed to the total baryonic mass in each halo, at time $t=3.0~{\rm Gyr}$ after the start of the simulations, and for two different efficiencies of cosmic ray production by supernovae. Comparison with the case without cosmic ray physics shows that star formation is strongly suppressed in small halos, by up to a factor $\sim$ 10-20, but large systems are essentially unaffected.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[height=4.3cm,width=1.1cm,clip]{5295f13w.eps}... ...5mm} \includegraphics[height=4.3cm,width=4.5cm,clip]{5295f13l.eps} \end{figure}$ Figure 13: Effect of cosmic ray feedback on star formation in simulations of isolated disk galaxy formation. Each row shows results for a different halo mass, for $M_{\rm halo} = 10^9$ , 10¹⁰, 10¹¹ and $10^{12}~h^{-1}~{M}_\odot$ from top to bottom. We compare the projected gas density fields at time $t= 2.0 ~{{\rm Gyr}}$ of runs without cosmic ray feedback ( left column) to that of runs with cosmic ray production by supernovae ( middle column). The gas density field is colour-coded on a logarithmic scale. For the simulation with cosmic rays, we overplot contours that show the contribution of the projected cosmic ray energy density to the total projected energy density (i.e. thermal plus cosmic rays), with contour levels as indicated in the panels. Finally, the right column compares the azimuthally averaged stellar surface density profiles at time $t= 2.0 ~{{\rm Gyr}}$ for these runs. Results for simulations without cosmic ray physics are shown with a solid line, those for simulations with CR feedback with a dot-dashed line.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.6cm,clip]{5295f14.eps} \end{figure}$ Figure 14: Resolution study of the star formation rate during the formation of a galactic disk in a halo of mass $10^{10}~h^{-1}~{M}_\odot$ , including production of CRs with an efficiency of $\zeta _{\rm SN}=0.1$ . We compare results computed with 10³, 10⁴, 10⁵, 4 $\times$ 10⁵, and 1.6 $\times$ 10⁶ gas particles, respectively.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.1cm,clip]{5295f15.eps} \end{figure}$ Figure 15: Relative suppression of star formation in simulations of isolated halos when a fraction of 0.3 of the initial thermal pressure is replaced by a CR component of equal pressure. We show results as a function of halo virial mass for two different times after the simulations were started, for $t=1.0~{\rm Gyr}$ (solid line), and for $t=3.0~{\rm Gyr}$ (dot-dashed). For halos of low mass, the cosmic ray pressure contribution can delay the cooling in the halos.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.1cm,clip]{5295f16a.eps}\vspace*{5mm} \includegraphics[width=7.1cm,clip]{5295f16b.eps} \end{figure}$ Figure 16: Time evolution of the mean thermal energy and the cosmic ray energy content of the gas in non-radiative cosmological simulations. In the top panel, the solid thick line shows the mass-weighted temperature for a simulation where the efficiency of cosmic ray production at structure formation shocks is treated based on our on-the-fly Mach number estimator. The dashed line is the corresponding mean cosmic ray energy, which we here converted to a fiducial mean temperature by applying the same factor that converts thermal energy per unit mass to temperature. For comparison, the thin solid line shows the evolution of the mean mass-weighted temperature in an ordinary non-radiative simulation without cosmic ray physics. In the bottom panel, we show the ratio of the mean thermal energy in the cosmic ray case relative to the energy in the simulation without cosmic rays (solid line), while the dashed line is the corresponding ratio for the cosmic ray component. Finally, the dotted line gives the total energy in the cosmic ray simulation relative to the ordinary simulation without cosmic rays.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7cm,clip]{5295f17a.eps}\hspace*{0.9cm} \includegraphics[width=7cm,clip]{5295f17b.eps} \end{figure}$ Figure 17: Mean relative contribution of the cosmic ray pressure to the total pressure, as a function of gas overdensity in non-radiative cosmological simulations. We show measurements at epochs z=0, 1, 3, and 6. The panel on the left gives our result for a simulation where the injection efficiency and slope of the injected cosmic ray spectrum are determined based on our on-the-fly Mach number estimation scheme. For comparison, the panel on the right shows the result for a simulation with a fixed injection efficiency $\zeta _{\rm lin}=0.5$ and a soft spectral injection index of $\alpha _{\rm inj}=2.9$ . Clearly, the relative contribution of cosmic ray pressure becomes progressively smaller towards high densities. It is interesting that the trends with redshift are reversed in the two cases.
Open with DEXTER

In the text

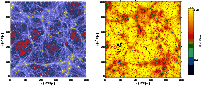$\begin{figure} \par\mbox{\resizebox{8.3cm}{!}{\includegraphics{5295f18a.eps}}\re... ...95f18b.eps}}\resizebox{!}{8.3cm}{\includegraphics{5295f18c.eps}} } \end{figure}$ Figure 18: Projected gas density field ( left panel) in a slice of thickness $20~h^{-1}~{\rm Mpc}$ through a non-radiative cosmological simulation at z=0. The simulation includes cosmic ray production at structure formation shocks using Mach-number dependent efficiencies based on an on-the-fly Mach number estimation scheme. The panel on the right shows the ratio of the projected cosmic ray energy density to the projected thermal energy density. We clearly see that the local contribution of cosmic rays is largest in voids. It is also still large in the accretion regions around halos and filaments, but is lower deep inside virialized objects.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5295f19.eps} \end{figure}$ Figure 19: Mean baryon fraction within the virial radius as a function of halo mass, normalized by the universal baryon fraction. We compare results for two non-radiative simulations, one with cosmic ray production by shocks, the other without cosmic ray physics. The bars show the $1\sigma$ scatter among the halos in each bin. When cosmic rays are included, the compressibility of the gas in halos becomes larger, leading to a slight increase of the enclosed baryon fraction.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5295f20.eps} \end{figure}$ Figure 20: Ratio of energy in cosmic rays to thermal energy within the virialized region of halos, shown as a function of halo mass. We compare results for two different non-radiative simulations, one treating the production of cosmic ray at shocks fronts using a Mach number estimator, the other invoking a constant injection efficiency. The bars give the $1\sigma$ scatter among the halos in each bin. Interestingly, the Mach-number dependent injection scheme predicts a lower CR energy content in more massive systems. In contrast, a constant shock injection efficiency produced no significant trend of the CR energy content with halo mass.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5295f21.eps} \end{figure}$ Figure 21: Evolution of the cosmic star formation rate density in simulations of galaxy formation at high redshift. We compare results for three simulations that include different physics, a reference simulation without cosmic ray physics, a simulation with CR production by supernovae, and a third simulation which in addition accounts for CR acceleration at structure formation shocks with an efficiency that depends on the local Mach number.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5295f22.eps}\end{figure}$ Figure 22: Comparison of the averaged total mass-to-light-ratio within the virial radius of halos formed in two high-resolution cosmological simulations up to z=3. Both simulations follow radiative cooling and star formation, but one also includes CR-feedback in the form of cosmic production by supernovae, with an efficiency of $\zeta _{\rm SN}=0.35$ and an injection slope of $\alpha _{\rm SN}=2.4$ . The bars indicate the scatter among halos in the logarithmic mass bins (68% of the objects lie within the range marked by the bars). Clearly, for halo masses below $10^{11}~h^{-1}~{M}_\odot$ , CR feedback progressively reduces the overall star formation efficiency in the halos.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{5295f23.eps} \end{figure}$ Figure 23: The K-band galaxy luminosity functions at z=3 in two high-resolution cosmological simulations. One of the simulations follows ordinary radiative cooling and star formation only (blue), the other additionally includes cosmic ray production by supernovae (red). The latter reduces the faint-end slope of the Schechter function fit (solid lines) to the data measured from the simulations (histograms). It is reduced from -1.15 to -1.10 in this case.
Open with DEXTER

In the text

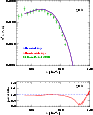$\begin{figure} \par\resizebox{8.3cm}{!}{\includegraphics{5295f24a.eps}}\\ % \resizebox{8.3cm}{!}{\includegraphics{5295f24b.eps}} % \end{figure}$ Figure 24: Ly- $\alpha$ flux power spectrum ( top) at z=3 in simulations with and without cosmic ray production in structure formation shocks. The results lie essentially on top of each other, and only by plotting their ratio ( bottom panel), it is revealed that there are small differences. In the simulation with cosmic rays, the power is suppressed by up to $\sim$ $15\%$ on scales $0.1~{\rm km^{-1}s} < k < 0.7~{\rm km^{-1}s}$ , while there is an excess on still smaller scales. However, on large scales $k< 0.1~{\rm km^{-1}s}$ , which are the most relevant for determinations of the matter power spectrum from the Ly- $\alpha$ forest, the power spectrum is not changed by including CR physics. For comparison, we have also included observational data from McDonald et al. (2000) in the top panel (the open symbols are corrected by removing metal lines). A slightly warmer IGM in the simulations could account for the steeper thermal cut-off observed in the data.
Open with DEXTER

In the text

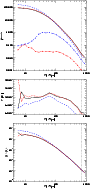$\begin{figure} \par\resizebox{8.2cm}{!}{\includegraphics{5295f25a.eps}}\vspace*{... ...cm}\\ % \resizebox{8.2cm}{!}{\includegraphics{5295f25c.eps}} % \\ % \end{figure}$ Figure 25: Spherically averaged radial profiles of thermodynamic gas properties in three re-simulations of the same cluster of galaxies. All three simulations were not following radiative cooling and star formation, and the reference simulation shown with a solid line does not include any CR physics. However, the simulation shown with a dashed line accounted for CR production at structure formation shocks with a fixed efficiency ( $\zeta _{\rm inj}=0.5$ , $\alpha _{\rm inj}=2.9$ ) while for the simulation shown with dot-dashed lines, the shock injection efficiency was determined with our Mach number estimation scheme. The panel on top compares the thermal pressure in the three simulations. For the two simulations with cosmic rays, we additionally plot the CR-pressure, marked with symbols. The panel in the middle compares the gas temperature, while the panel on the bottom shows the radial run of the gas density. The vertical dotted line marks the virial radius of the cluster.
Open with DEXTER

In the text

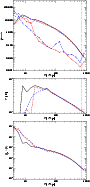$\begin{figure} \par\resizebox{8.2cm}{!}{\includegraphics{5295f26a.eps}}\vspace*{... ...esizebox{8.2cm}{!}{\includegraphics{5295f26c.eps}}\vspace*{-0.2cm}% \end{figure}$ Figure 26: Spherically averaged radial profiles of thermodynamic gas properties in three re-simulations of the same cluster of galaxies. All three simulations included radiative cooling of the gas, star formation and supernova feedback. The solid lines show the results of a reference simulation which did not include any cosmic ray physics. The other two simulations included CR production by supernovae, and the one shown with dot-dashed lines in addition accounted for CR injection at structure formation shocks, using Mach-number dependent efficiencies based on our Mach number estimation scheme. The panel on top compares the thermal pressure in the three simulations. For the two simulations with cosmic rays, we additionally plot the CR-pressure marked with symbols. The panel in the middle compares the gas temperature for the three cases, and the panel on the bottom shows the radial run of the gas density.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{5295f27.eps} \end{figure}$ Figure 27: Cumulative radial stellar mass profile in three re-simulations of the same cluster of galaxies. The simulations are the same ones also shown in Fig. 26. The solid line gives the result for a reference simulation without CR physics, the dashed line includes CR production by supernovae, and the dot-dashed line additionally accounts for CR injection at structure formation shocks. The vertical dotted line marks the virial radius of the cluster.
Open with DEXTER

In the text

$\begin{figure} \par {\hspace*{15mm}\includegraphics[height=6.7cm,width=6.8cm,cli... ...*{8mm} \includegraphics[height=6cm,width=1.15cm,clip]{5295f28z.eps} \end{figure}$ Figure 28: Effects of cosmic ray diffusion on the star formation and the pressure distribution in isolated halos of mass $10^{9}~h^{-1}~{M}_\odot$ and $10^{10}~h^{-1}~{M}_\odot$ . The panels on top compare the star formation rate when CR diffusion is included (thick blue line) to the case where it is neglected (thin green line). The dotted lines show the result when CR-production by supernovae is not included. In the bottom panels, we show projected gas density fields through the halos at time $t= 2.0 ~{{\rm Gyr}}$ , with contours overlaid that give the fractional contribution of the projected CR energy to the total projected energy. These panels correspond directly to equivalent maps shown in Fig. 13 for the case without CR diffusion.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{5295f2.eps} \end{figure}$	Figure 2: The function $\beta _\alpha (q)$ introduced in Eq. (5), for several different values of the spectral slope $\alpha$ .
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.3cm,clip]{5295f3.eps} \end{figure}$	Figure 3: The distribution of cosmic ray energy per unit logarithmic interval of proton momentum, for several different values of the spectral slope $\alpha$ . The distributions have been normalized to $\tilde{\varepsilon}(0)$ in each case.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.6cm,clip]{5295f14.eps} \end{figure}$	Figure 14: Resolution study of the star formation rate during the formation of a galactic disk in a halo of mass $10^{10}~h^{-1}~{M}_\odot$ , including production of CRs with an efficiency of $\zeta _{\rm SN}=0.1$ . We compare results computed with 10³, 10⁴, 10⁵, 4 $\times$ 10⁵, and 1.6 $\times$ 10⁶ gas particles, respectively.
Open with DEXTER