... recombination[*]
Appendix B is only available in electronic form at http://www.aanda.org 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... non-resonant[*]
We base our definition of this terminus on the energies of the involved intermediate states (see Sect. 2 for details). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... atom[*]
We restrict ourselves to the non-relativistic formulation of the hydrogen atom and assume that it is at rest in the lab frame. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... processes[*]
More rigorously, collisions more likely destroy the coherence for photons emitted very close to the line center, since in the distant wings the typical characteristic time of processes involving the corresponding quantum-states is much shorter (e.g. Karshenboim & Ivanov 2007). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... virtual[*]
Strictly speaking, photons appearing in the distant wings of the resonance are also connected with virtual states (e.g. Karshenboim & Ivanov 2007). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... like[*]
Within the non-relativistic treatment of the hydrogen atom, this is equivalent to separating the cases n<ni and $n\geq n_i$. Since the energy of the continuum states is always greater than for the bound states, the former are associated with the case $n\geq n_i$. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... interference[*]
In principle one should be more accurate by calling this contribution resonant/non-resonant-interference term, since also some level of interference is already included inside the resonant and non-resonant-term, which is absent in the 1+1-photon picture. However, we generally do not make this distinction. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... 1s-level[*]
The authors wish to thank E.E. Kholupenko for pointing out some inaccuracies related to this aspect. However, the modification did not affect the results of this paper. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... energy[*]
We neglect the small correction to the real part of the energy caused by the Lamb-shift. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... s/d-state[*]
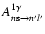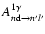Here $A^{1\gamma}_{n{\rm s/d}\rightarrow n'l'}$ refers to either the $A^{1\gamma}_{n{\rm s}\rightarrow n'l'}$ or the $A^{1\gamma}_{n{\rm d}\rightarrow n'l'}$ decay rate. We use this notation more often below. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... by[*]
The factor of 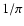$1/\pi$ is required due to the normalization of L(a, b). 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
... used[*]
In both cases the branching ratios are very close to unity. 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Copyright ESO 2008