A&A 478, 429-434 (2008)
DOI: 10.1051/0004-6361:20066802

Gravitational lensing as a probe of compact object populations in the Galaxy

S. Os\lowski1 - R. Moderski2 - T. Bulik1,2 - K. Belczynski3,[*]


1 - Astronomical Observatory, Warsaw University, Aleje Ujazdowskie 4, 00478 Warsaw, Poland
2 - Nicolaus Copernicus Astronomical Center, Bartycka 18, 00716 Warsaw, Poland
3 - Department of Astronomy, New Mexico State University, Frenger Mall, Las Cruces, NM, USA

Received 23 November 2006 / Accepted 4 October 2007

Abstract
Aims. The population of solitary compact objects in the Galaxy is very difficult to investigate. In this paper we examine the possibility of using microlensing searches to detect and to analyze the properties of solitary black holes and neutron stars.
Methods. Evolution of single and binary stars is followed using the StarTrack population synthesis code. The spatial distribution of compact objects in the Galaxy is determined by propagating them in the Galactic gravitational potential. Lensing events are found by tracing individual stars and compact objects.
Results. We find that compact object lensing events are concentrated in a region with a radius of $\approx $5 degrees around the Galactic center. The distribution of masses of the lenses for the models we consider differs, but only slightly, from the underlying mass distribution of compact objects. The expected detection rates are of the order of a few per year.

Key words: gravitational lensing - Galaxy: stellar content

1 Introduction

Assuming that the supernova rate in the Galaxy is about 10-2 yr-1, the Galactic population of compact objects - neutron stars and black holes - numbers somewhere between 107 and 109 objects. Most of them are solitary and only a small fraction resides in binaries. A small fraction of solitary neutron stars is visible as radio pulsars. The properties of black holes and neutron star populations in our Galaxy depend on the history of star formation rate, evolution of metallicity, on the initial mass function, and on details of compact object formation in supernovae explosions.

The properties of the population of solitary black holes can only be investigated indirectly, through observation of their interaction with the interstellar matter or light emitted by stars. Solitary black holes should be accreting gas from the interstellar medium. Therefore some of them should be observable in X-rays (Beskin & Karpov 2005; Agol & Kamionkowski 2002). The luminosity in X-rays , on the one hand, is less than for solitary neutron stars, where the surface emission plays a significant role, but on the other hand it may be increased due to the fact that black holes may have lower velocities with respect to the interstellar medium and higher masses in comparison with neutron stars. Searches for such objects have not been successful thus far.

Solitary black holes are also detectable with current microlensing searches (Paczynski 2003) like OGLE (Udalski 2003) and MOA (Bond et al. 2001). These campaigns have already yielded several black hole detections. Bennett et al. (2002) have presented two events: MACHO 96-BLG-5 and MACHO 98-BLG-6, with the mass estimates $6^{+10}_{-3}~M_{\odot}$ and $6^{+7}_{-3}~M_{\odot}$ respectively. Mao et al. (2002) showed that EWS 1999-BUL-32, identified also as MACHO 99-BLG-22, is a black hole candidate with a minimum mass of $10.5~M_{\odot}$. A further search for X-rays from MACHO 96-BLG-5 (Maeda et al. 2005) yielded an upper limit corresponding to a luminosity of less than (8- $9)\times 10^{-10}$ of its Eddington luminosity. A recent likelihood analysis of 22 microlensing events by Poindexter et al. (2005) lead to confirmation of the black hole candidate MACHO 99-BLG-22, while the other candidates are less probable.

Determination of the mass of an object with gravitational lensing is difficult because of the severe degeneracy between the parameters. However,it has been shown that these degeneracies can be broken to reveal bounds on the true mass of the lens. In order to achieve this one needs long lasting events for which the effects of microlens parallax can be measured. This still leaves a degeneracy between the lens mass and the relative distance of the source and the lens. However, bounds on the mass of the lens can be placed by statistical analysis of the probability distribution of a lensing event with observed properties given the mass and velocity distribution of stars in the Galaxy (Mao et al. 2002; Bennett et al. 2002). A detailed analysis of the microlens parallax and and bounds on the masses of lenses is presented by Poindexter et al. (2005)

The sample of microlensing by compact objects and black hole candidates will increase with time. It is therefore interesting to determine what constraints can be imposed by these observations on models of compact object formation and evolution. In this paper we present a simulation of the stellar evolution leading to the production of solitary black holes and neutron stars in our Galaxy. We analyze two scenarios: single stellar evolution and the formation of solitary compact objects through disruption of binaries. We then examine the motion of black holes and neutron stars in the Galactic potential and search for possible microlensing events observable from the Earth.

In Sect. 2 we present the basic ingredients of the calculation: the stellar evolution model, the Galactic potential, mass distribution used, and the lensing search algorithm. Section 3 contains the results and Sect. 4 the discussion.

   
2 Description of the model

In order to model the population of compact objects in the Galaxy we use the model of stellar single and binary evolution described below in Sect. 2.1. Each star is initially placed in the Galactic disc with a local rotational velocity and it moves in the Galactic potential described in Sect. 2.2. We take into account the kick velocities obtained in supernova explosions and binary disruptions (Blaauw 1961; Hobbs et al. 2005) and follow the motion of each compact object. We also populate the Galaxy with other stars that can be lensed by the compact objects and search for lensing events with the algorithm described in Sect. 2.3.

   
2.1 Compact object formation

The single star evolution is modeled using the modified formulae of Hurley et al. (2000) as presented by Belczynski et al. (2005) and we use the StarTrack population synthesis code (Belczynski et al. 2002a) to model binary evolution. The StarTrack population synthesis code was initially developed for the study of double compact object mergers in the context of gamma-ray bursts progenitors (Belczynski et al. 2002a) and gravitational-wave inspiral sources (Belczynski et al. 2002b). In recent years StarTrack has undergone major updates and revisions in the physical treatment of various binary evolution phases. For a detailed description of the revised code we refer the reader to Belczynski et al. (2005).

The simplest scenario leading to a single compact object is through evolution of single stars (model S). In this case a newly formed compact object receives a kick velocity (Hobbs et al. 2005). This is later used in the dynamical calculation of motion of the compact object in the Galactic gravitational potential.

Additional formation scenarios for solitary compact objects stems from the binary progenitors. For the standard model of evolution we denote it as model A. A binary already can be disrupted as a result of the first supernova explosion. A large fraction (0.8 for the binaries, where both components are massive enough to undergo a supernova explosion, see Belczynski & Bulik 1999) of binaries containing massive stars is disrupted in this way. This leads to the formation of a single compact object and a single companion which may still be massive enough to produce another compact object. The first supernova explosion takes place in the Galactic disc, where we initially place the stars with their Galactic rotational velocities and we add additional systemic velocities received as a result of the supernova explosion. We then follow each compact object as it moves in the Galactic potential.

A much smaller contribution comes from the disruption of a binary during the second supernova explosion since at this point the binary is already tight. In this case two single compact objects are formed. We follow the motion of the system after the first supernova until the second one. Thus the newly formed single compact objects start at the actual location of the second supernova, usually outside the disc, with appropriate velocities obtained in the disruption, and we then compute the trajectories of the two solitary compact objects.

Finally, we also investigate compact object formation through mergers - model M. This path usually leads to formation of a black hole. This includes mergers of stars during their nuclear evolution, as well as mergers of a compact object with a massive companion as a result of binary interaction. In the first case we assume that a single star is formed with a mass equal to the sum of the masses of the two merging components. Such a newly formed star may have higher metallicity than the initial one of the two stars because of their chemical evolution. We evolve this star neglecting the potential changes in metallicity. In general stars with higher metallicity lead to formation of compact objects with lower masses. In the case of a merger of a compact object with a massive companion we assume that a single black hole is formed with a mass equal to the sum of the masses of the compact object and the core of the companion while the envelope is expelled. The newly formed black holes do not gain additional velocity during mergers.

We ignore the contribution of double black hole systems, and single black holes formed in mergers of double black holes as they represent a much smaller population than the ones mentioned above (Belczynski et al. 2006).

We consider several models of binary evolution to assess the sensitivity of the results. We decrease the strength of the stellar winds which mainly affects the masses of the newly formed compact objects (model W05). A second parameter that may influence the results significantly is the distribution of the kicks received by the newly formed compact object. Apart from the standard model, in which the value of the kick is decreased with increasing fall-back mass, we consider two extreme cases. In the first model, black holes receive no kicks at all (model K0) and in the second one the kick distribution is the same for black holes as for neutron stars (model K1). Finally in model C we allow for survival in the CE evolution initiated by stars passing through the HG as opposed to the standard model in which we assume that such cases always lead to a merger (Belczynski et al. 2007).

The list of the models considered is shown in Table 1.

Table 1: Models of compact object formation considered in this paper.

   
2.2 Galactic model

We consider a model of the Galaxy consisting of three components: bulge, disc, and halo. The bulge and disc potentials are described by the Miyamoto & Nagai (1975) type potential (Paczynski 1990; Bulik et al. 1999)

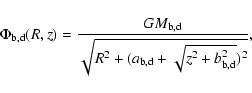\begin{displaymath}\Phi_{\rm b,d}(R,z) = \frac{GM_{\rm b,d}}{\sqrt{R^2 + (a_{\rm b,d} + \sqrt{z^2 + b_{\rm b,d}^2})^2} } , \end{displaymath} (1)

where M is the mass of a given component, R is the projection of the distance from the Galactic center, r, onto the Galactic plane, z is the height above the Galactic plane, and a, b are the parameters. Subscript b stands for the bulge component, while subscript d stands for the disc component.

The halo is described by the density distribution $\rho = \rho_{\rm c} [1+(r/r_{\rm c})^2]^{-1}$, where $\rho_{\rm c}$ is the characteristic density and $r_{\rm c}$ is the characteristic radius of the halo, with a cutoff at $r_{\rm cut}=100$ kpc, beyond which the halo density is zero. The corresponding potential for $r<r_{\rm cut}$ is

\begin{displaymath}\Phi_{\rm h}(r) = - \frac{GM_{\rm h}}{r_{\rm c}} \left[ \frac... ...c}}{r} \arctan\left(\frac{r}{r_{\rm c}} \right) \right] \cdot \end{displaymath} (2)

We use the following values of the parameters (Blaes & Rajagopal 1991) describing the potentials: $a_{\rm b}=0$ kpc, $b_{\rm b}=0.277$ kpc, $a_{\rm d}=4.2$ kpc, $b_{\rm d}=0.198$ kpc, $M_{\rm b}=1.12 \times 10^{10} ~M_{\odot}$, $M_{\rm d} = 8.78 \times 10^{10} ~M_{\odot}$, $M_{\rm h}=5.0 \times 10^{10} ~M_{\odot}$, and $r_{\rm c}=6.0$ kpc.

The distribution of stars in the disc, P(R,z), is assumed to be that of a young disc (Paczynski 1990). The radial and vertical distributions are independent i.e. the distributions factor out:

 \begin{displaymath}P (R,z) \propto p(R) R{\rm d}R ~ p(z) {\rm d}z , \end{displaymath} (3)

where the radial distribution is

 \begin{displaymath}p(R) \propto \exp~(-R/R_{\exp}), \end{displaymath} (4)

$R_{\exp} = 4.5~$kpc, and we introduce an upper cutoff at $R_{\max}=20$ kpc, beyond which the distribution is zero. The vertical distribution is exponential $p(z) \propto \exp\left(-z/75~{\rm pc}\right)$ . This is not a self consistent approach since the matter density corresponding to the disc potential is not the same as the stellar density. A self consistent approach has been investigated by Bulik et al. (1998) using the potentials calculated by Kuijken & Gilmore (1989), who found that the differences influence the motion in the disc plane for large radii R>20 kpc, which is not relevant for this calculation.

   
2.3 Lens search algorithm

A naive search for lenses i.e. testing for events when a star and a compact object are aligned with Earth on its Galactic orbit would require nearly infinite computational resources. Therefore we look for the lens events that take place anywhere on the Galactic orbit of the Earth. This is much easier computationally as this approach makes use of the cylindrical symmetry of the Milky Way.

We assume that the Earth's orbit in the Galaxy is circular with a radius of 8.5 kpc. Let us consider a sphere $\cal S$ of radius $R_{\rm E} = 8.5$ kpc (which is equal to Earth's Galactic orbit radius) and centered in the center of the Galaxy. Let us also consider a star-lens system located somewhere in the Galaxy. The position of the system is characterized by two vectors: $\vec{P}$ - the position vector of the star in the Galaxy, and $\vec{D}$ - the star-lens vector (see Fig. 1). We search for a point Q in which the line passing through the position of the star and the lens pierces the sphere. The vector $\vec{R}$ can be calculated for each pair of a star and a compact object and it changes as the two move in the Galactic gravitational potential. Looking for lensing events is equivalent to searching for the cases when the line traced by the $\vec{R}$ on the sphere $\cal S$ crosses the orbit of the Earth.


  \begin{figure} \par\includegraphics[width=6.4cm,clip]{6802fig1.ps}\end{figure} Figure 1: Geometry of the lensing event. Star and the lens are located inside a sphere of radius $R_{\rm E}$ equal to the radius of the Earth's orbit. Vector $\vec{P}$ denotes the position of the star in the Galaxy, while $\vec{D}$ is a star-lens vector. We look for a situation when star-lens line crosses the Earth's orbit during the evolution of the system.
Open with DEXTER

We first look for the factor u which satisfies the condition

 \begin{displaymath}\left \vert \vec{P} + u\vec{D} \right \vert = \left \vert \vec{R}\right \vert = R_{\rm E} . \end{displaymath} (5)

Equation (5) is a quadratic equation in u

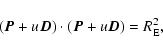\begin{displaymath}\left( \vec{P} + u\vec{D} \right) \cdot \left( \vec{P} + u\vec{D} \right) = R_{\rm E}^2 , \end{displaymath} (6)


 \begin{displaymath}D^2 u^2 + 2\vec{D} \cdot \vec{P} u + (P^2 - R_{\rm E}^2) = 0 . \end{displaymath} (7)

Providing that $\Delta = 4 \left( \vec{D} \cdot \vec{P} \right)^2 - 4 D^2 \left(P^2 - R_{\rm E}^2 \right) \geq 0$ Eq. (7) has a formal, real solution:

 \begin{displaymath}u_{1,2} = \frac{1}{D^2} \left[ -\vec{D} \cdot \vec{P} \pm \sq... ...P} \right)^2 - D^2 \left( P^2 - R_{\rm E}^2 \right)} \right] . \end{displaymath} (8)

Now, for each pair of a star and a compact object, we calculate $\Delta$ taking into account their position at the beginning of a calculation step. Let us denote the values corresponding to the end of a time step by primes. If $\Delta>0$ we calculate $\Delta'$ using the position of the pair at the end of the step, which in our calculations was one month. We look for lensing events in twelve such one month steps. If it is also positive, then we calculate both u1,2 and u'1,2, respectively. We are only interested in a configuration for which u1,2>1 and u'1,2>1. If u<0 the compact object is located behind the star, and for $0 \le u \le 1$ the compact object and the star reside inside and outside of the sphere $\cal S$, respectively. In both such cases the lensing event cannot be observed on Earth. For both u and u' we then calculate positions of the points defined by the vector $\vec{R}$ on the sphere at the beginning and at the end of the examined evolution period. The lensing event occurs when these points are located in different hemispheres (z'z<0). This is so because it means that the end of vector $\vec{R}$ crossed the Earth's orbit.

This algorithm is not sensitive to some special configurations when, during the evolution, the star or compact object are located outside the sphere at very high azimuthal angles (as seen from Earth). We checked for these special occasions with two additional algorithms. We conclude that such events are extremely rare (there was not even one such case) and do not influence our results. The results are also not sensitive to the specific choice of the orbit of the Earth, it does not have to lie exactly in the z=0 plane. We do not assume the symmetry with respect to this plane.

2.4 Lensing rate

In order to estimate the true lensing rate one has to scale the number of the lensing events found in the simulation to match the physical conditions in our Galaxy. There are two scaling factors involved. One results from the number of stars and compact objects used in the simulation and the second from the fact that we look for the lensing events that happen over the whole Earth orbit. Let us denote the Earth orbital period in the Milky way as $P_{\rm E} = 250$ Myr. Let the true number of stars in the Milky Way be $N^*=N^*_{11} \times 10^{11}$, and $f_{\rm lens} =10^{-2} f_{\rm lens,-2}$ represent the fraction of the stars in the Galaxy that can be detected by lens search experiments. This fraction can be estimated by integrating the distributions given by Eqs. (3) and (4) and assuming (a) that the limiting magnitude of microlensing searches is $m_{\rm V} = 18$, (b) that a typical lens is an $0.5~M_\odot$ main sequence star, and (c) that the field of view has a diameter of $10{\hbox{$^\circ$ }}$. The resulting value of $f_{\rm lens} =10^{-2}$ is consistent within an order of magnitude with the fact that OGLE monitors $1.2 \times 10^8$ stars. We assume that a compact object has been formed in the Galaxy every 100 yrs so that the number of compact objects in the Galaxy is $N^{\rm CO}=N^{\rm CO}_8\times10^8$. Our simulations include 106 stars that can be lensed. Thus the expected rate of lenses due to the compact objects per year is

 \begin{displaymath}{\cal R} = {f_{\rm lens}\over P_{\rm E}} N^* N^{\rm CO} {N_{\... ...^{\rm CO}_8 \frac{N_{\rm lens}}{N_{\rm sim}}~ [{\rm yr}^{-1}], \end{displaymath} (9)

where $N_{\rm sim}$ is the number of compact objects (potential lenses) in the simulation, and $N_{\rm lens}$ is the number of lenses we find in one year.

   
3 Results

Table 2: Number of compact objects, $N_{\rm sim}$, used in simulations, obtained number of lensing events, $N_{\rm lens}$, and expected lensing rate for compact objects formation models described in Table 1. See text for details on these rates.

Using the StarTrack population synthesis code we evolved 105binary systems, obtaining data about compact objects (neutron stars and black holes). We put those objects (only solitary, from disrupted systems) into the model of the Galaxy assuming a constant star formation rate throughout the history of the Galaxy. We also introduced 106 stars in the Milky Way. All the stars and compact objects were then evolved for 10 Gyr in Galactic potential taking into account the initial velocities that the compact objects received at birth due to asymmetric kicks and disruptions of the binary systems. We then searched for lensing events that take place anywhere over the Earth orbit in the Galaxy in one year of simulation. The resulting rates, calculated using Eq. (9), are presented in Table 2 for each model assuming that N*11=1, and $N^{\rm CO}_8=1$. The typical values obtained are a few per year, however these expected rates have to be considered as rough estimates given the number of assumptions used in Eq. (9). These assumption include the Galactic supernova rate, star formation rate history, a static model of the Galactic potential over the 10 Gyr timescale, as well as the number of stars to be lensed in the Galaxy. Note that the Table 2 gives the values of the rates assuming that all compact objects are formed in the particular scenario. The true lensing rate depends on the assumed binary fraction, and will be a weighted average of the appropriate binary evolution model and the single star scenario.


  \begin{figure} \par\includegraphics[width=8cm,clip]{6802fig2.ps}\end{figure} Figure 2: Map of the lensing events found in the simulation (as seen from Earth) for the model A of compact object formation.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{6802fig3.ps}\end{figure} Figure 3: Cumulative distributions of the angular distance of the lensing events from the Galactic center for the models considered in this paper.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.9cm,clip]{6802fig4.ps}\end{figure} Figure 4: The cumulative distributions of masses of compact objects in the standard model A. The solid line denotes the intrinsic distribution of compact object masses while the dashed line corresponds to the mass distribution of of the lenses. Each plot is labeled by the model as in Table 1.
Open with DEXTER

In each simulation we have noted the positions of the lensing events on the sky. We present the sky maps of these positions in Fig. 2. The lenses are strongly concentrated around the Galactic center. In Fig. 3 we present the cumulative distribution of the fraction of events as a function of the distance from the Galactic Center. Typically 70% of the lensing events take place within a circle with a radius $\approx $ $5\hbox{$^\circ$ }$ around the Galactic Center, while 90% of the events happen within $20\hbox{$^\circ$ }$.

We also note the mass of the gravitational lens for each lensing event. In Figs. 4 and 5 we present the distribution of masses of compact objects for each model and the mass distribution of lenses. In the case of models S, M, K0, and K1 the distributions are similar. They do differ in the remaining models, but in the same manner: the distribution of observed masses shows a deficiency of low mass compact objects (neutron stars) and an increased fraction of high mass objects (black holes). The distributions are similar for the models in which the velocities of compact objects weakly depend on their masses: K0, and K1. The higher velocities for low mass compact objects (models A, S, W0.5, C) decrease their density and therefore decrease the lensing rate. This effect is not very strong: in the cases when the distributions differ the suppression of low mass compact objects is not more than about 20% of the number of the high mass compact objects, see Figs. 4 and 5.

With each lensing event we noted the positions of the lens and the lensed star. We present the distributions of the distance between the Earth and the lensed star as a solid line in Fig. 6. The lensed stars are concentrated around the Galactic center: 75% of the lenses lie at distances of between 7 and 10 kpc. The lenses are spread roughly uniformly between the Earth and the Galactic center. Thus given a detection of a lens one can assume that the lensed object lies in the Galactic center. The position of the lens has to be deduced from the variation of the light curve due to the motion of the Earth around the Sun.

   
4 Summary

We have considered several scenarios leading to formation of Galactic compact objects and calculated their velocity distributions. We then simulate the spatial and velocity distributions of these objects in our Galaxy. We simulate the microlensing events and note both mass of the lens and position of the lens and the lensed object.

We use the Monte Carlo method to calculate the lensing rate and properties. This is a novel algorithm presented and used here for the first time. It is equivalent to the widely used method of integrating the volume defined by the Einstein ring behind a lens with the density of stars (Griest 1991). In order to verify this equivalence we estimate below the chance that a lensing event could be missed in the Monte Carlo method because of too large a time step. The Einstein radius $r_{\rm E}$ is

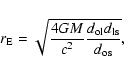\begin{displaymath}r_{\rm E} = \sqrt{\frac{4GM}{c^2} \frac{d_{\rm ol}d_{\rm ls}}{d_{\rm os}}} , \end{displaymath} (10)

where $d_{\rm ol}$, $d_{\rm ls}$, $d_{\rm os}$ are distances from the observer to a lens, from a lens to a source and from the observer to a source, respectively, and M is the mass of a lens. Taking $d_{\rm os}\approx 8$ kpc, $M\approx 1~M_{\odot}$, and denoting $x=d_{\rm ls}/d_{\rm os}$, we obtain a typical Einstein radius for a lens in our Galaxy $r_{\rm E} = 8~{\rm AU}\sqrt{x(1-x)}$, which has a maximum of $r_{\rm E} =4~{\rm AU} \approx 2 \times 10^{-8}$ kpc. Typical velocities of potential compact object lenses do not exceed $300~{\rm km~s}^{-1} \approx 3 \times 10^{-7}$ kpc yr-1. Therefore, during one year, it will shift its position by about $l = 3 \times 10^{-7}$ kpc. The volume in which we can look for potential sources is a slice swept by a moving cone with the radius of $r_{\rm E}$ and length equal to a few kpc; we assume h = 8 kpc. These values yield the volume $V \approx 10^{-14}~{\rm kpc}^3$. In our simulations, we are using 106stars that can be lensed thus the mean density of star in the simulation is

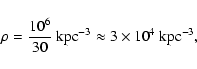\begin{displaymath}\rho = \frac{10^6}{30}~{\rm kpc}^{-3} \approx 3 \times 10^{4}~{\rm kpc}^{-3} , \end{displaymath} (11)

where we approximate the Galaxy as a uniform disc with a radius of 10 kpc and height 0.1 kpc. The number of stars in such a slice in our simulation is $N = \rho V \approx 10^{-10}$. Thus the probability that there is an additional lens that we miss in a single time step is negligible. The Monte Carlo method used here and the analytical methods (Griest 1991) are equivalent.


  \begin{figure} \par\includegraphics[width=15.7cm,clip]{6802fig5.ps}\end{figure} Figure 5: Same as Fig. 4 but for the remaining models.
Open with DEXTER

We estimate the rates of lensing events due to compact objects. These estimates show that they can be observed. The rates in Table 2 must be taken as rough estimates since there are some poorly known factors that are included in these rates - see Eq. (9). The fraction of objects detectable by the lens searches $f_{\rm lens}$ can be increased for searches conducted in the infrared. On the other hand we know that there already are some events that are interpreted as microlensing events by black holes, and thus the calculated rate is consistent with observations.

The most robust result of the simulations is the distribution of lensing events in the sky. All the events are well concentrated around the Galactic center. Thus the lens searches should concentrate on this region. This is due to the fact that the dominant factor determining the position on the sky is the density of the lensed stars and not the lenses themselves. We find that most of the lensed stars lie in the Galactic center, while the lenses are distributed uniformly between the Earth and Galactic center with no preferred distances.

Finally, we find that the observed mass distributions differ by less than 20% from the underlying one. The observations of several tens of gravitational lenses from black holes or neutron stars should lead to relatively accurate estimates of the compact object mass distribution. The observation of the mass distribution of compact objects is extremely important since this is a unique way to probe the final stages of massive star evolution. Observations of black holes in massive accreting binaries may suffer from numerous selection effects and their masses do not necessarily reflect the underlying distribution. Such selection effects may be due to the fact that some binaries are visible in X-rays because of their initial parameters. Additionally, the observability of X-ray binaries is influenced by amount of time they spend in the active X-ray phase. Thus, estimates of mass distributions of compact objects based just on the observations of X-ray binaries must take into account models of their origin and evolution.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{6802fig6.ps}\end{figure} Figure 6: The cumulative distributions of distances: between the lensed object and the Earth - solid line, and between the lens and the Earth - dashed line. The lensed objects are concentrated in the Galactic center, while the lenses are spread uniformly between the Earth and the Galactic center.
Open with DEXTER

The lensing events due to massive lenses will have long duration and therefore require long observational campaigns that preferably would cover the central circle with $R=20^\circ$ of our Galaxy. We emphasize the importance of such searches, as their potential results will have significance for the theory of compact object formation and models of massive star evolution, provided that those searches are able to measure the masses of lenses.

Acknowledgements
This research was supported by the KBN grants 1PO3D00530 (S.O., T.B., R.M.) 1P03D02228 (T.B., K.B.). The authors thank A. Udalski for useful comments on the manuscript. We are also grateful to A. Sadowski for help with the merger calculation.

References

 
Copyright ESO 2008