A&A 478, 219-233 (2008)
DOI: 10.1051/0004-6361:20078469

The most massive stars in the Arches cluster[*],[*]

F. Martins1 - D. J. Hillier2 - T. Paumard3 - F. Eisenhauer1 - T. Ott1 - R. Genzel1,4


1 - Max-Planck Instit $\ddot{\rm u}$t f $\ddot{\rm u}$r extraterrestrische Physik, Postfach 1312, 85741 Garching bei M $\ddot{\rm u}$nchen, Germany
2 - Department of Physics and Astronomy, University of Pittsburgh, 3941 O'Hara St., Pittsburgh, PA 15260, USA
3 - LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris Direrot, 5 Place Jules Janssen, 92195 Meudon Cedex, France
4 - Department of Physics, University of California, CA 94720, Berkeley, USA

Received 11 August 2007 / Accepted 5 November 2007

Abstract
Aims. We study a sample composed of 28 of the brightest stars in the Arches cluster. Our aim is to constrain their stellar and wind properties and to establish their nature and evolutionary status.
Methods. We analyze K-band spectra obtained with the integral field spectrograph SINFONI on the VLT. Atmosphere models computed with the code CMFGEN are used to derive the effective temperatures, luminosities, stellar abundances, mass loss rates and wind terminal velocities.
Results. We find that the stars in our sample are either H-rich WN7-9 stars (WN7-9h) or supergiants, where two are classified as OIf+. All stars are 2-4 Myr old. There is marginal evidence for a younger age among the most massive stars. The WN7-9h stars reach luminosities as high as 2 $\times $ $10^{6}~L_{\odot}$, consistent with initial masses of $\sim $120 $M_{\odot }$. They are still quite H-rich, but show both N enhancement and C depletion. They are thus identified as core H-burning objects showing products of the CNO equilibrium on their surface. Their progenitors are most likely supergiants of spectral types earlier than O4-6 and initial masses >60 $M_{\odot }$. Their winds follow a well-defined modified wind momentum - luminosity relation (WLR): this is a strong indication that they are radiatively driven. Stellar abundances tend to favor a slightly super-solar metallicity, at least for the lightest metals. We note, however, that the evolutionary models seem to under-predict the degree of N enrichment.

Key words: stars: early-type - stars: Wolf-Rayet - stars: atmospheres - stars: winds, outflows - Galaxy: center

   
1 Introduction

The center of our Galaxy is a unique environment for studying massive stars. It harbors three massive clusters - the Arches, Quintuplet and central cluster - which together contain about 30% of the number of Wolf-Rayet stars known in the Galaxy (van der Hucht 2006). Interestingly, the three clusters have different ages, ranging from $\sim $2 Myr for the Arches to $\sim $6 Myr for the central cluster. Consequently, they host different populations of massive stars and sample the entire upper part of the HR diagram. Studying their stellar content gives us a unique opportunity to understand how massive stars evolve.

Although there is a global framework explaining the evolution of stars more massive than $\ga$20 $M_{\odot }$, a quantitative description is still lacking. According to Crowther et al. (1995), stars with masses in the range 25-60 $M_{\odot }$ experience the sequence O  $\rightarrow$ Of  $\rightarrow$ LBV or RSG  $\rightarrow$ WN8  $\rightarrow$ WNE  $\rightarrow$ WC, while for more massive stars, the sequence O  $\rightarrow$ Of  $\rightarrow$ WNL+abs  $\rightarrow$ WN7 ( $\rightarrow$ WNE) $\rightarrow$ WC is preferred (LBV = luminous blue variable; RSG = red supergiant; WNE = early type WN; WNL = late type WNL). Langer et al. (1994) favor another scenario in which all stars have a H-rich WN phase prior to an LBV event: O  $\rightarrow$ H-rich WN  $\rightarrow$ LBV  $\rightarrow$ H-poor WN  $\rightarrow$ H-free WN  $\rightarrow$ WC. We see that there are still some qualitative differences between the proposed scenarios. Furthermore, the evolutionary sequences are not mature enough to allow a refinement of the classification of the stars in the different evolutionary states. For example, the spectral types of the O or WC stars entering the above scenarios are not specified. The question of whether or not all massive stars go through an LBV phase is also not answered. This is an important caveat, especially since this phase has recently been argued to be the one in which most of the mass removal happens (Smith & Owocki 2006).

In a previous study (Martins et al. 2007), we analyzed 18 massive stars in the central cluster of the Galaxy. This cluster is especially intriguing since it hosts the supermassive black hole SgrA* (Ghez et al. 1998; Genzel et al. 1996). In spite of the drastic tidal forces, several tens of massive stars formed recently (Paumard et al. 2006; Allen et al. 1990; Krabbe et al. 1995). Some of them are approaching the black hole at distances of only a few light hours (Ghez et al. 2003; Eisenhauer et al. 2005). The presence of young stars in the Galactic Center together with the apparent implausibility of forming stars so close to the central supermassive black hole is a puzzle usually referred to as "the paradox of youth''. Studying the dynamics of these young stars, Paumard et al. (2006) (see also Levin & Beloborodov 2003; Genzel et al. 2003) have shown that they orbit SgrA* in two counter-rotating disks. Together with other proofs (total mass and structure of the disks), this points to a local, "in situ'' star formation event. The detailed analysis of the post-main sequence massive stars has revealed that, surprisingly, their evolution follows almost perfectly the predictions of evolutionary models (Martins et al. 2007). This implies that whatever the exact formation mechanism is, the subsequent evolution is not different from that predicted for normal stars. We found that all stars seem to have progenitors in the mass range 25-60 $M_{\odot }$ and that they follow relatively well the evolutionary scenario proposed by Crowther et al. (1995) for this mass range. We have been able to refine this scenario, pinpointing the relation between different spectral types: O  $\rightarrow$ (Ofpe/WN9  $\leftrightarrow$ LBV)  $\rightarrow$ WN8  $\rightarrow$ WN8/WC9  $\rightarrow$ WC9. This was made possible by the detailed study of stellar abundances in various Wolf-Rayet stars and related objects. Abundance analysis is a powerful tool to constrain stellar evolution since it gives direct access to the evolutionary state of a star.

The above study focused on stars in the mass range 25-60 $M_{\odot }$ due to the age of the central cluster (more massive stars do not exist any more). In order to constrain stellar evolution at very high mass, we need to study younger clusters. The Arches cluster in the Galactic Center, only 30 pc away from the central cluster, is the ideal target. Not only is it believed to be quite young (2 to 4.5 Myr, see Figer et al. 1999; Blum et al. 2001 and the present study), but it also shares the same environment as the central cluster, and hence has the same metallicity. Hence, its study ensures to obtain a homogeneous view of stellar evolution among all types of massive stars in the Galactic Center. The Arches cluster, first discovered by Nagata et al. (1995) and Cotera et al. (1996), is also one the most massive and densest cluster of the Galaxy. Figer et al. (1999) first showed that the mass function (MF) of its central regions might be shallower than the typical Salpeter IMF. This result was confirmed by Stolte et al. (2002). Although there are indication that high mass star formation might be favored in the Galactic Center (Klessen et al. 2007; Morris & Serabyn 1996), recent simulations of the dynamical evolution of the cluster by Kim et al. (2006) indicate that we might in fact witness the effects of mass segregation in the cluster core rather than an actual top-heavy initial mass function. Whatever the physical reason, there are nearly 100 massive stars in the Arches cluster. From K-band spectroscopy of the brightest members, Blum et al. (2001) and Figer et al. (2002) identified several late WN stars and early O supergiants. The analysis of five of these stars by Najarro et al. (2004) revealed, by an indirect method, that their metallicity was close to solar.

Here, we analyze a much larger sample (28 stars in total) in order to better constrain their stellar and wind parameters. We rely on high quality data obtained with the integral field spectrograph SINFONI on the VLT. The K-band spectra extracted from this data set are analyzed with atmosphere models computed with the code CMFGEN (Hillier & Miller 1998). In Sect. 2 we describe the observations, our sample and the spectroscopic classification; in Sect. 3 our method to analyze the stars are presented; the results are summarized in Sect. 4 and discussed in Sects. 5-7. We give our conclusions in Sect. 8.

   
2 Spectroscopic data

   
2.1 Observations and data reduction

The Arches cluster was observed in service mode between May 3rd and June 27th 2005 with SINFONI on the ESO/VLT (Eisenhauer et al. 2003; Bonnet et al. 2004). K band data were obtained with a pixel scale of 0.1 $^{\prime\prime}$. Adaptive optics was used to improve the spatial resolution. The seeing varied between 0.5 and 1.2 arcsec during the different runs. Four sub-fields were observed at the core of the cluster, as well as 12 fields in the outer part. For each sub-field, the integration time on source was 240 s. One sky exposure was obtained every two object exposures. Early B stars were observed as telluric standards.

Data were reduced with the SPRED software (Abuter et al. 2006) as in Eisenhauer et al. (2005) and Paumard et al. (2006). The reduction steps include: sky subtraction, flat field and bad pixel correction, distortion correction, wavelength calibration and atmosphere correction. In the last step, the telluric standard is used after its intrinsic Br$\gamma$ line is removed by a simple interpolation of the continuum red and blueward of the line. Individual frames were subsequently combined to obtain mosaics of the observed regions (when frames overlap). We refer the reader to Abuter et al. (2006) for a comprehensive description of the software used. Spectra were then carefully extracted by selection of individual "source'' pixels from which "background'' pixels are removed to correct for light contamination. The final spectra have a resolution of $\sim $4000 and a signal to noise ratio of 10 to 80 depending on the brightness of the star.

   
2.2 Sample

We selected the stars with high enough signal to noise ratio spectra (S/N $\ga$ 10) for a subsequent quantitative analysis with atmosphere models. Equivalently, this means that we studied the brightest members of the Arches cluster. The list is given in Table 1. The name of the stars is taken from the list of Figer et al. (2002). NICMOS photometry in the F205W filter was taken from Figer et al. (2002), and was assumed to be equivalent to K-band photometry. We also included star number 1 of Blum et al. (2001) which is not in the list of Figer et al. (2002). It is designated by the name B1. Its K-band magnitude is taken as the 2.14  $\mu \rm {m}$ magnitude of Blum et al. (2001). This wavelength range is free of strong line. We estimated the absolute K-band magnitudes adopting a distance to the Galactic Center of 7.62 kpc (Eisenhauer et al. 2005). We also adopted a constant extinction AK = 2.8 for all stars. This value is slightly lower than the average AK derived by Stolte et al. (2002) and Kim et al. (2006). However, as noticed by these two studies, the extinction is smaller in the cluster center (inner 5 $^{\prime\prime}$). In this region, AK is between 2.6 and 2.95 Stolte et al. (2002). This behavior is interpreted as evidence that dust is swept by stellar winds and/or photo-evaporation by the intense UV radiation of massive stars. Since most of the stars in our selected sample are in the cluster center, the choice of AK = 2.8 is a reasonable assumption. From the adopted distance and extinction, we can derive the absolute magnitudes of our sample stars: they are reported in Col. 3 of Table 1.

   
2.3 Spectral classification

Spectral classification in the K band is more difficult than in the classical optical range due to the limited number of lines. However, catalogs of K band spectra of objects with spectral types derived from optical studies are becoming available, making the spectral classification easier (Hanson et al. 2005; Morris et al. 1996; Figer et al. 1997; Hanson et al. 1996). The main lines observed in our SINFONI spectra are the following: He I 2.058 $\mu $m, He II 2.189 $\mu $m, He II 2.037 $\mu $m, He II 2.346 $\mu $m, Br$\gamma$, N III 2.247, 2.251 $\mu $m, C IV 2.070-2.084 $\mu $m, Si IV 2.428 $\mu $m and the complex at 2.112-2.115  $\mu \rm {m}$ (composed of He I, N III, C III and O III). They are identified in Figs. A.1 to A.4. The most prominent line, Br$\gamma$, goes from a strong emission in the brightest stars to an absorption profile when the stars become fainter. He II 2.189 $\mu $m shows a similar behavior. He II 2.037 $\mu $m and He II 2.346 $\mu $m have a weak P-Cygni profile when present. C IV 2.070-2.084 $\mu $m, N III 2.247, 2.251 $\mu $m and Si IV 2.428 $\mu $m, when present, are always in emission. Finally, the 2.112-2.115  $\mu \rm {m}$ complex is in emission in most of the spectra.

Table 1: Photometry of the stars analyzed in the present paper. The stars are identified by their number in the list of Figer et al. (2002). Observed magnitudes are also from this source. A distance of 7.62 kpc is assumed (Eisenhauer et al. 2005), as well as a uniform extinction AK=2.8 in the K band (Stolte et al. 2002).

The K band spectra we obtained are typical of late WN (WNL) and early O type stars, in agreement with Figer et al. (2002). WN stars earlier than WN7 have He II 2.189 $\mu $m stronger than Br$\gamma$, which is observed in none of our sample stars. The distinction between late WN subclasses is difficult when only the K band is available (Morris et al. 1996). In WN7 stars, the He II 2.189 $\mu $m emission is strong (although not as much as Br$\gamma$). In later type stars, He II 2.189 $\mu $m is much weaker. In general, this morphology is associated with a strong He I 2.058 $\mu $m emission. However, in H-rich late type WN stars (the so-called WNh stars) He I 2.058 $\mu $m can be seen in absorption (Crowther & Smith 1996; Crowther & Bohannan 1997; Bohannan & Crowther 1999), which can be qualitatively understood by a lower He content. According to the atlas of Hanson et al. (1996) and Hanson et al. (2005), late type O stars have a weak He II 2.189 $\mu $m absorption, and the 2.112-2.115  $\mu \rm {m}$ line complex in absorption or weak P-Cygni. Our sample stars do not contain these spectral morphologies. We thus have only early type O stars (O4-6). Among them, main sequence stars can be distinguished from supergiants by the shape of Br$\gamma$: it is in absorption on the main sequence and either absent (because filled by wind emission) or in emission (usually with a weak central absorption) in supergiants. Some O supergiants have stronger lines than standard O4-6I stars (especially Br$\gamma$) and are identified as OIf+ supergiants[*]. Figer et al. (2002) argued that the distinction between WNL (especially WN7) and OIf+ is very difficult. Both types have strong emission lines, but WNL stars usually have He II 2.189 $\mu $m in emission or at least with a P-Cygni profile while OIf+ have mainly He II 2.189 $\mu $m in absorption. However, Conti et al. (1995) showed that exceptions exist: HD 16691 and HD 190429 are two OIf+ with He II 2.189 $\mu $m in emission. Figer et al. (2002) suggested that the presence of the N III 2.247, 2.251 $\mu $m emission in WNL stars but not in OIf+ supergiants could be used to break the degeneracy in the spectroscopic classification. Based on these considerations, we classify the Arches SINFONI spectra using the following criteria (restricted to early O and late WN stars):

$\bullet$
WNL stars have a strong Br$\gamma$ and 2.112-2.115  $\mu \rm {m}$ emission. Br$\gamma$ is stronger than the 2.112-2.115  $\mu \rm {m}$ complex. They show N III 2.247, 2.251 $\mu $m (emission). He I 2.058 $\mu $m is weak and/or in absorption, so all our WNL stars are H-rich (which is confirmed by our quantitative analysis, see below) and thus are classified as WNh. When He II 2.189 $\mu $m is purely in emission the spectral type WN7-8h is assigned. When it is in absorption or shows a P-Cygni profile, the star is classified as WN8-9h.

$\bullet$
OIf+ have He II 2.189 $\mu $m in absorption, a weak or no N III 2.247, 2.251 $\mu $m line, the 2.112-2.115  $\mu \rm {m}$ line complex and Br$\gamma$ in emission. The strength of Br$\gamma$ is similar to that of the 2.112-2.115  $\mu \rm {m}$ complex.

$\bullet$
O supergiants (OI) have the same morphological properties as OIf+ stars, except that Br$\gamma$ is in emission but weaker than the 2.112-2.115  $\mu \rm {m}$ complex, or in weak absorption.
These criteria remain qualitative on purpose, so that broad groups of stars can be defined without preventing the possibility that some stars are intermediate between the groups, as is likely to be the case in a population of massive stars with such a narrow age spread. The criteria we defined should also be seen as relative criteria to compare the different stars of our sample. Our final spectral classification for each star is given in Table 1. The spectra of our sample stars are also displayed in Figs. A.1-A.4.

   
3 Spectroscopic modeling of individual stars

In this section we describe our method to derive the stellar and wind properties of the selected stars. We also present an estimate of the uncertainties on the derived parameters.

   
3.1 Atmosphere models

We used the atmosphere code CMFGEN (Hillier & Miller 1998) to derive the stellar and wind properties of a sample of Wolf-Rayet and O stars. CMFGEN calculates non-LTE atmosphere models with winds and includes a robust treatment of line-blanketing. A detailed description of the code was given by Hillier & Miller (1998). Its main characteristics are also presented in Martins et al. (2005b,2004,2007). Here, we simply highlight a few important features:

$\diamond$
hydrodynamic structure: CMFGEN does not compute self-consistently the density (and velocity) structure of the atmosphere. The standard procedure consists in adopting a pseudo-hydrostatic structure on top of which a "$\beta$ velocity law'' is connected. Such a law is expected from theoretical ground (e.g. Pauldrach et al. 1986). Here, we used the TLUSTY structures of Lanz & Hubeny (2003) for the hydrostatic part of the atmosphere. We chose $\beta = 0.8$ since it is the typical value for O stars (Repolust et al. 2004; Puls et al. 1996). It also leads to good fits of the of the observed line profile. Only for stars B1 and F5 did we have to use values of 1.2 and 1.8 respectively to better fit the overall shape of the emission lines, especially Br$\gamma$: larger $\beta$ produce more centrally peaked lines (for the adopted clumping factor, see below). High values of $\beta$ are also found for O supergiants (Hillier et al. 2003; Crowther et al. 2002a). The use of such a structure may be questionable in the case of extreme supergiants and Wolf-Rayet stars. However, the wind density in these stars is usually so high that the photosphere is beyond the hydrostatic layers, so that the underlying structure has little impact on the observed spectrum.

$\diamond$
line-blanketing and super-levels: CMFGEN includes line-blanketing through the super-level approximation. In practice, levels of similar energies are grouped in a single super-level which is then used to compute the atmospheric structure. Within a super-level, individual levels have the same departure coefficient from LTE. This is a very convenient way to treat directly line-blanketing, without using statistical methods such as opacity sampling. Usually, only levels with large energies are grouped into super-levels. This may affect the strength of infrared lines since they mainly arise from transitions between such high energy levels. As a consequence, we decided not to use super-levels for H, He, NIII and CIV which contribute most of the K band lines: we used the full atom. In addition to H, He, C and N, we included O, Si, S and Fe in our models. No other elements could be treated due to the increased memory requirement implied by the large number of levels (typically about 3000 levels and 1300 super-levels). The elements included are anyway the ones responsible for most of the line-blanketing effects. Tests with additional species confirmed that adding other elements did not significantly affect the results. Similarly, tests run with different super-levels assignments lead to minor changes insufficient to modify quantitatively our results.

$\diamond$
microturbulent velocity: a value of 15 km s-1 was used in the computation of the atmospheric structure. For the detailed emergent spectrum resulting from the formal solution of the radiative transfer equation, we adopted $v_{\rm turb}$ = 10 km s-1. This is a reasonable value for O stars (Villamariz & Herrero 2000). For WR stars, it might be a little too low. However, test models with $v_{\rm turb}$ = 50 km s-1 indicate barely any change in the resulting line profiles, because they are dominated by the wind.

$\diamond$
clumping: CMFGEN allows the inclusion of clumping. In practice, a volume filling factor approach is used. The filling factor is described by an exponential law starting from a value of 1.0 at the base of the wind and declining to f in the outer atmosphere, where the velocity reaches $v_{\infty }$. Given the limited number of diagnostics in the K band, we have adopted f = 0.1 in our computations. This is a standard value for WR stars (Crowther et al. 2006; Hillier et al. 2001; Morris et al. 2000; Hillier & Miller 1999; Crowther et al. 2002a; Hamann & Koesterke 1998). For O stars, the amount of clumping is still a matter of debate. Values of f as low as 0.01 have been derived by Bouret et al. (2005), Martins et al. (2005b), Fullerton et al. (2006). But larger values are also found: f=0.2 by Repolust et al. (2004) or f=0.1 by Crowther et al. (2002b), Martins et al. (2005b). Recently, Puls et al. (2006) also showed that the clumping factor might vary non monotonically with radius in the wind, contrary to the usual assumption of atmosphere models. Given these uncertainties, the adopted value for f (0.1) is not unrealistic. If the clumping factor was smaller, then our mass loss rates for O supergiants would be overestimated by  $\sqrt{0.1/f}$.

   
3.2 Method

We briefly describe here the method we used to constrain the main stellar and wind parameters.

$\diamond$
Effective temperature: $T_{{\rm eff}}$ was constrained from the strength of He I and He II lines, as in most studies of massive stars. In practice, we used He I 2.058 $\mu $m, He I 2.112 $\mu $m, He II 2.189 $\mu $m, He II 2.037 $\mu $m and He II 2.346 $\mu $m as the main diagnostics. We note that $T_{{\rm eff}}$ is defined at the radius in the atmosphere model where the Rosseland optical depth reaches 2/3. For comparison with evolutionary models, it is usually useful to define T* as the temperature where the opacity is 20. This corresponds to a deeper, quasi hydrostatic layer of the atmosphere, which is more similar to the outer radius of the evolutionary models. In general, $T_{{\rm eff}}$ and T* are almost identical for O stars, while for WR stars with denser winds they can differ by several thousands of degrees.

$\diamond$
Luminosity: the K-band flux was used as the main indicator. The luminosity was adjusted so that the K-band magnitude of the models could match the absolute magnitude of the stars. In practice, the K-band flux depends not only on the stellar luminosity, but also on the mass loss rate since in the near infrared the ionized wind produces free-free emission. Hence, the luminosity was derived in parallel to $\dot{M}$.

$\diamond$
Mass loss rate and He abundance: $\dot{M}$ and the ratio of H to He content were constrained from the strength of the emission of Br$\gamma$ and the He lines. A change of $\dot{M}$ leads to a general increase of the emission in all the lines, while an increase of He/H strengthens the He lines and weakens Br$\gamma$.

$\diamond$
C and N abundances: The carbon and nitrogen content was derived from C IV 2.070-2.084 $\mu $m and N III 2.247, 2.251 $\mu $m respectively. We also use the Si IV 2.428 $\mu $m line when observed to constrain the Si abundance. We note however that this last abundance determination is less reliable than for the other elements since the spectrum is much noisier at the position of the Si IV 2.428 $\mu $m line (at the red end of the K band).

$\diamond$
Terminal velocity: the terminal velocity of the wind ( $v_{\infty }$) was determined from the width of the Br$\gamma$ and the extend of the absorption dip of the P-Cygni profile of He I 2.058 $\mu $m (when present). When none of these indicators could be used, we simply adopted $v_{\infty} = 2.6$ $\times $ $v_{\rm esc}$ (Lamers et al. 1995), $v_{\rm esc}$ being the escape velocity.
Due to the absence of strong gravity indicators, we adopted $\log g$ = 3.25 for the coolest stars, and $\log g$ = 3.50 for the hottest. This is a reasonable assumption in view of the calibrations of Martins et al. (2005a). Finally, the solar abundances of Grevesse & Sauval (1998) were used as references[*].

   
3.3 Accuracy of parameters determination

The determination of the stellar and wind parameters is a long iterative process: most spectral diagnostics depend on several parameters. To estimate the uncertainties on our determinations, one would ideally need to run tens of models covering the parameter space from which some kind of chi-square procedure (to be defined) could provide statistical errors. In practice, this is not possible in the present approach since this would lead to a prohibitively long process: a model and the associated spectrum require between 24 and 48 h of cpu time; sampling correctly the parameter space (10 to 20 models for each parameter, and $\sim $10 parameters) for each of the 28 stars would imply several months of computations. This is in addition to the time needed to actually find the best fit model for each star.

Hence, we prefer to rely on a more empirical way to estimate the uncertainties. For this, we chose to run a few test models for two typical stars (one WN8-9h and one O supergiant). We varied the parameters around the values of the best fit model and judged by eye when the resulting spectrum was not satisfactory any more: this was used to define our uncertainty. This gives a reasonable estimate of the accuracy with which the stellar and wind parameters are derived. Figure 1 illustrates this procedure for $\dot{M}$ and N/H.

In practice, we focused on the models for star F2 (WN8-9h) and star F21 (O4-6I). They were chosen as typical of their class of objects, both in terms of spectral morphology and derived parameters. The typical errors are: $\pm $3000 K (2000 K) on $T_{{\rm eff}}$ for O stars (WNLh), $\pm $0.2 dex on $\log \frac{L}{L_{\odot}}$, 0.2 (0.1)  $\log \dot{M}$, 100 km s-1 on terminal velocities and $\pm $50% ($\pm $30%) on abundances. The uncertainty on $\log \frac{L}{L_{\odot}}$ depends mainly on the adopted distance and extinction, and is thus similar for WNLh and O stars. The uncertainty on abundances does not take into account any possible systematics due to uncertainties in atomic data and model assumptions.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig1.eps}\end{figure} Figure 1: Uncertainty estimate for $\dot{M}$ and N/H for one WNLh star (F2) and one O supergiant (F21). The solid line is the observed spectrum, while the colored broken lines are the models. The red dot-dashed lines correspond to the best fit model. In the other models, only $\dot{M}$ ( left panels) or N/H ( right panels) have been varied.
Open with DEXTER

   
4 Derived stellar and wind parameters

The results of our analysis are summarized in Table 2. The final fits are shown in Figs. A.1-A.4. A summary of the general properties is given in Sect. 4.1 while a comparison to previous studies is made in Sect. 4.2.

   
4.1 General properties

To avoid lengthy discussions, we do not describe the stars one by one but focus on their global properties. They can be summarized as follows:

$\diamond$
The stars have very similar $T_{{\rm eff}}$: out of 28 stars, 17 have $32~500 < \mbox{$T_{{\rm eff}}$ }< 37~500$. The average effective temperatures of WN7-9h and O4-6I stars are 33 600 K and 37 600 K respectively. Considering the error on the temperature estimate ($\pm $2000-3000 K), there is very little dispersion in $T_{{\rm eff}}$ among our sample. This explains partly the similarity in the morphology of the K-band spectra. This has the important consequence that all stars lie almost on a vertical line in the HR diagram (see Sect. 5). Such a feature can be used to trace the age of the cluster. One can also note that the average temperature of the O4-6 supergiants is similar to the calibrated values of Martins et al. (2005a) for O5-5.5I stars.

$\diamond$
The stars are luminous: all the stars we analyzed have $\log \frac{L}{L_{\odot}}$ > 5.7, some of them reaching $\log \frac{L}{L_{\odot}}$ = 6.35. WN7-9h stars have, on average, $\log \frac{L}{L_{\odot}}$ = 6.14, O4-6 supergiants have $\log \frac{L}{L_{\odot}}$ = 5.84. Contrary to the case of effective temperatures, there is a clear luminosity difference between the classes of objects, WN7-9h stars being the most luminous. Luminosities in excess of $10^{6}~L_{\odot}$ are indicative of very high mass stars. This characteristic will be further discussed in Sect. 6. Early type supergiants/giants have luminosities in agreement with the expectations: the calibrations of Martins et al. (2005a) indicate $\log \frac{L}{L_{\odot}}$ = 5.78-5.95 for O4-6I stars.

$\diamond$
The stars are usually H rich: all the stars have a ratio He/H < 1.0. The WN7-9h stars are He enriched, but not excessively, with He/H between 0.1 and 1.0. Actually, only three WN7-9h stars have He/H > 0.5: all the other WNLh stars have a lower He content. It is interesting to note that some WNLh stars do not seem to be He enriched (stars B1, F1, F9, F14, F16). All the other types of stars show a solar helium abundance (with the exception of star F10 which is slightly enriched - He/H = 0.2).

$\diamond$
The stars show various degrees of chemical enrichment: as expected, WNLh stars have the strongest nitrogen enrichment, with X(N) between 0.005 and 0.028. O supergiants, including the O4-6If+ stars, have solar or slightly enriched N abundances (X(N) = 0.002-0.007). In parallel, WN stars are carbon deficient (X(C) < 1.3 $\times $ 10-3; exception: star F16) compared to O supergiants. This is a clear indication of CNO processing.

$\diamond$
Mass loss rates are stronger in WN stars: all WN7-9h stars have $\dot{M}$ > 10-5 $M_{\odot }$ yr-1 (exception: star F16, $\dot{M}$ = 6.3 $\times $ 10-6 $M_{\odot }$ yr-1). The O4-6 supergiants have lower mass loss rates (in the range 2-4.5 $\times $ 10-6 $M_{\odot }$ yr-1).
From this general overview, one sees that the stars analyzed here share some common properties ( $T_{{\rm eff}}$) but also are very different in terms of abundance patterns. This will be discussed in greater depth in Sect. 6.1.

Table 2: Derived stellar and wind parameters. The typical errors are: $\pm $3000 K on temperatures, $\pm $0.2 dex on $\log \frac{L}{L_{\odot}}$ and $\log \dot{M}$, 100 km s-1 on terminal velocities and $\pm $30% on abundances. Terminal velocities are adopted from $v_{\infty }$ = 2.6 $\times $ $v_{\rm esc}$ for O stars (except the two O4-6If+ supergiants).

Table 3: Comparison between our results and the study of Najarro et al. (2004) for the five stars in common. For each star, the first row gives our results, and the second one the results of Najarro et al. (2004). Only the main parameters are listed.

   
4.2 Comparison to previous studies

The only attempt to derive quantitative properties of the Arches massive stars is by Najarro et al. (2004). The authors focused on five stars (F3, F4, F8, F10 and F15) and used a similar technique to determine the stellar and wind parameters. They relied on Keck/NIRSPEC spectra with a high resolution ($\sim $23 300) but a narrower spectral coverage than our VLT/SINFONI data (only four windows centered on He I 2.058 $\mu $m, He I 2.112 $\mu $m, Br$\gamma$ and N III 2.247, 2.251 $\mu $m were observed).

The parameters derived in both the present study and the analysis of Najarro et al. (2004) are summarized in Table 3. Generally, there is a rather good agreement between both studies for the WN stars. Note in particular the similar luminosities, mass loss rates, terminal velocities and He and N abundances. We find effective temperatures systematically higher (by $\sim $2000 K), but the difference is within the uncertainties (except for star F4). The largest difference is found for the carbon abundance, although, with one exception (star F3), the discrepancy is only a factor of 2 or smaller. Here, we argue that Najarro et al. (2004) did not cover the full spectral range around 2.07  $\mu \rm {m}$ to observe the C IV 2.070-2.084 $\mu $m lines (see their Fig. 1), which is included in our SINFONI spectra. We have consequently a larger number of diagnostics and we are able to better derive the C content.

The differences are larger for the two O4-6If+ stars. We think the better quality of our spectra allows a better estimate of the terminal velocity (the full width of Br$\gamma$ is well observed), the C and N content (we unambiguously detect the C IV 2.070-2.084 $\mu $m lines and the N III 2.247, 2.251 $\mu $m doublet). The mass loss rates being similar, the wind densities are not (due to the difference in $v_{\infty }$), which partly explains the different luminosities. The different effective temperatures, well constrained by our well resolved He I and He II lines (especially He II 2.189 $\mu $m) complete this explanation.

   
5 HR diagram and cluster age

The stars analyzed in the present study are placed in the HR diagram in Fig. 2. The Geneva evolutionary tracks including rotation from Meynet & Maeder (2005) are used to build the diagram. Isochrones are also shown. As previously described, there is a clear difference in the position of stars of different spectral types. The WN7-9h stars (filled circles) are brighter than the normal O supergiants. The extreme supergiants are intermediate. One can immediately conclude that the WN7-9h stars of the Arches cluster are very massive stars: only the 120 $M_{\odot }$ evolutionary track is able to reach luminosities higher than $10^{6}~L_{\odot}$. Even the less luminous WN7-9h stars are accounted for only by the tracks with $M > 60~M_{\odot}$. One concludes that in the Arches cluster, the WN7-9h stars are the descendent of stars more massive than 60 $M_{\odot }$. The position of the extreme early supergiants (the O4-6If+ stars) overlaps with the position of the less luminous WN7-9h stars. It is thus likely that they are closely related to them (see also the next sections).


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig2.eps}\end{figure} Figure 2: HR diagram of the Arches cluster. Filled symbols are the stars analyzed in this work. The Geneva evolutionary tracks including rotation from Meynet & Maeder (2005) are plotted, as well as isochrones. For clarity, only the first $\sim $4 Myr of the tracks are plotted. The solid line in the right upper part of the figure is the Humphreys-Davidson limit. The typical error on the position of the stars is shown at the bottom left.
Open with DEXTER

From the position of the stars in the HR diagram, one can attempt to estimate their age. For that, isochrones are indicated in Fig. 2. The most luminous WN7-9h stars are 2-3 Myr old. The O supergiants (with the exception of the O4-6If+ stars) seem to span a slightly wider age range (2-4 Myr). There is however an overlap between the brightest supergiants and the faintest WN7-9h stars. This suggests that on average the most massive stars are slightly younger than less massive stars (in the mass range 40-120 $M_{\odot }$): one can clearly exclude an age of 3 Myr for the most luminous WN7-9h stars, while some of the O supergiants with $L \sim 10^{5.8}~L_{\odot}$ could be $\sim $4 Myr old. This may be an indication that the most massive stars formed at the end of the star forming event that gave birth to the Arches cluster. This would be consistent with the scenario according to which the most massive stars are the last to form in a starburst event since their presence immediately imply a strong negative feedback which removes material for star formation. We note however that we are probing a small region of the HR diagram and this would need to be confirmed by a deeper study of intermediate and low mass stars. Within the uncertainty on the effective temperature and luminosity of the O supergiants, one cannot exclude either that they have the same age as the WNLh stars. Besides, binarity may change the picture. If the most luminous stars were found to be binary stars, the luminosity of each component would have to drop (by as much as 0.3 dex in case of equally luminous companions). This would translate into an older age for the stars, now closer to the 3 Myr isochrones in Fig. 2. Hence, the suggestion of a late formation of the most massive stars still needs to be confirmed, but is worth being mentioned in view of the present results. We note also that in NGC 3603, a galactic cluster quite similar to the Arches, there exists a population of pre-main sequence stars younger than the most massive components (Harayama et al. 2007; Stolte et al. 2006). Clearly, a study of fainter components of the cluster is required to confirm the suggestion of a correlation between age and initial mass.

Figer et al. (1999) derived an age of 2 $\pm $ 1 Myr for the Arches cluster based on photometry of the massive components. A better estimate was given by Blum et al. (2001) who used information on the spectral types in combination to evolutionary models to constrain the age of the Arches to the range 2-4.5 Myr. Finally, comparing the types of Wolf-Rayet stars present in the cluster to the predictions of starburst models of Meynet (1995), as well as using the detailed properties of one star (F8), Figer et al. (2002) concluded that the age of the cluster is 2.5 $\pm $ 0.5 Myr. Our determination, which relies on a more quantitative basis and uses the most recent evolutionary tracks, agrees nicely with this estimate (especially if only WR stars are considered).

Finally, one should mention that the above results were obtained using solar metallicity tracks. As we will see later, the metallicity in the cluster might be slightly super-solar. In that case, the age we derived would be only an upper limit. Indeed, for Z=2 $\times $ $Z_{\odot }$, comparison to the corresponding evolutionary tracks show that all the stars we analyzed would be younger than 3 Myr.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig3.eps}\end{figure} Figure 3: Hydrogen mass fraction as a function of luminosity in the solar metallicity Geneva evolutionary models of Meynet & Maeder (2005) (solid line) and as derived in the stars analyzed in this work (symbols).
Open with DEXTER

   
6 Nature of the most luminous stars

In this section we investigate the nature of the Arches stars studied here as well as the possible relation between the different types of stars (O, WNLh). We first focus on the chemical evolutionary status, then discuss the wind properties before drawing our conclusions.

   
6.1 Chemical evolution

In the previous section we have seen that the stars classified WN7-9h in our sample appear to be very massive stars. To better unravel the nature of these objects, the analysis of their abundance pattern is a powerful tool since it informs about their evolutionary status.

In Fig. 3 we plot the hydrogen mass fraction as a function of luminosity. The symbols have the same meaning as in Fig. 2. The relation from the Geneva evolutionary tracks are overplotted (solid lines). One can immediately conclude that the WN7-9h stars are the only ones of our sample showing H depletion. However, even some of the WN7-9h stars appear not to be He enriched (none of the O stars are H depleted). Overall, the H mass fraction of WN7-9h stars ranges between 0.2 and 0.7. We interpret this pattern as a sign that the Arches WNLh stars are objects which left the main sequence recently, some of them being almost unevolved in terms of H depletion. This is a very important conclusion, because it means that some (and maybe all) of these stars are still core H burning objects. This implies that these stars are young, consistent with our age estimate (see Sect. 5). The comparison with the evolutionary tracks in Fig. 3 also indicates that they have masses in the range 60-120 $M_{\odot }$, similar to what was inferred from their position in the HR diagram.

A quantitative confirmation of the young evolutionary status of the Arches WNLh stars is given by Fig. 4. In this figure, the carbon mass fraction (X(C)) is shown as a function of the nitrogen mass fraction (X(N)). According to stellar evolution, X(C) decreases in the earliest phases while X(N) increases when H is burnt through the CNO cycle. Then when He burning starts, C is produced at the expense of N (and He). Figure 4 reveals that the WN7-9h stars are all carbon poor and N rich compared to the O stars of the sample (with the exception of star 14 which is more similar to O stars). In fact, they cluster in a rather small region of the X(C)-X(N) diagram, which suggests that they show the pattern of CNO equilibrium. Contrarily to Fig. 3, there is a clear distinction between WN7-9h and O stars which are more C rich and N poor. This allows us to unambiguously state that the WN7-9h stars are evolved objects but are still at the beginning of their post main sequence evolution.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig4.eps}\end{figure} Figure 4: Carbon mass fraction as a function of Nitrogen mass fraction in the Geneva evolutionary models of Meynet & Maeder (2005) (solid line: solar metallicity; dashed line: twice solar metallicity) and as derived in the stars analyzed in this work (symbols). The evolutionary tracks plotted are for 20, 40 and 85 $M_{\odot }$.
Open with DEXTER

Figure 4 shows that although the trend of decreasing X(C) with increasing X(N) predicted by the evolutionary models is qualitatively reproduced by the observations, quantitatively the agreement is not perfect. In particular, the WN7-9h stars span a wider range in X(N) (0.005 to 0.028) than expected from the models. In the models, at the level of X(C) seen in the WN7-9h stars, X(N) should be around 0.013 according to the solar metallicity track. The track at twice the solar metal content allows X(N) as large as 0.025. But for the level of X(N) observed, the C content in this track should be up to 4-5 times larger. An explanation purely by a non solar metallicity is not satisfying. Different initial rotational velocities cannot fully explain this scatter in X(N) values. Between two stars with initial rotational velocities of 0 and 300 km s-1, the difference of maximum value of the N mass fraction X(N) is 0.002. This is about one tenth of the range spanned by the WNLh stars (from $\sim $0.01 to $\sim $0.03, excluding star F14). Hence, a spread in initial rotational velocities cannot be fully responsible for the observed scatter in X(N).

One can also speculate that the evolutionary models do not predict a strong enough N enrichment in the early phases of evolution of massive stars. One important ingredient which is still neglected in most evolutionary models is magnetic fields. Recently, Maeder & Meynet (2005) have shown that the presence of magnetic fields in massive stars could favor solid body rotation and consequently chemical mixing. Their Fig. 10 reveals that He and N abundances can be significantly increased compared to non magnetic models. Interestingly, the effect of magnetic fields on chemical enrichment are larger for older stars. This is to be compared to the larger spread in X(N) for more evolved stars (WNLh compared to O supergiants) in Fig. 4. We do not claim that magnetic field can explain all the trends seen in this figure, but it might be an important ingredient. In that context, it is worth noting that Trundle & Lennon (2005) report a similar discrepancy between derived (by atmosphere modeling) and predicted (by evolutionary tracks) N abundances for B supergiants in the SMC.

To further investigate the chemical evolutionary status of the Arches stars, we have plotted in Fig. 5 the ratio of N to He abundance (by mass) as a function of effective temperature. Here again, the Geneva evolutionary tracks for solar and twice solar metallicity are overplotted. Theoretically, the N/He ratio probes the first phases of evolution. Indeed, while both N and He are produced during the H burning phase, the relative increase of the abundances relative to the initial values is larger for N than for He, simply because He is already a main element in the star while N is not. In practice, the N mass fraction changes by an order of magnitude, while the He mass fraction increases by only a factor of 2-3 (see for example Fig. 16 of Meynet & Maeder 2003). The N/He ration thus evolves from the initial value to a value corresponding to the CNO equilibrium. Stars which have not yet reached this equilibrium will show intermediate values of N/He. Focusing on the left part of Fig. 5 corresponding to the case of solar metallicity tracks, we see again a clear difference between the WNLh and the O stars: the latter appear to lie on evolutionary tracks where the N/He ration is still rising, while the former are all in the region where N/He is constant. This confirms our previous finding that the WNLh stars are core H burning stars which have reached the CNO equilibrium. On the contrary, the O stars are still in the process of reaching this equilibrium. An important discrepancy between evolutionary tracks and observed stars is the very large values of N/He in the Arches WNLh stars compared to the tracks: for some stars, no track seems to be able to reproduce their position. Even tracks for stars more massive than 120 $M_{\odot }$ (the most massive star for which evolutionary tracks exist) would not help, since all the tracks between 60 and 120 $M_{\odot }$ seem to predict about the same amount of N/He at equilibrium. More massive stars would show the same values. If we turn to the right part of Fig. 5 where the twice solar metallicity tracks are shown together with the derived stellar properties of the Arches stars, the situation dramatically improves. All stars can now be represented by the theoretical tracks, even the WN7-9h stars with the largest N/He ratios. The ones with the lowest ratios now appear not to have reached completely the CNO equilibrium. The reason for the largest theoretical N/He ratio at twice solar metallicity is that between $Z_{\odot }$ and Z=2 $\times $ $Z_{\odot }$ the initial He fraction barely changes, while the N content is much larger. The initial N/He ratio is thus larger. Does that mean that the Arches cluster metallicity is super solar? Although Fig. 5 makes a good case for it, we have seen that the interpretation was a bit different for Fig. 4 for which a super solar metallicity did not fully explain the observed trend. The question of the Arches cluster metallicity will be debated in Sect. 7.


  \begin{figure} \par\mbox{\includegraphics[width=8.1cm,clip]{8469fig5a.eps}\hspace*{0.6cm} \includegraphics[width=8.1cm,clip]{8469fig5b.eps} } \end{figure} Figure 5: Logarithm of the ratio of nitrogen to helium mass fraction in the Geneva evolutionary models of Meynet & Maeder (2005) and as derived in the stars analyzed in this work (symbols). Left: solar metallicity evolutionary tracks. Right: twice solar metallicity tracks.
Open with DEXTER

A final plot which combines the two previous ones is shown in Fig. 6. It displays the abundance ratio N/C as a function of $T_{{\rm eff}}$. Here again, this ratio reaches a maximum value when the stars is at the CNO equilibrium. The WNLh stars and the O stars are clearly separated, the former being more N rich-C poor than the latter. Note however the existence of some overlap, two WNLh stars having N/C ratios similar to O stars. We note that some WN7-9h stars still show N/C ratios larger than predicted. Using evolutionary tracks with Z=2 $\times $ $Z_{\odot }$ does not really improve the situation in this case, since the initial N and C abundances are changed in a very similar way when Z is increased, so that the initial N/C ratio does not vary a lot. Finally, it is interesting to note that the scatter of the N/C ratio seen in Fig. 6 among WN7-9h stars is real. An observational demonstration is made in Fig. 7 where we see that the two stars F6 and F7 have very similar spectra (and thus similar parameters, see Table 2) but different C IV 2.070-2.084 $\mu $m and N III 2.247, 2.251 $\mu $m lines. This means that stars at the same position in the HR diagram can be in slightly different states of chemical evolution.

From this analysis, we can safely conclude that the WN7-9h stars in the Arches are core H burning objects showing products of the CNO equilibrium at their surface. They are clearly distinct from the less evolved O supergiants.


  \begin{figure} \par\includegraphics[width=7.65cm,clip]{8469fig6.eps}\end{figure} Figure 6: Logarithm of the ratio of nitrogen to carbon mass fraction in the Geneva evolutionary models of Meynet & Maeder (2005) and as derived in the stars analyzed in this work (symbols).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig7.eps}\end{figure} Figure 7: Comparison between the spectra of stars F6 and F7 showing that stars with similar main lines and thus similar parameters ( $T_{{\rm eff}}$, $\log \frac{L}{L_{\odot}}$, $\dot{M}$) can have different C and N abundances, as revealed by the different strengths of the C IV 2.070-2.084 $\mu $m and N III 2.247, 2.251 $\mu $m lines.
Open with DEXTER

   
6.2 Winds

In Fig. 8 we show the mass loss rates of the Arches stars studied here as a function of luminosity (left). It is clear that the WNLh stars have stronger winds than the O stars. Indeed, although mass loss increases with luminosity as predicted by the theory of radiation driven winds (Castor et al. 1975), there is a separation between the O and WNLh stars for the luminosity range 5.7-6.2 in which both types of stars are found. This is another indication that WN7-9h stars are more evolved than O stars. It is also very interesting to note that the extreme supergiants (O4-6If+ stars) seem to have mass loss rates intermediate between normal O supergiants and WN7-9h stars. As we will see in Sect. 6.3, this is an indication of an evolutionary link between early O supergiants and WNLh stars.


  \begin{figure} \par\mbox{\includegraphics[width=8.15cm,clip]{8469fig8a.eps}\hspace*{0.6cm} \includegraphics[width=8.15cm,clip]{8469fig8b.eps} } \end{figure} Figure 8: Left: Mass loss rates as a function of luminosity for the Arches cluster stars. Right: clumping corrected mass loss rates for the Arches cluster stars (filled symbols) as well as comparison objects (open symbols): early type (extreme) supergiants from Repolust et al. (2005); Bouret et al. (2005); Herrero et al. (2002) and WN6-9h stars from Crowther & Dessart (1998); Crowther & Bohannan (1997).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig9.eps}\end{figure} Figure 9: Modified wind momentum - luminosity for the Arches cluster stars. The solid line is the theoretical prediction from Vink et al. (2000). The red dashed line is the linear fit to the O stars, excluding the O4-6If+ supergiants. The blue dot dashed line is the fit to the WN7-9h stars. The dotted line is our WLR for O stars if we use unclumped mass loss rates. See text for discussion.
Open with DEXTER

On the right part of Fig. 8, we show the clumping corrected mass loss rates ( $\dot{M}/\sqrt{f}$) as a function of luminosity for our sample stars as well as for comparison objects. We see that qualitatively, the mass loss rates we derive are consistent with previous studies of Galactic stars. Given the scatter in $\dot{M}$ among the various types of stars, it is not possible to make a quantitative comparison. Instead, the so-called modified wind momentum - luminosity relation, or WLR, is a better tool. The modified wind momentum, $\dot{M} v_{\infty} \sqrt{R}$ (R being the stellar radius), is expected on theoretical grounds to depend only on luminosity (e.g. Kudritzki & Puls 2000). Figure 9 shows the relation for the Arches cluster stars. On average, all stars follow the qualitative increase of the modified wind momentum as a function of luminosity. It is very important to note that this is also true to a large extent for the WN7-9h stars: they clearly show a correlation between modified wind momenta and luminosity. More specifically, we have:

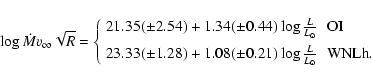\begin{displaymath}% \log \dot{M} v_{\infty} \sqrt{R} = \left\{ \begin{array}{l}... ...{L}{L_{\odot}} \hspace{0.2cm} {\rm WNLh}. \end{array} \right. \end{displaymath} (1)

The existence of a WLR for WN7-9h stars is a strong indication that radiative acceleration plays an important in driving their winds. This is a fundamental result, since the question of whether or not radiative acceleration is efficient enough to produce the large WR stars outflows is not entirely settled yet (see Crowther at al. 2007, for a recent review). Recent theoretical simulations by Gräfener & Hamann (2005) and Vink & de Koter (2005) convincingly indicate that radiative acceleration might explain the large mass loss rates of WR stars. Here, we provide an observational evidence that at least qualitatively, the O and WNLh stars winds in the Arches cluster rely on the same physics. Another argument in favor of line driving for the winds of the WN7-9h stars comes from the values of $\eta = \dot{M}$ $\times $ $v_{\infty} /(L/c)$ listed in the last column of Table 2. We see that for these stars, it is close to 1, meaning that radiation alone is in principle able to drive the wind, even in the single scattering limit.

The WLR followed by the WN7-9h stars is systematically shifted towards higher values (by $\sim $0.4 dex) compared to the O stars relation. This is not surprising since such an effect is also seen among O stars with different luminosity classes as well as between O, B and A stars (Repolust et al. 2004; Kudritzki et al. 1999). This is usually interpreted as a change in the number of lines effectively driving the acceleration (see discussion in Kudritzki & Puls 2000). We also note that the WLR we derive is flatter for WN7-9h stars: the slope is 1.34 for O stars, and 1.08 for WN7-9h stars. Given the errors, we cannot exclude however that the slopes are similar. Note that if we calculate the slope of the WLR regardless of the spectral types, i.e. including all stars of our sample, we get a value of 2.00 $\pm $ 0.19.

In Fig. 9, we have also plotted the theoretical relation of Vink et al. (2000) for O stars. Its slope is 1.83 $\pm $ 0.04. We see that given our limited sample and the errors, our WLR slope for O stars is rather similar. The absolute position of the WLR is however different. This is a known effect usually attributed to the use of clumping in our models, while the models of Vink et al. (2000) are homogeneous. Note however that hydrodynamical confirmations of this effect are still lacking. Including clumping in atmosphere models leads to systematically lower values of $\dot{M}$ compared to studies with homogeneous winds, the difference being $\sqrt{f}$ with f the clumping factor. In our case, we use f=0.1 so that we can expect a shift of 0.5 dex in the WLR of O stars (see dotted line in Fig. 9). We see that if we correct our derived relation by this amount, we end up slightly above the relation of Vink et al. (2000), by a factor $\sim $0.2 dex (the difference between their theoretical relation and ours is $\sim $0.2-0.3 dex depending on the luminosity). How can we explain this remaining discrepancy? One might argue that our value of the clumping factor, assumed to be 0.1, is not appropriate for O stars. Our relation would be consistent with that of Vink et al. (2000) if we had chosen $f \sim 0.2{-}0.3$, a value that we cannot discard from our modeling. As previously recalled, we note however that recent studies indicate smaller f for O supergiants (Hillier et al. 2003; Bouret et al. 2005; Crowther et al. 2002a). Another interesting possibility to explain the difference between our and Vink et al.'s WLR is that we see the effects of high metal content. Mass loss rates of O stars are expected to scale as Z0.85 (Vink et al. 2001). If the difference we observe between the theoretical relation of Vink et al. (2000) and our derived relation for O stars was due to such an effect, this would mean that the metallicity of the Arches stars should be $Z/Z_{\odot} = 10^{\frac{0.2}{0.85}} \sim 1.7$. This is an intriguing possibility that we will discuss further in Sect. 7. Finally, we should mention that the prediction of Vink et al. (2000) might not be correct. However, several recent studies seem to confirm its validity, at least at high luminosities (Mokiem et al. 2006; Markova et al. 2004).

To conclude this section on the wind properties of the Arches stars, we summarize in Table 4 the mass loss rates of the stars analyzed in the present study which have been observed at radio wavelengths by Lang et al. (2005). From these detections, the authors derive values of the mass loss rates using the standard relation of Wright & Barlow (1975). Since this relation implies that stellar winds are homogeneous, we have to compare the mass loss rates of Lang et al. (2005) to our clumping corrected $\dot{M}$(i.e. $\frac{\dot{M}}{\sqrt{f}}$). Lang et al. (2005) also use a different distance (8.0 kpc instead of 7.62 kpc) and assume $\mu = 2.0$ to derive their mass loss rates. We also have to correct for this. The initial and corrected values of $\dot{M}$ of Lang et al. (2005) are given in Cols. 3 and 4 of Table 4. For stars 3, 5, 8 and 18, we see that both our and the radio determination are consistent within a factor of 2. For the remaining stars (1, 2, 4, 6), the differences can be as large as almost an order of magnitude. Star F6 is suspected to be the counterpart of the X-ray source A1N (Law & Yusef-Zadeh 2004), indicating that it might be a non-thermal emitter (colliding winds). Besides, Lang et al. (2005) report that star F6 is variable. Hence, differences between our determination and the radio mass loss rate is not surprising. For the three remaining stars (F1, F2 and F4), we have no explanation so far of the disagreement. One might invoke binarity (although our spectra exclude the presence of a spectroscopic companion) or crowding which may affect the radio determination (the resolution - $0.42\hbox{$^{\prime\prime}$ }$ $\times $ $0.17\hbox{$^{\prime\prime}$ }$ - being lower than in our SINFONI data - 0.20 $^{\prime\prime}$).

Excluding star F6 (suspected binary), it is interesting to note that the radio mass loss rates are systematically lower than the IR unclumped ones (exception: F18). This effect was noted by Figer et al. (2002) for one star (F8). In our case, he difference is 0.36 dex, with a rather large dispersion (0.32). Since the ratio of unclumped mass loss rates is virtually similar to the ratio of wind densities (recall that the $\dot{M}$ diagnostics are in fact density indicators), this difference might tell us something about the different clumping factors in the IR and radio emitting regions. Density is $\propto$ $\dot{M}/\sqrt{f}$, where $\dot{M}$ is the "true'' mass loss rate. Hence, the ratio of radio to IR unclumped mass loss rates is $\propto$ $\sqrt{f_{\rm IR}/f_{\rm radio}}$ where $f_{\rm IR}$( $f_{\rm radio}$) is the clumping factor in the IR (radio) emitting region. With the observed trend, it seems that clumping is stronger in the IR than in the radio emitting region (by a factor of $\sim $5). This is in agreement (qualitatively and quantitatively) with the recent findings of Puls et al. (2006) and with the theoretical predictions of Runacres & Owocki (2002). This might partly explain the systematic differences seen in Table 4.

Table 4: Clumping corrected mass loss rates for the stars in common between the present sample and the sample of Lang et al. (2005).

   
6.3 Nature and evolution of the most luminous stars

The discussion in the last sections has lead to a clear picture for the nature of the WN7-9h stars in the Arches cluster: they are very massive ( $60<M<120~\mbox{$M_{\odot}$ }$) post main sequence objects still in the H burning phase and have reached the CNO equilibrium. They clearly separate from the rest of the O stars studied here. As such, they are very reminiscent of the H rich WN stars in the core of the NGC 3603 and R136 clusters (Crowther & Dessart 1998).

From the analysis of several Galactic WN stars, Crowther et al. (1995) built the following evolutionary sequence for stars more massive than 60 $M_{\odot }$:

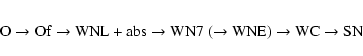
\begin{eqnarray*}\rm O \rightarrow Of \rightarrow WNL+abs \rightarrow WN7 \; (\rightarrow WNE) \rightarrow WC \rightarrow SN \end{eqnarray*}


where WNL (WNE) stands for W6-9 (WN2-5) stars. Langer et al. (1994) describe a similar sequence except that 1) they include a Luminous Blue Variable phase after the H-rich (=WNL + abs) phase, and 2) they do not explicitely list WN7 types in their scenario but replace them by the term H-poor WN. However, they tentatively identify H-rich WN stars as core H burning objects. They also note that these objects are the most luminous WN stars.

The Arches WNLh stars nicely fit the global picture drawn in these scenarios: they are very luminous, young, H rich objects clearly still in the H burning phase and with masses in excess of 60 $M_{\odot }$. Besides, our detailed analysis of the C and N abundance patterns of these stars quantitatively strengthens the conclusion that they are in a relatively early evolutionary state. The direct link between O and WNLh stars is also confirmed by our analysis. The O supergiants of our sample all appear to be less evolved than the WNLh stars (see Figs. 3-6). And the two O4-6If+ extreme supergiants have properties intermediate between normal supergiants and WNLh stars: this is best seen in Fig. 5 where they bridge the two latter classes of objects. Note however that we cannot state that there is a direct link between specific sub-classes of stars in the Arches cluster, namely between O4-6 supergiants and WNLh stars: Fig. 2 reveals that the former probably have lower initial masses than the latter. But we can safely conclude that WNLh stars have early O stars as progenitors, since they should evolve from more massive (and consequently hotter) O stars than the O supergiants of our sample. In practice, the Arches WNLh stars should be the descendant of O2-4 stars. We note that Crowther & Bohannan (1997) argued for a direct link between O8If and WN9ha stars. However, this was based on the study of only 3 stars, compared to 28 in the present paper. The WN9ha of their study had in addition a lower luminosity and temperature than the Arches WN7-9h stars, and might thus be a different, initially less massive type of WN9h star. Consequently, we do not think that our results are in contradiction with Crowther & Bohannan (1997), but rather that they refer to different kinds of stars.

In conclusion, our findings strongly support the scenario according to which, in the Arches cluster, the most massive O stars evolve into extreme supergiants and then into H-rich WNL stars.

   
7 Stellar metallicity

In the previous sections we have seen that several elements pointed towards a super solar metallicity for the Arches cluster stars: the N enrichment might be too large to be accounted for by solar metallicity evolutionary models, and the winds might be stronger than expected for a solar composition. This is somewhat in contradiction with the recent results of Najarro et al. (2004) who favored a solar metallicity for the five stars they analyzed. Their determination was based on the interesting finding that the N mass fraction reaches a maximum in evolutionary tracks when the star is in the WN phase. This maximum does not depend on the initial mass, but is sensitive to the initial global metallicity. In practice, comparing the mass fraction of a sample of WN stars to such tracks should then constrain the metallicity. Najarro et al. (2004) used the three WN stars they analyzed to make such an estimate. They found that a solar metallicity was preferred. In Table 3 we have shown that for these three stars, we find similar X(N) for one (F8), and slightly larger values than Najarro et al. (2004) for the other two (F3 and F4). Figure 10 is the figure Najarro et al. used to estimate Z in the Arches cluster, but now using the 13 WN stars of our sample: the shaded area corresponds to the range of X(N) covered by these 13 stars. From this, we see that a wide range of metallicity is possible. If real, this can be attributed to two factors. First, there may be a scatter in the initial metallicity of the Arches stars. However, a difference of a factor of 2 seems quite large. The second possibility is that the WN stars might not all have reached the phase of their evolution were X(N) is maximum. In that sense, Fig. 10 provides only a lower limit on the metallicity. Note that this effect most likely influences the results when a small number of stars is used. One might also wonder whether the scatter we see is not purely statistical. If we assume it is the case, we can run a $\chi ^{2}$ analysis to find the preferred metallicity, using

 \begin{displaymath}% \chi^{2}(Z) = \sum \frac{(X_{\rm i}-X_{\rm max}(Z))^{2}}{\sigma_{\rm i}^{2}} \end{displaymath} (2)

where $X_{\rm i}$ are the individual N mass fraction, $\sigma_{\rm i}$ the associated uncertainties, and $X_{{\rm max}}(Z)$ the maximum N mass fraction reached at a given metallicity. The evolution of $\chi ^{2}/n$ with Z is shown in Fig. 11 (n being the number of free parameters, equal to 12 in our case - 13 stars included and one fitted parameter). We see that there is a clear minimum for Z = 1.3-1.4 $Z_{\odot }$, and that a twice solar metallicity is clearly excluded. The minimum  $\chi ^{2}/n$ is 1.88, so a unique metallicity is not completely satisfactory to explain the distribution of $X({\rm N})_{\rm max}$. One has to keep in mind that this analysis is also correct only if the evolutionary models correctly predict the evolution of surface abundances.


  \begin{figure} \par\includegraphics[width=8.15cm,clip]{8469fig10.eps}\end{figure} Figure 10: N mass fraction as a function of age in evolutionary models for solar (solid line) and twice solar (dotted line) metallicity. The Geneva evolutionary tracks including rotation of Meynet & Maeder (2005) are used. Tracks for M = 120, 85, 60 and 40 $M_{\odot }$ are shown from from left to right. The shaded area indicates the range of X(N) covered by the WN7-9h stars analyzed in the present study.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{8469fig11.eps}\end{figure} Figure 11: Determination of metallicity from the N mass fraction of WNLh stars. $\chi ^{2}$ is defined in Eq. (2). $\chi ^{2}/n$ is shown as a function of metallicity. n is the number of free parameters (12 is the present case). If the scatter in X(N) is purely statistical, then a slightly super-solar metallicity (Z = 1.3-1.4 $Z_{\odot }$) is preferred.
Open with DEXTER

Altogether, our results tend to favor a slightly super solar metallicity. Najarro et al. (2004) concluded that Z = $Z_{\odot }$ was preferred. The difference is likely due to the use of different evolutionary tracks: we use the recent tracks from Meynet & Maeder (2005), while Najarro et al. use the obsolete tracks from Schaller et al. (1992). Since for a given metallicity, these old tracks have a larger maximum X(N), a lower metallicity is derived for a given range of observed X(N)[*]. In our sample, the average value of X(N) in WNLh stars is 1.70( $\pm 0.60)\%$. The three stars of Najarro et al. have on average X(N) = $1.57(\pm 0.15)\%$. Hence, within the errors, the values are similar. The different derived metallicity we find is thus likely due to the use of different evolutionary tracks.

An important comment to make is that the approach described above is only valid if the CNO abundances and the global metallicity Z scale similarly, or stated differently if all the metals have the same relative overabundance compared to the solar composition. Let us assume we have a model in which the initial CNO content is larger than solar, while all the other metals have solar abundances. The global metallicity will then be slightly above solar. Let us consider a second model in which the global metallicity is the same as in the first one, but now all the elements have the same abundance excess relative to the solar composition. In the two models, the global metallicity is the same, but the first one will produce a much higher N mass fraction. If we use this mass fraction to asses the global metallicity using the method presented above, then we will overestimate the global metallicity of the star.

Studies of abundances of individual elements not affected by stellar evolution would help to better constrain the metallicity of the Arches cluster stars. Unfortunately, very few lines are available for such a purpose. The only one which could be of help is the Si IV line at 2.428  $\mu \rm {m}$. Interestingly, it turns out that to correctly reproduce it in all the stars we have studied so far, we need a silicon abundance between solar and twice solar. Given that the line is located at the end of the K band where the S/N degrades rapidly and where the spectrum normalization is less straightforward than at shorter wavelengths, we claim that this is only an indication that individual abundances of light metals might be super-solar. It is nonetheless interesting that this would be consistent with the various indications gathered so far. If we assume that the Fe content is about solar as studies of red supergiants in the central cluster show (Ramírez et al. 2000; Carr et al. 2000), it might well mean that there is an excess of light metals relative to heavier metals in the Arches cluster. Such a conclusion would thus weaken the results of the Z determination by the method presented by Najarro et al. (2004). But this would be a very attractive possibility, since this could indicate a larger $\alpha$/Fe abundance ratio, which in turn is usually interpreted as the imprint of a top-heavy IMF. A recent study of stellar abundances in cool luminous stars by Cunha et al. (2007) concluded that O and Ca (two $\alpha$ elements) were overabundant compared to Fe in the central cluster. Our suggestion of a super-solar Si abundance in the Arches cluster is consistent with their findings.

In conclusion, we tentatively suggest that in the Arches cluster, the lightest elements most likely have a super-solar abundance while the iron peak elements have a solar metallicity.

   
8 Conclusions

We have presented a quantitative study of the most massive stars in the Arches cluster. K-band spectra have been obtained with SINFONI on the VLT. A detailed spectral classification has revealed the presence of WN7-9h stars as well as O supergiants, including two extreme OIf+ stars. We have quantified the main stellar and wind parameters of 28 stars using the atmosphere code CMFGEN. The main results of our study are:

In order to test the indication that the most massive stars are the last to form, intermediate mass stars must be analyzed. The question of the metallicity in the Galactic Center, and the Arches cluster in particular, is clearly not answered yet. New observations/analysis of cooler stars showing a larger number of metallic lines are needed. We will present such a study in a forthcoming paper.

Acknowledgements
We thank F. Najarro for useful comments and for sharing his O III model atom. This paper benefited from interesting discussions with G. Meynet. F.M. acknowledges partial support from the Alexander von Humboldt foundation. Finally, we thank an anonymous referee for a careful reading of the manuscript and valuable comments.

References

 

  
Online Material

Appendix A: Best fits

In this section, we gather the figures showing the comparison of our best fit models with the observed spectra of our program stars.


  \begin{figure} \par\includegraphics[height=22.3cm,width=16.75cm,clip]{8469fig12.eps}\end{figure} Figure A.1: Best fits (red dot-dashed lines) of the observed K-band spectra (black solid line).


  \begin{figure} \par\includegraphics[height=22.3cm,width=16.75cm,clip]{8469fig13.eps}\end{figure} Figure A.2: Best fits (red dot-dashed lines) of the observed K-band spectra (black solid line).


  \begin{figure} \par\includegraphics[height=22.3cm,width=17.25cm,clip]{8469fig14.eps}\end{figure} Figure A.3: Best fits (red dot-dashed lines) of the observed K-band spectra (black solid line).


  \begin{figure} \par\includegraphics[height=22.3cm,width=17.25cm,clip]{8469fig15.eps}\end{figure} Figure A.4: Best fits (red dot-dashed lines) of the observed K-band spectra (black solid line).


Copyright ESO 2008