A&A 475, 901-914 (2007)
DOI: 10.1051/0004-6361:20078271
D. Koutroumpa1 - F. Acero2 - R. Lallement1 - J. Ballet2 - V. Kharchenko3
1 - UMR 7620, IPSL/Service d'Aéronomie, CNRS, Université Pierre et Marie Curie, Université Versailles-Saint-Quentin, Verrières-le-Buisson, France
2 - UMR 7158, DSM/DAPNIA/SAp, CEA Saclay, 91191 Gif-sur-Yvette, France
3 - Harvard-Smithsonian Center for Astrophysics, Cambridge, MA, USA
Received 13 July 2007 / Accepted 10 September 2007
Abstract
Aims. We study the 0.57 keV (O VII triplet) and 0.65 keV (O VIII) diffuse emission generated by charge transfer collisions between solar wind (SW) oxygen ions and interstellar H and He neutral atoms in the inner Heliosphere. These lines which dominate the 0.3-1.0 keV energy interval are also produced by hot gas in the galactic halo (GH) and possibly the Local Interstellar Bubble (LB).
Methods. We developed a time-dependent model of the Solar Wind Charge-Exchange (SWCX) X-ray emission, based on the localization of the Solar Wind Parker spiral at each instant. We include input SW conditions affecting three selected fields, as well as shadowing targets observed with XMM-Newton, Chandra and Suzaku satellites and calculate X-ray emission in the oxygen lines O VII and O VIII in order to determine the SWCX contamination and the residual emission to attribute to the galactic soft X-ray background. We obtain ground level intensities and/or simulated lightcurves for each target and compare to X-ray data from the three instruments mentioned.
Results. The local 3/4 keV emission (due essentially to O VII and O VIII) detected in front of shadowing clouds is found to be entirely explained by the CX heliospheric emission. No emission from the LB is needed at these energies. The observed and modeled range of the foreground oxygen emission is 0.3-4.6 LU (Line Units = photons cm-2 s-1 sr-1) for OVII and 0.02-2.1 LU for OVIII depending on directions and conditions. Using the model predictions we subtract the heliospheric contribution to the measured emission and derive the halo contribution. We also correct for an error in the preliminary analysis of the Hubble Deep Field North (HDFN). We find intensities of 4.9
+1.29-1.04 LU, 6.25
+0.63-0.98 LU, 11.15
+2.36-1.41 LU for OVII and 1.41
+0.60-0.49 LU, 1.62
+0.35-0.49 LU, 1.97
+1.11-0.71 LU for OVIII towards the Marano Field, the Hubble Deep Field-North, and the Lockman Hole respectively.
Key words: solar wind - X-rays: diffuse background - X-rays: ISM - ISM: general - Galaxy: halo
Charge-eXchange (CX) collisions between highly charged Solar Wind ions and solar system neutrals was identified as a very efficient mechanism of soft X-ray emission by Cravens et al. (1997), following the discovery of X-ray emission from comets (Lisse et al. 1996). Immediately after that, Cox (1998) suggested that X-ray emission induced in Solar Wind Charge-eXchange (SWCX) with interstellar (IS) neutrals flowing across the Heliosphere would be an additional component of the diffuse soft X-ray background (SXRB), not to be considered lightly.
Signs of the SWCX diffuse emission had already been detected during the ROSAT all-sky survey, as a background component varying in scales of one to several days and contaminating all observations with count rates comparable to the cosmic background (Snowden 1993). These temporal variations called long-term enhancements (LTEs; Snowden et al. 1995) had been associated to solar wind variations (Freyberg 1994) although their origin remained unknown until the discovery of SWCX emission.
Cravens et al. (2001) and Robertson et al. (2001) modeled the heliospheric SWCX emission with a simple model of the SW radial propagation without solar rotation, and explained satisfactorily the global correlation between the LTEs and strong solar wind enhancements. Moreover, the geocoronal emission was examined by Robertson & Cravens (2003a,b) and measured during Chandra observations of the dark moon (Wargelin et al. 2004). The temporal variations of the X-ray emission (including the ROSAT LTE's) were proved to be as much due to the geocoronal emission, as due to the heliospheric emission (H and He). However, the geocoronal emission consists mainly of short-term, intense peaks and is more tightly correlated to SW enhancements than the He and especially the H component of LTE's (Fig. 2 in Cravens et al. 2001) which makes it much easier to identify. Their analysis showed that the geocoronal emission can reach the same order of magnitude as the heliospheric contribution during only short-time intervals.
LTEs were, in general, easily identified in ROSAT lightcurves, and time-variable contaminated data were systematically removed (Snowden & Freyberg 1993), removing mainly the geocoronal component, but not all of the heliospheric emission. In general, it was proved that the contamination could be quite significant in the case of large solar wind enhancements, as has been demonstrated by the long-duration XMM-Newton exposure towards the Hubble Deep Field-North (Snowden et al. 2004, hereafter SCK04).
However, the ground level of the heliospheric SWCX emission has been a subject of debate. Cravens (2000) estimated that it could be of the same order as the soft X-ray emission of the so-called Local Interstellar Bubble (hereafter LB). On the other hand, Cox (1998) predicted that the heliospheric CX emission maxima should be aligned
along the interstellar wind axis (i.e. towards galactic coordinates lII,bII = 4![]() , +16
, +16![]() and in the opposite direction), a trend which was not observed in ROSAT survey maps. Lallement (2004) warned that parallax effects due to the ROSAT observation geometry destroy this axial symmetry and that as a consequence the absence of such maxima does not allow to draw conclusions. The reconstruction of the heliospheric emission sky map
for the ROSAT survey geometry and the comparison with the data and the LB geometry suggested that, apart from a few specific regions and from high latitude directions, a significant contribution of the heliosphere is not precluded.
and in the opposite direction), a trend which was not observed in ROSAT survey maps. Lallement (2004) warned that parallax effects due to the ROSAT observation geometry destroy this axial symmetry and that as a consequence the absence of such maxima does not allow to draw conclusions. The reconstruction of the heliospheric emission sky map
for the ROSAT survey geometry and the comparison with the data and the LB geometry suggested that, apart from a few specific regions and from high latitude directions, a significant contribution of the heliosphere is not precluded.
The Local Interstellar Bubble is a ![]() 100 pc cavity surrounding the Solar System and presumably filled with rarefied, hot plasma. The idea of the Hot LB derived from the need to explain the fraction of the soft X-ray background
that does NOT anticorrelate with the interstellar column density, and thus can not be attributed to distant galactic emission but needed a local origin (Sanders et al. 1977;
Snowden et al. 1990). The temperature of the emitting gas has been inferred by the Wisconsin (Fried et al. 1980; McCammon & Sanders 1990; Snowden et al. 1990) and ROSAT (Snowden 1993) surveys band ratios in the 1/4 keV energy range, and found to be around 106 K.
100 pc cavity surrounding the Solar System and presumably filled with rarefied, hot plasma. The idea of the Hot LB derived from the need to explain the fraction of the soft X-ray background
that does NOT anticorrelate with the interstellar column density, and thus can not be attributed to distant galactic emission but needed a local origin (Sanders et al. 1977;
Snowden et al. 1990). The temperature of the emitting gas has been inferred by the Wisconsin (Fried et al. 1980; McCammon & Sanders 1990; Snowden et al. 1990) and ROSAT (Snowden 1993) surveys band ratios in the 1/4 keV energy range, and found to be around 106 K.
Apart from distinct features like supernovae and superbubbles (e.g. Loop I), the diffuse SXRB below 1 keV is still largely considered to be consisting of three major components: (i) an unabsorbed
![]() 106 K thermal component originating from the LB, (ii) an absorbed
106 K thermal component originating from the LB, (ii) an absorbed ![]() 2
2 ![]() 106 K thermal component associated with the galactic halo and (iii) an absorbed extragalactic power law (Kuntz & Snowden 2000; also see review of McCammon & Sanders 1990, and references within).
106 K thermal component associated with the galactic halo and (iii) an absorbed extragalactic power law (Kuntz & Snowden 2000; also see review of McCammon & Sanders 1990, and references within).
In Koutroumpa et al. (2006) we have presented a thorough analysis of the total ground level SWCX heliospheric emission and exposed a detailed list of the factors influencing this emission, such as the solar cycle phase, the observer position, and the line of sight (LOS), as well as a preliminary analysis of a time-dependent model.
In this paper we present a more detailed comparison between soft X-ray observations from XMM-Newton, Chandra and Suzaku and time-dependent simulations of heliospheric CX-induced soft X-ray emission. Our goal is to try and distinguish the post-CX heliospheric component within the soft X-ray background, in the range 0.5-1.0 keV and more specifically separate the oxygen (O VII 0.57 keV; O VIII 0.65 keV) heliospheric emission from the Local Interstellar Bubble (LB) and Galactic Halo emission in the same energy range. The two oxygen lines are of primary importance in the study of the LB, because if the 1/4 keV emission is usually analysed to derive the Bubble's temperature, the oxygen line ratio is used to constrain, or rule out, higher temperatures for the LB models (Henley et al. 2007, here after HSK07), as well as to constrain the halo emission characteristics.
X-ray data selection criteria and processing are presented in Sect. 2, followed by a thorough presentation of the time-dependent SWCX heliospheric model in Sect. 3. Case to case results are detailed in Sects. 4.1 to 4.5. Finally, conclusions and global comparison to ROSAT 3/4 keV maps are discussed in Sect. 5.
The targets selected are summarized in Table 1 and can be assembled in two major groups according to the criteria upon which they were selected.
| Name | Gal. Coord. | Instrument | Obs. period |
| Marano Field | (269.8 |
XMM | 22-30/08/2000 |
| HDFN | (126.0 |
XMM | 01/06/2001 |
| Lockman Hole | (149.1 |
XMM | 15-27/10/2002 |
| 2*MBM 12 | 2*(159.2 |
Chandra | 17/08/2000 |
| Suzaku | 03-08/02/2006 | ||
| 2*Filament | 2*(278.7 |
XMM | 03/05/2002 |
| Suzaku | 01-03/03/2006 |
The initial goal of this study was to model short-scale variations of the soft X-ray heliospheric background due to temporary SW enhancements. This idea was inspired by the SWCX X-ray detection during the Hubble Deep Field North (HDFN here after) observation of June, 1, 2001 with XMM-Newton (SCK04). The HDFN exposure was long enough to detect one of the most beautiful examples of CX emission in the Heliosphere, due to a large SW flux enhancement (SCK04; Koutroumpa et al. 2006).
Such long-lasting exposures are not very frequent in the observation schedules of X-ray observatories, so we decided to look in the XMM-Newton database for short-spaced repeated exposures on the same target-fields and preferentially associated with some medium or large SW enhancements recorded in the same periods by SW instruments (WIND, ACE/SWEPAM, OMNIWEB database). We thus collected three targets, including the HDFN, the Marano Field and the Lockman Hole, which compose our first group. We chose XMM-Newton because it disposes of a large Database of easy access. We needed a large spectral resolution in the 0.5-0.7 keV energy range, where the O VII and O VIII lines are dominant, so we used only MOS 1 and 2 spectra, which have the best resolution in this domain and the least calibration problems. The data extraction and analysis with XMM MOS 1 and 2 are detailed in Sects. 2.2 and 2.3.
Since the initial idea, the goal of this study has evolved. We decided to include two shadowing targets in the study, the molecular cloud MBM12 and a nearby filament in the Southern Galactic hemisphere (here after called South Galactic Filament = SGF). Each of these two shadows, has been observed during a minimum and maximum solar activity period. The observations are separated by several years, 2000 and 2006 for the MBM 12, and 2002 and 2006 for the SGF. Also, the observations were not made with the same instrument, Chandra and Suzaku for MBM 12, and XMM and Suzaku for the SGF. Even though the characteristics of these cases are quite different from the first group, we feel we can include them in this study since they are made in different solar conditions, and give an idea of the large-scale mean temporal variations of the SWCX X-ray emission level. Moreover, some of them are associated with quite particular SW conditions, either CMEs (MBM 12-Chandra observation, Filament-XMM observations), or sudden SW enhancement (MBM 12-Suzaku exposures). Each of the MBM 12 and SGF fields are detailed in paragraphs 4.1 and 4.2 respectively.
In any case, all observation fields are as clear as possible of large diffuse sources, in order to distinguish the post-CX heliospheric emission. We avoid the galactic plane and compile target fields with as few bright point sources as possible.
In Table 1 we list, besides the target name and central coordinates, the instrument used for each series of observations, and the observing period(s) for each field. Details on the data and model results will be given for each field in Sect. 4. General discussions on the data-model comparisons will also be given in Sect. 5.
All XMM observations were reprocessed using the Science Analysis System (SAS version 6.5; the software is based on the model described in SCK04). We used only MOS data to take advantage of its better spectral resolution. All the spectra used are an average of MOS1 and MOS2 detectors. To clean the event files from soft proton flare contamination, we used the MOS-FILTER process available in the Extended Source Analysis Software (XMM-ESAS).
By building a histogram of counts/s in the 2.5-12 keV energy range and fitting a gaussian
distribution upon it, it retains only the time intervals where the count rates are within a 3![]() range.
range.
The different fields contain moderately bright sources that may have emission lines in the same energy bands as the charge exchange induced soft X-ray emission. The XMM SSC (Survey Science Center) produces a summary source list file providing information such as the coordinates and the flux of the detected sources in various energy bands for each observation. Using the 0.5-2 keV energy band, we removed all the sources that contribute to more than 1% to the background emission in this particular energy band. The region subtracted was a disk covering 90% of the total flux of the sources. We then checked the results of the filter by building a "cheese'' map (full field of view with sources removed) in a small energy band around the OVII and OVII emission lines (0.5-0.7 keV) to check that no sources remained. All spectra were extracted from this filtered event file. In this study we did not use any astrophysical nor instrumental background spectrum since the charge exchange induced X-ray emission is present in the entire field of view and any background spectrum may contain the emission we are trying to measure.
The purpose of our simple model is to extract the flux of the O VII and O VIII emission lines respectively at 0.57 keV and 0.65 keV. To do so with minimal assumptions, we add narrow lines at the expected energies to a continuum emission. In the imaging mode, the spectral resolution of XMM is much broader than any astrophysical line width. Concerning the continuum emission we assume, there are many origins to it but we decided to make a simple modelization with only two power laws.
We fit the soft X-ray spectra between 0.5 and 1.2 keV with XSPEC (11.3.2ad; Arnaud 1996). The first component used in the model accounts for the residual soft proton contamination which is convolved by the redistribution matrix but not folded by the instrumental efficiency. The index and the normalization of this power law were free to vary.
The second component is an absorbed power law accounting for the extragalactic component. Its index was fixed to 1.46 (Chen et al. 1997) for all the observations. The absorption depends on the H column density of the part of the Galaxy each field is situated and the values are specified for each case in Sect. 4. We note that our modelling of the continuum is not realistic but it is sufficient for our study since we are mostly interested in charge exchange (CX) emission, which contains only lines.
Part of the spectral lines observed will be astrophysical emission from the Local Interstellar Bubble (LB) or a galactic corona. We prefer not to model this astrophysical emission to avoid underestimating the heliospheric component. We decided to model the following spectral lines with a gaussian distribution: O VII 0.57 keV, O VIII 0.65 and 0.81 keV, and Ne IX 0.91 keV.
The model (that we name PLC = PowerLaw Continuum) we used in our analysis can be described as follows: powerlaw/b + phabs(powerlaw) + Gaussian + Gaussian + Gaussian + Gaussian. The Gaussian width was set to 0. This resulted most of the time
in a good fit (
![]() 140-170 for 135 d.o.f).
140-170 for 135 d.o.f).
To test the robustness of our simple model for the continuum, we also tried a more sophisticated model for the continuum inspired by (and applied on) the SGF data analysis in HSK07 (see Sect. 4.2.1). This model consisted of a thermal plasma in collisional ionization equilibrium of temperature T = 106.06 K to model the LB, with oxygen abundance set to zero and two gaussians to account for the O VII and O VIII lines. The Galactic halo emission was modeled as two absorbed thermal plasma components of temperatures T = 105.93 K and T = 106.43 K respectively.
In our test (that we name TCZEROX = Thermal Continuum ZERo OXygen), we used the LB model of HSK07 and we also forced a zero oxygen abundance for the halo components, keeping the same temperatures, so that all O VII and O VIII intensities are included in the gaussians. This test gave only a 15% difference in the O VII strengths with respect to our simplified model, which gives us confidence in our procedure. The mean difference in the O VIII line flux is around 40%, but does not affect our confidence, since this line measurements are much more uncertain than the O VII line. The results on the SGF data analysis are thoroughly detailed in Sect. 4.2.1.
CX collisions, producing X-ray photons, are described by the reaction:
The model used to calculate the ground level heliospheric CX-induced soft X-rays is detailed in Koutroumpa et al. (2006). It calculates the dynamical distribution of interstellar H (
![]() )
and He (
)
and He (
![]() ) atoms in the inner Heliosphere with respect to
distance r from the Sun, considering solar cycle variations effects and solar wind anisotropies for both H and He ionization processes.
) atoms in the inner Heliosphere with respect to
distance r from the Sun, considering solar cycle variations effects and solar wind anisotropies for both H and He ionization processes.
It then calculates the SW heavy ion radial propagation and loss due to
CX occuring from collisions with IS atoms. We obtain then, the radial distribution of the SW heavy ion
![]() ,
depending on the density of ion XQ+ at 1 AU:
,
depending on the density of ion XQ+ at 1 AU:
![\begin{displaymath}%
N_{{X}^{Q+}o}=[{X}^{Q+}~/~{\rm O}]~[{\rm O~/~H^+}]~n_{{\rm H}^+o}
\end{displaymath}](/articles/aa/full/2007/45/aa8271-07/img17.gif) |
(2) |
For each selected target field and observation date, we calculate the path on the line of sight (LOS), decomposed in ![]() segments of increasing step dsj as we move away from the observer, from 0.1 AU at 1 AU up to 8.5 AU at the final distance of
segments of increasing step dsj as we move away from the observer, from 0.1 AU at 1 AU up to 8.5 AU at the final distance of ![]() 85 AU, and
the corresponding emissivity in units of (photons cm-3 s-1):
85 AU, and
the corresponding emissivity in units of (photons cm-3 s-1):
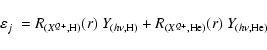 |
(3) |
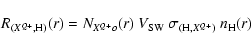 |
(4) |
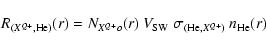 |
(5) |
The integrated emission for the particular spectral line on the LOS is given by the following Eq. (6):
Whenever solar instruments (WIND, ACE/SWEPAM) measure an important SW increase, due to solar flares, CMEs or other, within a few days of the observation dates of our selected fields, we apply a time-dependent simulation on the ground emission level to account for the variations induced in the total X-ray emission levels due to the enhancement. This was made for all of our targets except the Suzaku SGF exposure (Mars 2006) when the SW was rather calm. For each field we model the SW enhancements as one or multiple step functions, if there are more than one events during the observations period. The general procedure is similar for each simulation, based on the localization of the SW enhancements as a function of time along a Parker-type spiral, but we care to take into account the specific observation geometry and SW conditions for each target and date. These specific conditions will be detailed for each target in the Sects. 4.1 to 4.5.
The general principle of modeling the impact of the SW enhancements on the segmented LOS is resumed in the following. Detailed calculations, formulas and schematic view of possible observation geometries are given in Appendix A.
In our modeling we are compelled to consider two cases, whether the LOS is pointing forward on the Earth's orbit, or backwards on it, as explicitely shown in Fig. A.1. In fact, when the LOS is pointing forward on the orbit, the spiral is affecting the LOS progressively, starting from the observer on the Earth's position (Fig. A.1a). In the second case of the LOS pointing backwards, the combined effect of the solar rotation and of the SW radial propagation acts in such a way that the LOS is affected starting at an intermediate point, dividing the LOS in two parts: (i) one on which the spiral is moving away from the observer, and (ii) a second (usually smaller) on which the spiral is approaching the observer (Fig. A.1b). We will go through the differences in modeling the two cases in Appendix A.
The Active Region (AR) causing the SW enhancement is supposed to extend from North to South Solar Poles and is continuously emitting a SW proton (p+) flux enhanced by a factor
![]() with respect to normal values
with respect to normal values ![]() = 2.6
= 2.6 ![]() 108 cm-2 s-1, at a speed of
108 cm-2 s-1, at a speed of
![]() .
The solar longitudinal extend of the AR is defined such that the total duration of the enhancement is
.
The solar longitudinal extend of the AR is defined such that the total duration of the enhancement is ![]() as measured in SW instruments.
as measured in SW instruments.
Equivalently, associated with the SW p+ flux enhancement, we consider measured variation factor
![]() in
the heavy ion relative abundances with respect to normal slow SW abundances
in
the heavy ion relative abundances with respect to normal slow SW abundances
![]() ,
in the particular circumstances
the relative abundances of O7+ (0.2) and O8+ (0.07), obtained with ACE/SWICS intrument.
,
in the particular circumstances
the relative abundances of O7+ (0.2) and O8+ (0.07), obtained with ACE/SWICS intrument.
At each instant Ti we define the form of the Parker spiral taking into account solid solar rotation (27-day period),
the radial propagation speed (
![]() ), the "ignition'' time on the solar disk towards each radial direction (Tdj), and the total width of the spiral (
), the "ignition'' time on the solar disk towards each radial direction (Tdj), and the total width of the spiral (
![]() ). Only in the cases of CMEs, we neglect the solar rotation,
since radial propagation is dominating the CME structure.
). Only in the cases of CMEs, we neglect the solar rotation,
since radial propagation is dominating the CME structure.
Depending on the spiral's width and time Ti, the segment dsj can be affected either completely, or partially, as shown
in Figs. A.1a and b. This latter case is especially encountered when we model explosive CME's which are usually very brief. We include a correction ![]() and
and ![]() ,
adjusting the enhancement factor and the abundance variation factor respectively, according to the total width of the sub-segment really touched by the enhancement
at each instant Ti. These corrections are calculated for each LOS according to the observation geometry (LOS pointing forward or backwards, details in Appendix A).
,
adjusting the enhancement factor and the abundance variation factor respectively, according to the total width of the sub-segment really touched by the enhancement
at each instant Ti. These corrections are calculated for each LOS according to the observation geometry (LOS pointing forward or backwards, details in Appendix A).
Once we have defined the sub-segment(s) really affected by the spiral at instant Ti we calculated the "new temporary'' total heliospheric intensity Ii, modified because of the SW enhancement:
The model is dealing only with soft X-ray emission generated in the Heliosphere, not accounting for the geocoronal emission. Although we cannot exclude that some residual geocoronal emission remains in the data and should be included in a more complete modeling of SWCX emission, we can consider, here, that the major part of the geocoronal emission is removed along with proton events (data processing, Sect. 2.2), since it is exactly correlated with the SW variations (Cravens et al. 2001). Moreover, a quick look on the observation geometries and the fact that XMM is in high orbit seems to indicate that most of the observations avoided the geocorona. Therefore, we decide to neglect any residual geocoronal emission in the SWCX analysis.
MBM 12 is a nearby molecular cloud in the southern Galactic hemisphere (l, b = 159
![]() 2, -34
2, -34![]() ). It's distance is estimated with much uncertainty between 60 and 360 pc, according to various studies (Hobbs et al. 1986; Andersson et al. 2002; Lallement et al. 2003). MBM 12, with a column density of
). It's distance is estimated with much uncertainty between 60 and 360 pc, according to various studies (Hobbs et al. 1986; Andersson et al. 2002; Lallement et al. 2003). MBM 12, with a column density of
![]()
![]() 1021 cm-2, is optically thick in the energy range 0.5-0.7 keV where the O VII
(0.57 keV) and the O VIII (0.65 keV) lines are dominant. Therefore when observing on-cloud at this energy range, the emission flux detected must be generated nearby, partly by the CX process in the Heliosphere and a small residual emission due to the Galactic background.
1021 cm-2, is optically thick in the energy range 0.5-0.7 keV where the O VII
(0.57 keV) and the O VIII (0.65 keV) lines are dominant. Therefore when observing on-cloud at this energy range, the emission flux detected must be generated nearby, partly by the CX process in the Heliosphere and a small residual emission due to the Galactic background.
MBM 12 was frequently used as a shadow for the soft X-ray background, allowing to determine what fraction of the emission is generated in local regions, close to the Sun, and what fraction belongs to the Galactic (disk + halo) or extragalactic components. The first time the MBM 12 was observed as a shadow, was with ROSAT XRT/PSPC on July 31/ August 1, 1991
(Snowden et al. 1993, here after SMV93), which yielded an upper limit for the observed ON-CLOUD emission of 23 ROSAT Units and ![]() 75 ROSAT Units for the observed OFF-CLOUD emission (see Fig. 3 in SMV93).
75 ROSAT Units for the observed OFF-CLOUD emission (see Fig. 3 in SMV93).
ROSAT Units (RU) characteristic of the ROSAT measurements correspond to 10-6 counts s-1 arcmin-2. An approximate
equivalence between RU and LU (Line Units = photons cm-2 s-1 sr-1) can be estimated based on Smith et al. (2007)
reasoning on the line flux measured in ROSAT observations. SMV93 fitted the ROSAT data with a Raymond & Smith (1977) model,
simulating a standard LB of a temperature of 106 K which fits adequately the 1/4 keV band.
For such a model, the 3/4 keV (0.5-0.8 keV) band produces only 47 counts s-1 sr-1 (=3.98 RU, since 1 sr = 1.18 ![]() 107 arcmin2) which are essentially due to the O VII triplet intensity producing 0.28 LU for such a model (according to ATOMDB). The PSPC instrument on ROSAT has very low resolution in the 3/4 keV band and cannot resolve
O VII and O VIII lines of continuum. If we assume, keeping in mind the large uncertainties, that all of the emission detected in the 3/4 keV ROSAT band is due to the O VII triplet alone, then, 1 RU = 0.07 LU. With this equivalence we conclude that the intensity measured by ROSAT for the MBM 12 was
107 arcmin2) which are essentially due to the O VII triplet intensity producing 0.28 LU for such a model (according to ATOMDB). The PSPC instrument on ROSAT has very low resolution in the 3/4 keV band and cannot resolve
O VII and O VIII lines of continuum. If we assume, keeping in mind the large uncertainties, that all of the emission detected in the 3/4 keV ROSAT band is due to the O VII triplet alone, then, 1 RU = 0.07 LU. With this equivalence we conclude that the intensity measured by ROSAT for the MBM 12 was ![]() 1.6 LU for the ON-CLOUD emission and
1.6 LU for the ON-CLOUD emission and ![]() 5.25 LU for the OFF-CLOUD emission.
5.25 LU for the OFF-CLOUD emission.
Chandra observed MBM 12 on August 17, 2000, for a total interval of ![]() 56 ks (Smith et al. 2005). A first observation on July 9-10
of the same year was excluded by the authors because of a severe solar flare. For the 17/08/2000 observation, the authors report an unexpected strong foreground emission in the O VII (0.57 keV) and especially the O VIII (0.65 keV) lines. Their best fit of the
spectra yielded a foreground flux of 1.79
56 ks (Smith et al. 2005). A first observation on July 9-10
of the same year was excluded by the authors because of a severe solar flare. For the 17/08/2000 observation, the authors report an unexpected strong foreground emission in the O VII (0.57 keV) and especially the O VIII (0.65 keV) lines. Their best fit of the
spectra yielded a foreground flux of 1.79 ![]() 0.55 LU for the O VII line and 2.34
0.55 LU for the O VII line and 2.34 ![]() 0.36 LU for the O VIII line. They discuss the possibility of the emission being due to a non-equilibrium nature of the LB, but rather conclude that their observations
were contaminated by CX induced emission inside the Heliosphere.
0.36 LU for the O VIII line. They discuss the possibility of the emission being due to a non-equilibrium nature of the LB, but rather conclude that their observations
were contaminated by CX induced emission inside the Heliosphere.
Indeed, on August 12, 2000 at 10:35 UT, SOHO/LASCO observed a CME, which we name CME-1 here after, associated with an M-class flare from active region (AR) 9119, behind the west limb (Edgar et al. 2006). The CME was on the high end of CME masses, with a total mass of M = 1.2 ![]() 1016 g ejected, during a total of
1016 g ejected, during a total of
![]() h. It's speed was evaluated at about
660 km s-1. Apparently, the Chandra observation geometry (Fig. 1a) shows that Chandra was pointing through the interplanetary region affected by the CME material. A second CME (named CME-2) of equivalent mass, with a mean speed of 900 km s-1 and originating from AR 9114 near the first one, was recorded four hours later. In addition,
ACE/SWICS measurements indicate that SW O8+ had a relative abundance of 25% during the week preceeding the Chandra observation, and during the observation.
h. It's speed was evaluated at about
660 km s-1. Apparently, the Chandra observation geometry (Fig. 1a) shows that Chandra was pointing through the interplanetary region affected by the CME material. A second CME (named CME-2) of equivalent mass, with a mean speed of 900 km s-1 and originating from AR 9114 near the first one, was recorded four hours later. In addition,
ACE/SWICS measurements indicate that SW O8+ had a relative abundance of 25% during the week preceeding the Chandra observation, and during the observation.
We model the CME(s) propagation through the interplanetary space and how it affected the Chandra observation of MBM 12. In Fig. A.2 (Online Material, here after OM)
we present a series of LASCO/C3 images of CME-1, begining at 11:18 UT and ending at 14:18 UT. In the figures, the inner white circle represents the Solar disk while the outer circle traces the sphere limits at R =
![]() .
This is the surface crossed by the CME in the temporal interval showed in the figures. We can consider, then, that all of the CME mass crossed this sphere in
.
This is the surface crossed by the CME in the temporal interval showed in the figures. We can consider, then, that all of the CME mass crossed this sphere in
![]() h and we can calculate the
SW proton flux
h and we can calculate the
SW proton flux
![]() in the CME, according to Eq. (8):
in the CME, according to Eq. (8):
The CME speed and angular width are the two parameters that influence the most the post-CX X-ray emission, because they define the part of the LOS to be affected and also the timing for the CME to impact on it. The LOS emissivity is maximum near the observer, up to 3-4 AU, therefore, from Fig. 1a we understand that the CME width and speed will determine if the MBM 12 LOS is to be strongly affected during the Chandra observation or not.
The angular width of a CME is very difficult to evaluate since the apparent width can be much larger than the actual width because of projection effects, so that it reaches 360![]() for a CME originating at the Sun Center. CME-1 and CME-2 were classified as Partial Halo events because their total angular widths were estimated at
for a CME originating at the Sun Center. CME-1 and CME-2 were classified as Partial Halo events because their total angular widths were estimated at
![]()
![]() and 161
and 161![]() respectively. The LASCO/C2 and C3 images of CME-1 (OM - Fig. A.2) show a
latitudinal apparent width of
respectively. The LASCO/C2 and C3 images of CME-1 (OM - Fig. A.2) show a
latitudinal apparent width of ![]() 40
40![]() ,
but since the
CME-1 occured just behind the west limb, it must have had a rather large width. CME-2 could have a smaller width as it was on the visible part of the Solar Disk. If we consider an intermediate angular width of CME-1 and CME-2,
,
but since the
CME-1 occured just behind the west limb, it must have had a rather large width. CME-2 could have a smaller width as it was on the visible part of the Solar Disk. If we consider an intermediate angular width of CME-1 and CME-2,
![]()
![]() and
and
![]()
![]() ,
we obtain from Eq. (8) a SW proton flux of
,
we obtain from Eq. (8) a SW proton flux of ![]() 5
5 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1 and
108) cm-2 s-1 and ![]() 10
10 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1 for each respectively.
108) cm-2 s-1 for each respectively.
In this context, the LOS is "touched'' at a point near 1 AU away from the observer by CME-1 and around 2 AU away from the observer by CME-2 a little later. The simulated lightcurves of O VII and O VIII emission modified because of the interaction with CME-1 and CME-2 material are presented in Fig. 2. This interaction, in combination with the strongly enhanced O8+ relative abundance
![]() ,
gave a mean photon flux of
1.49 LU for the O VII triplet and 2.13 LU for the O VIII line in the same interval as the Chandra exposure. The ground level emission of the Heliosphere for the MBM 12 direction observed on the 17/08/2000 was modeled as a maximum solar activity period
and yielded 1.33 LU and 0.52 LU respectively for O VII and O VIII lines, which means a 12% increase for the O VII triplet and over 300% increase for the O VIII line due to the abundance/CME perturbations.
,
gave a mean photon flux of
1.49 LU for the O VII triplet and 2.13 LU for the O VIII line in the same interval as the Chandra exposure. The ground level emission of the Heliosphere for the MBM 12 direction observed on the 17/08/2000 was modeled as a maximum solar activity period
and yielded 1.33 LU and 0.52 LU respectively for O VII and O VIII lines, which means a 12% increase for the O VII triplet and over 300% increase for the O VIII line due to the abundance/CME perturbations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig8271dir/8271f2.ps}\end{figure}](/articles/aa/full/2007/45/aa8271-07/Timg55.gif) |
Figure 2: Simulated lightcurves of O VII (red plain line) and O VIII (blue dashed line) emission in LU for the MBM 12 Chandra exposure (17/08/2000 01:04 UT) under the combined impact of CME-1 and CME-2 (see details in text). X-ray data is also presented (Smith et al. 2005): O VII red dot, O VIII blue triangle. The horizontal double arrow delimits the Chandra exposure duration. |
These values are very close to the ones measured by Chandra On-Cloud, which reinforces the conclusion of Smith et al. (2005) that the emission detected was entirely due to SWCX, not only for the O VIII line which was the most affected by the CMEs and the changes in abundances they induced, but also for the O VII triplet.
The observation of MBM 12 with Suzaku on February 3-8, 2006 was performed in two consecutive exposures, ON-CLOUD (3-6/02/2006, for a total of 231 ks) and immediately after that, OFF-CLOUD (6-8/02/2006, for a total of 168 ks) (Smith et al. 2007).
The ON-CLOUD exposure was pointing at galactic coordinates (159.2![]() ,
-34.47
,
-34.47![]() ), which translates to 47
), which translates to 47![]() ,
3
,
3![]() of helioecliptic coordinates, while the OFF-CLOUD exposure was about 3
of helioecliptic coordinates, while the OFF-CLOUD exposure was about 3![]() away from the cloud, at galactic coordinates (157.3
away from the cloud, at galactic coordinates (157.3![]() ,
-36.8
,
-36.8![]() )
equal to 44
)
equal to 44![]() ,
2
,
2![]() in helioecliptic coordinates.
in helioecliptic coordinates.
ON-CLOUD the authors detect a local O VII line flux of (3.34 ![]() 0.26) LU and an O VIII line flux of (0.24
0.26) LU and an O VIII line flux of (0.24 ![]() 0.10) LU, while OFF-CLOUD the total line flux, including local (SWCX + LB?) and unabsorbed distant (galactic disk + halo) emission, rises at (5.68
0.10) LU, while OFF-CLOUD the total line flux, including local (SWCX + LB?) and unabsorbed distant (galactic disk + halo) emission, rises at (5.68 ![]() 0.59) LU and (1.01
0.59) LU and (1.01 ![]() 0.26) LU for O VII and O VIII respectively. The authors note that SW conditions were quite stable
during the Suzaku exposures, except a short period of the ON-CLOUD observation, and conclude that the discrepancies with their previous
results on MBM-12 observation with Chandra (4.1.1; Smith et al. 2005) were due to uncertainties on the background, especially in the case of Chandra, as well as to the large solar flare/CME influencing the Chandra background even more. However, they acknowledge
once more the probability that SWCX emission may be contaminating at an unknown degree the MBM 12 O VII and O VIII detection.
0.26) LU for O VII and O VIII respectively. The authors note that SW conditions were quite stable
during the Suzaku exposures, except a short period of the ON-CLOUD observation, and conclude that the discrepancies with their previous
results on MBM-12 observation with Chandra (4.1.1; Smith et al. 2005) were due to uncertainties on the background, especially in the case of Chandra, as well as to the large solar flare/CME influencing the Chandra background even more. However, they acknowledge
once more the probability that SWCX emission may be contaminating at an unknown degree the MBM 12 O VII and O VIII detection.
In this study, we model the MBM 12 Suzaku observations, taking into account the short SW perturbation recorded at the end of the ON-CLOUD pointing and the influence it had on the measured data. We note first three factors partly responsible for: (i) the Chandra - Suzaku discrepancy and (ii) the ON/OFF difference during the Suzaku observations.
The first point is the very strong difference between the solar maximum conditions in 2000 (Chandra observations) and the 2006 solar minimum conditions (Suzaku data). Indeed,
as demonstrated in the monochromatic maps in Koutroumpa et al. (2006), for low helioecliptic latitudes
![]() the SWCX X-ray
emission is higher for solar minimum than for solar maximum. This is due to the fact that at solar minimum the radiation pressure is weakened with respect to gravity and the IS H and He trajectories are more convergent. This, in addition with the fact that ionization
processes are less efficient, favours a better concentration of IS neutrals around the Sun (and the observer), filling more efficiently the ionization cavity for H, and enlarging the gravitational cone extent and density for He atoms. Therefore, it is quite logical that
Suzaku measurements find a higher O VII and O VIII levels, since the SWCX emission is closer and brighter at solar minimum.
the SWCX X-ray
emission is higher for solar minimum than for solar maximum. This is due to the fact that at solar minimum the radiation pressure is weakened with respect to gravity and the IS H and He trajectories are more convergent. This, in addition with the fact that ionization
processes are less efficient, favours a better concentration of IS neutrals around the Sun (and the observer), filling more efficiently the ionization cavity for H, and enlarging the gravitational cone extent and density for He atoms. Therefore, it is quite logical that
Suzaku measurements find a higher O VII and O VIII levels, since the SWCX emission is closer and brighter at solar minimum.
Second, we must point out the observation geometry differences between the Chandra and Suzaku exposures (Fig. 1). The Chandra observation, on August 17, 2000 was pointing downwind, but almost parallel to the He gravitational cone, thus missing the enhancement due to this part of the Heliosphere (Koutroumpa et al. 2006). On the contrary, Suzaku in February was pointing directly inside the He cone, which was only 1-2 AU away from the observer, where the emissivity on the LOS is maximum. Therefore, the Suzaku measurements should be normally much larger than the Chandra data.
Finally, the OFF-CLOUD LOS of Suzaku was pointing through a denser region of the He cone with respect to the ON-CLOUD LOS in the same period. Consequently, the OFF-CLOUD emission should be slightly higher than the ON-CLOUD emission,
even for calm SW conditions. Indeed, ground level O VII and O VIII fluxes for the ON-CLOUD pointing are 3.82 LU and 1.48 LU respectively, while for the OFF-CLOUD exposure they are 4.05 LU and 1.57 LU respectively. The ON-CLOUD ground level fluxes
are ![]() 3 times higher than the equivalent fluxes in the Chandra simulation.
3 times higher than the equivalent fluxes in the Chandra simulation.
Naturally, only the difference of the observing geometry between ON and OFF cloud pointings is not enough to explain the ON/OFF difference in X-ray emission intensities. We model the temporal variations of the X-ray emission in the 0.5-0.7 keV including a step function
of 2.01 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1, to account for the SW "spike'' recorded on day
108) cm-2 s-1, to account for the SW "spike'' recorded on day ![]() = 2.2, starting on 03/02/2006 00:00 UT, and propagating at a
particularly low speed (
= 2.2, starting on 03/02/2006 00:00 UT, and propagating at a
particularly low speed (
![]() = 350 km s-1) for 0.75 d. The SW proton flux remained at a high, but stable, level equal to 1.7
= 350 km s-1) for 0.75 d. The SW proton flux remained at a high, but stable, level equal to 1.7 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1after the spike. The modeled step function is presented with the black plain line in the lower panel of Fig. 3.
108) cm-2 s-1after the spike. The modeled step function is presented with the black plain line in the lower panel of Fig. 3.
O7+ relative abundance was at about half its normal value (
![]() = 0.11) before the SW spike which reduced the ground level of around the same factor. During and after the SW enhancement the relative abundance remained at lower
(
= 0.11) before the SW spike which reduced the ground level of around the same factor. During and after the SW enhancement the relative abundance remained at lower
(
![]() = 0.18) than normal values. Data for the O8+ relative abundance are very poor, but indicate that O8+ was also very scarce in the SW (
= 0.18) than normal values. Data for the O8+ relative abundance are very poor, but indicate that O8+ was also very scarce in the SW (
![]() = 0.01) before the SW enhancement, which also reduced
the initial ground level. Abundance remains very low throughout all the Suzaku observations, so we considered a very slow recovery, with
a value of 0.02 during the SW enhancement and 0.03 after that.
= 0.01) before the SW enhancement, which also reduced
the initial ground level. Abundance remains very low throughout all the Suzaku observations, so we considered a very slow recovery, with
a value of 0.02 during the SW enhancement and 0.03 after that.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fig8271dir/8271f3.ps}\end{figure}](/articles/aa/full/2007/45/aa8271-07/Timg60.gif) |
Figure 3: Upper panel: simulated lightcurves for the O VII and O VIII line emission in Line Units (photons cm-2 s-1 sr-1) for the MBM12 ON and OFF observations during the period 03-08/02/2006. The plain red line is for the O VII emission and the dashed blue line is for the O VIII emission. Red circles represent the measured ON and OFF O VII line flux, while the blue triangles represent the measured ON and OFF fluxes for O VIII line (Smith et al. 2007). Lower panel: solar wind proton flux (dotted line) in units of 108 cm-2 s-1 for the same period. The step function simulating the SW enhancement is presented with the plain black line. In both panels, the vertical plain lines represent the start and end of the observation period, while the dashed vertical line is the separation between the ON and OFF exposures. |
The simulation results combining the difference in the ON and OFF observation geometries, the SW enhancement and reduced abundances are shown in the upper panel of Fig. 3. The X-ray emission starts at a lower than ground level, due to the initial very low abundances of both O7+ and O8+. Then, the model is predicting a rise in both ON and OFF X-ray background emission, which accentuates even more the difference due to geometry effects. The mean O VII line fluxes for the ON and OFF observations are 3.56 LU and 4.62 LU respectively. On the other hand, the O VIII line fluxes for the ON and OFF exposures are 0.5 LU and 0.77 LU respectively. The ON-CLOUD simulation values for both O VII and O VIII lines are slightly above, but within error bars, the corresponding measured data, strongly implying that the foreground local emission detected on the MBM 12 cloud could be exclusively originating from within the Heliosphere.
On the other hand, for the OFF-CLOUD pointing the model results are lower than the measured values. Nevertheless, it is strongly implied that besides the large ground level foreground contamination from heliospheric X-rays, the distant component could be lower
than what was suggested by Smith et al. (2007), due to local temporal enhancements of the heliospheric component. Indeed, the ![]() 30%
and
30%
and ![]() 55% increase respectively in the O VII and O VIII line intensities have been attributed to the Galactic Halo oxygen emission, since in the Smith et al. (2007) analysis the foreground emission is considered stable. In this case, what was
attributed to distant galactic disk and halo should be revised to the residual flux of O VII and O VIII lines noted in Table 5.
55% increase respectively in the O VII and O VIII line intensities have been attributed to the Galactic Halo oxygen emission, since in the Smith et al. (2007) analysis the foreground emission is considered stable. In this case, what was
attributed to distant galactic disk and halo should be revised to the residual flux of O VII and O VIII lines noted in Table 5.
HSK07 and Henley & Shelton (2007) have observed an absorbing filament in the Southern galactic Hemisphere. They fitted simultaneously the ON-Filament and OFF-Filament exposures obtained with XMM-Newton (HSK07) and Suzaku (Henley & Shelton 2007) respectively.
Their goal was to use the difference in the galactic column density in the two directions (ON: 9.6 ![]() 1020 cm-2 and OFF: 1.9
1020 cm-2 and OFF: 1.9 ![]() 1020 cm-2) in order to disentangle the unabsorbed foreground emission attributed to the LB and the absorbed extragalactic and galactic halo component.
1020 cm-2) in order to disentangle the unabsorbed foreground emission attributed to the LB and the absorbed extragalactic and galactic halo component.
| SWCX | HSK07 | XMM/PLC | XMM/TCZEROX | ||||
| ON | OFF | LB | ON | OFF | ON | OFF | |
| O VII | 3.16 | 3.47 |
|
|
|
13.23 |
16.55 |
| O VIII | 1.02 | 1.11 | 1.0 |
|
|
|
|
Their basic spectral modeling was the same for both XMM and Suzaku observations and was composed of: (i) a thermal plasma model in collisional ionization equilibrium for the LB, (ii) two absorbed thermal plasma components for the Galactic halo, and (iii) an absorbed power law for the unresolved extragalactic sources (AGN). The absorption was determined by the column density for the ON and OFF exposures as mentioned before.
In the following paragraphs 4.2.1 and 4.2.2 we will detail the results obtained by HSK07 and Henley & Shelton (2007) for the O VII and O VIII line emission in the case of XMM and Suzaku respectively, as well as the SWCX simulations we applied on the XMM observations.
XMM observed the SGF on May 3, 2002 in two consecutive exposures ON and OFF for a total 12.8 ks and 27.8 ks respectively. After flare removal with standard XMM data analysis procedures, the useful time remaining was 11.9 ks for the ON exposure and only 4.4 ks for the OFF exposure.
HSK07 fitted the ON and OFF spectra obtained with MOS-1 and 2 cameras simultaneously, applying the standard model described previously. Their standard LB model assumed a thermal plasma with a temperature of 106.06 K and emission measure EM = 0.018 cm-6 pc. For these parameters, the LB standard model line emission yields 2.9 LU for O VII and 0.017 LU for O VIII (HSK07, ATOMDB database).
In order to measure more precisely the O VII and O VIII line emission from the LB in the XMM data, they replaced the standard thermal plasma model with a variation including two Gaussians for the oxygen lines and a thermal plasma model with frozen parameter of zero oxygen abundance to account for the continuum and remaining spectral lines. The Gaussians' widths were fixed at zero and the energies were fixed at 0.5681 keV for the O VII triplet and 0.6536 keV for the O VIII line. The two Gaussians yield O VII and O VIII line fluxes of 3.4 +0.6-0.4 LU and 1.0 LU respectively, which is higher than what is predicted by the standard LB models (HSK07, ATOMDB database).
We need, at this point, to comment on the central energy position of the O VII triplet. The O VII central energy was biased by the assumption that emission is due to thermal plasma, and was chosen as the mean energy of the resonance (O6r: 574 eV), intercombination (O6i: 568.5 eV) and forbidden (O6f: 560.9 eV) lines, weighted by the line emissivities
for a 106.06 K plasma. Indeed, the location of the centroid of the O VII triplet depends on the emission mechanism considered and can be represented by the line ratio G =
![]() .
In the case of hot plasmas ratio G is less than 1,
but larger than 3 in the case of charge-exchange (Kharchenko 2005). Future instruments with better spectral resolution should be able to separate the oxygen triplet lines and give more information on the nature of the soft X-ray background.
.
In the case of hot plasmas ratio G is less than 1,
but larger than 3 in the case of charge-exchange (Kharchenko 2005). Future instruments with better spectral resolution should be able to separate the oxygen triplet lines and give more information on the nature of the soft X-ray background.
The XMM-Earth system was positioned at a heliospheric longitude of 222![]() on 03/05/2002, and the SGF LOS were pointing at high south heliospheric latitudes (ON: 352
on 03/05/2002, and the SGF LOS were pointing at high south heliospheric latitudes (ON: 352![]() ,
-75
,
-75![]() ,
OFF: 353
,
OFF: 353![]() ,
-73
,
-73![]() ). The SWCX model for the SGF observation
geometry on 03/05/2002, considered with maximum solar conditions, predicts a ground
level O VII line emission of 2.32 LU and an equivalent O VIII line emission of 0.92 LU. Near-Earth SW measurements show moderate variations, but not neat enhancements to be modeled as step functions.
). The SWCX model for the SGF observation
geometry on 03/05/2002, considered with maximum solar conditions, predicts a ground
level O VII line emission of 2.32 LU and an equivalent O VIII line emission of 0.92 LU. Near-Earth SW measurements show moderate variations, but not neat enhancements to be modeled as step functions.
However, in the LASCO/CME catalog we find a CME starting on 30/04/2002 23:32 UT (
![]() = -2.02 + 0.167 d), and progressing at a speed of
= -2.02 + 0.167 d), and progressing at a speed of
![]() = 1100 km s-1 centered at a helioecliptic longitude of about 307
= 1100 km s-1 centered at a helioecliptic longitude of about 307![]() and with half width angle
and with half width angle ![]()
![]() 65
65![]() .
These parameters give a SW proton flux at
.
These parameters give a SW proton flux at
![]() = 6
= 6 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1. If we adopt
moderately enhanced relative abundances during the observation period for both O7+ and O8+, 0.30 and 0.08 respectively, we obtain the following line fluxes for the ON and OFF exposures: 3.16 LU (ON) and 3.47 LU (OFF) for the O VII triplet
and 1.02 LU (ON) and 1.11 LU (OFF) for the O VIII line. These simulated flux values, along with those obtained by HSK07 and attributed to the LB, as well as those measured for the total line intensity (foreground + distant halo component) in the
two XMM data fits (PLC, TCZEROX) are summarized in Table 2.
108) cm-2 s-1. If we adopt
moderately enhanced relative abundances during the observation period for both O7+ and O8+, 0.30 and 0.08 respectively, we obtain the following line fluxes for the ON and OFF exposures: 3.16 LU (ON) and 3.47 LU (OFF) for the O VII triplet
and 1.02 LU (ON) and 1.11 LU (OFF) for the O VIII line. These simulated flux values, along with those obtained by HSK07 and attributed to the LB, as well as those measured for the total line intensity (foreground + distant halo component) in the
two XMM data fits (PLC, TCZEROX) are summarized in Table 2.
Compared to HSK07 results on the LB line intensities, both ground level and especially CME-modified line intensities could account for most (if not all) of the emission attributed to the LB (3.4 LU and 1. LU respectively for O VII and O VIII). Moreover, the CME impact on the OFF-SGF exposure, produces a 10% enhancement with respect to the ON-SGF exposure, especially in the O VII intensity. HSK07 assumed that the foreground LB emission was identical for the two exposures, thus, the 10% enhancement of the heliospheric component was probably erroneously attributed to the Galactic Halo. We regret that HSK07 did not provide equivalent line intensity values for the galactic halo to compare to.
In our XMM data processing and modeling we made no assumptions on the nature of the O VII and O VIII line emission (see Sect. 2.3), and removed only the continuum from XMM data (columns XMM/PLC and XMM/TCZEROX in Table 2). Subtraction of the SWCX heliospheric component should give the residual emission, to really be separated in LB and Galactic halo emission, which can radically modify the parameters initially assumed for those components.
SGF is a medium-size absorber. In fact, HSK07 comment the fact that the SGF-ON column density is much lower than other shadowing observations: 4 ![]() 1021 cm-2 for MBM 12 (Smith et al. 2005, 2007), up to
1021 cm-2 for MBM 12 (Smith et al. 2005, 2007), up to ![]() 1023 cm-2
for Barnard 68 (Freyberg et al. (2004), which gave higher temperature results for the LB (106.21 K). For these absorbers, it is easier to conclude that what is measured as foreground emission is really local (LB according to HSK07,
SWCX according to our study), because transmissivity of O VIII radiation is less than 14%. On the contrary, the SGF has a higher transmissivity (up to 61% for O VIII energies) and therefore it is more difficult to really determine what originates
from the local component or leaks through the filament from distant components.
1023 cm-2
for Barnard 68 (Freyberg et al. (2004), which gave higher temperature results for the LB (106.21 K). For these absorbers, it is easier to conclude that what is measured as foreground emission is really local (LB according to HSK07,
SWCX according to our study), because transmissivity of O VIII radiation is less than 14%. On the contrary, the SGF has a higher transmissivity (up to 61% for O VIII energies) and therefore it is more difficult to really determine what originates
from the local component or leaks through the filament from distant components.
In their study, HSK07 test the case of a hotter LB (106.21 K), which would give higher O VIII emission, but conclude that such a case predicts far too much intrinsic halo O VI intensity, which is incompatible with FUSE measurements (Shelton et al. 2007). They are, thus, constrained to admit that the different temperatures of the LB resulting from the various shadowing observations, are due to anisotropies inside the LB for the different LOS.
What we could propose is the contrary: if the emission attributed to the LB is largely or entirely heliospheric, as it is suggested in our analysis, there is no need to look for a hotter or anisotropic bubble and hence, no need for a cooler halo and no discrepancy with FUSE measurements.
The Suzaku observations of the SGF were performed on March 1, 2006 16:56 UT for a total of ![]() 80 ks (ON-Filament), and on March 3, 2006 20:52 UT for a total of
80 ks (ON-Filament), and on March 3, 2006 20:52 UT for a total of ![]() 100 ks (OFF). Henley & Shelton (2007) fit the same basic model
(unabsorbed LB + absorbed
100 ks (OFF). Henley & Shelton (2007) fit the same basic model
(unabsorbed LB + absorbed ![]() (halo + extragalactic)) on the spectra and find LB and halo parameters very different from those obtained
with the XMM data in 2002. In detail, they detect a much fainter O VII triplet of 0.17 LU only for the LB, while O VIII line flux is not detected with certainty. No details on the halo absolute line fluxes for the two oxygen lines are given.
(halo + extragalactic)) on the spectra and find LB and halo parameters very different from those obtained
with the XMM data in 2002. In detail, they detect a much fainter O VII triplet of 0.17 LU only for the LB, while O VIII line flux is not detected with certainty. No details on the halo absolute line fluxes for the two oxygen lines are given.
The authors are perplexed by the difference of their Suzaku spectra of the SGF and their equivalent XMM spectra previously analyzed in HSK07. They report steady SW conditions within normal measured values, and claim that "the SWCX emission should be the same for both (XMM and Suzaku) observations, composing a fixed fraction of the foreground emission''.
At this point, we need to stress once more the effect of the solar cycle phase on the SWCX component and thus on the soft X-ray data. As we mentioned earlier, there is a large difference on the O VII and O VIII line fluxes between solar maximum (years 2000-2002) and solar minimum (2006), because of the difference in the distributions of IS neutrals in the Heliosphere. In the case of SGF, which points at very high southern ecliptic latitude (353![]() ,
-73
,
-73![]() )
the effect is
the opposite with respect to MBM 12, which was in low ecliptic latitude, because it is dominated by differences in the solar ions relative abundances.
)
the effect is
the opposite with respect to MBM 12, which was in low ecliptic latitude, because it is dominated by differences in the solar ions relative abundances.
At solar maximum, the SW is merely isotropic and the ion relative abundances are homogeneous and close to slow SW conditions. On the other hand, at solar minimum we find a SW highly anisotropic and composed of equatorial regions of slow wind and high latitude regions
of fast wind. In this latter case, LOS pointing at high ecliptic latitudes are partly affected by fast SW (above ![]()
![]() )
and the X-ray emission is dominated by differences of ion relative abundances with respect to maximum cycle phase. Indeed,
O8+ is completely absent from the fast SW and O7+ is strongly depleted (
)
and the X-ray emission is dominated by differences of ion relative abundances with respect to maximum cycle phase. Indeed,
O8+ is completely absent from the fast SW and O7+ is strongly depleted (
![]() = 0.07). Therefore, X-ray emission on high latitude LOS is expected to be much fainter at solar minimum than solar maximum.
= 0.07). Therefore, X-ray emission on high latitude LOS is expected to be much fainter at solar minimum than solar maximum.
During the Suzaku observations of the SGF SW flux was very calm, but also there was rather low O7+ and O8+ relative abundances as recorded by ACE/SWICS in the ecliptic plane (in general the ecliptic plane is dominated by slow SW conditions). The O7+ was only 0.083 during the ON-Filament exposure, while it rose to 0.13, 1.5 d after, for the OFF exposure. O8+ statistics were very poor in the SWICS data for this period, but show very low values, of 0.02 for the period of the exposures. For lack of data, we assume that high latitude abundances were lower than average by the same amount as in the ecliptic.
The ground level model predicts an O VII line flux of 0.83 LU and an O VIII line flux of 0.07 LU (for solar minimum conditions in the LOS of the SGF). After abundance correction (0.083/0.2 for O7+ and 0.02/0.07 for O8+) we predict 0.34 LU in O VII and 0.02 LU in O VIII for the ON-Filament exposure. These values are about an order of magnitude below the equivalent values in the SGF-XMM simulation, which is the same difference Henley & Shelton (2007) state for their Suzaku and XMM spectra in the Suzaku band (0.3-0.7 keV). Besides the two oxygen lines we analyze here, which are the most important in the range 0.5-0.7 keV, the main ion lines dominating the Suzaku band, are due to CX collisions of C6+, N7+ and N6+ with IS neutrals. These ions, although not treated in this study, are known to have equivalent abundance variations as O7+ and O8+ between solar maximum and solar minimum, and thus, an equivalent trend in the SWCX X-ray emissions they generate (Koutroumpa et al. 2006).
The simulated O VII and O VIII intensities we derive are of the same order and even slightly higher than the ones attributed to the LB by Henley & Shelton (2007). We conclude that, as in the case of the XMM data, the foreground emission in the 0.5-0.7 keV band can be exclusively attributed to the Heliosphere. We must also note, that according to O7+ abundance measurements, the SWCX O VII emission is likely to have risen by a factor of 1.6 during the OFF exposure, with respect to the ON exposure. Therefore, the background emission attributed to the absorbed distant component should be revised, by subtracting properly the heliospheric contribution (see Table 4).
The Hubble Deep Field-North has been observed with XMM-Newton as a test case for the noncosmic background modeling and subtraction for the European Photon Imaging Camera. The total length of the observation was broken in four exposures scheduled over a period of 16 days. The fourth pointing, on June 1, 2001 offered an exemplary case of SWCX emission detection, which was analysed by SCK04.
The authors, in a useful exposure time of 38.1 ks out of a total 95.4 ks, after removal of flaring periods, discerned a drop in the 0.52-0.75 keV band lightcurve, occuring in the last quarter of the interval. They used a separate spectral fit for the HIGH
and LOW regime, as they define the intervals before and after the drop respectively, with four main components: (i) an unabsorbed thermal component with ![]() keV for the LB, (ii) an absorbed thermal component with also
keV for the LB, (ii) an absorbed thermal component with also ![]() keV for the
lower halo emission, (iii) an absorbed, hotter component (
keV for the
lower halo emission, (iii) an absorbed, hotter component (![]() keV) for the Galactic halo or Local Group emission, and (iv) an absorbed power law with spectral index of 1.46 for the unresolved extragalactic sources. The absorption was fixed to the
Galactic column density
keV) for the Galactic halo or Local Group emission, and (iv) an absorbed power law with spectral index of 1.46 for the unresolved extragalactic sources. The absorption was fixed to the
Galactic column density
![]()
![]() 1020 cm-2. In the HIGH state of the exposure only, a series of spectral lines
to represent the SWCX emission was added in the fitting process. The lines included were the C VI 0.37 and 0.46 keV lines, the O VII triplet at 0.57 keV, the O VIII lines at 0.65 and 0.81 keV, the Ne IX line at 0.91 keV and the Mg XI line at 1.34 keV.
Their analysis yielded a SWCX induced line flux of 7.39 LU and 6.54 LU for the O VII and O VIII lines respectively in the HIGH state only, while the contribution of SWCX in the LOW state regime and the remaining pointing was completely neglected.
1020 cm-2. In the HIGH state of the exposure only, a series of spectral lines
to represent the SWCX emission was added in the fitting process. The lines included were the C VI 0.37 and 0.46 keV lines, the O VII triplet at 0.57 keV, the O VIII lines at 0.65 and 0.81 keV, the Ne IX line at 0.91 keV and the Mg XI line at 1.34 keV.
Their analysis yielded a SWCX induced line flux of 7.39 LU and 6.54 LU for the O VII and O VIII lines respectively in the HIGH state only, while the contribution of SWCX in the LOW state regime and the remaining pointing was completely neglected.
| Proton flux step function | Ion relative abundances | |||||||
| Simulation 1 | Simulation 2 | HIGH | LOW | |||||
|
|
|
|
|
|
|
|
|
|
| (0.5 + 0.5) | 4 | (0.5 + 1.) | 10 | 0.488 | 0.28 | 0.125 | 0.038 | |
| Line flux (LU = photons cm-2 s-1 sr-1) | ||||||||
| Simulation 1 | Simulation 2 | SCK04 | Data | |||||
| High | Low | High | Low | High | High | Low | ||
| O VII | 4.20 | 3.22 | 9.06 | 2.02 | 7.39 | 15.44 | 8.14 | |
| O VIII | 1.99 | 1.40 | 5.69 | 1.18 | 6.54 | 8.14 | 1.96 | |
In Sect. 5 of Koutroumpa et al. (2006), we presented a first time-dependent modeling of the SWCX emission, based on the same method
presented in this study and applied on the HDFN June 1, 2001 exposure. We have used a simplified geometry of the LOS, supposing that it was lying in the ecliptic plane instead of pointing at a helioecliptic latitude of 57![]() .
We have presented simulated
lightcurves for two different sets of SW parameters and concluded that the heliospheric X-rays were responsible for the observed enhancement and mainly that the LOW state spectrum still contained a large fraction of heliospheric emission. Unfortunately,
an error in taking into account the variable steps on the LOS, which was discovered after publication annuls our results, but not
our main conclusions which we attempt to validate in the present re-analysis of the HDFN simulation.
.
We have presented simulated
lightcurves for two different sets of SW parameters and concluded that the heliospheric X-rays were responsible for the observed enhancement and mainly that the LOW state spectrum still contained a large fraction of heliospheric emission. Unfortunately,
an error in taking into account the variable steps on the LOS, which was discovered after publication annuls our results, but not
our main conclusions which we attempt to validate in the present re-analysis of the HDFN simulation.
We performed two simulations, taking into account the real geometry of the HDFN observation (Observer at
![]() = 251
= 251![]() ,
LOS pointing backwards at
,
LOS pointing backwards at ![]() ,
,
![]() = 48
= 48![]() ,
57
,
57![]() ,) and considering O7+ and O8+ relative abundances as implied by the O VIII and O VII lines ratio calculation in SCK04 (SCK04; Koutroumpa et al. 2006, see Table 3). The difference in the two simulations
lies on the step function adopted for the SW enhancement and how it affects the high latitude LOS of the HDFN.
,) and considering O7+ and O8+ relative abundances as implied by the O VIII and O VII lines ratio calculation in SCK04 (SCK04; Koutroumpa et al. 2006, see Table 3). The difference in the two simulations
lies on the step function adopted for the SW enhancement and how it affects the high latitude LOS of the HDFN.
In the first case, we take equivalent conditions as those presented in Koutroumpa et al. (2006), with a step function occuring on day
![]() = (0.5 + 0.5) d, and a SW proton flux of 4 SPFU. The results are presented in the upper panel of Fig. 4a.
= (0.5 + 0.5) d, and a SW proton flux of 4 SPFU. The results are presented in the upper panel of Fig. 4a.
We can see from Fig. 4a that timing between model and data seems correct, as it did for the simplified geometry used in Koutroumpa et al. (2006). The simulated lightcurve, within the observation limits, starts at an already higher value, dropping at the end of the SW enhancement. Nevertheless, the absolute difference between HIGH and LOW regimes in the simulation is far too low to explain the large drop measured in XMM data. Indeed the HIGH to LOW drop is of 0.98 LU and 0.59 LU only, in the model for the line O VII and O VIII respectively, while it is of 7.3 LU for O VII and of 6.18 for O VIII in the data.
The HDFN is the only exposure divided in two states. Since the target field is the same for the two states, the column density is identical, thus, we are confident that such a variation in the soft X-ray background is mainly due to the heliospheric emission. The Geocorona could partly be responsible for the variation, but as explained in Cravens et al. (2001) and SCK04 it should be temporally correlated with the SW rising and dropping with it. Moreover, SCK04 analyze the XMM-Newton geometry for the 01/06/2001 and conclude that the satellite avoids the main zones that could be contaminated by the Geocorona.
As a consequence, we wished to test our SWCX model and see if we can find reasonable SW enhancement conditions that could fit better this strong variation in the Soft X-ray background. We consider then, a step function occuring on
![]() = (0.5 + 1.0) d and
with a SW proton flux of 10
= (0.5 + 1.0) d and
with a SW proton flux of 10 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1, which is quite rare, but not impossible to occur. We assume that the AR producing this enhancement is not infinitely ancient on the solar disk, as assumed in the general time-dependant modeling described
in Sect. 3, but appears
108) cm-2 s-1, which is quite rare, but not impossible to occur. We assume that the AR producing this enhancement is not infinitely ancient on the solar disk, as assumed in the general time-dependant modeling described
in Sect. 3, but appears ![]() 7 d earlier than 01/06/2001 00:00 UT (day 0), while pointing radially at a helioecliptic longitude of
7 d earlier than 01/06/2001 00:00 UT (day 0), while pointing radially at a helioecliptic longitude of ![]()
![]() 219
219![]() .
.
Under such conditions, the LOS will be affected only up to the segment
(
![]() 219
219![]() ,
40
,
40![]() )
which lies at phase angle
)
which lies at phase angle
![]() 32
32![]() and distance 1.08 AU with respect to the observer (see Fig. A.1b and Sect. 3). We, therefore, assume that the SW leaving the Sun on day -7 d and affecting the major emitting part of the LOS was quite different than the one measured on day 0.5
at the Earth's position. This is a plausible hypothesis, since the SW variation time-scales can be much shorter than 7 days. In addition, we cannot be certain for the SW conditions at a
and distance 1.08 AU with respect to the observer (see Fig. A.1b and Sect. 3). We, therefore, assume that the SW leaving the Sun on day -7 d and affecting the major emitting part of the LOS was quite different than the one measured on day 0.5
at the Earth's position. This is a plausible hypothesis, since the SW variation time-scales can be much shorter than 7 days. In addition, we cannot be certain for the SW conditions at a ![]() 30
30![]() angular distance from the Earth, since there are no in situ measurements at such distances.
angular distance from the Earth, since there are no in situ measurements at such distances.
The results of this simulation are presented in Fig. 4b with the same annotations as in Fig. 4a. The "truncation'' of the spiral's effect on the LOS at 40![]() forces a harder drop between the HIGH and LOW states,
which correspond better to the observed temporal profile. Moreover, the increase of the SW proton flux we imposed allows a better comparison between the simulated and measured HIGH-LOW differences. Indeed, the drop of the O VII line flux is of 7.04 LU.
The O VIII line drops by 4.51 LU which is still a little low with respect to the data drop, but we could suppose that ion relative abundances are also very different than the ones measured in Earth orbiting solar instruments.
forces a harder drop between the HIGH and LOW states,
which correspond better to the observed temporal profile. Moreover, the increase of the SW proton flux we imposed allows a better comparison between the simulated and measured HIGH-LOW differences. Indeed, the drop of the O VII line flux is of 7.04 LU.
The O VIII line drops by 4.51 LU which is still a little low with respect to the data drop, but we could suppose that ion relative abundances are also very different than the ones measured in Earth orbiting solar instruments.
What we need to stress as a conclusion to these simulation tests we performed, is the importance of accurate and multi-positioned in-situ measurements of the SW properties. Since SWCX emission is so sensitive to SW flux and abundance variations, precise simulations can only be improved with detailed and liable input parameters.
The Marano Field was named by an optical quasar survey by Marano et al. (1988) and was frequently surveyed in optical wavelengths,
X-rays (ROSAT, XMM) and radio wavelengths (Krumpe et al. 2007, and references within). The mean galactic H I column density in the Marano
Field is ![]() = 2.7
= 2.7 ![]() 1020 cm-2. XMM-Newton observed the Marano Field 7 times in the period between August 22, and August 27, 2000. The mean total exposure time was
1020 cm-2. XMM-Newton observed the Marano Field 7 times in the period between August 22, and August 27, 2000. The mean total exposure time was ![]() 10 ks for each observation.
10 ks for each observation.
The SWCX model ground level is taken for maximum solar activity for 2000. Marano field is pointing at -67![]() of helioecliptic latitude which means the SW affecting the outer parts of the LOS could have been very different than the one measured in the ecliptic.
of helioecliptic latitude which means the SW affecting the outer parts of the LOS could have been very different than the one measured in the ecliptic.
The SW variations measured form WIND instrument at this time period can be modeled as 3 step functions starting on days (from date 22/08/2000 00:00 UT): 0 d (step-1), 1.625 d (step-2) and 5 d (step-3) lasting 1.4 d, 0.4 d and 1.8 d respectively. Step-1 yields an enhancement of 2.12 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1, step-2 an enhancement of 2.7
108) cm-2 s-1, step-2 an enhancement of 2.7 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1 and finaly step-3 gives an enhancement
of 1.8
108) cm-2 s-1 and finaly step-3 gives an enhancement
of 1.8 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1. There are ACE/SWICS measurements showing high values of O
8+ = 0.14 and O
7+ = 0.3 abundances before and during step-1 and step-2.
108) cm-2 s-1. There are ACE/SWICS measurements showing high values of O
8+ = 0.14 and O
7+ = 0.3 abundances before and during step-1 and step-2.
In figure OM-A.3, we present the lightcurves for O VII and O VIII lines resulting from the simulation, as well as the XMM-data for the 7 Marano exposures. The variations measured with XMM in the Marano field are not very large, mainly inside the error bars of each data point. The model predicts relative variations of the same order and with the right timing as well. We see a moderate mean increase around day 2 (24/08/2000) of about 38% in the O VII line, which is reproduced with a relative strength of 34% in the model. The O VIII data points have larger uncertainties, but the mean relative increase in the exposures period is around 50-80% (considering the points with the smallest error bars), while the model predicts a relative increase of 40%.
The Lockman Hole is the sky region with the absolute lower H I column density (
![]()
![]() 1019 cm-2). XMM-Newton observed the Lockman Hole 7 times in the period between October 15, and October 28, 2002. The total exposure time
spans from
1019 cm-2). XMM-Newton observed the Lockman Hole 7 times in the period between October 15, and October 28, 2002. The total exposure time
spans from ![]() 80 ks to
80 ks to ![]() 105 ks for each observation.
105 ks for each observation.
The SWCX model ground level is taken for maximum solar activity, 2002 being closer to maximum.
To model the Lockman Hole exposures during the period 15-28/10/2002 we use two step functions starting at days -9.25 (step-1) and 0 (step-2). Step-1 has a SW proton flux of 1.7 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1 lasting for about 2 days, while step-2 has a proton flux
of
108) cm-2 s-1 lasting for about 2 days, while step-2 has a proton flux
of ![]() 2
2 ![]() (2.6
(2.6 ![]() 108) cm-2 s-1 lasting for about 2 days. O7+ relative abundances could be slightly enhanced during the two SW enhancements (
108) cm-2 s-1 lasting for about 2 days. O7+ relative abundances could be slightly enhanced during the two SW enhancements (![]() 0.3-0.4, although not used in the figure), but O8+ abundances are very difficult to estimate
because of big lack of data. The Lockman Hole is pointing at an helioecliptic latitude of 45
0.3-0.4, although not used in the figure), but O8+ abundances are very difficult to estimate
because of big lack of data. The Lockman Hole is pointing at an helioecliptic latitude of 45![]() which could allow very different
SW caracteristics affecting the LOS than those measured in Solar instruments.
which could allow very different
SW caracteristics affecting the LOS than those measured in Solar instruments.
The resulting lightcurves are presented in figure OM-A.4. Clearly besides the discrepancies in the variation amplitudes, we also have a timing problem in the comparison, the model predicting an emission rising too fast with respect to the measured enhancement for step-1 and too late for step-2 respectively. These discrepancies do not have any obvious explanation but an inherent variation in the O VII and O VIII emission of the Lockman Hole field (more discussion in Sect. 5.1).
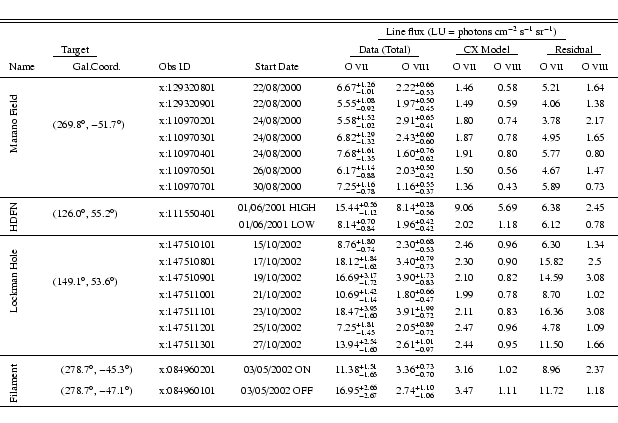
|
In Table 4 we resume all the XMM observation fields modeled in the SWCX simulations. We include the SG Filament XMM ON exposure, since it is a minor absorber and substantial emission of the halo remains. The data results are for the total O VII and O VIII line intensity as calculated in the XMM/PLC spectral model we defined in Sect. 2.3. The data contain, thus, both local foreground and distant components of the O VII, O VIII diffuse emission. Model results stand for the heliospheric O VII and O VIII line emission, ONLY, due to charge-exchange collisions. Finally in the last two columns we present the residual diffuse SXRB emission when we subtract the SWCX component from the total data results. This residual emission, should be originating in the Galactic Halo (or the border regions of the Loop I), since from what we already demonstrated in the shadowing results, the LB emission can be accounted as exclusively CX-induced heliospheric emission (see also following Sect. 5.2).
The residual emission is quite variable, since the SWCX temporal model did not succeed in correlating temporally all series of observations. Notably, the Lockman Hole variations are due to the complete lack of temporal correlation between
the observed X-ray emission variations and the SWCX model predictions. These variations, we do not manage to explain, unless there is an inherent variation in the Galactic halo emission between the different Lockman Hole exposures. But, according to the absorption law:
| (9) |
For the HDFN field we have retained the simulation 2 results of the SWCX model, since they are the ones that give the most stable residual emission as required for a unique long-lasting exposure towards a constant field (see Sect. 4.3). The Marano field is the only one to have relatively constant residual emission, since already data were quite stable even before the CX component subtraction.
We understand that, in general, XMM data comparison to model results provides quite poor correlation, especially for the O VII line intensity. The data are systematically higher than model predictions, by factors ranging from 2 to 10. This is expected, naturally, since the model accounts only for the CX heliospheric component of the SXRB. In addition, the residual emission, after the CX subtraction is quite different for each target region. This is due to the different H I column density in each field, or, to intrinsic variations of the Galactic Halo emission from one region to another.
![\begin{displaymath}\begin{tabular}{lclccccccc}
\hline \hline
&&&&&&&&& \\ [-8pt]...
...0.02:: & 0:: & 0::\\
&&&&&&&&& \\ [-4pt]
\hline
\end{tabular}\end{displaymath}](/articles/aa/full/2007/45/aa8271-07/img87.gif)
|
The O VII data points (and thus the residual intensity) exhibit a higher dispersion than the O VIII data points for each target. Except for the HDFN which, as we explained in Sect. 4.3, was temporally divided in two exposures towards the exact same field,
all the other targets, were observed in repeated exposures in which the central field of view was pointing in slightly different
directions. In the O VIII line energies, the transmission is very high, larger than 60% for column densities less than ![]() 1021 (Freyberg 2004; HSK07), like our XMM targets, and thus is less sensitive to column density
variations. However, the O VII line is much more absorbed, so even minor variations of the
1021 (Freyberg 2004; HSK07), like our XMM targets, and thus is less sensitive to column density
variations. However, the O VII line is much more absorbed, so even minor variations of the ![]() column density induce large dispersion in the emission measured for the repeted exposures at each galactic region.
column density induce large dispersion in the emission measured for the repeted exposures at each galactic region.
In the future, we need to pursue the study with better statistics for each target field, i.e. apply the SWCX model to more exposures towards each field so as to fit separately each target results.
The most important result in our analysis is the one deriving from the shadowing observations, which is that the emission initially attributed to the Local Interstellar Bubble till now, is probably originating entirely from within the Heliosphere.
In Table 5, constructed in the same principle as Table 4, we resume the MBM 12 and SG Filament shadowing observations. In Fig. 5 we linearly fit the data over the SWCX model results for each shadowing observation. We did not use data errorbars as
standard deviation to weight the fit, because not all data errorbars were communicated (HSK07 and Henley & Shelton 2007). The fit coefficients
![]() for the O VII and O VIII lines are also noted on the figure.
for the O VII and O VIII lines are also noted on the figure.
The observations data represent the LB O VII and O VIII line intensities as derived from the authors (Smith et al. 2005, 2007; HSK07; Henley & Shelton 2007). As explained individually for each case in Sects. 4.1 and 4.2, the shadows block more or less efficiently the Galactic Halo oxygen emission, and in their analysis the authors derive only the local foreground emission of the oxygen lines.
The only exception is in the Suzaku/MBM 12 observation (Smith et al. 2007) where the O VII and O VIII halo emission is added to the foreground emission for the OFF-CLOUD exposure. However, as we demonstrated in Sect. 4.1.2, there is a ![]() 30% and
30% and ![]() 55% increase in the OFF-CLOUD simulated SWCX O VII and O VIII line intensities respectively,
due to the brief SW enhancement at the end of the ON-CLOUD exposure. Smith et al. (2007) supposed that the foreground (LB) emission
was constant between the ON and OFF cloud exposures, thus this increase was erroneously attributed to the Galactic Halo emission which should be revised. For this reason, we include these values in the linear data-model fits as well.
55% increase in the OFF-CLOUD simulated SWCX O VII and O VIII line intensities respectively,
due to the brief SW enhancement at the end of the ON-CLOUD exposure. Smith et al. (2007) supposed that the foreground (LB) emission
was constant between the ON and OFF cloud exposures, thus this increase was erroneously attributed to the Galactic Halo emission which should be revised. For this reason, we include these values in the linear data-model fits as well.
The linear fit has a slope of 1.19 (![]() 0.14; 0.19 (1
0.14; 0.19 (1![]() )
for O VII and O VIII resp.) which means that the SWCX model reproduces very well the local foreground emission measured in shadows. Moreover, the intersection of the linear fit with the
data axis should give an estimate of the residual foreground emission to be attributed to the LB. The foreground is found to be (-0.26
)
for O VII and O VIII resp.) which means that the SWCX model reproduces very well the local foreground emission measured in shadows. Moreover, the intersection of the linear fit with the
data axis should give an estimate of the residual foreground emission to be attributed to the LB. The foreground is found to be (-0.26 ![]() 0.43 (1
0.43 (1![]() )) LU for O VII and (-0.17
)) LU for O VII and (-0.17 ![]() 0.24 (1
0.24 (1![]() )) LU for O VIII, which means that with a high probability
the LB O VII and O VIII emission is negligible compared to the heliospheric emission.
)) LU for O VIII, which means that with a high probability
the LB O VII and O VIII emission is negligible compared to the heliospheric emission.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{fig8271dir/8271f5.ps}\end{figure}](/articles/aa/full/2007/45/aa8271-07/Timg89.gif) |
Figure 5: Foreground emission data from shadowing observations in litterature (MBM 12: Smith et al. 2005, 2007, and SGF: HSK07; Henley et al. 2007b) versus SWCX model results for the O VII and O VIII line intensities. Linear fits are calculated with no error-bar weighting, since not all data error-bars were communicated (see Table 5 and Sect. 5.2 for details). |
In Fig. 6 we present a 3/4 keV all-sky map of the ROSAT survey in galactic coordinates, extracted from Wang (1998). The map colorscales are in ROSAT units (1 RU = 0.07 LU). On the map we have marked the positions of the target fields we have presented in our analysis. The survey maps were constructed during a 6-month period, due to the constraints of the ROSAT observation geometry scanning the sky through a great circle perpendicular to the Sun-ROSAT direction. Data decontamination removed contamination due to LTEs to some extent, but not all of the heliospheric emission.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{fig8271dir/8271f6.ps}\end{figure}](/articles/aa/full/2007/45/aa8271-07/Timg90.gif) |
Figure 6: ROSAT 3/4 keV all-sky map (Wang 1998) in ROSAT units (10-6 cts s-1 arcmin-2) including target fields modeled with the SWCX model. |
North Galactic hemisphere fields have lower column density than the ones in the South Galactic hemisphere. HDFN, Lockman give an equivalent mean residual emission for the Halo, except for unexplicable variations of the Lockman Hole. The Marano Field should have similar residual emission as the SGF, since they lie in the same region, but the column density is different for Marano (Krumpe et al. 2007) than the two SGF ON and OFF fields (HSK07).
MBM 12 has the largest column density, especially compared to the other shadowing case we analyze, the SGF. Moreover, it is the only field pointing at no particular emissive feature in the 3/4 keV band. MBM 12 has only 23 ![]() I
I ![]() 75 ROSAT units
(10-6 counts s-1 arcmin-2), ON and OFF limits as measured by SMV93. The equivalence between Line Units and ROSAT Units being 1RU = 0.07 LU, MBM 12 counts
75 ROSAT units
(10-6 counts s-1 arcmin-2), ON and OFF limits as measured by SMV93. The equivalence between Line Units and ROSAT Units being 1RU = 0.07 LU, MBM 12 counts ![]() 1.6 LU ON-CLOUD and
1.6 LU ON-CLOUD and ![]() 5.25 LU OFF-CLOUD. The ROSAT observation of MBM 12 was also during a solar maximum, which is why the ON-CLOUD measurements are of the same order as the ON-CLOUD
O VII measurements (1.79 LU) from the Chandra/MBM 12 observation (the OFF-CLOUD Chandra O VII; O VIII data were not communicated) and as the solar maximum SWCX model towards the MBM 12 (1.33 (ground level) - 1.49 LU). Summing the O VII and O VIII line
intensities in the Chandra observations would highly exceed the ROSAT observations, but O VIII was highly contaminated by transient SWCX emission, as discussed in Sect. 4.1.1.
5.25 LU OFF-CLOUD. The ROSAT observation of MBM 12 was also during a solar maximum, which is why the ON-CLOUD measurements are of the same order as the ON-CLOUD
O VII measurements (1.79 LU) from the Chandra/MBM 12 observation (the OFF-CLOUD Chandra O VII; O VIII data were not communicated) and as the solar maximum SWCX model towards the MBM 12 (1.33 (ground level) - 1.49 LU). Summing the O VII and O VIII line
intensities in the Chandra observations would highly exceed the ROSAT observations, but O VIII was highly contaminated by transient SWCX emission, as discussed in Sect. 4.1.1.
All the other fields are in the vicinity of the Loop I limits were and could be contaminated by the Loop's emission as well. The HDFN, Lockman Hole, SGF and Marano fields yield around 100-150 ROSAT units, i.e. 7-10.5 LU, which is of the same order of magnitude as the XMM O VII and O VIII data reported in Table 4 (except HDFN which is highly contaminated by SWCX emission). The SWCX model predicts a heliospheric emission at least one fifth of the ROSAT emission maps in the brightest regions in the map, besides the Loop I, which leaves substantial contamination of the Heliosphere to the Galactic Halo emission.
For a series of deep field and shadow X-ray observations we have calculated the X-ray emission due to charge-exchange collisions in the Heliosphere, taking into account the temporal evolution of the emission due to solar cycle phase and/or solar wind enhancements.
This analysis yields estimates of the SWCX heliospheric component within the diffuse Soft X-ray Background and confirms the large contamination of X-ray data by the heliospheric emission.
The local 3/4 keV emission (due essentially to O VII and O VIII) detected in front of shadowing clouds is found to be entirely explained by the CX heliospheric emission. No emission from the LB is needed at these energies. Such a negative result will have to be taken into account in future determinations of the LB temperature and pressure.
Galactic (halo + Loop I) oxygen line intensities need to be corrected for heliospheric contamination. We provide some corrections appropriate to the directions we have considered. Again, halo gas determinations must include these new constraints.
Our analysis is limited by the absence of out-of-ecliptic solar wind measurements and ionic abundances with enough statistics. Nevertheless, if pursued for a large sample of observations, it should better constrain the galactic emission. Future X-ray instruments with higher spectral resolution should allow a more precise determination of oxygen (and other) emission lines and better disentangle the different sources of emission.
Acknowledgements
We wish to thank John C. Raymond and Richard J. Edgar for useful information and enriching discussions. We would also like to thank our referee, Thomas E. Cravens, for his attentive report and valuable comments.
At each instant Ti we define the form of the Parker spiral by calculating the radial distance
![]() (if
(if
![]() ,
else Dj = 0) the front of the spiral has reached, and the total width
,
else Dj = 0) the front of the spiral has reached, and the total width
![]() of the spiral. Tdj is the instant
when the spiral leaves the Sun along the radial rj, depending on the radial propagation of the SW and the solar rotation (considered as solid for simplicity with a 27-day period), and defined by the Eq. (A.1):
of the spiral. Tdj is the instant
when the spiral leaves the Sun along the radial rj, depending on the radial propagation of the SW and the solar rotation (considered as solid for simplicity with a 27-day period), and defined by the Eq. (A.1):
When the segment AB = dsj is only partially affected by the SW enhancement, we need to define a new enhancement factor
![]() to apply on the entire segment dsj to account for the difference between the sub-segment really affected, SS', and the total length dsj of the segment. An equivalent adjustment is to be applied in the abundances variation factor:
to apply on the entire segment dsj to account for the difference between the sub-segment really affected, SS', and the total length dsj of the segment. An equivalent adjustment is to be applied in the abundances variation factor:
![]() .
We will at first describe the procedure for the simplest case,
when the LOS is ponting forward (Fig. A.1a), and then the more complicated case of the LOS pointing backwards (Fig. A.1b). In the two figures the length of segment dsj is exagerated with respect to real dimensions for better legibility.
.
We will at first describe the procedure for the simplest case,
when the LOS is ponting forward (Fig. A.1a), and then the more complicated case of the LOS pointing backwards (Fig. A.1b). In the two figures the length of segment dsj is exagerated with respect to real dimensions for better legibility.
We calculate the sub-segment SS' indirectly by defining the segments AS' and SB:
SS' = dsj - AS' - SB. We assume that the arcs
DjD(j+1) and
D'jD'(j+1)
are small enough to be considered as straight lines. This is
reasonable, for the segments dsj are narrow, especially near the observer (0 to 5 AU) where the emissivity is maximum and needs to be defined accurately. Then, from the opposed triangles (
S'BD'(j+1) and S'AD'j) and (
SBD(j+1) and SADj)
we can have respectively:
In the second case of the LOS pointing backwards, the combined effect of the solar rotation and of the SW radial propagation acts in such a way that the LOS is affected starting at an intermediate point, dividing the LOS in two parts:
(i) one on which the spiral is moving away from the observer, and (ii) a second (usually smaller) on which the spiral is
approaching the observer (Fig. A.1b). For the first part, where the spiral is moving away from the observer, Eqs. (A.2) and (A.3) remain unchanged. In the second
part, where the spiral is approaching the observer, we have named the segment
dsj = A1B1 in Fig. A.1b to avoid confusion. Respectively, we have named
OA1 = rj,
OB1 = rj+1,
![]() and
SS' = dsj - A1S' - SB1. Thus, we calculate the segments A1S' and SB1 from the opposed triangles (S'A1Dj and
S'B1D(j+1)) and (
SB1D'(j+1) and SA1D'j) respectively:
and
SS' = dsj - A1S' - SB1. Thus, we calculate the segments A1S' and SB1 from the opposed triangles (S'A1Dj and
S'B1D(j+1)) and (
SB1D'(j+1) and SA1D'j) respectively: