A&A 472, 131-140 (2007)
DOI: 10.1051/0004-6361:20066945
Tanuka Chattopadhyay1 - Asis Kumar Chattopadhyay2
1 - Shibpur Dinobundhoo College, 412/1 G.T. Road
(South), Howrah 711102, India,
Visiting Associate, Inter-University
Center for Astronomy and Astrophysics, Post Bag 4,
Ganeshkhind,
Pune 411007, India
2 -
Department of Statistics, Calcutta University,
35 Ballygunge Circular Road, Calcutta 700019, India
Received 15 December 2006 / Accepted 10 April 2007
Abstract
Aims. To find an objective classification of the globular clusters in our Galaxy, M 31, and LMC.
Methods. A new method of Cluster Analysis (CA)was carried out and the set of parameters for this method was selected through an objective process, Principal Component Analysis (PCA). Robustness of the classification was established using bootstrap samples.
Results. In every case they exhibit multi-population structure instead of bimodality as is found in many spirals and giant elliptical galaxies. The kinematics of MW and M 31 GCs are examined in support of these sub-populations in the cluster system. It is found that for MW and M 31 GCs a disc, inner halo, and outer halo populations of GCs are more likely to exist than only the disc and halo populations of GCs in MW as concluded by Zinn (1985, ApJ, 293, 424). This supports the existence of three populations more firmly explained by Zinn (1993, Globular Cluster-Galaxy Connection, 38) and Mackey & Gilmore (2004, MNRAS, 355, 504) whereas only two populations are found for LMC GCs. The new multivariate analysis increases the importance of the inclusion of many parameters while at the same time it eliminates less significant parameters and helps to enunciate a unique theory of galaxy formation.
Key words: Galaxy: kinematics and dynamics - galaxy: globular clusters: general - galaxies: Local Group - methode: statistical
Globular clusters have long been considered as the unique tool for studying galaxy formation and evolution, but the first step is to study the formation process of the globular clusters (GCs) themselves. There are various theories regarding the formation of GCs. Among them (1) gaseous merger, (2) in situ GC formation, and (3) tidal stripping are important. According to merger theory, GCs in gE and cD galaxies were created by the gaseous merger of two progenitor spiral galaxies (Ashman & Zepf 1992; Zepf & Ashman 1993) so that there are two populations of GCs. One is the metal-poor GCs of the progenitor spirals and other is the metal-rich GCs formed in the collision of high velocity gas. One of the most noteworthy success of this model is the discovery of the protoglobular clusters in the currently merging galaxies (Whitmore et al. 1993; Schweizer et al. 1996). In the merger model the high SN galaxies said to be created by the merger of several normal SN galaxies. But in practice the GC systems of high SN galaxies do not have more metal-rich GCs but instead have more metal-poor ones. This means that GC metallicity gradients are steeper in high SN galaxies contrary to the prediction of Ashman & Zepf (1992). According to the most favourable theory (Forbes et al. 1997) GCs are considered to be formed in situ star formation episodes during a collapse process. In the first episode a chaotic merging of many small gaseous subunits (Searle & Zinn 1978; Katz 1992) occurs. During this phase a small fraction of the gas turns into stars and most of them reside in GCs, i.e. the ratio of stars in GCs to field stars is large (Forbes et al. 1997). So, the GCs formed in this phase are metal-poor. In the second phase, the stars enrich the medium and now field stars form in large numbers (due to more efficient cooling at high metallicity) and the GCs which form in this phase are metal-rich. In the third phase the remaining gas settles as a galactic disc at the centre of the galaxy. Spiral galaxies may be considered as an extreme case of this process. Here there is almost no pre-galaxy star formation. So the GCs which form in the second phase are metal-poor compared to the metal-rich GCs in the second phase for elliptical galaxies. Spirals then go on to form a prominent disc and associated GCs in the third phase of collapse. But the main difficulty of this process is the lack of a detailed mechanism for creating distinct phases of GCs formation from a single halo collapse. Also, this analysis is intended to find the bimodality of a single parameter which is colour.
In the present study we carry out a multivariate analysis, which is likely to be more appropriate in a multivariate set up. Early attempts to analyse the characteristics of the Galaxy and GCs by statistical methods were carried out by Brosche (1973), Peterson & King (1975), Brosche & Lentes (1984), Eigenson & Yatsyk (1989), Djorgovski (1991), Covino & Fracassini (1993). Some correlations of the slope of GCs present day mass function (PDMF) with other parameters were studied by Capaccioli et al. (1991) who found that two or at most three significant parameters determine the PDMF slope. This problem was also discussed by Djorgovski (1991). Several correlations among GCs metallicity and galaxy parameters were studied by van den Bergh (1975), Brodie & Huchra (1991), Forbes et al. (1996), Harris (1991), Djorgovski (1995). Djorgovski (1995) uses core radius, velocity dispersion, central surface brightness, and mass-to-light ratio to define a Fundamental Plane for the GCs of elliptical galaxies. These correlations provide rough distance indicators for GCs. In an earlier work Covino & Fracassini (1993) carried out a Principal Component Analysis (PCA) followed by Cluster Analysis (CA) for more than one parameter at a time to study the clustering nature of GCs in different galaxies in the Local Group. Their analysis suffers from several difficulties. First in their study the parameter set is not same for all galaxies. Also the number of parameters is very large (6 for M 31, 8 for LMC, and 10 for Milky Way) so that it is difficult to study the clustering nature in finer details and their interrelations. Finally, the number of clusters, which they selected in an ad hoc manner, is the eighth hierarchy stage. Also the sample size is small.
In the present problem we have first used PCA to search for the optimum set of parameters which gives the maximum variation for the globular clusters in Milky Way, M 31, and LMC. This method reduces the number of parameters to be selected for CA and hence serves the purpose of PCA. Then we took that optimum set of parameters and applied a new method of CA (Sugar & James 2003) which finds the optimum number of groups of GCs instead of choosing group in an ad hoc manner. Also in our case the sample size of Milky Way is almost double. This helps to sort out the optimum number of clusters and optimum set of parameters so that a more efficient theory of galaxy formation can be developed on the basis of this multivariate analysis. In this connection it is also important to mention that under the given set up a partitioning algorithm for cluster analysis is more appropriate than a hierarchical algorithm since the set up is not nested. The new method for finding the optimum number of clusters is based on partitioning algorithm.
In the present paper we closely follow the approach of Covino & Fracassini (1993) in order to classify GCs. The new aspects of our study are as follows:
In Principal Component Analysis (Chattopadhyay & Chattopadhyay 2006) we are interested in discovering which parameters in a data set form coherent subgroups that are relatively independent of one another. The specific aim of the analysis is to reduce a large number of parameters to a smaller number while retaining maximum spread among experimental units. The analysis therefore helps us to determine the optimum set of parameters causing the overall variations in the nature of GCs. PCA has been discussed in detail in Appendix A.
Cluster analysis is the art of finding groups in data. Over the last forty years different algorithms and computer programs have been developed for CA. The choice of a clustering algorithm depends both on the type of data available and on the particular purpose. Generally clustering algorithms can be divided into two principal types viz. partitioning and hierarchical methods.
A partitioning method constructs K clusters i.e. it classifies the data into K groups which together satisfy the requirement of a partition such that each group must contain at least one object and each object must belong to exactly one group. So there are at most as many groups as there are objects (K <=n). Two different clusters cannot have any object in common and the K groups together add up to the full data set. Partitioning methods are applied if one wants to classify the objects into K clusters where K is fixed (which should be selected optimally). The aim is usually to uncover a structure that is already present in the data. The K- means method of (MacQueen 1967) is probably the most widely applied partitioning clustering technique.
Hierarchical algorithms do not construct single partition with K clusters but they deal with all values of K in the same run. The partition with K=1 is a part of the output (all objects are together in the same cluster) and also the situation with K=n (each object forms a separate cluster). In between all values of K=2,3,... n-1 are covered in a kind of gradual transition. The only difference between K=r and K=r+1 is that one of the r clusters splits in order to obtain r+1 clusters or two of the (r+1) clusters combined to yield r clusters. Under this method either we start with K=n and move hierarchically step-by-step, where at each step two clusters are merged, depending on similarity until only one is left i.e. K=1 (agglomerative) or the reverse, i.e. start with K=1 and move step-by-step, where at each step one cluster is divided into two- (depending on dissimilarity) until K=n (divisive). Most of the previous works (Covino & Fracassini 1993) were done on the basis of hierarchical clustering. But we feel that for the problem under consideration the partitioning method is more applicable because (a) A partitioning method tries to select best clustering with K groups which is not the goal of hierarchical method. (b) A hierarchical method can never repair what was done in previous steps. (c) Partitioning methods are designed to group items rather than variables into a collection of K clusters. (d) Since a matrix of distances (similarities) does not have to be determined and the basic data do not have to be stored during the computer run partitioning methods can be applied to much larger data sets. For K- means algorithm (Hartigan 1975) the optimum value of K can be obtained in different ways.
By using this algorithm we first determined the structures of sub
populations (clusters) for varying numbers of clusters taking
K=2, 3, 4 etc. For each such cluster formation we computed the
values of a distance measure
![]() which is defined as the distance of
the xK vector (values of the parameters) from the centre
cK (which is estimated as the mean value) p is the order of
the xK vector. Then the algorithm for determining the optimum
number of clusters is as follows (Sugar & James 2003). Let us
denote by d'K the estimate of dK at the Kth
point. Then d'K is the minimum achievable distortion
associated with fitting K centres to the data. A natural way of
choosing the number of clusters is to plot d'K versus Kand look for the resulting distortion curve (Fig. 5). This curve is
always monotonic decreasing. Initially one would expect much
smaller drops for K greater than the true number of clusters
because past this point adding more centres simply partitions
within groups rather than between groups. According to Sugar &
James (2003), for a large number of items the distortion curve
when transformed to an appropriate negative power (p/2), will
exhibit a sharp "jump'' (if we plot K versus transformed d'K). Then we calculated the jumps in the transformed
distortion as
which is defined as the distance of
the xK vector (values of the parameters) from the centre
cK (which is estimated as the mean value) p is the order of
the xK vector. Then the algorithm for determining the optimum
number of clusters is as follows (Sugar & James 2003). Let us
denote by d'K the estimate of dK at the Kth
point. Then d'K is the minimum achievable distortion
associated with fitting K centres to the data. A natural way of
choosing the number of clusters is to plot d'K versus Kand look for the resulting distortion curve (Fig. 5). This curve is
always monotonic decreasing. Initially one would expect much
smaller drops for K greater than the true number of clusters
because past this point adding more centres simply partitions
within groups rather than between groups. According to Sugar &
James (2003), for a large number of items the distortion curve
when transformed to an appropriate negative power (p/2), will
exhibit a sharp "jump'' (if we plot K versus transformed d'K). Then we calculated the jumps in the transformed
distortion as
![]() ).
).
The optimum number of clusters is the value of K associated with the largest jump. The largest jump can be determined by plotting JK against K and the highest peak will correspond to the largest jump (Figs. 6, 7 and 17).
Our analysis is based on three samples of
GCs in Milky Way, M 31, and LMC which have appropriate photometric
and
structural parameter values.
Sample 1.
This consists of 135 GCs taken from the catalogue
of Harris (1996) which have nonzero values of all the parameters
used for CA. The parameters used for PCA are distance from the
galactic centre (
![]() ), absolute visual magnitude (MV),
colour (B-V), concentration parameter (c), core radius (
), absolute visual magnitude (MV),
colour (B-V), concentration parameter (c), core radius (![]() ),
central surface brightness (
),
central surface brightness (![]() ), radial velocity
(
), radial velocity
(![]() ), metallicity ([Fe/H]), and horizontal branch
ratio (HBR). We are mainly concentrating on parameters which are
intrinsic and independent in
nature.
), metallicity ([Fe/H]), and horizontal branch
ratio (HBR). We are mainly concentrating on parameters which are
intrinsic and independent in
nature.
Sample 2. This consists of 35 GCs of the catalogue of Barmby
et al. (2002). The parameters used are
![]() ,
MV, b(B-V),
[Fe/H], c,
,
MV, b(B-V),
[Fe/H], c, ![]() ,
Vr, and
,
Vr, and ![]() .
We have converted the visual
magnitudes from Barmby et al. (2000) to absolute visual magnitudes
using a distance of 770 kpc (Sparke & Gallagher 2000) for M 31.
.
We have converted the visual
magnitudes from Barmby et al. (2000) to absolute visual magnitudes
using a distance of 770 kpc (Sparke & Gallagher 2000) for M 31.
Sample 3. This consists of 23 GCs used in the paper by
Mackey & Gilmore (2003). The parameters used are
![]() ,
MV, (B-V), c,
,
MV, (B-V), c, ![]() ,
Vr, [Fe/H], and
,
Vr, [Fe/H], and ![]() .
We
have converted the visual magnitudes from Mackey & Gilmore
(2003) to absolute
visual magnitudes using a distance of 49 kpc (Sparke & Gallagher 2000) for LMC.
.
We
have converted the visual magnitudes from Mackey & Gilmore
(2003) to absolute
visual magnitudes using a distance of 49 kpc (Sparke & Gallagher 2000) for LMC.
In Tables 3, 5, and 7 we have mentioned the elements of the correlation matrices corresponding to Samples 1, 2, and 3 respectively.
After finding the different groups by cluster analysis it is necessary to study the properties of the groups identified in terms of their ages along with other parameters. Again we have used B-V as one of the parameters in PCA. As ages and B-Vvalues are subjected to measurement errors it is worthwhile to identify the nature of errors included in the data.
| MW GCs | LMC GCs | ||||
| ID | Errors | E(B-V) | ID | Errors | E(B-V) |
| Gyr | log (age) (Gyr) | ||||
| 104 | 1.3 | Harris (1996) | 1711 | +.05-.05 | |
| 288 | 1.6 | 1754 | +0.06-0.07 | ||
| 362 | 2.0 | 1755 | 0.01 | ||
| 1261 | 1.3 | 1805 | +.30-.10 | ||
| 1851 | 1.0 | 1810 | 0.34 | ||
| 1904 | 1.5 | 1818 | +.3-.1 | 0.25 | |
| 2298 | 2.2 | 1831 | +.3-.3 | ||
| 2808 | 1.6 | 1835 | +.07-.08 | ||
| 3201 | 1.6 | 1850 | +.2-.2 | 0.13 | |
| 4147 | 1.6 | 1854 | 0.11 | ||
| 4590 | 1.0 | 1856 | +.3-.3 | 0.07 | |
| 5024 | 1.6 | 1866 | 0.01 | ||
| 5053 | 1.5 | 1885 | 0.23 | ||
| 5272 | 1.0 | 1898 | +.3-.3 | ||
| 5466 | 2.0 | 2004 | +.2-.2 | 0.36 | |
| 5897 | 2.1 | 2019 | +.07-.09 | ||
| 5904 | 1.3 | 2031 | +.1-.1 | .06 | |
| 6101 | 1.3 | 2100 | +.2-.2 | ||
| 6121 | 2.0 | 2121 | +.06-.07 | ||
| 6171 | 2.3 | 2136 | +.1-.1 | ||
| 6205 | 2.6 | 2156 | +.2-.2 | -0.16 | |
| 6218 | 1.3 | 2157 | +.2-.2 | ||
| 6254 | 2.0 | 2164 | +.2-.2 | ||
| 6341 | 1.7 | 2173 | +.07-.09 | ||
| 6352 | 1.3 | 2213 | +.1-.12 | ||
| 6397 | 1.9 | 2214 | +.2-.2 | ||
| 6535 | 2.4 | 2231 | +.1-.13 |
| MW GCs | ||
| ID | Errors | E(B-V) |
| Gyr | ||
| 6584 | 1.4 | Harris (1996) |
| 6652 | 1.7 | |
| 6752 | 2.2 | |
| 6809 | 1.3 | |
| 6838 | 1.1 | |
| 7006 | 1.3 | |
| 7078 | 2.0 | |
| 7099 | 1.8 | |
| 7492 | 2.0 | |
| Ter 7 | 0.8 | |
| Ter 8 | 1.7 | |
| Rup 106 | 0.9 | |
| Pal5 | 1.6 | |
| Pal12 | 1.7 | |
| Ic4499 | 1.2 | |
| Arp2 | 1.0 |
| Name | Errors in Age | E(B-V) | ||
| positive error | ||||
| LMC GCs | Mean | 0.16 | 0.13 | |
| SD | 0.09 | 0.16 | ||
| AD | 1.36 | 0.23 | ||
| Remark | Good fit | Very Good fit | ||
| negative error | ||||
| Mean | -0.15 | |||
| SD | 0.08 | |||
| AD | 1.27 | |||
| Remark | Good fit | |||
| MW GCs | Mean | 1.59 | 1.95 | |
| SD | 0.44 | 0.62 | ||
| AD | 0.45 | 0.11 | ||
| Remark | Good fit | Very good fit |
| Parameter |
|
MV | c | B-V | [Fe/H] | HBR | Vr | ||
|
|
1 | ||||||||
| MV | 0.22 | 1 | |||||||
| c | -0.32 | -0.25 | 1 | ||||||
| 0.38 | 0.72 | -0.52 | 1 | ||||||
| B-V | -0.29 | -0.02 | 0.05 | 0.16 | 1 | ||||
| [Fe/H] | -0.29 | 0.10 | 0.10 | 0.07 | 0.60 | 1 | |||
| 0.04 | 0.11 | -0.68 | 0.11 | -0.16 | -0.15 | 1 | |||
| HBR | -0.13 | 0.26 | 0.09 | -0.26 | -0.44 | -0.77 | 0.11 | 1 | |
| 0.03 | 0.03 | -0.05 | 0.09 | -0.02 | 0.06 | 0.17 | -0.03 | 1 |
For Milky Way we considered 43 GCs and for LMC we considered 23 GCs. Their ages and corresponding errors can be obtained from Chaboyer et al. (1992) and Mackey & Gilmore (2003) respectively and are listed in Table 1. The means and standard deviations of these errors are listed in Table 2. The means and standard deviations (SD) of extinctions in colour E(B-V) for Milky Way (MW) and LMC GCs are also listed in Table 2. It is interesting to note that most of the error and extinction distributions are Gaussian as indicated in Table 2 and Figs. 1-4 respectively. These show that the ages and colours of Milky Way and LMC GCs are consistent with respect to the measurement errors and extinctions. To study errors corresponding to ages for MW GCs we excluded some of the outliers and the fit is good which is evident from the Anderson Darling (AD) statistic. In Appendix B we have discussed Quantile Quantile Plot and Anderson Darling Statistic which have been used for fitting of Normal Distribution.
From the above findings it may be inferred that since the error distributions are Gaussian (symmetric), the errors are supposed to be averaged out in final analysis and results are not likely to be affected by them.
| Set | Principal Component | Eigen value | Cumulative |
| S1(
|
1 | 1.6 | 53.1 |
| 2 | 0.8 | 79.9 | |
| 3 | 0.6 | 100.0 | |
| S2(
|
1 | 1.4 | 47.3 |
| 2 | 1.1 | 82.9 | |
| 3 | 0.5 | 100.0 | |
| S3(
|
1 | 1.3 | 43.7 |
| 2 | 0.9 | 75.3 | |
| 3 | 0.7 | 100.0 | |
| S4(
|
1 | 1.5 | 51.5 |
| 2 | 0.9 | 81.9 | |
| 3 | 0.5 | 100.0 | |
| S5(
|
1 | 2.0 | 50.7 |
| 2 | 0.8 | 71.3 | |
| 3 | 0.7 | 88.9 | |
| 4 | 0.4 | 100.0 | |
| S6(MV,c, [Fe/H]) | 1 | 1.6 | 53.0 |
| 2 | 0.8 | 80.0 | |
| 3 | 0.6 | 100.0 | |
| S7(
|
1 | 1.6 | 54.7 |
| 2 | 0.9 | 85.7 | |
| 3 | 0.4 | 100.0 | |
| S8(HBR, [Fe/H], c) | 1 | 1.5 | 49.7 |
| 2 | 0.9 | 79.2 | |
| 3 | 0.6 | 100.0 |
| Parameter |
|
MV | c | B-V | [Fe/H] | ||
|
|
1 | ||||||
| MV | -0.34 | 1 | |||||
| c | -0.01 | -0.058 | 1 | ||||
| -0.24 | 0.76 | -0.33 | 1 | ||||
| B-V | -0.25 | 0.16 | 0.39 | -0.214 | 1 | ||
| [Fe/H] | -0.215 | 0.66 | -0.26 | 0.48 | 0.68 | 1 | |
| 0.25 | -0.01 | -0.82 | 0.34 | -0.46 | 0.09 | 1 |
| Set | Principal Component | Eigen value | Cumulative |
| S1(
|
1 | 1.4 | 47.7 |
| 2 | 1.0 | 80.6 | |
| 3 | 0.6 | 100.00 | |
| S2(
|
1 | 1.3 | 44.5 |
| 2 | 1.0 | 78.2 | |
| 3 | 0.7 | 100.00 | |
| S3(
|
1 | 1.5 | 48.8 |
| 2 | 1.0 | 81.8 | |
| 3 | 0.5 | 100.0 | |
| S4(
|
1 | 2.1 | 71.0 |
| 2 | 0.7 | 94.0 | |
| 3 | 0.2 | 100.0 | |
| S5(
|
1 | 1.9 | 46.5 |
| 2 | 1.3 | 79.9 | |
| 3 | 0.6 | 96.3 | |
| 4 | 0.2 | 100.0 | |
| S6(
|
1 | 1.8 | 60.5 |
| 2 | 1.0 | 93.9 | |
| 3 | 0.2 | 100.0 | |
| S7([Fe/H],
|
1 | 1.9 | 62.7 |
| 2 | 1.0 | 94.4 | |
| 3 | 0.2 | 100.0 |
| Parameter |
|
c | [Fe/H] | MV | |||
|
|
1 | ||||||
| 0.32 | 1 | ||||||
| 0.09 | 0.19 | 1 | |||||
| c | -0.19 | -0.03 | -0.88 | 1 | |||
| 0.61 | -0.13 | 0.13 | -0.38 | 1 | |||
| [Fe/H] | 0.46 | 0.44 | 0.16 | -0.11 | 0.28 | 1 | |
| MV | 0.52 | -0.26 | -0.03 | -0.18 | 0.75 | -0.12 | 1 |
It is found that the statistical dimensionality for the GCs in all
the galaxies in the Local Group is two which involves the
parameters core radius (![]() ), concentration parameter (c) and
metallicity. This is minimum but gives a total variation as high
as 96 percent. This is maximum compared to all previous analyses
(Kormendy & Djorgovski 1989; Djorgovski & de Carvalho 1990;
Santiago & Djorgovski 1993; De Carvalho & Djorgovski 1992).
This is the goal of PCA.
), concentration parameter (c) and
metallicity. This is minimum but gives a total variation as high
as 96 percent. This is maximum compared to all previous analyses
(Kormendy & Djorgovski 1989; Djorgovski & de Carvalho 1990;
Santiago & Djorgovski 1993; De Carvalho & Djorgovski 1992).
This is the goal of PCA.
We found in the
previous analysis that the maximum variation among the GCs in the
Milky Way, M 31, and, LMC is due to the parameter set (
![]() ). The metallicity values for GCs in M 31 are available for 35 clusters. So the sample size is slightly reduced for M 31 in our
case compared to Covino & Fracassini (1993). The results for CA
for Sample 1 are shown in Table 9 and Figs. 5 and 6 respectively.
The jumps are at 4 and 6 respectively. To test the robustness of
the classification we took several bootstrap samples generated
from the original sample. In most of the situations it was found
both from the jumps and from the (
). The metallicity values for GCs in M 31 are available for 35 clusters. So the sample size is slightly reduced for M 31 in our
case compared to Covino & Fracassini (1993). The results for CA
for Sample 1 are shown in Table 9 and Figs. 5 and 6 respectively.
The jumps are at 4 and 6 respectively. To test the robustness of
the classification we took several bootstrap samples generated
from the original sample. In most of the situations it was found
both from the jumps and from the (
![]() )
plots that the
proper number of groups (clusters) should be 3. We took
this decision because of the following reasons.
)
plots that the
proper number of groups (clusters) should be 3. We took
this decision because of the following reasons.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{6945fig5.eps}
\end{figure}](/articles/aa/full/2007/34/aa6945-06/Timg28.gif) |
Figure 5: xy diagram for the number of clusters (K) and corresponding distortions (d'K) for Sample 1. |
| Set | Principal Component | Eigen value | Cumulative |
| S1(
|
1 | 1.5 | 50.9 |
| 2 | 1.0 | 84.6 | |
| 3 | 0.5 | 100.0 | |
| S2(
|
1 | 1.6 | 54.4 |
| 2 | 0.9 | 84.1 | |
| 3 | 0.5 | 100.0 | |
| S3(
|
1 | 2.0 | 50.0 |
| 2 | 1.4 | 85.7 | |
| 3 | 0.5 | 97.7 | |
| 4 | 0.1 | 100.0 | |
| S5(
|
1 | 1.7 | 58.3 |
| 2 | 1.0 | 91.9 | |
| 3 | 0.2 | 100.0 | |
| S6(
|
1 | 1.9 | 64.1 |
| 2 | 1.0 | 96.1 | |
| 3 | 0.1 | 100.0 | |
| S7(
|
1 | 2.3 | 75.5 |
| 2 | 0.5 | 92.2 | |
| 3 | 0.2 | 100.0 | |
| S8(
|
1 | 1.8 | 60.5 |
| 2 | 0.7 | 83.3 | |
| 3 | 0.5 | 100.0 |
| No of clusters at the peaks | 4, 6 | |||
| Variables | Cluster 1 | Cluster 2 | Cluster 3 | Cluster 4 |
| No. of members | 37 | 41 | 45 | 12 |
|
|
-0.59 | -1.54 | -1.69 | -1.29 |
|
|
1.66 | 2.11 | 1.21 | 0.92 |
|
|
2.66 | 0.59 | 3.86 | 17.53 |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{6945fig7.eps}
\end{figure}](/articles/aa/full/2007/34/aa6945-06/Timg35.gif) |
Figure 7: xy diagram for the number of clusters (K) and jumps for Bootstrap Samples, dash for second, solid line for fourth and dotted line for third Bootstrap Sample respectively. |
Now the kinematics
of MW GCs are studied to examine the physical consistency of the
classification following Zinn (1985). The basic assumption is that
the rotational velocity of each sub group in the classification is
constant. For this it is necessary to know the distances of GCs
from the galactic centre and the results depend slightly on the
values adopted for ![]() and the velocity of the LSR about
the galactic centre (
and the velocity of the LSR about
the galactic centre (![]() )
which are taken as 8.2 kpc and
220 km s-1 for the present situation. The analysis follows the
method of Frenk & White (1980). The values of rotational
velocities (
)
which are taken as 8.2 kpc and
220 km s-1 for the present situation. The analysis follows the
method of Frenk & White (1980). The values of rotational
velocities (
![]() )
and velocity dispersion (
)
and velocity dispersion (
![]() )
are listed in Table 11 for each group. Also the group means for
heights from the galactic plane (|z|), distances from the
galactic centre (
)
are listed in Table 11 for each group. Also the group means for
heights from the galactic plane (|z|), distances from the
galactic centre (
![]() ), metallicities, concentration
parameters (c), core radii, and central surface brightness (
), metallicities, concentration
parameters (c), core radii, and central surface brightness (![]() )
are listed for these sub groups. It is found that for
)
are listed for these sub groups. It is found that for
![]() the cluster group has substantial rotation for
the cluster group has substantial rotation for
![]() kpc (Cluster 1) and for
kpc (Cluster 1) and for
![]() and GCs have
less rotation for
and GCs have
less rotation for
![]() kpc. This supports the analysis
by Zinn (1985). The innermost group (Cluster 1) has substantial
rotational velocity (
kpc. This supports the analysis
by Zinn (1985). The innermost group (Cluster 1) has substantial
rotational velocity (![]() 124 km s-1), highly metal rich (
124 km s-1), highly metal rich (![]() -0.64) having smaller core radii (
-0.64) having smaller core radii (![]() 2.71 pc).
2.71 pc).
| |
Figure 9:
[Fe/H] vs. |
| |
Figure 10:
[Fe/H] vs. |
| |
Figure 11:
[Fe/H] vs. |
| Bootstrap samples | No of clusters | Variables | Cluster 1 | Cluster 2 | Cluster 3 |
| at peaks | |||||
| No. of members | 36 | 68 | 31 | ||
| 1 | 3, 5 |
|
-0.59 | -1.46 | -1.80 |
|
|
1.42 | 2.00 | 0.93 | ||
|
|
2.84 | 0.92 | 12.66 | ||
| No. of members | 41 | 66 | 28 | ||
| 2 | 3 |
|
-0.73 | -1.61 | -1.67 |
|
|
1.50 | 1.86 | 0.82 | ||
|
|
3.06 | 1.26 | 13.36 | ||
| No. of members | 43 | 68 | 24 | ||
| 3 | 3,5 |
|
-0.57 | -1.58 | -1.60 |
|
|
1.70 | 1.8 | 0.87 | ||
|
|
2.84 | 1.32 | 10.45 | ||
| No. of members | 56 | 65 | 14 | ||
| 4 | 3,7 |
|
-0.89 | -1.65 | -1.01 |
|
|
1.97 | 1.44 | 1.24 | ||
|
|
1.17 | 2.81 | 17.49 |
| |
Figure 12:
[Fe/H] vs. |
| |
Figure 13:
[Fe/H] vs. |
| |
Figure 14: [Fe/H] vs. c diagram for final cluster analysis result for Sample 1. The suffixes indicate the cluster number. |
| |
Figure 15:
[Fe/H], |
| Variables | Cluster 1 | Cluster 2 | Cluster 3 |
| No. of members | 41 | 69 | 25 |
|
|
-0.64 | -1.61 | -1.58 |
|
|
1.60 | 1.82 | 0.91 |
|
|
2.71 | 10.16 | 12.12 |
|
|
1.73 | 5.49 | 18.81 |
|
|
4.196 | 10.16 | 31.69 |
|
|
18.792 | 17.28 | 22.32 |
|
|
124 | 5 | 20 |
|
|
88 | 129 | 131 |
|
|
11.81 | 14.83 | 14.66 |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{6945fig16.eps}
\end{figure}](/articles/aa/full/2007/34/aa6945-06/Timg63.gif) |
Figure 16: Scatter diagram of age in logarithmic scale (yr) vs. metallicity with available values of ages in clusters 1, 2 and 3 respectively as a result of cluster analysis for Sample 1. |
| Variables | Cluster 1 | Cluster 2 | Cluster 3 |
| No. of members | 9 | 19 | 7 |
|
|
-0.43 | -1.51 | -1.41 |
|
|
1.06 | 0.76 | 0.73 |
|
|
1.67 | 1.55 | 1.08 |
|
|
0.545 | 0.92 | 1.93 |
|
|
5.28 | 8.78 | 8.17 |
|
|
16.28 | 16.01 | 16.56 |
|
|
52.87 | 31.16 | 51.90 |
The CA for M 31 GCs are shown in Table 12 and Fig. 17 respectively.
The optimum number in this case is also three like those in MW.
Cluster 1 has high metallicity, very low core radii and close to
the galactic centre. Cluster 2 has minimum metallicity,
comparatively lower core radii, and is very far from the centre.
Cluster 3 has comparatively low metallicity, maximum core radii.
For calculating the rotational velocities of these groups the
function
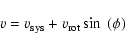
| |
Figure 18:
[Fe/H], |
| Variables | Cluster 1 | Cluster 2 | Cluster 3 |
| No. of members | 16 | 4 | 3 |
|
|
-0.37 | -1.6 | -0.34 |
|
|
0.33 | 0.55 | 0.18 |
|
|
18.33 | 17.40 | 18.49 |
|
|
1.39 | 1.26 | 0.68 |
|
|
2.62 | 3.72 | 10.87 |
|
|
3.18 | 1.5 | 2.85 |
|
|
8.09 | 10.20 | 7.77 |
| |
Figure 19:
[Fe/H], |
| |
Figure 20:
B-V, |
We have applied multivariate analysis for the reclassification of the globular clusters of our Galaxy, M 31, and LMC. First a Principal Component Analysis is performed to search for the optimum set of parameters giving the maximum over all variation among the GCs in these galaxies. It is found that metallicity, concentration parameter and core radius are the parameters responsible for maximum variation in the GCs of Milky Way and M 31. The statistical dimensionality is two in every situation which is less than those of elliptical galaxies (Santiago & Djorgovski 1992). This procedure is completely different from the method of studying two point correlation or studying the properties of GCs with respect to a single parameter like colour or HB morphology as done by previous authors (Zinn 1985, 1993; Mackey & Gilmore 2004). As the present set up is multivariate, it is quite likely to carry out the analysis by multivariate methods. Also there are various parameters responsible for the variation among GCs. It is better to select the optimum set giving maximum variation. This reduces the difficulty in handling large number of parameters simultaneously and drawing any physical conclusions while at the same time restores the significant parameters responsible for maximum variation. This is the goal of PCA. In the present situation the optimum set does not include HB morphology parameter which is HBR but includes chemical composition and morphological parameters instead (Table 4, S7, and S8). So it is more scientific to perform classification on the basis of these significant parameters selected objectively instead of taking any parameter in a subjective way. Then Cluster Analysis is carried out with respect to this optimum set. Here two and three clusters are found in case of MW, M 31, and LMC GCs. The robustness of the classification is tested by taking a few bootstrap samples generated from the original one. The classification differs from that by Zinn (1985) and is in agreement with Zinn (1993) and Mackey & Gilmore (2004). For MW and M 31 three clusters, disc, inner halo, and outer halo GCs are found. The kinematic properties, age metallicity diagram, metallicity gradients studied for these groups also support the true nature of the classification. The analogous behaviour of the GCs with MW GCs in different parametric planes shows that they have a similar nature as those of MW GCs. Perrett et al. (2002) have calculated the kinematic properties of some 200 GCs in M 31 and have found two groups, disc and halo GCs with metallicities peaked at -0.5 and -1.41 respectively. In the present analysis, three groups have been found with mean metallicities -0.43, -1.41, and -1.51 respectively. The existence of the third group with minimum metallicity is analogous in properties with inner halo GCs of MW. For LMC GCs two groups have been found instead of three though the conclusion is not very firm due to the small size of the sample. The evolution history is likely to differ from those of MW and M 31. As there is controversy in the formation of GCs in disc (Schommer et al. 1992) or in pressure supported halo (van den Bergh 2004) so more clear picture will come out from the spectroscopic study of GCs with a larger sample size.
Acknowledgements
One of the the authors (Tanuka Chattopadhyay) wishes to thank University Grants Commission (UGC), India for awarding her a major research project for the work.The authors are grateful to Prof. Rajaram Nityananda for his useful suggestions. The authors are also thankful to Prof. Duncan Forbes for his careful reading and important suggestions. The authors are grateful to the referee for his careful reading and valuable suggestions to improve the quality of the work.
The purpose of the principal component analysis is to reduce the complexity of multivariate data by transforming the data into the principal components space and choosing the first n principal components that explain most of the variation in the original variables.
Let the components xi of a random vector
![]() are measured in the same or comparable units. Also assume
that the variances of the variables do not vary too much. Let
are measured in the same or comparable units. Also assume
that the variances of the variables do not vary too much. Let
![]() denote the covariance matrix of the random vector
denote the covariance matrix of the random vector
![]() is assumed to be at least positive semi definite rank
is assumed to be at least positive semi definite rank
![]() .
All the eigen values of
.
All the eigen values of ![]() are real and non
negative. Let
are real and non
negative. Let
![]() be the ordered eigen value of
be the ordered eigen value of ![]() .
Then there exists an
orthogonal matrix
.
Then there exists an
orthogonal matrix
![]() such that
such that
![]() ,
,
![]()
Consider the transformation
| y = G'x | (A.1) |
| (A.2) |
| |
= | ||
| = | |||
From the above result it follows that for any set of orthogonal
vectors
hi, h'i hi = 1 and for any ![]()
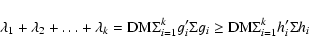
For this reason, the component
| y1 = g'1 x | (A.3) |
| y2 = g'2 x | (A.4) |
Here Var(
![]() ,
Because
,
Because
![]() ,
y1 has the largest variance
,
y1 has the largest variance
![]() has
the second largest variance
has
the second largest variance ![]() and so on.
Since
and so on.
Since
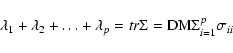 |
(A.5) |
Many criteria have been suggested by different authors for deciding how many principal components to retain. Some of these criteria are as follows:
The quantile-quantile (q-q) plot is a graphical technique for
determining if two data sets come from populations with a common
distribution. A q-q plot is a plot of the quantiles of the first
data set against the quantiles of the second data set. By a
quantile, we mean the fraction (or percent)
of points below the given value. That is, the 0.3 (or 30![]() )
quantile is the point
at which 30
)
quantile is the point
at which 30![]() of the data fall below and 70
of the data fall below and 70![]() fall above that value.
fall above that value.
A 45-degree reference line is also plotted. If the two sets come from a population with the same distribution, the points should fall approximately along this reference line. The greater the departure from this reference line, the greater the evidence for the conclusion that the two data sets have come from populations with different distributions.
In order to fit a theoretical distribution to a data set we take
the data set as the first sample and observations from the
theoretical distribution under consideration (in our case
Normal) as the second sample.
Anderson-Darling test
The Anderson-Darling test (Stephens 1974) is used to test if a sample of data came from a population with a specific distribution. It is a modification of the Kolmogorov-Smirnov (K-S) test and gives more weight to the tails than does the K-S test. The K-S test is distribution free in the sense that the critical values do not depend on the specific distribution being tested. The Anderson-Darling test makes use of the specific distribution in calculating critical values. This has the advantage of allowing a more sensitive test and the disadvantage that critical values must be calculated for each distribution.
The Anderson-Darling test is an alternative to the chi-square and
Kolmogorov-Smirnov goodness-of-fit tests.
Definition: The Anderson-Darling test is defined as:
H0: The data follow a specified distribution.
Ha: The data do not follow the specified distribution.
Test Statistic: The
Anderson-Darling test statistic is defined as
![\begin{displaymath}S ={\Sigma}^N_{i=1}((2i-1)/N)[{\rm ln}~(F(Y_{i})+{\rm ln}~(1-F(Y_{N+1-i}))]\end{displaymath}](/articles/aa/full/2007/34/aa6945-06/img100.gif)
Significance Level: Critical Region: The critical values for the Anderson-Darling test are dependent on the specific distribution that is being tested. Tabulated values and formulas have been published (Stephens 1974, 1976, 1977, 1979) for a few specific distributions (normal, lognormal, exponential, Weibull, logistic, extreme value type 1). The test is a one-sided test and the hypothesis that the distribution is of a specific form is rejected if the test statistic, A, is greater than the critical value.