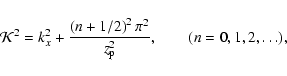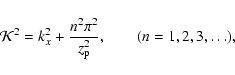A&A 471, 1023-1033 (2007)
DOI: 10.1051/0004-6361:20077633
R. Soler - R. Oliver - J. L. Ballester
Departament de Física, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
Received 12 April 2007 / Accepted 8 June 2007
Abstract
Context. One of the typical features shown by observations of solar prominence oscillations is that they are damped in time and that the values of the damping times are usually between one and three times the corresponding oscillatory period. However, the mechanism responsible for the attenuation is still not well-known.
Aims. Thermal conduction, optically thin or thick radiation and heating are taken into account in the energy equation, and their role on the attenuation of prominence oscillations is evaluated.
Methods. The dispersion relation for linear non-adiabatic magnetoacoustic waves is derived considering an equilibrium made of a prominence plasma slab embedded in an unbounded corona. The magnetic field is orientated along the direction parallel to the slab axis and has the same strength in all regions. By solving the dispersion relation for a fixed wavenumber, a complex oscillatory frequency is obtained, and the period and the damping time are computed.
Results. The effect of conduction and radiation losses is different for each magnetoacoustic mode and depends on the wavenumber. In the observed range of wavelengths the internal slow mode is attenuated by radiation from the prominence plasma, the fast mode by the combination of prominence radiation and coronal conduction and the external slow mode by coronal conduction. The consideration of the external corona is of paramount importance in the case of the fast and external slow modes, whereas it does not affect the internal slow modes at all. When a thinner slab representing a filament thread is considered, the fast mode is less attenuated whereas both internal and external slow modes are not affected.
Conclusions. Non-adiabatic effects are efficient damping mechanisms for magnetoacoustic modes, and the values of the obtained damping times are compatible with those observed.
Key words: Sun: oscillations - Sun: magnetic fields - Sun: corona - Sun: prominences
Prominences are dense coronal structures which appear as thin, dark filaments on the solar disc when observed in H![]() .
On the contrary, they show up as bright objects above the solar limb. The coronal magnetic field is responsible for the support of prominences against
gravity, and it also plays a fundamental role in the thermal confinement of the
cool prominence plasma embedded in the much hotter coronal environment. Nevertheless, the structure, orientation and strength of the magnetic field in prominences and the surrounding corona is still enigmatic and not well-known. High resolution observations reveal that prominences are composed of numerous very thin, thread-like structures, called fibrils, piled up to form the body of the prominence (Lin et al. 2003, 2005, 2007) and measures also indicate that magnetic field lines are orientated along these thin threads.
.
On the contrary, they show up as bright objects above the solar limb. The coronal magnetic field is responsible for the support of prominences against
gravity, and it also plays a fundamental role in the thermal confinement of the
cool prominence plasma embedded in the much hotter coronal environment. Nevertheless, the structure, orientation and strength of the magnetic field in prominences and the surrounding corona is still enigmatic and not well-known. High resolution observations reveal that prominences are composed of numerous very thin, thread-like structures, called fibrils, piled up to form the body of the prominence (Lin et al. 2003, 2005, 2007) and measures also indicate that magnetic field lines are orientated along these thin threads.
The observational evidence of small-amplitude oscillations in quiescent solar
prominences goes back to 40 years ago (Harvey 1969). These oscillations, whose amplitude typically goes from less than 0.1 km s-1 to 2-3 km s-1, were
historically classified, according to their periods, in short- (P <
10 min), intermediate- (10 min < P < 40 min) and long-period oscillations
(P > 40 min), although very short-periods of less than 1 min (Balthasar et al.
1993) and extreme ultra-long-periods of more than 8 h (Foullon et al. 2004)
have been reported. Nevertheless, the value of the period seems not to be related with the
nature or the source of the trigger and is probably linked to the prominence eigenmode that is excited. There are also a few determinations of the wavelength and phase speed of standing oscillations and propagating waves in large regions of prominences (Molowny-Horas et al. 1997; Terradas et al. 2002) and in single filament threads (Lin et al. 2007). On the other hand, several observations (Molowny-Horas et al. 1999; Terradas et al. 2002) showed evidence of the attenuation of the oscillations in Doppler velocity time series, which is a common feature observed in large areas. By fitting a sinusoidal function multiplied by a factor
![]() to the Doppler series, these authors obtained values of the damping time,
to the Doppler series, these authors obtained values of the damping time,
![]() ,
which were usually between 1 and 3 times the corresponding oscillatory period. The reader is referred to some recent reviews for more information about the observational background (Oliver & Ballester 2002; Wiehr 2004; Engvold 2004; Ballester 2006).
,
which were usually between 1 and 3 times the corresponding oscillatory period. The reader is referred to some recent reviews for more information about the observational background (Oliver & Ballester 2002; Wiehr 2004; Engvold 2004; Ballester 2006).
From the theoretical point of view, small-amplitude prominence oscillations can be interpreted in terms of linear magnetohydrodynamic (MHD) waves. Although there is a wide bibliography of works that investigate the ideal MHD wave modes supported by prominence models (see Oliver & Ballester 2002, for an extensive review of theoretical studies), the investigation of the wave damping has been broached in few papers. By removing the ideal assumption and including dissipative terms in the basic MHD equations, several works studied the attenuation of prominence oscillations considering radiative losses based on the Newtonian law of cooling with a constant relaxation time (Terradas et al. 2001), or performing a more complete treatment of non-adiabatic effects, assuming optically thin radiation, heating and thermal conduction (Carbonell et al. 2004; Terradas et al. 2005). The main conclusion of these previous studies is that only the slow wave is attenuated by thermal effects, radiation being the dominant damping mechanism in the range of typically observed wavelengths in prominences, but the fast wave remains practically undamped. On the other hand, Forteza et al. (2007) proposed ion-neutral collisions as a damping mechanism on the basis that prominences are partially ionised plasmas, but they found that this mechanism is only efficient in attenuating the fast mode in quasi-neutral plasmas, the slow mode being almost unaffected.
In the light of these referred studies, non-adiabatic effects likely are the best candidates for the damping of small-amplitude oscillations, at least for slow modes. However, previous results do not assess the influence of the corona. The main aim of the present work is to perform a step forward in the investigation of the effect of non-adiabatic mechanisms (radiation losses, thermal conduction and heating) on the time damping of prominence oscillations. We consider a slab model with a longitudinal magnetic field and take into account the external coronal medium. So, we explore for the first time the joint effect of prominence and coronal mechanisms on the attenuation of oscillations. The magnetoacoustic normal modes of this equilibrium were previously investigated by Edwin & Roberts (1982) and Joarder & Roberts (1992) in the adiabatic case. Later on, a revision of these works was done in Soler et al. (2007), hereafter Paper I, and the normal modes were studied and reclassified according to their magnetoacoustic properties.
This paper is organised as follows. The description of the equilibrium model and the linear non-adiabatic wave equations are given in Sect. 2, whereas the dispersion relation for the magnetoacoustic modes is derived in Sect. 3. Then, the results are plotted and investigated in Sect. 4. Finally, Sect. 5 contains the conclusions of this work.
Our equilibrium configuration (Fig. 1) is made of a homogeneous plasma layer with prominence conditions (density
![]() and temperature
and temperature ![]() )
embedded in an unbounded corona (density
)
embedded in an unbounded corona (density
![]() and temperature
and temperature ![]() ). The coronal density is computed by fixing the coronal temperature and imposing pressure continuity across the interfaces. The magnetic field is
). The coronal density is computed by fixing the coronal temperature and imposing pressure continuity across the interfaces. The magnetic field is
![]() ,
with B0 a constant everywhere. Both media are unlimited in the x- and y-directions. The half-width of the prominence slab is
,
with B0 a constant everywhere. Both media are unlimited in the x- and y-directions. The half-width of the prominence slab is ![]() .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7633f01.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg19.gif) |
Figure 1: Sketch of the equilibrium. |
| Open with DEXTER | |
The basic magnetohydrodynamic equations for the discussion of non-adiabatic processes are:
Table 1: Parameter values of the radiative loss function corresponding to the considered regimes. The three prominence regimes represent different plasma optical thicknesses. Prominence (1) regime corresponds to an optically thin plasma whereas Prominence (2) and Prominence (3) regimes represent greater optical thicknesses. All quantities are expressed in MKS units.
Following the same process as in Carbonell et al. (2004), we consider small perturbations from the equilibrium state, linearise the basic Eqs. (1)-(6) and obtain their Eqs. (9)-(14). Since our model is unlimited in the x- and y-directions, we assume all perturbations are in the form
![]() ,
and considering only motions and propagation in the xz-plane (vy=0, ky=0), which excludes Alfvén waves, the linearised equations become
,
and considering only motions and propagation in the xz-plane (vy=0, ky=0), which excludes Alfvén waves, the linearised equations become
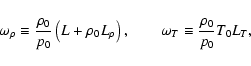
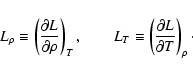
We impose some restrictions on the solutions of Eq. (13) in order to obtain the dispersion relation for the linear non-adiabatic magnetoacoustic waves. We restrict this analysis to body waves which are evanescent in the corona, since we are looking for solutions which are essentially confined to the slab. For such solutions, vz(z) is of the form
Imposing continuity of vz and the total (gas plus magnetic) pressure perturbation across the interfaces, we find four algebraic relations between the constants A1, A2, A3 and A4. The non-trivial solution of this system gives us the dispersion relation
The dispersion relation for the magnetoacoustic waves presented in Eq. (18) is equivalent to the relation investigated in Edwin & Roberts (1982) and Joarder & Roberts (1992), and revised Paper I, in the case of adiabatic perturbations, since all non-adiabatic terms are now enclosed in
![]() and
and
![]() through Eq. (14).
through Eq. (14).
Now, we assume Prominence (1) conditions inside the slab (i.e. an optically thin prominence) and a heating mechanism given by a=b=0. Unless otherwise stated, the following equilibrium parameters are considered in all computations:
![]() K,
K,
![]()
![]() 10-11 kg m-3,
10-11 kg m-3,
![]() K,
K,
![]()
![]() 10-13 kg m-3, B0=5 G and
10-13 kg m-3, B0=5 G and
![]() km. The solution of the dispersion relation (Eq. (18)) for a fixed real kx gives us a complex frequency
km. The solution of the dispersion relation (Eq. (18)) for a fixed real kx gives us a complex frequency
![]() .
We then compute the oscillatory period, the damping time and the ratio of the damping time to the period because this is an important quantity from the observational point of view,
.
We then compute the oscillatory period, the damping time and the ratio of the damping time to the period because this is an important quantity from the observational point of view,
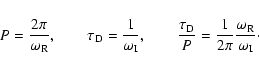
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{7633f02.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg72.gif) |
Figure 2: Phase speed versus the dimensionless wavenumber for the three fundamental oscillatory modes. Solid lines denote kink modes whereas dotted lines correspond to sausage modes. The shaded zones are projections of the forbidden (or leaky) regions on the plane of this diagram. Note that the vertical axis is not drawn to scale. |
| Open with DEXTER | |
In Fig. 3 P,
![]() and
and
![]() are represented for the fundamental modes and for a range of the longitudinal wavenumber between
are represented for the fundamental modes and for a range of the longitudinal wavenumber between
![]() and
and
![]() .
The shaded zones correspond to wavelengths between 5
.
The shaded zones correspond to wavelengths between 5 ![]()
![]() and
and
![]() ,
the typically observed values. It turns out that the values of the period are very similar to those obtained in the adiabatic case (Joarder & Roberts 1992; Paper I). The damping time presents a strong dependence with the wavenumber and its behaviour is very different from one mode to another. This fact suggests that the non-adiabatic mechanisms can affect each mode in a different way (Carbonell et al. 2004). This is studied in detail in Sect. 4.1. Observations show that prominence oscillations are typically attenuated in a few periods (Terradas et al. 2002), so a damping time of the order of the period is expected. In our results, the fundamental modes present values of
,
the typically observed values. It turns out that the values of the period are very similar to those obtained in the adiabatic case (Joarder & Roberts 1992; Paper I). The damping time presents a strong dependence with the wavenumber and its behaviour is very different from one mode to another. This fact suggests that the non-adiabatic mechanisms can affect each mode in a different way (Carbonell et al. 2004). This is studied in detail in Sect. 4.1. Observations show that prominence oscillations are typically attenuated in a few periods (Terradas et al. 2002), so a damping time of the order of the period is expected. In our results, the fundamental modes present values of
![]() in the range 1 to 10 in the observed wavelength region, which is in agreement with observations.
in the range 1 to 10 in the observed wavelength region, which is in agreement with observations.
The importance of the different non-adiabatic terms included in the energy equation (Eq. (3)) depends on the wavenumber. In order to know which is the range of dominance of each mechanism, we compare the damping time obtained when considering all non-adiabatic terms (displayed in the middle column of Fig. 3) with the results obtained when a specific mechanism is removed from the energy equation. With this analysis, we are able to know where the omitted mechanism has an appreciable effect on the damping. The results of these computations for the fundamental kink modes (Fig. 4) are summarised as follows:
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{7633f03.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg78.gif) |
Figure 3: Period ( left), damping time ( centre) and ratio of the damping time to the period ( right) versus the longitudinal wavenumber for the fundamental oscillatory modes. Upper panels: internal slow kink (solid line), fast kink (dotted line) and external slow kink (dashed line). Lower panels: internal slow sausage (solid line) and fast sausage (dotted line). Shaded zones correspond to those wavelengths typically observed. Note the cut-offs of the external slow kink mode and the fast sausage mode. Prominence (1) radiation conditions have been taken for the prominence plasma and the heating scenario is given by a=b=0. |
| Open with DEXTER | |
| |
Figure 4: Damping time versus the longitudinal wavenumber for the three fundamental kink oscillatory modes: internal slow ( left), fast ( centre) and external slow ( right). Different linestyles represent the omitted mechanism: all mechanisms considered (solid line), prominence conduction eliminated (dotted line), prominence radiation eliminated (dashed line), coronal conduction eliminated (dot-dashed line) and coronal radiation eliminated (three dot-dashed line). Prominence (1) radiation conditions have been taken for the prominence plasma and the heating scenario is given by a=b=0. |
| Open with DEXTER | |
Approximate values of kx for which the transitions between regimes take place can be computed by following a process similar to that in Carbonell et al. (2006). The thermal ratio, d, and the radiation ratio, r, quantify the importance of thermal conduction and radiation, respectively (De Moortel & Hood 2004),
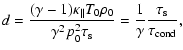 |
(19) | ||
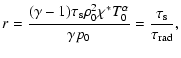 |
(20) |
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{7633f05.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg98.gif) |
Figure 5: Same as Fig. 4 for the fundamental fast sausage mode. |
| Open with DEXTER | |
| |
Figure 6:
Damping time versus the longitudinal wavenumber for the fundamental internal slow kink mode ( left), the fundamental fast kink mode ( centre) and the fundamental external slow kink mode ( right). The different linestyles represent different values of the prominence temperature:
|
| Open with DEXTER | |
| |
Figure 7:
Same as Fig. 6 with
|
| Open with DEXTER | |
| |
Figure 8: Same as Fig. 6 with B0 = 5 G (solid line), B0 = 2 G (dotted line) and B0 = 10 G (dashed line). |
| Open with DEXTER | |
Now, we use prominence values to compute k* for the prominence radiation-prominence conduction transition (
![]() ), and coronal values for the coronal radiation-coronal conduction transition (
), and coronal values for the coronal radiation-coronal conduction transition (
![]() ). This gives the values
). This gives the values
![]()
![]() 10-3 m-1, and
10-3 m-1, and
![]()
![]() 10-8 m-1. For the transition of the fast kink mode between the coronal conduction and the prominence radiation regimes, the boundary wavenumber
10-8 m-1. For the transition of the fast kink mode between the coronal conduction and the prominence radiation regimes, the boundary wavenumber
![]() can be roughly calculated by imposing
can be roughly calculated by imposing
![]() ,
that gives
,
that gives
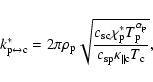 |
(22) |
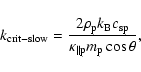 |
(23) |
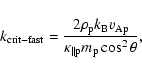 |
(24) |
| |
Figure 9: Same as Fig. 6 with the prominence optical thickness given by Prominence (1) (solid line), Prominence (2) (dotted line) and Prominence (3) (dashed line) conditions. |
| Open with DEXTER | |
In this section, we compute the solutions for different values of the equilibrium physical conditions. We only present the results for the fundamental kink modes since they are equivalent to those of sausage modes. Figures 6-8 display the damping time as function of kx for some selected values of the prominence temperature, the prominence density and the magnetic field, respectively.
For the internal slow mode, a decrease of the prominence temperature or the prominence density raises the position of the radiative plateau and increases its length. The opposite behaviour is seen when the density or the temperature are increased. However, the value of the magnetic field does not influence the attenuation of this mode, such as expected for a slow wave.
Increasing the value of the prominence temperature causes a vertical displacement of
![]() of the fast mode in those regions in which prominence mechanisms dominate. The value of the prominence density has a smaller effect and its main influence is in changing the coupling point with the external slow mode, which moves to higher kx for greater values of the density. The magnetic field strength has a more complex effect on
of the fast mode in those regions in which prominence mechanisms dominate. The value of the prominence density has a smaller effect and its main influence is in changing the coupling point with the external slow mode, which moves to higher kx for greater values of the density. The magnetic field strength has a more complex effect on
![]() and also modifies the coupling point.
and also modifies the coupling point.
Finally, the external slow mode is only slightly affected by a modification of the prominence physical parameters since it is mainly dominated by coronal conditions, and the influence of the magnetic field is very small due to the slow-like magnetoacoustic character of this solution.
The optically thin radiation assumption is a reasonable approximation in a plasma with coronal conditions but prominence plasmas often are optically thick. In this section we compare the results obtained considering different optical thicknesses for the prominence plasma (see Fig. 9 for the fundamental kink modes). The results corresponding to the slow sausage mode have not been plotted since they are equivalent to those obtained for slow kink mode; those for the fundamental fast sausage mode, however, are displayed in Fig. 10.
The variation of the prominence optical thickness modifies the prominence conduction-prominence radiation critical wavenumber,
![]() (see analytical approximation of Eq. (21)). For the internal slow mode, an increase in the optical thickness raises the position of the radiative plateau and shifts it to smaller wavenumbers. This fact causes an a priori surprising result in the observed wavelength range, since
(see analytical approximation of Eq. (21)). For the internal slow mode, an increase in the optical thickness raises the position of the radiative plateau and shifts it to smaller wavenumbers. This fact causes an a priori surprising result in the observed wavelength range, since
![]() has a smaller value for optically thick radiation, Prominence (3), than for optically thin radiation, Prominence (1). Regarding fast modes, the damping time increases when the optical thickness is increased, but only in the region in which prominence radiation dominates. The value of
has a smaller value for optically thick radiation, Prominence (3), than for optically thin radiation, Prominence (1). Regarding fast modes, the damping time increases when the optical thickness is increased, but only in the region in which prominence radiation dominates. The value of
![]() inside the observed wavelength range is partially affected and raises an order of magnitude for Prominence (3) conditions in comparison with the results for Prominence (1) conditions. Finally, the damping time of the external slow mode is not affected by the prominence optical thickness since it is entirely dominated by the corona, as it has been noticed in Sect. 4.1.
inside the observed wavelength range is partially affected and raises an order of magnitude for Prominence (3) conditions in comparison with the results for Prominence (1) conditions. Finally, the damping time of the external slow mode is not affected by the prominence optical thickness since it is entirely dominated by the corona, as it has been noticed in Sect. 4.1.
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{7633f10.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg126.gif) |
Figure 10: Same as Fig. 9 for the fundamental fast sausage mode. |
| Open with DEXTER | |
| |
Figure 11: Same as Fig. 6 with the heating scenario given by a=b=0 (solid line); a=1, b=0 (dotted line); a=b=1 (dashed line); a=b=7/6 (dot-dashed line); a=1/2, b=-1/2 (three dot-dashed line). |
| Open with DEXTER | |
Now, we compute the damping time for the five possible heating scenarios. For simplicity, we only consider the fundamental kink modes (Fig. 11). Carbonell et al. (2004) showed that in a plasma with prominence conditions the different heating scenarios have no significant influence on the damping time. Nevertheless, in coronal conditions wave instabilities can appear depending on the heating mechanism. In our results, we see that the heating scenario affects the value of
![]() only in the ranges of kx in which radiation is the dominant damping mechanism. The heating scenario has a negligible effect when prominence radiation dominates, since
only in the ranges of kx in which radiation is the dominant damping mechanism. The heating scenario has a negligible effect when prominence radiation dominates, since
![]() is only slightly modified. On the contrary, wave instabilities appear in those regions in which coronal radiation dominates. Thermal destabilisation occurs when the imaginary part of the frequency becomes negative, so oscillations are not attenuated but amplified in time. Instabilities only occur in the fundamental fast kink and the external slow modes for very small values of kx, outside the observed wavelength range.
is only slightly modified. On the contrary, wave instabilities appear in those regions in which coronal radiation dominates. Thermal destabilisation occurs when the imaginary part of the frequency becomes negative, so oscillations are not attenuated but amplified in time. Instabilities only occur in the fundamental fast kink and the external slow modes for very small values of kx, outside the observed wavelength range.
In order to assess the effects arising from the presence of two different media in the equilibrium, a comparison between the previous results and those corresponding to a single medium is suitable. So, we consider a simpler equilibrium made of an isolated prominence slab with the magnetic field parallel to its axis. The external medium is not taken into account. Magnetoacoustic non-adiabatic perturbations are governed by Eq. (13), and rigid boundary conditions for vz are imposed at the edges of the prominence slab,
Next, considering only the fundamental kink modes for simplicity, we compute the period and the damping time and compare with those obtained when the surrounding corona is taken into account (Fig. 12). We see that there is a perfect agreement between both results in the case of the internal slow mode, whereas the solutions for the fast mode only coincide for intermediate and large wavenumbers, and show an absolutely different behaviour in the observed wavelength range and for smaller wavenumbers. Additionally, one must bear in mind that the external slow mode exists because of the presence of the coronal medium, hence it is not supported by an isolated slab.
In Paper I we proved that the internal slow mode is essentially confined within the prominence slab and that the effect of the corona on its oscillatory period can be neglected. Now, we see that the corona has no influence on the damping time either. On the other hand, the confinement of the fast mode is poor for small wavenumbers, the isolated slab approximation not being valid. As it has been noted in Sect. 4.1, the corona has an essential effect on the attenuation of the fast mode in the observed wavelength range.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{7633f12.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg134.gif) |
Figure 12: Comparison between the solutions for a prominence plus corona system and for an isolated slab with prominence conditions. The upper panels correspond to the fundamental internal slow kink mode and the lower panels to the fundamental fast kink mode. The solid lines are the solutions for a prominence plus corona equilibrium whereas the dotted lines with diamonds represent the solutions for an isolated slab. Prominence (1) parameters and a=b=0 have been used in the computations. |
| Open with DEXTER | |
Since magnetic field lines are orientated along fibrils, our model can also be applied to study the oscillatory modes supported by a single prominence fibril. In order to perform this investigation, we reduce the slab half-width, ![]() ,
to a value according to the typical observed size of filament threads, which is between 0.2 to 0.6 arcsec (Lin et al. 2005). Since these values are close to the resolution limit of present-day telescopes, it is likely that thinner threads could exist. So, assuming now
,
to a value according to the typical observed size of filament threads, which is between 0.2 to 0.6 arcsec (Lin et al. 2005). Since these values are close to the resolution limit of present-day telescopes, it is likely that thinner threads could exist. So, assuming now
![]() km, we compute P,
km, we compute P,
![]() and
and
![]() for the fundamental kink modes and compare these results with those obtained for
for the fundamental kink modes and compare these results with those obtained for
![]() km.
km.
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{7633f13.eps}\end{figure}](/articles/aa/full/2007/33/aa7633-07/Timg135.gif) |
Figure 13:
Period ( left), damping time ( centre) and ratio of the damping time to the period ( right) versus kx for the fundamental kink oscillatory modes: internal slow ( top panels), fast ( mid panels) and external slow ( bottom panels). Solid lines correspond to
|
| Open with DEXTER | |
Such as displayed in Fig. 13, both internal and external slow modes are not affected by the width of the prominence slab since they are essentially polarised along the x-direction and so they are not influenced by the equilibrium structure in the z-direction. Nevertheless, the location of the cut-off of the external slow mode and the coupling point with the fast mode are shifted to larger values of kx when the slab width is reduced. On the other hand, the fast mode, which is responsible for transverse motions, is highly influenced by the value of ![]() .
The
.
The
![]() curve for the fast mode is displaced to larger values of kx when smaller
curve for the fast mode is displaced to larger values of kx when smaller ![]() is considered. This causes that higher values of
is considered. This causes that higher values of
![]() are obtained in the observed wavelength range. Hence, these results suggest that local prominence oscillations related with transverse fast modes supported by a single fibril could be less affected by non-adiabatic mechanisms than global fast modes supported by the whole or large regions of the prominence. However, according to the results pointed out by Díaz et al. (2005) and Díaz & Roberts (2006), large groups of fibrils tend to oscillate together since the separation between individual fibrils is of the order of their thickness. In a very rough approximation one can consider that a thick prominence slab could represent many near threads which oscillate together and that the larger the slab width is, the more threads fit inside it. So, our results show that the slab size (i.e. the number of threads which oscillate together in this rough approximation) has important repercussions on the damping time of collective transverse oscillations, hence the oscillations could be more attenuated when the number of oscillating threads is larger. This affirmation should be verified by investigating the damping in multifibril models.
are obtained in the observed wavelength range. Hence, these results suggest that local prominence oscillations related with transverse fast modes supported by a single fibril could be less affected by non-adiabatic mechanisms than global fast modes supported by the whole or large regions of the prominence. However, according to the results pointed out by Díaz et al. (2005) and Díaz & Roberts (2006), large groups of fibrils tend to oscillate together since the separation between individual fibrils is of the order of their thickness. In a very rough approximation one can consider that a thick prominence slab could represent many near threads which oscillate together and that the larger the slab width is, the more threads fit inside it. So, our results show that the slab size (i.e. the number of threads which oscillate together in this rough approximation) has important repercussions on the damping time of collective transverse oscillations, hence the oscillations could be more attenuated when the number of oscillating threads is larger. This affirmation should be verified by investigating the damping in multifibril models.
In this paper, we have studied the time damping of magnetoacoustic waves in a prominence-corona system considering non-adiabatic terms (thermal conduction, radiation losses and heating) in the energy equation. Small amplitude perturbations have been assumed, so the linearised non-adiabatic MHD equations have been considered and the dispersion relation for the slow and fast magnetoacoustic modes has been found assuming evanescent-like perturbations in the coronal medium. Finally, the damping time of the fundamental oscillatory modes has been computed and the relevance of each non-adiabatic mechanism on the attenuation has been assessed. Next, we summarise the main conclusions of this work:
Acknowledgements
The authors acknowledge the financial support received from the Spanish Ministerio de Ciencia y Tecnología under grant AYA2006-07637. R. Soler thanks the Conselleria d'Economia, Hisenda i Innovació for a fellowship.
Combining Eqs. (7)-(12), one can obtain the expressions for the perturbed quantities as functions of vz and its derivative
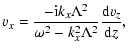 |
(A.1) | ||
| (A.2) | |||
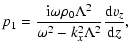 |
(A.3) | ||
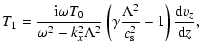 |
(A.4) | ||
| (A.5) | |||
| (A.6) |
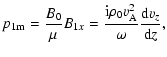 |
(A.7) | ||
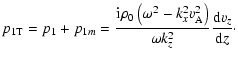 |
(A.8) |
Internal slow modes are almost non-dispersive and for adiabatic perturbations a good approximation for the frequency is
![]() ,
,
![]() being the prominence sound speed. In the non-adiabatic case, we can consider the equivalence between
being the prominence sound speed. In the non-adiabatic case, we can consider the equivalence between
![]() and
and ![]() to propose
to propose
![]() as an approximate dispersion relation. Taking into account Eq. (15) for
as an approximate dispersion relation. Taking into account Eq. (15) for ![]() ,
the approximate dispersion relation for the internal slow modes is a third order polynomial in
,
the approximate dispersion relation for the internal slow modes is a third order polynomial in ![]() ,
,
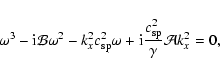 |
(B.1) |
We here deduce a polynomial dispersion relation for the magnetoacoustic normal modes of a slab with a longitudinal magnetic field. Taking Eqs. (27) and (28) as the dispersion relations for the kink and sausage modes, respectively, one can replace kz and ![]() with their correspondent expressions (Eqs. (14)-(15)), and the following fifth order polynomial equation is found,
with their correspondent expressions (Eqs. (14)-(15)), and the following fifth order polynomial equation is found,