A&A 469, 861-872 (2007)
DOI: 10.1051/0004-6361:20077407
R. Barrena1 - W. Boschin2,3 - M. Girardi3,4 - M. Spolaor3,5
1 - Instituto de Astrofísica de Canarias, C/Vía
Láctea s/n, 38200 La Laguna, Tenerife, Spain
2 -
Fundación Galileo Galilei - INAF, C/Alvarez de Abreu 70,
38700 Santa Cruz de La Palma, Canary Islands, Spain
3 -
Dipartimento di Astronomia of the Università degli Studi di
Trieste, via Tiepolo 11, 34131 Trieste, Italy
4 -
INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11,
34131 Trieste, Italy
5 -
Centre for Astrophysics & Supercomputing, Swinburne University,
Hawthorn, VIC 3122, Australia
Received 5 March 2007 / Accepted 19 April 2007
Abstract
Aims. We present the results of a new spectroscopic and photometric survey of the hot, binary X-ray cluster A115 at z=0.193, containing a radio relic.
Methods. Our analysis is based on new spectroscopic data obtained at the Telescopio Nazionale Galileo for 115 galaxies and on new photometric data obtained at the Isaac Newton Telescope in a large field. We combine galaxy velocity and position information to select 85 galaxies recognized as cluster members, determine global dynamical properties and detect substructures.
Results. We find that A115 appears as a well isolated peak in the redshift space, with a global line-of-sight (LOS) velocity dispersion
![]() km s-1. Our analysis confirms the presence of two structures of cluster-type well recognizable in the plane of the sky and shows that they differ of
km s-1. Our analysis confirms the presence of two structures of cluster-type well recognizable in the plane of the sky and shows that they differ of ![]() 2000 km s
2000 km s![]() in the LOS velocity. The northern, high velocity subcluster (A115N) is likely centred on the second brightest cluster galaxy (BCM-A, coincident with radio source 3C28) and the northern X-ray peak. The southern, low velocity subcluster (A115S) is likely centred on the first brightest cluster galaxy (BCM-B) and the southern X-ray peak. We estimate that A115S is slightly dynamically more important than A115N having
in the LOS velocity. The northern, high velocity subcluster (A115N) is likely centred on the second brightest cluster galaxy (BCM-A, coincident with radio source 3C28) and the northern X-ray peak. The southern, low velocity subcluster (A115S) is likely centred on the first brightest cluster galaxy (BCM-B) and the southern X-ray peak. We estimate that A115S is slightly dynamically more important than A115N having
![]() km s
km s![]() vs.
vs.
![]() km s-1. Moreover, we find evidence for two small groups at low velocities. We estimate a global cluster virial mass of 2.2-3.5
km s-1. Moreover, we find evidence for two small groups at low velocities. We estimate a global cluster virial mass of 2.2-3.5
![]() .
.
Conclusions. Our results agree with a pre-merging scenario where A115N and A115S are colliding with a LOS impact velocity
![]() km s-1. The most likely solution to the two-body problem suggests that the merging axis lies at
km s-1. The most likely solution to the two-body problem suggests that the merging axis lies at ![]() 20 degrees from the plane of the sky and that the cores will cross after
20 degrees from the plane of the sky and that the cores will cross after ![]() 0.1 Gyr. The radio relic with its largest dimension perpendicular to the merging axis is likely connected to this merger.
0.1 Gyr. The radio relic with its largest dimension perpendicular to the merging axis is likely connected to this merger.
Key words: galaxies: clusters: general - galaxies: clusters: individual: Abell 115 - galaxies: distances and redshifts - cosmology: observations
The evolution of clusters of galaxies as seen in numerical simulations is characterized by the asymmetric accretion of mass clumps from surrounding filaments (e.g. Diaferio et al. 2001). Nearby clusters are characterized by a variety of morphologies, indicative of different dynamical properties, elongated distribution, traced by several galaxy clumps (e.g., Barrena et al. 2002; Boschin et al. 2006; Sauvageot et al. 2005; Yuan et al. 2005). The presence of substructure is indicative of a cluster in an early phase of the process of dynamical relaxation or of secondary infall of clumps into already virialized clusters (see Girardi & Biviano 2002, for a review).
An interesting aspect of these investigations is the possible
connection of cluster mergers with the presence of extended, diffuse
radio sources. These sources are large (up to ![]() 1
h70-1 Mpc), amorphous
cluster sources of uncertain origin and generally steep radio spectra
(Hanisch 1982; see also and Giovannini & Feretti 2002,
for a review). They are classified as halos, if they are
located in the cluster centre, or relics, if they appear in the
peripheral regions of the cluster. Halos and relics are rare sources
that appear to be associated with very rich clusters that have
undergone recent mergers and thus it has been suggested by various
authors that cluster halos/relics are related to recent merger
activity (e.g., Tribble 1993; Burns et al. 1994;
Feretti 1999).
1
h70-1 Mpc), amorphous
cluster sources of uncertain origin and generally steep radio spectra
(Hanisch 1982; see also and Giovannini & Feretti 2002,
for a review). They are classified as halos, if they are
located in the cluster centre, or relics, if they appear in the
peripheral regions of the cluster. Halos and relics are rare sources
that appear to be associated with very rich clusters that have
undergone recent mergers and thus it has been suggested by various
authors that cluster halos/relics are related to recent merger
activity (e.g., Tribble 1993; Burns et al. 1994;
Feretti 1999).
The synchrotron radio emission of halos and relics demonstrates the
existence of large scale cluster magnetic fields, of the order of
0.1-1 ![]() G, and of widespread relativistic particles of energy
density 10-14-10-13 erg cm-3. The difficulty in
explaining halos/relics arises from the combination of their large
size and the short synchrotron lifetime of relativistic electrons.
The expected diffusion velocity of the electron population is on the
order of the Alfvén speed (
G, and of widespread relativistic particles of energy
density 10-14-10-13 erg cm-3. The difficulty in
explaining halos/relics arises from the combination of their large
size and the short synchrotron lifetime of relativistic electrons.
The expected diffusion velocity of the electron population is on the
order of the Alfvén speed (![]() 100 km s-1) making it difficult for the
electrons to diffuse over a megaparsec-scale region within their
radiative lifetime. Therefore, one needs a mechanism by which the
relativistic electron population can be transported over large
distances in a short time, or a mechanism by which the local electron
population is reaccelerated and the local magnetic fields are
amplified over an extended region. The cluster-cluster merger can
potentially supply both mechanisms (e.g., Giovannini et al. 1993; Burns et al. 1994; Röttgering et al. 1994; see also Feretti et al. 2002; Sarazin
2002, for reviews). However, the question is still debated
since the diffuse radio sources are quite uncommon and only recently
we can study these phenomena on the basis of a sufficient statistics
(a few dozens of clusters up to
100 km s-1) making it difficult for the
electrons to diffuse over a megaparsec-scale region within their
radiative lifetime. Therefore, one needs a mechanism by which the
relativistic electron population can be transported over large
distances in a short time, or a mechanism by which the local electron
population is reaccelerated and the local magnetic fields are
amplified over an extended region. The cluster-cluster merger can
potentially supply both mechanisms (e.g., Giovannini et al. 1993; Burns et al. 1994; Röttgering et al. 1994; see also Feretti et al. 2002; Sarazin
2002, for reviews). However, the question is still debated
since the diffuse radio sources are quite uncommon and only recently
we can study these phenomena on the basis of a sufficient statistics
(a few dozens of clusters up to ![]() ,
e.g., Giovannini et al. 1999; see also Giovannini & Feretti 2002; Feretti
2005).
,
e.g., Giovannini et al. 1999; see also Giovannini & Feretti 2002; Feretti
2005).
Growing evidence of the connection between diffuse radio emission and cluster merging is based on X-ray data (e.g., Böhringer & Schuecker 2002; Buote 2002). Studies based on a large number of clusters have found a significant relation between the radio and the X-ray surface brightness (Govoni et al. 2001a,b) and between the presence of radio-halos/relics and irregular and bimodal X-ray surface brightness distribution (Schuecker et al. 2001). New unprecedented insights into merging processes in radio clusters are offered by Chandra and XMM-Newton observations (e.g., Markevitch & Vikhlinin 2001; Fujita et al. 2004).
Optical data are a powerful way to investigate the presence and the dynamics of cluster mergers (e.g., Girardi & Biviano 2002), too. The spatial and kinematical analysis of member galaxies allow us to detect and measure the amount of substructure, to identify and analyse possible pre-merging clumps or merger remnants. This optical information is really complementary to X-ray information since galaxies and ICM react on different time scales during a merger (see numerical simulations by Roettiger et al. 1997). Unfortunately, to date optical data is lacking or poorly exploited and sparse literature concerns some few individual clusters. In this context we have carried on an intensive program to study the clusters containing extended, diffuse radio emission (Boschin et al. 2004; Boschin et al. 2006; Girardi et al. 2006; Barrena et al. 2007). In particular, we have conducted a study of Abell 115 (hereafter A115) having an extended arc-shape relic (Feretti et al. 1984; Giovannini et al. 1987; Govoni et al. 2001b).
A115 is a rich cluster (Abell richness class = 3; Abell et al. 1989) known in the literature to be characterized by a
double X-ray peak (A115N and A115S; Forman et al. 1981) and
by the presence of a strong cooling flow in its northern component
(White et al. 1997). White et al. (1997) give the
following values for the X-ray luminosity and temperature:
![]() ,
,
![]() erg s-1 (in their cosmology) and
erg s-1 (in their cosmology) and
![]() ,
5.7 keV for the
northern and southern components, respectively. Slightly smaller
temperatures are also found in the literature:
,
5.7 keV for the
northern and southern components, respectively. Slightly smaller
temperatures are also found in the literature:
![]() and 5.2 keV for the northern
component, and
and 5.2 keV for the northern
component, and
![]() and 4.8 keV for the
southern component (from Shibata et al. 1999; and Gutierrez &
Krawczynski 2005, respectively). Both ASCA and Chandra data
show that the temperature of the ICM is highly nonuniform across the
cluster suggesting that the merger is well underway, but not
disturbing the cool subcluster cores (Shibata et al. 1999;
Gutierrez & Krawczynski 2005). From the optical point of
view, Beers et al. (1983) mapped the galaxy distribution
finding three major clumps of galaxies (A, B, and C in Fig. 4a of
their paper). Northern and southern clumps A and B correspond to the
peaks of the X-ray surface brightness distribution. However, no
X-ray emission has been found associated with the third eastern
clump.
and 4.8 keV for the
southern component (from Shibata et al. 1999; and Gutierrez &
Krawczynski 2005, respectively). Both ASCA and Chandra data
show that the temperature of the ICM is highly nonuniform across the
cluster suggesting that the merger is well underway, but not
disturbing the cool subcluster cores (Shibata et al. 1999;
Gutierrez & Krawczynski 2005). From the optical point of
view, Beers et al. (1983) mapped the galaxy distribution
finding three major clumps of galaxies (A, B, and C in Fig. 4a of
their paper). Northern and southern clumps A and B correspond to the
peaks of the X-ray surface brightness distribution. However, no
X-ray emission has been found associated with the third eastern
clump.
The northern subcluster contains the very strong radio galaxy 3C28
(Riley & Pooley 1975; Feretti et al. 1984; Giovannini
et al. 1987). Its host galaxy is the brightest galaxy of the
northern subcluster and is classified as "elliptical'' by Schombert
1987. The strong X-ray and radio emissions of this cluster
member seem to be explained by the presence of a large amount of hot
gas which is likely to be accreting onto the galaxy.
This scenario agrees with the observation in the
spectrum of this galaxy of the H![]() -line and other emission
lines, likely tracing a cooling flow system (Crawford et al. 1999).
-line and other emission
lines, likely tracing a cooling flow system (Crawford et al. 1999).
The diffuse radio source belongs to A115N, and extends from this sub-cluster to the periphery. According to its non-central location and its elongated structure, it is classified as a cluster relic. However, elongated relics are generally at the cluster periphery, and with the largest dimension roughly perpendicular to the cluster radial orientation. So this source is quite unusual although several considerations confirm that it should be a cluster relic (Govoni et al. 2001b).
To date few spectroscopic data are reported in the literature. Beers et al. (1983) measured the redshift for 19 cluster members (see also Zabludoff et al. 1990 for a later re-reduction with a new template). In December 2003 we obtained spectra of 115 galaxies in the cluster region, with the purpose of constraining its dynamical status.
The plan of this paper is the following. In Sect. 2 we describe our new photometric and spectroscopic observations. In Sect. 3 we provide our results about cluster membership, global properties, and substructure. In Sect. 4 we draw our conclusion about cluster structure and estimate cluster mass. In Sect. 5 we discuss our results and posit a plausible scenario for the dynamical status of A115. We summarize our results in Sect. 6.
Throughout this paper, we use
H0=70 h70 km s-1 Mpc-1 in a
flat cosmology with
![]() and
and
![]() .
In the
adopted cosmology, 1
.
In the
adopted cosmology, 1![]() corresponds to
corresponds to ![]() 192
h70-1 kpc
192
h70-1 kpc![]() at the
cluster redshift.
at the
cluster redshift.
Multi-object spectroscopic observations of A115 were carried out at
the TNG telescope in December 2003 during the program of proposal
AOT8/CAT-G6. We used DOLORES/MOS with the LR-B Grism 1, yielding a
dispersion of 187 Å/mm, and the Loral CCD of
![]() pixels
(pixel size of 15
pixels
(pixel size of 15 ![]() m). This combination of grating and detector
results in dispersions of 2.8 Å/pix. We have taken five MOS masks
for a total of 152 slits. We acquired three exposures of 1800 s for
each masks. Wavelength calibration was performed using helium-argon
lamps. Reduction of spectroscopic data was carried out with IRAF
m). This combination of grating and detector
results in dispersions of 2.8 Å/pix. We have taken five MOS masks
for a total of 152 slits. We acquired three exposures of 1800 s for
each masks. Wavelength calibration was performed using helium-argon
lamps. Reduction of spectroscopic data was carried out with IRAF![]() package.
package.
Radial velocities were determined using the cross-correlation
technique (Tonry & Davis 1979) implemented in the RVSAO
package (developed at the Smithsonian Astrophysical Observatory
Telescope Data Center). Each spectrum was correlated against six
templates for a variety of galaxy spectral types: E, S0, Sa, Sb, Sc,
Ir (Kennicutt 1992). The template producing the highest value
of ![]() ,
i.e., the parameter given by RVSAO and related to the
signal-to-noise of the correlation peak, was chosen. Moreover, all
spectra and their best correlation functions were examined visually to
verify the redshift determination. In some cases (IDs 85, 112 and 115,
see Table 1) we took the EMSAO redshift as a reliable
estimate of the redshift.
,
i.e., the parameter given by RVSAO and related to the
signal-to-noise of the correlation peak, was chosen. Moreover, all
spectra and their best correlation functions were examined visually to
verify the redshift determination. In some cases (IDs 85, 112 and 115,
see Table 1) we took the EMSAO redshift as a reliable
estimate of the redshift.
For eleven galaxies we obtained two redshift determinations, which are
of similar quality. This allow us to obtain a more rigorous estimate
for the redshift errors since the nominal errors as given by the
cross-correlation are known to be smaller than the true errors (e.g.,
Malumuth et al. 1992; Bardelli et al. 1994; Ellingson
& Yee 1994). We fit the first determination vs. the second
one by using a straight line and considering errors in both
coordinates (e.g., Press et al. 1992). The fitted line agrees
with the one to one relation, but, when using the nominal
cross-correlation errors, the small value of ![]() -probability
indicates a poor fit, suggesting the errors are underestimated. Only
when nominal errors are multiplied by a
-probability
indicates a poor fit, suggesting the errors are underestimated. Only
when nominal errors are multiplied by a ![]() 1.3 factor the observed
scatter can be explained. Therefore, hereafter we assume that true
errors are larger than nominal cross-correlation errors by a factor 1.3. For the eleven galaxies we used the average of the two redshift
determinations and the corresponding error.
1.3 factor the observed
scatter can be explained. Therefore, hereafter we assume that true
errors are larger than nominal cross-correlation errors by a factor 1.3. For the eleven galaxies we used the average of the two redshift
determinations and the corresponding error.
Our spectroscopic survey consists of 115 galaxies taken in a
field of ![]()
![]() .
.
We also determined the equivalent widths (EW hereafter) of the
absorption line H![]() and the emission line [OII], in order to
classify post-starburst and starburst galaxies. We estimated the
minimum measurable EW of each spectrum as the width of a line spanning 2.8 Å (our dispersion) in wavelength, with an intensity three times
the rms noise in the adjacent continuum. This estimation yields upper
measurable limits of
and the emission line [OII], in order to
classify post-starburst and starburst galaxies. We estimated the
minimum measurable EW of each spectrum as the width of a line spanning 2.8 Å (our dispersion) in wavelength, with an intensity three times
the rms noise in the adjacent continuum. This estimation yields upper
measurable limits of ![]() 4.5 Å in EW.
4.5 Å in EW.
We use a conservative approach leading to a sparse spectral
classification (![]() 50% of the sample, see Table 1). We
follow the classification by Dressler et al. (1999; see also
Poggianti et al. 1999). We define "e''-type galaxies those
showing active star formation as indicated by the presence of an [OII] and, in particular, "e(b)'' galaxies when the equivalent width of
EW([OII]) is
50% of the sample, see Table 1). We
follow the classification by Dressler et al. (1999; see also
Poggianti et al. 1999). We define "e''-type galaxies those
showing active star formation as indicated by the presence of an [OII] and, in particular, "e(b)'' galaxies when the equivalent width of
EW([OII]) is ![]() -40 Å (likely starburst galaxies);
"e(a)''-type galaxies those having EW(H
-40 Å (likely starburst galaxies);
"e(a)''-type galaxies those having EW(H
![]() Å;
"e(c)''-type galaxies those having moderate emission lines and
EW(H
Å;
"e(c)''-type galaxies those having moderate emission lines and
EW(H![]() Å (likely spiral galaxies). We define "k+a''
and "a+k''-type galaxies those having
Å (likely spiral galaxies). We define "k+a''
and "a+k''-type galaxies those having
![]() H
H
![]() Å and EW(H
Å and EW(H![]() Å, respectively, and no emission lines
(the so called "post-starbust''). Moreover, out of galaxies having
the cross-correlation coefficient
Å, respectively, and no emission lines
(the so called "post-starbust''). Moreover, out of galaxies having
the cross-correlation coefficient
![]() -
corresponding to
-
corresponding to
![]() as obtained using A773 data (Barrena
et al. 2007) - we define "k''-type galaxies those having
EW(H
as obtained using A773 data (Barrena
et al. 2007) - we define "k''-type galaxies those having
EW(H![]() Å and no emission lines (likely passive
galaxies). We classify 62 galaxies finding 38 "passive'' galaxies, 24 "active'' galaxies (i.e., 14 "k+a''/"a+k'' and 10 "e'' galaxies).
Å and no emission lines (likely passive
galaxies). We classify 62 galaxies finding 38 "passive'' galaxies, 24 "active'' galaxies (i.e., 14 "k+a''/"a+k'' and 10 "e'' galaxies).
The WFC consists of a 4 chip mosaic covering a
![]() field of view, with only a 20% marginally vignetted area. We took 10 exposures of 720 s in
field of view, with only a 20% marginally vignetted area. We took 10 exposures of 720 s in ![]() and 360 s in
and 360 s in ![]() Harris
filters (a total of 7200 s and 3600 s in each band) developing a
dithering pattern of ten positions. This observing mode allowed us to
build a master "supersky'' image that was used to correct our images
for vignetting and fringing patterns (Gullixson 1992). In
addition, the dithering helped us to clean cosmic rays and avoid gaps
between CCD chips. The complete reduction process (including flat
fielding, bias subtraction and bad-columns elimination) yielded a
final co-added image where the variation of the sky was lower than 0.4% in the whole frame. Another effect associated with the wide
field frames is the distortion of the field. In order to match the
photometry of several filters (in our case, only
Harris
filters (a total of 7200 s and 3600 s in each band) developing a
dithering pattern of ten positions. This observing mode allowed us to
build a master "supersky'' image that was used to correct our images
for vignetting and fringing patterns (Gullixson 1992). In
addition, the dithering helped us to clean cosmic rays and avoid gaps
between CCD chips. The complete reduction process (including flat
fielding, bias subtraction and bad-columns elimination) yielded a
final co-added image where the variation of the sky was lower than 0.4% in the whole frame. Another effect associated with the wide
field frames is the distortion of the field. In order to match the
photometry of several filters (in our case, only ![]() and
and ![]() ), a good astrometric solution taking into account these
distortions is needed. Using IRAF tasks and taking as reference the
USNO B1.0 catalog we were able to find an accurate astrometric
solution (
), a good astrometric solution taking into account these
distortions is needed. Using IRAF tasks and taking as reference the
USNO B1.0 catalog we were able to find an accurate astrometric
solution (
![]() )
across the full frame. The photometric
calibration was performed using Landolt standard fields achieved
during the observation.
)
across the full frame. The photometric
calibration was performed using Landolt standard fields achieved
during the observation.
We finally identified galaxies in our ![]() and
and ![]() images and measured their magnitudes with the SExtractor package
(Bertin & Arnouts 1996) and AUTOMAG procedure. In few cases,
(e.g., close companion galaxies, galaxies close to defects of CCD),
the standard SExtractor photometric procedure failed. In these cases
we computed magnitudes by hand. This method consists in assuming a
galaxy profile of a typical elliptical and scale it to the maximum
observed value. The integration of this profile give us an estimate of
the magnitude. The idea of this method is similar to the PSF
photometry, but assuming a galaxy profile, more appropriate in this
case.
images and measured their magnitudes with the SExtractor package
(Bertin & Arnouts 1996) and AUTOMAG procedure. In few cases,
(e.g., close companion galaxies, galaxies close to defects of CCD),
the standard SExtractor photometric procedure failed. In these cases
we computed magnitudes by hand. This method consists in assuming a
galaxy profile of a typical elliptical and scale it to the maximum
observed value. The integration of this profile give us an estimate of
the magnitude. The idea of this method is similar to the PSF
photometry, but assuming a galaxy profile, more appropriate in this
case.
We transformed all magnitudes into the Johnson-Cousins system (Johnson
& Morgan 1953; Cousins 1976). We used
![]() and
and
![]() ,
as derived from the Harris fil- ter characterization
(http://www.ast.cam.ac.uk/~wfcsur/technical/photom/colours/) and
assuming a
,
as derived from the Harris fil- ter characterization
(http://www.ast.cam.ac.uk/~wfcsur/technical/photom/colours/) and
assuming a
![]() for E-type galaxies (Poggianti
1997). As a final step, we estimated and corrected the
galactic extinction
for E-type galaxies (Poggianti
1997). As a final step, we estimated and corrected the
galactic extinction
![]() ,
,
![]() from Burstein &
Heiles (1982) reddening maps. We estimated that our
photometric sample is complete down to B=19.5 (21.0) and R=22.0(23.0) for S/N=5 (3) within the observed field.
from Burstein &
Heiles (1982) reddening maps. We estimated that our
photometric sample is complete down to B=19.5 (21.0) and R=22.0(23.0) for S/N=5 (3) within the observed field.
We assigned B and R magnitudes to the whole spectroscopic sample.
We measured redshift for galaxies down to
![]() mag, but we are
complete to 60% down to R=18 mag (within a region of
mag, but we are
complete to 60% down to R=18 mag (within a region of
![]() around
around
![]() ,
,
![]() (J2000.0)).
(J2000.0)).
Table 1 lists the velocity catalogue (see also
Figs. 1 and 2): identification number
of each galaxy, ID (Col. 1); ID code following the IAU nomenclature
(Col. 2); right ascension and declination, ![]() and
and ![]() (J2000, Col. 3); B and R magnitudes (Cols. 4 and 5, respectively);
heliocentric radial velocities,
(J2000, Col. 3); B and R magnitudes (Cols. 4 and 5, respectively);
heliocentric radial velocities,
![]() with errors,
with errors,
![]() (Cols. 6 and 7, respectively); spectral
classification SC (Col. 8).
(Cols. 6 and 7, respectively); spectral
classification SC (Col. 8).
To select cluster members out of the 115 galaxies having redshifts, we
follow the two steps procedure. First, we perform the
adaptive-kernel method (hereafter DEDICA, Pisani 1993 and
1996; see also Fadda et al. 1996; Girardi et al. 1996; Girardi & Mezzetti 2001). We find the
significant peaks in the velocity distribution >99% c.l. This
procedure detects A115 as a one-peak structure at
![]() populated by 88 galaxies considered as candidate cluster members (see
Fig. 3). Out of non-member galaxies, 12 and 15 are
foreground and background galaxies, respectively.
populated by 88 galaxies considered as candidate cluster members (see
Fig. 3). Out of non-member galaxies, 12 and 15 are
foreground and background galaxies, respectively.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7407fig3.eps}
\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg68.gif) |
Figure 3: Redshift galaxy distribution. The solid line histogram refers to galaxies assigned to the cluster according to the DEDICA reconstruction method. |
The projected clustercentric distance vs. the rest-frame velocity of
the 88 galaxies is shown in Fig. 4 where we also show
the three brightest galaxies in our sample, each of
them corresponding to a different galaxy density clumps as found by
Beers et al. (1983), i.e. IDs 54, 21(=3C28) and 104 (hereafter
BCM-B, BCM-A, and BCM-C) corresponding to B (A115S), A (A115N), and
C clumps, respectively. The position of BCM-B is very close to that
of the southern X-ray peak
(
![]() ,
,
![]() (J2000.0) as recovered from
X-ray Chandra data, see Fig. 2). BCM-A = 3C28 is
coincident with the northern X-ray peak and is very close to the
position of the X-ray centroid when masking the X-ray emission of
the point source (
(J2000.0) as recovered from
X-ray Chandra data, see Fig. 2). BCM-A = 3C28 is
coincident with the northern X-ray peak and is very close to the
position of the X-ray centroid when masking the X-ray emission of
the point source (
![]() ,
,
![]() (J2000.0) by Govoni et al. 2001b). We also consider the bright galaxy ID 81
(hereafter BCM-D, see Sect. 3.3) located in the middle of
the above three galaxies.
(J2000.0) by Govoni et al. 2001b). We also consider the bright galaxy ID 81
(hereafter BCM-D, see Sect. 3.3) located in the middle of
the above three galaxies.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7407fig4.eps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg74.gif) |
Figure 4:
Projected clustercentric distance vs. rest-frame velocity
|
All the galaxies assigned to the A115 peak are analysed in a second
step by applying the "shifting gapper'' technique by Fadda et
al. (1996), which uses the combination of position and
velocity information. This procedure rejects galaxies that are too
far in velocity from the main body of galaxies and within a fixed bin
that shifts along the distance from the cluster centre. The procedure
is iterated until the number of cluster members converges to a stable
value. Following Fadda et al. (1996) we use a gap of 1000 km s![]() - in the cluster rest-frame - and a bin of 0.6
h70-1 Mpc, or large
enough to include 15 galaxies. In the case of the A115 complex, which
is not an individual system, we fix alternatively BCM-A and -B as
cluster centres. Figure 4 shows the results. The very
high velocity galaxy (ID 91) is a clear interloper far more than
3000 km s
- in the cluster rest-frame - and a bin of 0.6
h70-1 Mpc, or large
enough to include 15 galaxies. In the case of the A115 complex, which
is not an individual system, we fix alternatively BCM-A and -B as
cluster centres. Figure 4 shows the results. The very
high velocity galaxy (ID 91) is a clear interloper far more than
3000 km s![]() from other galaxies. The other two high velocity galaxies
(IDs 96 and 100), that are close enough in 2D and far from the high
velocity BCM-A galaxy (see Fig. 1), are rejected in both
our analyses. The conclusion about the low velocity tail is less clear
also because few of these galaxies lie in the eastern region of the
cluster and might be associated to the C clump (or to the D clump, see
Sect. 3.3). We decide to define 85 likely cluster members
rejecting the three highest velocity galaxies (basic sample). In some
analyses we also consider an alternative sample of 80 galaxies -
Sample2 - also rejecting the low velocity galaxies indicated in
Fig. 4 (the crosses in the middle panel).
from other galaxies. The other two high velocity galaxies
(IDs 96 and 100), that are close enough in 2D and far from the high
velocity BCM-A galaxy (see Fig. 1), are rejected in both
our analyses. The conclusion about the low velocity tail is less clear
also because few of these galaxies lie in the eastern region of the
cluster and might be associated to the C clump (or to the D clump, see
Sect. 3.3). We decide to define 85 likely cluster members
rejecting the three highest velocity galaxies (basic sample). In some
analyses we also consider an alternative sample of 80 galaxies -
Sample2 - also rejecting the low velocity galaxies indicated in
Fig. 4 (the crosses in the middle panel).
By applying the bi-weight estimator to cluster members (Beers et al. 1990), we compute a mean cluster redshift of
![]() ,
i.e.
,
i.e.
![]() km s-1. We estimate the LOS velocity
dispersion,
km s-1. We estimate the LOS velocity
dispersion,
![]() ,
by using the bi-weight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
,
by using the bi-weight estimator and
applying the cosmological correction and the standard correction for
velocity errors (Danese et al. 1980). We obtain
![]() km s-1, where errors are estimated through a
bootstrap technique. Consistent results are found for Sample2 (see
Table 2).
km s-1, where errors are estimated through a
bootstrap technique. Consistent results are found for Sample2 (see
Table 2).
Hereafter, for practical reasons, we consider as centre of the whole
A115 complex the position of the bi-weight centre obtained using
bi-weight mean estimators for RA and Dec separately
(
![]() ,
,
![]() (J2000.0)).
(J2000.0)).
We analyse the velocity distribution to look for possible deviations from Gaussianity that could provide important signatures of complex dynamics. For the following tests the null hypothesis is that the velocity distribution is a single Gaussian.
We estimate three shape estimators, i.e. the kurtosis, the skewness, and the scaled tail index (see, e.g., Beers et al. 1991). The value of the skewness (-0.462) shows evidence that the velocity distribution differs from a Gaussian at the 95-99% c.l. (see Table 2 of Bird & Beers 1993). Moreover, the W-test (Shapiro & Wilk 1965) marginally rejects the null hypothesis of a Gaussian parent distribution at the 92% c.l.
Then we investigate the presence of gaps in the distribution. A weighted gap in the space of the ordered velocities is defined as the difference between two contiguous velocities, weighted by the location of these velocities with respect to the middle of the data. We obtain values for these gaps relative to their average size, precisely the midmean of the weighted-gap distribution. We look for normalized gaps larger than 2.25 since in random draws of a Gaussian distribution they arise at most in about 3% of the cases, independent of the sample size (Wainer & Schacht 1978; see also Beers et al. 1991). Two significant gaps in the ordered velocity dataset are detected individuating two groups in the low velocity tail of the velocity distribution, of eight and six galaxies (see WGAP1 and WGAP2 in Table 2 and Fig. 5).
We use the results of the gap analysis to determine the first guess when using the Kaye's mixture model (KMM) to find a possible group partition of the velocity distribution (as implemented by Ashman et al. 1994). The KMM algorithm fits an user-specified number of Gaussian distributions to a dataset and assesses the improvement of that fit over a single Gaussian. In addition, it provides the maximum-likelihood estimate of the unknown n-mode Gaussians and an assignment of objects into groups. We do not find any two- or three-groups partition which is a significant better descriptor of the velocity distribution with respect to a single Gaussian.
When applying the DEDICA method to the 2D distribution of A115 galaxy members we find three significant peaks. The position of the highest peak is close to the location of the BCM-B and of the southern peak of X-ray emission (XS in Fig.6). Another peak is close to the location of the BCM-A, of the northern peak of X-ray emission (XN) and of the X-ray centroid when masking the X-ray emission of the point source (X, Govoni et al. 2001b). When dividing the sample in bright and faint galaxies - using the median magnitude value R=18.32 - we find that the 2D distributions of the two samples are different at the 98.5% c.l. according to the two-dimensional Kolmogorov-Smirnov test (hereafter 2DKS-test; see Fasano & Franceschini 1987, as implemented by Press et al. 1992). In fact, the faint galaxies sample shows both peaks A and B, while the bright galaxies sample only shows the peak B.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{7407fig6.eps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg82.gif) |
Figure 6: Spatial distribution on the sky of spectroscopically confirmed cluster members and the relative isodensity contour map. The three brightest galaxies BCM-A -B, and -C corresponding to Beers et al. (1983) groups, a fourth bright galaxy (BCM-D) and the X-ray peaks are indicated by large squares, too. The plot is centred on the cluster centre defined as the bi-weight centre (see text). |
The existence of correlations between positions and velocities of cluster galaxies is a footprint of real substructures. Here we use different approaches to analyse the structure of A115 combining velocity and position information.
The cluster velocity field may be influenced by the presence of
internal substructures. To investigate the velocity field of the A115
complex we divide galaxies in a low and a high velocity samples by
using the median cluster velocity and check the difference between the
two distributions of galaxy positions. Figure 9 shows that
low and high velocity galaxies are segregated roughly in the E-W
direction. The two distributions are different at the 99.5% c.l.
according to the 2DKS-test. In order to estimate the direction of
the velocity gradient we perform a multiple linear regression fit to
the observed velocities with respect to the galaxy positions in the
plane of the sky (see also den Hartog & Katgert 1996; Girardi
et al. 1996). We find a position angle on the celestial sphere
of
![]() degrees (measured counter-clock-wise from
north), i.e. higher velocity galaxies lie in the western region of the
cluster (see Fig. 9). To assess the significance of this
velocity gradient we perform 1000 Monte Carlo simulations by randomly
shuffling the galaxy velocities and for each simulation we determine
the coefficient of multiple determination (RC2, see e.g., NAG
Fortran Workstation Handbook 1986). We define the
significance of the velocity gradient as the fraction of times in
which the RC2 of the simulated data is smaller than the observed
RC2. We find that the velocity gradient is marginally significant
at the 90% c.l. Similar results are obtained for the Sample2
(
degrees (measured counter-clock-wise from
north), i.e. higher velocity galaxies lie in the western region of the
cluster (see Fig. 9). To assess the significance of this
velocity gradient we perform 1000 Monte Carlo simulations by randomly
shuffling the galaxy velocities and for each simulation we determine
the coefficient of multiple determination (RC2, see e.g., NAG
Fortran Workstation Handbook 1986). We define the
significance of the velocity gradient as the fraction of times in
which the RC2 of the simulated data is smaller than the observed
RC2. We find that the velocity gradient is marginally significant
at the 90% c.l. Similar results are obtained for the Sample2
(
![]() degrees at the 91% c.l.).
degrees at the 91% c.l.).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{7407fig9.eps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg91.gif) |
Figure 9: Spatial distribution on the sky of 85 cluster members. Open and solid circles indicate low and high velocity galaxies, the cross the galaxy with median velocity. The larger the symbol, the smaller is the radial velocity. The solid and faint lines indicate the position angle of the cluster gradient and relative errors, respectively. The faint big squares indicate the 14 galaxies belonging to WGAP1 and WGAP2 (see Sect. 3.2). The plot is centred on the cluster centre. |
We combine galaxy velocity and position information to compute the
![]() -statistics devised by Dressler & Schectman (1988).
This test is sensitive to spatially compact subsystems that have
either an average velocity that differs from the cluster mean, or a
velocity dispersion that differs from the global one, or both. We
find
-statistics devised by Dressler & Schectman (1988).
This test is sensitive to spatially compact subsystems that have
either an average velocity that differs from the cluster mean, or a
velocity dispersion that differs from the global one, or both. We
find
![]() for the value of the parameter which gives the
cumulative deviation. This value is an indication of substructure,
significant at the 96% c.l., as assessed computing 1000 Monte Carlo
simulations, randomly shuffling the galaxy velocities.
Figure 10 shows the distribution on the sky of all galaxies,
each marked by a circle: the larger the circle, the larger the
deviation
for the value of the parameter which gives the
cumulative deviation. This value is an indication of substructure,
significant at the 96% c.l., as assessed computing 1000 Monte Carlo
simulations, randomly shuffling the galaxy velocities.
Figure 10 shows the distribution on the sky of all galaxies,
each marked by a circle: the larger the circle, the larger the
deviation ![]() of the local parameters from the global cluster
parameters, i.e. the higher the evidence for substructure. This
figure provides information on the positions of substructures: one in
the eastern region corresponding to the clump C and one in the
northern region corresponding to the clump A. Similar results
obtained for Sample2 (
of the local parameters from the global cluster
parameters, i.e. the higher the evidence for substructure. This
figure provides information on the positions of substructures: one in
the eastern region corresponding to the clump C and one in the
northern region corresponding to the clump A. Similar results
obtained for Sample2 (
![]() and a c.l. of 95%), but the
eastern substructure is no longer so obvious in the relative plot.
and a c.l. of 95%), but the
eastern substructure is no longer so obvious in the relative plot.
To obtain further information, we resort to the technique developed by
Biviano et al. (2002), who used the individual
![]() -values of the Dressler & Schectman method. The critical
point is to determine the value of
-values of the Dressler & Schectman method. The critical
point is to determine the value of ![]() that optimally indicates
galaxies belonging to substructure. To this aim we consider the
that optimally indicates
galaxies belonging to substructure. To this aim we consider the
![]() -values of all 1000 Monte Carlo simulations already used to
determine the significance of the substructure (see above). The
resulting distribution of
-values of all 1000 Monte Carlo simulations already used to
determine the significance of the substructure (see above). The
resulting distribution of ![]() is compared to the observed one
finding a difference of P>99.99% c.l. according to the KS-test.
The "simulated'' distribution is normalized to produce the observed
number of galaxies and compared to the observed distribution in
Fig. 11: the latter shows a tail at large values. The
tail with
is compared to the observed one
finding a difference of P>99.99% c.l. according to the KS-test.
The "simulated'' distribution is normalized to produce the observed
number of galaxies and compared to the observed distribution in
Fig. 11: the latter shows a tail at large values. The
tail with
![]() is populated by galaxies that presumably
are in substructures. For the selection of galaxies within
substructures we choose the value of
is populated by galaxies that presumably
are in substructures. For the selection of galaxies within
substructures we choose the value of
![]() ,
since the
galaxies with
,
since the
galaxies with
![]() are well separated in the sky
(see Fig. 10) and assign three and eleven galaxies to the
clumps C and A, respectively (hereafter DS-C and DS-A). The northern
structure is populated by high velocity galaxies, while the poor
statistics prevent us to obtain firm conclusions about the eastern
structure (see Table 2).
are well separated in the sky
(see Fig. 10) and assign three and eleven galaxies to the
clumps C and A, respectively (hereafter DS-C and DS-A). The northern
structure is populated by high velocity galaxies, while the poor
statistics prevent us to obtain firm conclusions about the eastern
structure (see Table 2).
The Gaussian model for the 2D galaxy distribution is poorly supported by theoretical and/or empirical arguments and, however, our galaxy catalogue is not complete down to a magnitude limit. However, since the 3D diagnostics is in general the most sensitive indicators of the presence of substructure (e.g., Pinkney et al. 1996), we apply the 3D version of the KMM software using simultaneously galaxy velocity and positions. We use the galaxy assignment given by Dressler-Schectman method to determine the first guess when fitting three groups. The algorithm fits a three-groups partition at the 97% c.l. according to the likelihood ratio test (hereafter KMM1, KMM2, KMM3 groups from low to high mean velocities). The results for the three groups are shown in Table 2 and Fig. 12. KMM1 group is sparse in the sky, but well distinct in velocity from the other two groups. Several of its galaxies were already detected by the weighted gap analysis as belonging to WGAP1 and WGAP2 (see Sect. 3.2). Moreover, KMM1 contains BCM-D. KMM2 and KMM3 groups are well distinct in the sky. KMM2 contains both BCM-B and BCM-C, while KMM3 contains BCM-A.
The spatial agreement between the two brightest cluster members (BCM-A and -B) and the peaks of X-ray emission as well as the high density of galaxies around BCM-A and -B prompts us to analyse the profiles of the mean velocity and the velocity dispersion of galaxy systems surrounding these two galaxies (see Figs. 13 and 14, respectively). This allows an independent analysis of the individual galaxy clumps. Although an increase in the velocity-dispersion profile in the cluster central regions might be due to dynamical friction and galaxy merging (e.g., Menci & Fusco-Femiano 1996; Girardi et al. 1998; Biviano & Katgert 2004), in the case of A115 it might be simply induced by the contamination of the galaxies of a secondary clump (e.g., Girardi et al. 1996; Girardi et al. 2005). The latter hypothesis can be investigated by looking at the behaviour of the mean velocity profile.
Since from the above sections we know the presence of one or likely a few low velocity groups, we analyse the Sample2 to avoid, at least partially, the possible contamination. We also consider the results obtained rejecting all galaxies belonging to low velocity WGAP1 and WGAP2. Figures 13 and 14 show velocity-dispersion and mean-velocity profiles, as well as regions not likely to be contaminated by other galaxy systems and thus reliable for kinematical analysis. Detailed results of this analysis are included in Table 2 where the "uncontaminated'' galaxy systems are named as CORE-A and CORE-B.
Figure 13 shows how the integral velocity-dispersion
slightly increases with the distance from the BCM-A. Simultaneously,
the mean velocity shows a continuous decline from high values ![]() 59 000 km s
59 000 km s![]() suggesting a strong contamination of galaxies from
structures connected with BCM-B, -C and -D, all having lower mean
velocities. In a conservative view we consider the likely
uncontaminated region within 0.25
h70-1 Mpc, where we find
suggesting a strong contamination of galaxies from
structures connected with BCM-B, -C and -D, all having lower mean
velocities. In a conservative view we consider the likely
uncontaminated region within 0.25
h70-1 Mpc, where we find
![]() km s-1. Figure 14 shows an enough robust mean
velocity and a sharp increase of the integral velocity-dispersion
with the distance from the BCM-B up to a peak value
km s-1. Figure 14 shows an enough robust mean
velocity and a sharp increase of the integral velocity-dispersion
with the distance from the BCM-B up to a peak value ![]() 1450 km s
1450 km s![]() at
at ![]() 0.3
h70-1 Mpc. We interpret these features as the contamination of
the structures connected with BCM-A, -C and -D with higher and lower
mean velocities. Their combination does not affect the mean velocity
but strongly increases the velocity dispersion. In fact, the peak
value of the velocity dispersion goes down from 1450 to 1200 km s
0.3
h70-1 Mpc. We interpret these features as the contamination of
the structures connected with BCM-A, -C and -D with higher and lower
mean velocities. Their combination does not affect the mean velocity
but strongly increases the velocity dispersion. In fact, the peak
value of the velocity dispersion goes down from 1450 to 1200 km s![]() when
rejecting low velocity galaxies of WGAP1 and WGAP2. We then consider
the likely uncontaminated region within 0.25
h70-1 Mpc, where we find
when
rejecting low velocity galaxies of WGAP1 and WGAP2. We then consider
the likely uncontaminated region within 0.25
h70-1 Mpc, where we find
![]() km s-1.
km s-1.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7407fig13.eps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg103.gif) |
Figure 13:
Kinematical profiles of the northern subcluster A115N obtained
assuming BCM-A as centre. The vertical line indicates the region
likely not contaminated from other galaxy clumps (see text). Top
panel: rest-frame velocity vs. projected distance from the
subcluster centre (BCM-A): crosses indicate the galaxies belonging to
WGAP1 and WGAP2. Differential (big circles) and integral (small
points) mean velocity and LOS velocity-dispersion profiles are shown
in middle and bottom panels, respectively. For the differential
profiles we plot the values for seven annuli from the centre of the
subcluster, each of 0.25
h70-1 Mpc. For the integral profiles, the mean and
dispersion at a given (projected) radius from the subcluster-centre
is estimated by considering all galaxies within that radius - the
first value computed on the five galaxies closest to the centre. The
error bands at the |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{7407fig14.eps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg104.gif) |
Figure 14:
The same as in Fig. 13, but referring to the southern
subcluster A115S centred around BCM-B. The dashed line in the bottom
panel gives the integral velocity dispersion profile when rejecting
the low velocity galaxies of WGAP1 and WGAP2. In the bottom panel,
the horizontal line represents the range of X-ray temperatures as
given in the literature for A115S (see Sect. 1)
transformed in
|
On the basis of the above section we conclude that A115 is formed by two subclusters well distinct in the sky and centred around BCM-A and -B, hereafter A115N and A115S, with the addition of several low velocity galaxies, above all in the eastern cluster region, likely organised in small groups (see Fig. 9 and the PA of the velocity gradient).
As for the low velocity groups we detect two 2D galaxy concentrations around the two bright, low velocity galaxies BCM-C and -D. Moreover, we find two possible groups in the low velocity tail of the velocity distribution (WGAP1 containing BCM-D and WGAP2). The Dressler-Schectman test detects a substructure around the BCM-C, too. The presence of a group around BCM-D finds some support in the faint X-ray emission shown there (see Gutierrez & Krawczynski 2005 and Fig. 2). That we find evidence of a few groups rather than of an individual massive cluster agrees with the absence of a third X-ray luminous peak.
As for A115N, we find comparable kinematical properties in the
analysis of DS-A and CORE-A, i.e.
![]() km s
km s![]() and
and
![]() km s-1. Instead KMM3 is
contaminated by the presence of low velocity galaxies, e.g. IDs 10
and 19 close to BCM-A. As for A115S, we find
km s-1. Instead KMM3 is
contaminated by the presence of low velocity galaxies, e.g. IDs 10
and 19 close to BCM-A. As for A115S, we find
![]() km s
km s![]() and
and
![]() km s
km s![]() (see KMM2 and
CORE-B). The velocity dispersion of the two subclusters are roughly
comparable to their average X-ray temperature as listed in the
literature and transformed in
(see KMM2 and
CORE-B). The velocity dispersion of the two subclusters are roughly
comparable to their average X-ray temperature as listed in the
literature and transformed in
![]() assuming the
density-energy equipartition between gas and galaxies, i.e.
assuming the
density-energy equipartition between gas and galaxies, i.e.
![]()
![]() (see Figs. 13 and 14). The two subclusters
differ by
(see Figs. 13 and 14). The two subclusters
differ by ![]() 2000 km s
2000 km s![]() in the LOS velocity, i.e. almost three times
more than what found by Beers et al. (1983) with only 19 cluster members. In agreement with Beers et al. (1983), we
find that A115S is dynamically somewhat more important than A115N,
while the contrary is found by X-ray data (Jones & Forman
1999; White et al. 1997; Gutierrez & Krawczynski
2005; but see Shibata et al. 1999). As already
suggested by Beers et al. (1983) the presence of 3C28 might
affects the X-ray results overestimating the X-ray luminosity and
the temperature of A115N.
in the LOS velocity, i.e. almost three times
more than what found by Beers et al. (1983) with only 19 cluster members. In agreement with Beers et al. (1983), we
find that A115S is dynamically somewhat more important than A115N,
while the contrary is found by X-ray data (Jones & Forman
1999; White et al. 1997; Gutierrez & Krawczynski
2005; but see Shibata et al. 1999). As already
suggested by Beers et al. (1983) the presence of 3C28 might
affects the X-ray results overestimating the X-ray luminosity and
the temperature of A115N.
Although A115 is likely in a phase of interaction (see the following
section), the two main galaxy subclusters are still well detectable
and roughly well coincident with the X-ray peaks. Thus we assume
that each subcluster is in dynamical equilibrium to compute virial
quantities. Hereafter we assume
![]() km s
km s![]() and 900-1000 km s
and 900-1000 km s![]() for A115N and A115S, respectively.
for A115N and A115S, respectively.
Following the prescriptions of Girardi & Mezzetti (2001), we
assume for the radius of the quasi-virialized region
![]() h70-1 Mpc
h70-1 Mpc![]() and
and
![]() h70-1 Mpc
h70-1 Mpc![]() for A115N and A115S, respectively - see their
eq. 1 after introducing the scaling with H(z) (see also Eq. (8) of
Carlberg et al. 1997 for R200). Therefore, our
spectroscopic catalogue samples most of the virialized region.
for A115N and A115S, respectively - see their
eq. 1 after introducing the scaling with H(z) (see also Eq. (8) of
Carlberg et al. 1997 for R200). Therefore, our
spectroscopic catalogue samples most of the virialized region.
One can compute the mass using the virial theorem (Limber & Mathews
1960; see also, e.g., Girardi et al. 1998) under the
assumption that mass follows galaxy distribution:
![]() ,
where
,
where
![]() is the standard virial mass,
is the standard virial mass,
![]() a projected
radius (equal two times the harmonic radius), and SPT is the surface
pressure term correction (The & White 1986). The value of
a projected
radius (equal two times the harmonic radius), and SPT is the surface
pressure term correction (The & White 1986). The value of
![]() depends on the size of the considered region, so that the
computed mass increases (but not linearly) with the increasing
considered region. Since the two subclusters are interacting and we
do not cover the whole virialized region we use an alternative
estimate which was shown be good when
depends on the size of the considered region, so that the
computed mass increases (but not linearly) with the increasing
considered region. Since the two subclusters are interacting and we
do not cover the whole virialized region we use an alternative
estimate which was shown be good when
![]() is computed within
is computed within
![]() (see Eq. (13) of Girardi et al. 1998). This
alternative estimate is based on the knowledge of the galaxy
distribution and, in particular, a galaxy King-like distribution with
parameters typical of nearby/medium-redshift clusters: a core radius
(see Eq. (13) of Girardi et al. 1998). This
alternative estimate is based on the knowledge of the galaxy
distribution and, in particular, a galaxy King-like distribution with
parameters typical of nearby/medium-redshift clusters: a core radius
![]() and a slope-parameter
and a slope-parameter
![]() ,
i.e. the volume galaxy density at large radii
as
,
i.e. the volume galaxy density at large radii
as
![]() (Girardi & Mezzetti
2001). For the whole virialized region we obtain
(Girardi & Mezzetti
2001). For the whole virialized region we obtain
![]() h70-1 Mpc
h70-1 Mpc![]() and
and
![]() h70-1 Mpc. As for the SPT
correction, we assume a 20% computed combining data on many clusters
one (e.g., Carlberg et al. 1997; Girardi et al. 1998).
This leads to virial masses
h70-1 Mpc. As for the SPT
correction, we assume a 20% computed combining data on many clusters
one (e.g., Carlberg et al. 1997; Girardi et al. 1998).
This leads to virial masses
![]()
![]() and
and
![]()
![]() for the two subclusters.
for the two subclusters.
To compare our results with the estimate recovered from a X-ray
surface brightness deprojection analysis (White et al. 1997)
we assume that each subcluster is described by a King-like mass
distribution (see above) or, alternatively, a NFW profile where the
mass-dependent concentration parameter is taken from Navarro et al. (1997) and rescaled by the factor 1+z (Bullock et al. 2001; Dolag et al. 2004). We obtain
![]()
![]() and
and
![]()
![]() .
The first
estimate is somewhat smaller and the second one is in agreement with
those found by White et al. (1997, see their Table 3 where
.
The first
estimate is somewhat smaller and the second one is in agreement with
those found by White et al. (1997, see their Table 3 where
![]()
![]() and
and
![]()
![]() in our cosmology).
in our cosmology).
As for the mass of the whole system, the contribution of the low
velocity groups is of minor importance since they likely have low
velocity dispersion and the virial mass scales with
![]() .
E.g., we estimate that
.
E.g., we estimate that ![]()
![]() for a
for a
![]() km s
km s![]() group (see WGAP1 in Table 2). Considering the
possible presence of, at most, two of these
group (see WGAP1 in Table 2). Considering the
possible presence of, at most, two of these
![]() km s
km s![]() groups, a reliable mass estimate of the whole system is then
M=2.2-3.5
groups, a reliable mass estimate of the whole system is then
M=2.2-3.5
![]() ,
in agreement with rich clusters reported in the
literature (e.g., Girardi et al. 1998; Girardi & Mezzetti
2001). A smaller mass estimate is given by Govoni et al.
(2001b;
,
in agreement with rich clusters reported in the
literature (e.g., Girardi et al. 1998; Girardi & Mezzetti
2001). A smaller mass estimate is given by Govoni et al.
(2001b;
![]()
![]() centred on the
X-ray centroid in A115N), but notice that it refers to a smaller
cluster region, i.e. likely excluding a large part of A115S.
centred on the
X-ray centroid in A115N), but notice that it refers to a smaller
cluster region, i.e. likely excluding a large part of A115S.
Since A115N and A115S are well detectable and optical and X-ray data indicate a very similar location we are likely looking at the cluster prior to merging. However, A115N and A115S subclusters are already starting to interact, as suggested by several pieces of evidence: the slight displacement between peaks of gas distribution and of galaxy distribution (see our Fig. 8); the presence of an hot region likely due to the interaction (Shibata et al. 1999; Gutierrez & Krawczynski 2005). Very noticeably, the largest dimension of the radio relic is somewhat perpendicular to the axis connecting A115N and A115S in agreement with being originated by shock waves connected to the ongoing merger (e.g., Ensslin & Brüggen 2002).
When the merging scenario is assumed to explain the presence of the
hot region located between A115N and A115S, a relative colliding
velocity is necessary to heat up the ICM temperature kT from ![]() 4 to
4 to ![]() 9 keV (see Gutierrez & Krawczynski
2005). Assuming that the two subclusters are to cause a
head-on collision and that their kinetic energies are completely
converted to thermal energy, the necessary value of the colliding
velocity is
9 keV (see Gutierrez & Krawczynski
2005). Assuming that the two subclusters are to cause a
head-on collision and that their kinetic energies are completely
converted to thermal energy, the necessary value of the colliding
velocity is
![]() (see Shibata et al. 1999). We find
(see Shibata et al. 1999). We find
![]() km s
km s![]() in good agreement with the observed relative LOS velocity in
the rest frame
in good agreement with the observed relative LOS velocity in
the rest frame
![]() km s
km s![]() as recovered from CORE-A
and CORE-B in the cluster rest frame, i.e. (
as recovered from CORE-A
and CORE-B in the cluster rest frame, i.e. (
![]() ).
).
Here we investigate the relative dynamics of A115N and A115S using
different analytic approaches which are based on an energy integral
formalism in the framework of locally flat spacetime and Newtonian
gravity (e.g., Beers et al. 1982). The values of the relevant
observable quantities for the two-clumps system are: the relative LOS
velocity in the rest frame,
![]() km s
km s![]() (as recovered
from CORE-A and CORE-B); the projected linear distance between the
two clumps, D=0.89
h70-1 Mpc
(as recovered
from CORE-A and CORE-B); the projected linear distance between the
two clumps, D=0.89
h70-1 Mpc![]() (as recovered from BCM-A and -B cluster rest
frame); the mass of the system obtained by adding the masses of the
two subclusters each within its virial radius,
(as recovered from BCM-A and -B cluster rest
frame); the mass of the system obtained by adding the masses of the
two subclusters each within its virial radius,
![]() (see Sect. 4).
(see Sect. 4).
First, we consider the Newtonian criterion for gravitational binding
stated in terms of the observables as
![]() ,
where
,
where ![]() is the projection angle
between the plane of the sky and the line connecting the centres of
two clumps. The faint curve in Fig. 15 separates the bound
and unbound regions according to the Newtonian criterion (above and
below the curve, respectively). Considering the value of
is the projection angle
between the plane of the sky and the line connecting the centres of
two clumps. The faint curve in Fig. 15 separates the bound
and unbound regions according to the Newtonian criterion (above and
below the curve, respectively). Considering the value of
![]() ,
the A115N+S system is bound between
,
the A115N+S system is bound between
![]() and
and
![]() ;
the corresponding probability, computed considering the
solid angles (i.e.,
;
the corresponding probability, computed considering the
solid angles (i.e.,
![]() ), is 65%. We also consider the implemented
criterion
), is 65%. We also consider the implemented
criterion
![]() ,
which introduces different angles
,
which introduces different angles
![]() and
and
![]() for projection of distance and velocity, not
assuming strictly radial motion between the clumps (Hughes et al. 1995). We obtain a binding probability of 60%.
for projection of distance and velocity, not
assuming strictly radial motion between the clumps (Hughes et al. 1995). We obtain a binding probability of 60%.
Then, we apply the analytical two-body model introduced by Beers et al. (1982) and Thompson (1982; see also Lubin et al. 1998, for a recent application). This model assumes radial
orbits for the clumps with no shear or net rotation of the
system. Furthermore, the clumps are assumed to start their evolution
at time t0=0 with separation d0=0, and are moving apart or
coming together for the first time in their history; i.e. we are
assuming that we are seeing the cluster prior to merging (at the time
t=11.106 Gyr at the cluster redshift). The bimodal model solution
gives the total system mass
![]() as a function of
as a function of ![]() (e.g., Gregory & Thompson 1984). Figure 15 compares
the bimodal-model solutions with the observed mass of the system,
which is the most uncertain observational parameter. The present
bound outgoing solutions (i.e. expanding), BO, are clearly
inconsistent with the observed mass. The possible solutions span
these cases: the bound and present incoming solution
(i.e. collapsing), BIa and BIb, and the unbound-outgoing solution, UO.
For the incoming case there are two solutions because of the ambiguity
in the projection angle
(e.g., Gregory & Thompson 1984). Figure 15 compares
the bimodal-model solutions with the observed mass of the system,
which is the most uncertain observational parameter. The present
bound outgoing solutions (i.e. expanding), BO, are clearly
inconsistent with the observed mass. The possible solutions span
these cases: the bound and present incoming solution
(i.e. collapsing), BIa and BIb, and the unbound-outgoing solution, UO.
For the incoming case there are two solutions because of the ambiguity
in the projection angle ![]() .
We compute the probabilities
associated to each solution assuming that the region of
.
We compute the probabilities
associated to each solution assuming that the region of
![]() values between uncertainties are equally probable for individual
solutions:
values between uncertainties are equally probable for individual
solutions:
![]() ,
,
![]() ,
,
![]() %.
%.
Between the two possible bound solutions,
![]() and 76 degrees, the second one is rather unlikely since it means a distance
of
and 76 degrees, the second one is rather unlikely since it means a distance
of ![]() 3.7
h70-1 Mpc
3.7
h70-1 Mpc![]() between A115N and A115S, i.e. well larger than the
virial radii, while the second solution means a distance of
between A115N and A115S, i.e. well larger than the
virial radii, while the second solution means a distance of ![]() 1.0
h70-1 Mpc
1.0
h70-1 Mpc![]() in agreement with a certain degree of interaction. When assuming
in agreement with a certain degree of interaction. When assuming
![]() degrees the present colliding velocity is very large
(
degrees the present colliding velocity is very large
(![]() 4400 km s-1) and the cluster cores will cross after 0.08 Gyr.
4400 km s-1) and the cluster cores will cross after 0.08 Gyr.
The characterization of the dynamics of A115 using these models is
affected by several limitations. For instance, possible underestimates
of the masses - e.g., if the subclusters extend outside the virial
radius - lead to binding probabilities larger than those computed
above. The models do not take the mass distribution in the
subclusters into account when the separation of the subclusters is
comparable with their size (i.e. at small ![]() )
and do not
consider the possible effect of small, low velocity groups. Moreover,
the two-body model breaks down in a regime where A115N and A115S subclusters are already strongly interacting.
)
and do not
consider the possible effect of small, low velocity groups. Moreover,
the two-body model breaks down in a regime where A115N and A115S subclusters are already strongly interacting.
Finally, the two-body model does not consider the possibility of an off-axis merger as suggested by the X-ray surface brightness distribution (Gutierrez & Krawczynski 2005). For an analytical treatment which assumes that A115N and A115S are in a circular Keplerian orbit with the orbital plane perpendicular to the LOS, we refer to those authors.
As for the low velocity groups, we consider a group corresponding to
WGAP1 likely centred around BCM-D and possibly interacting with the
A115N+S complex. The values of the relevant observable quantities for
the two-clumps system are then: the relative LOS velocity in the rest
frame,
![]() km s
km s![]() (as recovered from WGAP1 and the mean
velocity of CORE-A and CORE-B cluster rest frame); the projected
linear distance between the two clumps, D=0.89
h70-1 Mpc
(as recovered from WGAP1 and the mean
velocity of CORE-A and CORE-B cluster rest frame); the projected
linear distance between the two clumps, D=0.89
h70-1 Mpc![]() (as recovered from
BCM-D and the mean position between BCM-A and -B); the mass of the
system obtained by adding the mass of a
(as recovered from
BCM-D and the mean position between BCM-A and -B); the mass of the
system obtained by adding the mass of a
![]() km s
km s![]() group to A115N+S, i.e.
group to A115N+S, i.e.
![]() .
According to the Newtonian criterion for
gravitational binding we find a binding probability of 38%. The
bimodal model indicates that the group is infalling onto the A115N+S
complex with a merging axis intermediate between the LOS and the plane
of sky (i.e.,
.
According to the Newtonian criterion for
gravitational binding we find a binding probability of 38%. The
bimodal model indicates that the group is infalling onto the A115N+S
complex with a merging axis intermediate between the LOS and the plane
of sky (i.e.,
![]() degrees).
degrees).
It has been suggested that cluster-cluster collisions may trigger star formation in cluster galaxies (Bekki 1999; Moss & Whittle 2000; Girardi & Biviano 2002, and references therein). Caldwell & Rose (1997) noticed that post-starburst galaxies are frequently found in clusters with evidence of past collision events. Here we analyse possible segregations between passive and active galaxy populations.
Out of 85 cluster members we classify 48 galaxies finding 34 "passive'' galaxies ("k'' in Table 1) and 14 "active'' galaxies (i.e., 9 "k+a''/"a+k'' and 5 "e'' galaxies, respectively), see also Fig. 7.
The velocity distribution of passive galaxies differs from that of active galaxies at the 99.47% c.l. according to the KS-test, active galaxies having a larger mean velocity (see Table 2). With present data this difference seems due to both Balmer absorption lines ("k+a''/"a+k'') and emission lines "e'' galaxies. This suggests that the galaxy population of the high velocity subcluster (A115N) is very active with respect to other A115 galaxies. Indeed, we find that two out three classified galaxies in CORE-A are active galaxies (in particular BCM-A), while no active galaxy is found in CORE-B. That A115S has a rich, red galaxy population is also found by Rakos et al. (2000) suggesting that this system is evolutionarily "developed''. Analysing the 2D distributions we only find a marginal difference between passive and Balmer absorption lines galaxies (at the 92% c.l. according to the 2dKS-test) with three out of nine Balmer absorption lines galaxies closely located to BCM-A. Assuming that galaxy activity is connected with the merging phenomena, our results point out that A115N subcluster is more affected than A115S in agreement with our finding that A115N is less massive than A115S (see Sect. 4).
We present the results of the dynamical analysis of the rich, X-ray luminous, and hot cluster of galaxies A115, showing a binary apparency (A115N and A115S) and containing a diffuse arc-shape radio emission, connected to A115N. This emission is considered a very anomalous relic since elongated relics are generally located at the cluster periphery, and with the largest dimension roughly perpendicular to the cluster radial orientation.
Our analysis is based on new redshift data for 115 galaxies, measured
from spectra obtained at the TNG in a cluster region within a radius
of
![]() .
We also use new photometric data
obtained at the INT telescope in a field larger than
.
We also use new photometric data
obtained at the INT telescope in a field larger than
![]() .
.
We select 85 cluster members around
![]() and compute a global
LOS velocity dispersion of galaxies,
and compute a global
LOS velocity dispersion of galaxies,
![]() km s-1.
km s-1.
Our analysis confirms the presence of two structures of cluster-type
well recognizable in the plane of the sky and shows that they differ
by ![]() 2000 km s
2000 km s![]() in LOS velocity. The northern, high velocity
subcluster (A115N) is likely centred on the second brightest cluster
galaxy (BCM-A, coincident with radio source 3C28) and the northern
X-ray peak. The southern, low velocity subcluster (A115S) is likely
centred on the first brightest cluster galaxy (BCM-B) and the
southern X-ray peak. We estimate that A115S is slightly dynamically
more important than A115N having a velocity dispersion of
in LOS velocity. The northern, high velocity
subcluster (A115N) is likely centred on the second brightest cluster
galaxy (BCM-A, coincident with radio source 3C28) and the northern
X-ray peak. The southern, low velocity subcluster (A115S) is likely
centred on the first brightest cluster galaxy (BCM-B) and the
southern X-ray peak. We estimate that A115S is slightly dynamically
more important than A115N having a velocity dispersion of
![]() km s
km s![]() vs.
vs.
![]() km s-1. The virial mass
estimates for the two subclusters are
km s-1. The virial mass
estimates for the two subclusters are
![]()
![]() and
and
![]()
![]() .
.
Moreover, we find evidence for two small groups at low velocities. In fact, the galaxy distribution obtained from our INT data shows the presence of two concentrations (C and D) in addition to A115N and A115S (A and B). The C group surrounds the third brightest cluster member and coincides with the clump already found by Beers et al. (1983; see also our Dressler-Schectman analysis). The D group surrounds another bright galaxy (BCM-D in this paper) and likely coincides with a faint X-ray emission shown by Chandra data (Gutierrez & Krawczynski 2005).
Considering the complex structure of A115 we estimate a global cluster
virial mass of 2.2-3.5
![]() .
.
Our results agree with a pre-merging scenario where A115N and A115S
are colliding with a LOS impact velocity
![]() km s-1. The most likely solution to the two-body problem
suggests that the merging axis lies at
km s-1. The most likely solution to the two-body problem
suggests that the merging axis lies at ![]() 20 degrees from the
plane of the sky and that the cores will cross after
20 degrees from the
plane of the sky and that the cores will cross after ![]() 0.1 Gyr.
0.1 Gyr.
In our scenario where 1) A115S is more massive than A115N; 2) the dynamically important axis is the axis connecting the two merging subclusters; 3) this axis is perpendicular to the largest dimension of the relic, the anomaly of the A115 radio diffuse source is likely overcome supporting its relic nature (Govoni et al. 2001b).
Acknowledgements
We thank Andrea Biviano for useful discussions.
This publication is based on observations made on the island of La Palma with the Italian Telescopio Nazionale Galileo (TNG), operated by the Fundación Galileo Galilei - INAF (Istituto Nazionale di Astrofisica), and with the Isaac Newton Telescope (INT), operated by the Isaac Newton Group (ING), in the Spanish Observatorio of the Roque de Los Muchachos of the Instituto de Astrofisica de Canarias.
This publication also makes use of data obtained from the Chandra data archive at the NASA Chandra X-ray centre (http://cxc.harvard.edu/cda/).
This work was partially supported by a grant from the Istituto Nazionale di Astrofisica (INAF, grant PRIN-INAF2006 CRA Ref. number 1.06.09.09).
![\begin{figure}
\par\includegraphics[width=14.5cm,,angle=180,clip]{7407fig1.ps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg156.gif) |
Figure 1: R-band image of A115 taken with the WFC camera of the INT. Targets with successful velocity measurements are labeled as in Table 1. Circles and boxes indicate cluster members and non member galaxies, respectively. |
![\begin{figure}
\par\includegraphics[width=14.5cm,,angle=180,clip]{7407fig2.ps}\end{figure}](/articles/aa/full/2007/27/aa7407-07/Timg157.gif) |
Figure 2: R-band image of the cluster A115 with, superimposed, the smoothed contour levels of the Chandra X-ray image ID#3233 (photons in the energy range 0.5-5 keV; blue) and the contour levels of the NVSS (Condon et al. 1998) radio image (red). Letters A, B, C and D indicate the three brightest cluster members each one corresponding to Beers et al. (1983) clumps and a fourth bright galaxy (see text). |
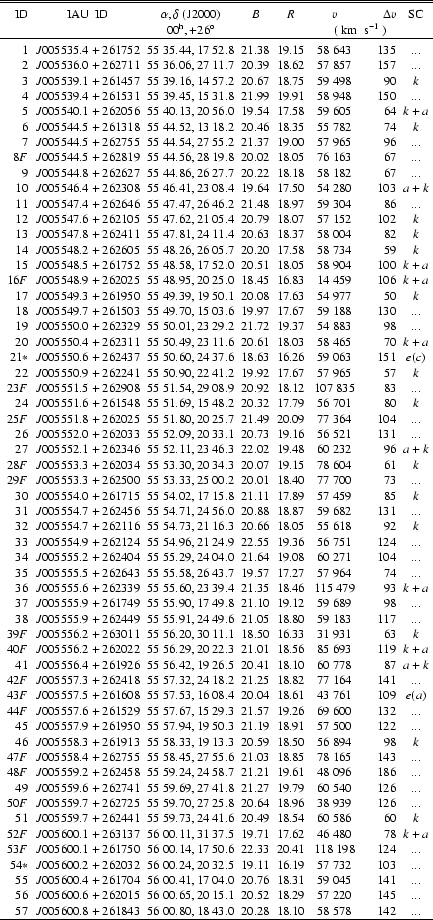 |
 |