A&A 469, 633-637 (2007)
DOI: 10.1051/0004-6361:20077079

Interferometric observations of the multiple stellar system $\delta $ Velorum
(Research Note)

A. Kellerer1 - M. G. Petr-Gotzens1 - P. Kervella2 - V. Coudé du Foresto2


1 - European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
2 - LESIA, Paris observatory, France

Received 10 January 2007 / Accepted 26 March 2007

Abstract
Context. The nearby ($\sim$24 pc) triple stellar system $\delta $ Velorum contains a close, eclipsing binary (Aa, Ab) discovered in 2000. Multiple systems provide an opportunity to determine the set of fundamental parameters (mass, luminosity, size, chemical composition) of coeval stars.
Aims. These parameters can be obtained with particular precision in the case of eclipsing binaries; so we exploited this potential for $\delta $ Velorum's components (Aa, Ab).
Methods. We have analysed interferometric observations of the close binary (Aa, Ab), obtained with the VINCI instrument and two VLTI siderostats. The measurements, which resolve the two components for the first time, are fitted onto the simple model of two uniformly bright, spherical stars.
Results. The observations suggest that Aa and Ab have larger diameters than expected for stars on the main sequence, hence they must be in a later evolutionary state.

Key words: binaries: eclipsing - stars: fundamental parameters - techniques: interferometric - binaries: visual - binaries: spectroscopic

1 Introduction

One of the fifty brightest stars on the sky, with a visual magnitude of $m_{\rm V\/}=1.96$ mag (Johnson et al. 1966), $\delta $ Velorum (HD 74956), is a multiple stellar system (e.g. Worley & Douglass 1997). But in spite of its brightness and proximity, $\pi=(40.90\pm 0.38)$ mas (Perryman et al. 1997), the issue of its composition remains unresolved. As early as 1847, Herschel published his detection of two faint visual companions, $\delta $ Vel C and D, at a distance of $69^{\prime\prime}$ from $\delta $ Vel A. Another companion - $\delta $ Vel B at the time separated by $\sim$ $3\hbox{$^{\prime\prime}$ }$ from $\delta $ Vel A - was later discovered by Innes (1895). The separation $0\hbox{$.\!\!^{\prime\prime}$ }736\pm0\hbox{$.\!\!^{\prime\prime}$ }014$ between components A and B appeared surprising when measured by Hipparcos, but it was explained later in terms of the orbit computation of Argyle et al. (2002), which showed a highly elliptical orbit of component B with period P=142 yr. In 1979, preliminary results from speckle interferometry suggested yet another component of the system (Tango et al. 1979). This apparent companion was found at a separation of $\sim$ $ 0\hbox{$.\!\!^{\prime\prime}$ }6$ and was taken to be a further component, because the separation for star B at the time was believed to be $\sim$ $3^{\prime\prime}$.

By now, however, it seems very likely that the speckle observations resolved $\delta $ Vel B; while there is still an unexplained disagreement for the position angle, the measured small separation does fit well with the orbital solution found by Argyle et al. (2002). As noted in earlier publications (Hoffleit et al. 1991; Otero et al. 2000), the two stars that are currently termed $\delta $ Vel C and D were taken to be associated with the pair AB because of seemingly similar proper motion. However, we have not found the source of the proper motion measurement of C and D. Finally, the most luminous component, A, was recently recognized to be a close eclipsing binary with a period T=45.15 days (Otero et al. 2000). Since then, $\delta $ Vel has been classified as a quintuple stellar system.

This investigation is focussed on the bright eclipsing binary, $\delta $ Vel A, but we also argue that $\delta $ Vel C and D are not physically associated with $\delta $ Vel A, B. While this makes $\delta $ Vel a triple system, it takes little away from its challenging potential for obtaining important information on stellar evolution. As the inclination, i, of its orbital plane is constrained to be close to  $90^{\circ}$, an eclipsing binary system provides one of the best means to obtain, in terms of the Kepler laws of motion, fundamental stellar parameters.

In this research note, we present the first interferometric observations of the eclipsing binary $\delta $ Vel A, obtained with ESO's Very Large Telescope Interferometer (VLTI) and its "commissioning instrument'' VINCI. The measurements resolve this binary system for the first time. They are analysed here with non-linear least-square fitting methods. We combine our interferometric results with existing photometric and spectroscopic observations, estimate some orbital parameters of the $\delta $ Vel A binary system, and discuss the stellar properties of the individual components based on the results.

  
2 Characteristics of $\delta $ Vel A derived from previous measurements

In the following, a priori estimates of two orbital parameters for the $\delta $ Vel (Aa-Ab) system are derived from the time interval between the eclipses and their durations. In subsection 2.2, stellar properties are then estimated from existing photometric and spectroscopic observations.

   
2.1 Orbit orientation and eccentricity

As reported by Otero et al. (2000) and Otero (2006), the fractional orbital period from the primary to the secondary eclipse equals $\tau _{\rm f}=0.43\pm 0.05$. The secondary eclipse was observed by the Galileo satellite in 1989, and its duration and depth were fairly precisely established as $0.91\pm0.01$ days and $\Delta m_{\rm II}=0.32\pm0.02$ (Otero 2006). The same spacecraft observed the primary eclipse several years later, although its measurements had become less accurate by then. The approximate duration and depth of the primary eclipse are $0.51\pm0.05$ days and $\Delta m_{\rm I}=0.51\pm0.05$(Otero 2006). The ratio of durations thus amounts to $\rho _{\rm f}=1.78\pm 0.19$. As will be seen now, the eccentricity, e, and the angle, $\omega $, between the semi-major axis and the line of sight, are constrained by $\tau_{\rm f}$ and $\rho_{\rm f}$. The angle $\omega $ is similar to, but must not be confused with, the more generally used parameter longitude of periastron.

The relative motion of the two stars $\delta $ Vel Aa and Ab is taken to be independent of external forces, and the vector, $\vec{s}$, from Ab to Aa traces an elliptical orbit around Ab as a focal point. Because the photometric light curve indicates a total eclipse for $\delta $ Vel A, the inclination of the orbit needs to be close to 90$^\circ$. To simplify the equations, we assume $i=90^\circ$, and Ab is taken to be the star with the higher surface brightness. During the primary eclipse, which is deeper, Ab is thus eclipsed by Aa. The angle $\theta$ of $\vec{s}$, also called the true anomaly, is zero at periastron and increases to $\pi$ as the star moves towards apastron. The distance between the stars depends on $\theta$ according to the relation:

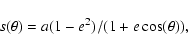\begin{displaymath}s(\theta) = a(1 - e^{2})/(1+e \cos(\theta)), \end{displaymath} (1)

where a denotes the semi-major axis. In line with Kepler's second law, the vector $\vec{s}$ covers equal areas per unit time. The fractional orbital period to reach angle $\theta$ is, accordingly:
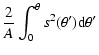                              $\displaystyle \tau (\theta)$ = $\displaystyle \frac{2}{A} \int_{0}^{\theta} s^{2}(\theta') {\rm d\/}\theta'$ (2)
  = $\displaystyle [2 {\rm arctan\/}(f_{1} \tan(\theta/2) - f_{2} \sin(\theta)/(1+ e \cos(\theta))] / 2\pi,$ (3)

where $A = \pi a^{2} \sqrt{(1 - e^{2})}$ equals the area of the ellipse, and $f_{1} = \sqrt{((1-e)/(1+e))}$ and $f_{2} = e \sqrt{(1-e^{2})}$.

During the primary eclipse, when the star with the lower surface brightness, Aa, covers Ab, the vector $\vec{s}$ is directed towards Earth, and $\theta$ equals $\omega $. During the secondary eclipse $\theta$ equals $\omega+\pi$. Thus:

 
                             $\displaystyle \tau_{\rm f}$ = $\displaystyle 0.43 \pm0.05$ (4)
  = $\displaystyle \int_{\omega}^{\omega+\pi} {\rm d\/}\theta/(1+e \cos(\theta))^{2}$ (5)
  = $\displaystyle [{\rm arctan\/}(f_{1} \tan((\omega+\pi)/2))-{\rm arctan\/}(f_{1} \tan (\omega/2))$  
    $\displaystyle +f_{2} \sin(\omega)/(1-e^{2} \cos(\omega)^{2})] / \pi,$ (6)

which determines $\omega $ for any given eccentricity, e (Fig. 1). The orbital velocity decreases as $\theta$ goes from zero to $\pi$, i.e. from the periastron to the apastron. In the subsequent interval, $\pi$ to 2$\pi$ (or -$\pi$ to 0), it increases again. If the line of sight contained the orbital major axis, i.e. $\omega= 0$ or $\pi$, the fractional duration between eclipses $\tau$ would equal 0.5. Note that for such values of $\omega $, Eq. (6) is not defined, yet $\tau$ tends towards 0.5 when $\omega $ approaches 0, or $\pi$. If the line of sight contained the orbital minor axis, i.e. $\omega= \pi$/2 or -$\pi$/2, the maximum and minimum values of $\tau$ would be reached. Values of $\tau$ less than 0.5 are thus associated with negative $\omega $ values. Since the fractional orbital period from the primary to the secondary eclipse is 0.43, the angle $\omega $ must lie between -$\pi$ and 0. As Fig. 1 shows, the eccentricity needs to be larger than $\approx$0.03.
  \begin{figure} \par\includegraphics[angle=90,width=6.5cm,clip]{7079fig1.eps} \end{figure} Figure 1: The angle, $\omega $, at primary eclipse and the eccentricity, e, as constrained by the fractional durations between the eclipses, $\tau _{\rm f}=0.43\pm 0.05$, and the fractional durations of the eclipses, $\rho _{\rm f}=1.78\pm 0.19$.
Open with DEXTER

On the other hand, $\omega $ can be further constrained through the ratio of the eclipse durations as follows. The eclipse durations are inversely proportional to the product $r~{\rm d\/}\theta/{\rm d\/}t$of radius and angular velocities during the eclipses. They are thus proportional to $s(\theta$), and their ratio is:

$\displaystyle \rho(\omega) = (1 - e \cos(\omega)) / (1 + e \cos(\omega)).$     (7)

Given $\rho _{\rm f}=1.78\pm 0.19$, this leads to a second relation between e and $\omega $. As illustrated by Fig. 1, simultaneous agreement with both observed values $\tau_{\rm f}$ and $\rho_{\rm f}$is reached only if $e\;\in\;[0.23 {-} 0.37]$ and $\omega\;\in\;-[0.1 {-} 0.7]$ rad.

   
2.2 Semi-major axis and stellar parameters

Orbital motion in the triple system $\delta $ Vel(Aa+Ab+B) has recently been substantiated and analysed by Argyle et al. (2002). From position measurements taken over a period of roughly 100 years, the authors inferred a P = 142 yr orbit for component B and deduced a total dynamical mass $M({\rm Aa})+M({\rm Ab})+M(B)=5.7^{+1.27}_{-1.08}\;M_{\odot}$. Photometric and spectroscopic measurements of the individual components being few and partly inconclusive, individual mass estimates are still difficult.

Hipparcos measured an apparent magnitude of $H_{\rm P}=1.991$ for $\delta $ Vel A and $H_{\rm P}=5.570$ for $\delta $ Vel B. With the transformations given by Harmanec (1998), the approximate Johnson V magnitudes are $m_{\rm V\/} = 1.99$ and $m_{\rm V\/} = 5.5$ for $\delta $ Vel A and $\delta $ Vel B, respectively. With the colours of the individual $\delta $ Vel components being unknown, it needs to be noted that the uncertainty of $m_{\rm V\/}$can be as high as $\sim$0.07 mag. Since $\delta $ Vel  is close (d = 24.45 pc according to Hipparcos), no interstellar reddening towards the source needs to be assumed, making the absolute magnitudes are $M_{\rm V\/} \sim 0.05$ for $\delta $ Vel A and $M_{\rm V\/} \sim 3.6$ for $\delta $ Vel B.

Several authors have analysed spectra of $\delta $ Vel A (e.g. Wright 2003; Alekseeva 1997; Levato 1972; Gray & Garrison 1987). Many of their measurements have probably included $\delta $ Vel B, but its flux is too low to add a significant contribution. From the metal line ratios and Balmer line equivalent widths, all authors deduced either spectral type A0 V or A1 V. This being most likely an average classification of the two stars, Aa and Ab, one star should be slightly hotter and the other cooler than an A0/1V star. No signatures of a double-lined spectroscopic binary were reported in any of the spectroscopic observations.

Based on the spectrophotometric information referred to above and under the assumption that all $\delta $ Vel components are on the main sequence, it is suggested that Aa and Ab have spectral type between A0V and A5V with masses in the range 2.0-3.0 $M_{\odot}$. Furthermore, it follows that B is an F-dwarf with mass about $\sim$ $ 1.5~M_{\odot}$. This agrees reasonably well with the total dynamical mass derived by Argyle et al. (2002).

An a priori estimate of the semi-major axis, a, of the Aa-Ab system is next derived from the mass sum of Aa+Ab ( $5\pm1~M_\odot$) and its orbital period ( $T=45.150\pm0.001$ days), which leads to $a = (6.4\pm0.5)\times 10^{10}$ m =  $0.43\pm0.04$ AU.
If they are main sequence early A stars, Aa and Ab should have stellar diameters between $1.7{-}2.4~D_{\odot}$.

Finally, the depths of the eclipses can be used to constrain the surface brightness ratio $\phi$ of the two eclipsing components, $\delta $ Vel Aa and Ab,

 \begin{displaymath} 1.28 \leq \phi = \frac{1-10^{-\Delta m_{\rm I}/2.5}}{1-10^{-\Delta m_{\rm II}/2.5}}\leq 1.67. \end{displaymath} (8)

Table 1: Details of the VINCI measurements. The uncertainty on the phase determination equals $\pm 0.002$.

3 VLT interferometer/VINCI observations

  
3.1 Data description

During April-May 2003, the ESO Very Large Telescope Interferometer (VLTI) was used to observe the eclipsing binary $\delta $ Vel(Aa+Ab) in the K-band at four orbital phases with the single-mode fiber-based instrument VINCI (Glindemann 2001; Kervella et al. 2003). The observations were performed with two siderostats, placed at stations B3 and M0, separated by 155.368 m. Table 1 lists the observing dates, the orbital phases of $\delta $ Vel (Aa+Ab), the calibrated squared visibilities V2 and their standard deviations $\sigma_{V^2}$, and the number of accepted scans $N_{\rm S}$ (out of 500).

Every interferometric observation yields a fringe contrast or squared visibility, V2, whose variations are due not only to interferometric modulation, but also to atmospheric and instrumental fluctuations. Accordingly the raw squared visibilities need to be calibrated by a reference star. To this purpose the observations of $\delta $ Vel were combined with observations of HD 63744, a star of spectral type K0III, with an estimated diameter of $1.63\pm0.03$ mas (Bordé et al. 2002). The interferometric measurements were then analysed by use of the VINCI data reduction pipeline, described in detail in Kervella et al. (2003).

Additionally, the calibrated V2 values need to be corrected for the influence of the nearby component $\delta $Vel B. The diffraction on the sky (through an individual VLTI 0.4 m siderostat) of the fundamental fiber mode, which defines the interferometric field of view, is equivalent to an Airy disk with a 1 $.\!\!^{\prime\prime}$38 diameter. At the time of the observations, Aa+Ab and B were separated by $\sim$ $(1.0\pm0.3)\hbox{$^{\prime\prime}$ }$. Depending on atmospheric conditions, the interferograms are, therefore, contaminated by a random and time-varying fraction of light, i.e. an incoherent signal, from star B. The visibilities must, accordingly, be multiplied by a factor:

\begin{displaymath}V_{\rm c\/} =V\times (1+I_{\rm B\/}/I_{\rm Aa+Ab\/}) = (1.05\pm0.05)\times V, \end{displaymath} (9)

where $I_{\rm B\/}$ and $I_{\rm Aa+Ab\/}$ are the intensities collected by the interferometer from $\delta $Vel B and $\delta $Vel (Aa+Ab). The value of $I_{\rm B}/I_{\rm Aa+Ab}$ lies between 0 (no light from B) and $10^{-\Delta m/2.5}=0.09$ (star B is completely in the field of view), where $\Delta m\sim2.6$ equals the K-band magnitude difference between B and Aa+Ab.

  
3.2 Comparison to a model


  \begin{figure} \par\includegraphics[width=16cm,clip]{7079fig2.eps} \end{figure} Figure 2: Corrected visibility values and standard deviation, compared to a model of two uniformly luminous, spherical stars. The parameter values of the best fit (solid line) are indicated in the upper left corner.
Open with DEXTER

The 17 visibility measurements, ${V_{\rm c}}^2$, were fitted to a model of a binary system of two uniformly bright spherical stellar discs, observed at K-band with a filter of finite bandwith. Five parameters of the binary model (stellar diameters Da, Db, position angle of the ascending node $\Omega$, semi-major axis a, eccentricity e) were adjusted for optimum fit to the observations. The fitting procedure utilises a non-linear least-square algorithm (Markwardt 2005) that follows the direction of steepest descent of $\chi ^2$ in the parameter space, $\chi ^2$ being the reduced sum of squared deviations, i.e. the sum divided by the 13 degrees of freedom. To distinguish between local and absolute minima, the initial parameters were varied over the broad ranges of their potential values: The semi major axis, a, was considered between $5.4\times 10^{10}$ m and $8.0\times 10^{10}$ m, which corresponds to a total mass of Aa and Ab in the range $3 {-} 10~M_\odot$. As specified in Sect. 2, $e\in[0.23, 0.37]$. The stellar diameters were examined between 0.4 and 12.4 mas. These limits refer respectively to the resolution limit of the interferometer and to the Roche lobe volume diameter $D_{\rm L}$. The latter is approximated to better than 1$\%$ by $D_{\rm L}/d\sim 12.4$ mas (Eggleton 1983). If one of the stars were to have a diameter larger than $D_{\rm L}$, the system would be an interacting binary and the simple model of two spherical, uniformly bright stars would not apply. The position angle of the ascending node $\Omega$, measured from North to East, equals 0 if the projected orbital plane and the North-South axes are aligned. No previous measurement of $\Omega$ exists, and the angles $\Omega$ and $\Omega+\pi$ cannot be distinguished through interferometric measurements; therefore, $\Omega$ is considered between 0 and $\pi$. Varying the surface brightness ratio $\phi$ over the range specified in Eq. (8) has virtually no effect on $\chi ^2$, $\phi$is so fixed at 1.46. Likewise, the period of the binary $\delta $ Vel (Aa-Ab) is fixed at T=45.150 days. No apsidal motion of the eclipsing system has been noted since its discovery in 2000. The orbital inclination has been fixed at $90^{\circ}$, although given the stellar diameters and separations deduced in Section 2.2, the actual inclination could lie between $87.5^\circ$ and $92.5^\circ$.

The best adjustment of the model to the measured visibilities and their 1-sigma statistical errors is shown in Fig. 2. It corresponds to a reduced mean squared deviation $\chi_0^2=2.6$ and is obtained for the following parameter values: $ a = (5.7\pm0.3)\times10^{10} ~{\rm m\/}, e = 0.230\pm0.005, \Omega = (27.4\pm1.2)^{\circ}, D_a = (6.0\pm0.5)~D_\odot, D_b = (3.3\pm0.6)~D_\odot.$The angle at primary eclipse is derived by the eccentricity as specified in Sect. 2.1: $\omega=-(20\pm3)^{\circ}$. The parameter uncertainties equal the statistical errors, $\sigma$, scaled by the reduced mean deviation of the model to the measurements, i.e. $\chi_0~\sigma$. The dependence of $\chi ^2$ on the stellar diameters is illustrated in Fig. 3.

The three visibilities measured on May 10, 2003 systematically deviate from the model fit (see Fig. 2). There is no evident explanation for this deviation: the data were obtained under good atmospheric conditions and the calibrator was the same as on the other nights. If the three points are removed, the quality of the fit is improved, $\chi_0^2=1.4$, but within the uncertainties, the resulting parameter values are unchanged: $ a = (5.4\pm0.5)\times10^{10}~ {\rm m\/}, e = 0.230\pm0.005, \Omega = (29.2\pm2.4)^{\circ}, D_a = (6.6\pm0.5)~D_\odot, D_b = (3.2\pm0.5)~D_\odot.$

It is apparent from the relatively high $\chi_0^2$ that there are deviations in addition to the purely statistical errors. They might be due to an underestimation of the calibrator's size or might reflect some inaccuracies in the model for two uniformly bright, spherical stars. This is discussed in the subsequent section.

  
4 Results and discussion

4.1 The close eclipsing binary $\delta $ Vel (Aa-Ab)

The computations could be slightly biased if the diameter of the calibrator star were substantially misestimated or if HD 63744 were a - still undiscovered - binary system. On the other hand, HD 63744 is part of the catalog of interferometric calibrator stars by Bordé et al. 2002, with its diameter ( $1.63\pm0.03$) mas specified to a precision of $1.8\%$. Furthermore, it has been studied simultaneously with other calibrator stars in VINCI observations by one of the authors (P.  Kervella). In these investigations the visibilities of HD 63744 equal those expected for a single star of $1.63\pm0.03$ mas diameter. Thus, HD 63744 appears to be a reliable calibrator.

Perhaps more relevant are the possible astrophysical complexities of $\delta $ Vel (Aa+Ab) that are disregarded in the model of two uniformly bright, spherical stars. In particular, the rotational velocities of Aa and/or Ab are found to be high, with values of $\sim$150-180 km s-1 (Royer et al. 2002; Hempel et al. 1998; Holweger et al. 1999), which indicates that the two stars need not be uniformly luminous or circular.

Another possible over-simplification of our binary model is the constraint on the orbital inclination, i, being fixed at 90$^\circ$. Given the fitted semi-major axis and stellar diameters, we note that the eclipse durations ( $0.51\pm0.05$ days and $0.91\pm0.01$ days) are shorter than they should be in the case of $i=90^\circ$, where the duration of the longer eclipse would have to exceed $D_a\;T/(2\pi~a)=1.06$ days. We conclude that i is $\sim$$88^\circ$ or $\sim$$ 92^\circ$, rather than $90^{\circ}$. All observations were performed out of eclipse and, therefore, the visibility values are nearly unaffected by such a small variation in i. With substantially more visibility measurements and an increased number of fitted parameters, the issue on the precise orbital inclination might be addressed in more detail.

  \begin{figure} \par\includegraphics[width=6.5cm,clip]{7079fig3.eps} \end{figure} Figure 3: $\chi ^2$ as a function of the stellar diameters. The three other parameters of the model are set equal to: $a=(5.7\pm 0.3)10^{10}$ m, $e=0.230\pm 0.05$ and $\Omega =27.4\pm 1.2^\circ $.
Open with DEXTER

The most important and remarkable result of our analysis is that the stellar diameters of Aa and Ab are found to equal $6.0\pm0.5~D_{\odot}$ and $3.3\pm0.6~D_{\odot}$, respectively. This exceeds significantly, by factors $\sim$1.4-3, the values expected if Aa and Ab are main sequence stars. If both diameters are constrained to lie below $2.5~D_{\odot}$, the best fit corresponds to $\chi^2=16.7$, which is far beyond the present result and confirms that large diameters are required to account for the measured visibilities.

4.2 The physical association of $\delta $Vel C and D

Ever since the observations of Herschel (1847), $\delta $Vel has been taken to be a visual multiple star, with $\delta $Vel C and D the outer components of the system. With $m_{\rm V}$ of 11.0 mag and 13.5 mag (Jeffers et al. 1963), C and D would need to be of late spectral type, certainly no earlier than M, if they were as distant as $\delta $Vel (Aa+Ab+B). To our knowledge, the only existing spectra of C and D were recorded during a survey of nearby M dwarfs (Hawley et al. 1996). While the limited range and resolution of the spectra precluded ready determination of the spectral types of C and D, they were nevertheless estimated as $\sim$G8V and $\sim$K0V. Therefore, given their apparent magnitudes, C and D must be much farther away than $\delta $Vel (Aa+Ab+B). We conclude that $\delta $Vel C and D are not physically associated. Hence, $\delta $Vel ought to be only classified as a triple stellar system.

  
5 Summary

Seventeen VINCI visibility measurements of $\delta $ Vel (Aa+Ab) were fitted onto the model of two uniformly bright, spherical stars. The adjustment to the measurements does not provide individual diameters compatible with A-type main sequence stars. The two stars thus appear to be in a more advanced evolutionary stage. More data are needed however to confirm this result. As the stellar evolution is fast during this period, more detailed knowledge of the system might also constrain the models more tightly. Precise photometric and spectroscopic observations ofthe eclipses should provide the separate intensities and chemical compositions of Aa and Ab and, hence, permit further inferences on the age and evolutionary state of $\delta $ Vel.

Acknowledgements
We thank Rosanna Faraggiana for her extensive help, Sebastian Otero for providing the light curves $\delta $ Vel Aa, Ab, and Neil Reid for making the spectra of $\delta $ Vel C, D available. The manuscript was improved by helpful comments from the referee.

References

 
Copyright ESO 2007