A&A 469, 213-222 (2007)
DOI: 10.1051/0004-6361:20077385
A. Isella1,2 - L. Testi1 - A. Natta1 - R. Neri3 - D. Wilner4 - C. Qi4
1 - Osservatorio Astrofisico di Arcetri, INAF, Largo E.Fermi 5,
50125 Firenze, Italy
2 -
Dipartimento di Fisica, Universitá di Milano, via Celoria 16,
20133 Milano, Italy
3 -
Institut de Radio Astronomie Millimétrique (IRAM), 300 rue de la
Piscine, Domaine Universitaire de Grenoble, 38406 St. Martin d'Hères, France
4 -
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, MS
42, Cambridge, MA 02138, USA
Received 1 March 2007 / Accepted 4 April 2007
Abstract
We present new multi-wavelength millimeter interferometric
observations of the Herbig Ae star HD 163296 obtained with the
IRAM/PBI, SMA and VLA arrays both in continuum and in the 12CO,
13CO and C18O emission lines. Gas and dust properties
have been obtained comparing the observations with self-consistent
disk models for the dust and CO emission. The circumstellar
disk is resolved both in the continuum and in CO. We find
strong evidence that the circumstellar material is in Keplerian
rotation around a central star of 2.6 ![]() .
The disk inclination
with respect to the line of sight is 46
.
The disk inclination
with respect to the line of sight is 46![]()
![]() 4
4![]() with a position angle of 128
with a position angle of 128![]()
![]() 4
4![]() .
The slope of the dust opacity measured between 0.87 and 7 mm
(
.
The slope of the dust opacity measured between 0.87 and 7 mm
(![]() )
confirms the presence of mm/cm-size grains in the disk
midplane. The dust continuum emission is asymmetric and
confined inside a radius of 200 AU while the CO emission extends up
to 540 AU. The comparison between dust and CO temperature indicates
that CO is present only in the disk interior. Finally, we
obtain an increasing depletion of CO isotopomers from 12CO to
13CO and C18O. We argue that these results support the
idea that the disk of HD 163296 is strongly
evolved. In particular, we suggest that there is a strong depletion
of dust relative to gas outside 200 AU; this may be due to the
inward migration of large bodies that form in the outer disk or
to clearing of a large gap in the dust distribution by a low mass
companion.
)
confirms the presence of mm/cm-size grains in the disk
midplane. The dust continuum emission is asymmetric and
confined inside a radius of 200 AU while the CO emission extends up
to 540 AU. The comparison between dust and CO temperature indicates
that CO is present only in the disk interior. Finally, we
obtain an increasing depletion of CO isotopomers from 12CO to
13CO and C18O. We argue that these results support the
idea that the disk of HD 163296 is strongly
evolved. In particular, we suggest that there is a strong depletion
of dust relative to gas outside 200 AU; this may be due to the
inward migration of large bodies that form in the outer disk or
to clearing of a large gap in the dust distribution by a low mass
companion.
Key words: accretion, accretion disks - techniques: interferometric - stars: planetary systems: protoplanetary disks - stars: circumstellar matter
Millimeter and sub-millimeter interferometers are providing an increasingly detailed description of disks around pre-main sequence
stars of solar (T Tauri stars; TTS) and intermediate mass (Herbig Ae;
HAe). Both dust continuum emission and emission in molecular
lines are observed and spatially resolved in a number of disks,
yielding information on the disk density and temperature, the dust
properties, and the gas chemistry and dynamics in the outer disk
(e.g., Natta et al. 2007; Dutrey et al. 2006, and
references therein). Thanks to the recent instrumental improvements,
it is now possible to build upon the original detections and
study more accurately the disk structure details.
The number of well-studied disks is however still very small,
practically restricted to the most massive and luminous
ones; still, it is clear that disks differ from one another. Recently,
evidence of spiral structures and of deviations from Keplerian rotation have been reported in AB Aur, a 2-3 Myr old intermediate mass star, (Piétu et al. 2005; Corder
et al. 2005); the classical TTS LkCa15 has a large inner hole of size ![]() 50 AU
depleted of dust, while the HAe star MWC 480 has a smooth disk with an optically thick (at millimeter wavelengths) inner region of radius
50 AU
depleted of dust, while the HAe star MWC 480 has a smooth disk with an optically thick (at millimeter wavelengths) inner region of radius
![]() 35 AU (Piétu et al. 2006). Both spiral structures
and large gaps are evidence of dynamical perturbations, possibly due
to the effect of large planets. The existence of both unperturbed and
distorted disks among pre-main sequence stars suggests that the planet
formation is actively occurring during this evolutionary stage,
leaving detectable marks on the parent disks. It is therefore
important to study in detail as many disks as possible, in order to
characterize their basic properties and to detect deviations from the
simple patterns of homogeneous disks in Keplerian rotation.
35 AU (Piétu et al. 2006). Both spiral structures
and large gaps are evidence of dynamical perturbations, possibly due
to the effect of large planets. The existence of both unperturbed and
distorted disks among pre-main sequence stars suggests that the planet
formation is actively occurring during this evolutionary stage,
leaving detectable marks on the parent disks. It is therefore
important to study in detail as many disks as possible, in order to
characterize their basic properties and to detect deviations from the
simple patterns of homogeneous disks in Keplerian rotation.
We report in this paper a detailed study of the disk associated to the
HAe star HD 163296, using observations in the continuum and CO lines
obtained with three different interferometers, namely the Very Large
Array (VLA) at 7 mm, IRAM Plateau de Bure Interferometer (PBI) at 1.3
and 2.6 mm and the Submillimeter Array (SMA) at 0.87 mm. HD 163296 is
a star of spectral type A1, mass of roughly 2.3 ![]() ,
distance
122 pc (van den Ancker et al. 1998). Early OVRO observations
(Mannings & Sargent 1997) have shown the presence of a disk
with a minimum mass
,
distance
122 pc (van den Ancker et al. 1998). Early OVRO observations
(Mannings & Sargent 1997) have shown the presence of a disk
with a minimum mass ![]() 0.03
0.03 ![]() and evidence of rotation from
the CO lines. The disk is seen in scattered light by Grady et al. (2000, 1999), with radius of
and evidence of rotation from
the CO lines. The disk is seen in scattered light by Grady et al. (2000, 1999), with radius of ![]() 500 AU; it has an associated jet seen in Ly-
500 AU; it has an associated jet seen in Ly-![]() with HST, extending on both sides of the disk orthogonally to it (Devine et al. 2000;
Wassell et al. 2006). Natta et al. (2004) found evidence
of evolved dust in the outer disk of HD 163296 by comparing the VLA
7 mm flux to the OVRO observations.
with HST, extending on both sides of the disk orthogonally to it (Devine et al. 2000;
Wassell et al. 2006). Natta et al. (2004) found evidence
of evolved dust in the outer disk of HD 163296 by comparing the VLA
7 mm flux to the OVRO observations.
The results we present here have much higher spatial resolution and wavelength coverage than what has been previously reported. They allow us to measure accurately the dynamics of the disk as well as the disk and dust properties and to test the capability of disk models to account for the observations. As we will show, they suggest that the HD 163296 system is probably evolving towards a debris disk phase.
The structure of the paper is as follows. Section 2 will describe the observations. The results will be presented in Sect. 3, where we will derive some of the disk parameters. A more detailed analysis, using self-consistent disk models of the dust and CO line emission will be presented in Sect. 4; Sect. 5 contains the results, which will be further discussed in Sect. 6. Summary and conclusions follow in Sects. 7 and 8.
The PBI observations were carried over the 2003/2004 winter season. The six 15 m dishes were used in the most extended configuration providing a baseline coverage between 25 and 400 m. The corresponding angular resolutions are reported in Table 1. The receivers were tuned to observe the 12CO J = 2-1 line and the nearby continuum at 1.3 mm, while at 2.8 mm the 13CO J = 1-0, and C18O J = 1-0 lines were observed along with the continuum. Bandpass and complex gain calibrations were ensured by observations of standard IRAM calibrators. The phase stability was excellent during our observations and only a minimal amount of editing of the data was necessary. All calibrations were performed using the standard CLIC suite of programmes within the GILDAS software package. The calibrated uv data were then exported for the subsequent analysis. The accuracy of the flux density scale calibration is expected to be within 20% at these wavelengths.
The SMA observations of HD 163296 were made on August 23rd, 2005 using the Compact
Configuration of seven of the 6 m diameter antennas, which
provided 21 independent baselines ranging in length from 8 to 80 m. The SMA digital correlator was configured with a narrow band of 512 channels over 104 MHz, which provided 0.2 MHz frequency
resolution, or 0.18 km s-1 velocity resolution at 345 GHz, and
the full correlator bandwidth was 2 GHz. The weather was good with
![]() (225 GHz) around 0.06 and the double-sideband (DSB) system
temperature were between 200 and 500 K. The source HD 163296 was
observed from HA -3 to 4.5. Calibration of the visibility phases and
amplitudes was achieved with observations of the quasar 1921-293,
typically at intervals of 25 min. Observations of Uranus provided
the absolute scale for the flux density calibration and the
uncertainties in the flux scale are estimated to be 20%. The data
were calibrated using the MIR software
package
(225 GHz) around 0.06 and the double-sideband (DSB) system
temperature were between 200 and 500 K. The source HD 163296 was
observed from HA -3 to 4.5. Calibration of the visibility phases and
amplitudes was achieved with observations of the quasar 1921-293,
typically at intervals of 25 min. Observations of Uranus provided
the absolute scale for the flux density calibration and the
uncertainties in the flux scale are estimated to be 20%. The data
were calibrated using the MIR software
package![]() .
.
HD 163296 was observed at the NRAO/VLA as part of a larger survey for 7 mm disk emission around Herbig Ae stars (see Natta et al. 2004). Data were obtained with the array in the C and D configurations, in several occasions from Dec. 2001 through May 2003. Accurate pointing was ensured by hourly pointing sessions at
3.6 cm on a bright extra galactic object. The array offered baselines
from the shadowing limit through ![]() 3.4 km, although some data was
obtained in a hybrid DnA configuration, all the data from the longer
baselines had to be rejected due to large phase fluctuations that
could not be corrected. The resulting uv-plane coverage offered an angular resolution of 0.5
3.4 km, although some data was
obtained in a hybrid DnA configuration, all the data from the longer
baselines had to be rejected due to large phase fluctuations that
could not be corrected. The resulting uv-plane coverage offered an angular resolution of 0.5
![]() and a maximum recoverable size of
the order of
and a maximum recoverable size of
the order of ![]() 40
40
![]() .
All the data was edited and calibrated
using standard recipes in AIPS. The short term complex gain variations
were corrected using frequent (few minutes cycle) observations of the
quasar 1820-254, while the flux scale was set observing the VLA calibrator 1331+305. This procedure is expected to be accurate
within
.
All the data was edited and calibrated
using standard recipes in AIPS. The short term complex gain variations
were corrected using frequent (few minutes cycle) observations of the
quasar 1820-254, while the flux scale was set observing the VLA calibrator 1331+305. This procedure is expected to be accurate
within ![]() 15% at 7 mm.
15% at 7 mm.
The continuum maps obtained at 0.87 mm, 1.3 mm, 2.8 mm and 7 mm are shown in Fig. 1. Channel maps, integrated intensity and mean velocity maps of the 12CO J = 2-1, 13CO J = 1-0 and 12CO J = 3-2 transitions are shown in Figs. 2-4 respectively. At the wavelength corresponding to the C18O J = 1-0 transition we did not detect any emission; the continuum integrated fluxes are reported in Table 1.
With simple physical assumptions, these observations allow us to determine some fundamental parameters of the star+disk system as the stellar and the disk masses, the contribution to the observed fluxes of free-free gas emission, the wavelength dependence of the observed flux at millimeter wavelengths and the related dust grain opacity.
![\begin{figure}
\par\includegraphics[angle=270,width=16.45cm,clip]{7385fig1.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg27.gif) |
Figure 1:
Continuum maps of HD 163296 at 0.87, 1.3,
2.8 and 7 mm, starting from the left. In order to highlight the
extended morphology of the disk, the first contour level in the
0.87 mm map corresponds to 30 mJy (3 |
| Beam | Emission | Flux | ||
| (mm) | FWHM | PA | FWHM | (mJy) |
| 0.87 |
|
20 |
|
1910 |
| 1.3 |
|
7 |
|
705 |
| 2.8 |
|
8 |
|
77.0 |
| 7 |
|
172 |
|
4.5 |
The
![]() continuum maps of HD 163296 are shown
in Fig. 1. At all wavelengths, the peak is coincident
with the position of the optical star as measured from Hipparcos and,
given the respective synthesized beams FWHM (see Table 1),
the emission is resolved and elongated approximately in the east-west
direction. Approximating the source with a circularly symmetric
geometrically thin disk and taking into account the beam shape, the
observed aspect ratio of the level contours implies an inclination of
the disk plane from the line of sight of 45
continuum maps of HD 163296 are shown
in Fig. 1. At all wavelengths, the peak is coincident
with the position of the optical star as measured from Hipparcos and,
given the respective synthesized beams FWHM (see Table 1),
the emission is resolved and elongated approximately in the east-west
direction. Approximating the source with a circularly symmetric
geometrically thin disk and taking into account the beam shape, the
observed aspect ratio of the level contours implies an inclination of
the disk plane from the line of sight of 45![]()
![]() 20
20![]() and a position angle of 120
and a position angle of 120![]()
![]() 30
30![]() ,
in rough agreement
with the values obtained by Mannings & Sargent (1997)
using marginally resolved OVRO observations (58
,
in rough agreement
with the values obtained by Mannings & Sargent (1997)
using marginally resolved OVRO observations (58![]() and 126
and 126![]() respectively).
respectively).
The emission is resolved at all the wavelengths in the East-West direction. The fainter contour levels are not centrally symmetric, showing excess emission in the east half of the image, better visible in the 0.87 and 1.3 mm maps. Both the disk size and the morphology will be discussed in more detail in Sect. 6.
As shown in Figs. 2-3, in all the detected molecular line transitions,
the emission is resolved, showing a velocity pattern typical of an inclined rotating disk characterized by a position angle of about 130![]() (a more precise estimate of the position angle will be presented in Sect. 5). The velocity-position diagram
calculated along this direction (see Fig. 5) shows a well defined "butterfly shape'' typical of Keplerian rotation. A first estimate of the mass of the central
object and of the dimension of the disk can be obtained by comparing
the observed velocities with the Keplerian law:
(a more precise estimate of the position angle will be presented in Sect. 5). The velocity-position diagram
calculated along this direction (see Fig. 5) shows a well defined "butterfly shape'' typical of Keplerian rotation. A first estimate of the mass of the central
object and of the dimension of the disk can be obtained by comparing
the observed velocities with the Keplerian law:
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{7385fig6.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg48.gif) |
Figure 6:
HD 163296 spectral energy distribution. Data
from literature are shown with empty squares (Mannings 1994;
Natta et al. 2004; de Winter et al. 2001) and dots
(ISO-SW). Our new measurements (see Table 1) are shown
with full squares. The observed fluxes at 3.6 cm and 6.1 cm have
been used to calculate the free-free contribution (dashed line) to
the observed flux assuming a free-free spectral index of 0.6. Free-free subtracted fluxes are shown at 7 mm while at shorter wavelength the free-free contribution is
negligible. The solid line shows the prediction of our disk model as
discussed in Sect. 5.2. The resulting spectralindex
|
The continuum spatially integrated fluxes of HD 163296 and the corresponding spectral energy distribution are given in Table 1 and shown in Fig. 6, respectively. In addition to our measurements (full squares), observations at 0.7, 1.3, 3.6 and 6.1 mm are from Natta et al. (2004, and references therein) while observations at 0.75, 0.8, 0.85, 1.1 and 1.3 mm are from Mannings (1994).
Assuming that the observed flux at 3.6 and 6.1 cm is dominated by free-free emission from a wind (with a spectral index of 0.6), the free-free contribution at 7 mm corresponds to 1.2 mJy (27% of the observed flux), while it is negligible at shorter wavelengths.
After the subtraction of the free-free component, the millimeter
spectral index
![]() (
(
![]() )
calculated between 1 mm and 7 mm is 3.0
)
calculated between 1 mm and 7 mm is 3.0 ![]() 0.1, slightly higher than the value
0.1, slightly higher than the value
![]()
![]() 0.2
obtained by Natta et al. (2004) using VLA and OVRO fluxes only.
0.2
obtained by Natta et al. (2004) using VLA and OVRO fluxes only.
Assuming that the dust emission is optically thin at millimeter
wavelengths and that the dust is isothermal, the measured flux can be
used to estimate the product of the disk total mass M times the dust
opacity ![]() ,
through the relation:
,
through the relation:
With these simplifying assumptions, the slope of the dust
opacity is
![]() ,
where
,
where ![]() is the spectral
index obtained in the previous section.
is the spectral
index obtained in the previous section.
The disk parameters derived in Sect. 3 under a number of very crude assumptions can only provide order-of-magnitude estimates. A more quantitative analysis requires comparison of the observations to more sophisticated model predictions. We chose to perform the comparison using the observed visibilities (rather than reconstructed images), following an approach similar to the one discussed by Dutrey et al. (2006).
| Parameters | Continuum | 12CO J = 2-1 | 12CO J = 3-2 | 13CO J = 1-0 |
| 2.6a | 2.6+0.3-0.5 | 2.4 |
2.6 |
|
| PA | 120 |
128 |
130 |
130 |
| Incl | 40 |
45 |
45 |
50 |
|
|
200 |
550 |
550 |
500 |
|
|
46 |
90 |
90a |
|
| p | 0.8 |
|
0.6a | 1.0 |
|
|
|
60 |
||
| q |
|
0.8 |
0.8 |
|
| 1.0 |
1.0a | 1.0a | 1.0a | |
| 2.6 | 1.17 | 1.05 | 1.15 |
a Fixed parameter.
This method requires to decide "a priori'' which family of models
is likely to describe the observed object. In view of the results
described in Sect. 3, we model the millimeter
emission of HD 163296 (continuum and CO lines) as coming from a circumstellar disk. We assume that the disk is heated by the stellar
radiation only, and that any viscous contribution can be
neglected. This is very likely a good approximation, given the
relatively low accretion rate measured in HD 163296 (![]() 10-7
10-7 ![]() /yr; Garcia Lopez et al. 2006).
/yr; Garcia Lopez et al. 2006).
The disk structure and emission is computed using the 2-layer approximation of Chiang & Goldreich (1997), as developed by Dullemond et al. (2001). Similar models have been used in Testi et al. (2003) and Natta et al. (2004), to analyze the (sub)millimeter emission of a number of Herbig Ae stars. We refer to these papers for a more detailed description.
The inner disk is characterized by the presence of a puffed-up inner rim located at the dust evaporation radius (Isella & Natta 2005). The combined rim+disk flux is calculated taking into account the shadow that the rim casts over the outer disk.
The disk geometry can be fully flared, as in hydrostatic equilibrium disks where gas and dust are well mixed. If dust growth and settling are important, the flaring angle decreases: the resulting radial temperature profile is flatter, affecting the SED in the mid and far infrared (D'Alessio et al. 2006, and references therein). As shown in Fig. 6, the SED of HD 163296 is well reproduced by a fully flared disk model. The fit of the SED becomes very poor if the flaring angle is reduced by more than a factor of two, which corresponds to a small variation of the temperature radial profile.
Once the stellar properties are known, the disk structure is
completely characterized by the following parameters: the disk mass (![]() ), the disk outer radius (
), the disk outer radius (
![]() ), the dependence of the surface density on radius (
), the dependence of the surface density on radius (
![]() )
and the properties of dust on the disk surface and midplane. In
addition, the observed emission depends on the orientation of the disk
with respect to the observer, which is characterized by the
inclination
)
and the properties of dust on the disk surface and midplane. In
addition, the observed emission depends on the orientation of the disk
with respect to the observer, which is characterized by the
inclination ![]() of the disk with respect to the line of sight
(
of the disk with respect to the line of sight
(![]() for face-on disks), and the position angle PA.
for face-on disks), and the position angle PA.
The continuum emission at millimeter and sub-millimeter wavelengths
is computed by ray integration as in Dullemond et al. (2001).
We describe the midplane dust opacity at long wavelengths as a power law of index ![]() ,
with
,
with ![]() a free parameter, as in Eq. (3). At short wavelengths and in the disk surface we adopt the dust opacity of astronomical silicates (Weingartner &
Draine 2001). The inner disk radius is the dust sublimation
radius, as in the rim models of Isella et al. (2006) for
large (
a free parameter, as in Eq. (3). At short wavelengths and in the disk surface we adopt the dust opacity of astronomical silicates (Weingartner &
Draine 2001). The inner disk radius is the dust sublimation
radius, as in the rim models of Isella et al. (2006) for
large (![]()
![]() m) grains, and it is equal to 0.45 AU; the dust on
the disk surface is as in Natta et al. (2004). Neither of
these two quantities is relevant for the following analysis.
m) grains, and it is equal to 0.45 AU; the dust on
the disk surface is as in Natta et al. (2004). Neither of
these two quantities is relevant for the following analysis.
The observed CO emission originates in the outer layers of the disk,
at heights that depend on the optical depth of the specific
transition. Once the disk structure is specified, as described above,
one needs to compute, at each radius, the gas temperature profile in
the vertical direction. This is a complex problem, whose results
depend on a number of not well known properties, among them the X-ray
field and the role of very small grains in heating the gas (e.g.,
Dullemond et al. 2006). Therefore, we use a parametric
description assuming that for each CO transition the excitation
temperature is the same at all z and can be described as a power-law of r in the form:
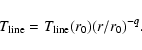 |
(4) |
In the analysis of CO observations we have assumed 12CO/H2 = 7.0 ![]() 10-5, 13CO/H2 = 1.0
10-5, 13CO/H2 = 1.0 ![]() 10-6 and C18O/H2 = 1.3
10-6 and C18O/H2 = 1.3 ![]() 10-7, which correspond to the ratios 12CO/13CO = 70, 12CO/C18O = 550 (Beckwith
& Sargent 1993; Dutrey et al. 1996, and reference therein)
10-7, which correspond to the ratios 12CO/13CO = 70, 12CO/C18O = 550 (Beckwith
& Sargent 1993; Dutrey et al. 1996, and reference therein)
As described in detail in the Appendix, we have developed a code which computes, for each CO transition, the line intensity and profile as function of the disk parameters, namely the inclination and PA, the density and temperature profile, and the disk outer radius. In addition, we assume that the disk is in Keplerian rotation around the central star and vary the stellar mass independently for each line.
In the following, we assume a gas turbulence velocity
![]() km s-1. Note that for
km s-1. Note that for
![]() in the
range observed in other TTS and HAe (0.07-0.38 km s-1 from
Piétu et al. 2007, 2005, 2003; Dutrey et al. 1994, 1996; Dartois et al. 2003; Simon et al. 2001) the results does not change. This is due
to the fact that, for the inclination of the HD 163296 disk, the CO lines width is dominated by the differential disk rotation.
in the
range observed in other TTS and HAe (0.07-0.38 km s-1 from
Piétu et al. 2007, 2005, 2003; Dutrey et al. 1994, 1996; Dartois et al. 2003; Simon et al. 2001) the results does not change. This is due
to the fact that, for the inclination of the HD 163296 disk, the CO lines width is dominated by the differential disk rotation.
The observations of HD 163296 have been analyzed by comparing the
observed and the model predicted complex visibilities. For each set of
data, the best fit model has been obtained minimizing the
![]() ,
where
,
where
![]() and
and
![]() are the real and the imaginary part of
the complex visibility measured (obs) and predicted (mod) in the
point i of the uv-plane, and Wi is the weight of each
measure. For each CO transition, the
are the real and the imaginary part of
the complex visibility measured (obs) and predicted (mod) in the
point i of the uv-plane, and Wi is the weight of each
measure. For each CO transition, the ![]() has been computed by the
simultaneous fitting of 14 velocity channels chosen in order to
optimize the sampling of the line profile. The
has been computed by the
simultaneous fitting of 14 velocity channels chosen in order to
optimize the sampling of the line profile. The ![]() minimization
has been performed exploring a wide region of the space of model
parameters. For each parameter, the 1
minimization
has been performed exploring a wide region of the space of model
parameters. For each parameter, the 1![]() uncertainties are
estimated as
uncertainties are
estimated as
![]() ,
where n is
the number of degrees of freedom and
,
where n is
the number of degrees of freedom and
![]() is the
is the ![]() value
of best fit model.
value
of best fit model.
![\begin{figure}
\par\includegraphics[angle=270,width=16.45cm,clip]{7385fig7.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg81.gif) |
Figure 7:
Maps of the residuals relative to the
best fit model for the continuum emission (see Fig. 1
for the observations). The contour level are spaced by |
The continuum data at the four observed wavelengths
(0.87, 1.3, 2.7, 7 mm) have been analyzed independently to estimate
the best disk parameters and their uncertainties. We have varied the two parameters that define the position of the disk on the plane of the
sky, namely the inclination and position angle, as well as the three physical parameters which affect the continuum dust emission, namely
the disk outer radius
![]() ,
the slope p of the surface density
profile and the product
,
the slope p of the surface density
profile and the product
![]() .
Since the continuum emission has a very weak dependence on the mass of
the central star, we fixed
.
Since the continuum emission has a very weak dependence on the mass of
the central star, we fixed ![]() = 2.6
= 2.6 ![]() (see Sect. 5.3).
(see Sect. 5.3).
The values of the parameters obtained at different wavelengths are the same within the uncertainties. In Col. 1 of Table 2 we show the values of the resulting best fit model obtained by combining the independent results at the four different wavelengths. The constraints are dominated by the 1.3 mm data, which have the best sensitivity and resolution.
The surface density radial profile has a slope p = 0.81 ![]() 0.01 and
the disk outer radius is
0.01 and
the disk outer radius is
![]()
![]() 15 AU. The very good
constraints on both parameters are due to the favorable orientation
of the beam at 1.3 mm with the maximum resolution (0.42
15 AU. The very good
constraints on both parameters are due to the favorable orientation
of the beam at 1.3 mm with the maximum resolution (0.42
![]() )
in
almost the same direction of the major axis of the disk.
Note that the formal error on p is extremely low. On the other
hand, small variations on the disk flaring (that allow to fit the SED)
lead to correspondingly small variation of the disk radial temperature
profile and on the value of p. Taking into account this fact,
)
in
almost the same direction of the major axis of the disk.
Note that the formal error on p is extremely low. On the other
hand, small variations on the disk flaring (that allow to fit the SED)
lead to correspondingly small variation of the disk radial temperature
profile and on the value of p. Taking into account this fact, ![]() 0.1 is a more reasonable uncertainty for p. The formal uncertainties on the other parameters are much larger than those
introduced by small variations of the flaring angle.
0.1 is a more reasonable uncertainty for p. The formal uncertainties on the other parameters are much larger than those
introduced by small variations of the flaring angle.
The four values of
![]() are used to
constrain the slope
are used to
constrain the slope ![]() of the dust opacity law (see
Eq. (3)) between 0.87 and 7 mm, which turns out to be 1.0
of the dust opacity law (see
Eq. (3)) between 0.87 and 7 mm, which turns out to be 1.0 ![]() 0.1. This confirms the presence of large grains in the HD 163296
circumstellar disk (Natta et al. 2004). Note that the optically thick disk region at 1.3 mm
has size of
0.1. This confirms the presence of large grains in the HD 163296
circumstellar disk (Natta et al. 2004). Note that the optically thick disk region at 1.3 mm
has size of ![]() 6 AU and contributes only 4% of the observed
flux, so that
6 AU and contributes only 4% of the observed
flux, so that ![]() is very similar to that derived in
Sect. 3.3. The observations constrain only the dependence of
the dust opacity on wavelength, not its absolute value. The value of
is very similar to that derived in
Sect. 3.3. The observations constrain only the dependence of
the dust opacity on wavelength, not its absolute value. The value of
![]() given in Table 2 is obtained from
given in Table 2 is obtained from
![]() assuming
assuming
![]() cm2/g.
cm2/g.
The residuals for each wavelength
are shown in Fig. 7. They have been reconstructed
from the residuals in the uv-plane with the same procedure used to
obtain the images in Fig. 1. Residual contours are
generally lower than ![]() with the exception of the 0.87 and
1.3 mm maps, where a flux asymmetry in the east half of the map (see
also Sect. 3.1) is clearly visible. This structure, not
detected at longer wavelengths, requires more resolved observations to
be investigated in detail.
with the exception of the 0.87 and
1.3 mm maps, where a flux asymmetry in the east half of the map (see
also Sect. 3.1) is clearly visible. This structure, not
detected at longer wavelengths, requires more resolved observations to
be investigated in detail.
The analysis of the CO emission has been carried out separately for the different CO transitions and the corresponding best fit parameters are given in Table 2.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{7385fig8.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg86.gif) |
Figure 8:
Comparison between the observed and the
model predicted 12CO J = 2-1 emission. The upper panel shows the
position-velocity diagram for the 12CO J = 2-1 transition (as in
Fig. 5). The lower panel shows the residuals relative
to the best fit model parameters reported in Table 2. The
contour levels are at 2 |
The observed 12CO J = 2-1 emission is well fitted by a Keplerian disk orbiting a central star with mass
![]()
![]() .
Figure 8 shows the
position-velocity residuals obtained subtracting the best fit model
from the observed uv-table: no evidence of non-Keplerian rotation or
stellar outflow is detected, within the actual instrumental
sensitivity. Both the position angle and the
inclination are in agreement with the values
obtained from the continuum. Since the line is optically thick, the
constraint on the gas surface density is poor. The
inferred outer radius of the disk is 550
.
Figure 8 shows the
position-velocity residuals obtained subtracting the best fit model
from the observed uv-table: no evidence of non-Keplerian rotation or
stellar outflow is detected, within the actual instrumental
sensitivity. Both the position angle and the
inclination are in agreement with the values
obtained from the continuum. Since the line is optically thick, the
constraint on the gas surface density is poor. The
inferred outer radius of the disk is 550 ![]() 50 AU, more than two times larger than the value obtained from the continuum and similar to
the result obtained by Thi et al. (2004) from the model
fitting of single dish line profiles. The
radial temperature profile of the 12CO has a slope
q=0.5+0.2-0.1 and a value of
40+2-5 K at 100 AU.
50 AU, more than two times larger than the value obtained from the continuum and similar to
the result obtained by Thi et al. (2004) from the model
fitting of single dish line profiles. The
radial temperature profile of the 12CO has a slope
q=0.5+0.2-0.1 and a value of
40+2-5 K at 100 AU.
Since the 12CO J = 3-2 line is optically thick and given the
relatively low resolution of the SMA observations, the
measurements do not constrain the CO radial density profile. In this
case we fix both p and
![]() equal to the values obtained
for the 12CO J = 2-1 and vary the other parameters. The
results for the inclination, position angle, disk outer radius and CO temperature are in good agreement with the values obtained for the
12CO J = 2-1, with larger uncertainties due to the lower spatial
resolution.
equal to the values obtained
for the 12CO J = 2-1 and vary the other parameters. The
results for the inclination, position angle, disk outer radius and CO temperature are in good agreement with the values obtained for the
12CO J = 2-1, with larger uncertainties due to the lower spatial
resolution.
Finally, the model fit to the 13CO J = 1-0 line gives results
consistent with those obtained from the 12CO lines with the exception
of the value of
![]() which is significantly smaller. This
discrepancy may be due to a depletion of the 13CO and will be
discussed in Sect. 6.5. The radial temperature profile of
the 13CO has a slope q=0.8
which is significantly smaller. This
discrepancy may be due to a depletion of the 13CO and will be
discussed in Sect. 6.5. The radial temperature profile of
the 13CO has a slope q=0.8 ![]() 0.4 and a value of 30
0.4 and a value of 30 ![]() 10 K
at 100 AU. We will comment on the gas physical conditions in
Sect. 6.5. In general, the parameter constraints obtained
from the 13CO are not as good as those obtained for the 12CO J = 2-1, as expected given the lower resolution of the observations.
10 K
at 100 AU. We will comment on the gas physical conditions in
Sect. 6.5. In general, the parameter constraints obtained
from the 13CO are not as good as those obtained for the 12CO J = 2-1, as expected given the lower resolution of the observations.
The disk orientation is well determined by our set of
measurements: it has a moderate inclination with respect to the
line of sight (the mean of the inclination values is
46![]()
![]() 4
4![]() )
with a position angle of 128
)
with a position angle of 128![]()
![]() 4
4![]() .
.
All the observations are consistent with the emission of a circumstellar disk in Keplerian rotation around a star of 2.6 ![]() ,
assuming the Hipparcos distance of
122+17-13 pc (van den Ancker et al. 1998). Within the
error, the stellar mass is in agreement with the value of 2.3
,
assuming the Hipparcos distance of
122+17-13 pc (van den Ancker et al. 1998). Within the
error, the stellar mass is in agreement with the value of 2.3 ![]() (Natta et al. 2004) obtained from the location of the star on
the HR diagram, using Palla & Stahler (1993) evolutionary
tracks; the corresponding stellar age is of about 5 Myr.
(Natta et al. 2004) obtained from the location of the star on
the HR diagram, using Palla & Stahler (1993) evolutionary
tracks; the corresponding stellar age is of about 5 Myr.
The model fitting (Table 2) shows that the value of the disk
outer radius inferred from the continuum dust emission
(200 ![]() 15 AU) is almost three times smaller than the value obtained
from the CO analysis (where 540
15 AU) is almost three times smaller than the value obtained
from the CO analysis (where 540 ![]() 40 AU is the mean value). Since
our method takes into account the sensitivity limits of the different
interferometric observations, this discrepancy can not be explained by
the fact that the disk outer regions have a continuum surface
brightness below the sensitivity limit. If we extend
the disk model that fits the continuum to the outer radius of the CO,
we predict a continuum emission between 200 AU and 550 AU which would
be easily detected in our observations (see Fig. 9). A similar difference in the dust and gas outer radii has been also
reported by Piétu et al. (2005) for the Herbig Ae star AB Aur.
40 AU is the mean value). Since
our method takes into account the sensitivity limits of the different
interferometric observations, this discrepancy can not be explained by
the fact that the disk outer regions have a continuum surface
brightness below the sensitivity limit. If we extend
the disk model that fits the continuum to the outer radius of the CO,
we predict a continuum emission between 200 AU and 550 AU which would
be easily detected in our observations (see Fig. 9). A similar difference in the dust and gas outer radii has been also
reported by Piétu et al. (2005) for the Herbig Ae star AB Aur.
To reconcile the CO and the dust observations, it is necessary to introduce a sharp drop in the continuum emission of a factor >30 at a radius of about 200 AU. With such a drop, the millimeter fluxes at larger r will be below the sensitivity of our observations and will be lost in the observational noise. What can be the origin of such a drop?
In the optically thin regime, which is appropriate for the outer
regions of the disk, the continuum flux emitted at distance r from the star depends on the mass surface density ![]() ,
the dust/gas ratio
,
the dust/gas ratio ![]() ,
the dust opacity
,
the dust opacity ![]() and the midplane dust temperature T(r) through the relation
and the midplane dust temperature T(r) through the relation
A second possibility to explain the observed flux depletion is that
the dust opacity ![]() at distance larger than 200 AU is much
lower because most of the grains have grown into very large
bodies.
at distance larger than 200 AU is much
lower because most of the grains have grown into very large
bodies.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{7385fig9.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg93.gif) |
Figure 9:
Model predicted 1.3 mm continuum
emission obtained extrapolating the dust surface density inferred
inside the radius of 200 AU to the CO outer radius of 550 AU. The
contours are spaced by 3 |
Finally, a third possibility is that the dust density, i.e.
![]() ,
is in some way depleted at large distances. The values
of the gas density
,
is in some way depleted at large distances. The values
of the gas density ![]() obtained by the CO lines analysis (see Table 2) induce however to exclude the existence of the strong discontinuity in the gas radial density
profile required to explain a flux depletion factor >30 since a drop of a factor
obtained by the CO lines analysis (see Table 2) induce however to exclude the existence of the strong discontinuity in the gas radial density
profile required to explain a flux depletion factor >30 since a drop of a factor ![]() 10 in the 13CO distribution at r>200 AU will already produce small but observable
effects on the line emission. On the other hand, it is possible that
the ratio dust/gas
10 in the 13CO distribution at r>200 AU will already produce small but observable
effects on the line emission. On the other hand, it is possible that
the ratio dust/gas ![]() decreases very
rapidly in the outer disk either due to the formation and fast
migration of meter size bodies or to the presence of planetesimals or
planets which create a gap in the dust distribution. It is worth
noting that the dynamical perturbation induced by such large bodies on
the surrounding material (see the review of Papaloizou et al. 2007) may also account for the asymmetric dust density distribution detected in the continuum maps
(Fig. 7).
decreases very
rapidly in the outer disk either due to the formation and fast
migration of meter size bodies or to the presence of planetesimals or
planets which create a gap in the dust distribution. It is worth
noting that the dynamical perturbation induced by such large bodies on
the surrounding material (see the review of Papaloizou et al. 2007) may also account for the asymmetric dust density distribution detected in the continuum maps
(Fig. 7).
The presence of a giant planet, or a brown dwarf, orbiting in the outer disk of HD 163296 has also be suggested by Grady et al. (2000), in order to explain the dark line observed in the scattered light HST images between 300 AU and 350 AU from the central star. While planets are invoked to explain the large inner gaps observed in the dust distribution in the so called "transitional disks'' (i.e., Calvet et al. 2005), HD 163296 will be, if confirmed by future observations, the first case in which a sub-stellar mass companion is found in the outer disk of a pre-main sequence star.
Both the dust continuum emission and the CO lines indicate a rather
shallow surface density profile,
![]() corresponding to a gas + dust mass of 0.05
corresponding to a gas + dust mass of 0.05 ![]() 0.01
0.01 ![]() if the
disk outer radius is 200 AU. However, if, as we believe, the gaseous
disk extends with the same surface density profile all way to 540 AU
the inferred disk mass is much larger, 0.17
if the
disk outer radius is 200 AU. However, if, as we believe, the gaseous
disk extends with the same surface density profile all way to 540 AU
the inferred disk mass is much larger, 0.17 ![]() .
.
An additional uncertainty on the disk mass comes from the
uncertainty on the dust opacity, as discussed in Natta et al. (2007). Although a disk mass of 0.17 ![]() (6% of
(6% of ![]() )
is probably a lower limit, the observed Keplerian rotation pattern
indicates that the disk should not be much more massive. In this case
one expects deviations from Keplerian rotation (Lodato & Bertin 2003) as observed in massive disks (Cesaroni et al. 2005).
)
is probably a lower limit, the observed Keplerian rotation pattern
indicates that the disk should not be much more massive. In this case
one expects deviations from Keplerian rotation (Lodato & Bertin 2003) as observed in massive disks (Cesaroni et al. 2005).
The example of HD 163296 illustrates how the simple disk mass
derivation from the observed millimeter flux (see
Sect. 3.4) can be wrong for a variety of reasons, even
when the emission is optically thin. In the case of HD 163296, only
30% of the total mass (i.e., the fraction inside 200 AU)
contributes to the continuum millimeter flux. On the other hand, the
disk is hotter than the 30 K assumed in Eq. (2). The two effects cancel in part so that the "simple'' and "correct'' values
differ by about 50% (for the same
![]() normalization).
normalization).
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{7385fi10.ps}\end{figure}](/articles/aa/full/2007/25/aa7385-07/Timg97.gif) |
Figure 10: Comparison between the dust and the CO temperature. As labelled in the figure, the thin-solid line correspond to the dust temperature in the optically thin disk surface, while the thick solid line corresponds to the dust temperature in the disk interior. The CO temperature is indicated with the shaded region, taking into consideration the uncertainties. The model parameters are those reported in Col. 3 of Table 2. |
At the actual gas density both the 12CO and 13CO lines
are optically thick and lead to similar CO excitation temperatures
expressed by the relation
![]() K
K
![]() AU)-0.5.
Figure 10 shows the comparison between this CO temperature
(shaded region) and the dust temperature corresponding to the same
disk model. The disk interior temperature Ti (thick-solid
line) and the disk surface temperature
AU)-0.5.
Figure 10 shows the comparison between this CO temperature
(shaded region) and the dust temperature corresponding to the same
disk model. The disk interior temperature Ti (thick-solid
line) and the disk surface temperature ![]() (thin-solid line),
calculated using our two-layer disk model, correspond respectively to
disk regions where
(thin-solid line),
calculated using our two-layer disk model, correspond respectively to
disk regions where
![]() and
and
![]() (Dullemond et al. 2002);
(Dullemond et al. 2002);
![]() is the optical depth
for the stellar radiation calculated along the radial direction. The
equivalence between the CO and the dust temperature can thus be
interpreted as the evidence that the CO, and in particular the
12CO, lines are emitted by the gas present at such values of the
optical depth, e.g. well under the disk surface. Is this result
compatible with the high optical depth of the 12CO lines?
is the optical depth
for the stellar radiation calculated along the radial direction. The
equivalence between the CO and the dust temperature can thus be
interpreted as the evidence that the CO, and in particular the
12CO, lines are emitted by the gas present at such values of the
optical depth, e.g. well under the disk surface. Is this result
compatible with the high optical depth of the 12CO lines?
Assuming that H2 and CO are well mixed all over the vertical
extension of the disk and assuming also the standard ratio
12CO/H2 = 7.0 ![]() 10-5, the 12CO lines should be
emitted by disk regions well above the disk surface, defined as the
height where
10-5, the 12CO lines should be
emitted by disk regions well above the disk surface, defined as the
height where
![]() .
In this situation, we expect a CO temperature close to the disk surface temperature, or even higher if the gas and the dust are decoupled (Jonkheid et al. 2007). On the other hand CO molecules on the superficial layers of the
disk are expected to be photo-dissociated by the UV photons emitted by
the hot central star. In particular, for an Herbig Ae star similar to
HD 163296, Jonhkeid et al. (2007) show that the CO photo-dissociation occurs in the disk regions where the optical depth
to the stellar UV radiation field is
.
In this situation, we expect a CO temperature close to the disk surface temperature, or even higher if the gas and the dust are decoupled (Jonkheid et al. 2007). On the other hand CO molecules on the superficial layers of the
disk are expected to be photo-dissociated by the UV photons emitted by
the hot central star. In particular, for an Herbig Ae star similar to
HD 163296, Jonhkeid et al. (2007) show that the CO photo-dissociation occurs in the disk regions where the optical depth
to the stellar UV radiation field is
![]() (see Fig. 5.6 therein). Therefore, the CO and disk interior temperature are
expected to be similar if
(see Fig. 5.6 therein). Therefore, the CO and disk interior temperature are
expected to be similar if
![]() ,
i.e.,
if
,
i.e.,
if
![]() ,
where
,
where
![]() is the dust
opacity averaged on the stellar spectrum. We think that this is the
case in HD 163296.
is the dust
opacity averaged on the stellar spectrum. We think that this is the
case in HD 163296.
The dust opacity is a complex quantity that depends on the dust
chemical composition, structure and on the grain size
distribution. The condition
![]() is generally
satisfied by large grains. In the case of HD 163296 one needs, for
example, compact silicate grains larger than 0.1
is generally
satisfied by large grains. In the case of HD 163296 one needs, for
example, compact silicate grains larger than 0.1 ![]() m or porous
grains of silicate and carbonaceous materials larger than few microns
(see Fig. 11). Cooler stars require larger grains,
unless significant UV excess is present.
m or porous
grains of silicate and carbonaceous materials larger than few microns
(see Fig. 11). Cooler stars require larger grains,
unless significant UV excess is present.
If CO survives only in the disk interior, we expect that lines with different optical depth will have similar temperatures. On the contrary, if CO is present in the disk surface layers, lines with higher optical depth should have higher excitation temperatures.
The few existing observations indicate that all cases occur. Piétu et al. (2007) have recently reported that for the HAe stars MWC 480 and AB Aur and the TTS DM Tau, the 12CO and 13CO lines are characterized by different temperatures, while in the case of the TTS LkCa 15 the CO temperatures are all similar. We suggest that these differences are due to different dust properties (i.e. different composition, grain growth and settling) and stellar spectra.
The values of
![]() reported in Table 2 indicate
that the 13CO J = 1-0 emission requires a ratio
13CO/H2
reported in Table 2 indicate
that the 13CO J = 1-0 emission requires a ratio
13CO/H2 ![]() 10-7, about a factor 10 lower than what found in
interstellar clouds. From the non-detection of the C18O J = 1-0 line we estimate that the C18O should be depleted of a factor >60 with respect to the typical ratio
12CO/C18O = 550. We note that a similar trend of depletion from 12CO to 13CO
and C18O has been found by Dutrey et al. (1994, 1996) in a number of TTS. On the other hand an over-abundance of 13CO has been found in DM Tau, MWC 480 and
LkCa 15 (Piétu et al. 2007) while for DM Tau, Dartois et al. (2003) find that all the CO isotopomers (12CO, 13CO and C18O) are depleted by the same factor
10-7, about a factor 10 lower than what found in
interstellar clouds. From the non-detection of the C18O J = 1-0 line we estimate that the C18O should be depleted of a factor >60 with respect to the typical ratio
12CO/C18O = 550. We note that a similar trend of depletion from 12CO to 13CO
and C18O has been found by Dutrey et al. (1994, 1996) in a number of TTS. On the other hand an over-abundance of 13CO has been found in DM Tau, MWC 480 and
LkCa 15 (Piétu et al. 2007) while for DM Tau, Dartois et al. (2003) find that all the CO isotopomers (12CO, 13CO and C18O) are depleted by the same factor
![]() 10. The observational picture is still very uncertain and
deserves further investigations.
10. The observational picture is still very uncertain and
deserves further investigations.
In the case of HD 163296, the gas temperature always higher than 20 K rules out the condensation of CO onto dust grains as possible cause of the CO isotopomers depletion. Alternatively, Jonkheid et al. (2007) have recently pointed out that a higher ratio between the 12CO and its isotopomers may be the consequence of grain growth and settling. This latter hypothesis is more convincing given the evidence of grain growth in the HD 163296 disk discussed in this work (see Sects. 5.2 and 6.5).
This paper presents new observations of the disk of HD 163296 in the dust continuum from 0.87 to 7 mm, 12CO (J = 2-1 and J = 3-2) and 13CO (J = 1-0) lines. The disk is resolved in all lines and continuum.
We have compared the observations to the predictions of self-consistent disk models. We find that the disk, as seen in CO lines, is very large (R=540 AU), with a Keplerian rotation
pattern consistent with a central mass of 2.6 ![]() .
Within the
observational errors, there is no evidence of non-Keplerian motions
and/or significant turbulent broadening. We obtain a disk inclination
of 46
.
Within the
observational errors, there is no evidence of non-Keplerian motions
and/or significant turbulent broadening. We obtain a disk inclination
of 46![]() ,
significantly lower than the value of
,
significantly lower than the value of ![]() 60
60![]() found
in literature.
found
in literature.
The dust opacity has a power law dependence on wavelength
![]() with
with ![]()
![]() 0.1 in the interval
0.87-7 mm. This value is similar to what has been measured in a number
of spatially resolved disks of HAe and TTS (e.g., Natta et al. 2004; Rodmann et al. 2006), and is very likely an indication that the bulk of the solid material in these
disks has coagulated into very large bodies, of millimeter and
centimeter size (Natta et al. 2007). Within the accuracy
of our data we do not confirm the possible variation of
0.1 in the interval
0.87-7 mm. This value is similar to what has been measured in a number
of spatially resolved disks of HAe and TTS (e.g., Natta et al. 2004; Rodmann et al. 2006), and is very likely an indication that the bulk of the solid material in these
disks has coagulated into very large bodies, of millimeter and
centimeter size (Natta et al. 2007). Within the accuracy
of our data we do not confirm the possible variation of ![]() with r discussed in Natta et al. (2007).
with r discussed in Natta et al. (2007).
The continuum observations constrain the surface density profile
(
![]() )
for
)
for
![]() AU. At larger radii,
the continuum emission drops with respect to the model predictions by
a factor 30 at least (at 1.3 mm). We argue that this may be due to the
clearing of a very large gap by dynamical perturbations from a low
mass companion or to the inward migration of the large bodies that may
form in the outer disk.
AU. At larger radii,
the continuum emission drops with respect to the model predictions by
a factor 30 at least (at 1.3 mm). We argue that this may be due to the
clearing of a very large gap by dynamical perturbations from a low
mass companion or to the inward migration of the large bodies that may
form in the outer disk.
The temperatures derived for CO lines of different optical depth are
similar and equal to the dust temperature in the disk interior (
![]() ). This requires that the dust
opacity in the UV (which controls the CO dissociation) and in the
wavelength range where the stellar radiation peaks are similar, as
expected if grains have grown to micron size.
Differences in the temperature of the CO lines can only be expected if
CO is present in the disk surface layers. A variety of situations can
occur depending on the exact dust composition and sizes and on the
stellar radiation field.
). This requires that the dust
opacity in the UV (which controls the CO dissociation) and in the
wavelength range where the stellar radiation peaks are similar, as
expected if grains have grown to micron size.
Differences in the temperature of the CO lines can only be expected if
CO is present in the disk surface layers. A variety of situations can
occur depending on the exact dust composition and sizes and on the
stellar radiation field.
A comparison of the disk properties derived from the dust continuum and the CO lines shows that the 13CO J = 1-0 emission is consistent with a ratio of 13CO/H2 and C18O/H2 about a factor 10 and 60 lower than what is found in interstellar clouds.
The results discussed in this work can be interpreted as clues to the evolution occurring in the HD 163296 system. The presence of large grains in the disk midplane, the equivalence between the dust and CO temperature, the drop in the continuum dust emission further out 200 AU, its detected asymmetry and, maybe, the CO isotopomers depletion, all support the idea that the circumstellar disk is probably harboring the formation of large bodies, being in between a Class II pre-main sequence disk and an older debris disk.
On the other hand, it is important to underline that HD 163296 strongly differs from the so called transitional disks (Calvet et al. 2005) characterized by a clearing of the inner disk supposed to be originated by the presence of a giant planet. In the case of HD 163296, it is the outer disk that appear dust depleted. This conclusion opens a number of theoretical problem about how dust grains can growth in the low density outer disk environment. In this respect the recently improved PBI array, the new CARMA array and ALMA will bring in the next future to real observational breakthrough in the comprehension of circumstellar disk evolution and planetary formation.
Acknowledgements
The authors acknowledge partial support for this project by MIUR PRIN grant 2003/027003-001. A.I. acknowledge Riccardo Cesaroni, Malcolm Walmsley, Giuseppe Bertin, Ewine van Dishoek and Anneila Sargent for their help and useful suggestions.
In order to analyze the CO emission we developed a numerical code
that solve the general formulation of the radiation transfer
equation along each direction between the observer and the
emitting source. If s is the linear coordinate along the line of
sight, increasing from the observer (
![]() )
towards the source,
the observed emission in each direction is given by the relation
)
towards the source,
the observed emission in each direction is given by the relation
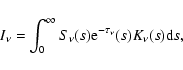 |
(A.1) |
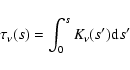 |
(A.2) |
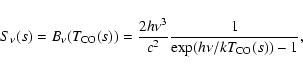 |
(A.3) |
The absorbing coefficient of the circumstellar medium is due both to
gaseous CO and dust:
![]() .
For
the dust
.
For
the dust
![]() ,
where
,
where ![]() is
the local density of the circumstellar material (gas+dust) and
is
the local density of the circumstellar material (gas+dust) and ![]() is the dust absorbing coefficient for total mass unit given in
Eq. (3). The CO absorbing coefficient is given by the
relation
is the dust absorbing coefficient for total mass unit given in
Eq. (3). The CO absorbing coefficient is given by the
relation
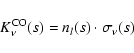 |
(A.4) |
Calling m0 and
![]() the mean molecular weight of the gas and
the fraction of CO present in the gas respectively, the number of
molecules nl(s) is given by the Boltzman equation
the mean molecular weight of the gas and
the fraction of CO present in the gas respectively, the number of
molecules nl(s) is given by the Boltzman equation
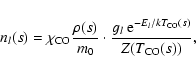 |
(A.5) |
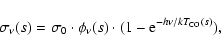 |
(A.6) |
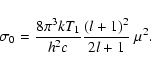 |
(A.9) |
As shown in Fig. 5 and described in
Sect. 3.2, the observed velocity patterns in the CO transitions are in good agreement with the Keplerian rotation of the disk. We can thus assume that gas moves on circular orbits around
the star characterized by a tangential velocity
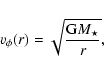 |
(A.10) |
 |
(A.11) |
Finally, the velocity vk(s) can be calculated for each direction,
knowing the geometrical transformations between the coordinate salong the line of sight and the cylindrical coordinates r and ![]() .
.
In order to solve the described set of equations, we thus need an expression for the circumstellar mass density ![]() and the temperature of the emitting gas
and the temperature of the emitting gas
![]() .
In both cases we can
assume the cylindrical symmetry and write
.
In both cases we can
assume the cylindrical symmetry and write
![]() and
and
![]() .
.
For the emitting gas temperature, we choose the parameterization
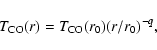 |
(A.12) |
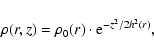 |
(A.13) |
Finally, the pressure scale h(r) is given by the relation
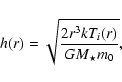 |
(A.15) |
Note that the emitting gas temperature
![]() has been parametrized
independently of the disk interior temperature Ti, which governs
the density structure of the disk. As pointed out by Dartois et al. (2003), the more optically thick CO transitions may by
good tracer of the disk surface where the gas temperature is different
from the disk interior.
has been parametrized
independently of the disk interior temperature Ti, which governs
the density structure of the disk. As pointed out by Dartois et al. (2003), the more optically thick CO transitions may by
good tracer of the disk surface where the gas temperature is different
from the disk interior.
The resulting model, produces brightness maps for each frequency (see Fig. A.2) that can be compared with the observations presented in Figs. 2 and 3.