A&A 467, 375-383 (2007)
DOI: 10.1051/0004-6361:20066287
G. A. Gary1 - C. Pietraszewski2 - E. A. West1 - T. C. Dines2
1 - National Space Science and Technology Center,
Marshall Space Flight Center, Huntsville, AL, 35812, USA
2 -
IC Optical Systems Ltd., Beckenham, Kent, BR34TW, UK
Received 22 August 2006 / Accepted 23 January 2007
Abstract
Aims. The confocal Fabry-Pérot interferometer allows sub-picometer spectral resolution of Fraunhofer line profiles. Such high spectral resolution is needed to keep pace with the higher spatial resolution of the new set of large-aperture solar telescopes. The line-of-sight spatial resolution derived for line profile inversions would then track the improvements of the transverse spatial scale provided by the larger apertures. In particular, profile inversion allows improved velocity and magnetic field gradients to be determined independent of multiple line analysis using different energy levels and ions. The confocal interferometer's unique properties allow a simultaneous increase in both étendue and spectral power. The higher throughput for the interferometer provides significant decrease in the aperture, which is important in spaceflight considerations.
Methods. We have constructed and tested two confocal interferometers. A slow-response thermal-controlled interferometer provides a stable system for laboratory investigation, while a piezoelectric interferometer provides a rapid response for solar observations.
Results. In this paper we provide design parameters, show construction details, and report on the laboratory test for these interferometers. The field of view versus aperture for confocal interferometers is compared with other types of spectral imaging filters. We propose a multiple etalon system for observing with these units using existing planar interferometers as pre-filters. The radiometry for these tests established that high spectral resolution profiles can be obtained with imaging confocal interferometers. These sub-picometer spectral data of the photosphere in both the visible and near-infrared can provide important height variation information. However, at the diffraction-limited spatial resolution of the telescope, the spectral data is photon starved due to the decreased spectral passband.
Key words: Sun: atmosphere - instrumentation: interferometers - Sun: magnetic fields - Sun: general - Sun: infrared
Solar physicists are beginning, on a regular basis, to spatially
resolve below 100 kilometer on the sun by employing optical 1-m class, and larger, aperture telescopes (Schlichenmaier 2006;
Bettonvil 2004; Keil et al. 2004; Bernasconi et al. 1999). It
is conceivable to resolve to ![]() 10 km in the next couple
of decades with semi-monolithic or interferometric telescopes
(Davis et al. 2005; Hammerschlag et al. 2004; Damé 1994). These operational,
under-construction, or conceived telescopes include Flare-Genesis
(0.8 m), Themis (0.9 m), Swedish Solar Telescope (1.0 m), SunRise
(1.0 m), McMath-Pierce (1.5 m), Gregor (1.5 m), Dutch Open Telescope++
(1.5 m), New Big Bear Solar Telescope (1.6 m), Advance Technology
Solar Telescope (4.0 m), Magnetic Transition Region Probe (6.0 m)
and Giant Solar Optical Telescope (11.0 m). This effort of larger
apertures for improved spatial resolution has been conducted in unison with superior
designs and techniques (e.g., improvements in (i) image stabilization
by adaptive optics for ground-based observatories, (ii) thermal designs to reduce
locally induced seeing effects, (iii) polarization resolution by lowering instrumental effects,
(iv) the size of the CCD arrays to increase the field of view, and (v)
imaging processing to allow improved data analysis). Radiative
transfer theory has improved with advanced magnetohydrodynamical numerical
simulations at the sub-granular scales to resolve elemental
flux tubes. However, visible-infrared, high-spectral-resolution
narrow-band imaging filters at a spectral resolution of
10 km in the next couple
of decades with semi-monolithic or interferometric telescopes
(Davis et al. 2005; Hammerschlag et al. 2004; Damé 1994). These operational,
under-construction, or conceived telescopes include Flare-Genesis
(0.8 m), Themis (0.9 m), Swedish Solar Telescope (1.0 m), SunRise
(1.0 m), McMath-Pierce (1.5 m), Gregor (1.5 m), Dutch Open Telescope++
(1.5 m), New Big Bear Solar Telescope (1.6 m), Advance Technology
Solar Telescope (4.0 m), Magnetic Transition Region Probe (6.0 m)
and Giant Solar Optical Telescope (11.0 m). This effort of larger
apertures for improved spatial resolution has been conducted in unison with superior
designs and techniques (e.g., improvements in (i) image stabilization
by adaptive optics for ground-based observatories, (ii) thermal designs to reduce
locally induced seeing effects, (iii) polarization resolution by lowering instrumental effects,
(iv) the size of the CCD arrays to increase the field of view, and (v)
imaging processing to allow improved data analysis). Radiative
transfer theory has improved with advanced magnetohydrodynamical numerical
simulations at the sub-granular scales to resolve elemental
flux tubes. However, visible-infrared, high-spectral-resolution
narrow-band imaging filters at a spectral resolution of
![]() /
/
![]() have not received much attention. This spectral
resolution is currently provided by the non-imaging Fourier Transform
Spectrometer (FTS) on the
National Solar Observatory (NSO)/McMatch-Pierce Telescope. Using
the FTS and studying elemental flux tubes, Stenflo et al. (1984)
point out that the spectral measurements can be independent of the
unresolved spatial elements, and hence high spectral resolution
is a key component to understanding the structure of the sun.
Mathew et al. (2003) have used the 3 pm full width half maximum
(FWHM) spectral resolution Tenerife Infrared
Polarimeter (TIP) and inverted the FeI 1.56
have not received much attention. This spectral
resolution is currently provided by the non-imaging Fourier Transform
Spectrometer (FTS) on the
National Solar Observatory (NSO)/McMatch-Pierce Telescope. Using
the FTS and studying elemental flux tubes, Stenflo et al. (1984)
point out that the spectral measurements can be independent of the
unresolved spatial elements, and hence high spectral resolution
is a key component to understanding the structure of the sun.
Mathew et al. (2003) have used the 3 pm full width half maximum
(FWHM) spectral resolution Tenerife Infrared
Polarimeter (TIP) and inverted the FeI 1.56 ![]() m Stokes
profiles using the SPINOR code to obtain an estimate of the magnetic
fields gradient in an umbral region. In general, the line-of-sight
spatial resolution derived from profile inversions should follow
the improvements in the transverse (i.e., image plane) spatial resolution with larger
apertures; however this will require sub-picometer spectral resolution.
It is clear that the use of several lines with different magnetic,
thermal, and Doppler sensitivities will help resolve the vertical information.
However this process has its problems associated directly with the sensitivity
variation which is used, i.e. different mass, different ions, different transitions,
and different Landé factors. Through using a single transition and exploring the depth by
its variation of opacity with position in the line (or response function) we avoid
these sensitivity differences. Furthermore we will show that the trade-off between
the signal-to-noise ratio and spectral resolution is acceptable.
In this paper we present the spherical or confocal interferometer,
an unnoticed technique in solar physics, which shows promise
in combining high-spectral resolution and imaging, such that
vertical gradients in mass advective flows and magnetic field
gradients can be derived on a scale compatible with the horizontal
gradients.
m Stokes
profiles using the SPINOR code to obtain an estimate of the magnetic
fields gradient in an umbral region. In general, the line-of-sight
spatial resolution derived from profile inversions should follow
the improvements in the transverse (i.e., image plane) spatial resolution with larger
apertures; however this will require sub-picometer spectral resolution.
It is clear that the use of several lines with different magnetic,
thermal, and Doppler sensitivities will help resolve the vertical information.
However this process has its problems associated directly with the sensitivity
variation which is used, i.e. different mass, different ions, different transitions,
and different Landé factors. Through using a single transition and exploring the depth by
its variation of opacity with position in the line (or response function) we avoid
these sensitivity differences. Furthermore we will show that the trade-off between
the signal-to-noise ratio and spectral resolution is acceptable.
In this paper we present the spherical or confocal interferometer,
an unnoticed technique in solar physics, which shows promise
in combining high-spectral resolution and imaging, such that
vertical gradients in mass advective flows and magnetic field
gradients can be derived on a scale compatible with the horizontal
gradients.
Normal or planar Fabry-Pérot interferometers (FPP) have a
pair of mirrored parallel plates (etalons) and the light passes
through the system when the gap between the plates is an integer
number of the wavelength (Fabry and Pérot 1902; Vaughan 1989).
The FWHM spectral passband
(
![]() )
is dependent on the separation between the plates. These FPPs
are used as standard narrow passband imaging filters in solar
physics in the US Air Forces Optical Solar Patrol Network (OSPAN,
)
is dependent on the separation between the plates. These FPPs
are used as standard narrow passband imaging filters in solar
physics in the US Air Forces Optical Solar Patrol Network (OSPAN,
![]() FWHM
FWHM ![]() 10 pm), University of Hawaii's Mees Solar Magnetograph
(
10 pm), University of Hawaii's Mees Solar Magnetograph
(
![]() FWHM
FWHM ![]() 7 pm), Göttingen Astrophysical
Institute's FPI (
7 pm), Göttingen Astrophysical
Institute's FPI (
![]() FWHM
FWHM ![]() 6.6 pm),
Arcetri Observatory's Interferometric BIdimensional Spectrometer
(IBIS,
6.6 pm),
Arcetri Observatory's Interferometric BIdimensional Spectrometer
(IBIS,
![]() FWHM
FWHM ![]() 2.3 pm), Kiepenheuer
Solar Physics Institute's Triple Etalon Solar Spectrometer (TESOS,
2.3 pm), Kiepenheuer
Solar Physics Institute's Triple Etalon Solar Spectrometer (TESOS,
![]() FWHM
FWHM ![]() 1.9 pm), and
NSO/Sacromento
Peak Observatory's dual etalon systems (
1.9 pm), and
NSO/Sacromento
Peak Observatory's dual etalon systems (
![]() FWHM
FWHM![]() 1.7 pm). For narrower FWHM filters with larger gap distances,
the confocal interferometer should be considered. A confocal (spherical)
Fabry-Pérot interferometer (FPS) differs from the parallel-plate
interferometer in that the mirrored etalons are identical spherical
surfaces where the center of radius is at the surface
of the other mirror. (Confocal means having the same foci.).
Because of the spherical surfaces, the confocal interferometer
can increase simultaneously both the spectral resolution and
throughput and should be the preferred choice of interferometers
for sub-picometer spectral filters (Hercher
1968; Vaughan 1989).
1.7 pm). For narrower FWHM filters with larger gap distances,
the confocal interferometer should be considered. A confocal (spherical)
Fabry-Pérot interferometer (FPS) differs from the parallel-plate
interferometer in that the mirrored etalons are identical spherical
surfaces where the center of radius is at the surface
of the other mirror. (Confocal means having the same foci.).
Because of the spherical surfaces, the confocal interferometer
can increase simultaneously both the spectral resolution and
throughput and should be the preferred choice of interferometers
for sub-picometer spectral filters (Hercher
1968; Vaughan 1989).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{6287fg01.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg21.gif) |
Figure 1:
The confocal optical configuration. In this configuration, the
distance, d, between the two spherical mirrors (bold arcs) is set
equal to the confocal distance, r, the radius of the spherical mirrors.
To the upper left of the confocal mirrors,
a real object is located at S1. The transmitted light paths through the
confocal mirrors and a lens are shown with the
two resulting real images
|
| Open with DEXTER | |
The path of the light through the confocal interferometer is typically
a figure-eight shape (Fig. 1) with the exit beam re-entering the direction
of the initial beam (to within paraxial approximation) (Connes
1958; Hercher 1968; Clark 1972; Vaughan 1989). For the initial
incident direction, the interference contributions to an exit
ray come after 22k reflections, where k is a positive integer.
The spherical mirrors and their associated thickness affect the
final imaging and spectral resolution however we shall show this
is not a significant effect. A main point of this paper is to describe
the imaging quality of the confocal interferometers and the possible
improvements that they could provide for solar physics, since
the confocal interferometers have greater throughput and greater
alignment tolerances than parallel plate interferometers under
certain circumstances. An offset in confocal mirror alignment
results in only a change in the optical axis of the system,
when the confocal distance, r, is corrected by normal tuning. This results in a necessary
alignment of the mirror centers to only the order of ![]() 0.1D/ r;
where as a planar Fabry-Pérot interferometer,
the alignment tolerance for parallelism is on the order of
0.1D/ r;
where as a planar Fabry-Pérot interferometer,
the alignment tolerance for parallelism is on the order of ![]()
![]() ,
where
,
where ![]() is the wavelength and D is the aperture.
is the wavelength and D is the aperture.
One concern with increasing the spectral resolution is that this implies a deficit of photons as the spectral passband is reduced, causing longer exposure times. This is obviously problematic if the diffraction-limited spatial resolution is retained. For then the dependency of the size of the telescope is canceled since the light collected is a product of the telescope area and the spatial area sampled. If the aperture is varied it will be found that the product of the telescope's aperture area and the area of the diffraction-limited resolution element on the sun is constant. At the diffraction limit resolution, the exposure times are independent of the aperture size (Table 1, last column). Therefore, to collect a reasonable number photons for spectral analysis a reduced spatial resolution is require, as we will demonstrate. We will now consider the exposure times for two wavelengths, one in the visible and one in the near infrared.
The exposure time is
determined by the time it takes to fill each detector pixel well with
electrons. This time is governed by the well capacity of the CCD and
the numbers of electrons generated each second by the light incident
on each pixel. This latter parameter is itself determined by the quantum
efficiency of the CCD and the number of photons incident each
second on the pixel, ![]() .
To determine
.
To determine ![]() ,
we consider
the total radiant energy incident on a detector pixel
per second,
,
we consider
the total radiant energy incident on a detector pixel
per second, ![]() .
.
![]() is equal to the solar radiant power per second per unit
area per unit wavelength interval at the wavelength of interest,
is equal to the solar radiant power per second per unit
area per unit wavelength interval at the wavelength of interest,
![]() ,
multiplied by the wavelength passband,
,
multiplied by the wavelength passband,
![]() ,
the area of
the telescope
,
the area of
the telescope ![]() ,
and the effective
area of a pixel on the sun,
,
and the effective
area of a pixel on the sun,
![]() ,
and corrected for transmission losses,
,
and corrected for transmission losses, ![]() :
:
![]() .
The fraction of the total area collected by the telescope that is
imaged on a detector pixel is equal to the ratio of solid angle of
the projected pixel and the solid angle of the sun.
.
The fraction of the total area collected by the telescope that is
imaged on a detector pixel is equal to the ratio of solid angle of
the projected pixel and the solid angle of the sun.
Table 1:
The diffraction limit resolution for large solar telescopes using
values in the text (
![]() nm/ 1564.8 nm).
nm/ 1564.8 nm).
Observing at the telescope diffraction-limited resolution
with the detector pixel size set
by the Nyquist spatial frequency, the pixel size is half the
diffraction-limited size. The projected solid angle of the pixel is then given
by
![]() .
The solid
angle of the sun is
.
The solid
angle of the sun is
![]() sr, hence
sr, hence
![]() .
Assuming
.
Assuming
![]() nm, a telescope
with an effective area of
nm, a telescope
with an effective area of
![]() cm2, (i.e.,
cm2, (i.e.,
![]() m), gives
m), gives
![]() sr, and
sr, and
![]() .
In the continuum, the incident solar flux is
.
In the continuum, the incident solar flux is
![]() erg cm-2 nm-1 s-1 at the wavelength
erg cm-2 nm-1 s-1 at the wavelength
![]() .
With optics providing a total optical transmittance of
.
With optics providing a total optical transmittance of
![]() and a filter of
and a filter of
![]() pm, we have:
pm, we have:
![]() = (1645 erg cm-2 nm-1 s-1)(0.001 nm)
(7845 cm2) (
= (1645 erg cm-2 nm-1 s-1)(0.001 nm)
(7845 cm2) (
![]() )
(0.01) =
)
(0.01) =
![]() erg s-1.
At a wavelength of
erg s-1.
At a wavelength of
![]() nm, each photon has an
energy of
nm, each photon has an
energy of
![]() erg, so there is a flux of
erg, so there is a flux of
![]() photons per second on a pixel.
With a 0.8 quantum-efficiency (QE)
detector the number of electrons per sec is determined (
photons per second on a pixel.
With a 0.8 quantum-efficiency (QE)
detector the number of electrons per sec is determined (
![]() ). For a
signal to noise of
S/N = 1000, the number of electrons needed to be
collected is a million. Hence, the exposure time is 18 s.
However for photometry we can use
). For a
signal to noise of
S/N = 1000, the number of electrons needed to be
collected is a million. Hence, the exposure time is 18 s.
However for photometry we can use ![]() pixel binning, i.e., a
resolution element, and reduce the exposure time to 4.5 s to collect a
million photons. In the near infrared
at
pixel binning, i.e., a
resolution element, and reduce the exposure time to 4.5 s to collect a
million photons. In the near infrared
at ![]()
![]() nm
where the diffraction limit spatial resolution is larger but the solar flux
is lower,
nm
where the diffraction limit spatial resolution is larger but the solar flux
is lower,
![]() erg cm-2 nm-1 s-1; the photon
flux is
erg cm-2 nm-1 s-1; the photon
flux is
![]() photons per second per pixel
and the exposure time is 2.9 s with an IR 0.5 QE detector. At both
wavelengths it is assumed that the pixel well depth is
photons per second per pixel
and the exposure time is 2.9 s with an IR 0.5 QE detector. At both
wavelengths it is assumed that the pixel well depth is
![]() e-. Assuming Poisson counting noise is the
dominate noise, the detector digitation then must be able to
resolve
e-. Assuming Poisson counting noise is the
dominate noise, the detector digitation then must be able to
resolve
![]() ,
e.g., 10 bit A/D.
Multiple reads of the CCD is necessary but we have assumed that
the readout rate is a fraction of the exposure time, hence the
readout is ignored. We also assumed that the dark current can be
ignored when compared with the Poisson noise.
,
e.g., 10 bit A/D.
Multiple reads of the CCD is necessary but we have assumed that
the readout rate is a fraction of the exposure time, hence the
readout is ignored. We also assumed that the dark current can be
ignored when compared with the Poisson noise.
For one spectral position the exposure times are acceptable
considering the solar dynamics time scales with respect to a diffraction-limited resolution
element on the sun. However to obtain a high-spectral-resolution line
profile at 1 pm spectral resolution and at the diffraction
limit, the exposure time become
problematic. Stepping at an interval of 0.5 pm over a spectral scan range of 30 pm, the photoelectrons for this line profile are obtained in 270 s
at
![]() V and 171 s for
V and 171 s for
![]()
![]() .
Of course, this is over the full field of view.
To obtain the full Stokes profiles, the addition
polarimetry requirements increase the total time by a factor of 6.
Therefore, to obtain full Stokes profile scans in a time significantly shorter than the solar
oscillation period, the spatial resolution must be larger than the
diffraction limit. For extended, horizontal stratified regions (e.g., penumbral Evershed flow regions)
where resolving the vertical stratification is important, the
employment of larger than diffraction-limited resolution would
be acceptable and allow shorter exposure times.
.
Of course, this is over the full field of view.
To obtain the full Stokes profiles, the addition
polarimetry requirements increase the total time by a factor of 6.
Therefore, to obtain full Stokes profile scans in a time significantly shorter than the solar
oscillation period, the spatial resolution must be larger than the
diffraction limit. For extended, horizontal stratified regions (e.g., penumbral Evershed flow regions)
where resolving the vertical stratification is important, the
employment of larger than diffraction-limited resolution would
be acceptable and allow shorter exposure times.
A main emphasis for imaging interferometry is to provide high
spatial resolution compatible with the spectral line information
to be derived. The larger the gap between the etalon
plates in either
the parallel or spherical interferometers, the higher the spectral
resolution becomes, i.e. the smaller the spectral passband. Since
the large ground-based and space-based solar telescopes,
which are planned or being built, produce higher transverse spatial
resolution on the scale of 10-200 km (Table 1); it is desirable
and necessary to also increase the spectral power to isolate
the solar physics to a comparable spatial scale in the vertical
direction. That is to dissect the line profile structure of the
line formation region (e.g., photospheric lines have a height
of formation FWHM ![]() 200-500 km). In particular to determine
the vertical (or line-of-sight) gradients of flows and fields, to the same scale
as the transverse gradients of the flows and fields, and to interrupt
the corresponding line asymmetries. The pressure scale height
for the photosphere is
200-500 km). In particular to determine
the vertical (or line-of-sight) gradients of flows and fields, to the same scale
as the transverse gradients of the flows and fields, and to interrupt
the corresponding line asymmetries. The pressure scale height
for the photosphere is ![]() 150 km and the photon mean path
is also on this scale.
150 km and the photon mean path
is also on this scale.
Having high spectral resolution is important in determining the
vertical gradients. Balasubramaniam & Uitenbroek (2001) investigated
the velocity gradients over the height of formation of the non-magnetic
sensitive iron line FeI 557.6 nm (Landé factor of g=0). They showed with numerical
modeling that a 0.5 pm passband is required to resolve the ![]() 100 m/s
advective flows. A second example infers that a sub-picometer
passband in the near infrared can determine the vertical magnetic
gradient of the normal field. Sanchez Almeida (2006) showed theoretically that the vertical
magnetic gradient can be derived from high spectral resolution observations
of a single Zeeman sensitive line. As an example of this,
the difference between the spectral Stokes V profiles of a
line formed within a magnetic field region with a decreasing gradient
and of a line formed within a constant magnetic field
is plotted in Fig. 2.
Using the umbra M model of Maltby et al. (1986) with
a magnetic field strength of B = 3000 G, velocities of
100 m/s
advective flows. A second example infers that a sub-picometer
passband in the near infrared can determine the vertical magnetic
gradient of the normal field. Sanchez Almeida (2006) showed theoretically that the vertical
magnetic gradient can be derived from high spectral resolution observations
of a single Zeeman sensitive line. As an example of this,
the difference between the spectral Stokes V profiles of a
line formed within a magnetic field region with a decreasing gradient
and of a line formed within a constant magnetic field
is plotted in Fig. 2.
Using the umbra M model of Maltby et al. (1986) with
a magnetic field strength of B = 3000 G, velocities of
![]() km s-1 and
km s-1 and
![]() km s-1,
an inclination of 45 deg, and an azimuth of 45 deg,
these magnetic field calculations were generated with vertical
field gradients of 0, -3 and -6 G/km. Independent of the polarization
strength, these differences can be resolved with sub-picometer
spectral resolution. Observationally, Mathew et al. (2003) used a profile
inversion program to infer a vertical magnetic gradient from
the TIP observations (
km s-1,
an inclination of 45 deg, and an azimuth of 45 deg,
these magnetic field calculations were generated with vertical
field gradients of 0, -3 and -6 G/km. Independent of the polarization
strength, these differences can be resolved with sub-picometer
spectral resolution. Observationally, Mathew et al. (2003) used a profile
inversion program to infer a vertical magnetic gradient from
the TIP observations (
![]() FWHM =
FWHM = ![]() 3 pm) and obtained a value of
3 pm) and obtained a value of
![]() -4 G/km.
With sub-picometer resolution, the magnetic gradient can be improved
and compared with values from other Zeeman sensitive lines at
higher heights.
-4 G/km.
With sub-picometer resolution, the magnetic gradient can be improved
and compared with values from other Zeeman sensitive lines at
higher heights.
Increasing the spatial resolution to well below 100 km has brought
about a bogus concern that visible photospheric structure will
be limited by photon diffusion to an optical mean-free-path,
i.e. about one pressure scale height, due to smoothing by radiative
transfer. If this were true, it would also effect the inversion
of the line profile and hence set a limit on the useful spectral
resolution. The argument was that the photon mean free path
is ![]() 200 km for unity optical depth at 500 nm (
200 km for unity optical depth at 500 nm (
![]() 5=1)
(Allen 1973). Countering that argument, visible observations
by Rouppe van der Voort et al. (2004, 2005) and
Stein & Nordlund's
(2006) hydrodynamic simulations have shown that much smaller structures
exist and a resolution of less than 100 km is required for the
photosphere. Bruls & von der Lühe (2001), in an analysis
of radiative transfer effects on the visibility of small-scale
structures, performed 2D non-LTE radiative transfer computations
for thin flux sheets with widths ranging from 10 to 160 km in
the solar photosphere. They demonstrated that such small structures
could be observed as small scale variations of intensity and
polarization. With the conclusion that the size limit where the
photospheric structure cannot be observed (due to smoothing radiative
transfer effects) must lie well below 10 km. Synthesis of line
profiles from dynamical flux tube simulations suggests that visible
structure in Stokes V will exist down to size scales of 5 km (Stein & Nordlund 2006). Hence scales much smaller than
100 km should be resolvable with imaging and spectral profile
inversions.
5=1)
(Allen 1973). Countering that argument, visible observations
by Rouppe van der Voort et al. (2004, 2005) and
Stein & Nordlund's
(2006) hydrodynamic simulations have shown that much smaller structures
exist and a resolution of less than 100 km is required for the
photosphere. Bruls & von der Lühe (2001), in an analysis
of radiative transfer effects on the visibility of small-scale
structures, performed 2D non-LTE radiative transfer computations
for thin flux sheets with widths ranging from 10 to 160 km in
the solar photosphere. They demonstrated that such small structures
could be observed as small scale variations of intensity and
polarization. With the conclusion that the size limit where the
photospheric structure cannot be observed (due to smoothing radiative
transfer effects) must lie well below 10 km. Synthesis of line
profiles from dynamical flux tube simulations suggests that visible
structure in Stokes V will exist down to size scales of 5 km (Stein & Nordlund 2006). Hence scales much smaller than
100 km should be resolvable with imaging and spectral profile
inversions.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6287fg02.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg58.gif) |
Figure 2:
For the infrared iron Zeeman line at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm]{6287fg03.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg59.gif) |
Figure 3:
The upper panel plots the wavelength shift ( |
| Open with DEXTER | |
In the next section we will compare the confocal interferometer with other spectral filters in terms of field of view and aperture size. Then we will provide initial design parameters, explain the construction details for two designs, and report on the laboratory test of these units. In the conclusion, we will propose a multiple etalon system for future testing the piezoelectric-controlled unit to obtain sub-picometer spectral profiles of photospheric in both the visible and near-infrared. These observations will employ existing planar Fabry-Perót interferometers as prefilters to the confocal system.
We will now compare the confocal interferometer with other imaging
filter systems. For a 4-meter aperture telescope and for a given
set of field of views (FOVs), Fig. 3 compares the optical aperture
requirement for the confocal interferometer with an air-gap and
solid planar Fabry-Pérot interferometer (FPI), a Lyot filter, and
a Michelson interferometer. It shows that for a particular on-axis
spectral resolution (e.g., 0.5 pm, dash horizontal line in upper
panel) that the off-axis oblique chief ray at the incident angle produces
an identical wavelength shift at the edge of the FOV of the same
size as the on-axis resolution. For the particular filters this
spectral shift is dependent on the refractive index of the gap
or the particular type of interferometers. This typically sets
the spectral resolution requirement for a collimated or telecentric
optical system (Gary et al. 2003) and is due to the fact that
the oblique chief ray angle in the interferometer sets the limits to
the FOV for a given spectral resolution, via the Lagrange invariant
or the ratio of the telescope aperture to the interferometer aperture.
The confocal interferometer is similar to the Michelson
interferometers in that it allows for a small aperture
interferometer, compared to the 100 mm plus etalons for the air
gap etalon. The solid Michelson interferometer is designed for
one wavelength while confocal interferometers can cover a wide
range of wavelengths dependent on the reflectivity function of
the etalon coatings. The relative wavelength shift, ![]()
![]() /
/![]() ,
as a function of the off-axis oblique chief-ray incident angle
,
as a function of the off-axis oblique chief-ray incident angle ![]() is given by
is given by ![]()
![]() /
/
![]() ,
where constant K is 1, 1/
,
where constant K is 1, 1/![]() 2, (
2, (
![]() )/2
)/2![]()
![]() 2, (p2/
n2-p1/n1)/(p2
n2-p1n1), and
2, (p2/
n2-p1/n1)/(p2
n2-p1n1), and ![]() 2/2 respectively, for a air-gap
Fabry-Pérot filter, a solid Fabry-Pérot filter, a wide field
Lyot filter, a solid polarizing Michelson interferometer, and
the confocal interferometer, where (
2/2 respectively, for a air-gap
Fabry-Pérot filter, a solid Fabry-Pérot filter, a wide field
Lyot filter, a solid polarizing Michelson interferometer, and
the confocal interferometer, where (![]() ,
,
![]() ,
n1, and n2)
and (p1 and p2) are particular refractive indices and thicknesses
(Gary et al. 2003; Hercher 1968). From these wavelength relationships,
the confocal interferometer is nearly equivalent
to the Michelson filters, and these have an advantage
over an air-gap Fabry-Pérot interferometer because a larger
effective field of view can be obtained, or, equivalently, a
smaller aperture can be used with a given field of view. The
decrease in aperture for an air-gap interferometer is a factor
of
,
n1, and n2)
and (p1 and p2) are particular refractive indices and thicknesses
(Gary et al. 2003; Hercher 1968). From these wavelength relationships,
the confocal interferometer is nearly equivalent
to the Michelson filters, and these have an advantage
over an air-gap Fabry-Pérot interferometer because a larger
effective field of view can be obtained, or, equivalently, a
smaller aperture can be used with a given field of view. The
decrease in aperture for an air-gap interferometer is a factor
of ![]() 2 for a solid-gap (LiNbO3) etalon, a factor of
2 for a solid-gap (LiNbO3) etalon, a factor of ![]() 10
for a wide field, birefringent, Lyot filter with split-calcite
elements, and a factor of
10
for a wide field, birefringent, Lyot filter with split-calcite
elements, and a factor of ![]() 100 for a confocal and a polarizing
Michelson interferometer. However, for the ability to make multi-wavelength observations
at sub-picometer spectral resolution, the
advantage goes to a confocal interferometer.
100 for a confocal and a polarizing
Michelson interferometer. However, for the ability to make multi-wavelength observations
at sub-picometer spectral resolution, the
advantage goes to a confocal interferometer.
The characterization of a parallel plate Fabry-Pérot interferometer
(FPP) for a telecentric beam configuration gives an effective
FWHM dependent on the maximum angle of incident (![]() ),
while for a collimated beam configuration there is a variation
of line center across the FOV. The single etalon equations for
the central wavelength
),
while for a collimated beam configuration there is a variation
of line center across the FOV. The single etalon equations for
the central wavelength ![]()
![]() ,
free spectral range FSR,
total finesse F, reflectance finesse
,
free spectral range FSR,
total finesse F, reflectance finesse ![]() ,
integer order number m, and passband (
,
integer order number m, and passband (
![]() )
are given by the well-known relations: (i)
)
are given by the well-known relations: (i)
![]()
![]() n
n ![]() cos(
cos(![]() )/m, (ii)
)/m, (ii)
![]() =
=
![]() 2 /2 n
2 /2 n ![]() cos(
cos(![]() ),
(iii)
),
(iii) ![]() =
=
![]() R1/2/(1-R)
R1/2/(1-R)
![]() -
-
![]() /ln R,
and (iv)
/ln R,
and (iv)
![]() FWHM = FSR/F, where
FWHM = FSR/F, where ![]() is the etalon
gap distance for parallel plates, n is the refractive index of the gap, R is the
coating reflectance, and assuming no optical defects, i.e.,
is the etalon
gap distance for parallel plates, n is the refractive index of the gap, R is the
coating reflectance, and assuming no optical defects, i.e.,
![]() (Vaughan
1989). For small angles the wavelength shift is
(Vaughan
1989). For small angles the wavelength shift is
![]()
![]() =
= ![]()
![]()
![]() 2/2
(Fig. 3). These inter-relationships determine the specific
requirements for the parallel-plate filter. In particular for
the planar Fabry-Pérot the ratio of the spectral resolution
(
2/2
(Fig. 3). These inter-relationships determine the specific
requirements for the parallel-plate filter. In particular for
the planar Fabry-Pérot the ratio of the spectral resolution
(
![]() )
to the
étendue (
)
to the
étendue (
![]() )
is
given by
)
is
given by
![]() ,
where D is the aperture size (Herscher 1968; Vaughan 1989). Increasing
the gap distance increases the spectral power
,
where D is the aperture size (Herscher 1968; Vaughan 1989). Increasing
the gap distance increases the spectral power
![]()
![]()
![]() but decreases the étendue
but decreases the étendue
![]() /
/![]() .
.
Setting the distance between mirror centers, d, to the exact confocal
separation, r, the corresponding on-axis, paraxial formulae for the confocal (spherical)
Fabry-Pérot interferometer (FPS) are: (i) ![]()
![]() n r/m, (ii) FSR =
n r/m, (ii) FSR = ![]()
![]() 2/4 n r, (iii)
2/4 n r, (iii) ![]() =
=
![]() ,
and (iv)
,
and (iv)
![]() = FSR/F
(Vaughan 1989). The useable aperture or pupil spot radius is given
by
= FSR/F
(Vaughan 1989). The useable aperture or pupil spot radius is given
by ![]()
![]() = (
= (
![]() /
/![]() )1/4, assuming the FWHM
at this edge is within 2-1/2 of the central FWHM (Vaughan 1989).
If
)1/4, assuming the FWHM
at this edge is within 2-1/2 of the central FWHM (Vaughan 1989).
If ![]() is the beam solid angle, A is
the usable aperture area, and the refractive index is set to
unity, n = 1, the confocal étendue is given by
is the beam solid angle, A is
the usable aperture area, and the refractive index is set to
unity, n = 1, the confocal étendue is given by
![]() 2][
2][
![]() ] =
] =
![]() 2 r
2 r ![]() /
/![]() and the spectral power
and the spectral power
![]() =
= ![]() /
/
![]() FWHM = 4
FWHM = 4
![]() /
/![]() ;
hence the ratio of the resolving power to étendue
for the confocal Fabry-Pérot interferometer is given by
;
hence the ratio of the resolving power to étendue
for the confocal Fabry-Pérot interferometer is given by
![]() /
/
![]()
![]() 0.7 (2
0.7 (2 ![]() /
/
![]()
![]() )2. Hence both the
resolving power
)2. Hence both the
resolving power
![]() /
/
![]() FWHM
FWHM ![]() r and the étendue
r and the étendue
![]() increases with the confocal separation
distance. For a fixed finesse, the confocal interferometer can increase
simultaneously, both, the spectral power and throughput. For
the same FSR and for
increases with the confocal separation
distance. For a fixed finesse, the confocal interferometer can increase
simultaneously, both, the spectral power and throughput. For
the same FSR and for
![]() /2, the FPS becomes a better
choice than the FPP when
/2, the FPS becomes a better
choice than the FPP when ![]() mm because of the defect finesse (Hercher
1968). For the FPP parameters,
mm because of the defect finesse (Hercher
1968). For the FPP parameters, ![]() > 21/2D, the étendue
relation
> 21/2D, the étendue
relation
![]() states that the confocal interferometer
has greater light collecting property (Vaughan 1989, p. 194). For large-aperture solar telescopes,
the critical result is that a smaller aperture can be used for the same number of photons passing
through.
states that the confocal interferometer
has greater light collecting property (Vaughan 1989, p. 194). For large-aperture solar telescopes,
the critical result is that a smaller aperture can be used for the same number of photons passing
through.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6287fg04.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg92.gif) |
Figure 4:
The relation between the FWHM and the FSR as a function
of confocal separation (r) and reflectance (R) is plotted. The
confocal separation distances r in millimeters associated with
|
| Open with DEXTER | |
We have designed and built two sub-picometer confocal interferometer both
performing in the visible and near infrared. Each FPS was
designed with a
![]() FWHM=0.13 pm (FSR = 2 pm)
at
FWHM=0.13 pm (FSR = 2 pm)
at ![]() V=630.2 nm and
V=630.2 nm and
![]() FWHM =0.8 pm
(FSR = 12 pm) at
FWHM =0.8 pm
(FSR = 12 pm) at ![]()
![]() nm. This allows the solar
FeI Zeeman sensitive lines at
nm. This allows the solar
FeI Zeeman sensitive lines at ![]() V and
V and ![]()
![]() to be scanned and allows a frequency stabilized HeNe laser line
(
to be scanned and allows a frequency stabilized HeNe laser line
(![]()
![]() nm) to be employed for laboratory test.
The relationship between FSR, FWHM, reflectance, and confocal
separation is shown in Fig. 4 for the visible and near infrared
lines. Although the plot of reflectance versus FSR and FWHM is independent of the wavelength,
we have separated the line plots into two reflectance
groups in order to show their correlation with the confocal separation
distances for
nm) to be employed for laboratory test.
The relationship between FSR, FWHM, reflectance, and confocal
separation is shown in Fig. 4 for the visible and near infrared
lines. Although the plot of reflectance versus FSR and FWHM is independent of the wavelength,
we have separated the line plots into two reflectance
groups in order to show their correlation with the confocal separation
distances for ![]() V and
V and ![]()
![]() .
For the two wavelengths,
the largest two squares plot the corresponding design values for R=0.92for the same separation distance, r=50 mm. The set of box symbols
at the ordinate FSR = 1 pm refer to a separation of r=100 mm for
.
For the two wavelengths,
the largest two squares plot the corresponding design values for R=0.92for the same separation distance, r=50 mm. The set of box symbols
at the ordinate FSR = 1 pm refer to a separation of r=100 mm for ![]() V.
The reflectance finesse is
V.
The reflectance finesse is ![]() =
=
![]() R/(1-R2) = 18.8 and
the resolving power is
R/(1-R2) = 18.8 and
the resolving power is
![]() =
=
![]() FWHM/
FWHM/![]() = 4
= 4
![]() /
/![]() =
=
![]() for
for ![]() V and
V and
![]() for
for ![]()
![]() .
This implies a confocal separation distance of r =50 mm for sub-picometer spectral resolution, and for
ease of manufacturing the first units for testing have an aperture
of 25 mm. Because of the root-mean-square (rms) irregularities and roughness
of the spherical surfaces, the total finesse is a combination
of the reflectance finesse
.
This implies a confocal separation distance of r =50 mm for sub-picometer spectral resolution, and for
ease of manufacturing the first units for testing have an aperture
of 25 mm. Because of the root-mean-square (rms) irregularities and roughness
of the spherical surfaces, the total finesse is a combination
of the reflectance finesse ![]() and the defect finesse
and the defect finesse
![]() .
For a rms irregularity of
.
For a rms irregularity of ![]()
![]() =
= ![]() /
/
![]() ,
the
defect finesse is
,
the
defect finesse is
![]() =
=
![]() /2 (Hercher 1968). Hence
to have
/2 (Hercher 1968). Hence
to have
![]() to match the
to match the ![]() (R=0.92) then
(R=0.92) then
![]() = 38
and
= 38
and ![]()
![]() =
= ![]() /38, which is a reasonable smoothness
for the spherical etalons. For these values the total finesse
F is then F = (1/(1/
/38, which is a reasonable smoothness
for the spherical etalons. For these values the total finesse
F is then F = (1/(1/![]() 2+ 1/
2+ 1/
![]() 2))
1/2=2-1/2
2))
1/2=2-1/2![]() = 13.3.
This is an effective reflectivity of 0.88. The FWHM design values
become
= 13.3.
This is an effective reflectivity of 0.88. The FWHM design values
become
![]() FWHM=0.15 pm and 0.90 pm. Inversely,
if we had selected the total finesse to be 18.8, then the reflectance
and detect finesse must be 26.5 which give R=0.943. Hence the
final design reflectance value was set to be
FWHM=0.15 pm and 0.90 pm. Inversely,
if we had selected the total finesse to be 18.8, then the reflectance
and detect finesse must be 26.5 which give R=0.943. Hence the
final design reflectance value was set to be
![]() with surface figure to be better than
with surface figure to be better than ![]() /40.
/40.
An optical configuration for the confocal interferometer is shown
in Fig. 1 within the paraxial approximation. The rays starting
from S1 after making quadruple (or 22k) reflections are reentrant
with the original direction. After making two reflections or
22k+1, another set of rays emerge and form an additional image (S'2).
For each of the two beams, the FPS intensity is 50% that of a FPP, however,
in principle, the second beam could be recombined or used.
This second image appears to be coming from the virtual source at S2.
There are two beams that emerge back toward the source side (dashed arrows in Fig. 1).
Clark (1972) gives the imaging relationships for an imaging confocal
optical interferometer with the etalon plates with a radius of
curvature given by r and a separation of d = r+e, where e is a small
displacement. For e=0, the separation is the exact
confocal distance. The phase difference for the rays is given
by
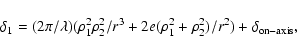 |
(1) |
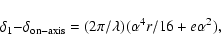 |
(2) |
![\begin{displaymath}I({\alpha})=(I_{0}/2)/[1+(2F/{\pi})^{2} \sin^{2}(\delta_{1}/2)],
\end{displaymath}](/articles/aa/full/2007/19/aa6287-06/img111.gif) |
(3) |
![\begin{displaymath}{\alpha}_{\pm}=\pm(-1) [-(8e/r) \pm (16\lambda/rF)^{1/2}]^{1/2},
\end{displaymath}](/articles/aa/full/2007/19/aa6287-06/img115.gif) |
(4) |
which gives the variation of acceptable angles for which the
passband is within FWHM. Hence if
![]() -=0 then
-=0 then
![]() + = (64
+ = (64![]() /rF)1/4
/rF)1/4 ![]() 2.8 (
2.8 (
![]() FWHM/
FWHM/![]() )1/4
)1/4
![]() 5.15 deg. This is consistent with the angle 2
5.15 deg. This is consistent with the angle 2![]()
![]()
![]() 2(
2(![]() /
/
![]() )1/4
)1/4 ![]() 3.6 deg, derived form Hercher's (1968, Eq. (17)) spot radius.
Therefore the FOV is approximately 4 deg.
3.6 deg, derived form Hercher's (1968, Eq. (17)) spot radius.
Therefore the FOV is approximately 4 deg.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6287fg05.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg118.gif) |
Figure 5: Schematic of both of the confocal Fabry-Pérot interferometers. Two sets of lines (dotted) shown have radii of confocal radii R1=50.065 and R2=60.30 with their radii centered at the center of interior mirror surfaces M1 and M2. |
| Open with DEXTER | |
For testing the image quality of the confocal interferometers,
we have constructed two confocal interferometer using IC Optical
Systems spherical mirrors of
r=r1=50.065 mm internal confocal
radius and external radius of
r2=60.30 mm.
These 25 mm diameter fused silica plates (n=1.459) have a 15 mm clear aperture and
a plate thickness of 10.235 mm. The measured mirror coating
transmittances is 5.13% at 630.98 nm and 4.97% at
1564.2 nm. The exterior surfaces, with anti-reflecting coatings
for both wavelengths (R
![]() 0.25%), were made concentric
with a radius of curvature of 60.25 mm. By employing concave-convex
etalon plates and the plate thickness, the optical power of each
etalon plate is minimized for imaging quality and spectral resolution.
The thick lens formula f-1 =
(n-1)(1/r1-1/r2 +
(n-1)/n r1 r2)
gives a relative low-power, large focal length of f
0.25%), were made concentric
with a radius of curvature of 60.25 mm. By employing concave-convex
etalon plates and the plate thickness, the optical power of each
etalon plate is minimized for imaging quality and spectral resolution.
The thick lens formula f-1 =
(n-1)(1/r1-1/r2 +
(n-1)/n r1 r2)
gives a relative low-power, large focal length of f ![]() 623 mm (while an optical Zemax code
gives f
623 mm (while an optical Zemax code
gives f ![]() -925 mm).
-925 mm).
In order to calibrate the etalon we need to be able to scan j-free
spectral ranges, i.e., the confocal displacement should be
![]() ,
a few microns. The spectral resolution
should be
,
a few microns. The spectral resolution
should be ![]() 1/10
1/10![]() of the
of the
![]() FWHM,
or about (
FWHM,
or about (
![]() )/(10 F). To infinitesimally displace the
mirrors by this amount, the two confocal interferometers
were designed to have good mechanical and environmental stability
(Fig. 5). The piezoelectric-controlled interferometer follows
the design by Budker et al. (1999) (cf., Vaughan 1989, Sect. 5.5.1).
The thermally-controlled FPS design was engineered to allow
initial precise displacement near the confocal separation.
)/(10 F). To infinitesimally displace the
mirrors by this amount, the two confocal interferometers
were designed to have good mechanical and environmental stability
(Fig. 5). The piezoelectric-controlled interferometer follows
the design by Budker et al. (1999) (cf., Vaughan 1989, Sect. 5.5.1).
The thermally-controlled FPS design was engineered to allow
initial precise displacement near the confocal separation.
The piezoelectric controller utilizes a thin-wall hallow cylinder
of lead zirconate titanate (PbZr0.52Ti0.48O3, PZT)
made of Channel Industries C-5700 and milled by Boston Piezo
Optics to a length of 10 mm, outside diameter 25 mm, and wall thickness
of 1 mm, and nickel plated (Fig. 7, lower panel). For a voltage V, the linear displacement along the
cylindrical axis is given by ![]() d =d31 L V/t, where
d31= -0.25 nm/volt is the piezoelectric constant, L is the
length of the cylinder, and t is the wall thickness of the cylinder;
then
d =d31 L V/t, where
d31= -0.25 nm/volt is the piezoelectric constant, L is the
length of the cylinder, and t is the wall thickness of the cylinder;
then ![]() d = 2.5 nm
d = 2.5 nm ![]() V or
V or
![]()
![]()
![]() V at
V at ![]() V=630.2 nm.
A voltage of 60 volts allows tuning through one free spectral range for the visible
line. For a finesse of F=13, then the displacement resolution of the tube
should be 1.2 nm or
V=630.2 nm.
A voltage of 60 volts allows tuning through one free spectral range for the visible
line. For a finesse of F=13, then the displacement resolution of the tube
should be 1.2 nm or ![]()
![]() /500 with a voltage resolution of
/500 with a voltage resolution of ![]()
![]() volt.
The coefficient of thermal expansion led to a displacement of
volt.
The coefficient of thermal expansion led to a displacement of
![]() 40 nm/C, hence the temperature needs to be stable or
known to within
40 nm/C, hence the temperature needs to be stable or
known to within ![]() 0.1 C. The calibration between voltage
and displacement is required to correct for hysteresis and nonlinearity (Fig. 8).
0.1 C. The calibration between voltage
and displacement is required to correct for hysteresis and nonlinearity (Fig. 8).
The construction schematic is shown in Fig. 5. The rear fixed mirror (M2) is in a grove attached with cyanoacrilate adhesive. The front mirror (M1) is attached to the piezoelectric cylinder (PZT) with epoxy. Between the Invar steel mounting tube and the PZT ceramics cylinder, a thin plastic-shim angular ring is placed to insure that the nickel electrodes of the PZT will not be shorted by touching the steel tube. The shim is attached to the Invar by cyanoacrilate adhesive. The PZT cylinder is attached to the shim and to the Invar via epoxy. There is a section of the shim material (1/8th of the ring) that is missing and hence the epoxy over this section is directly attached to the Invar. The wires to the PZT cylinder were attached to the nickel coated walls using Sn-62 solder. The steel parts are milled Free-Cut Invar 36 Alloy which is a low thermal expansion alloy, and allow a threaded-screw displacement for setting the initial separation of the mirrors.
The thermally-controlled design uses a 50 mm-long glass cylinder
between the confocal interferometer mirrors (Fig. 7, upper panel). Initially an all
Zerodur glass cylinder was considered with a thermal coefficient
of expansion of
![]() ppm/C. Using a thermal system that
controls the temperature to
ppm/C. Using a thermal system that
controls the temperature to ![]() T=0.1 C, implies controlling
the spacing by steps of
T=0.1 C, implies controlling
the spacing by steps of ![]()
![]()
![]() T = 50 mm
T = 50 mm ![]() 0.05
0.05
![]() 10
10
![]() nm. However, for a system
working in the IR at
nm. However, for a system
working in the IR at ![]()
![]() (or in the visible at
(or in the visible at ![]() V)
this change represents a change in the filter wavelength of
V)
this change represents a change in the filter wavelength of
![]()
![]() = 4
= 4
![]() ;
note that
;
note that ![]() refers to a small displacement associated with a wavelength change
refers to a small displacement associated with a wavelength change
![]()
![]() and
and ![]() is a
small displacement associated with a temperature change
is a
small displacement associated with a temperature change ![]() .
The offset order
.
The offset order ![]() is given by
is given by
![]() /
/![]() ,
hence
,
hence ![]()
![]() = (
= (![]() e/e)
e/e) ![]() = 5
= 5
![]() 10-9
10-9![]() and
for
and
for ![]()
![]()
![]()
![]() (or
(or ![]()
![]()
![]() V),
then
V),
then ![]()
![]()
![]()
![]() 10-5 pm
(or
10-5 pm
(or ![]()
![]() V=3.1
V=3.1
![]() 10-5 pm)
which is quite small and implies prohibitively large changes in temperature. The FWHM is
given by FSR,
10-5 pm)
which is quite small and implies prohibitively large changes in temperature. The FWHM is
given by FSR,
![]() ,
divided by the finesse F. Hence, with the refractive
index n=1, the intensity profile FWHM is
,
divided by the finesse F. Hence, with the refractive
index n=1, the intensity profile FWHM is
![]() FWHM =
FWHM = ![]() 2/(4 e F).
For
2/(4 e F).
For ![]() ,
the confocal finesse is
,
the confocal finesse is ![]() ;
;
![]()
![]() pm for
pm for ![]()
![]() ;
and
;
and
![]() FWHM
FWHM ![]() 0.13 pm for
0.13 pm for ![]() V. Again,
V. Again, ![]()
![]() needs to be some fraction of the FWHM in order to measure the
line profile, i.e.,
needs to be some fraction of the FWHM in order to measure the
line profile, i.e., ![]()
![]() /
/
![]() FWHM < 1, but
FWHM < 1, but
![]()
![]() /
/
![]()
![]() /0.8 = 9.7 for
/0.8 = 9.7 for ![]()
![]() (or
(or ![]()
![]() /
/
![]()
![]() /
/
![]() for
for ![]() V). Hence, with
Zerodur, the spectral line profile is unresolved by thermal tuning
for reasonable total changes in temperature. Therefore, the thermal control design
was refined.
V). Hence, with
Zerodur, the spectral line profile is unresolved by thermal tuning
for reasonable total changes in temperature. Therefore, the thermal control design
was refined.
The refinement was produced by employing a dual-glass cylinder
(BK7 and Zerodur) separating the spherical mirrors, where the
thermal expansion of the glass cylinder controls the inter-etalon
spacing. Assuming a set of characteristics for the FWHM and FSR
at ![]() V and
V and ![]()
![]() and assuming that at least
5 points are needed across the FWHM to define the profile sufficiently,
then Table 2 was generated assuming that the thermal control
resolution is 0.1 C. Using (
and assuming that at least
5 points are needed across the FWHM to define the profile sufficiently,
then Table 2 was generated assuming that the thermal control
resolution is 0.1 C. Using (![]() e/e) = (
e/e) = (
![]()
![]() T) = (
T) = (![]()
![]() /
/![]() )
and with the assumption that
set
)
and with the assumption that
set ![]()
![]() V = 0.02 pm, i.e. the step size, and
V = 0.02 pm, i.e. the step size, and ![]()
![]()
![]() = 0.08 pm for a change of
= 0.08 pm for a change of ![]() T=0.1 C, then
(
T=0.1 C, then
(![]() e/e)V = (
e/e)V = (
![]() ) =
) =
![]() ,
(
,
(
![]() )
)![]() = (
= (
![]() /1564.85) =
/1564.85) =
![]() for
for ![]() T=0.1 C. Therefore, with a change of
T=0.1 C. Therefore, with a change of ![]() T=1.0 C,
we have the thermal coefficient of expansion requirements for the respective wavelengths:
T=1.0 C,
we have the thermal coefficient of expansion requirements for the respective wavelengths:
![]() = (
= (![]() e/e)V =
e/e)V =
![]() and
and
![]() = (
= (![]() e/e)
e/e)![]() =
=
![]() .
Using a segment
of length of L1 of Zerodur (denoted by Z) with its TCE
.
Using a segment
of length of L1 of Zerodur (denoted by Z) with its TCE
![]() =
=
![]() and
a segment of length L2 of BK7 with
and
a segment of length L2 of BK7 with
![]() =
=
![]() then
we can obtained the correct overall CTE by solving:
then
we can obtained the correct overall CTE by solving:
![]() +
+
![]() = (L1 + L2)
= (L1 + L2)
![]() for 630.2 nm. Hence if the
overall length is
L=L1+L2 then L1(
for 630.2 nm. Hence if the
overall length is
L=L1+L2 then L1(
![]() ) = (L-L1)
(
) = (L-L1)
(
![]() )
or L1= L (
)
or L1= L (
![]() )/
(
)/
(
![]() ).
For L1/L = (
).
For L1/L = (
![]() )/(
)/(
![]() ) = 0.962 and for L=50 mm, then
L1=48.1 mm for Zerodur and
L2=1.89 mm
for BK7. Therefore by introducing a 1.89 mm segment of BK7, the
combination provides the correct over all CTE need for the visible.
The values to meet the correct CTE for the IR needs to be
L1=46.74 mm and
L2=3.26 mm
which was the final design specifications, since they also satisfy the visible requirement.
The electric requirement for 20 C temperature range and controlling the individual tripod
of legs to 0.1 C is provided by a temperature
transducer (type AD590) with a heater strip.
The measured time constant for the constructed interferometer
was 360 s. The resulting temporal sensitivity is too long for solar observations; however the
dual-glass cylinder has no associated hysteresis.
) = 0.962 and for L=50 mm, then
L1=48.1 mm for Zerodur and
L2=1.89 mm
for BK7. Therefore by introducing a 1.89 mm segment of BK7, the
combination provides the correct over all CTE need for the visible.
The values to meet the correct CTE for the IR needs to be
L1=46.74 mm and
L2=3.26 mm
which was the final design specifications, since they also satisfy the visible requirement.
The electric requirement for 20 C temperature range and controlling the individual tripod
of legs to 0.1 C is provided by a temperature
transducer (type AD590) with a heater strip.
The measured time constant for the constructed interferometer
was 360 s. The resulting temporal sensitivity is too long for solar observations; however the
dual-glass cylinder has no associated hysteresis.
The parallel plates of a FPP must be exactly parallel, i.e.,
to within ![]() /D
/D ![]() 10-6 radians. Conversely, because
of the spherical shape of the FPS, the alignment of the centers
of the mirrors needs to be only roughly aligned, to within about
0.1D/r
10-6 radians. Conversely, because
of the spherical shape of the FPS, the alignment of the centers
of the mirrors needs to be only roughly aligned, to within about
0.1D/r ![]() 10-2 radians. This allows the axial alignment
to be glued in place with no further improvement in tilt. However,
for the axial separation of the confocal mirrors, the precision
is more critical than the axial alignment and is given by
10-2 radians. This allows the axial alignment
to be glued in place with no further improvement in tilt. However,
for the axial separation of the confocal mirrors, the precision
is more critical than the axial alignment and is given by ![]() = (
= (![]()
![]() )1/2, hence, for r = 50 mm,
)1/2, hence, for r = 50 mm, ![]() = 1.564
= 1.564 ![]() m, F=15,
m, F=15, ![]() = 13
= 13 ![]() m
m
![]() 8
8 ![]() (Vaughan 1989, p. 195). However, setting
the initial separation is straight forward (Hercher 1968), and
is based on the fringe movement about the confocal separation.
The fringe pattern radius for fringe orders
(Vaughan 1989, p. 195). However, setting
the initial separation is straight forward (Hercher 1968), and
is based on the fringe movement about the confocal separation.
The fringe pattern radius for fringe orders
![]() is plotted
versus the departure from the confocal position in Fig. 6.
The thick solid line is for
is plotted
versus the departure from the confocal position in Fig. 6.
The thick solid line is for ![]() .
The dotted line is the maximum
radial dispersion curve (
.
The dotted line is the maximum
radial dispersion curve (![]() /
/![]() ). For scale,
a rectangle is defined by the spot radius of
). For scale,
a rectangle is defined by the spot radius of ![]()
![]() and
departure of
and
departure of
![]() .
The wavelength is for the photospheric visible Zeeman
sensitive line (
.
The wavelength is for the photospheric visible Zeeman
sensitive line (
![]() nm). Spot radius
nm). Spot radius ![]()
![]() is defined when the actual FWHM is
is defined when the actual FWHM is
![]() .
If the confocal departure is less than the confocal distance
(e <0), as e is decreased, the low order fringe
pattern moves outward and for e >0, as e is increased
the fringes move inwards. For the piezoelectric tuned FPS, a
fine screw adjustment allowed the confocal separation adjustment.
For the thermally tuned FPS, the glass tube was carefully polished
and checked for the proper separation and then optically contacted
to the mirrors.
.
If the confocal departure is less than the confocal distance
(e <0), as e is decreased, the low order fringe
pattern moves outward and for e >0, as e is increased
the fringes move inwards. For the piezoelectric tuned FPS, a
fine screw adjustment allowed the confocal separation adjustment.
For the thermally tuned FPS, the glass tube was carefully polished
and checked for the proper separation and then optically contacted
to the mirrors.
Table 2: Initial thermal design requirements with R=0.9.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{6287fg06.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg179.gif) |
Figure 6: Near confocal Fabry-Pérot fringe patterns. The curves give the radii of the circular interference pattern for collimated light in the paraxial approximation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{6287fg07.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg180.gif) |
Figure 7: The two constructed confocal interferometers with sub-picometer spectral resolution. For each, the confocal distance is 50 mm and the aperture is 25 mm. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{6287fg08.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg181.gif) |
Figure 8: Piezoelectric-controlled FPS scans of the HeNe laser line. The data is partially corrected for thermal drift. The solid lines are scans with the PZT voltage increasing and the dotted lines are with voltage decreasing. The separation of profiles set shows the hysteresis effect which can be corrected. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{6287fg09.eps}
\end{figure}](/articles/aa/full/2007/19/aa6287-06/Timg182.gif) |
Figure 9:
An image of part of an Air Force Resolution Chart imaged
at
|
| Open with DEXTER | |
The confocal interferometer sub-picometer test results are given
in terms of profile line scanning and imaging. In Fig. 8, the
results are shown using the piezoelectric-controlled FPS.
The scans show the hysteresis effect of the lead zirconate titanate
cylinder (cf. Crawford 1961). A Powell multiple parameter least-squares
fit of the scans determined that the sub-picometer spectral resolution was
![]() pm
with FSR = 1.99 pm, F= 6.0, and effective reflectivity of 0.77. These acceptable values include the effect of
complete optical configuration and hence the finesse is lower than the theoretical value.
pm
with FSR = 1.99 pm, F= 6.0, and effective reflectivity of 0.77. These acceptable values include the effect of
complete optical configuration and hence the finesse is lower than the theoretical value.
Figure 9 shows the imaging capability of the confocal interferometer.
An US Air Force Resolution Chart is imaged at
![]() nm.
For this large field of view, the two images of the FPS are captured by the CCD camera,
and the effects of spherical aberrations can be seen at the outer edge of the
image. The center of the optical axis is near the center of the figure.
For this magnification, the resolution is limited by the CCD.
nm.
For this large field of view, the two images of the FPS are captured by the CCD camera,
and the effects of spherical aberrations can be seen at the outer edge of the
image. The center of the optical axis is near the center of the figure.
For this magnification, the resolution is limited by the CCD.
Employing larger magnification with a zoom lens, Fig. 10 shows the center of USAF resolution charts imaged
employing an entrance mask with an aperture of
![]()
![]() mm were
F=6 and
mm were
F=6 and
![]() nm.
The image was formed using an negative pattern, 1951 USAF resolution
chart (Edumund Optics NT38-256, maximum resolution 228 lp/mm, i.e., Group 7/Element 6) using a
175 mm focal length lens with the image and object distances equal (350 mm).
The 4 mm aperture was slightly offset from the optical axis. The FOV is 2.5 deg.
With this optical configuration, the spatial resolution is only slightly degraded,
nm.
The image was formed using an negative pattern, 1951 USAF resolution
chart (Edumund Optics NT38-256, maximum resolution 228 lp/mm, i.e., Group 7/Element 6) using a
175 mm focal length lens with the image and object distances equal (350 mm).
The 4 mm aperture was slightly offset from the optical axis. The FOV is 2.5 deg.
With this optical configuration, the spatial resolution is only slightly degraded, ![]() 11%,
as seen by comparing the two images
and by comparing the images with the diffraction limit of a 4 mm aperture, which is
at the frequency giving by Group 4/Element 4 of the resolution
chart. These test result show that a FPS allows imaging interferometry at high spectral resolution.
11%,
as seen by comparing the two images
and by comparing the images with the diffraction limit of a 4 mm aperture, which is
at the frequency giving by Group 4/Element 4 of the resolution
chart. These test result show that a FPS allows imaging interferometry at high spectral resolution.
| |
Figure 10:
Images of an USAF resolution Chart at
|
| Open with DEXTER | |
The confocal interferometer sub-picometer FWHM spectral filters for visible and near-IR solar magnetography and Dopplergraphy will lead to a better understanding of the magnetic field and advective flow gradients through the solar atmosphere and links observation between different spectral lines at various heights. For high spectral resolution, a confocal (also called a spherical or Connes) interferometer enhances the scientific value of future solar satellite missions by increasing the field of view and throughput of magnetographs, decreases the cost of the mission by allowing smaller optical components, and increases the mission probability of success by relaxing optical tolerances of the interferometer. We have developed, tested, and demonstrated the imaging capabilities of a very narrow-passband confocal interferometer. The FOV and spatial resolution of a FPS is set by the diffraction limit of the confocal spot size. The spectral resolution is set by the adjustment of the confocal separation. The FPS can be use for imaging and provides sub-picometer spectral resolution. The high throughput of the FPS as compared to the FPP makes this interferometer the choice for obtaining high resolution solar line profiles.
For future studies, there are two imaging FPP instruments that
can be used as prefilters for our FPS research on solar
phenomena. In the visual and the near IR, the NSO Sacramento
Peak's high-resolution dual Queensgate Fabry-Pérot interferometers can be
employed, with the narrowest passband compatible with the FPS's
FSR. At
![]() nm the NSO's 50 mm etalons ET50-1001
(FWHM = 9.0 pm, FSR = 327 pm) and ET50-1046 (FWHM = 1.7 pm,
FSR = 72.1 pm)
can be employed. In the near IR, the etalons ET50-993 (FWHM = 11.3 pm,
FSR = 522.5 pm) and ET50-998 (FWHM = 168.3 pm, FSR = 3932 pm) could be
employed as a prefilter for the FPS. For a S/N of 500,
a 15-point
nm the NSO's 50 mm etalons ET50-1001
(FWHM = 9.0 pm, FSR = 327 pm) and ET50-1046 (FWHM = 1.7 pm,
FSR = 72.1 pm)
can be employed. In the near IR, the etalons ET50-993 (FWHM = 11.3 pm,
FSR = 522.5 pm) and ET50-998 (FWHM = 168.3 pm, FSR = 3932 pm) could be
employed as a prefilter for the FPS. For a S/N of 500,
a 15-point ![]()
![]() spectral profile scan time
is estimated to be 40 minutes using
the Dunn Solar Telescope. Also for the NIR, the New
Jersey Institute of Technology/Big Bear Solar Observatory's Near
Infrared Magnetograph (NIRM) could be employed which has a FPP
with FWHM = 8.8 pm and FSR = 548.7 pm. We plan to employ these systems
to obtain sub-picometer spectral resolution Stokes I and V line
profiles in the umbral regions to determine the vertical magnetic
field and velocity gradients across the height of formation of
the spectral lines FeI
spectral profile scan time
is estimated to be 40 minutes using
the Dunn Solar Telescope. Also for the NIR, the New
Jersey Institute of Technology/Big Bear Solar Observatory's Near
Infrared Magnetograph (NIRM) could be employed which has a FPP
with FWHM = 8.8 pm and FSR = 548.7 pm. We plan to employ these systems
to obtain sub-picometer spectral resolution Stokes I and V line
profiles in the umbral regions to determine the vertical magnetic
field and velocity gradients across the height of formation of
the spectral lines FeI
![]() and
and
![]() .
However, the final spectral information will degraded by the relatively long
integration times.
.
However, the final spectral information will degraded by the relatively long
integration times.
With the construction of ground-based solar telescopes with aperture larger than a meter and the planned National Solar Observatory's 4-m Advanced Technology Solar Telescope, the observed transverse spatial resolution will be less than the half-width of the vertical height of formation of the observed spectral lines. Using a confocal sub-picometer interferometer,the observations can be made of the same spectral line to produce vertical height information compatible to the transverse scale within a time frame consistent with the resolution. These observations can be supplemented with multiple line observations; however, multiple line analysis relies on the assumption that the height of formation of the atomic levels can be directly related to the height of formation of the observed line. The radiometry calculations given in the introduction confirm that such observations can be made, and we argue that these should be pursued. With the completion of the future observations listed in the last paragraph, the usefulness of the observations will be tested.
Acknowledgements
We would like to thank D. Budker (UC Berkeley), E. Bickel (Channel Industries), and N. Benoit (Boston Piezo Optics) for their assistance on the design and mechanical construction of the PZT interferometer. We thank J. Sanchez Almeida (IAC), L. Bellot Rubio (IAA), J. Bruls (KIS), and W. Cao (NJIT) for there comments and calculations on the possibilities of high spectral resolution in the near infrared. We would like thank the V. Martinez Pillet for helping to greatly clarify the manuscript through a careful reading of the paper. This research was supported by the Marshall Space Flight Center's Institutional Research and Development Program.