- ... coordinates
![[*]](/icons/foot_motif.gif)
- Throughout this paper we use galactic coordinates with origin at
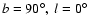 ,
and
equator defined by
,
and
equator defined by
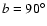 ,
and
,
and
![$l \in [0^\circ,360^\circ]$](/articles/aa/full/2007/11/aa5585-06/img14.gif) ,
with
,
with 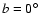 in the galactic North-pole.
in the galactic North-pole.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pixels
![[*]](/icons/foot_motif.gif)
- We shall see below that, subject to certain
reasonable constraints, the details of this subdivision
will not change our results significantly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![$\alpha_i \in (0, 180^\circ]$](/articles/aa/full/2007/11/aa5585-06/img31.gif)
![[*]](/icons/foot_motif.gif)
- In this connection it is instructive to note that, for a homogeneous distribution of points on S2, all angular separations
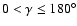 are allowed, and the corresponding
probability distribution can be calculated to give
are allowed, and the corresponding
probability distribution can be calculated to give
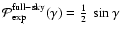 .
This represents the limit of a statistically isotropic distribution
of points in S2 as the number of points go to infinity.
One can thus quantify departure from statistical isotropy by
calculating the departure of the mean observed probability distribution
.
This represents the limit of a statistically isotropic distribution
of points in S2 as the number of points go to infinity.
One can thus quantify departure from statistical isotropy by
calculating the departure of the mean observed probability distribution
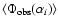 from this quantity, i.e. by
evaluating
from this quantity, i.e. by
evaluating
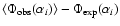 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variance
![[*]](/icons/foot_motif.gif)
- We have checked numerically that the blms of the
 -maps derived from the Monte Carlo CMB maps do follow Gaussian distributions,
which justifies the use of cosmic variance bounds and the
-maps derived from the Monte Carlo CMB maps do follow Gaussian distributions,
which justifies the use of cosmic variance bounds and the 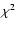 test.
test.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.