A&A 462, 1127-1135 (2007)
DOI: 10.1051/0004-6361:20065122

Energy leakage as an attenuation mechanism for vertical kink oscillations in solar coronal wave guides

M. Selwa1 - K. Murawski1 - S. K. Solanki2 - T. J. Wang2,3


1 - Group of Astrophysics and Gravity Theory, Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
2 - Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
3 - Department of Physics, Montana State University, Bozeman, MT 59717-3840, USA

Received 1 March 2006 / Accepted 8 October 2006

Abstract
Aims. We study wave leakage as a possible attenuation mechanism of coronal loop oscillations in the ideal MHD regime.
Methods. We consider impulsively generated oscillations in solar coronal magnetic wave guides such as a straight slab and a curved arcade loop. The two-dimensional numerical model we implement includes the effects of nonlinearity and line curvature on attenuation of fast magnetosonic kink waves.
Results. We show that these waves are more strongly attenuated in the arcade loop than in the slab and provide evidence that the curvature of magnetic field lines results in excess energy leakage. For parameters appropriate for a coronal loop the kink oscillation is too efficiently attenuated by energy leakage, suggesting that in the solar atmosphere wave leakage must be reduced compared to our simulations. We conclude that energy leakage is an efficient source of attenuation of coronal loop oscillations.

Key words: magnetohydrodynamics (MHD) - Sun: corona - Sun: oscillations

1 Introduction

The good spatial resolution of highly sensitive instruments such as SUMER (SOHO) and TRACE resulted in the detection of various oscillations in solar coronal loops. These include propagating (De Moortel et al. 2002) and standing (Wang et al. 2002) slow magnetosonic waves. There are also observations of different polarizations of fast magnetosonic waves: horizontal kink (Aschwanden et al. 1999; Schrijver et al. 2002), vertical kink (Wang & Solanki 2004), and fast sausage waves (Nakariakov et al. 2003; Aschwanden 2004). We refer to the vertical and horizontal polarizations of kink waves separately as vertical and horizontal kink waves, since they show somewhat different properties (e.g. signs of compressibility are displayed by the vertical kink oscillations only).

Oscillations of magnetic loops have been studied analytically over the last few decades by Edwin & Roberts (1983,1982), Roberts et al. (1984), Cally (1986), Nakariakov (2003), Van Doorsselaere et al. (2004a, b), but restricted to idealized situations. Numerical simulations are required to tackle more complex models and both excitation and attenuation of coronal loop oscillations have been extensively studied by numerical means. Oscillations in curved coronal loops were considered for the first time by Smith et al. (1997). More recent studies were made by Murawski et al. (2005a, b), del Zanna et al. (2005), Brady & Arber (2005), and (Selwa et al. 2005b - hereafter Paper I, Selwa et al. 2006 - hereafter Paper II).

The current work is motivated by the observed rapid attenuation of magnetohydrodynamic (MHD) waves. A number of attenuation mechanisms have been studied theoretically. For instance, Ofman & Wang (2002) and Selwa et al. (2005a) considered attenuation of oscillations of hot loops by thermal conduction. Resonant absorption was studied by Ruderman & Roberts (2002) and by Goossens et al. (2002). De Moortel et al. (2004) discussed the effect of attenuation of slow waves due to mode coupling. Ofman & Aschwanden (2002) studied phase mixing as an attenuation mechanism of transverse oscillations, while Zaqarashvili et al. (2004) suggested that global kink modes may be attenuated by resonant generation of slow waves at half the frequency of the kink wave. Ofman (2002) discussed chromospheric leakage of Alfvén waves and Selwa et al. (2005a) showed that slow waves can be efficiently attenuated by foot-point leakage. Attenuation of quasi-modes in curved loops was recently considered by Van Doorsselaere et al. (2004b).

Another mechanism which may be responsible for wave attenuation is energy leakage. In this context, Murawski & Roberts (1993a,b) showed by numerical simulations that for a smooth coronal slab there is energy leakage from the slab, associated with the propagation of sausage and kink waves. Wave energy leakage in the kink wave is generally small, whereas the energy in sausage waves leaks more strongly for long wavelengths and smoother slabs. For fast oscillations leakage was proposed to be very efficient only for high harmonics (Smith et al. 1997; Cally 2003; Díaz et al. 2004). Smith et al. (1997) examined the effect of curvature on fast magnetoacoustic waves in dense coronal loops situated in a potential coronal arcade. They showed that due to the curvature of the structure, leaky waves occur. The sausage mode is more affected by curvature and is more leaky than the kink mode. An increase in loop length, width, and gas density ratio reduces the leakage. Odd modes of oscillations (zero velocity at the loop summit) are more strongly confined than even modes. Brady & Arber (2005) found that leakage is more efficient for higher wavelengths (lower harmonics). However, they limited their studies to harmonics higher than four. Verwichte et al. (2006a) showed that for a circular loop only an equilibrium Alfvén frequency, whose cross-section is modeled by a top-hat profile, leads to trapped modes. Other profiles result in energy leakage into the ambient medium through wave tunneling. The authors also found a similar behavior for a straight slab model of a coronal loop. Díaz et al. (2006) showed that in an arcade loop with constant density all fast modes are leaky and attenuation times correspond to their observed values.

Since there is no convincing observational evidence of energy leakage as the main mechanism that is responsible for attenuation of global fast modes, the goal of this paper is to perform detailed studies of leakage as an attenuation mechanism for vertical kink oscillations.

This paper is organized as follows. The numerical models are described in Sect. 2. The numerical results are presented and discussed in Sect. 3. This is followed by a discussion of the main results in Sect. 4.

   
2 Numerical models

Our model system is taken to be composed of a magnetized plasma with polytropic index $\gamma=5/3$. We neglect gravitational stratification and non-ideal MHD effects. As kink oscillations are mainly observed by TRACE in cold ($\sim$1 MK) loops we will model them using the ideal MHD equations:

    
                           $\displaystyle {\partial\varrho\over \partial t}$ + $\displaystyle \nabla\cdot \left(\varrho{\vec V}\right)=0,$ (1)
$\displaystyle \varrho{\partial {\vec V}\over\partial t}$ + $\displaystyle \left(\varrho{\vec V}\cdot \nabla\right){\vec V}= -\nabla p+{1\over\mu}(\nabla\times{\vec B})\times{\vec B},$ (2)
$\displaystyle \frac{\partial E}{\partial t}$ + $\displaystyle \nabla\cdot\left[\left( E + p + \frac{B^2}{2\mu}\right) {\vec V}- \frac{{\vec B} ({\vec B} \cdot {\vec V})}{\mu}\right] = 0,$ (3)
$\displaystyle {\partial{\vec B}\over\partial t}$ = $\displaystyle \nabla\times \left({\vec V}\times {\vec B}\right),$ (4)

where $\mu$ is the magnetic permeability, ${\varrho}$ is mass density, ${\vec V}$ is flow velocity, p is gas pressure, ${\vec B}$ is a divergence free, $\nabla\cdot{\vec B} = 0$, magnetic field. The plasma energy density is expressed as

 \begin{displaymath}E = \frac{{\varrho} V^2}{2} + \frac{p}{\gamma-1} + \frac{B^2}{2\mu}\cdot \end{displaymath} (5)

2.1 Equilibrium configurations

We limit our discussion to a two-dimensional magnetically structured atmosphere for which the plasma quantities are independent of the spatial coordinate y, $\partial / \partial y = 0$, as well as we neglect the polarization along the y-direction by setting Vy=By=0. To study energy leakage as an attenuation mechanism of vertical kink oscillations we use two models of coronal loops: (a) an arcade model and (b) a slab model for a straight magnetic field topology. The model (b) will serve for comparison purposes to discuss curvature effects on wave attenuation in the model (a).

2.1.1 A coronal arcade model
We adopt the coronal arcade model that was recently described in Papers I and II. In this model the coronal arcade is settled in a two-dimensional, gravity-free and motionless environment ( ${\vec V}=0$). From the momentum Eq. (1) it follows for a constant pressure that at the equilibrium the Lorentz force must vanish.

This condition is satisfied by the equilibrium magnetic field components

                  Bex = $\displaystyle \;\; B_{\rm0} \cos{(x/{\Lambda}_{\rm B})} {\rm e}^{-z/{\Lambda}_{\rm B}},$ (6)
Bez = $\displaystyle -B_{\rm0} \sin{(x/{\Lambda}_{\rm B})} {\rm e}^{-z/{\Lambda}_{\rm B}},$ (7)

where $B_{\rm0}$ is the magnetic field at the level z=0 and ${\Lambda}_{\rm B}$ is the magnetic scale height taken as

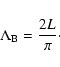\begin{displaymath}\nonumber {\Lambda}_{\rm B} = \frac{2L}{\pi}\cdot \end{displaymath}  

Here L=100 Mm is the horizontal half-width of the arcade. As in Papers I and II a background mass density $\varrho _{\rm e}$ is assumed constant. With such assumption the background Alfvén speed is chosen as: $V_{\rm A}=V_{\rm A0}{\rm e}^{-z/{\Lambda}_{\rm B}}$, where $V_{\rm A0}={\rm const.}$ is the Alfvén speed at the reference level z=0. In this case $V_{\rm A}$ decays exponentially with height z but as ${\Lambda}_{\rm B}=200/\pi$ Mm, the decay rate is small.
  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5122f1a.eps}\par\includegraphics[width=7.8cm,clip]{5122f1b.eps}\end{figure} Figure 1: Initial configurations for a curved arcade loop ( top panel) and a straight slab ( bottom panel). The density (color bar) is given in arbitrary units (10-12 kg m-3). The loop and the slab are seen as regions of condensed plasma. Magnetic field lines are shown as solid white lines. Note that the loop apex and the middle of the slab are denser than the surrounding plasma as a consequence of hot dense initial pulses, which due to their finite width protrude into loop/slab.
Open with DEXTER

We consider a loop which is embedded in the arcade in such a way that its edges follow two specific magnetic field lines. A cut along the loop does not have a perfect circular shape, but its average radius and length can be estimated as 70 Mm and 190 Mm, respectively. The equilibrium structure of the loop is shown in the top panel of Fig. 1. The mass density is enhanced in the loop comparing to the ambient medium. We choose the mass density contrast $d={\varrho}_{\rm i}/{\varrho}_{\rm e}=10$, where ${\varrho}_{\rm i}$ denotes the mass density within the loop and $\varrho _{\rm e}$ corresponds to the ambient medium. This density contrast has been chosen in order to remain consistent with our earlier computations (Papers I and II). In Sect. 4 we also estimate the density contrast between the background and the TRACE loop actually exhibiting the oscillation and discuss its implications. Note that the Alfvén speed within the loop is smaller than in the ambient medium ( $V_{{\rm A}{\rm i}}=V_{{\rm A}{\rm e}}/\!\sqrt{d}$). This depression in the Alfvén speed forms a wave guide for fast magnetosonic waves. For a potential magnetic arcade the equilibrium pressure $p_{\rm e}=\varrho_{\rm e}c_{{\rm s e}}^2/\gamma$ has to be constant. Here $c_{{\rm se}}$ is the sound speed in the ambient medium. All equilibrium parameters are listed in Table 1.

Table 1: Scale and Equilibrium and normalization parameters.

2.1.2 A slab model
For a straight slab model we choose a value of the Alfvén speed, $V_{\rm As}$, which is the same as at the curved loop apex:

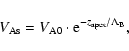\begin{displaymath}V_{\rm As}=V_{{\rm A}{\rm0}}\cdot {\rm e}^{-z_{\rm apex}/{\Lambda}_{\rm B}}, \end{displaymath} (8)

where $z_{\rm apex}=48$ Mm is the position of the curved loop apex. The slab half-width, a=2.5 Mm, is chosen equal to the half-width of the curved loop at its apex. The slab is centered at z=0. Within such a slab a mass density, ${\varrho}_{\rm i}$, is d times higher than in the ambient medium, $\varrho _{\rm e}$. The value of the gas pressure is the same both for the curved loop and the straight slab. Magnetic field has only the x-component equal to $B_{\rm xs}=V_{\rm As}\sqrt{\mu{\varrho}_{\rm e}}$. In such a model the Alfvén speed does not vary along the slab. The length of the straight slab is chosen as 2L, which is close to the curved loop length. The initial configuration of the straight slab is shown in the lower panel of Fig. 1.

2.2 Perturbations

As our interest is in impulsively excited waves, we set perturbations in Eqs. (1)-(2) by launching a hot pulse in the pressure and mass density, i.e.

 \begin{displaymath}\delta{f}(x,z,t=0) = f_{\rm0}~ {\rm e}^{-\left[({x-x_{\rm0}})^2+({z-z_{\rm0}})^2\right]/w^2}, \end{displaymath} (9)

where $\delta{f}=({\delta{\varrho}}/{{\varrho}_{\rm0}},{\delta{p}}/{p_{\rm0}})$and $f_{\rm0}=(0.1,1)A_{\rm p}$. The initial position of the pulse is denoted by $(x_{\rm0},z_{\rm0})$ and its width is w. For such a choice the amplitude of the pressure pulse is ten times higher than the amplitude of the mass density pulse. As a result of that the pulse is 6.4 times hotter than the ambient corona. Both for the curved loop and the slab we set $A_{\rm p}=7.5$, w=35 Mm and choose the same pulse position with respect to the loop: $x_{\rm0}=z_{\rm0}=0$ ( $x_{\rm0}=L$, $z_{\rm0}=-0.5\ L$) in the case of the curved loop (slab). As a consequence of the same powers of the initial pulse, the initial shifts for the curved loop and the slab are close one to each other.

  
3 Numerical results

Numerical simulations are performed with the code EMILY (Jones et al. 1997). This code adopts a finite-volume TVD scheme which uses an approximate Riemann solver for the hyperbolic fluxes. The scheme is second-order accurate in space and time.

Equations (1)-(4) are solved numerically in Eulerian boxes with the x- and z-dimensions $(-L,L)\times(0, 2L)$ and $(0, 2L)\times(-L,L)$ in the case of the curved loop and the slab, respectively. These boxes are covered by uniform grids of $600\times 800$ and $300\times 400$ numerical cells, respectively. Grid convergence studies based on grid refinement were performed to show that the numerical results are not affected by insufficient spatial resolution.

Open boundary conditions, with zero-gradient extrapolation of all plasma variables, were applied at the left, right and top sides of the simulation region in the case of the curved loop, and at the bottom and top sides of the simulation region in the case of the slab. Such a choice allows a wave signal to freely leave the simulation region at the sides of the simulation region where the open boundary conditions are imposed. Line-tying boundary conditions are implemented by imposing ${\vec V}=0$ at the bottom of the curved loop and at the left and right sides of the slab simulation region. These boundary conditions model wave reflections from the denser photospheric regions. We have also tested the case when the bottom boundary of the slab box is also closed. The results remained relatively unchanged.


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{5122f2a.eps}\par\includegraphics[width=7.8cm,clip]{5122f2b.eps}\end{figure} Figure 2: Time-signatures of the mass density (color scale; arbitrary units) at the loop apex for the curved loop ( top panel) and the straight slab ( bottom panel). Spatial coordinates and time are measured in units of L and in seconds, respectively. Note the difference in time scale between the top and bottom panels.
Open with DEXTER

3.1 Wave attenuation mechanisms

Let us first contrast the behaviour of the loop apex with the centre of the slab. In Fig. 2 we plot the density along z/L near the loop apex (x=0) in the upper panel and at the centre of the slab (x/L=1) in the lower panel. The difference between the behaviour between the loop and the slab is striking. Whereas the kink mode excited by the initial pulse in the curved loop decays in less than a full wave period, the kink mode excited in the slab exhibits little sign of any decay. In the following we consider the cause of this difference. First of all we note that the periods of kink oscillations are not the same for the curved loop (P=499 s) and the slab (P=929 s). The difference in the periods results from the fact that the Alfvén speed in the slab is different than in the loop and that the lengths of these features are slightly different. In the case of the slab the Alfvén speed is uniform along the slab and is equal to the Alfvén speed at the loop apex ( $V_{{\rm A,slab}}=2.2\times 10^5$ ms-1), which is its minimum value within the loop. The average Alfvén speed in the curved loop is $V_{{\rm A,loop}}=6.1\times 10^5$ ms-1. As the period of standing kink oscillations, P, in 2D geometry is determined by the loop length l, and the Alfvén speed inside the loop, $V_{\rm Ai}$: $P=2l/V_{\rm Ai}$, for similar loop length P is larger for loops with lower Alfvén speeds (slab case). In our further studies we consider $A_{\rm p}=15$ in case of the curved loop case to emphasize more details. The derived properties are practically independent of the amplitude of the oscillation.

We note that for the curved loop the ratio of the attenuation time, $\tau $, to the period, P, is $\tau/P \sim 0.5$. For the straight slab we do not observe significant attenuation and $\tau $ is very large; $\tau $ could not be reliably evaluated for the slab case.

One possibility for the strong decay displayed by the loop is numerical diffusion in the loop model. This is unlikely for two reasons. Firstly, the same code is used for both geometries, which otherwise have similar properties. Secondly, the numerical diffusion is small. We estimate the numerical diffusion by measuring the total mass in the curved loop above a given density threshold value. The total mass is evaluated by numerical integration of the mass density at each grid point inside the loop above the chosen threshold value. We compare the time dependence of the total mass computed with a density threshold of 3 (in arbitrary units) to that with a threshold of 7. The higher threshold value lies close to the minimum density attained inside the loop. The lower threshold value lies slightly above the maximum density reached in the ambient region. Comparing the total mass for the two threshold values we estimate that $\sim$17% of the mass moves out of the central part of the loop during the simulation time (dotted line, corresponding to the higher threshold value in Fig. 3). This makes the loop broader and its boundaries become smoothed. The total mass in the loop remains roughly constant, however (solid line in Fig. 3). Another proof of the low level of diffusion is given in Paper II (Fig. 4).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f3.eps}\end{figure} Figure 3: Total mass in the loop with a given threshold of 3 (solid line) and 7 (dotted line) vs. time.
Open with DEXTER

Our simulation results described in Paper II clearly show that the ratio of attenuation time $\tau $to wave period P decreases with P. Values of P and $\tau $ are obtained by fitting the attenuated sine function to the appropriate time-signature. As the applied MHD equations are ideal and numerical diffusion is small, dissipative effects are not present in this system. We infer that the mechanism of wave attenuation acting in these simulations differs from viscous attenuation.

Another mechanism, which might be responsible for the attenuation of kink oscillations is resonant absorption of Alfvén and slow magnetosonic waves. However, since our models are 2D and there is no variation in the y-direction, we have no Alfvén waves in the system. Moreover, it is rather unlikely that cusp resonances are important in a low $\beta$ plasma. Such a mechanism cannot play any important role in attenuation of kink oscillations for the chosen geometries. Consequently, we conclude that attenuation is due to energy leakage. Longer wavelength waves experience more difficulties in fitting into a curved loop structure and as a result they leak energy into the ambient medium (Wentzel 1974). Brady et al. (2006) showed that the ability of waves to leak is intrinsically Alfvén speed profile. Energy leakage can also result from wave tunneling which is present (absent) for the considered curved loop (straight slab). Wave tunneling was recently discussed by Verwichte et al. (2006a) in the context of normal modes in the limit of cold plasma ($\beta=0$) approximation. Verwichte et al. (2006b) dealt with the leaking waves for non top-hat Alfvén frequency profiles and showed the behaviour of tunneling modes and "straight'' leaky modes (leaking without tunneling). Verwichte et al. (2006c) showed how such a model can be implemented for coronal seismology. This process leads to a decrease of the wave amplitude - a process which is characteristic of wave attenuation. These findings are in general agreement with the results of Murawski & Roberts (1993a,b), Verwichte et al. (2006a), Díaz et al. (2006) and Zaqarashvili (2006) who studied energy leakage of normal modes in coronal structures.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f4a.eps}\par\includegr... ...lip]{5122f4b.eps}\par\includegraphics[width=7.5cm,clip]{5122f4c.eps}\end{figure} Figure 4: Evolution of perturbed energy density for the curved loop present in the system (t=300 s - top panel, t=800 s - middle panel, t=1300 s - bottom panel). The perturbed energy density is given in arbitrary units (initial energy of the loop apex). The position of the loop corresponds to the black contour lines at the bottom.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f5a.eps}\par\includegr... ...lip]{5122f5b.eps}\par\includegraphics[width=7.5cm,clip]{5122f5c.eps}\end{figure} Figure 5: Evolution of perturbed energy density in a case when the curved loop is absent in the system (t=300 s - top panel, t=800 s - middle panel, t=1300 s - bottom panel). The perturbed energy density is given in arbitrary units (initial energy of the loop apex).
Open with DEXTER

Evidence of energy leakage from the curved loop is provided by perturbed energy density profiles (Fig. 4). Perturbed energy density is defined as $\Delta E=E(t)-E(0)$, where E is given by Eq. (5). The position of the loop corresponds to the black contour lines near the bottom of the panels. The maximum at around z/L=1.2 in the top frame, represented by a red-yellow patch, results from the initial pulse (also the maximum at the top of the central frame), but other local maxima (e.g. at z/L=0.9 in the top frame) result from energy leakage (red areas above the loop). Compare with Fig. 5 which illustrates the same system but without the loop.

While in Fig. 4 we observe a series of wave fronts leaking from the loop, Fig. 5 reveals essentially a single wave front. When this wave front leaves the simulation region there are no more wave fronts present in the system (bottom panel of Fig. 5) except some signatures of weak reflections at the side edges of the numerical box (which are also present in the bottom panel of Fig. 4). The difference between the figures results from the fact that some energy is trapped in the loop, while in the loop-less case the pulse propagates freely through the corona. It is noteworthy that waves leaving the loop in Fig. 4 do not have their origin in multiple reflections between the loop and the bottom boundary, as such reflections would cause periodical shifts of the loop apex or compression at this place, that is not observed in the top panel of Fig. 2.

Evidence that energy leaks from the loop via fast magnetosonic waves is provided by their propagation across the field lines. Also, perturbations in the thermal and magnetic pressures are in-phase outside the loop (shown along x=0 line for three consecutive times in Fig. 6). The position of $z\sim 0.5\ L$(where thermal and magnetic pressures are in antiphase) corresponds to the position of the loop. Since the initial pulse is quite strong and the fast speed is non-uniform along x=0 we do not observe regular periodic sine waves. Similar patterns are visible in the mass density and z-component of velocity.

  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f6a.eps}\par\includegr... ...lip]{5122f6b.eps}\par\includegraphics[width=7.5cm,clip]{5122f6c.eps}\end{figure} Figure 6: Evolution of magnetic pressure perturbations (solid line) and thermal pressure perturbations (dashed line) along the line x=0 above the curved loop (t=300 s - top panel, t=800 s - middle panel, t=1300 s - bottom panel).
Open with DEXTER

To identify the fast mode which leaks from the loop, we study mass density profiles outside the loop, where leaky waves are able to propagate. Figure 7 shows the mass density and x-component of velocity profiles plotted in flux coordinates for t=800 s. For such a choice of coordinates the pulse was launched at a $\psi=1$ line. In the flux coordinate system ( $\chi, \psi$), which covers the whole arcade, the unperturbed curved loop in Cartesian coordinates becomes a straight slab. These coordinates were used by Oliver et al. (1996) to study linear waves in coronal arcades. The pattern outside the loop in Fig. 7 shows a similar behaviour to the right panels of Figs. 2 and 3 from Cooper et al. (2003), who illustrated the transversal component of velocity and mass density profiles for the sausage mode.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f7a.eps}\par\includegraphics[width=7.5cm,clip]{5122f7b.eps}\end{figure} Figure 7: Top panel: mass density outside the loop (colour scale, units of $\varrho _{\rm e}$) at t=800 s plotted in flux coordinates. The white area corresponds to the position of the loop. Compare with the right panel of Fig. 3 from Cooper et al. (2003). Bottom panel: x-component of velocity (colour scale, units of $V_{\rm A0}$) at t=800 s. The white contour corresponds to the position of the loop. Compare with the right panel of Fig. 2 from Cooper et al. (2003).
Open with DEXTER

It is noteworthy that wave attenuation is stronger for longer period kink oscillations (top panel of Fig. 8). Such a behavior was found by Selwa et al. (2006). Longer period oscillations result from a stronger pulse which stretches the loop more and causes a larger displacement of the loop. A stretched loop is more curved (supposing that positions of the loop foot-points are fixed in time). As a consequence of that a loop leaks more energy, resulting in a smaller attenuation time. Top panel of Fig. 8 shows also two fits to the numerical data: linear $a_1+b_1\cdot P$ and polynomial $a_2\cdot P^{-b_2}$ function. Best fits lead to the following values of the parameters: a1 = 1.31066, b1 = -0.00166, a2 = 721673, b2 = 2.29382. Note, that according to Ofman & Aschwanden (2002) $\tau \sim P$ in the case of resonant absorption of Alfvén waves and $\tau \sim P^{4/3}$ in the case of phase mixing, while in contrast to their findings energy leakage exhibits a decreasing trend.

However, for more energetic pulses the period grows by about a factor of 1.5, but the ratio of attenuation time to the period differs by a factor of 2.7 (see Fig. 8, top panel). It is possible that in such a case non-linear effects play some role in the attenuation of the kink oscillations.

The same argument can explain the decrease of $\tau /P$ for longer loops with higher curvature obtained by varying the position of the foot-point, $x_{\rm f}$ (bottom panel of Fig. 8). Varying the foot-point position, $x_{\rm f}$, with the fixed half-width of the arcade, L, allows us to switch between different field lines of the arcade bounding the loop and change curvature of the loop defined as the ratio of the height of the loop's apex to the position of its foot-point.

Another indication that the vertical kink oscillations are attenuated as a result of energy leakage comes from a comparison of the attenuation rate, $\tau /P$, for different loop densities, widths and lengths. Figure 9 shows $\tau /P$ vs. the density ratio between the loop and the ambient corona, d (top panel), vs. half-width of the loop measured at the foot-point, a (medium panel), and vs. half-width of the arcade, L (bottom panel), that corresponds to different lengths of the loops. It is noteworthy that $\tau /P$ grows with d, a and L. As loops with different lenghts in the potential arcade modelled with the various positions of the foot-point (bottom panel of Fig. 8) have different parameters, e.g. average Alfvén speed, curvature and $\beta$, we change the length of the loop by varying the half-width of the arcade, L, that allows us to hold curvature fixed by fixing field lines of the arcade bounding the loop. Note, that there is no contradiction between bottom panels of Figs. 8 and 9. The former one shows mainly the role of the curvature (by varying $x_{\rm f}$), although the loop length also changes, while the latter one presents only the role of loop length (by varying L) on $\tau /P$. Also, from the bottom panel of Fig. 8 it follows that $\tau /P$ grows with L for fixed $x_{\rm f}$. These findings serve as evidence of weaker wave attenuation for higher values of these parameters. These results are in good agreement with the findings by Smith et al. (1997) who showed that increase of the loop length, loop width or the density ratio reduces the leakage.


  \begin{figure} \par\includegraphics[scale=0.475, bb=0 30 504 310]{5122f8a.eps}\par\includegraphics[scale=0.475, bb=0 30 504 310]{5122f8b.eps}\end{figure} Figure 8: Top panel: the ratio of attenuation time $\tau $ to period P, $\tau /P$of vertical loop oscillations vs. period. The solid (dotted) line corresponds to the best quadratic (linear) fit. The different periods were obtained by changing the total energy of the initial pulse (Selwa et al. 2006). Bottom panel: $\tau /P$ vs. position of the right foot-point of the loop, $x_{\rm f}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=6.5cm,clip]{5122f9a.eps}\\ [2.5mm] \pa... ...b.eps}\\ [2.5mm] \par\includegraphics[width=6.5cm,clip]{5122f9c.eps}\end{figure} Figure 9: Top panel: the ratio of attenuation time $\tau $ to period P, $\tau /P$, of vertical loop oscillations vs. density ratio between the loop and the ambient medium, d. middle panel: $\tau /P$ vs. half-width of the loop at the foot-point, a. bottom panel: $\tau /P$ vs. half-width of the arcade L.
Open with DEXTER

  
4 Discussion

We now compare with observations. Wang & Solanki (2004) presented evidence for vertical kink oscillations of a coronal loop observed in the 195 Å bandpass by TRACE. Following the method of Aschwanden et al. (2003) we estimate the density contrast of the loop. By fitting the flux profile (Fig. 10) we obtain the loop radius a=3.9 Mm and the skin depth l=3.6 Mm. Hence we evaluate the mean loop width $w_{\rm loop}=4.3$ Mm (Aschwanden et al. 2003, Eq. (2)). For the loop flux $F_{\rm subtr}=0.34$ DN s-1 pix-1 (where DN = data number) we get according to Eq. (14) in Aschwanden et al. (2003):

 \begin{displaymath}\sqrt{n_{\rm i}^2-n_{\rm e}^2}\approx3.9\times 10^8~{\rm cm}^{-3}. \end{displaymath} (10)

By assuming a hydrostatically stratified atmosphere we obtain the equivalent column depth $z_{\rm eq}=32.7$ Mm at the loop apex for a plasma temperature T=1.5 MK. With the background flux $F_{\rm back}=11$ DN s-1pix-1 and the altitude of the oscillating loop segment $h_{\rm osc}=[98.2,\ 100.1,\ 99.7]$ Mm respectively. We get $n_{\rm e}=[1.98,\ 1.93,\ 1.94]\times 10^8$ cm-3 and $n_{\rm i}=[4.37,\ 4.35,\ 4.36]\times 10^8$ cm-3 for three types of loop shapes (Table 1, Wang & Solanki 2004). As a consequence, the density enhancement is $d=n_{\rm i}/n_{\rm e}\approx 2.3$.

Suppose that resonant absorption is the main attenuation mechanism. Then, $\tau/P\sim0.98$ for the measured density contrast of 2.3 (Eq. (4), Aschwanden et al. 2003). Wang & Solanki (2004) measured $\tau/P=3.05$, but this value could be too large with the uncertainty due to only 1.5 visible wave-periods (interrupted by a data gap), since it means 4-5 visible periods of oscillations, i.e. we should still see oscillations after the gap, but actually we did not. Therefore, the resonant absorption could also explain the observed damping of vertical loop oscillations as shown by Aschwanden et al. (2003) for the horizontal kink oscillations.


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{5122f10.eps}\end{figure} Figure 10: Estimation of the density contrast of the loop observed by Wang & Solanki (2004) (their Fig. 2a): observed flux profile obtained by averaging 31 images before the oscillation started ( top panel) with linear background (dotted line); normalized flux profile together with theoretical fit ( middle panel); density profile ( bottom panel, Eq. (1) in Aschwanden et al. 2003). The dashed lines in bottom panel represent the inner/outer loop radius.
Open with DEXTER

As indicated by the top panel of Fig. 9, a lower density contrast leads to stronger attenuation by wave leakage. For the density ratio d=3 the simulation provide $\tau/P<0.2$ (see Fig. 11 for the corresponding time series). As the attenuation is very strong the vertical oscillations are hardly seen, which is inconsistent with the observations (Wang & Solanki 2004). Since the observed oscillations are less strongly damped, wave leakage must be reduced in the solar atmosphere compared to our simple model.

We stress, however, that the measurement of the loop density contrast with the method of Aschwanden et al. (2003) is based on an a priori assumption that the loop density profile is monolithic. If, e.g., the loop consists of multiple unresolved threads or the loop has a low filling factor, the density contrast could be higher than the present estimate. Such a finely structured loop would be more vulnerable to phase mixing (Ofman & Aschwanden 2002) and wave scattering (Gruszecki et al. 2006).

As was shown by Smith et al. (1997), a lower density contrast leads to a stronger attenuation. From the top panel of Fig. 9 we infer that $\tau/P<0.2$ for the density ratio d=3 that is close to the observational value, which is obtained by the simulations for the case of d=3.

The numerical simulations we performed provide some insight into the attenuation of the vertical kink oscillations. The literature on wave attenuation is vast (e.g., Ye et al. 1993; Ofman & Aschwanden 2002; Ruderman & Roberts 2002; Van Doorsselaere et al. 2004a; Van Doorsselaere et al. 2004b; Andries et al. 2005). The proposed models differ to various extents in the boundary conditions (bc) they use. For instance, Ye et al. (1993) applied bc that sets the radial electric field $E_{\rm r}=0$ on the loop's surface. This is proper for the Toroidal Alfvén Eigenmode (TAE). The main conclusions are that the Alfvén continuum modes of the non-curved structure (a cylinder) are attenuated due to curvilinear perturbations. However, the attenuation rates were not calculated. Ofman & Aschwanden (2002) showed that phase mixing leads to rapid dissipation of Alfvén waves due to the variation of the Alfvén speed across the wave front which results in the formation of small scales. However, they suggested that the loop oscillations are dissipated by phase mixing with anomalously high viscosity. Ruderman & Roberts (2002) dealt with continuum attenuation due to resonant absorption. The model was a straight cylinder with smooth edges and a homogeneous central core. In the limit where the edges become discontinuous, the kink modes of Edwin & Roberts (1983) were retrieved. The attenuation rate was calculated (their Eq. (56)) in the limit of thin edges and it is, of course, small. Van Doorsselaere et al. (2004b) built on Ruderman & Roberts (2002) and found the roots of the dispersion function without the thin edge constraint, i.e. allowing for a diffuse edge. The attenuation rate by resonant absorption increased by 20% at best with respect to the one calculated by Ruderman & Roberts (2002). Van Doorsselaere et al. (2004b) added the effects of curvature and showed that the attenuation rate increased by 12% at best with respect to the value calculated by Ruderman & Roberts (2002). Andries et al. (2005) implemented a longitudinal stratification along a cylindrical loop and pointed out that this can significantly alter both the real and imaginary parts of the quasi-mode frequency. This statement was validated by Arregui et al. (2005) for non-thin edges who showed that the period and attenuation of coronal loop oscillations essentially depend on the density contrast and the inhomogeneity length-scale. Both Andries et al. (2005) and Arregui et al. (2005) show that the ratio of attenuation time to the period based on resonant absorption is almost not affected by gravitational stratification.


  \begin{figure} \par\includegraphics[width=8cm,clip]{5122f11.eps}\end{figure} Figure 11: Time-signatures of the mass density (color scale; arbitrary units) at the loop apex for the curved loop with the density contrast d=3. Compare with top panel of Fig. 2.
Open with DEXTER

We note the following: (a) in Ye et al. (1993) TAEs have a different boundary condition than the one we implemented; (b) Ruderman & Roberts (2002), Van Doorsselaere et al. (2004a), Van Doorsselaere et al. (2004b), and Andries et al. (2005) basically deal with kink modes and their work can be related to what we observe. Our conclusion that energy leakage from the loop into the ambient medium is an efficient mechanism responsible for attenuation of vertical kink oscillations complements the results of these studies. The conclusion that kink oscillations are attenuated stronger in a curved loop is consistent with findings of Van Doorsselaere et al. (2004b) for quasi-modes which show similar behavior and are more attenuated in curved configurations. However, there is no explanation of such a behavior in terms of energy given in their paper.

A comparison with observed vertical oscillations clearly shows that, as a damping mechanism, wave leakage is too efficient in our simulations. Leakage can be reduced by improving the wave-guiding properties of a loop. Indeed, the relative attenuation time $\tau /P$ grows with mass density, width and length of the loop (Fig. 9). Another possibility is to implement a twisted magnetic field, which requires a 3D computation. Implementation of different Alfvén speed profiles which eliminate wave tunneling (Verwichte et al. 2006a) that takes place in the discussed curved loop configuration can reduce energy leakage out of the loop. Finally, a different excitation mechanism than the single pulse used here may also have the potential of reducing wave attenuation. An example is the excitation by a train of pulses which mimics better impulsive waves that result from natural sources (flares, EIT waves), exhibiting finite life time scales.

It is worthwhile to discuss briefly the relevance of the recent results of Díaz et al. (2006) to our paper. Díaz et al. (2006) studied linear fast magnetosonic waves in a semi-circular loop in the limit of the cold and linear MHD approximations. They derived the dispersion relation for various modes. As a result of energy leakage these modes are characterized by a complex frequency, $\omega$. The imaginary parts of $\omega$ are usually small compared with the real parts. As a result of that wave attenuation due energy leakage is weak and the oscillations typically last for 2-5 wave periods, which is about twice longer than in our simulations. Spatial structures of these oscillations exhibit exponential growth with height far away from the arcade (their Figs. 5, 6), which is similar to the results of our Fig. 6. The normalized attenuation time, $\tau /P$, lies in the range of values found in our studies, and it grows for denser loops (their Fig. 9).

A number of improvements to this study are possible. The most obvious is switching to 2.5-D geometry in order to study also other mechanisms, such as resonant absorption of Alfvén waves. It is also not clear to what extent the inclusion of gravity will affect the results.

Acknowledgements
K.M. expresses his sincere thanks to Drs. Luigi Nocera and Erwin Verwichte for stimulating discussions. MS thanks Dr. Andreas Lagg for his help on IDL visualization. The magnetohydrodynamic code EMILY used in this study was developed at the University of Washington by Ogden S. Jones, Uri Shumlak, Scott Eberhardt, Bogdan Udrea, and provided through the sponsorship of AFOSR program. We thank an anonymous referee for comments that helped to improve this paper. M.S.'s & K.M.'s work was financially supported by a grant from the State Committee for Scientific Research Republic of Poland, with KBN grant No. 2 PO3D 016 25. T.J.W.'s work was supported in part through NASA grant NAS5-38099 for TRACE mission operations and data analysis, through a subcontract of Lockheed-Martin Solar and Astrophysics Laboratory with Montana State University.

References

 
Copyright ESO 2007