A&A 460, 145-153 (2006)
DOI: 10.1051/0004-6361:20065128
J. Krticka1 - J. Kubát2 - D. Groote3
1 - Ústav teoretické fyziky a astrofyziky PrF MU,
611 37 Brno, Czech Republic
2 -
Astronomický ústav, Akademie ved Ceské
republiky, 251 65 Ondrejov, Czech Republic
3 -
Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 2 March 2006 / Accepted 16 July 2006
Abstract
We study the possibility of the helium decoupling in the
stellar wind of ![]() Ori E. To obtain reliable wind parameters
for this star we first calculate NLTE wind model and
derive wind mass-loss rate and terminal velocity.
Using corresponding force multipliers we study the possibility of
helium decoupling. We find that helium decoupling is not possible for realistic
values of helium charge (calculated from NLTE wind models).
Helium decoupling only seems possible for a very low helium charge.
The reason for this behavior is the strong coupling between helium and hydrogen.
We also find that frictional heating becomes important in the outer parts of the
wind of
Ori E. To obtain reliable wind parameters
for this star we first calculate NLTE wind model and
derive wind mass-loss rate and terminal velocity.
Using corresponding force multipliers we study the possibility of
helium decoupling. We find that helium decoupling is not possible for realistic
values of helium charge (calculated from NLTE wind models).
Helium decoupling only seems possible for a very low helium charge.
The reason for this behavior is the strong coupling between helium and hydrogen.
We also find that frictional heating becomes important in the outer parts of the
wind of ![]() Ori E due to the collisions between some heavier elements and the
passive components - hydrogen and helium. For a metallicity ten times lower than the solar
one, both hydrogen and helium decouple from the metals and may fall
back onto the stellar surface. However, this does not explain the
observed chemical peculiarity since both these components decouple together
from the absorbing ions. Although we do not include the effects of
the magnetic field into our models, we argue that the presence of
a magnetic field will likely not significantly modify the derived results because
in such case model equations describe the motion parallel to the magnetic field.
Ori E due to the collisions between some heavier elements and the
passive components - hydrogen and helium. For a metallicity ten times lower than the solar
one, both hydrogen and helium decouple from the metals and may fall
back onto the stellar surface. However, this does not explain the
observed chemical peculiarity since both these components decouple together
from the absorbing ions. Although we do not include the effects of
the magnetic field into our models, we argue that the presence of
a magnetic field will likely not significantly modify the derived results because
in such case model equations describe the motion parallel to the magnetic field.
Key words: stars: winds, outflows - stars: mass-loss - stars: early-type - hydrodynamics - stars: chemically peculiar
The radiative force plays an important role in the atmospheres of early-type stars. In luminous early-type stars it may be greater than the gravitational force. In such a case, the outer stellar layers can hardly be in hydrostatic equilibrium. Consequently, the radiatively driven wind is blowing from these stars (see, e.g., Kudritzki & Puls 2000; Owocki 2004; or Krticka & Kubát 2006, for a review). For many cooler early-type stars the radiative force is not able to expel the material into the circumstellar environment; however, it is able to cause elemental drift and, consequently, abundance stratification (e.g., Vauclair 2003; Michaud 2005) and becomes manifested as chemical peculiarity.
Hot stars with radiatively driven stellar winds and hot chemically peculiar stars seem to form two diverse groups of stars. While the flow in the atmospheres of stars with strong winds would eliminate any possible abundance stratification and chemical peculiarity, the atmospheres of chemically peculiar stars are supposed to be very quiet (likely due to magnetic fields) to enable elemental diffusion (e.g., Vauclair 1975).
However, there exists a small group of hot stars for which both effects, stellar wind and chemical peculiarity, seem to be important. The sparsely populated group of helium-rich stars probably exhibits both effects. In some cases, chemical peculiarity can be even used as a test of wind existence (Landstreet et al. 1998; Dworetsky & Budaj 2000). Some of the stars with parameters corresponding to hot chemically peculiar stars may have also purely metallic winds, as proposed by Babel (1996).
One of the most enigmatic stars of the group of helium-rich
stars is the star denoted as ![]() Ori E or HD 37479.
To our knowledge, this star is the only
known Bp star with hydrogen lines in emission. Its
photometrical and emission line profile variability can be explained assuming the
circumstellar cloud model (Smith & Groote 2001;
Townsend et al. 2005). Similarly to the star HD 37776 (Mikulásek et al.
2006), this star may exhibit rotational braking,
probably due to the magnetically controlled stellar wind (Oksala & Townsend
2006).
Ori E or HD 37479.
To our knowledge, this star is the only
known Bp star with hydrogen lines in emission. Its
photometrical and emission line profile variability can be explained assuming the
circumstellar cloud model (Smith & Groote 2001;
Townsend et al. 2005). Similarly to the star HD 37776 (Mikulásek et al.
2006), this star may exhibit rotational braking,
probably due to the magnetically controlled stellar wind (Oksala & Townsend
2006).
Stellar winds of hot stars are accelerated mainly due to the light scattering in the lines of elements like carbon, nitrogen, oxygen, or iron. Because these heavier elements have much lower density than the bulk of the flow (composed of hydrogen and helium), hot star winds have a multicomponent nature (Castor et al. 1976; Springmann & Pauldrach 1992; Curé 1992; Babel 1995; Krticka & Kubát 2000, 2001, hereafter KKII). Momentum is transferred from low-density heavier elements to the high-density component composed of hydrogen and helium due to Coulomb collisions of charged particles. The corresponding frictional force depends on the velocity difference between wind components. For very low velocity differences, lower than the mean thermal velocity (basically for stars with dense winds), the flow is well coupled. For higher velocity differences (basically for stars with low density winds) the Coulomb collisions are not able to efficiently transfer momentum from heavier ions to hydrogen and helium, and frictional heating becomesimportant (KKII) or wind components may even decouple (Owocki & Puls 2002; Krticka & Kubát 2002).
The chemical peculiarity of helium strong stars is explained in the literature
either by radiative diffusion moderated by the stellar wind
(Vauclair 1975; Michaud et al. 1987) or by helium
decoupling in the stellar wind and its consecutive fall back (Hunger
& Groote 1999). To test whether the wind decoupling model is able to provide a reliable
explanation of helium chemical peculiarity, we decided to calculate
multicomponent wind models suitable for the Bp star ![]() Ori E.
Ori E.
Since there is no accurate determination of ![]() Ori E wind parameters
from observation, we decided to calculate wind mass-loss rate and
terminal velocity using our NLTE wind models (Krticka & Kubát
2004) first.
Ori E wind parameters
from observation, we decided to calculate wind mass-loss rate and
terminal velocity using our NLTE wind models (Krticka & Kubát
2004) first.
These models make it possible to solve (generally multicomponent) hydrodynamical equations for radiatively driven winds and enable prediction of mass-loss rates and terminal velocities. The radiative force and the radiative heating/cooling term are calculated with NLTE level populations obtained using atomic data based on an extended set of the TLUSTY input files (Hubeny 1988; Hubeny & Lanz 1992, 1995; Lanz & Hubeny 2003). The data are based on the Opacity Project (Seaton 1987; Luo & Pradhan 1989; Sawey & Berrington 1992; Seaton et al. 1992; Butler et al. 1993; Nahar & Pradhan 1993), the Iron Project (Hummer et al. 1993; Bautista 1996; Nahar & Pradhan 1996; Zhang 1996; Bautista & Pradhan 1997; Zhang & Pradhan 1997; Chen & Pradhan 1999), and the VALD database (Piskunov et al. 1995; Kupka et al. 1999). The most important simplification of our code compared to other models available in the literature (Vink et al. 1999; Pauldrach et al. 2001; Gräfener & Hamann 2005) is the simplified treatment of the radiative transfer equation. We use the Sobolev approximation for the solution of the radiative transfer equation in lines (Sobolev 1947; Rybicki & Hummer 1978), and we neglect UV line blocking as well as line overlaps.
For the calculation of wind models we assume spherical symmetry.
Since it is well-known that ![]() Ori E has a magnetic field
(Landstreet & Borra 1978) that generally breaks down the assumption of spherical symmetry, our models, at least approximately, describe the flow along individual field lines.
Note that to obtain a more realistic description of the multicomponent wind in
the presence of a stellar magnetic field, it would be necessary to
solve the hydrodynamical equations along the field lines with an inclusion of the proper
projections of individual forces acting on the wind or to use the magnetohydrodynamical simulations.
In the case of a one-component wind model, the former was done in a simplified form by
Friend & MacGregor (1984) and MacGregor & Friend (1987),
and more recently, the latter, using magnetohydrodynamical simulations by
ud-Doula & Owocki (2002).
Ori E has a magnetic field
(Landstreet & Borra 1978) that generally breaks down the assumption of spherical symmetry, our models, at least approximately, describe the flow along individual field lines.
Note that to obtain a more realistic description of the multicomponent wind in
the presence of a stellar magnetic field, it would be necessary to
solve the hydrodynamical equations along the field lines with an inclusion of the proper
projections of individual forces acting on the wind or to use the magnetohydrodynamical simulations.
In the case of a one-component wind model, the former was done in a simplified form by
Friend & MacGregor (1984) and MacGregor & Friend (1987),
and more recently, the latter, using magnetohydrodynamical simulations by
ud-Doula & Owocki (2002).
Stellar parameters appropriate for ![]() Ori E (Hunger et al. 1989) are given in Table 1. The stellar radiative flux (the lower boundary of the wind solution)
of
Ori E (Hunger et al. 1989) are given in Table 1. The stellar radiative flux (the lower boundary of the wind solution)
of ![]() Ori E is calculated using the spherically symmetric NLTE model
atmosphere code described in Kubát (2003).
Ori E is calculated using the spherically symmetric NLTE model
atmosphere code described in Kubát (2003).
Since we intend to study self-initiation of the chemical peculiarity of
![]() Ori E, we also assume solar helium abundance. If not explicitly stated, we
assume solar chemical composition for heavier elements.
Ori E, we also assume solar helium abundance. If not explicitly stated, we
assume solar chemical composition for heavier elements.
| Effective
temperature
|
22 500 K |
| Stellar mass M |
|
| Stellar radius R* |
|
| 3.94 | |
| Mass-loss
rate
|
|
| Terminal
velocity |
|
Using our NLTE wind model, in which we neglected the multicomponent effects,
we calculated wind parameters for ![]() Ori E.
The predicted wind mass-loss rate
Ori E.
The predicted wind mass-loss rate
![]()
![]()
![]() is in
agreement with the order-of-magnitude estimate inferred from observations
(see the discussion in Groote & Hunger 1997).
The derived terminal velocity
is in
agreement with the order-of-magnitude estimate inferred from observations
(see the discussion in Groote & Hunger 1997).
The derived terminal velocity
![]() implies the ratio
of terminal velocity to escape velocity
implies the ratio
of terminal velocity to escape velocity
![]() (note that the radiative force due to light scattering on free
electrons has only a small influence here since the Eddington parameter
(note that the radiative force due to light scattering on free
electrons has only a small influence here since the Eddington parameter
![]() is low). The derived ratio of terminal velocity to escape velocity
is consistent with that for stars close to the bistability jump
(see Pauldrach & Puls 1990; Lamers et al. 1995;
Crowther et al. 2006).
is low). The derived ratio of terminal velocity to escape velocity
is consistent with that for stars close to the bistability jump
(see Pauldrach & Puls 1990; Lamers et al. 1995;
Crowther et al. 2006).
Since we want to study helium decoupling that is charge-dependent
(as follows from the frictional term due to the Coulomb collisions - see
Eqs. (6) here or (40) in KKII), we have to study the calculated variation of He ionization in the wind. From Fig. 1 we conclude that helium is mostly singly ionized
in the stellar wind with only a small contribution of doubly ionized
helium. The fraction of neutral helium in the wind is very small, less than 10-4(for
![]() ).
).
Before studying helium decoupling, we shall discuss another aspect of a wind model for ![]() Ori E, namely, multicomponent effects due to
friction of individual heavier elements with hydrogen and helium.
Ori E, namely, multicomponent effects due to
friction of individual heavier elements with hydrogen and helium.
Since the radiative acceleration acting on individual heavier elements
is different, each element moves with slightly different velocity.
The dimensionless velocity difference between a given
individual heavier element h and hydrogen and helium,
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5128fig2.eps}\end{figure}](/articles/aa/full/2006/46/aa5128-06/Timg34.gif) |
Figure 2:
Calculated relative velocity differences (see Eq. (1))
between individual heavier elements and the passive component.
Velocity differences for elements with low
|
![\begin{figure}
\par\hspace*{-1.5mm}\includegraphics[width=7.5cm,clip]{5128fig3.e...
...4.eps}\vspace*{3mm}
\includegraphics[width=7.4cm,clip]{5128fig5.eps}\end{figure}](/articles/aa/full/2006/46/aa5128-06/Timg35.gif) |
Figure 3:
Four component NLTE wind model with components hydrogen and
helium (p), electrons, nitrogen (N), and remaining heavier ions.
Upper panel: radial velocity of the passive component p
and nitrogen. The velocities of wind components are nearly
indistinguishable in the plot. Middle panel: plot of dimensionless velocity difference
between the passive component and nitrogen
|
Using Eq. (2) we calculated the approximate velocity
differences between hydrogen and helium and individual
heavier ions (see Fig. 2). Apparently, the relative velocity differences between silicon or nitrogen and the hydrogen-helium component are so high that frictional heating
may be enabled. To test this possibility we calculated
four-component wind models. Despite the fact that the relative velocity difference between silicon
and the passive component is slightly higher than that of nitrogen, we
selected the nitrogen component for this test because nitrogen has higher
abundance and, consequently, heating effects caused by friction
are expected to be higher for this element. Resulting four-component wind model (with wind components hydrogen plus helium, free electrons, nitrogen,
and the remaining heavier ions) is given in Fig. 3.
Apparently, the stellar wind temperature significantly increases in the outer parts due to
frictional heating. However, no decoupling occurs in this case (since
![]() is too low to enable the decoupling). The wind terminal velocity significantly increases compared to the case when the frictional heating is neglected. This is caused by the change in the ionization and excitation equilibrium due to a higher wind temperature. Since this effect occurs for velocities higher than that at the critical point, the mass-loss
rate is not essentially modified in four-component models. A similar effect,
but to a lesser extent, was already reported by Krticka (2006).
is too low to enable the decoupling). The wind terminal velocity significantly increases compared to the case when the frictional heating is neglected. This is caused by the change in the ionization and excitation equilibrium due to a higher wind temperature. Since this effect occurs for velocities higher than that at the critical point, the mass-loss
rate is not essentially modified in four-component models. A similar effect,
but to a lesser extent, was already reported by Krticka (2006).
Because the effects of frictional heating between heavier elements (in
our case nitrogen) and the passive component are important basically only
for velocities higher than the escape velocity (which is
![]() at the stellar surface), they do not
significantly modify the flow properties close to the stellar surface.
Since this region is important for the study of the helium decoupling
and its reaccretion, we neglect the effect of friction caused by the distinct properties of
all individual heavier elements. However, heating due to friction between hydrogen and helium ions is properly taken into account.
at the stellar surface), they do not
significantly modify the flow properties close to the stellar surface.
Since this region is important for the study of the helium decoupling
and its reaccretion, we neglect the effect of friction caused by the distinct properties of
all individual heavier elements. However, heating due to friction between hydrogen and helium ions is properly taken into account.
To test the possibility of helium decoupling we calculated four-component wind models with the four following explicitly included wind components: hydrogen, helium, heavier ions, and free electrons. For this purpose we did not use our NLTE models, but simpler (and faster) models with the radiative force in the CAK approximation (Castor et al. 1975; see KKII for the description of these models). The parameterized description of the radiative force in these models enables us to vary both wind parameters and wind ionization state independently to discuss the parameter space for which helium decoupling seems possible.
To model the mass and charge of heavier ions, we selected parameters corresponding to oxygen
(because elements like C, N, O, Si, and S are important for radiative driving).
The selection of oxygen does not have a significant impact on derived results.
The CAK force parameters
We calculated four-component wind models with the realistic value of the
helium charge taken from the previously discussed NLTE model.
Since helium is mostly singly ionized in the wind region
(see Fig. 1), we simply assume
![]() ,
where
,
where
![]() is the relative charge in units of the elementary charge e,
is the relative charge in units of the elementary charge e,
![]() .
.
The velocity profile of a calculated four-component wind model is shown in Fig. 4. Evidently, the radial velocities of all wind components are nearly the same and the wind components are well coupled. Consequently, helium decoupling cannot be found in this case.
For a very low helium charge, significantly lower than that calculated
from NLTE equations, helium decoupling is possible. As an example, in Fig. 5 we plot
a comparable wind model, but for helium charge
![]() .
Apparently, the wind density at the wind base is high enough to
accelerate helium from the stellar surface to supersonic velocities.
However, due to its very low charge, helium decouples from the mean flow
at velocities lower than the escape velocity.
Consequently, helium remains bound to the star and may fall back to the stellar surface.
Hydrodynamical simulations are necessary to study this process in detail
(cf. Porter & Skouza 1999; Votruba et al. 2006).
.
Apparently, the wind density at the wind base is high enough to
accelerate helium from the stellar surface to supersonic velocities.
However, due to its very low charge, helium decouples from the mean flow
at velocities lower than the escape velocity.
Consequently, helium remains bound to the star and may fall back to the stellar surface.
Hydrodynamical simulations are necessary to study this process in detail
(cf. Porter & Skouza 1999; Votruba et al. 2006).
The main result of this paper - that for realistic values of
its charge helium does not decouple from the wind flow for parameters suitable for a star like ![]() Ori E - seems to be in contradiction to the result of Hunger & Groote
(1999), who argued on the basis of the work of Babel (1995,
1996) for the decoupling hypothesis that explains the
observational results. To find the reason for this difference, we
study the hydrodynamical equations analytically. The equation of motion for helium (neglecting
the radiative force acting on helium, the gas-pressure term, and the
charge separation electric field) has the form of (Burgers 1969)
Ori E - seems to be in contradiction to the result of Hunger & Groote
(1999), who argued on the basis of the work of Babel (1995,
1996) for the decoupling hypothesis that explains the
observational results. To find the reason for this difference, we
study the hydrodynamical equations analytically. The equation of motion for helium (neglecting
the radiative force acting on helium, the gas-pressure term, and the
charge separation electric field) has the form of (Burgers 1969)
However, the situation may differ from the extreme case described above.
The contributions of hydrogen and heavier ions to helium acceleration
may be equally important due to different values of the relative
velocity differences
![]() and
and
![]() that
are arguments of the Chandrasekhar function (see Appendix A for a more detailed approximate description of the flow). However, in the case where
the velocity difference between helium and
heavier ions is large,
that
are arguments of the Chandrasekhar function (see Appendix A for a more detailed approximate description of the flow). However, in the case where
the velocity difference between helium and
heavier ions is large,
![]() ,
the frictional
force due to hydrogen dominates. Note that after the decoupling of helium and hydrogen
(in the particular case displayed in Fig. 5 for
,
the frictional
force due to hydrogen dominates. Note that after the decoupling of helium and hydrogen
(in the particular case displayed in Fig. 5 for
![]() ),
helium still remains coupled to electrons. This is due to the fact that
),
helium still remains coupled to electrons. This is due to the fact that
![]() .
The coupling of helium to electrons, however,
modifies the helium velocity only slightly.
.
The coupling of helium to electrons, however,
modifies the helium velocity only slightly.
The only possibility of how to enable helium to fall back onto the stellar surface is to break the strong coupling between helium and hydrogen while keeping the coupling between hydrogen and heavier ions. The only way to secure this in our self-consistent models is to lower the helium charge. This is why for very low helium charges, helium decoupling is possible.
We may derive an approximate condition for the helium decoupling in
the stellar wind. If helium decouples from the stellar wind and subsequently falls back,
there is a point where the helium velocity gradient is zero (see
Fig. 5). The helium momentum Eq. (5)
has, at this point, the form of
Our conclusion that helium decoupling is unlikely in the case of a realistic helium charge is based on the assumption that all helium ionization stages can be treated as a single wind component. This means physically that the processes of ionization and recombination are so rapid that the typical time of recombination or ionization is much shorter than the characteristic time of change in flow properties (i.e., velocity and density). While the violation of this condition would not affect the results in the case of doubly ionized helium (because it has higher charge than the singly ionized helium and, consequently, is more tightly coupled to hydrogen, see Eq. (6)), the violation of this condition in the case of neutral helium may offer an interesting possibility of a helium decoupling mechanism. The reason for this is that the cross-section of collisions of protons with neutral helium is much lower than the effective cross-section for collisions between charged particles (Krstic & Shultz 1999).
To test this, we compare the characteristic time of change in
flow properties (roughly corresponding to the time during which the velocity increases
to its actual value)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5128fig8.eps}\end{figure}](/articles/aa/full/2006/46/aa5128-06/Timg65.gif) |
Figure 6:
Comparison of the characteristic time of change in flow properties
|
Comparison of characteristic times
![]() and
and
![]() is given in Fig. 6. The characteristic time
is given in Fig. 6. The characteristic time
![]() first slightly decreases with radius and then increases again.
This marks the region of fast wind acceleration. Also, the He I ionization time
increases with radius. However, the characteristic time
first slightly decreases with radius and then increases again.
This marks the region of fast wind acceleration. Also, the He I ionization time
increases with radius. However, the characteristic time
![]() is much larger than the He I ionization time
is much larger than the He I ionization time
![]() .
Consequently, helium may be treated as one component
and no decoupling between different helium ionization stages occurs.
.
Consequently, helium may be treated as one component
and no decoupling between different helium ionization stages occurs.
Since the metallicity of individual surface elements of ![]() Ori E varies
with location on the stellar surface, we also studied
the influence of different metallicity on the
possibility of helium decoupling. In particular, we selected the
metallicity to be
Ori E varies
with location on the stellar surface, we also studied
the influence of different metallicity on the
possibility of helium decoupling. In particular, we selected the
metallicity to be
![]() ,
as derived by Smith & Groote
(2001) for
,
as derived by Smith & Groote
(2001) for ![]() Ori E.
Ori E.
Our NLTE wind model for metallicity
![]() (not shown here) predicts a very low mass-loss rate of
(not shown here) predicts a very low mass-loss rate of
![]()
![]()
![]() .
This is much lower than that which can be inferred from the simple relation
.
This is much lower than that which can be inferred from the simple relation
![]() derived by Krticka (2006) for SMC
O stars. This indicates that for lower wind densities the dependence of
mass-loss rate on metallicity is more pronounced.
derived by Krticka (2006) for SMC
O stars. This indicates that for lower wind densities the dependence of
mass-loss rate on metallicity is more pronounced.
Steeper metallicity dependence of mass-loss rates for small
metallicities may seem unexpected. To explain this
behavior, let us first discuss the contribution
of lines of different elements to the radiative force.
This is connected with the value of the line optical depth ![]() ,
which is in the Sobolev approximation given by (e.g.,
Abbott 1982, Eq. (1), neglecting the finite-disk correction)
,
which is in the Sobolev approximation given by (e.g.,
Abbott 1982, Eq. (1), neglecting the finite-disk correction)
Very close to the star, the Sobolev optical depth, Eq. (13),
is large for many lines both of iron group elements and of lighter elements (like carbon,
nitrogen, etc.), mainly due to the very large wind density. Since iron group elements
have effectively larger number of lines than lighter elements, the former
dominate the radiative force close to the star. Farther out in the
wind, the line optical depth, Eq. (13),
is lower (mainly due to decreasing wind density). Since iron
group elements have lower abundances than carbon and nitrogen
(i.e., effectively lower ni), many lines, e.g. iron ones,
become optically thin (![]() ), and these lines do not significantly contribute to the radiative force at higher wind velocities. Consequently, the relative contribution of iron group elements to
the radiative force decreases with increasing wind velocity,
and lighter elements become more important for the radiative acceleration (see also Vink et al. 2001). This behavior can also be interpreted as the result of
the fact that lighter elements and iron group elements dominate different parts
of the line-strength distribution function (Puls et al. 2000). In our
case (even for the solar metallicity model) the iron lines
already become inefficient close to the critical point due to a very low wind density.
), and these lines do not significantly contribute to the radiative force at higher wind velocities. Consequently, the relative contribution of iron group elements to
the radiative force decreases with increasing wind velocity,
and lighter elements become more important for the radiative acceleration (see also Vink et al. 2001). This behavior can also be interpreted as the result of
the fact that lighter elements and iron group elements dominate different parts
of the line-strength distribution function (Puls et al. 2000). In our
case (even for the solar metallicity model) the iron lines
already become inefficient close to the critical point due to a very low wind density.
However, for low metallicities and densities, many lines of lighter elements that are
optically thick for higher metallicities, also become optically thin. This
leads to a significant decrease of the mass-loss rate. In our specific case there is only one optically thick line (the C III resonance line at
![]() Å) that significantly contributes to the radiative force at the critical point. From the contribution of this optically thick line we can calculate the value of the
Å) that significantly contributes to the radiative force at the critical point. From the contribution of this optically thick line we can calculate the value of the
![]() parameter
(cf. Puls et al. 2000, Eq. (26)) as
parameter
(cf. Puls et al. 2000, Eq. (26)) as
![]() .
Using Eq. (87) of Puls et al. (2000), we can roughly estimate
the dependence of the mass-loss rate on the metallicity as
.
Using Eq. (87) of Puls et al. (2000), we can roughly estimate
the dependence of the mass-loss rate on the metallicity as
![]() .
This is more consistent with the decrease of the mass-loss rate with metallicity
obtained in our case than the dependence
.
This is more consistent with the decrease of the mass-loss rate with metallicity
obtained in our case than the dependence
![]() derived by
Krticka (2006) for the denser wind of SMC stars.
Note however that the value of
derived by
Krticka (2006) for the denser wind of SMC stars.
Note however that the value of
![]() may itself depend on the
metallicity. In terms of the line-strength distribution functions (Puls et al. 2000),
the steepening of the dependence of mass-loss
rate on metallicity may be explained as a consequence of the steepening
of the line-strength distribution function for high line-strengths.
Our result supports the findings of Kudritzki (2002,
see Fig. 9 therein), who also found more pronounced dependence of
mass-loss rate on metallicity for a very low-metallicity environment.
may itself depend on the
metallicity. In terms of the line-strength distribution functions (Puls et al. 2000),
the steepening of the dependence of mass-loss
rate on metallicity may be explained as a consequence of the steepening
of the line-strength distribution function for high line-strengths.
Our result supports the findings of Kudritzki (2002,
see Fig. 9 therein), who also found more pronounced dependence of
mass-loss rate on metallicity for a very low-metallicity environment.
The calculated wind model is indeed very close to the wind existence limit. As discussed above, iron lines become inefficient for wind driving and the stellar wind itself is accelerated mainly due to carbon and nitrogen lines. CAK critical point is located closer to the stellar surface as a result of the decrease of a number of optically thick lines (cf. Babel 1995; Vink 2006).
For the calculation of NLTE models we neglected the multicomponent effects; however, from the values of relative velocity differences, Eq. (2), it is clear, that the stellar wind would decouple relatively close to the stellar surface. We have tested this possibility in the three-component model where the metallic ions are described as one component and concluded that already in this model the decoupling occurs close to the stellar surface.
The wind terminal velocity
![]() is lower than in the case of a solar-metallicity model
(cf. Fig. 4). The lowering of the terminal velocity with respect to the solar
metallicity model is an example of the dependence of the terminal velocity on metallicity.
is lower than in the case of a solar-metallicity model
(cf. Fig. 4). The lowering of the terminal velocity with respect to the solar
metallicity model is an example of the dependence of the terminal velocity on metallicity.
The most important parameter that influences the possibility of helium decoupling is the helium charge. However, due to the lower wind density, helium is even more ionized than in the case of the solar metallicity model.
We have calculated low-metallicity four-component wind models with helium as
the fourth component again with the simpler models using the
CAK radiative force. Although the helium ionization is slightly higher than that
in the solar metallicity model, we assumed
![]() .
To obtain
the lower mass-loss rate inferred from NLTE calculations,
we used k=0.23. The other force multipliers are the same as in
Eq. (4). It may seem that the adopted value for kwas not adequately lowered compared to the value adopted for the solar metallicity model
(where k=0.38 was used), because k scales with metallicity as
.
To obtain
the lower mass-loss rate inferred from NLTE calculations,
we used k=0.23. The other force multipliers are the same as in
Eq. (4). It may seem that the adopted value for kwas not adequately lowered compared to the value adopted for the solar metallicity model
(where k=0.38 was used), because k scales with metallicity as
![]() (e.g., Puls et al. 2000). However, the value k=0.23is appropriate for a four-component wind model of a star with low metallicity
(i.e.,
(e.g., Puls et al. 2000). However, the value k=0.23is appropriate for a four-component wind model of a star with low metallicity
(i.e.,
![]() ). Because the radiative force
in the four-component models is calculated using metal density,
the decrease of wind metallicity causes lower
radiative force and lower mass-loss rate.
Consequently, with decreasing metallicity the value of k in
the four-component models varies only slightly.
). Because the radiative force
in the four-component models is calculated using metal density,
the decrease of wind metallicity causes lower
radiative force and lower mass-loss rate.
Consequently, with decreasing metallicity the value of k in
the four-component models varies only slightly.
The results from the calculated four-component wind model can be seen in Fig. 7. Apparently, the friction between metallic ions and the passive component is low and is not able to accelerate the passive component to velocities higher than the escape velocity. Consequently, the wind components decouple and the passive component may start to fall back to the stellar surface. However, hydrogen and helium are still coupled together.
From the first point of view it could be expected that there would be a very high velocity gradient of heavier elements downstream from the point where the decoupling occurs. However, this is not the case; the velocity increase of heavier elements is only moderate after the decoupling. The reason for this behavior is the same as that which causes non-decoupling described for the two-component flow by Krticka & Kubát (2000; see the arguments in Sect. 3.2 therein). According to the momentum equation of heavier ions, the radiative force is approximately equal to the frictional force. Since there is a deficit of the frictional force in the region where decoupling starts to be effective, the radiative force is lower there. Consequently, due to the dependence of the radiative force on the velocity gradient in the Sobolev approximation, the velocity gradient of heavier ions decreases. Because the velocity of the passive component (hydrogen and helium) is lower than the escape velocity, this component decelerates and may fall back onto the stellar surface (Porter & Skouza 1999). The wind in this region is likely to be unstable for the perturbations of a multicomponent flow (Owocki & Puls 2002; Krticka & Kubát 2002).
The derived terminal velocity for the absorbing ions is very low in this case,
roughly
![]() .
Consequently, due to low
wind velocities there would be basically no X-rays emitted in this case by the
possible wind shocks (provided that the absorbing ion component does not accelerate
as a result of other instabilities). This model corresponds to models discussed by
Groote & Schmitt (2004), who argued that the possible explanation of missing periodic X-rays
coming from
.
Consequently, due to low
wind velocities there would be basically no X-rays emitted in this case by the
possible wind shocks (provided that the absorbing ion component does not accelerate
as a result of other instabilities). This model corresponds to models discussed by
Groote & Schmitt (2004), who argued that the possible explanation of missing periodic X-rays
coming from ![]() Ori E may be connected with too low wind velocities.
Ori E may be connected with too low wind velocities.
Although we have used the best models available to us, there are many simplifications that may slightly modify the results obtained (see also KKII; Krticka 2006).
Helium-rich stars could also eventually have a purely metallic wind, as proposed by Babel (1996). However, it is not clear how this could lead to a helium chemical peculiarity.
Although MacGregor (1988) showed that strong magnetic fields may significantly influence the wind terminal velocity, Owocki & ud-Doula (2004) concluded that the change of the terminal velocity is only moderate. The latter argument supports our basic results to be valid also in the case of a strong magnetic field.
The magnetic field, however, may also change the frictional coefficients
due to the particle gyration induced by the magnetic field or may also alter
the velocity distribution function of individual species.
The modification of a frictional coefficient due to the magnetic field
could explain the observational finding of Groote & Hunger (1997)
that the helium-enrichment in ![]() Ori E is found where the wind flow
in the non-magnetic case will be mostly parallel to the magnetic field lines of this star.
Similar findings for other helium strong stars were reported by Groote (2003).
Ori E is found where the wind flow
in the non-magnetic case will be mostly parallel to the magnetic field lines of this star.
Similar findings for other helium strong stars were reported by Groote (2003).
The importance of the magnetic field for the collision frequency of helium atoms
is given by the value of the product of the mean collision time between helium ions
and protons
![]() and gyration frequency of helium ions
and gyration frequency of helium ions
![]() (Mestel 2003, p. 18 therein; Braginskij 1963;
Imazu 1986). The mean collision time
(Mestel 2003, p. 18 therein; Braginskij 1963;
Imazu 1986). The mean collision time
![]() is given by
is given by
The application of Eqs. (14) and (15) to our
derived wind model has shown that for a typical magnetic field with intensities of
the order of 104 G, which corresponds to
the surface magnetic field of ![]() Ori E derived by
Landstreet & Borra (1978), in the outer parts of
the
Ori E derived by
Landstreet & Borra (1978), in the outer parts of
the ![]() Ori E wind, the inequality
Ori E wind, the inequality
![]() holds.
This inequality holds even for lower magnetic field intensities of the
order of 102 G (the lower value of the magnetic field intensity roughly
takes into the account its decrease with radius and its latitudinal
variations). Since wind flows along magnetic field lines due to the strong wind
confinement by the magnetic field, the above-mentioned variation of the
frictional coefficient with the magnetic field is likely not very important
in our case.
holds.
This inequality holds even for lower magnetic field intensities of the
order of 102 G (the lower value of the magnetic field intensity roughly
takes into the account its decrease with radius and its latitudinal
variations). Since wind flows along magnetic field lines due to the strong wind
confinement by the magnetic field, the above-mentioned variation of the
frictional coefficient with the magnetic field is likely not very important
in our case.
Even in the case when doubly ionized helium comprises a significant
fraction of all helium atoms, some of them remain neutral (Fig. 1).
This means that each helium atom for some (however very small) fraction
of time is neutral. Recall that in the case of ![]() Ori E,
some wind material may remain trapped in the minima of gravitational and centrifugal potential along
magnetic field lines (Townsend & Owocki 2005).
The non-zero fraction of time spent by each helium atom in the neutral
state may then induce the drift of helium atoms across magnetic field
lines. Let us at least approximatively derive the magnitude of such
an effect. Recall that the typical time of neutral helium ionization is
Ori E,
some wind material may remain trapped in the minima of gravitational and centrifugal potential along
magnetic field lines (Townsend & Owocki 2005).
The non-zero fraction of time spent by each helium atom in the neutral
state may then induce the drift of helium atoms across magnetic field
lines. Let us at least approximatively derive the magnitude of such
an effect. Recall that the typical time of neutral helium ionization is
![]() (see Eq. (12)) and the typical time of neutral helium recombination is introduced similarly as
(see Eq. (12)) and the typical time of neutral helium recombination is introduced similarly as
![]() .
During the time
.
During the time
![]() the helium atom is not supported by the magnetic field (since it is neutral) and its absolute value of the radial velocity increases by (neglecting the centrifugal force)
the helium atom is not supported by the magnetic field (since it is neutral) and its absolute value of the radial velocity increases by (neglecting the centrifugal force)
![]() where g=GM/r2.
During the time
where g=GM/r2.
During the time
![]() ,
the helium atom is supported by the
magnetic field and has zero radial velocity. Assuming that helium is mostly ionized,
,
the helium atom is supported by the
magnetic field and has zero radial velocity. Assuming that helium is mostly ionized,
![]() ,
this means that the average velocity is roughly
,
this means that the average velocity is roughly
![]() .
The typical time necessary to travel the distance R* is
.
The typical time necessary to travel the distance R* is
![]() .
For typical values for the outer wind parts
.
For typical values for the outer wind parts
![]() s
and
s
and
![]() s, the typical diffusion time
s, the typical diffusion time
![]() years is too large compared to the typical time for the emptying of
the magnetosphere, which is of the order of a hundred years (Townsend & Owocki 2005).
Moreover, the drift may occur in the outward direction,
since the total force acting on neutral helium atoms (i.e.,
the centrifugal force plus the gravitational force) may be directed
outwards, and in such a case no fall back will occur.
Note that the rotation of the magnetosphere containing charged particles
may be roughly approximated as a rigid body rotation, at least near
to the stellar surface.
years is too large compared to the typical time for the emptying of
the magnetosphere, which is of the order of a hundred years (Townsend & Owocki 2005).
Moreover, the drift may occur in the outward direction,
since the total force acting on neutral helium atoms (i.e.,
the centrifugal force plus the gravitational force) may be directed
outwards, and in such a case no fall back will occur.
Note that the rotation of the magnetosphere containing charged particles
may be roughly approximated as a rigid body rotation, at least near
to the stellar surface.
We have studied whether the helium decoupling can occur in the stellar
wind of ![]() Ori E and, consequently, we tested whether
this process may consistently explain enhanced helium
abundance in the atmospheres of Bp stars (as proposed by Hunger &
Groote 1999).
Ori E and, consequently, we tested whether
this process may consistently explain enhanced helium
abundance in the atmospheres of Bp stars (as proposed by Hunger &
Groote 1999).
For this purpose we first calculated an NLTE wind model
for ![]() Ori E and derived its mass-loss rate, terminal
velocity, and helium ionization. These parameters were consequently used for the calculation of
four-component wind models to test whether helium decoupling may occur.
As a by-product of our study, we have found that the frictional heating
due to collisions between individual heavier elements (for example
nitrogen) and the passive component (hydrogen and helium) is important in
the outer wind regions of
Ori E and derived its mass-loss rate, terminal
velocity, and helium ionization. These parameters were consequently used for the calculation of
four-component wind models to test whether helium decoupling may occur.
As a by-product of our study, we have found that the frictional heating
due to collisions between individual heavier elements (for example
nitrogen) and the passive component (hydrogen and helium) is important in
the outer wind regions of ![]() Ori E.
Ori E.
Our four-component wind models showed that for realistic values of
helium charge, the decoupling of helium from the stellar wind of
![]() Ori E is unlikely. Helium decoupling is possible only for
a very low helium charge, much lower than that derived from NLTE equations.
We discussed the possibilities that may change this result, however, we
were not able to find any consistent model that could lead to
helium decoupling in the wind under such conditions.
Ori E is unlikely. Helium decoupling is possible only for
a very low helium charge, much lower than that derived from NLTE equations.
We discussed the possibilities that may change this result, however, we
were not able to find any consistent model that could lead to
helium decoupling in the wind under such conditions.
The main result of our paper, that for realistic values of helium
charge helium will not decouple from the wind flow for parameters
suitable for a star like ![]() Ori E, is in contradiction to the result of Hunger & Groote (1999) who obtained the opposite behavior. The reason for this is that helium is strongly coupled to hydrogen and this coupling cannot be neglected in
model calculations.
Ori E, is in contradiction to the result of Hunger & Groote (1999) who obtained the opposite behavior. The reason for this is that helium is strongly coupled to hydrogen and this coupling cannot be neglected in
model calculations.
We have shown that for lower metallicities the wind mass-loss rate is significantly lower. This is caused by a significant decrease of the number of optically thick lines. For such low mass-loss rates the decoupling of wind components and a subsequent fall back of the passive component may occur. However, helium and hydrogen remain coupled in this case; consequently, this does not explain the chemical peculiarity.
We studied the multicomponent flow analytically and derived a simple condition for helium decoupling in the stellar wind. This analysis supports our basic result that helium decoupling is possible only for a very low helium charge (i.e., when helium is basically neutral).
We have also studied the possibility of the decoupling of neutral helium.
This could be an interesting way of helium decoupling (at least
partially), since the cross-section of collisions of protons with neutral
helium is much lower than the effective cross-section for collisions between
charged particles. However, the neutral helium atoms do not remain neutral for
a sufficiently long time since the characteristic helium
ionization time is much shorter than the characteristic time of change in
flow properties
![]() .
.
As observations seem to favor the hypothesis of helium decoupling (Groote & Hunger 1997; Hunger & Groote 1999), our result leaves us in the very unpleasant situation that we do not have any self-consistent explanation for the chemical peculiarity of He-strong stars. While the scenario proposed by Hunger & Groote (1999) requires artificial lowering of the helium charge, models for helium diffusion moderated by the stellar wind (Vauclair 1975; Michaud et al. 1987) require artificial lowering of the wind mass-loss rate. The only remaining influence on the helium decoupling, which is very difficult to calculate, is that of a strong magnetic field. Nevertheless, it seems clear that the decoupling of helium in normal (non-magnetic) stars with comparable stellar parameters can be excluded as a mechanism of creating the helium overabundance in the stellar atmosphere. Moreover, we were not able to find any self-consistent mechanism that would enable the decoupling in the case of magnetic stars.
Acknowledgements
We would like to thank to Dr. Marian Karlický for the discussion of the influence of the magnetic field on the frictional coefficients, and to Dr. Joachim Puls for his valuable comments on the manuscript. This research has made use of NASA's Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France. This work was supported by grants GA CR 205/03/D020, 205/04/1267. The Astronomical Institute Ondrejov is supported by project AV0 Z10030501.
To obtain an approximate description of a well coupled
multicomponent flow of hydrogen, helium,
and heavier ions![]() (neglecting electrons), we can write
the momentum equations of hydrogen (H) and helium (
(neglecting electrons), we can write
the momentum equations of hydrogen (H) and helium (![]() )
as (Burgers 1969; neglecting the gas-pressure term and
polarization electric field)
)
as (Burgers 1969; neglecting the gas-pressure term and
polarization electric field)
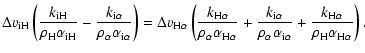 |
(A.3) |
The sign of
![]() depends on the sign of the first bracket in
Eq. (A.4). For
depends on the sign of the first bracket in
Eq. (A.4). For
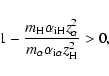 |
(A.5) |
Finally, let us compare the frictional force acting on helium due to
heavier ions and hydrogen in the case of a well coupled flow. The frictional acceleration
after Eq. (5), assuming
![]() and
and
![]() ,
is
,
is
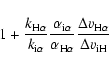 |
(A.7) |