- ... [C/Fe]
![[*]](/icons/foot_motif.gif)
- The usual spectroscopic notation
![${\rm [A/X]}=\log~({N_{\rm A}/N_{\rm X} })_{*}-\log~({N_{\rm A}/N_{\rm X} })_{\odot}$](/articles/aa/full/2006/42/aa5763-06/img24.gif) is used throughout.
is used throughout.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
NIST
![[*]](/icons/foot_motif.gif)
- http://physics.nist.gov/PhysRefData/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
approach
![[*]](/icons/foot_motif.gif)
- Because the fine-structure levels are not directly
included in the whole problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... MULTI
![[*]](/icons/foot_motif.gif)
- Available at
http://www.astro.uio.no/~matsc/mul22/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function
![[*]](/icons/foot_motif.gif)
- More explicitly,
assuming complete redistribution and in the Wien regime, the ratio of
the line source function to the Planck function can be expressed in
terms of the ratio of departure coefficients for the upper and lower
levels of a transition, as
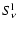 /
/
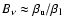 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... formed
![[*]](/icons/foot_motif.gif)
- It is
important to remember that, as mentioned, these weak lines form with
a significant contribution from a tail of atmospheric layers located
much higher up than one would expect in the simple Eddington-Barbier
approach, as we discovered by looking at their contribution
functions (Magain 1986). For example, at
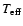 = 6000 K, log g = 4.50,
[Fe/H] = -3, the average height of formation actually moves
out to log
= 6000 K, log g = 4.50,
[Fe/H] = -3, the average height of formation actually moves
out to log
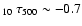 ,
with a significant
contribution to the absorption profile still coming from layers as
high up as log
,
with a significant
contribution to the absorption profile still coming from layers as
high up as log
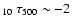 .
Also note the steep
increase of the level population at low metallicity, as one moves
outward in the atmospheric model
(Fig. 2).
.
Also note the steep
increase of the level population at low metallicity, as one moves
outward in the atmospheric model
(Fig. 2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... routine
![[*]](/icons/foot_motif.gif)
- Available via FTP from:
ftp://ftp.mso.anu.edu.au/pub/damian/corr_nlte/c/
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
al.
![[*]](/icons/foot_motif.gif)
- Namely,
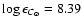 and
and
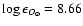 (Asplund et al. 2004; Asplund et al.
2005b), as compared to
(Asplund et al. 2004; Asplund et al.
2005b), as compared to
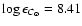 and
and
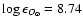 in Akerman et al. (2004). We believe
the values we adopt are best estimates since they are averaged over
different lines and they account for 3D/non-LTE effects.
in Akerman et al. (2004). We believe
the values we adopt are best estimates since they are averaged over
different lines and they account for 3D/non-LTE effects.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.