A&A 457, 823-839 (2006)
DOI: 10.1051/0004-6361:20064846
P. Sánchez-Blázquez1,2 - J. Gorgas2 - N. Cardiel2,3
1 - Laboratoire d'Astrophysique, École Polytechnique Fédérale de Lausanne (EPF
L), Observatoire, 1290 Sauverny, Switzerland
2 -
Dpto. de Astrofísica, Fac. de Ciencias Físicas, Universidad
Complutense de Madrid, 28040 Madrid, Spain
3 -
Calar Alto Observatory, CAHA, Apartado 511, 04004 Almería, Spain
Received 11 January 2006 / Accepted 19 April 2006
Abstract
Aims. This is the third paper of a series devoted to the study of the stellar content of early-type galaxies. The goal of the series is to set constraints on the evolutionary status of these objects.
Methods. We present line-strength gradients for 22 spectral indices measured in a sample of 82 early-type galaxies in different environments, including the high-density cores of the Coma cluster, the Virgo cluster, poor groups, and isolated field galaxies. Using new evolutionary population synthesis models, we derive age and metallicity gradients, and compare the mean values with the predictions of different galaxy formation models. We explore the behaviour of individual chemical species by deriving the metallicity gradient with different indicators.
Results. We find that the strength of the metallicity gradient inferred from stellar population models depends on the specific Lick index employed. In particular, metallicity gradients obtained with CN2 and C4668 combined with H![]() are steeper than those measured using Ca4227 or Fe4383. The correlation of the metallicity gradients with other parameters also depends on the specific index employed. If the metallicity gradient is obtained using CN2 and Mgb, then it correlates with the central age of the galaxies. On the contrary, if Fe4383 or Ca4227 is used, the metallicity gradient correlates with the velocity dispersion gradient.
are steeper than those measured using Ca4227 or Fe4383. The correlation of the metallicity gradients with other parameters also depends on the specific index employed. If the metallicity gradient is obtained using CN2 and Mgb, then it correlates with the central age of the galaxies. On the contrary, if Fe4383 or Ca4227 is used, the metallicity gradient correlates with the velocity dispersion gradient.
Conclusions. This may suggest that several mechanisms have helped to set the age and metallicity gradients in early-type galaxies. While we do not find any correlation between the metallicity gradient and the central velocity dispersion for galaxies in low-density environments, we find a marginal correlation between the metallicity gradient and the mass for galaxies in the centre of the Coma cluster. We also find a trend for which galaxies in denser environments show a steeper metallicity gradient than galaxies in less dense environments. We interpret these results in light of the different mechanisms proposed to explain the observed changes between galaxies as a function of environment.
Key words: Galaxy: abundances - galaxies: elliptical and lenticular, cD - galaxies: stellar content
This is the third paper in a series devoted to studying the properties of
the stellar populations in early-type galaxies as a function of their
local environment. In Sánchez-Blázquez et al. (2006a, hereafter
Paper I), we presented central Lick/IDS index measurements for a sample of
98 early-type galaxies and described their relation to the velocity
dispersion. In Sánchez-Blázquez et al. (2006b, hereafter Paper II), we
compared the indices with the stellar population synthesis models of
Vazdekis et al. (2006, in preparation, hereafter V06) to derive ages and
metallicities. These models are an improved
version of those described by Vazdekis et al. (2003),
strengthened by the addition of a new stellar library
(Sánchez-Blázquez et al. 2006c).
The synthetic spectra cover a spectral range of
![]() Å at resolution 2.3 Å.
The previous papers concentrated on the analysis of the
central regions of the galaxies. In this paper, we investigate the
behaviour of these properties as a function of galactocentric radius.
Å at resolution 2.3 Å.
The previous papers concentrated on the analysis of the
central regions of the galaxies. In this paper, we investigate the
behaviour of these properties as a function of galactocentric radius.
It is well-known that early-type galaxies show a variation of their
stellar population properties with radius. The first evidence of this
phenomenon was observed in the colours of bulges and elliptical galaxies
(see the review by Kormendy & Djorgovski 1989), and indicated that the
central regions tend to be redder than the outer parts. Other authors have
measured optical surface brightness profiles for large sets of local
ellipticals (e.g., Franx et al. 1989; Peletier et al. 1990), reaching the same conclusion. The first study of gradients in the
strength of absorption features was performed by McClure (1969). In a sample of 7 galaxies, McClure found that the C(41-42) index (a measure
of the CN![]() 4216 band strength) was stronger in the centres of the
galaxies than at a distance of 1-1.5 kpc, which he interpreted to be the
result of a metallicity difference between the two regions. Subsequent work in the
field has explored the strength of absorption feature
gradients using a broad range of line indices (Spinrad et al. 1971, 1972; Welch & Forrester 1972; Joly & Andrillat
1973; Oke & Schwarzschild 1975; Cohen 1979; Efstathiou & Gorgas 1985;
Couture & Hardy 1988; Peletier 1989; Thomsen & Baum 1989; Gorgas et al. 1990; Boroson & Thompson 1991; Bender & Surma 1992; Davidge 1992; Davies et al. 1993; Carollo et al. 1993; González 1993; Fisher et al. 1995; Gorgas et al. 1997; Cardiel et al. 1998a; Mehlert et al. 2003). In general, these studies indicate the existence of intense gradients in CN
4216 band strength) was stronger in the centres of the
galaxies than at a distance of 1-1.5 kpc, which he interpreted to be the
result of a metallicity difference between the two regions. Subsequent work in the
field has explored the strength of absorption feature
gradients using a broad range of line indices (Spinrad et al. 1971, 1972; Welch & Forrester 1972; Joly & Andrillat
1973; Oke & Schwarzschild 1975; Cohen 1979; Efstathiou & Gorgas 1985;
Couture & Hardy 1988; Peletier 1989; Thomsen & Baum 1989; Gorgas et al. 1990; Boroson & Thompson 1991; Bender & Surma 1992; Davidge 1992; Davies et al. 1993; Carollo et al. 1993; González 1993; Fisher et al. 1995; Gorgas et al. 1997; Cardiel et al. 1998a; Mehlert et al. 2003). In general, these studies indicate the existence of intense gradients in CN
![]() and CN
and CN
![]() ,
less
pronounced gradients in the Mg
,
less
pronounced gradients in the Mg
![]() ,
G band, NaD, Ca H&K features, and in some lines of Fe I, and a weak or null gradient in
H
,
G band, NaD, Ca H&K features, and in some lines of Fe I, and a weak or null gradient in
H![]() ,
MgH, TiO, Ca I, and in the calcium triplet in the
near-infrared. Most of these studies have suggested that the existence of
gradients in the metallic spectral features is a consequence of a decreasing metallicity with increasing galactocentric radius (e.g., McClure 1969; Cohen 1979; Davies et al. 1993; Kobayashi & Arimoto 1999;
Mehlert et al. 2003). Some, however, have argued that, apart from a variation of metallicity with radius, there is also a radial variation in
the luminosity-weighted mean age of the stellar populations, with the
central regions being younger than the outer regions (Gorgas et al. 1990;
Munn 1992; González 1993; González & Gorgas 1996).
,
MgH, TiO, Ca I, and in the calcium triplet in the
near-infrared. Most of these studies have suggested that the existence of
gradients in the metallic spectral features is a consequence of a decreasing metallicity with increasing galactocentric radius (e.g., McClure 1969; Cohen 1979; Davies et al. 1993; Kobayashi & Arimoto 1999;
Mehlert et al. 2003). Some, however, have argued that, apart from a variation of metallicity with radius, there is also a radial variation in
the luminosity-weighted mean age of the stellar populations, with the
central regions being younger than the outer regions (Gorgas et al. 1990;
Munn 1992; González 1993; González & Gorgas 1996).
How the physical properties of galaxies vary with radius can prove invaluable for constraining the processes of galaxy formation and evolution. For example, metallicity gradients are a measure of the quantity, velocity, and duration of gas dissipation. Likewise, age and metallicity gradients contain information concerning the relative importance of interactions during galaxy formation.
In the classical models of monolithic collapse (Eggen et al. 1962; Larson
1974a; Carlberg 1984; Arimoto & Yoshii 1987; Gibson 1997), stars form in
essentially all regions during the collapse and remain in their orbits
with little inward migration, whereas the gas dissipates inwards, being
continuously enriched by the evolving stars.
In this way, the stars formed at the centres of galaxies are predicted to
be more metal-rich than those born in the outer regions. Supernova-driven
galactic winds (Mathews & Baker 1971; Larson 1974b; Arimoto & Yoshii
1987; Gibson 1997), initiated when the energy injected into the
interstellar medium (ISM) by supernovae matches that of its binding
energy, act to evacuate the galaxy of gas, thereby eliminating the fuel
necessary for star formation. The external parts of the galaxy (with a shallower potential well) develop winds before the central regions, where
the star formation and, therefore, the chemical enrichment continue for
longer. The monolithic collapse models, therefore, predict very steep
metallicity gradients as both processes - the dissipation of gas toward
the central parts of the galaxy and the different timescales for the
occurrence of the galactic winds - act in the direction of steepening any
nascent metallicity gradient![]() .
.
Simulations of galaxy mergers within the concordant hierarchical clustering cold dark matter framework (e.g., Cole et al. 1994; Baugh et al. 1996; Kauffmann 1996; Kauffmann & Charlot 1998) offer somewhat contradictory predictions as to the radial variation of stellar properties in early-type galaxies - while some (e.g., White 1980; Bekki & Shioya 1999) suggest that mergers lead of a flattening of metallicity gradients, others (e.g., van Albada 1982) argue that the gradients are affected only moderately by the mergers, as the violent relaxation preserves the position of the stars in the local potential. This apparent dichotomy between the simulations is driven in part by the sensitivity of the outcome to the fraction of gaseous versus stellar mass present in the progenitor galaxies. Broadly speaking, the predicted gradients are steeper if the progenitor galaxies have a large fraction of their pre-merger baryonic mass in the form of gas. Furthermore, numerical simulations suggest that during the merger, a significant fraction of this gas migrates inward toward the central regions of the merging galaxies, resulting in increased central star formation (Barnes & Hernquist 1991). Mihos & Hernquist (1994) showed that the observed gradients in elliptical galaxies may be a consequence of the occurrence of secondary bursts of star formation triggered by these mergers.
One of the means to understanding the physical processes governing
galaxy formation and evolution is to study the relations between gradients
and other fundamental (global) properties of galaxies. For instance,
dissipational collapse models predict a strong positive correlation
between metallicity gradient and galactic mass. The empirical evidence
for such putative correlations remains contentious - e.g., Gorgas et al. (1990, hereafter G90) did not find any relation between the Mg2 gradient
and the rotation or total luminosity of a sample of early-type galaxies,
although they found some evidence of a positive correlation between the Mg2gradient and the central velocity dispersion (a probability of 95% in a
non-parametric Spearman test). Conversely, Franx & Illingworth (1990)
found a correlation between the colour gradient and local escape velocity (later
confirmed by other authors, such as Davies et al. 1993),
arguing that the aforementioned galactic winds were the dominant mechanism
controlling the metal content of early-type galaxies. Davidge (1992) analysed 12 bright
ellipticals, searching for correlations between the Mg2 gradients and the
central velocity dispersion (![]() ), the total luminosity, the shape
of the isophotes, the fine structure parameter (Schweizer et al. 1990),
and the anisotropy parameter (v/
), the total luminosity, the shape
of the isophotes, the fine structure parameter (Schweizer et al. 1990),
and the anisotropy parameter (v/![]() )*, which defines the degree of
rotation in a galaxy (Binney 1978). Davidge found weak correlations
between the Mg2 gradient, (v/
)*, which defines the degree of
rotation in a galaxy (Binney 1978). Davidge found weak correlations
between the Mg2 gradient, (v/![]() )* and
)* and ![]() ,
and an absence of correlation with any of the other parameters. Carollo et al. (1993) carried out an exhaustive study of the gradients of several spectral features (Mg1, Mg2, NaD, TiO1, TiO2, and Fe5270) in a sample of 42 galaxies. Carollo et al. found a tendency for the slope of
the gradients in the Mg2 index to increase with the mass of the galaxy,
but only for galaxies with masses below 10
,
and an absence of correlation with any of the other parameters. Carollo et al. (1993) carried out an exhaustive study of the gradients of several spectral features (Mg1, Mg2, NaD, TiO1, TiO2, and Fe5270) in a sample of 42 galaxies. Carollo et al. found a tendency for the slope of
the gradients in the Mg2 index to increase with the mass of the galaxy,
but only for galaxies with masses below 10
![]() .
Carollo &
Danziger (1994) studied the line-strength gradients in Mg2 and
.
Carollo &
Danziger (1994) studied the line-strength gradients in Mg2 and ![]() Fe
Fe![]() for five early-type galaxies, confirming the
dependency between metallicity and local potential well depth as a function of galactocentric radius, albeit with significant scatter.
González & Gorgas (1996) surveyed the Mg2 gradient literature
available at the time, discovering that galaxies with steeper Mg2 gradients also possess stronger central Mg2. They proposed a scenario
in which star formation episodes in the centre of the galaxies are
responsible for the correlation, pointing out that its existence implies
that the global mass-metallicity relation is flatter than the
mass-metallicity relation inferred from the central values. Recently,
Mehlert et al. (2003) found a correlation between the gradients of some
spectral features and the velocity dispersion gradient (which can be
considered a measure of the potential well depth gradient). In contrast
with González & Gorgas, Mehlert et al. did not find a correlation
between the line-strength index gradients and the central values, or
between the index gradients and the central velocity dispersion.
for five early-type galaxies, confirming the
dependency between metallicity and local potential well depth as a function of galactocentric radius, albeit with significant scatter.
González & Gorgas (1996) surveyed the Mg2 gradient literature
available at the time, discovering that galaxies with steeper Mg2 gradients also possess stronger central Mg2. They proposed a scenario
in which star formation episodes in the centre of the galaxies are
responsible for the correlation, pointing out that its existence implies
that the global mass-metallicity relation is flatter than the
mass-metallicity relation inferred from the central values. Recently,
Mehlert et al. (2003) found a correlation between the gradients of some
spectral features and the velocity dispersion gradient (which can be
considered a measure of the potential well depth gradient). In contrast
with González & Gorgas, Mehlert et al. did not find a correlation
between the line-strength index gradients and the central values, or
between the index gradients and the central velocity dispersion.
The results to date are, to some extent, contradictory and therefore incapable of providing unequivocal support to any particular galaxy formation scenario. This contradictory nature is driven, in part, by the requisite high signal-to-noise data and associated care in data reduction necessary to extract reliable gradients. Further, very few absorption features (mainly Mg2) have been systematically explored with a suitably large sample of ellipticals. Our work has been designed specifically to address these shortcomings which have plagued the interpretation of the extant data, using a sample of 82 galaxies populating a range of local environmental conditions.
In Sect. 2, we describe the measurement of the line-strength gradients within our dataset. In Sect. 3, we compare these gradients with synthesis models to derive explicit age and metallicity gradients. Sections 4 to 7 analyse the stellar population gradients for a sample drawn from low density environments. In particular, Sect. 4 discusses the mean age and metallicity gradients, while in Sect. 5 we explore the existence of possible variations of the chemical abundance ratios with radius. In Sect. 6, we explore the existence of putative correlations between metallicity gradient and other galactic parameters. In Sect. 7, we use the stellar population global parameters, derived with the help of the gradients, to study whether the trends found in Papers I and II hold only for the central parts, or can be extended to the entire galaxy. Section 8 studies the mean gradients in the sample of galaxies drawn from the high-density core of the Coma cluster. Finally, in Sect. 9, we summarise our findings and conclusions.
The parent sample from which galaxies are drawn consists of 98 early-type systems, of which 37 belong to the Coma cluster (high-density
environment galaxies, hereafter HDEGs), while the rest are drawn from the
field, small groups, and the Virgo cluster (low-density environment
galaxies, hereafter LDEGs). Details of the sample, the observations, and
associated data reduction, can be found in Paper I. From each fully
reduced galaxy frame, a final frame was created by extracting spectra
along the slit, binning in the spatial direction to guarantee a minimum
signal-to-noise ratio per Å (S/N) of 20 in the spectral region of the
H![]() index, ensuring a maximum relative error for this index (assuming
a typical value of 1.5 Å) of 20% (see Cardiel et al. 1998b). Those
galaxies that did not have a minimum of 4 spectra along the radius
meeting this criterion were eliminated from the final sample, which left a total of 82 galaxies of sufficient quality to measure gradients - 21 HDEGs and 61 LDEGs.
index, ensuring a maximum relative error for this index (assuming
a typical value of 1.5 Å) of 20% (see Cardiel et al. 1998b). Those
galaxies that did not have a minimum of 4 spectra along the radius
meeting this criterion were eliminated from the final sample, which left a total of 82 galaxies of sufficient quality to measure gradients - 21 HDEGs and 61 LDEGs.
An equivalent radius
![]() was assigned to each binned spectrum:
was assigned to each binned spectrum:
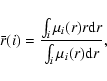 |
(1) |
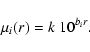 |
(2) |
| (3) |
Radial velocities and velocity dispersions were measured for each spectrum
as a function of galactocentric radius, as described in Paper I. The
rotation curve and the velocity dispersion profile were used to measure
the Lick/IDS indices at the resolution defined by this system and to
correct them for velocity broadening (again, as described in Paper I).
Instead of using the individual values of the velocity dispersion for each
spectrum measured at each radial "bin'', we fitted a smooth curve to the
![]() profile. This minimises the errors in the derived velocity
dispersion, due to the lower signal-to-noise ratios in the external parts
of the galaxies. Residual [OIII] emission profiles were also estimated as
described in Paper I. These values were used to correct the H
profile. This minimises the errors in the derived velocity
dispersion, due to the lower signal-to-noise ratios in the external parts
of the galaxies. Residual [OIII] emission profiles were also estimated as
described in Paper I. These values were used to correct the H![]() index
for emission, using the the relation derived by Trager et al. (2000a) -
index
for emission, using the the relation derived by Trager et al. (2000a) -
![]() H
H![]() = 0.6 [OIII], where
= 0.6 [OIII], where ![]() H
H![]() is the correction to
the index and [OIII] the equivalent width of the [OIII]
is the correction to
the index and [OIII] the equivalent width of the [OIII]
![]() emission line. The Mgb and Fe5015 indices were also corrected from
emission, as was done in the central spectra. The final kinematic, line-strength
and emission profiles, together with their associated errors, are
presented in Sánchez-Blázquez (2004).
emission line. The Mgb and Fe5015 indices were also corrected from
emission, as was done in the central spectra. The final kinematic, line-strength
and emission profiles, together with their associated errors, are
presented in Sánchez-Blázquez (2004).
We measured 19 Lick/IDS indices defined by Trager et al. (1998) for all the
galaxies except for those observed in Run 3, for which only 15 indices could be
measured. With the aim of reducing the random errors in the external parts of
the galaxies, we have defined the following composite indices:
| (4) | |||
| (5) |
Although the behaviour of the indices as a function of galactocentric
radius is not perfectly linear for all 82 galaxies, with the aim of
obtaining a quantitative measurement of their values, we performed a linear fit, weighted by the errors over all the indices, to the relation
![]() ,
where I' represents the index expressed in
magnitudes,
,
where I' represents the index expressed in
magnitudes, ![]() is the effective radius projected over the major axis,
i.e.,
is the effective radius projected over the major axis,
i.e.,
![]() (
(
![]() being the
effective radius), and d the index gradient, hereafter denoted by grad. This projection can be done under the assumption that the contours
of constant I' coincide with the isophotes, which has been confirmed by
several earlier studies (e.g., Davies et al. 1993). To avoid the
uncertainties and radial flattening due to seeing effects, the data within
the central area corresponding to the seeing were excluded from the fit.
The seeing was estimated directly from the observations on the 4 different
runs. Figure 1 shows some examples of the line-strength
gradients for the galaxy NGC 2832.
being the
effective radius), and d the index gradient, hereafter denoted by grad. This projection can be done under the assumption that the contours
of constant I' coincide with the isophotes, which has been confirmed by
several earlier studies (e.g., Davies et al. 1993). To avoid the
uncertainties and radial flattening due to seeing effects, the data within
the central area corresponding to the seeing were excluded from the fit.
The seeing was estimated directly from the observations on the 4 different
runs. Figure 1 shows some examples of the line-strength
gradients for the galaxy NGC 2832.
To check the assumption of linearity for the gradients, we have
compared the central values derived in Paper I (integrated within an equivalent aperture of 4
![]() at redshift z=0.016 - i.e.,
at redshift z=0.016 - i.e.,
![]() 1.3 kpc), with the expected values for this aperture inferred from
the gradients. Figure 2 shows this comparison for all the
indices. Within each panel, the mean offset (
1.3 kpc), with the expected values for this aperture inferred from
the gradients. Figure 2 shows this comparison for all the
indices. Within each panel, the mean offset (![]() )
and the root mean
square of the deviations (
)
and the root mean
square of the deviations (![]() )
are indicated. In general, the
agreement is very good - the offsets are not statistically significant
for any of the indices, and the scatter is compatible with the errors,
lending support to the adopted approximation of a linear fit.
)
are indicated. In general, the
agreement is very good - the offsets are not statistically significant
for any of the indices, and the scatter is compatible with the errors,
lending support to the adopted approximation of a linear fit.
Table 1, available in the electronic edition and
online![]() , lists the gradients in
all the line-strength indices measured for each of the 82 galaxies in our
sample. A portion of this table is reproduced here to demonstrate its
content and structure.
, lists the gradients in
all the line-strength indices measured for each of the 82 galaxies in our
sample. A portion of this table is reproduced here to demonstrate its
content and structure.
| Galaxy | D4000 | H
|
H
|
CN2 | Ca4227 | G4300 | H
|
H
|
Fe4383 | |
| NGC 221 | -0.0877 | -0.0520 | -0.0014 | 0.0008 | -0.0247 | -0.0110 | 0.0104 | 0.0018 | 0.0079 | 0.0025 |
| 0.0126 | 0.0058 | 0.0023 | 0.0026 | 0.0057 | 0.0035 | 0.0025 | 0.0020 | 0.0032 | 0.0017 | |
| Ca4455 | Fe4531 | C4668 | H |
Fe5015 | Mg1 | Mg2 | Mgb | Fe5270 | Fe5335 | |
| 0.0027 | -0.0030 | -0.0037 | -0.0021 | 0.0052 | -0.0007 | 0.0092 | -0.0017 | -0.0038 | 0.0020 | |
| 0.0019 | 0.0016 | 0.0017 | 0.0016 | 0.0019 | 0.0011 | 0.0022 | 0.0018 | 0.0011 | 0.0017 |
Figure 3 shows the line-strength gradients in Fe4383, Mgb,
and H![]() ,
presented in index-index diagrams that combine both the
central values and the line-strengths at one effective radius. Each
central measurement is connected to its corresponding
measurement in the outer region. The stellar population
models of V06 are overplotted.
As can be seen, most of the lines tend to be nearly
parallel (although, admittedly, not entirely) to the iso-age lines taken
from the theoretical grid, which indicates that the gradients are mostly
due to variations in metallicity. However, there are several galaxies
that show significant variations in both age and metallicity with radius.
We return to this point towards the end of this section.
,
presented in index-index diagrams that combine both the
central values and the line-strengths at one effective radius. Each
central measurement is connected to its corresponding
measurement in the outer region. The stellar population
models of V06 are overplotted.
As can be seen, most of the lines tend to be nearly
parallel (although, admittedly, not entirely) to the iso-age lines taken
from the theoretical grid, which indicates that the gradients are mostly
due to variations in metallicity. However, there are several galaxies
that show significant variations in both age and metallicity with radius.
We return to this point towards the end of this section.
To quantify this behaviour, we have transformed the line-strength gradients into age and metallicity gradients using the model predictions of V06, who make use of the code of Vazdekis (1999) updated with a new and improved stellar library (MILES, Sánchez-Blázquez et al. 2006c; these models will be presented in the forthcoming paper V06).
With the aim of minimising the effects of low signal-to-noise data, we
designed a method that makes simultaneous use of 10 different indices. The
selected indices are: H
![]() ,
CN2, Ca4227, G4300, H
,
CN2, Ca4227, G4300, H
![]() ,
Fe4383, H
,
Fe4383, H![]() ,
Fe5015, HA, and Balmer. We checked that the results
did not depend on the particular choice of indices. None of the Mg indices were
employed, as they could not have been measured in all the galaxies from Run 3,
due to the wavelength converage of the spectra.
To derive single estimates of age and metallicity gradients, we followed a procedure
that is divided into two steps: (i) obtaining individual errors for the
age and metallicity gradients for all the galaxies in each index-index
diagram; and (ii) deriving the final values of the age and metallicity
gradients, along with their associated errors.
,
Fe5015, HA, and Balmer. We checked that the results
did not depend on the particular choice of indices. None of the Mg indices were
employed, as they could not have been measured in all the galaxies from Run 3,
due to the wavelength converage of the spectra.
To derive single estimates of age and metallicity gradients, we followed a procedure
that is divided into two steps: (i) obtaining individual errors for the
age and metallicity gradients for all the galaxies in each index-index
diagram; and (ii) deriving the final values of the age and metallicity
gradients, along with their associated errors.
We first calculated the slopes of the constant age and metallicity lines
in the models. The slopes of these lines change with the absolute values
of age and metallicity but, in the region in which the galaxies are
located, the values are almost constant. The derived slopes define a new
diagram that we call "![]() index-
index-![]() index'' - in the associated
Fig. 4, the dashed line represents the expected gradients
in the indices if these were due, exclusively, to a variation in age
(assuming a constant solar metallicity). On the other hand, the solid
lines show the predicted gradients if the only parameter changing with
radius was the metallicity (assuming a constant age of 10 Gyr).
Figure 4 also shows the gradients in H
index'' - in the associated
Fig. 4, the dashed line represents the expected gradients
in the indices if these were due, exclusively, to a variation in age
(assuming a constant solar metallicity). On the other hand, the solid
lines show the predicted gradients if the only parameter changing with
radius was the metallicity (assuming a constant age of 10 Gyr).
Figure 4 also shows the gradients in H![]() and Fe4383
measured in the galaxy NGC 4842A. To derive the age and metallicity
gradients, we project the position of the galaxy over the lines
and Fe4383
measured in the galaxy NGC 4842A. To derive the age and metallicity
gradients, we project the position of the galaxy over the lines
![]() age = 0 and
age = 0 and ![]() [M/H] = 0,
and interpolate the projection over these lines.
[M/H] = 0,
and interpolate the projection over these lines.
For each galaxy, and in every ![]() index-
index-![]() index diagram, we
performed 104 Monte Carlo simulations in which each point was perturbed
with our errors, following a Gaussian probability distribution. For each
simulation, an age and metallicity gradient was obtained. This process was
repeated with all possible paired combinations of indices. As an illustration, Fig. 5 shows the values of age and
metallicity gradients derived for NGC 4842A, using the
index diagram, we
performed 104 Monte Carlo simulations in which each point was perturbed
with our errors, following a Gaussian probability distribution. For each
simulation, an age and metallicity gradient was obtained. This process was
repeated with all possible paired combinations of indices. As an illustration, Fig. 5 shows the values of age and
metallicity gradients derived for NGC 4842A, using the
![]() H
H![]() -
-![]() Mgb and
Mgb and ![]() Mgb-
Mgb-![]() Fe4383 diagrams. As
can be seen, due to the non-orthogonality of the index-index diagrams,
there is an artificial anti-correlation between the age and the
metallicity gradients. To obtain the error in the age and metallicity
gradient for each galaxy, in every diagram, we projected these ellipses
over the x- and y-axes and calculated the standard deviation of
the resultant Gaussian. We denote the typical errors by
Fe4383 diagrams. As
can be seen, due to the non-orthogonality of the index-index diagrams,
there is an artificial anti-correlation between the age and the
metallicity gradients. To obtain the error in the age and metallicity
gradient for each galaxy, in every diagram, we projected these ellipses
over the x- and y-axes and calculated the standard deviation of
the resultant Gaussian. We denote the typical errors by
![]() (grad [age])i and
(grad [age])i and ![]() (grad [M/H])i, where i refers
to each index-index diagram.
(grad [M/H])i, where i refers
to each index-index diagram.
Once we have obtained the typical errors associated with the inferred age and metallicity gradients for each index-index combination, we again performed (for each galaxy) 104 Monte Carlo simulations, into which Gaussian noise was added to each line-strength index. Simulations were performed for each index independently, as opposed to each index-index diagram (note that once an index value is simulated, its particular value is fed simultaneously to all the possible diagrams, taking into account the fact that not all of the different diagrams are independent).
We then measured the age and metallicity gradients of all the values obtained
in all the simulations j, using all the different diagrams i. The mean age
and metallicity gradient of simulation j was obtained as an average of
the age and metallicity gradients obtained for this particular simulation, using
all the different diagrams i, namely,
![\begin{displaymath}%
{\rm grad~[age]}_{j}=
\frac{\displaystyle\sum_{i=1}^{n_{\r...
...i=1}^{n_{\rm com}}
\frac{1}{\sigma({\rm grad~[age]})_{i}^2}},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img53.gif) |
(6) |
![\begin{displaymath}%
{\rm grad}~[{\rm M}/{\rm H}]_{j}=
\frac{\displaystyle\sum_...
...com}}
\frac{1}{\sigma({\rm grad}~ [{\rm M}/{\rm H}])_{i}^2}},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img54.gif) |
(7) |
Finally, the age and metallicity gradients for each galaxy were calculated as
the mean values of all the simulations, i.e.,
![\begin{displaymath}%
{\rm grad~[age]}_{\rm final}=\sum_{j=1}^{n_{\rm sim}}
\frac{{\rm grad}~[{\rm age}_{j}]}{n_{\rm sim}},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img56.gif) |
(8) |
![\begin{displaymath}%
{\rm grad~[M/H]}_{\rm final}=\sum_{j=1}^{n_{\rm sim}}
\frac{{\rm grad}~[{\rm M}/{\rm H}]_{j}}{n_{\rm sim}},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img57.gif) |
(9) |
![\begin{displaymath}%
\sigma_{(\rm age)}=\sqrt{\frac{\displaystyle\sum_{j=1}^{n_{...
..._{j}-{\rm grad~[age]}_{\rm final}\right)^2}
{n_{\rm sim}-1}},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img59.gif) |
(10) |
![\begin{displaymath}%
\sigma_{(\rm [M/H])}=\sqrt{\frac{\displaystyle\sum_{j=1}^{n...
...-{\rm grad~[M/H]}_{\rm final}\right)^2}
{n_{\rm sim}-1}}\cdot
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img60.gif) |
(11) |
Figure 6 shows three different ![]() index-
index-![]() index diagrams in which we have overplotted the galaxies in low-density
environments. The lines of constant age and metallicity divide these
diagrams into four distinct regimes. These regimes indicate the position
of the galaxies with positive/negative differences in age and metallicity
between the central and the external parts, as is labeled in the panels. As
can be seen, most of the galaxies are situated in the regime consistent
with their centres being younger and more metal-rich than their outer
regions. The bulk of the galaxies, however, are further away from the line
index diagrams in which we have overplotted the galaxies in low-density
environments. The lines of constant age and metallicity divide these
diagrams into four distinct regimes. These regimes indicate the position
of the galaxies with positive/negative differences in age and metallicity
between the central and the external parts, as is labeled in the panels. As
can be seen, most of the galaxies are situated in the regime consistent
with their centres being younger and more metal-rich than their outer
regions. The bulk of the galaxies, however, are further away from the line
![]() [M/H] = 0 than from the line
[M/H] = 0 than from the line ![]() age = 0, suggesting that the
gradients in the line-strength indices are due
(mostly) to variations of metallicity with radius.
age = 0, suggesting that the
gradients in the line-strength indices are due
(mostly) to variations of metallicity with radius.
The predicted mean values of the age and metallicity gradients are
dependent upon the merging history of the galaxies.
In general, dissipative processes tend to steepen the
metallicity gradient, while major mergers are expected
to dilute it. In the simulations of Kobayashi (2004), the
typical gradients for non-merger and merger galaxies are
![]() [Fe/H]/
[Fe/H]/
![]() ,
-0.38,
,
-0.38, ![]() [O/H]
[O/H]
![]() ,
-0.24, and
,
-0.24, and
![]() ,
-0.24,
respectively. We now analyse the mean age and metallicity gradients for
the sample of LDEGs. Table 3 lists these values,
together with relevant associated statistics (see below).
,
-0.24,
respectively. We now analyse the mean age and metallicity gradients for
the sample of LDEGs. Table 3 lists these values,
together with relevant associated statistics (see below).
| Mean | N |
|
t |
|
t | |||
| grad ( |
|
0.117 | 61 | 19.62 | 3.1 | 0.032 | 1.63E-13 | |
| grad [M/H] |
|
0.151 | 61 | 17.25 | 5.7 | 0.075 | 4.3E-22 | |
| grad [M/H] (CN2-H |
|
0.249 | 61 | 23.14 | 11.2 | 0.111 | 2.6E-31 | 5.94 |
| grad [M/H] (C4668-H |
|
0.219 | 61 | 21.78 | 9.8 | 0.078 | 0.000 | 4.26 |
| grad [M/H] (Fe4383-H |
|
0.197 | 61 | 15.31 | 3.9 | 0.109 | 1.2E-14 | 0.14 |
| grad [M/H] (Mgb-H |
|
0.302 | 61 | 14.53 | 5.1 | 0.138 | 5.3E-31 | 2.30 |
| grad [M/H] (Ca4227-H |
|
0.269 | 61 | 19.18 | 3.4 | 0.178 | 2.9E-7 | 0.45 |
The mean age gradient for the sample of LDEGs is
![]() (age)/
(age)/![]() = 0.082
= 0.082 ![]() 0.015. A t-test indicates that the
probability of this value being different from zero by chance is <0.1%.
The positive gradient indicates that, on average, the centres of the
galaxies are younger (or at least, they contain a percentage of younger
stars, which make the mean luminosity-weighted age lower) than the outer
parts. The existence of a significant age gradient is difficult to
explain within monolithic collapse scenarios, as the timescales for star
formation are necessarily very short, but it does suggest that secondary
episodes of star formation have occurred recently in the centres of the galaxies.
0.015. A t-test indicates that the
probability of this value being different from zero by chance is <0.1%.
The positive gradient indicates that, on average, the centres of the
galaxies are younger (or at least, they contain a percentage of younger
stars, which make the mean luminosity-weighted age lower) than the outer
parts. The existence of a significant age gradient is difficult to
explain within monolithic collapse scenarios, as the timescales for star
formation are necessarily very short, but it does suggest that secondary
episodes of star formation have occurred recently in the centres of the galaxies.
Little work has been done to date on the derivation of age gradients
within early-type galaxies. Indeed, most of the extant studies of
gradients in the literature assume the absence of an age gradient in
order to derive the metallicity gradient.
Munn (1992) was the first author who studied, in a systematic way, the variation
of age with the galactocentric radius.
From a sample of seven early-type galaxies, Munn combined the
CN![]() 3883 and CN
3883 and CN![]() 4216 features with the D4000 index to
compare them with the prediction of stellar population models. Since the age
calibration employed by Munn was necessarily restricted to the assumption
of solar metallicity, his ability to quantify the inferred gradients was
limited. He did, however, conclude that to explain the dispersion
and trends in the CN-D4000 diagrams, a variation of at least two parameters with radius was necessary (as suggested already by G90), with
age and metallicity being the obvious candidates. Using the stellar
population models of Worthey (1994), González (1993) found a mean
variation in the age of his sample of galaxies of
4216 features with the D4000 index to
compare them with the prediction of stellar population models. Since the age
calibration employed by Munn was necessarily restricted to the assumption
of solar metallicity, his ability to quantify the inferred gradients was
limited. He did, however, conclude that to explain the dispersion
and trends in the CN-D4000 diagrams, a variation of at least two parameters with radius was necessary (as suggested already by G90), with
age and metallicity being the obvious candidates. Using the stellar
population models of Worthey (1994), González (1993) found a mean
variation in the age of his sample of galaxies of ![]() 20% from the
centre to the effective radius (he also found a variation of
20% from the
centre to the effective radius (he also found a variation of ![]() 50% in
metallicity). Fisher et al. (1996) found
that the centres were slightly younger than the external
parts in their sample of lenticulars, although they did not quantify the result. Contrary to these
results, Mehlert et al. (2003) found a mean age gradient compatible with
being null in a sample of galaxies. The
discrepancy between the above results and those of Mehlert et al. (2003)
may be due to the different environments from which the samples were
drawn. We analyse the gradients for the HDEGs in Sect. 8.
50% in
metallicity). Fisher et al. (1996) found
that the centres were slightly younger than the external
parts in their sample of lenticulars, although they did not quantify the result. Contrary to these
results, Mehlert et al. (2003) found a mean age gradient compatible with
being null in a sample of galaxies. The
discrepancy between the above results and those of Mehlert et al. (2003)
may be due to the different environments from which the samples were
drawn. We analyse the gradients for the HDEGs in Sect. 8.
Table 3 also shows the values of the rms dispersion
about the mean value (![]() )
and the scatter expected from the errors (
)
and the scatter expected from the errors (
![]() ). We performed a
). We performed a ![]() test to compare these
values, and the results are shown in the 8th column of the table.
There is a real scatter in the age gradients between galaxies that cannot
be explained by the errors, which is consistent with the earlier results of G90. We
have explored possible correlations between the age gradients and other
parameters of the galaxies, including (but not limited to) the central
velocity dispersion, but we have not found any significant correlations.
test to compare these
values, and the results are shown in the 8th column of the table.
There is a real scatter in the age gradients between galaxies that cannot
be explained by the errors, which is consistent with the earlier results of G90. We
have explored possible correlations between the age gradients and other
parameters of the galaxies, including (but not limited to) the central
velocity dispersion, but we have not found any significant correlations.
The mean metallicity gradient in our sample of LDEGs is
![]() [M/H]/
[M/H]/
![]() = -0.206
= -0.206 ![]() 0.019. Earlier studies have
derived comparable gradients using, primarily,
0.019. Earlier studies have
derived comparable gradients using, primarily,
![]() Fe
Fe![]() and Mg indices. For example, Couture & Hardy (1988),
using the Mg2 index, found a variation in metallicity with radius of
and Mg indices. For example, Couture & Hardy (1988),
using the Mg2 index, found a variation in metallicity with radius of
![]() [M/H]
[M/H]
![]() .
G90 measured mean gradients in their sample
of early-type galaxies of
.
G90 measured mean gradients in their sample
of early-type galaxies of ![]() [M/H]
[M/H]
![]()
![]() 0.09 and
0.09 and
![]() [M/H]
[M/H]
![]()
![]() 0.10, using the Mg2 and
0.10, using the Mg2 and
![]() Fe
Fe![]() indices, respectively (later confirmed by Davies
et al. 1993). To transform the line-strength gradients into metallicity
gradients, each of these studies used the Mould (1978), Burstein (1979),
and Faber et al. (1985) calibrations. In all these cases, they assumed a null
age gradient. Fisher et al. (1995), through the comparison of the
gradients of Mg2, H
indices, respectively (later confirmed by Davies
et al. 1993). To transform the line-strength gradients into metallicity
gradients, each of these studies used the Mould (1978), Burstein (1979),
and Faber et al. (1985) calibrations. In all these cases, they assumed a null
age gradient. Fisher et al. (1995), through the comparison of the
gradients of Mg2, H![]() ,
and
,
and ![]() Fe
Fe![]() with the stellar
population models of Worthey (1994), obtained a metallicity gradient of
with the stellar
population models of Worthey (1994), obtained a metallicity gradient of
![]() [M/H]
[M/H]
![]()
![]() 0.1. Finally, Mehlert et al. (2003),
using the population synthesis models of Thomas et al. (2003), obtained a metallicity gradient of
0.1. Finally, Mehlert et al. (2003),
using the population synthesis models of Thomas et al. (2003), obtained a metallicity gradient of ![]() [M/H]
[M/H]
![]()
![]() 0.12,
significantly more shallow than previous studies had found. The values
derived in the current study are consistent with the extant literature and
suggest that early-type galaxies exhibit a reduction in metallicity of
0.12,
significantly more shallow than previous studies had found. The values
derived in the current study are consistent with the extant literature and
suggest that early-type galaxies exhibit a reduction in metallicity of
![]() 40% per decade of variation in radius. This value is considerably
lower than the values predicted by the dissipative collapse models. For
example, Larson's hydrodynamical simulations gave
40% per decade of variation in radius. This value is considerably
lower than the values predicted by the dissipative collapse models. For
example, Larson's hydrodynamical simulations gave
![]() (Larson 1974a,b) and -1.0 (Larson 1975), and
Carlberg's (1984) N-body simulations gave
(Larson 1974a,b) and -1.0 (Larson 1975), and
Carlberg's (1984) N-body simulations gave
![]() .
It should be stressed, though, that these particular models
leave significant room for improvement, due to the absence of essential
physical processes, including star formation, thermal feedback from
supernovae, and chemical enrichment.
.
It should be stressed, though, that these particular models
leave significant room for improvement, due to the absence of essential
physical processes, including star formation, thermal feedback from
supernovae, and chemical enrichment.
Finally, we compared the dispersion about the mean values (
![]() )
and the scatter expected from the errors (
)
and the scatter expected from the errors (
![]() = 0.075) by
performing a
= 0.075) by
performing a ![]() test. The hypothesis "
test. The hypothesis "
![]() ''
can be rejected at a low significance level (see Col. 8 of
Table 3). To investigate the causes of the variation
in the metallicity gradients among galaxies, we explore putative
correlations of the
gradients with other physical galaxy parameters in Sect. 6.
''
can be rejected at a low significance level (see Col. 8 of
Table 3). To investigate the causes of the variation
in the metallicity gradients among galaxies, we explore putative
correlations of the
gradients with other physical galaxy parameters in Sect. 6.
It is well-known that massive early-type galaxies have abundance patterns
that do not match that of the solar neighbourhood (see Paper II, and
references therein). Although the influence of non-scaled solar abundance
ratio patterns complicates the estimation of mean ages from integrated
light, it does provide an important clue as to the formation and chemical
enrichment histories of galaxies. In this section, we explore the
presence of relative abundance ratio gradients in our sample of LDEGs.
To do so, we compare the metallicity gradients
obtained with different indices (combined with H![]() )
and make the
assumption that the differences in the derived values are due
to the different sensitivities of the Lick indices to changes in the chemical
composition. While avoiding a detailed
quantitative analysis (due to the difficulty in performing this kind
of analysis with the current stellar population models, see Paper II for details),
the qualitative trends presented below do offer
invaluable information concerning the formation of these galaxies and the
timescales for star formation therein.
)
and make the
assumption that the differences in the derived values are due
to the different sensitivities of the Lick indices to changes in the chemical
composition. While avoiding a detailed
quantitative analysis (due to the difficulty in performing this kind
of analysis with the current stellar population models, see Paper II for details),
the qualitative trends presented below do offer
invaluable information concerning the formation of these galaxies and the
timescales for star formation therein.
Figure 7 shows three ![]() index-
index-![]() index diagrams in
which gradients of CN2, Mgb, and C4668 are compared to the
gradients of Fe4383. The lines corresponding to
index diagrams in
which gradients of CN2, Mgb, and C4668 are compared to the
gradients of Fe4383. The lines corresponding to ![]() age = 0 and
age = 0 and
![]() [M/H] = 0 are overplotted. Due to the low sensitivity to age of
all these indices, the diagrams appear highly degenerate - i.e., the
iso-age and iso-metallicity lines are almost parallel. If the galaxies did
not have a gradient in the relative abundances, we would expect to find
all the points distributed along these lines. However, they appear to be
systematically shifted toward the left of the diagram, although the
magnitude of these shifts is very different in the three plots. In the
first panel (
[M/H] = 0 are overplotted. Due to the low sensitivity to age of
all these indices, the diagrams appear highly degenerate - i.e., the
iso-age and iso-metallicity lines are almost parallel. If the galaxies did
not have a gradient in the relative abundances, we would expect to find
all the points distributed along these lines. However, they appear to be
systematically shifted toward the left of the diagram, although the
magnitude of these shifts is very different in the three plots. In the
first panel (![]() Mgb-
Mgb-![]() Fe4383), the metallicity gradients
measured with Mgb are slightly steeper than the metallicity gradients
inferred from Fe4383, although the differences are admittedly small.
In the second panel (
Fe4383), the metallicity gradients
measured with Mgb are slightly steeper than the metallicity gradients
inferred from Fe4383, although the differences are admittedly small.
In the second panel (![]() CN2-
CN2-![]() Fe4383),
the differences are more evident. The metallicity gradients obtained with CN2 are clearly steeper (in absolute value) than the ones inferred from Fe4383.
The last panel (
Fe4383),
the differences are more evident. The metallicity gradients obtained with CN2 are clearly steeper (in absolute value) than the ones inferred from Fe4383.
The last panel (![]() C4668-
C4668-![]() Fe4383) is an intermediate case. The metallicity gradient obtained with C4668 is slightly steeper than the one estimated from Fe4383.
Although the trend is not as evident as in the second panel, the points
are visibly shifted toward the left of the constant age and metallicity lines.
Fe4383) is an intermediate case. The metallicity gradient obtained with C4668 is slightly steeper than the one estimated from Fe4383.
Although the trend is not as evident as in the second panel, the points
are visibly shifted toward the left of the constant age and metallicity lines.
To analyse these differences in more detail, we calculated the metallicity
gradients in several index-index diagrams using the indices CN2,
C4668, Fe4383, Mgb, and Ca4227, combined with H![]() .
In
Fig. 8, we compare these gradients with the values
obtained from ten different indicators, as described in
Sect. 3. Clearly, while the values
obtained with Ca4227 and Fe4383 are compatible with the gradients obtained
in Sect. 3, the gradients calculated with CN2, C4668, and, perhaps, Mgb are steeper. We quantified these
differences by measuring the mean gradient using the various diagrams, the
results of which are summarised in Table 3. The final
column of the table shows the probability that the mean gradients
calculated with the various indicators are the same as the gradients
calculated Sect. 3. The gradients
calculated using CN2 and C4668 are almost twice as steep as the
gradients calculated with the average of ten indicators. In the case of Mgb, despite the mean gradient being almost twice as steep as the
mean metallicity gradient, the result is less significant. In that case,
the initial hypothesis can be rejected with a significance level lower
than 0.025.
.
In
Fig. 8, we compare these gradients with the values
obtained from ten different indicators, as described in
Sect. 3. Clearly, while the values
obtained with Ca4227 and Fe4383 are compatible with the gradients obtained
in Sect. 3, the gradients calculated with CN2, C4668, and, perhaps, Mgb are steeper. We quantified these
differences by measuring the mean gradient using the various diagrams, the
results of which are summarised in Table 3. The final
column of the table shows the probability that the mean gradients
calculated with the various indicators are the same as the gradients
calculated Sect. 3. The gradients
calculated using CN2 and C4668 are almost twice as steep as the
gradients calculated with the average of ten indicators. In the case of Mgb, despite the mean gradient being almost twice as steep as the
mean metallicity gradient, the result is less significant. In that case,
the initial hypothesis can be rejected with a significance level lower
than 0.025.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=5.15cm,clip]{4846fig8a...
...
\includegraphics[angle=-90,width=5.15cm,clip]{4846fig8e.ps} }
\par\end{figure}](/articles/aa/full/2006/39/aa4846-06/Timg86.gif) |
Figure 8:
Comparison of the metallicity gradient measured with different
indicators combined with H |
We could argue that the differences in the metallicities derived with different indicators are due to variations in the chemical composition as a function of galactocentric distance, as the sensitivity of different Lick indices to variations on the abundance of different chemical elements is not the same (Tripicco & Bell 1995; Korn et al. 2004). But the Lick indices show a dependence on gravity that, while not large (Gorgas et al. 1993; Worthey et al. 1994), is also not null. As the behaviour of each line index under variations in the underlying IMF is not identical, a change in the ratio of dwarf-to-giant stars with galactocentric radius could result in the metallicity gradient inferred from different indicators also being different.
![\begin{figure}
\par\includegraphics[angle=-90,width=5.5cm,clip]{4846fig9a.ps}\hs...
...ace*{3mm}
\includegraphics[angle=-90,width=5.5cm,clip]{4846fig9f.ps}\end{figure}](/articles/aa/full/2006/39/aa4846-06/Timg87.gif) |
Figure 9: Relation between the metallicity gradients obtained in different index-index diagrams (as indicated in the brackets) and the velocity dispersion gradient for the sample of LDEGs. In the top left panel, the metallicity gradient has been obtained using a combination of ten indices, as described in Sect. 3. |
Cenarro et al. (2003) calibrated the CaT* (calcium triplet) index in the
near-infrared and found a relationship between [Fe/H], velocity dispersion, and the slope of the IMF. One of the projections of this relationship is
![\begin{displaymath}%
\mu=2.41+2.78[{\rm M}/{\rm H}]-3.79[{\rm M}/{\rm H}]^2,
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img88.gif) |
(12) |
![\begin{eqnarray*}&& {\rm CN}_2 =
0.037 - 0.006 \mu + 0.135 [{\rm M}/{\rm H}] +...
...0.130 \mu + 2.257 [{\rm M}/{\rm H}] + 2.257 [{\rm M}/{\rm H}]^2.
\end{eqnarray*}](/articles/aa/full/2006/39/aa4846-06/img93.gif)
More likely, the differences in the metallicity gradients obtained with the different indices are due to changes in the relative abundance gradients of distinct elements. However, it is difficult to quantify the strength of those gradients with the present knowledge of line formation and the inherent limitations of stellar population synthesis models
There are several physical processes that can produce a metallicity gradient in early-type galaxies. The relationship between these gradients and other global properties of the galaxies afford an opportunity to discriminate among the competing processes. Previous attempts have searched for correlations using colours and empirical line-strength indices; in what follows, we study the correlation between the gradients of the derived simple stellar population (SSP) parameters and the global properties of the host galaxies. In this section, we only use the subsample of elliptical galaxies, excluding the lenticulars (S0) from the analysis. The reason for doing this is that the correlations between the gradients and other parameters are predicted by a specific mechanism of galaxy formation, and, although S0 and E galaxies seem to have the same relations between the central properties and other parameters, very different mechanisms have been proposed for their formation. As the sample of S0 is small, we could not perform a comparative study using only S0 galaxies.
As noted in Sect. 1, Franx & Illingworth (1990) found a correlation
between colour gradient and the gradient of escape velocity, which
they interpreted as a correlation between the local metallicity and the
local potential well depth in a sample of early-type galaxies. They
suggested that such a correlation was consistent with a galactic wind
origin, and inconsistent with a dissipative inward flow origin. Others,
including Davies et al. (1993), Carollo & Danziger (1994), and Mehlert
et al. (2003) find similar relations between the gradients of some
line-strength indices and the gradient of the potential
well![]() . We now examine the likelihood of the
existence of this correlation within our sample of LDEGs, using the
inferred metallicity gradients and empirical velocity dispersion gradients - Fig. 9 illustrates the observed trends.
. We now examine the likelihood of the
existence of this correlation within our sample of LDEGs, using the
inferred metallicity gradients and empirical velocity dispersion gradients - Fig. 9 illustrates the observed trends.
| N |
|
t | Pnc | |
| grad age | 54 |
|
0.56 | 0.885 |
| grad [M/H] | 54 |
|
0.65 | 0.238 |
| grad [M/H] (CN2-H |
54 |
|
2.04 | 0.002 |
| grad [M/H] (Ca4227-H |
54 |
|
0.65 | 0.063 |
| grad [M/H] (Fe4383-H |
54 |
|
0.89 | 0.900 |
| grad [M/H] (C4668-H |
54 |
|
1.27 | 0.062 |
| grad [M/H] (Mgb-H |
54 |
|
2.11 | 0.001 |
To study the degree of correlation, we have performed two different tests:
a non-parametric Spearman rank order test and a t-test. The Spearman
test does not take into account the errors in the individual points, while
the t-test has the limitation of considering just a linear relation, and
it assumes Gaussian probability distributions. A good estimate of the
degree of correlation between both magnitudes can be obtained by studying
the results of both tests. In the t-test, we check the hypothesis
"b=0'', where b is the slope of the linear fit to the data. The
errors in the slope were calculated through Monte Carlo simulations, where
each point was perturbed in both axes, assuming a Gaussian distribution
with standard deviation equal to the errors. For a significance level of
![]() ,
a t value higher than 1.96 indicates that a correlation
exists. The results of both tests are shown in
Table 4. In the second row of the table (and left top
panel in Fig. 9), we show the correlation when the
metallicity is measured with the ten indicators described in
Sect. 3. We do not find any correlation
between the metallicity gradients and the gradient of velocity dispersion.
The other panels in the figure show the metallicity gradients obtained in
different
,
a t value higher than 1.96 indicates that a correlation
exists. The results of both tests are shown in
Table 4. In the second row of the table (and left top
panel in Fig. 9), we show the correlation when the
metallicity is measured with the ten indicators described in
Sect. 3. We do not find any correlation
between the metallicity gradients and the gradient of velocity dispersion.
The other panels in the figure show the metallicity gradients obtained in
different ![]() index-
index-![]() index diagrams in which we combined
H
index diagrams in which we combined
H![]() with various metallicity indicators (as indicated between the
brackets). Surprisingly, we find a marginally significant correlation
between the metallicity gradients and grad
with various metallicity indicators (as indicated between the
brackets). Surprisingly, we find a marginally significant correlation
between the metallicity gradients and grad ![]() when the metallicity
gradient is measured using Mgb and CN2 indices, while we do not find
any correlation when the metallicity gradient is obtained using the other
indices. If the correlation between these parameters is indicative of the
importance of galactic winds during the evolution of early-type galaxies,
the fact that the correlation only exists when the metallicity gradient is
calculated with some specific indices may indicate that this process
affects some chemical species more than others. This could happen if, for
example, the relative abundance patterns were different when the galactic
winds occurred.
when the metallicity
gradient is measured using Mgb and CN2 indices, while we do not find
any correlation when the metallicity gradient is obtained using the other
indices. If the correlation between these parameters is indicative of the
importance of galactic winds during the evolution of early-type galaxies,
the fact that the correlation only exists when the metallicity gradient is
calculated with some specific indices may indicate that this process
affects some chemical species more than others. This could happen if, for
example, the relative abundance patterns were different when the galactic
winds occurred.
The dispersion in the relations is, in any case, very large. This large scatter may be a consequence of using the velocity dispersion as an indicator of the local potential and/or indicative that other processes are driving the variation of the local metal content with radius. Davies et al. (1993), in fact, suggest that the local velocity dispersion is a poor indicator of the local escape velocity, due to the (complicating) presence of rotation and anisotropies. On the other hand, the existence of kinematically decoupled cores in a large percentage of galaxies, the presence of shells, dust lanes, and the observation of interacting galaxies, seem to indicate that mergers and interactions are common processes in the lives of galaxies. If these interactions have some associated gas dissipation and/or star formation, it may produce dispersion in the correlation between local metallicity and local escape velocity. In fact, other authors (Davies et al. 1993; Carollo & Danziger 1994) have found correlations between the Mg2 and the velocity dispersion gradients using the local escape velocity instead of the velocity dispersion, also finding a large scatter in the relations.
We conclude that the local potential of early-type galaxies may play a role in defining the metallicity gradient. However, the large scatter in the derived correlation suggests that other processes may play a role in modulating the final metal content. These processes can be the consequence of differences in the merger histories of galaxies, as proposed by Kobayashi (2004). The fact that the inferred metallicity gradients differ depending upon the indicator adopted also suggests that the gradients of the various chemical species have probably been formed (and modified) through different physical mechanisms.
Dissipative collapse models of galaxy formation predict strong correlations between the metallicity gradients and certain global parameters, such as the luminosity, mass, and central velocity dispersion (Larson 1974a; Carlberg 1984; Arimoto & Yoshii 1987; Kawata 1999; Chiosi & Carraro 2002; Kawata & Gibson 2003), in the sense that more massive galaxies should possess steeper metallicity gradients. Such a prediction is driven primarily by the adopted mass-dependent feedback efficiency within the models. Conversely, galaxy formation through hierarchical clustering of small sub-units does not necessarily lead to a clear prediction of any putative correlations between metallicity gradients and global galactic properties - merger history can readily play a part in eroding any extant correlation (e.g., Kobayashi 2004).
With the aim of exploring the possible correlation between metallicity
gradient and galactic mass, we compare
the metallicity gradients (obtained as
described in Sect. 3) with the central
velocity dispersion for the sample of LDEGs in
Fig. 10. The other panels in the
figure show the relation between the metallicity gradient and the central
velocity dispersion when the metallicity gradient is measured using
CN2, C4668, Fe4383, Mgb, and Ca4227 combined with H![]() .
.
As in Sect. 6.1, we studied the degree of correlation through a t-test and a non-parametric Spearman test. The results of these tests are shown in Table 5. We did not find any correlation between the metallicity gradients and the central velocity dispersion, regardless of the line-strength indices used to derive the former.
In regards to putative correlations between line-strength indices and the
mass or the velocity dispersion, Peletier (1989), Peletier et al. (1990),
and G90, each found positive correlations between the Mg2 gradient and
the central velocity dispersion, while González (1993) and Davies &
Sadler (1987) found the opposite trend. Conversely, Davidge (1991, 1992)
and Davies et al. (1993) did not find any correlation between the
gradients of the indices Mg2, ![]() Fe
Fe![]() ,
or H
,
or H![]() and the central
velocity dispersion. In this work, we have doubled the sample size
compared to any of the extant studies, and instead of analysing the
colours or raw line-strength gradients, we employed the inferred
metallicity gradients. For the sample of LDEGs, we did not find any
correlation between these parameters and the central velocity dispersion.
and the central
velocity dispersion. In this work, we have doubled the sample size
compared to any of the extant studies, and instead of analysing the
colours or raw line-strength gradients, we employed the inferred
metallicity gradients. For the sample of LDEGs, we did not find any
correlation between these parameters and the central velocity dispersion.
![\begin{figure}
\par\includegraphics[angle=-90,width=5.5cm,clip]{4846fig10a.ps}\h...
...ce*{3mm}
\includegraphics[angle=-90,width=5.5cm,clip]{4846fig10f.ps}\end{figure}](/articles/aa/full/2006/39/aa4846-06/Timg108.gif) |
Figure 10: Metallicity gradients obtained in different index-index diagrams (as indicated in brackets) versus the central velocity dispersion. |
| N | t | Pnc | |
| grad age | 54 | -1.736 | 0.168 |
| grad [M/H] | 54 | 0.810 | 0.106 |
| grad [M/H] (CN2-H |
54 | 1.075 | 0.789 |
| grad [M/H] (Ca4227-H |
54 | 0.251 | 0.986 |
| grad [M/H] (Fe4383-H |
54 | 1.303 | 0.244 |
| grad [M/H] (C4668-H |
54 | 0.026 | 0.455 |
| grad [M/H] (Mgb-H |
54 | 0.578 | 0.934 |
In Sect. 6.1, we showed that, for the sample of LDEGs, the metallicity gradients tend to correlate with the velocity dispersion gradient when they are measured with some indicators (in particular CN2 and Mgb), but that this correlation disappears when the metallicity gradient is measured with Fe4383, Ca4227, and C4668.
In Sect. 4 we showed that the mean age gradient in our sample of LDEGs is not null, which might be indicative of the occurrence of star formation events in the centre of the galaxies. Furthermore, we showed in Paper II that in these events, the relative enrichment of some chemical species (the ones mainly released by low- and intermediate-mass stars, like Fe) might be more important than others (the ones mainly produced in type II supernovae, like Mg). With the aim of exploring whether the occurrence of star formation processes in the centre of the galaxies may be responsible for the abundance gradients in some chemical species, we now study the correlation between the metallicity gradients and the central ages obtained in Paper II. Figure 11 shows these correlations for different measurements of the metallicity gradient. When the correlation is statistically significant, a linear fit taking into account the errors in the x- and y-directions is also plotted. In these cases, the probability of no correlation (Pnc) obtained in a non-parametric Spearman test and the t parameter to verify the hypothesis b=0 (where b is the slope of the linear fit) are indicated in the panels. As can be seen in the different panels, while we do not find any significant correlation when the metallicity gradients are measured with CN2, Mgb, or Ca4227, we do find a correlation between the metallicity gradients and the central age of the galaxies, when the former is measured using Fe4383 and C4668. We also find a significant correlation between the metallicity gradient obtained with the ten indicators described in Sect. 3 and the central age of the galaxies. We interpret these correlations in Sect. 6.4.
In Sects. 6.1-6.3, we studied the putative correlations between metallicity gradient and other global properties of LDEGs. Broadly speaking, we found two distinct characteristics of the gradients depending upon the specific indicator used to derive them:
This view agrees with the results of Papers I and II. Note that in galaxies that have suffered star formation episodes in their centres, the [Mg/Fe] gradient flattens as a consequence of the Fe enrichment in the central parts, which is supported by the relation between [Mg/Fe] and age reported in Paper I. This is also in agreement with the result presented in Paper II, in which we found the existence of an age-metallicity relation when the metallicity was measured with Fe4383, but not when this parameter was measured with Mgb.
Conversely, in Sánchez-Blázquez et al. (2003), we reported differences in the N abundance between galaxies in different environments. If the star formation processes in the centres of the galaxies do not substantially affect the gradients in this element, then the differences must be visible not only in the centres, but also in the outer parts.
We also note the behaviour of the metallicity gradient when inferred from Ca4227. Specifically, the gradient does not correlate with any of the obvious physical parameters - i.e., neither with the central age nor with the velocity dispersion gradient.
Many of the results described in Papers I and II could be explained by
assuming the presence of a small percentage of young stars in the centre of
most of the galaxies, at least in the subsample of LDEGs. We have also argued
that this could be the cause of the existence of non-null age gradients in our
sample of galaxies (see Sect. 4). If this point of view is
correct, we would expect that the relations defined between the global
parameters of the galaxies (i.e., for the whole bodies of the galaxies) are
different than the one derived for the central regions. To investigate this
possibility, we now compare for the subsample of LDEGs, the
relation of these global values and the velocity dispersion with the relations
derived for the central values in Paper II. The global values can be
obtained from the gradients, assuming a linear behaviour of the indices with
radius and evaluating the integral
![\begin{displaymath}%
I_{\rm global}=\frac{\displaystyle\int_{0}^{\infty}
I(r)\...
...
2\pi I_{\rm e} \exp^{-7.67[(r/r_{\rm e})^{1/4}-1]}{\rm d}r},
\end{displaymath}](/articles/aa/full/2006/39/aa4846-06/img110.gif) |
(13) |
Figure 12 shows the relation between the global age and global metallicities (as derived from different indicators) and the central velocity dispersion. We plot a linear fit to the data weighted with the errors in both parameters, and to compare with the relations for the central regions, we have also plotted the linear fits obtained for the central values derived in Paper II. Table 6 summarises the parameters of the fits. We carried out a t-test to verify the existence of significant differences between the slopes of the trends defined by the central and the global SSP-parameters. A value of t higher than 1.96 indicates that there exist differences with a significance level lower than 0.05.
| Central | Global | ||||
| t | |||||
| [M/H] (CN2-H |
|
|
|
|
0.86 |
| [M/H] (Fe4383-H |
|
|
|
|
0.98 |
| [M/H] (Mgb-H |
|
|
|
|
0.88 |
| log age |
|
|
|
|
2.88 |
The only case in which the slopes defined by the central and the global values are significantly different is in the relation between the age and the central velocity dispersion. While the central age shows a significant correlation with the central velocity dispersion (see Paper II), the global age, as derived in this section, does not correlate with this parameter. This result favours the idea that, in a large percentage of galaxies, the young ages that we found in Paper II are due to a minor percentage of stars that formed in the centre of the galaxies at a later epoch than the bulk of the stars, as suggested by Trager et al. (2000b). It also supports the suggestion that this minor percentage of young stars in the centre of the galaxies is responsible for the age gradients reported in Sect. 4.
On the other hand, the slopes of the relations between the metallicity and
the central velocity dispersion do not show a statistically significant
variation between the central and the global values, although there is a tendency for the relations to be steeper for the global values. There are
also differences in the zero point as a consequence of the existence of
gradients, in disagreement with the earlier claims of González & Gorgas
(1996). These authors found that the relation Mg![]() is flatter
at one effective radii than in the center, concluding that the mass-metallicity
relation was much flatter at one effective radii than in the central parts
of the galaxies. In light of our present series of papers, the
results of González & Gorgas could be explained if the differences
between the central and global relation of the age with
is flatter
at one effective radii than in the center, concluding that the mass-metallicity
relation was much flatter at one effective radii than in the central parts
of the galaxies. In light of our present series of papers, the
results of González & Gorgas could be explained if the differences
between the central and global relation of the age with ![]() was causing these differences.
was causing these differences.
The lack of variation in the slope of the relation between the central and
the global metallicities measured with CN2 and Mgb was expected, since
we find a flat relation between the strength of the gradients
and the central velocity dispersion.
In the case of the metallicity measured with Fe4383, we might have expected to see a steepening of the slope in the
global relation compared with the central one. If the relative importance
of the star formation processes has been higher in the smaller galaxies
(as suggested by the age-![]() relation), the metallicity inferred
from Fe4383 in these galaxies should be also higher. The variation in the
slope obtained when comparing the central and the global relations goes in
this sense, but the differences are not statistically significant. We must
note that the errors in the global measurements are higher than for the
central values, which might explain the lack of statistical significance.
relation), the metallicity inferred
from Fe4383 in these galaxies should be also higher. The variation in the
slope obtained when comparing the central and the global relations goes in
this sense, but the differences are not statistically significant. We must
note that the errors in the global measurements are higher than for the
central values, which might explain the lack of statistical significance.
| Mean | N |
|
t |
|
t | LDEGs | t' | |||
| grad log age |
|
0.258 | 15 | 9.79 | 0.34 | 0.138 | 0.0003 |
|
0.8 | |
| grad [M/H] |
|
0.247 | 15 | 11.85 | 5.59 | 0.157 | 0.0017 |
|
1.8 | |
| grad [M/H] (CN2-H |
|
0.432 | 15 | 10.86 | 5.60 | 0.236 | 0.0003 | 2.10 |
|
0.5 |
| grad [M/H] (C4668-H |
|
0.358 | 15 | 9.18 | 5.71 | 0.185 | 4.2E-06 | 1.96 |
|
1.4 |
| grad [M/H] (Fe4383-H |
|
0.456 | 15 | 8.95 | 1.47 | 0.275 | 0.0014 | 0.95 |
|
0.2 |
| grad [M/H] (Mgb-H |
|
0.611 | 15 | 10.23 | 2.85 | 0.337 | 4.2E-05 | 1.02 |
|
0.8 |
| grad [M/H] (Ca4227-H |
|
0.831 | 15 | 11.16 | 0.70 | 0.434 | 1.7E-06 | 0.61 |
|
0.3 |
If the environment in which galaxies reside has any influence over the
timescales of the star formation, the number of interactions, or the
dissipation of gas, we might expect to see an environmental dependence
upon the inferred age and metallicity gradients. Fisher et al. (1995)
analysed a sample of bright cluster ellipticals, concluding that their
gradients and those of field ellipticals, were not significantly
different. When studying the photometry in the
B- and R-bands as a function of radius for galaxies in Abell 2199,
Tamura & Otha (2003) found
correlations between the colour gradients and some global properties of
the galaxies, such as the luminosity and effective radius, which had not
been found in studies of field galaxies. These authors, however, only
found these correlations amongst the most luminous galaxies (R<15 mag
and with an effective radius >3
![]() ). We now
examine the mean gradients of the SSP-parameters for the HDEGs and compare
these values with the ones obtained for the LDEGs.
). We now
examine the mean gradients of the SSP-parameters for the HDEGs and compare
these values with the ones obtained for the LDEGs.
The second column of Table 7 lists the mean values of
the SSP-parameter gradients obtained for the HDEGs in different
index-index diagrams (indicated between brackets). As in
Sect. 4, we quantified the probability that these
values are different from zero by chance. The results of a t-test
indicate that, while the metallicity gradients obtained in the
CN2-H![]() and C4668-H
and C4668-H![]() diagrams are not compatible with
being null, the metallicity gradients obtained in the Fe4383-H
diagrams are not compatible with
being null, the metallicity gradients obtained in the Fe4383-H![]() and
Ca4227-H
and
Ca4227-H![]() diagrams are compatible with zero, within the errors.
Furthermore, the mean age gradient for this subsample of galaxies is also
compatible with zero. We now analyse these results separately:
diagrams are compatible with zero, within the errors.
Furthermore, the mean age gradient for this subsample of galaxies is also
compatible with zero. We now analyse these results separately:
Acording to Kobayashi (2004), the absence of correlation between the metallicity
gradient and the central velocity dispersion may be the consequence of
differences in the merger history of the galaxies. If the star formation
processes in recent epochs have been less frequent in the Coma cluster
galaxies, one might expect that any in situ correlation would have been
less substantially impacted. To explore whether this is the case, in
Fig. 13 we present the metallicity gradients
measured in different ![]() index-
index-![]() index diagrams against the
central velocity dispersion for the elliptical galaxies of the Coma cluster. The table at the bottom of the figure shows the results of a t-test and a non-parametric Spearman rank test to check the degree of correlation between both variables. In this case, we find a correlation
between the metallicity gradient and the central velocity dispersion, but
only when the metallicity gradient is measured with the Fe4383 index.
While the correlation is not statistically significant when derived from
other indices, there does seem to be a marginal trend in the sense that more
massive galaxies also show a steeper gradient. To confirm this putative
mass trend and further constrain galaxy formation models, higher
signal-to-noise spectra must be obtained.
index diagrams against the
central velocity dispersion for the elliptical galaxies of the Coma cluster. The table at the bottom of the figure shows the results of a t-test and a non-parametric Spearman rank test to check the degree of correlation between both variables. In this case, we find a correlation
between the metallicity gradient and the central velocity dispersion, but
only when the metallicity gradient is measured with the Fe4383 index.
While the correlation is not statistically significant when derived from
other indices, there does seem to be a marginal trend in the sense that more
massive galaxies also show a steeper gradient. To confirm this putative
mass trend and further constrain galaxy formation models, higher
signal-to-noise spectra must be obtained.
![\begin{figure}
\par\mbox{\includegraphics[angle=-90,width=6.3cm,clip]{4846fig13a...
...ad [M/H] (Mgb--H$\beta$ ) & 1.40 & 0.18 \\
\hline
\end{tabular}\par\end{figure}](/articles/aa/full/2006/39/aa4846-06/Timg142.gif) |
Figure 13: Metallicity gradients versus central velocity dispersion for HDEGs. The different panels show the metallicity gradients obtained in different index-index diagrams (indicated between the brackets). The first panel ( top left) compares the metallicity gradients obtained as described in Sect. 3. In the case in which the correlation is statistically significant, an error weighted linear fit is also shown. The table at the bottom indicates the results of a t-test and a non-parametric Spearman rank test (see text for details). |
We have carried out a study of the gradients in 23 different spectral features for a sample of 82 early-type galaxies situated in different environments. Our results can be summarised thus:
Acknowledgements
We would like to thank the anonymous referee for very helpful comments. The WHT is operated on the island of La Palma by the Royal Greenwich Observatory at the Observatorio del Roque de los Muchachos of the Insituto de Astrofísica de Canarias. The Calar Alto Observatory is operated jointly by the Max-Planck Institute für Astronomie, Heidelberg, and the Spanish Instituto de Astrofísica de Andalucía (CSIC). This work was partially supported by the Spanish research project AYA 2003-01840 and by the Australian Research Council. We are grateful to the CATs for their generous allocations of telescope time.
| Nombre | D4000 | H |
H |
CN2 | Ca4227 | G4300 | H |
H |
Fe4383 | |
| NGC 221 | -0.0877 | -0.0520 | -0.0014 | 0.0008 | -0.0247 | -0.0110 | 0.0104 | 0.0018 | 0.0079 | 0.0025 |
| 0.0126 | 0.0058 | 0.0023 | 0.0026 | 0.0057 | 0.0035 | 0.0025 | 0.0020 | 0.0032 | 0.0017 | |
| NGC 315 | -0.0439 | -0.2038 | 0.0111 | -0.0016 | 0.0059 | -0.0081 | -0.0112 | 0.0424 | 0.0454 | -0.0110 |
| 0.0261 | 0.0177 | 0.0048 | 0.0064 | 0.0106 | 0.0076 | 0.0056 | 0.0057 | 0.0058 | 0.0048 | |
| NGC 507 | 0.0029 | 0.0276 | 0.0182 | 0.0179 | -0.0357 | 0.0123 | 0.0526 | -0.0447 | -0.0676 | 0.0334 |
| 0.0992 | 0.0554 | 0.0124 | 0.0293 | 0.0312 | 0.0425 | 0.0296 | 0.0142 | 0.0250 | 0.0236 | |
| NGC 584 | -0.0769 | -0.1955 | 0.0331 | 0.0312 | -0.0655 | -0.0139 | -0.0001 | 0.0313 | 0.0394 | -0.0204 |
| 0.0326 | 0.0582 | 0.0123 | 0.0108 | 0.0191 | 0.0210 | 0.0144 | 0.0124 | 0.0205 | 0.0079 | |
| NGC 636 | -0.0121 | -0.2441 | 0.0243 | 0.0285 | -0.0848 | -0.0011 | -0.0226 | 0.0419 | 0.0405 | -0.0374 |
| 0.0416 | 0.0483 | 0.0159 | 0.0221 | 0.0207 | 0.0222 | 0.0168 | 0.0164 | 0.0158 | 0.0198 | |
| NGC 821 | -0.0226 | -0.2749 | 0.0480 | 0.0225 | -0.1467 | -0.0506 | -0.0113 | 0.0251 | 0.0310 | -0.0217 |
| 0.0570 | 0.0602 | 0.0257 | 0.0277 | 0.0326 | 0.0220 | 0.0106 | 0.0119 | 0.0155 | 0.0127 | |
| NGC 1453 | -0.0419 | -0.0769 | 0.0332 | 0.0342 | -0.0583 | -0.0387 | 0.0060 | 0.0191 | 0.0162 | -0.0339 |
| 0.0224 | 0.0284 | 0.0150 | 0.0242 | 0.0234 | 0.0209 | 0.0163 | 0.0105 | 0.0148 | 0.0130 | |
| NGC 1600 | -0.0739 | -0.1825 | 0.0146 | -0.0017 | -0.0484 | -0.0234 | -0.0054 | 0.0182 | 0.0171 | -0.0150 |
| 0.0155 | 0.0098 | 0.0079 | 0.0080 | 0.0107 | 0.0116 | 0.0068 | 0.0050 | 0.0068 | 0.0067 | |
| NGC 1700 | -0.0031 | -0.0787 | 0.0170 | -0.0115 | -0.0813 | 0.0303 | -0.0075 | 0.0141 | 0.0078 | -0.0098 |
| 0.0362 | 0.0294 | 0.0176 | 0.0183 | 0.0144 | 0.0298 | 0.0147 | 0.0146 | 0.0152 | 0.0125 | |
| NGC 2300 | -0.1032 | 0.0088 | 0.0154 | 0.0100 | -0.0490 | 0.0060 | 0.0086 | 0.0090 | -0.0097 | -0.0165 |
| 0.0312 | 0.0697 | 0.0205 | 0.0222 | 0.0228 | 0.0276 | 0.0186 | 0.0175 | 0.0222 | 0.0091 | |
| NGC 2329 | 0.0502 | 0.0548 | 0.0254 | 0.0266 | -0.0554 | 0.0077 | 0.0018 | 0.0310 | 0.0193 | -0.0701 |
| 0.0330 | 0.0491 | 0.0313 | 0.0323 | 0.0312 | 0.0229 | 0.0262 | 0.0219 | 0.0142 | 0.0216 | |
| NGC 2693 | -0.0259 | -0.1256 | 0.0118 | 0.0110 | -0.0683 | -0.0373 | -0.0063 | 0.0156 | 0.0166 | -0.0181 |
| 0.0370 | 0.0300 | 0.0118 | 0.0127 | 0.0098 | 0.0152 | 0.0159 | 0.0080 | 0.0109 | 0.0135 | |
| NGC 2694 | -0.0885 | -0.9690 | 0.0647 | 0.0246 | -0.0138 | -0.0843 | 0.0306 | 0.0153 | 0.0842 | -0.0036 |
| 0.1337 | 0.1819 | 0.1381 | 0.1250 | 0.1186 | 0.0576 | 0.0660 | 0.0667 | 0.1095 | 0.0056 | |
| NGC 2778 | -0.2297 | -0.2964 | 0.0425 | 0.0342 | -0.1089 | -0.0156 | -0.0357 | 0.0415 | 0.0486 | -0.0209 |
| 0.0450 | 0.0141 | 0.0120 | 0.0115 | 0.0182 | 0.0132 | 0.0120 | 0.0210 | 0.0243 | 0.0109 | |
| NGC 2832 | -0.0646 | -0.1193 | 0.0226 | -0.0094 | -0.0783 | -0.0689 | -0.0244 | 0.0357 | 0.0162 | -0.0448 |
| 0.0152 | 0.0154 | 0.0087 | 0.0148 | 0.0086 | 0.0166 | 0.0084 | 0.0090 | 0.0097 | 0.0118 | |
| NGC 3115 | -0.1056 | -0.3075 | 0.0232 | 0.0146 | -0.1086 | -0.0149 | -0.0098 | 0.0223 | 0.0194 | -0.0228 |
| 0.0094 | 0.0114 | 0.0051 | 0.0063 | 0.0160 | 0.0068 | 0.0118 | 0.0127 | 0.0092 | 0.0054 | |
| NGC 3377 | -0.1624 | -0.2541 | 0.0292 | 0.0025 | -0.1134 | -0.0116 | -0.0320 | 0.0368 | 0.0280 | -0.0331 |
| 0.0672 | 0.0324 | 0.0102 | 0.0120 | 0.0122 | 0.0085 | 0.0063 | 0.0108 | 0.0136 | 0.0155 | |
| NGC 3379 | -0.0737 | -0.1927 | 0.0184 | 0.0155 | -0.0556 | -0.0189 | -0.0194 | 0.0245 | 0.0216 | -0.0189 |
| 0.0087 | 0.0072 | 0.0042 | 0.0046 | 0.0057 | 0.0046 | 0.0056 | 0.0044 | 0.0044 | 0.0038 | |
| NGC 3605 | -0.0594 | -0.2601 | 0.0111 | 0.0386 | -0.0040 | 0.0163 | 0.0285 | 0.0384 | 0.0284 | -0.0609 |
| 0.0683 | 0.0458 | 0.0235 | 0.0224 | 0.0188 | 0.0171 | 0.0239 | 0.0223 | 0.0175 | 0.0163 | |
| NGC 3608 | -0.0728 | -0.1859 | 0.0460 | 0.0438 | -0.1081 | -0.0085 | 0.0129 | 0.0128 | 0.0003 | -0.0226 |
| 0.0329 | 0.0349 | 0.0180 | 0.0141 | 0.0149 | 0.0107 | 0.0132 | 0.0092 | 0.0123 | 0.0061 | |
| NGC 3641 | -0.1151 | -0.5179 | 0.0831 | 0.0703 | -0.1777 | -0.0281 | -0.0341 | 0.0213 | 0.0707 | -0.0242 |
| 0.1236 | 0.0703 | 0.0307 | 0.0356 | 0.0436 | 0.0326 | 0.0344 | 0.0522 | 0.0542 | 0.0218 | |
| NGC 3665 | -0.0557 | -0.0052 | 0.0029 | 0.0120 | -0.0182 | 0.0087 | -0.0057 | 0.0110 | -0.0014 | -0.0151 |
| 0.0260 | 0.0289 | 0.0113 | 0.0155 | 0.0134 | 0.0136 | 0.0109 | 0.0069 | 0.0118 | 0.0071 | |
| NGC 3818 | -0.0992 | -0.2511 | 0.0304 | 0.0266 | -0.1078 | -0.0080 | -0.0222 | 0.0275 | 0.0349 | -0.0164 |
| 0.0176 | 0.0169 | 0.0079 | 0.0101 | 0.0141 | 0.0097 | 0.0099 | 0.0119 | 0.0133 | 0.0078 | |
| NGC 4261 | -0.0663 | -0.0881 | 0.0090 | 0.0085 | -0.0578 | -0.0096 | -0.0263 | 0.0279 | 0.0197 | -0.0138 |
| 0.0089 | 0.0100 | 0.0054 | 0.0064 | 0.0055 | 0.0106 | 0.0064 | 0.0066 | 0.0070 | 0.0044 | |
| NGC 4278 | -0.0856 | -0.2121 | 0.0441 | 0.0484 | -0.0978 | -0.0208 | -0.0138 | 0.0457 | 0.0604 | -0.0286 |
| 0.0082 | 0.0072 | 0.0044 | 0.0051 | 0.0066 | 0.0060 | 0.0072 | 0.0053 | 0.0068 | 0.0047 | |
| NGC 4365 | -0.0606 | -0.2294 | 0.0092 | 0.0122 | -0.0623 | -0.0193 | -0.0069 | 0.0272 | 0.0304 | -0.0247 |
| 0.0123 | 0.0086 | 0.0054 | 0.0067 | 0.0061 | 0.0065 | 0.0058 | 0.0052 | 0.0067 | 0.0043 | |
| NGC 4374 | -0.0255 | -0.1773 | 0.0138 | 0.0136 | -0.0612 | -0.0056 | -0.0132 | 0.0185 | 0.0343 | -0.0125 |
| 0.0201 | 0.0210 | 0.0097 | 0.0097 | 0.0113 | 0.0098 | 0.0082 | 0.0065 | 0.0084 | 0.0062 | |
| NGC 4415 | 0.0602 | -0.0585 | -0.0050 | 0.0052 | 0.0118 | -0.0325 | 0.0177 | 0.0124 | 0.0326 | -0.0015 |
| 0.0565 | 0.0205 | 0.0092 | 0.0106 | 0.0133 | 0.0095 | 0.0101 | 0.0096 | 0.0126 | 0.0050 | |
| NGC 4431 | 0.0436 | -0.0467 | 0.0015 | -0.0349 | -0.0398 | -0.0094 | -0.0083 | -0.0052 | 0.0023 | 0.0021 |
| 0.0881 | 0.0406 | 0.0176 | 0.0212 | 0.0153 | 0.0240 | 0.0115 | 0.0074 | 0.0134 | 0.0083 | |
| NGC 4464 | -0.0967 | -0.2536 | 0.0101 | 0.0017 | -0.0700 | -0.0004 | 0.0036 | 0.0179 | 0.0273 | -0.0119 |
| 0.0177 | 0.0155 | 0.0115 | 0.0125 | 0.0166 | 0.0125 | 0.0110 | 0.0282 | 0.0280 | 0.0082 | |
| NGC 4467 | -0.1443 | -0.2577 | 0.0208 | -0.0265 | -0.0763 | -0.0122 | 0.0095 | 0.0448 | 0.0375 | -0.0455 |
| 0.0946 | 0.0724 | 0.0263 | 0.0318 | 0.0433 | 0.0340 | 0.0346 | 0.0788 | 0.0896 | 0.0277 | |
| NGC 4472 | -0.0436 | -0.1140 | 0.0212 | 0.0118 | -0.0563 | -0.0320 | 0.0011 | 0.0084 | 0.0026 | -0.0156 |
| 0.0063 | 0.0069 | 0.0029 | 0.0034 | 0.0042 | 0.0051 | 0.0039 | 0.0034 | 0.0037 | 0.0033 | |
| NGC 4478 | -0.0727 | -0.1332 | 0.0076 | -0.0058 | -0.0389 | -0.0139 | -0.0161 | 0.0074 | 0.0000 | -0.0157 |
| 0.0240 | 0.0086 | 0.0059 | 0.0065 | 0.0073 | 0.0062 | 0.0100 | 0.0119 | 0.0111 | 0.0043 | |
| NGC 4486B | -0.2310 | -0.7128 | 0.0064 | 0.0056 | -0.0806 | 0.0103 | -0.0028 | 0.0045 | -0.0057 | -0.0001 |
| 0.0742 | 0.1373 | 0.0282 | 0.0459 | 0.0179 | 0.0297 | 0.0431 | 0.0440 | 0.0535 | 0.0305 | |
| NGC 4489 | 0.1483 | -0.4048 | 0.0159 | 0.0018 | -0.0061 | -0.0082 | -0.0216 | 0.0234 | 0.0109 | -0.0354 |
| 0.0666 | 0.0773 | 0.0219 | 0.0149 | 0.0220 | 0.0302 | 0.0135 | 0.0076 | 0.0160 | 0.0162 | |
| NGC 4552 | -0.0572 | -0.1592 | 0.0284 | 0.0098 | -0.0817 | -0.0063 | 0.0030 | 0.0059 | -0.0004 | -0.0117 |
| 0.0183 | 0.0258 | 0.0110 | 0.0148 | 0.0112 | 0.0174 | 0.0095 | 0.0102 | 0.0127 | 0.0088 | |
| NGC 4564 | -0.1740 | -0.1850 | 0.0019 | -0.0082 | -0.0909 | -0.0427 | -0.0078 | 0.0096 | 0.0145 | 0.0005 |
| 0.0157 | 0.0185 | 0.0062 | 0.0061 | 0.0103 | 0.0066 | 0.0068 | 0.0075 | 0.0084 | 0.0038 | |
| NGC 4594 | 0.0126 | -0.2270 | 0.0490 | 0.0307 | -0.1377 | -0.0005 | 0.0081 | 0.0286 | 0.0554 | -0.0096 |
| 0.0224 | 0.0257 | 0.0097 | 0.0158 | 0.0214 | 0.0249 | 0.0138 | 0.0226 | 0.0212 | 0.0173 | |
| NGC 4621 | -0.0720 | -0.1734 | 0.0134 | 0.0036 | -0.0755 | -0.0126 | 0.0060 | 0.0239 | 0.0125 | -0.0198 |
| 0.0080 | 0.0120 | 0.0070 | 0.0070 | 0.0081 | 0.0096 | 0.0061 | 0.0050 | 0.0059 | 0.0061 | |
| NGC 4636 | -0.0742 | -0.1762 | 0.0200 | 0.0287 | -0.0363 | 0.0024 | -0.0125 | 0.0256 | 0.0246 | -0.0109 |
| 0.0262 | 0.0322 | 0.0139 | 0.0142 | 0.0176 | 0.0168 | 0.0109 | 0.0066 | 0.0135 | 0.0089 | |
| NGC 4649 | -0.0641 | -0.0489 | 0.0044 | 0.0229 | -0.0477 | -0.0205 | -0.0105 | 0.0228 | 0.0260 | -0.0123 |
| 0.0198 | 0.0257 | 0.0133 | 0.0159 | 0.0165 | 0.0163 | 0.0134 | 0.0090 | 0.0110 | 0.0095 | |
| NGC 4673 | -0.3136 | -0.1806 | 0.0593 | 0.0560 | -0.0487 | -0.0530 | -0.0324 | 0.0424 | 0.0583 | -0.0036 |
| 0.0519 | 0.0138 | 0.0143 | 0.0169 | 0.0152 | 0.0187 | 0.0122 | 0.0088 | 0.0075 | 0.0124 | |
| NGC 4692 | -0.0808 | -0.1060 | 0.0231 | 0.0380 | -0.0885 | -0.0235 | -0.0171 | 0.0218 | 0.0166 | -0.0142 |
| 0.0601 | 0.0161 | 0.0183 | 0.0287 | 0.0198 | 0.0163 | 0.0166 | 0.0111 | 0.0147 | 0.0130 | |
| NGC 4697 | 0.0151 | -0.2025 | 0.0303 | 0.0181 | -0.0771 | -0.0112 | -0.0137 | 0.0244 | 0.0293 | -0.0126 |
| 0.0065 | 0.0221 | 0.0033 | 0.0042 | 0.0041 | 0.0049 | 0.0035 | 0.0028 | 0.0029 | 0.0032 | |
| NGC 4742 | -0.2420 | -0.1593 | -0.1027 | -0.1252 | 0.0109 | 0.0183 | 0.0351 | -0.0901 | -0.1320 | 0.0092 |
| 0.0276 | 0.0122 | 0.0129 | 0.0138 | 0.0097 | 0.0083 | 0.0103 | 0.0261 | 0.0303 | 0.0059 | |
| NGC 4839 | -0.0423 | -0.1857 | 0.0492 | 0.0356 | -0.0134 | 0.0385 | -0.0116 | 0.0433 | 0.0002 | -0.0311 |
| 0.1146 | 0.0319 | 0.0335 | 0.0355 | 0.0138 | 0.0359 | 0.0264 | 0.0208 | 0.0183 | 0.0274 | |
| NGC 4842A | -0.2731 | -0.0902 | -0.0263 | -0.0614 | -0.1362 | 0.0771 | -0.0711 | 0.0325 | -0.0027 | -0.0500 |
| 0.1125 | 0.0600 | 0.0441 | 0.0239 | 0.0715 | 0.0284 | 0.0474 | 0.0423 | 0.0267 | 0.0343 | |
| NGC 4864 | -0.0010 | -0.0811 | -0.0179 | 0.0077 | -0.0249 | -0.0171 | -0.0135 | 0.0477 | 0.0329 | -0.0620 |
| 0.1205 | 0.0244 | 0.0238 | 0.0304 | 0.0113 | 0.0258 | 0.0284 | 0.0265 | 0.0166 | 0.0487 | |
| NGC 4865 | -0.2596 | -0.1158 | -0.0129 | -0.0221 | -0.0461 | 0.0030 | 0.0139 | -0.0172 | -0.0081 | -0.0132 |
| 0.0400 | 0.0238 | 0.0319 | 0.0507 | 0.0374 | 0.0190 | 0.0158 | 0.0157 | 0.0257 | 0.0150 | |
| NGC 4874 | 0.0810 | -0.1949 | 0.0412 | 0.0643 | -0.0345 | -0.0317 | -0.0074 | -0.0228 | -0.0631 | -0.0021 |
| 0.0772 | 0.0258 | 0.0155 | 0.0204 | 0.0171 | 0.0188 | 0.0131 | 0.0129 | 0.0198 | 0.0121 | |
| NGC 4875 | -0.2320 | 0.0183 | -0.0267 | -0.0331 | -0.0529 | -0.0152 | 0.0297 | 0.0081 | -0.0117 | 0.0000 |
| 0.0774 | 0.0547 | 0.0068 | 0.0437 | 0.0102 | 0.0703 | 0.0138 | 0.0239 | 0.0402 | 0.0429 | |
| NGC 4889 | -0.0708 | -0.1506 | -0.0005 | 0.0119 | -0.0785 | 0.0128 | 0.0151 | 0.0131 | 0.0127 | -0.0347 |
| 0.0309 | 0.0163 | 0.0098 | 0.0112 | 0.0183 | 0.0188 | 0.0114 | 0.0069 | 0.0125 | 0.0103 | |
| NGC 4908 | -0.1810 | -0.1450 | 0.0389 | 0.0763 | -0.0266 | 0.0384 | -0.0588 | 0.0644 | 0.0381 | -0.0234 |
| 0.1363 | 0.0397 | 0.0225 | 0.0595 | 0.0410 | 0.0488 | 0.0488 | 0.0302 | 0.0423 | 0.0427 | |
| NGC 5638 | -0.0690 | -0.1999 | 0.0264 | 0.0256 | -0.0820 | 0.0007 | -0.0220 | 0.0265 | 0.0313 | -0.0114 |
| 0.0124 | 0.0092 | 0.0072 | 0.0084 | 0.0078 | 0.0099 | 0.0082 | 0.0081 | 0.0105 | 0.0046 | |
| NGC 5796 | -0.1814 | -0.1352 | 0.0026 | -0.0154 | -0.0340 | -0.0221 | 0.0009 | 0.0046 | 0.0048 | -0.0074 |
| 0.0381 | 0.0201 | 0.0095 | 0.0117 | 0.0121 | 0.0115 | 0.0125 | 0.0112 | 0.0151 | 0.0083 | |
| NGC 5812 | -0.1731 | -0.2445 | 0.0294 | 0.0124 | -0.0822 | -0.0272 | -0.0233 | 0.0342 | 0.0261 | -0.0250 |
| 0.0176 | 0.0118 | 0.0076 | 0.0078 | 0.0102 | 0.0116 | 0.0101 | 0.0119 | 0.0129 | 0.0067 | |
| NGC 5813 | -0.0064 | -0.2948 | 0.0364 | 0.0268 | -0.0791 | -0.0023 | -0.0193 | 0.0333 | 0.0363 | -0.0203 |
| 0.0146 | 0.0153 | 0.0070 | 0.0074 | 0.0090 | 0.0109 | 0.0069 | 0.0069 | 0.0089 | 0.0056 | |
| NGC 5831 | -0.0694 | -0.2808 | 0.0503 | 0.0362 | -0.0925 | -0.0326 | -0.0379 | 0.0546 | 0.0576 | -0.0355 |
| 0.0261 | 0.0150 | 0.0112 | 0.0131 | 0.0115 | 0.0129 | 0.0106 | 0.0077 | 0.0109 | 0.0083 | |
| NGC 5845 | -0.3136 | -0.3665 | 0.0338 | 0.0286 | -0.0628 | -0.0208 | -0.0211 | 0.0380 | 0.0239 | -0.0397 |
| 0.0300 | 0.0199 | 0.0135 | 0.0096 | 0.0237 | 0.0145 | 0.0152 | 0.0196 | 0.0218 | 0.0090 | |
| NGC 5846 | 0.0398 | -0.1676 | 0.0012 | -0.0230 | -0.0395 | 0.0292 | -0.0188 | 0.0216 | 0.0144 | -0.0512 |
| 0.0273 | 0.0089 | 0.0073 | 0.0082 | 0.0109 | 0.0128 | 0.0065 | 0.0054 | 0.0083 | 0.0097 | |
| NGC 5846A | 0.2745 | -0.1974 | 0.0027 | 0.0086 | -0.0477 | -0.0162 | -0.0379 | 0.0397 | 0.0215 | -0.0553 |
| 0.1293 | 0.0336 | 0.0141 | 0.0121 | 0.0239 | 0.0281 | 0.0134 | 0.0110 | 0.0185 | 0.0176 | |
| NGC 6127 | -0.0884 | -0.2386 | 0.0328 | 0.0337 | -0.0840 | -0.0085 | -0.0098 | 0.0316 | 0.0385 | -0.0122 |
| 0.0171 | 0.0173 | 0.0245 | 0.0234 | 0.0248 | 0.0206 | 0.0139 | 0.0090 | 0.0100 | 0.0107 | |
| NGC 6166 | -0.0096 | -0.0327 | 0.0270 | 0.0022 | -0.0323 | -0.0411 | -0.0172 | 0.0325 | 0.0209 | -0.0366 |
| 0.0415 | 0.0209 | 0.0121 | 0.0148 | 0.0115 | 0.0148 | 0.0154 | 0.0100 | 0.0131 | 0.0148 | |
| NGC 6411 | -0.0067 | -0.2148 | 0.0135 | -0.0137 | -0.0524 | -0.0136 | -0.0132 | 0.0259 | 0.0351 | -0.0207 |
| 0.0146 | 0.0116 | 0.0088 | 0.0123 | 0.0095 | 0.0094 | 0.0058 | 0.0054 | 0.0079 | 0.0068 | |
| NGC 6482 | -0.0696 | -0.0383 | 0.0253 | -0.0017 | -0.0586 | -0.0305 | 0.0066 | 0.0259 | 0.0335 | -0.0236 |
| 0.0270 | 0.0310 | 0.0147 | 0.0152 | 0.0146 | 0.0183 | 0.0125 | 0.0092 | 0.0124 | 0.0101 | |
| NGC 6702 | -0.0410 | -0.1912 | 0.0227 | 0.0342 | -0.0327 | 0.0126 | 0.0003 | 0.0246 | 0.0241 | -0.0063 |
| 0.0196 | 0.0130 | 0.0164 | 0.0165 | 0.0200 | 0.0204 | 0.0137 | 0.0090 | 0.0117 | 0.0079 | |
| NGC 6703 | -0.1053 | -0.1916 | 0.0189 | 0.0176 | -0.0577 | 0.0038 | -0.0267 | 0.0253 | 0.0171 | -0.0160 |
| 0.0246 | 0.0166 | 0.0043 | 0.0060 | 0.0100 | 0.0072 | 0.0062 | 0.0054 | 0.0043 | 0.0051 | |
| NGC 7052 | -0.0136 | -0.1008 | 0.0054 | 0.0106 | -0.0368 | 0.0040 | 0.0163 | 0.0138 | 0.0393 | -0.0140 |
| 0.0134 | 0.0212 | 0.0071 | 0.0100 | 0.0093 | 0.0099 | 0.0080 | 0.0064 | 0.0070 | 0.0061 | |
| NGC 7332 | -0.0232 | -0.3047 | 0.0199 | 0.0106 | -0.0871 | -0.0020 | -0.0208 | 0.0248 | 0.0237 | -0.0256 |
| 0.0178 | 0.0170 | 0.0039 | 0.0046 | 0.0080 | 0.0076 | 0.0059 | 0.0045 | 0.0050 | 0.0058 | |
| IC 767 | 1.4466 | -0.4829 | -0.0025 | -0.0427 | 0.0133 | 0.0050 | 0.0442 | -0.0333 | -0.0516 | -0.0179 |
| 2.3182 | 0.0591 | 0.0376 | 0.0736 | 0.0443 | 0.0360 | 0.0056 | 0.0415 | 0.0392 | 0.0994 | |
| IC 794 | -0.0303 | -0.1679 | 0.0388 | 0.0525 | -0.0160 | 0.0157 | -0.0148 | 0.0244 | 0.0222 | -0.0344 |
| 0.1655 | 0.0347 | 0.0132 | 0.0185 | 0.0229 | 0.0293 | 0.0250 | 0.0197 | 0.0307 | 0.0149 | |
| IC 832 | -0.1324 | 0.0138 | -0.0158 | -0.0387 | -0.0560 | -0.0128 | 0.0029 | -0.0081 | -0.0179 | -0.0018 |
| 0.0556 | 0.0410 | 0.0241 | 0.0258 | 0.0263 | 0.0431 | 0.0177 | 0.0153 | 0.0228 | 0.0192 | |
| IC 3957 | -0.0347 | -0.5857 | 0.0493 | -0.0335 | -0.0868 | -0.1265 | -0.0755 | 0.0577 | 0.0492 | -0.0094 |
| 0.0895 | 0.1203 | 0.0312 | 0.0572 | 0.0812 | 0.0323 | 0.1151 | 0.0680 | 0.0887 | 0.0325 | |
| IC 3959 | -0.2640 | -0.2479 | 0.0296 | 0.0259 | -0.1023 | -0.0299 | -0.0377 | 0.0549 | 0.0535 | 0.0114 |
| 0.1392 | 0.0275 | 0.0139 | 0.0268 | 0.0194 | 0.0310 | 0.0253 | 0.0227 | 0.0273 | 0.0230 | |
| IC 3963 | -0.0381 | -0.1294 | 0.0271 | 0.0248 | -0.0278 | -0.0665 | 0.0030 | 0.0238 | 0.0063 | -0.0250 |
| 0.1324 | 0.0293 | 0.0134 | 0.0189 | 0.0207 | 0.0284 | 0.0234 | 0.0109 | 0.0176 | 0.0186 | |
| IC 3973 | -0.3219 | -0.3314 | -0.0182 | -0.0551 | -0.0219 | 0.0161 | 0.0247 | -0.0368 | -0.0530 | 0.0058 |
| 0.0698 | 0.0733 | 0.0274 | 0.0440 | 0.0129 | 0.0344 | 0.0264 | 0.0220 | 0.0291 | 0.0106 | |
| IC 4042 | -0.2280 | -0.5860 | 0.0509 | 0.0194 | -0.0288 | 0.0369 | -0.0669 | 0.0307 | -0.0079 | 0.0550 |
| 0.1406 | 0.1258 | 0.1236 | 0.0971 | 0.2025 | 0.0791 | 0.0343 | 0.0412 | 0.0746 | 0.2003 | |
| IC 4051 | 0.0864 | -0.2565 | 0.0545 | 0.0231 | -0.1041 | 0.0015 | -0.0420 | 0.0385 | 0.0134 | -0.0277 |
| 0.0540 | 0.0333 | 0.0127 | 0.0128 | 0.0165 | 0.0262 | 0.0137 | 0.0153 | 0.0173 | 0.0120 | |
| CGCG159-041 | -0.2040 | -0.2805 | 0.1211 | 0.0866 | -0.0309 | 0.0743 | 0.1851 | -0.0545 | 0.0136 | 0.0354 |
| 0.2762 | 0.2039 | 0.0616 | 0.0416 | 0.1286 | 0.0289 | 0.1133 | 0.0343 | 0.0534 | 0.0748 | |
| CGCG159-043 | -0.1134 | -0.2382 | 0.0185 | 0.0453 | -0.0455 | -0.0001 | 0.0001 | 0.0151 | 0.0218 | 0.0080 |
| 0.1105 | 0.0371 | 0.0195 | 0.0265 | 0.0211 | 0.0321 | 0.0205 | 0.0166 | 0.0255 | 0.0209 | |
| CGCG159-083 | -0.2836 | 0.3389 | -0.0502 | -0.0509 | -0.0173 | 0.0039 | 0.0388 | -0.0289 | -0.0064 | 0.0045 |
| 0.1301 | 0.0403 | 0.0133 | 0.0151 | 0.0182 | 0.0152 | 0.0149 | 0.0148 | 0.0152 | 0.0183 | |
| CGCG159-089 | -0.0218 | -0.3534 | 0.0459 | 0.0544 | -0.1319 | 0.0219 | 0.0137 | -0.0226 | 0.0096 | 0.0156 |
| 0.0885 | 0.0636 | 0.0270 | 0.0266 | 0.0209 | 0.0317 | 0.0284 | 0.0238 | 0.0291 | 0.0228 | |
| NGC 221 | 0.0027 | -0.0030 | -0.0037 | -0.0021 | 0.0052 | -0.0007 | 0.0092 | -0.0017 | -0.0038 | 0.0020 |
| 0.0019 | 0.0016 | 0.0017 | 0.0016 | 0.0019 | 0.0011 | 0.0022 | 0.0018 | 0.0011 | 0.0017 | |
| NGC 315 | 0.0113 | -0.0275 | -0.0396 | -0.0039 | -0.0045 | 0.0030 | -0.0247 | -0.0666 | 0.0040 | -0.0210 |
| 0.0059 | 0.0051 | 0.0051 | 0.0048 | 0.0040 | 0.0031 | 0.0044 | 0.0072 | 0.0036 | 0.0057 | |
| NGC 507 | -0.0034 | 0.0150 | 0.0121 | 0.0352 | 0.0279 | 0.0160 | 0.0346 | -0.0119 | 0.0013 | -0.0026 |
| 0.0206 | 0.0215 | 0.0197 | 0.0109 | 0.0180 | 0.0147 | 0.0225 | 0.0345 | 0.0246 | 0.0241 | |
| NGC 584 | -0.0120 | -0.0113 | -0.0290 | -0.0036 | 0.0000 | -0.0126 | -0.0206 | -0.0193 | -0.0144 | -0.0197 |
| 0.0109 | 0.0076 | 0.0065 | 0.0071 | 0.0105 | 0.0061 | 0.0110 | 0.0120 | 0.0071 | 0.0094 | |
| NGC 636 | -0.0136 | 0.0028 | -0.0508 | 0.0064 | -0.0227 | -0.0216 | -0.0482 | -0.0230 | -0.0012 | -0.0106 |
| 0.0176 | 0.0117 | 0.0119 | 0.0095 | 0.0078 | 0.0129 | 0.0162 | 0.0124 | 0.0080 | 0.0119 | |
| NGC 821 | -0.0227 | -0.0302 | -0.0581 | -0.0124 | -0.0222 | -0.0472 | -0.0765 | -0.0417 | -0.0084 | -0.0129 |
| 0.0073 | 0.0145 | 0.0128 | 0.0167 | 0.0099 | 0.0169 | 0.0197 | 0.0143 | 0.0105 | 0.0148 | |
| NGC 1453 | -0.0073 | -0.0018 | -0.0286 | 0.0328 | -0.0143 | -0.0080 | -0.0148 | -0.0442 | -0.0218 | -0.0061 |
| 0.0165 | 0.0111 | 0.0076 | 0.0098 | 0.0113 | 0.0088 | 0.0114 | 0.0111 | 0.0133 | 0.0159 | |
| NGC 1600 | -0.0311 | 0.0005 | -0.0206 | -0.0251 | 0.0086 | -0.0074 | -0.0172 | -0.0048 | -0.0320 | -0.0271 |
| 0.0085 | 0.0045 | 0.0039 | 0.0055 | 0.0038 | 0.0085 | 0.0064 | 0.0114 | 0.0088 | 0.0135 | |
| NGC 1700 | -0.0101 | -0.0073 | -0.0426 | 0.0027 | -0.0143 | -0.0270 | -0.0392 | -0.0243 | -0.0069 | -0.0116 |
| 0.0149 | 0.0075 | 0.0102 | 0.0114 | 0.0086 | 0.0078 | 0.0097 | 0.0106 | 0.0087 | 0.0157 | |
| NGC 2300 | 0.0035 | 0.0006 | -0.0511 | -0.0068 | 0.0005 | 0.0063 | -0.0087 | -0.0288 | -0.0073 | 0.0071 |
| 0.0139 | 0.0141 | 0.0073 | 0.0150 | 0.0083 | 0.0112 | 0.0113 | 0.0131 | 0.0188 | 0.0096 | |
| NGC 2329 | -0.0250 | -0.0266 | -0.0278 | -0.0064 | -0.0233 | 0.0762 | ||||
| 0.0239 | 0.0107 | 0.0165 | 0.0169 | 0.0099 | 0.0489 | |||||
| NGC 2693 | -0.0147 | -0.0132 | -0.0216 | 0.0199 | -0.0019 | -0.0258 | -0.0260 | -0.0093 | -0.0056 | -0.0048 |
| 0.0130 | 0.0074 | 0.0082 | 0.0065 | 0.0063 | 0.0104 | 0.0100 | 0.0098 | 0.0070 | 0.0126 | |
| NGC 2694 | -0.0546 | -0.0403 | -0.0407 | 0.0211 | 0.0128 | 0.0700 | 0.0416 | -0.0119 | -0.0029 | 0.0259 |
| 0.0911 | 0.0194 | 0.0029 | 0.0318 | 0.0160 | 0.0396 | 0.0400 | 0.0380 | 0.0182 | 0.0170 | |
| NGC 2778 | -0.0279 | -0.0233 | -0.0441 | 0.0006 | -0.0212 | -0.0653 | ||||
| 0.0098 | 0.0099 | 0.0071 | 0.0072 | 0.0072 | 0.0075 | |||||
| NGC 2832 | -0.0060 | -0.0193 | -0.0424 | -0.0055 | -0.0140 | 0.2740 | ||||
| 0.0104 | 0.0068 | 0.0055 | 0.0079 | 0.0092 | 0.0698 | |||||
| NGC 3115 | -0.0268 | -0.0111 | -0.0387 | -0.0063 | -0.0219 | -0.0320 | ||||
| 0.0059 | 0.0045 | 0.0041 | 0.0037 | 0.0039 | 0.0046 | |||||
| NGC 3377 | -0.0246 | -0.0041 | -0.0565 | -0.0022 | -0.0219 | -0.0669 | -0.1011 | -0.0615 | -0.0146 | -0.0201 |
| 0.0095 | 0.0072 | 0.0052 | 0.0091 | 0.0050 | 0.0062 | 0.0096 | 0.0081 | 0.0069 | 0.0100 | |
| NGC 3379 | -0.0169 | -0.0102 | -0.0258 | 0.0017 | -0.0174 | -0.0669 | -0.1011 | -0.0615 | -0.0146 | -0.0201 |
| 0.0040 | 0.0029 | 0.0028 | 0.0035 | 0.0030 | 0.0052 | 0.0060 | 0.0065 | 0.0053 | 0.0052 | |
| NGC 3605 | -0.0095 | -0.0028 | -0.0226 | -0.0010 | -0.0392 | -0.0242 | ||||
| 0.0136 | 0.0104 | 0.0111 | 0.0114 | 0.0103 | 0.0118 | |||||
| NGC 3608 | -0.0278 | -0.0170 | -0.0392 | 0.0113 | -0.0263 | -0.0527 | -0.0788 | -0.0514 | -0.0151 | -0.0135 |
| 0.0160 | 0.0136 | 0.0117 | 0.0147 | 0.0082 | 0.0093 | 0.0062 | 0.0082 | 0.0128 | 0.0079 | |
| NGC 3641 | -0.0453 | -0.0086 | -0.0364 | 0.0086 | -0.0386 | -0.0569 | ||||
| 0.0306 | 0.0259 | 0.0195 | 0.0264 | 0.0144 | 0.0248 | |||||
| NGC 3665 | -0.0169 | -0.0168 | -0.0259 | 0.0070 | -0.0086 | -0.0242 | -0.0212 | -0.0122 | -0.0009 | -0.0086 |
| 0.0126 | 0.0082 | 0.0044 | 0.0094 | 0.0065 | 0.0052 | 0.0076 | 0.0076 | 0.0050 | 0.0065 | |
| NGC 3818 | -0.0114 | -0.0226 | -0.0505 | -0.0043 | -0.0238 | -0.0424 | ||||
| 0.0078 | 0.0071 | 0.0060 | 0.0070 | 0.0068 | 0.0068 | |||||
| NGC 4261 | -0.0087 | -0.0042 | -0.0216 | 0.0015 | -0.0211 | -0.0203 | ||||
| 0.0073 | 0.0117 | 0.0036 | 0.0048 | 0.0040 | 0.0059 | |||||
| NGC 4278 | -0.0245 | -0.0178 | -0.0359 | -0.0033 | -0.0244 | -0.0543 | ||||
| 0.0045 | 0.0036 | 0.0028 | 0.0048 | 0.0038 | 0.0050 | |||||
| NGC 4365 | -0.0238 | -0.0166 | -0.0286 | 0.0027 | -0.0200 | -0.0356 | ||||
| 0.0052 | 0.0036 | 0.0027 | 0.0036 | 0.0036 | 0.0038 | |||||
| NGC 4374 | -0.0147 | -0.0077 | -0.0203 | 0.0115 | -0.0075 | -0.0190 | -0.0322 | -0.0255 | -0.0088 | -0.0066 |
| 0.0081 | 0.0051 | 0.0048 | 0.0027 | 0.0053 | 0.0042 | 0.0055 | 0.0067 | 0.0052 | 0.0063 | |
| NGC 4415 | -0.0137 | -0.0031 | -0.0009 | -0.0033 | -0.0143 | 0.0012 | -0.0156 | -0.0204 | -0.0149 | -0.0142 |
| 0.0078 | 0.0079 | 0.0045 | 0.0056 | 0.0047 | 0.0115 | 0.0169 | 0.0129 | 0.0080 | 0.0129 | |
| NGC 4431 | 0.0059 | -0.0076 | -0.0049 | -0.0190 | 0.0062 | -0.0033 | 0.0037 | -0.0028 | -0.0299 | -0.0046 |
| 0.0125 | 0.0103 | 0.0078 | 0.0110 | 0.0101 | 0.0076 | 0.0126 | 0.0054 | 0.0080 | 0.0094 | |
| NGC 4464 | -0.0155 | -0.0079 | -0.0167 | 0.0104 | -0.0116 | -0.0319 | ||||
| 0.0066 | 0.0091 | 0.0084 | 0.0061 | 0.0062 | 0.0080 | |||||
| NGC 4467 | 0.0296 | -0.0208 | -0.0697 | -0.0053 | -0.0226 | -0.0318 | ||||
| 0.0094 | 0.0373 | 0.0303 | 0.0255 | 0.0250 | 0.0367 | |||||
| NGC 4472 | -0.0220 | -0.0113 | -0.0282 | -0.0001 | -0.0148 | -0.0184 | ||||
| 0.0036 | 0.0025 | 0.0019 | 0.0024 | 0.0024 | 0.0034 | |||||
| NGC 4478 | -0.0131 | -0.0078 | -0.0209 | -0.0112 | -0.0094 | -0.0101 | ||||
| 0.0045 | 0.0042 | 0.0029 | 0.0048 | 0.0046 | 0.0051 | |||||
| NGC 4486B | 0.0072 | -0.0062 | -0.0433 | -0.0237 | 0.0002 | 0.1090 | 0.0839 | -0.0411 | -0.0130 | -0.0313 |
| 0.0429 | 0.0229 | 0.0098 | 0.0184 | 0.0262 | 0.0257 | 0.0102 | 0.0174 | 0.0043 | 0.0039 | |
| NGC 4489 | -0.0292 | -0.0076 | -0.0348 | -0.0168 | -0.0208 | -0.0031 | -0.0160 | -0.0023 | -0.0218 | -0.0298 |
| 0.0098 | 0.0097 | 0.0094 | 0.0099 | 0.0104 | 0.0260 | 0.0206 | 0.0083 | 0.0101 | 0.0136 | |
| NGC 4552 | -0.0061 | -0.0066 | -0.0351 | 0.0004 | -0.0084 | -0.0362 | -0.0533 | -0.0309 | -0.0103 | -0.0047 |
| 0.0074 | 0.0071 | 0.0040 | 0.0064 | 0.0051 | 0.0047 | 0.0054 | 0.0051 | 0.0049 | 0.0059 | |
| NGC 4564 | -0.0022 | -0.0111 | -0.0455 | 0.0028 | -0.0109 | -0.0320 | ||||
| 0.0049 | 0.0040 | 0.0033 | 0.0042 | 0.0029 | 0.0046 | |||||
| NGC 4594 | -0.0137 | -0.0169 | -0.0501 | -0.0130 | -0.0084 | -0.0512 | ||||
| 0.0091 | 0.0068 | 0.0056 | 0.0162 | 0.0106 | 0.0118 | |||||
| NGC 4621 | -0.0152 | -0.0115 | -0.0405 | -0.0036 | -0.0150 | -0.0294 | ||||
| 0.0061 | 0.0032 | 0.0035 | 0.0055 | 0.0041 | 0.0059 | |||||
| NGC 4636 | -0.0335 | -0.0186 | -0.0216 | -0.0120 | -0.0134 | -0.0201 | -0.0287 | -0.0302 | -0.0108 | -0.0062 |
| 0.0111 | 0.0060 | 0.0069 | 0.0069 | 0.0086 | 0.0071 | 0.0066 | 0.0079 | 0.0066 | 0.0083 | |
| NGC 4649 | -0.0190 | 0.0037 | -0.0300 | 0.0051 | -0.0124 | -0.0263 | -0.0404 | -0.0257 | 0.0052 | 0.0089 |
| 0.0090 | 0.0066 | 0.0063 | 0.0042 | 0.0058 | 0.0043 | 0.0057 | 0.0069 | 0.0056 | 0.0078 | |
| NGC 4673 | -0.0006 | -0.0103 | -0.0407 | 0.0199 | -0.0096 | -0.0239 | -0.0599 | -0.0534 | -0.0239 | -0.0262 |
| 0.0127 | 0.0090 | 0.0103 | 0.0095 | 0.0105 | 0.0041 | 0.0064 | 0.0108 | 0.0080 | 0.0105 | |
| NGC 4692 | -0.0231 | -0.0088 | -0.0417 | -0.0057 | -0.0141 | -0.0392 | -0.0588 | -0.0388 | 0.0055 | -0.0205 |
| 0.0061 | 0.0169 | 0.0119 | 0.0124 | 0.0096 | 0.0082 | 0.0091 | 0.0123 | 0.0107 | 0.0081 | |
| NGC 4697 | -0.0096 | -0.0094 | -0.0313 | 0.0030 | -0.0137 | -0.0257 | ||||
| 0.0030 | 0.0022 | 0.0023 | 0.0024 | 0.0020 | 0.0032 | |||||
| NGC 4742 | -0.0113 | -0.0036 | -0.0192 | -0.0637 | -0.0164 | 0.0017 | ||||
| 0.0082 | 0.0055 | 0.0050 | 0.0082 | 0.0054 | 0.0060 | |||||
| NGC 4839 | -0.0311 | -0.0394 | -0.0080 | -0.0165 | -0.0261 | -0.0206 | -0.0279 | -0.0254 | -0.0226 | -0.0003 |
| 0.0274 | 0.0408 | 0.0098 | 0.0103 | 0.0216 | 0.0258 | 0.0139 | 0.0080 | 0.0304 | 0.0302 | |
| NGC 4842A | -0.0788 | 0.0045 | -0.0046 | 0.0248 | 0.0020 | -0.0011 | -0.0029 | 0.0553 | -0.0260 | -0.0109 |
| 0.0305 | 0.0525 | 0.0144 | 0.0283 | 0.0116 | 0.0243 | 0.0342 | 0.0264 | 0.0268 | 0.0228 | |
| NGC 4864 | -0.0463 | -0.0213 | -0.0332 | -0.0201 | -0.0546 | -0.0346 | -0.0846 | -0.0345 | -0.0176 | -0.0735 |
| 0.0220 | 0.0245 | 0.0128 | 0.0199 | 0.0217 | 0.0105 | 0.0401 | 0.0430 | 0.0143 | 0.0243 | |
| NGC 4865 | -0.0038 | -0.0181 | -0.0227 | 0.0028 | -0.0132 | -0.0171 | -0.0296 | -0.0327 | -0.0064 | -0.0230 |
| 0.0198 | 0.0113 | 0.0099 | 0.0116 | 0.0078 | 0.0050 | 0.0088 | 0.0158 | 0.0083 | 0.0144 | |
| NGC 4874 | 0.0337 | -0.0280 | -0.0413 | -0.0550 | -0.0234 | -0.0151 | -0.0366 | -0.0511 | -0.0290 | 0.0272 |
| 0.0096 | 0.0122 | 0.0062 | 0.0146 | 0.0109 | 0.0078 | 0.0075 | 0.0104 | 0.0114 | 0.0154 | |
| NGC 4875 | 0.0087 | -0.0172 | -0.0451 | -0.0163 | -0.0050 | -0.0055 | -0.0165 | 0.0087 | -0.0239 | -0.0059 |
| 0.0548 | 0.0173 | 0.0196 | 0.0745 | 0.0198 | 0.0241 | 0.0126 | 0.0221 | 0.0105 | 0.0291 | |
| NGC 4889 | 0.0087 | -0.0246 | -0.0385 | -0.0031 | -0.0303 | -0.0603 | -0.0505 | 0.0062 | -0.0132 | -0.0536 |
| 0.0114 | 0.0075 | 0.0064 | 0.0061 | 0.0069 | 0.0058 | 0.0091 | 0.0123 | 0.0081 | 0.0128 | |
| NGC 4908 | -0.0047 | -0.0120 | -0.0378 | 0.0004 | 0.0106 | -0.0463 | -0.0184 | -0.0487 | -0.0184 | -0.0014 |
| 0.0315 | 0.0322 | 0.0373 | 0.0152 | 0.0221 | 0.0104 | 0.0218 | 0.0274 | 0.0239 | 0.0381 | |
| NGC 5638 | -0.0258 | -0.0107 | -0.0314 | 0.0013 | -0.0135 | -0.0357 | ||||
| 0.0060 | 0.0052 | 0.0031 | 0.0056 | 0.0043 | 0.0064 | |||||
| NGC 5796 | -0.0004 | -0.0172 | -0.0235 | -0.0011 | -0.0110 | -0.0328 | ||||
| 0.0137 | 0.0096 | 0.0050 | 0.0066 | 0.0066 | 0.0100 | |||||
| NGC 5812 | -0.0177 | -0.0249 | -0.0338 | -0.0003 | -0.0272 | -0.0265 | ||||
| 0.0078 | 0.0060 | 0.0042 | 0.0062 | 0.0051 | 0.0076 | |||||
| NGC 5813 | -0.0179 | -0.0119 | -0.0168 | 0.0012 | -0.0116 | -0.0200 | ||||
| 0.0063 | 0.0048 | 0.0044 | 0.0057 | 0.0040 | 0.0070 | |||||
| NGC 5831 | -0.0245 | -0.0131 | -0.0386 | 0.0053 | -0.0154 | -0.0365 | ||||
| 0.0078 | 0.0069 | 0.0072 | 0.0063 | 0.0064 | 0.0059 | |||||
| NGC 5845 | -0.0161 | -0.0150 | -0.0293 | 0.0011 | -0.0188 | -0.0200 | ||||
| 0.0091 | 0.0069 | 0.0085 | 0.0097 | 0.0059 | 0.0075 | |||||
| NGC 5846 | -0.0011 | -0.0085 | -0.0199 | -0.0043 | -0.0102 | -0.0135 | -0.0440 | -0.0172 | -0.0103 | -0.0290 |
| 0.0078 | 0.0047 | 0.0053 | 0.0069 | 0.0047 | 0.0038 | 0.0062 | 0.0064 | 0.0056 | 0.0059 | |
| NGC 5846A | -0.0246 | -0.0161 | -0.0468 | -0.0093 | -0.0009 | -0.0227 | -0.0714 | -0.0499 | -0.0151 | -0.0308 |
| 0.0125 | 0.0104 | 0.0079 | 0.0132 | 0.0158 | 0.0101 | 0.0066 | 0.0086 | 0.0070 | 0.0129 | |
| NGC 6127 | -0.0072 | -0.0079 | -0.0374 | -0.0059 | -0.0227 | -0.0217 | ||||
| 0.0101 | 0.0073 | 0.0068 | 0.0074 | 0.0064 | 0.0202 | |||||
| NGC 6166 | -0.0207 | -0.0208 | -0.0271 | 0.0151 | -0.0081 | -0.0272 | -0.0300 | -0.0639 | -0.0068 | -0.0047 |
| 0.0122 | 0.0132 | 0.0109 | 0.0076 | 0.0100 | 0.0066 | 0.0140 | 0.0163 | 0.0100 | 0.0152 | |
| NGC 6411 | -0.0203 | -0.0105 | -0.0294 | 0.0023 | -0.0101 | -0.0200 | -0.0274 | -0.0176 | -0.0040 | -0.0150 |
| 0.0074 | 0.0045 | 0.0055 | 0.0057 | 0.0054 | 0.0046 | 0.0042 | 0.0068 | 0.0052 | 0.0052 | |
| NGC 6482 | -0.0249 | -0.0143 | -0.0190 | 0.0077 | -0.0175 | -0.0324 | -0.0624 | -0.0382 | -0.0077 | -0.0186 |
| 0.0139 | 0.0117 | 0.0063 | 0.0088 | 0.0090 | 0.0061 | 0.0059 | 0.0084 | 0.0092 | 0.0109 | |
| NGC 6702 | -0.0105 | 0.0039 | -0.0325 | -0.0174 | -0.0219 | -0.0058 | ||||
| 0.0106 | 0.0089 | 0.0082 | 0.0075 | 0.0075 | 0.0188 | |||||
| NGC 6703 | -0.0021 | -0.0165 | -0.0316 | 0.0025 | -0.0160 | -0.0152 | -0.0399 | -0.0245 | -0.0122 | -0.0157 |
| 0.0061 | 0.0044 | 0.0034 | 0.0039 | 0.0036 | 0.0032 | 0.0040 | 0.0035 | 0.0039 | 0.0057 | |
| IC 832 | 0.0031 | -0.0326 | 0.0040 | 0.0176 | -0.0078 | -0.0169 | -0.0537 | -0.0227 | -0.0269 | -0.0352 |
| 0.0240 | 0.0216 | 0.0099 | 0.0142 | 0.0129 | 0.0150 | 0.0114 | 0.0142 | 0.0153 | 0.0178 | |
| IC 3957 | -0.0385 | 0.0240 | -0.0543 | -0.0046 | -0.0366 | -0.0552 | -0.0292 | 0.0003 | -0.1654 | -0.0976 |
| 0.0067 | 0.0304 | 0.0164 | 0.0175 | 0.0378 | 0.0230 | 0.0185 | 0.0583 | 0.0726 | 0.0213 | |
| NGC 7052 | -0.0109 | -0.0038 | -0.0193 | 0.0117 | -0.0179 | -0.0188 | -0.0145 | -0.0263 | -0.0127 | -0.0101 |
| 0.0077 | 0.0071 | 0.0059 | 0.0064 | 0.0042 | 0.0037 | 0.0047 | 0.0056 | 0.0065 | 0.0069 | |
| NGC 7332 | -0.0239 | -0.0135 | -0.0483 | 0.0118 | -0.0028 | -0.0506 | -0.0646 | -0.0215 | -0.0195 | -0.0197 |
| 0.0055 | 0.0035 | 0.0042 | 0.0054 | 0.0064 | 0.0051 | 0.0113 | 0.0037 | 0.0043 | 0.0042 | |
| IC 767 | 0.0286 | -0.0388 | -0.0341 | -0.0631 | 0.0389 | 0.1132 | 0.1299 | 0.0308 | -0.0101 | 0.0096 |
| 0.0073 | 0.0240 | 0.0358 | 0.0198 | 0.0232 | 0.0673 | 0.0540 | 0.0294 | 0.0221 | 0.0322 | |
| IC 794 | 0.0369 | -0.0450 | -0.0470 | -0.0064 | -0.0198 | -0.0108 | ||||
| 0.0216 | 0.0206 | 0.0146 | 0.0085 | 0.0110 | 0.0146 | |||||
| IC 3959 | -0.0097 | 0.0242 | -0.0027 | -0.0045 | -0.0127 | -0.0325 | -0.0663 | -0.0257 | -0.0058 | -0.0449 |
| 0.0130 | 0.0287 | 0.0156 | 0.0112 | 0.0080 | 0.0090 | 0.0148 | 0.0141 | 0.0159 | 0.0169 | |
| IC 3963 | 0.0055 | 0.0022 | -0.0462 | -0.0131 | -0.0149 | -0.0302 | -0.0312 | -0.0289 | -0.0155 | -0.0204 |
| 0.0236 | 0.0158 | 0.0105 | 0.0205 | 0.0119 | 0.0059 | 0.0097 | 0.0129 | 0.0124 | 0.0213 | |
| IC 3973 | -0.0004 | -0.0194 | -0.0090 | -0.0403 | -0.0176 | -0.0227 | -0.0288 | -0.0184 | -0.0036 | -0.0400 |
| 0.0161 | 0.0291 | 0.0114 | 0.0318 | 0.0169 | 0.0117 | 0.0177 | 0.0271 | 0.0163 | 0.0161 | |
| IC 4042 | -0.0124 | -0.0252 | -0.0516 | 0.0097 | 0.0174 | 0.0370 | -0.0706 | -0.0256 | 0.0603 | -0.0823 |
| 0.1930 | 0.0702 | 0.0385 | 0.0917 | 0.0554 | 0.0417 | 0.0617 | 0.0738 | 0.0338 | 0.0872 | |
| IC 4051 | -0.0478 | 0.0055 | -0.0500 | 0.0108 | -0.0169 | -0.0480 | -0.0652 | -0.0318 | -0.0109 | 0.0066 |
| 0.0153 | 0.0106 | 0.0128 | 0.0057 | 0.0087 | 0.0080 | 0.0097 | 0.0123 | 0.0131 | 0.0165 | |
| CGCG159-041 | -0.0414 | 0.1280 | 0.0216 | -0.0290 | -0.0009 | -0.0557 | -0.1646 | -0.1203 | -0.1237 | -0.0292 |
| 0.0581 | 0.0502 | 0.0589 | 0.0668 | 0.1725 | 0.0105 | 0.0662 | 0.0453 | 0.0232 | 0.0269 | |
| CGCG159-043 | -0.0389 | -0.0126 | -0.0285 | -0.0389 | -0.0307 | -0.0343 | -0.0590 | -0.0318 | -0.0202 | -0.0390 |
| 0.0152 | 0.0134 | 0.0213 | 0.0181 | 0.0161 | 0.0089 | 0.0128 | 0.0121 | 0.0108 | 0.0114 | |
| CGCG159-083 | -0.0307 | -0.0317 | -0.0212 | 0.0527 | -0.0084 | -0.0165 | -0.0213 | -0.0334 | -0.0009 | -0.0249 |
| 0.0192 | 0.0158 | 0.0131 | 0.0145 | 0.0169 | 0.0098 | 0.0148 | 0.0177 | 0.0139 | 0.0176 | |
| CGCG159-089 | 0.0046 | 0.0084 | -0.0542 | 0.0231 | -0.0331 | -0.0371 | -0.0617 | -0.0271 | -0.0121 | -0.0188 |
| 0.0333 | 0.0223 | 0.0071 | 0.0107 | 0.0158 | 0.0140 | 0.0103 | 0.0264 | 0.0124 | 0.0220 |
| CN2 | C4668 | Fe4383 | Mgb | Ca4227 | |||
| Galaxy | grad (age) | grad ([M/H]) | grad ([M/H]) | grad ([M/H]) | grad ([M/H]) | grad ([M/H]) | grad ([M/H]) |
|
|
|
|
|
|
|
| |
| NGC 221 | 0.0151 | -0.0273 | -0.170 | -0.246 | 0.023 | -0.171 | 0.082 |
| 0.0180 | 0.0226 | 0.241 | 0.139 | 0.222 | 0.259 | 0.373 | |
| NGC 315 | 0.0850 | -0.2745 | 0.010 | -0.689 | -0.214 | -1.266 | -0.209 |
| 0.0486 | 0.0651 | 0.112 | 0.089 | 0.095 | 0.148 | 0.151 | |
| NGC 507 | -0.6291 | 0.5756 | 0.076 | 0.451 | 1.004 | 0.453 | 0.935 |
| 0.1508 | 0.2140 | 0.309 | 0.324 | 0.354 | 0.611 | 0.664 | |
| NGC 584 | 0.0814 | -0.1937 | -0.673 | -0.510 | -0.341 | -0.414 | -0.294 |
| 0.0868 | 0.1185 | 0.196 | 0.114 | 0.145 | 0.242 | 0.355 | |
| NGC 636 | 0.0779 | -0.3627 | -0.740 | -0.804 | -0.427 | -0.291 | 0.117 |
| 0.1148 | 0.1592 | 0.220 | 0.200 | 0.300 | 0.274 | 0.382 | |
| NGC 821 | 0.0563 | -0.8237 | -1.560 | -1.058 | -0.493 | -0.981 | -1.057 |
| 0.1157 | 0.9981 | 0.351 | 0.235 | 0.293 | 0.391 | 0.478 | |
| NGC 1453 | -0.2652 | -0.0141 | -0.170 | -0.246 | 0.023 | -0.171 | 0.082 |
| 0.1036 | 0.1259 | 0.241 | 0.139 | 0.222 | 0.259 | 0.373 | |
| NGC 1600 | 0.2293 | -0.0732 | -0.765 | -0.521 | -0.592 | -0.561 | -0.897 |
| 0.0504 | 0.0708 | 0.116 | 0.072 | 0.121 | 0.216 | 0.203 | |
| NGC 1700 | 0.0803 | -0.3432 | -0.750 | -0.693 | -0.096 | -0.384 | 0.534 |
| 0.1116 | 0.1349 | 0.186 | 0.183 | 0.237 | 0.274 | 0.508 | |
| NGC 2300 | 0.1531 | -0.2416 | -0.553 | -0.902 | -0.335 | -0.644 | -0.049 |
| 0.1284 | 0.1582 | 0.270 | 0.156 | 0.252 | 0.353 | 0.508 | |
| NGC 2329 | 0.2413 | -0.3977 | -0.610 | -0.510 | -1.081 | 1.243 | -0.014 |
| 0.1731 | 0.1840 | 0.346 | 0.284 | 0.377 | 0.884 | 0.478 | |
| NGC 2693 | -0.1917 | -0.0072 | -0.420 | -0.220 | 0.049 | 0.210 | -0.168 |
| 0.0786 | 0.0997 | 0.116 | 0.138 | 0.206 | 0.205 | 0.265 | |
| NGC 2694 | -0.1551 | -0.0214 | 0.119 | -0.531 | 0.270 | 0.186 | -0.882 |
| 0.2540 | 0.2572 | 1.146 | 0.218 | 0.467 | 0.853 | 1.057 | |
| NGC 2778 | 0.0644 | -0.3501 | -1.041 | -0.733 | -0.284 | -1.158 | -0.233 |
| 0.0879 | 0.1155 | 0.186 | 0.125 | 0.178 | 0.182 | 0.249 | |
| NGC 2832 | 0.1436 | -0.3521 | -0.819 | -0.747 | -0.712 | 4.801 | -1.200 |
| 0.0696 | 0.1046 | 0.120 | 0.102 | 0.196 | 1.205 | 0.297 | |
| NGC 3115 | 0.2518 | -0.4864 | -1.121 | -0.691 | -0.416 | -0.692 | -0.367 |
| 0.0501 | 0.0845 | 0.154 | 0.070 | 0.090 | 0.103 | 0.129 | |
| NGC 3377 | 0.0334 | -0.3600 | -1.118 | -0.960 | -0.498 | -1.143 | -0.229 |
| 0.0679 | 0.1147 | 0.152 | 0.103 | 0.241 | 0.214 | 0.222 | |
| NGC 3379 | 0.1055 | -0.2279 | -0.515 | -0.419 | -0.239 | -1.069 | -0.262 |
| 0.0347 | 0.0528 | 0.066 | 0.051 | 0.072 | 0.128 | 0.098 | |
| NGC 3605 | 0.0574 | -0.3890 | -0.050 | -0.385 | -0.869 | -0.452 | 0.235 |
| 0.1046 | 0.1486 | 0.218 | 0.191 | 0.278 | 0.288 | 0.348 | |
| NGC 3608 | 0.0595 | -0.3767 | -0.906 | -0.575 | -0.145 | -0.706 | 0.104 |
| 0.1043 | 0.1180 | 0.216 | 0.209 | 0.230 | 0.306 | 0.334 | |
| NGC 3641 | 0.0067 | -0.3821 | -1.608 | -0.547 | -0.209 | -0.856 | -0.261 |
| 0.2529 | 0.2634 | 0.501 | 0.359 | 0.491 | 0.636 | 0.731 | |
| NGC 3665 | 0.0616 | -0.1746 | -0.092 | -0.383 | -0.105 | -0.086 | 0.284 |
| 0.0716 | 0.0941 | 0.166 | 0.095 | 0.163 | 0.215 | 0.285 | |
| NGC 3818 | 0.1865 | -0.3875 | -1.089 | -0.874 | -0.295 | -0.840 | -0.216 |
| 0.0728 | 0.1087 | 0.152 | 0.106 | 0.147 | 0.172 | 0.203 | |
| NGC 4261 | 0.1011 | -0.2411 | -0.538 | -0.350 | -0.171 | -0.335 | -0.119 |
| 0.0453 | 0.0597 | 0.075 | 0.068 | 0.091 | 0.132 | 0.184 | |
| NGC 4278 | 0.1895 | -0.4505 | -0.981 | -0.623 | -0.451 | -1.034 | -0.397 |
| 0.0408 | 0.0647 | 0.081 | 0.056 | 0.095 | 0.121 | 0.132 | |
| NGC 4365 | 0.1087 | -0.2385 | -0.567 | -0.459 | -0.305 | -0.586 | -0.247 |
| 0.0378 | 0.0542 | 0.069 | 0.050 | 0.077 | 0.091 | 0.121 | |
| NGC 4374 | -0.1112 | -0.0716 | -0.452 | -0.258 | -0.000 | -0.239 | 0.154 |
| 0.0421 | 0.0668 | 0.109 | 0.077 | 0.092 | 0.126 | 0.158 | |
| NGC 4415 | 0.1048 | -0.0759 | 0.074 | -0.038 | -0.071 | -0.428 | -0.581 |
| 0.0625 | 0.0658 | 0.136 | 0.080 | 0.104 | 0.243 | 0.183 | |
| NGC 4431 | 0.1725 | -0.1285 | -0.610 | -0.216 | -0.260 | -0.409 | -0.548 |
| 0.0928 | 0.1048 | 0.189 | 0.145 | 0.194 | 0.219 | 0.423 | |
| NGC 4464 | -0.1041 | -0.0150 | -0.550 | -0.206 | -0.009 | -0.374 | 0.213 |
| 0.0796 | 0.0931 | 0.169 | 0.141 | 0.141 | 0.178 | 0.226 | |
| NGC 4467 | 0.0916 | -0.5234 | -0.798 | -1.202 | -0.719 | -0.669 | -0.303 |
| 0.2661 | 0.2767 | 0.492 | 0.504 | 0.526 | 0.782 | 0.719 | |
| NGC 4472 | 0.1062 | -0.3919 | -0.543 | -0.472 | -0.220 | -0.331 | -0.506 |
| 0.0252 | 0.0460 | 0.047 | 0.035 | 0.056 | 0.072 | 0.091 | |
| NGC 4478 | 0.1997 | -0.2858 | -0.508 | -0.428 | -0.391 | -0.393 | -0.454 |
| 0.0508 | 0.0667 | 0.087 | 0.056 | 0.090 | 0.122 | 0.135 | |
| NGC 4486B | 0.4092 | -0.3663 | -1.059 | -0.891 | -0.362 | -1.184 | -0.337 |
| 0.2165 | 0.2441 | 0.260 | 0.200 | 0.483 | 0.442 | 0.576 | |
| NGC 4489 | 0.3077 | -0.4354 | -0.259 | -0.700 | -0.752 | -0.359 | -0.483 |
| 0.1042 | 0.1423 | 0.228 | 0.164 | 0.260 | 0.228 | 0.492 | |
| NGC 4552 | 0.0526 | -0.2075 | -0.782 | -0.584 | -0.158 | -0.546 | -0.091 |
| 0.0674 | 0.0939 | 0.127 | 0.076 | 0.151 | 0.144 | 0.287 | |
| NGC 4564 | 0.1010 | -0.3264 | -0.842 | -0.740 | 0.050 | -0.520 | -0.613 |
| 0.0453 | 0.0635 | 0.107 | 0.059 | 0.080 | 0.109 | 0.131 | |
| NGC 4594 | 0.0938 | -0.3880 | -1.481 | -0.929 | -0.332 | -1.162 | -0.281 |
| 0.1078 | 0.1491 | 0.272 | 0.142 | 0.335 | 0.353 | 0.496 | |
| NGC 4621 | 0.1645 | -0.4335 | -0.770 | -0.702 | -0.332 | -0.594 | -0.274 |
| 0.0461 | 0.0718 | 0.097 | 0.067 | 0.114 | 0.143 | 0.184 | |
| NGC 4636 | 0.2275 | -0.3357 | -0.493 | -0.446 | -0.335 | -0.768 | -0.215 |
| 0.0766 | 0.0981 | 0.178 | 0.120 | 0.158 | 0.182 | 0.289 | |
| NGC 4649 | 0.0305 | -0.2151 | -0.398 | -0.465 | -0.095 | -0.364 | -0.215 |
| 0.0624 | 0.0845 | 0.159 | 0.105 | 0.142 | 0.137 | 0.261 | |
| NGC 4673 | -0.1593 | -0.1049 | -0.231 | -0.540 | 0.252 | -0.580 | -0.415 |
| 0.0960 | 0.1239 | 0.176 | 0.175 | 0.213 | 0.249 | 0.339 | |
| NGC 4692 | 0.1630 | -0.3817 | -0.920 | -0.737 | -0.286 | -0.802 | -0.490 |
| 0.1103 | 0.1285 | 0.233 | 0.204 | 0.251 | 0.305 | 0.349 | |
| NGC 4697 | 0.0425 | -0.1537 | -0.706 | -0.502 | -0.131 | -0.403 | -0.113 |
| 0.0248 | 0.0423 | 0.046 | 0.040 | 0.055 | 0.071 | 0.086 | |
| NGC 4742 | 0.7591 | -0.6467 | -0.655 | -0.771 | -0.840 | -1.174 | -1.053 |
| 0.0804 | 0.0949 | 0.129 | 0.098 | 0.143 | 0.182 | 0.207 | |
| NGC 4839 | 0.2800 | -0.3535 | -0.440 | -0.460 | -0.833 | -0.898 | 0.056 |
| 0.1708 | 0.1540 | 0.278 | 0.220 | 0.488 | 0.647 | 0.693 | |
| NGC 4842A | -0.2147 | 0.0637 | -1.015 | 0.098 | -0.324 | 1.459 | 1.735 |
| 0.2617 | 0.2364 | 0.721 | 0.295 | 0.619 | 0.676 | 0.709 | |
| NGC 4864 | 0.4900 | -0.5792 | -0.479 | -0.697 | -1.175 | -0.998 | -0.692 |
| 0.1762 | 0.1618 | 0.251 | 0.244 | 0.722 | 0.812 | 0.563 | |
| NGC 4865 | 0.0672 | -0.2587 | -0.410 | -0.359 | -0.143 | -0.532 | 0.106 |
| 0.1232 | 0.1416 | 0.370 | 0.175 | 0.261 | 0.339 | 0.368 | |
| NGC 4874 | 0.5845 | -0.7181 | -0.988 | -1.078 | -0.866 | -1.955 | -1.657 |
| 0.1029 | 0.1382 | 0.225 | 0.136 | 0.265 | 0.316 | 0.411 | |
| NGC 4875 | 0.1777 | -0.3231 | -0.704 | -0.869 | -0.248 | -0.152 | -0.582 |
| 0.1390 | 0.2141 | 0.852 | 0.588 | 1.212 | 1.398 | 1.876 | |
| NGC 4889 | 0.2578 | -0.4363 | -0.793 | -0.665 | -0.534 | 0.052 | 0.136 |
| 0.0711 | 0.1120 | 0.182 | 0.109 | 0.163 | 0.237 | 0.307 | |
| NGC 4908 | 0.0131 | -0.2354 | -0.251 | -0.629 | -0.322 | -0.864 | 0.613 |
| 0.2231 | 0.2812 | 0.419 | 0.604 | 0.618 | 0.549 | 0.794 | |
| NGC 5638 | 0.0766 | -0.3273 | -0.774 | -0.515 | -0.140 | -0.614 | 0.038 |
| 0.0524 | 0.0673 | 0.097 | 0.061 | 0.103 | 0.147 | 0.187 | |
| NGC 5796 | 0.1234 | -0.2664 | -0.340 | -0.400 | -0.120 | -0.608 | -0.371 |
| 0.0744 | 0.0938 | 0.133 | 0.091 | 0.148 | 0.208 | 0.216 | |
| NGC 5812 | 0.1436 | -0.3077 | -0.795 | -0.567 | -0.355 | -0.480 | -0.434 |
| 0.0645 | 0.0881 | 0.117 | 0.079 | 0.127 | 0.172 | 0.214 | |
| NGC 5813 | 0.0150 | -0.0826 | -0.747 | -0.272 | -0.266 | -0.335 | -0.011 |
| 0.0527 | 0.0634 | 0.105 | 0.078 | 0.113 | 0.156 | 0.202 | |
| NGC 5831 | 0.0299 | -0.2412 | -0.827 | -0.608 | -0.417 | -0.553 | -0.401 |
| 0.0682 | 0.0980 | 0.127 | 0.123 | 0.142 | 0.149 | 0.230 | |
| NGC 5845 | 0.0536 | -0.2156 | -0.591 | -0.482 | -0.540 | -0.337 | -0.304 |
| 0.1005 | 0.1117 | 0.244 | 0.150 | 0.180 | 0.216 | 0.287 | |
| NGC 5846 | 0.1258 | -0.2327 | -0.432 | -0.363 | -0.786 | -0.389 | 0.369 |
| 0.0554 | 0.0764 | 0.130 | 0.096 | 0.165 | 0.161 | 0.236 | |
| NGC 5846A | 0.1829 | -0.2979 | -0.570 | -0.848 | -0.917 | -1.069 | -0.451 |
| 0.1110 | 0.1620 | 0.265 | 0.156 | 0.305 | 0.278 | 0.488 | |
| NGC 6127 | 0.2307 | -0.4596 | -0.879 | -0.667 | -0.261 | -0.500 | -0.258 |
| 0.0855 | 0.1293 | 0.240 | 0.118 | 0.179 | 0.375 | 0.344 | |
| NGC 6166 | -0.1318 | -0.0738 | -0.131 | -0.346 | -0.284 | -0.858 | -0.329 |
| 0.0920 | 0.1051 | 0.137 | 0.178 | 0.228 | 0.310 | 0.271 | |
| NGC 6411 | 0.0348 | -0.1593 | -0.477 | -0.475 | -0.255 | -0.272 | -0.166 |
| 0.0528 | 0.0745 | 0.107 | 0.098 | 0.122 | 0.154 | 0.181 | |
| NGC 6482 | 0.0031 | -0.1937 | -0.472 | -0.263 | -0.214 | -0.538 | -0.318 |
| 0.0877 | 0.0951 | 0.170 | 0.117 | 0.185 | 0.214 | 0.321 | |
| NGC 6702 | 0.3652 | -0.5531 | -0.522 | -0.666 | -0.353 | -0.433 | -0.168 |
| 0.0854 | 0.1245 | 0.204 | 0.140 | 0.150 | 0.355 | 0.343 | |
| NGC 6703 | 0.0898 | -0.2319 | -0.526 | -0.510 | -0.186 | -0.391 | 0.112 |
| 0.0423 | 0.0684 | 0.102 | 0.059 | 0.089 | 0.093 | 0.132 | |
| NGC 7052 | -0.0011 | -0.1360 | -0.215 | -0.240 | -0.018 | -0.250 | 0.309 |
| 0.0596 | 0.0763 | 0.112 | 0.105 | 0.123 | 0.153 | 0.196 | |
| NGC 7332 | -0.0207 | -0.0314 | -0.698 | -0.724 | -0.180 | -0.162 | 0.217 |
| 0.0460 | 0.0768 | 0.096 | 0.075 | 0.110 | 0.113 | 0.157 | |
| IC 767 | 0.3838 | -1.1858 | -0.625 | -1.015 | -1.211 | -0.642 | -1.250 |
| 0.1290 | 0.2090 | 0.459 | 0.579 | 1.359 | 0.619 | 0.683 | |
| IC 794 | 0.2383 | -0.5238 | -0.230 | -0.831 | -0.580 | -0.314 | 0.112 |
| 0.1220 | 0.1673 | 0.229 | 0.240 | 0.236 | 0.293 | 0.472 | |
| IC 832 | -0.1432 | 0.0902 | -0.329 | 0.191 | 0.242 | -0.073 | 0.169 |
| 0.1404 | 0.1483 | 0.291 | 0.182 | 0.330 | 0.351 | 0.710 | |
| IC 3957 | 0.2298 | -0.4788 | -0.890 | -0.940 | -0.202 | -0.082 | -2.087 |
| 0.2385 | 0.2636 | 0.769 | 0.287 | 0.507 | 1.048 | 0.612 | |
| IC 3959 | 0.0731 | -0.1642 | -1.038 | -0.077 | 0.091 | -0.545 | -0.565 |
| 0.1344 | 0.1655 | 0.214 | 0.260 | 0.349 | 0.316 | 0.510 | |
| IC 3963 | 0.3360 | -0.5703 | -0.424 | -0.864 | -0.550 | -0.765 | -1.322 |
| 0.1340 | 0.1788 | 0.300 | 0.217 | 0.387 | 0.436 | 0.595 | |
| IC 3973 | 0.4122 | -0.3849 | -0.692 | -0.435 | -0.532 | -1.091 | -0.595 |
| 0.1776 | 0.1643 | 0.374 | 0.285 | 0.483 | 0.735 | 0.820 | |
| IC 4042 | -0.1029 | -0.3628 | -0.161 | -0.794 | 0.919 | -0.275 | 0.785 |
| 0.4661 | 0.6512 | 0.374 | 0.285 | 0.483 | 0.735 | 0.820 | |
| IC 4051 | -0.0582 | -0.3693 | -0.873 | -0.759 | -0.224 | -0.365 | 0.251 |
| 0.0852 | 0.1261 | 0.165 | 0.208 | 0.184 | 0.234 | 0.411 | |
| CGCG 159-41 | 0.1629 | -0.0679 | -0.643 | 0.156 | 0.055 | -2.702 | 0.558 |
| 0.5742 | 0.6968 | 1.401 | 1.034 | 1.372 | 1.443 | 1.416 | |
| CGCG 159-43 | 0.5593 | -0.6726 | -0.902 | -0.751 | -0.480 | -1.305 | -0.820 |
| 0.1614 | 0.1936 | 0.281 | 0.355 | 0.385 | 0.386 | 0.618 | |
| CGCG 159-83 | -0.4099 | 0.0939 | -0.902 | -0.751 | -0.480 | -1.305 | -0.820 |
| 0.1310 | 0.1566 | 0.281 | 0.355 | 0.385 | 0.386 | 0.618 | |
| CGCG 159-89 | -0.0815 | -0.3979 | -0.994 | -0.743 | 0.570 | -0.048 | 0.831 |
| 0.1410 | 0.1969 | 0.229 | 0.134 | 0.351 | 0.484 | 0.513 |