A&A 457, 265-280 (2006)
DOI: 10.1051/0004-6361:20065392
P. L. Dufton1 - S. J. Smartt1 - J. K. Lee1 - R. S. I. Ryans1 - I. Hunter1 - C. J. Evans2 - A. Herrero3,4 - C. Trundle1,3 - D. J. Lennon5,3 - M. J. Irwin6 - A. Kaufer7
1 - Department of Physics and Astronomy, Queen's University Belfast, BT7 1NN, UK
2 - UK Astronomy Technology Centre, Royal Observatory, Blackford Hill,
Edinburgh EH9 3HJ, Scotland, UK
3 - Instituto de Astrofísica de Canarias, Calle Vía Làctea, 38200
La Laguna, Tenerife, Canary Islands, Spain
4 - Departamento de Astrofísica, Avda. Astrof. Francisco Sanchez s/n,
Universidad de La Laguna, 38071 La Laguna, Tenerife, Canary Islands, Spain
5 - The Isaac Newton Group of Telescopes, Apartado de Correos 321, 38700
Santa Cruz de La Palma, Canary Islands, Spain
6 - Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
7 - European Southern Observatory, Alonso de Cordova 3107, Santiago 19, Chile
Received 7 April 2006 / Accepted 21 June 2006
Abstract
An analysis is presented of VLT-FLAMES spectroscopy for three
Galactic clusters, NGC 3293, NGC 4755 and NGC 6611. Non-LTE model
atmosphere calculations have been used to estimate effective temperatures
(from either the helium spectrum or the silicon ionization equilibrium)
and gravities (from the hydrogen spectrum). Projected rotational velocities
have been deduced from the helium spectrum (for fast and moderate rotators)
or the metal line spectrum (for slow rotators). The origin of the low gravity
estimates for apparently near main sequence objects is discussed and is
related to the stellar rotational velocity. The atmospheric parameters
have been used to estimate cluster distances (which are generally in
good agreement with previous determinations)
and these have been used to estimate stellar luminosities and evolutionary
masses. The observed Hertzsprung-Russell diagrams are compared with
theoretical predictions and some discrepancies including differences in the
main sequence luminosities are discussed. Cluster ages have been deduced
and evidence for non-coeval star formation is found for all three of the
clusters. Projected rotational velocities for targets in the
older clusters, NGC 3293 and NGC 4755, have been found to be systematically
larger than those for the field, confirming recent results in other
similar age clusters. The distribution of projected
rotational velocities are consistent with a Gaussian distribution of
intrinsic rotational velocities. For the relatively unevolved targets
in the older clusters, NGC 3293 and NGC 4755, the peak of the velocity
distribution would be 250
![]() with a full-width-half-maximum of
approximately 180
with a full-width-half-maximum of
approximately 180
![]() .
For NGC 6611, the sample size is relatively
small but implies a lower mean rotational velocity. This may be
evidence for the spin-down effect due to angular momentum loss through
stellar winds, although our results are consistent with those found
for very young high mass stars. For all three
clusters we deduce present day mass functions with
.
For NGC 6611, the sample size is relatively
small but implies a lower mean rotational velocity. This may be
evidence for the spin-down effect due to angular momentum loss through
stellar winds, although our results are consistent with those found
for very young high mass stars. For all three
clusters we deduce present day mass functions with ![]() -values
in the range of -1.5 to -1.8, which are similar to other young
stellar clusters in the Milky Way.
-values
in the range of -1.5 to -1.8, which are similar to other young
stellar clusters in the Milky Way.
Key words: stars: early-type - stars: fundamental parameters - stars: rotation - Hertzsprung-Russell (HR) and C-M diagrams - stars: evolution
As part of a European Southern Observatory Large Programme, we are using the Fibre Large Array Multi-Element Spectrograph (FLAMES) at the Very Large Telescope to survey the hot stellar populations in our Galaxy and in the Magellanic Clouds. We have observed in excess of 50 O-type stars and 500 B-type stars, in a total of seven clusters. These data have been supplemented with observations of our brighter targets using the Fibre-Fed Extended Range Optical Spectrograph (FEROS) at La Silla. Evans et al. (2005, hereafter Paper I) have given an overview of the scientific goals of the project, discussed the target selection and data reduction techniques, and presented some preliminary analysis for three Galactic clusters. The scientific aims of the survey as discussed in Paper I, included understanding how rotation and metallicity influence stellar evolution and stellar winds, calibration of the wind momentum-luminosity relationship and the nature of supernova progenitors. In the case of stellar evolution, theoretical studies (see, for example, Heger & Langer 2000; Maeder & Meynet 2000) provide predictions of the surface enhancements expected for helium and nitrogen. Of particular relevance to our survey are the larger logarithmic enhancements predicted for lower metallicity regimes (Maeder & Meynet 2001). Although there are many previous detailed quantitative studies of O- and B-type stars (Crowther et al. 2002,2006; Bouret et al. 2003; Hillier et al. 2003; Evans et al. 2004; Trundle et al. 2004; Walborn et al. 2004; Dufton et al. 2005; Trundle & Lennon 2005), these have tended to concentrate on narrow lined (and hence possibly slowly rotating) stars, whilst the sample sizes have been relatively small. The current survey will sample both the main sequence and supergiant regimes and include rapidly rotating stars, thereby extending the scope of such studies.
In order to have a sample of stars in the Milky Way to compare with the
FLAMES datasets for the SMC and LMC we have obtained spectra of likely
cluster members in the three Galactic Clusters, NGC 3293, NGC 4755 and
NGC 6611. These clusters were chosen so as to have a similar age range
to their lower metallicity Magellanic Cloud counterparts. Although the
Milky Way has an abundance gradient (see, for example,
Afflerbach et al. 1997; Rolleston et al. 2000;
Gummersbach et al. 1998; Daflon & Cunha 2004) these clusters are
relatively close to the solar position and appear to have a similar
metallicity to that of the Sun from a preliminary model atmosphere analysis
of selected narrow line targets (see Hunter et al. 2006, for details).
Previous studies have discussed the HR-diagrams, star
formation timescales, initial mass funtions and rotational velocity
distributions in young Galactic clusters and have highlighted the value
of spectroscopic analysis of cluster members rather than spectral type
assignments from photometric colours (e.g. see Massey et al.
1995; Hillenbrand et al. 1993).
Additionally there has been a revival of interest in the rotational
velocity distribution of large samples of massive stars for comparison
with the predictions of theoretical evolutionary models and also to
probe initial conditions during star-formation. Strom et al.
(2005) have measured projected rotational velocities for approximately
200 B-type stars in h&![]() Per and suggest that
differences between the mean values for the cluster and field stars are due
to the star-formation process rather than being a consequence of angular
momentum evolution as they have moved from the ZAMS. Huang & Gies
(2005) have presented rotational velocities of stars in
nine Galactic open clusters with age ranges of approximately 6 to 73 Myr, and
have provided an interpretation on the basis of evolutionary arguments.
Additionally the extensive field star sample of Abt et al.
(2002) remains a benchmark study with which to
compare cluster rotational velocities. All of these studies illustrate
the importance of large stellar samples in order to ameliorate statistical
significance problems arising from the random inclination angle of the
rotational axes. The availability of the FLAMES spectrograph on an
8m telescope has allowed studies of large samples to be extended
to the Magellanic Clouds. For example,
Martayan et al. (2006)
have studied the effects of metallicity on the rotational velocities of
B-type and Be stars in the LMC and find that the LMC stars rotate
faster than Be stars at solar metallicity.
Per and suggest that
differences between the mean values for the cluster and field stars are due
to the star-formation process rather than being a consequence of angular
momentum evolution as they have moved from the ZAMS. Huang & Gies
(2005) have presented rotational velocities of stars in
nine Galactic open clusters with age ranges of approximately 6 to 73 Myr, and
have provided an interpretation on the basis of evolutionary arguments.
Additionally the extensive field star sample of Abt et al.
(2002) remains a benchmark study with which to
compare cluster rotational velocities. All of these studies illustrate
the importance of large stellar samples in order to ameliorate statistical
significance problems arising from the random inclination angle of the
rotational axes. The availability of the FLAMES spectrograph on an
8m telescope has allowed studies of large samples to be extended
to the Magellanic Clouds. For example,
Martayan et al. (2006)
have studied the effects of metallicity on the rotational velocities of
B-type and Be stars in the LMC and find that the LMC stars rotate
faster than Be stars at solar metallicity.
In this paper we analyse the early type stars in the three Galactic clusters observed with the FLAMES spectrograph. Stellar atmospheric parameters are deduced using non-LTE model atmosphere calculations and rotational velocities are estimated by comparing observed and theoretical rotationally broadened spectra. The former are discussed with particular reference to the surface gravities found for near main sequence objects; evidence is presented that relates the lower gravity estimates to large stellar rotational velocities. Our projected rotational velocities are discussed both in the context of possible systematic differences between field and cluster populations and to infer the underlying rotational velocity distributions. The estimates of the atmospheric parameters are used to deduce cluster distances leading to estimates of stellar luminosities and evolutionary masses. The former are then used to generate Hertzsprung-Russell diagrams and the agreement with theoretical predictions is discussed, while present day mass functions are estimated from the latter.
The observational data have been obtained during a European
Southern Observatory (ESO) Large Programme to study early-type stars in
our Galaxy and the Magellanic Clouds. For the former, targets were
observed in three clusters - NGC 3293, NGC 4755 and
NGC 6611 - with the Fibre Large Array Multi-Element Spectrograph
(FLAMES,
![]() ,
see Pasquini et al. 2002)
on the Very Large Telescope (VLT). The targets
were selected based on astrometry and photometry from the pre-FLAMES
observations using the wide-field imager (WFI) on the 2.2-m Max Planck
Gesellschaft (MPG)/ESO telescope, whilst the brightest stars were
observed separately with the Fibre-Fed, Extended Range Optical Spectrograph
(FEROS,
,
see Pasquini et al. 2002)
on the Very Large Telescope (VLT). The targets
were selected based on astrometry and photometry from the pre-FLAMES
observations using the wide-field imager (WFI) on the 2.2-m Max Planck
Gesellschaft (MPG)/ESO telescope, whilst the brightest stars were
observed separately with the Fibre-Fed, Extended Range Optical Spectrograph
(FEROS,
![]() ,
see Kaufer et al. 1999) on
the MPG. Further details of the target
selection criteria and data acquisition are presented in Paper I.
Using six standard high-resolution GIRAFFE settings, the FLAMES data
cover a wavelength range of 3950-4755 Å and 6380-6620 Å
with a typical signal-to-noise (S/N) ratio of 100, whilst the FEROS
spectra range from 3600 to 9200 Å with a S/N ratio >100.
Reductions were performed using both IRAF
,
see Kaufer et al. 1999) on
the MPG. Further details of the target
selection criteria and data acquisition are presented in Paper I.
Using six standard high-resolution GIRAFFE settings, the FLAMES data
cover a wavelength range of 3950-4755 Å and 6380-6620 Å
with a typical signal-to-noise (S/N) ratio of 100, whilst the FEROS
spectra range from 3600 to 9200 Å with a S/N ratio >100.
Reductions were performed using both IRAF![]() software and the FLAMES pipeline (girBLDRS, Blecha et al. 2003),
which showed excellent agreement. Details of the data reduction
procedure, spectral classification and radial velocity measurements
of the targets were presented in Paper I, which also contains
the coordinates and cross-referencing for the designations of
the targets. As an appendix we include the
finding charts for all objects we observed in these clusters (available
on-line only).
software and the FLAMES pipeline (girBLDRS, Blecha et al. 2003),
which showed excellent agreement. Details of the data reduction
procedure, spectral classification and radial velocity measurements
of the targets were presented in Paper I, which also contains
the coordinates and cross-referencing for the designations of
the targets. As an appendix we include the
finding charts for all objects we observed in these clusters (available
on-line only).
In this paper, we have only considered targets classified as earlier than B9. This cutoff was adopted as for later spectral types the neutral helium lines, which have been used as a temperature diagnostic were not normally visible. One exception is the target 4755-001 (note we have adopted the nomenclature used in Paper I), which despite a classification of B9 Ia had a measurable helium spectrum.
In this section, we discuss the methods that were used to estimate the stellar atmospheric parameters, projected rotational velocities, masses and luminosities together with the cluster distances. We also discuss some problematic stars (Sect. 3.4) and also the criteria to identify cluster membership (Sect. 3.6).
The estimation of the stellar atmospheric parameters - effective
temperature (
![]() )
and logarithmic surface gravity (log g) -
requires an iterative process and we have adopted different
approaches depending on the stellar effective temperature.
For B2-B8 stars, which make up the majority of the sample,
the strengths of the hydrogen and neutral helium lines were utilized,
while the ionization balance of Si III/IV was used for the
earlier B spectral types. In the case of the O-type stars,
the hydrogen and neutral and ionized helium line profiles provided
diagnostics for the atmospheric parameters, together with those
of the wind. The different methodologies are discussed below:
)
and logarithmic surface gravity (log g) -
requires an iterative process and we have adopted different
approaches depending on the stellar effective temperature.
For B2-B8 stars, which make up the majority of the sample,
the strengths of the hydrogen and neutral helium lines were utilized,
while the ionization balance of Si III/IV was used for the
earlier B spectral types. In the case of the O-type stars,
the hydrogen and neutral and ionized helium line profiles provided
diagnostics for the atmospheric parameters, together with those
of the wind. The different methodologies are discussed below:
As the FLAMES dataset contains a relatively large number of mid
and late B-type stars, we have utilized relatively simple methods
to estimate their atmospheric parameters. The ratio of the strengths
of the neutral helium and hydrogen lines is sensitive to effective
temperature for spectral types later than B1, whilst the strength
of the hydrogen lines can be used to estimate the surface gravity
(see for example Dufton et al. 1999). For hydrogen,
the equivalent widths of the H ![]() and H
and H ![]() lines
were measured with the continuum defined at
lines
were measured with the continuum defined at ![]() 16 Å from
the line centre. For any given star these normally agreed
to within 3% (which is consistent with our theoretical calculations)
and hence their average was adopted. For helium, while a
number of different features were available, the best observed line
which was seen in effectively all our spectra was that at 4026 Å. Moreover,
this line has been found to yield reliable effective temperature estimates
in a study of hot stars towards the Galactic centre by Dufton et al.
(1999). The equivalent widths (EWs) of this line were estimated
with the continuum normally defined at
16 Å from
the line centre. For any given star these normally agreed
to within 3% (which is consistent with our theoretical calculations)
and hence their average was adopted. For helium, while a
number of different features were available, the best observed line
which was seen in effectively all our spectra was that at 4026 Å. Moreover,
this line has been found to yield reliable effective temperature estimates
in a study of hot stars towards the Galactic centre by Dufton et al.
(1999). The equivalent widths (EWs) of this line were estimated
with the continuum normally defined at ![]() 6 Å from the line centre,
although for some of the sharper and weaker He I lines a narrower range
was adopted where this was believed to increase the reliability of
the measurements.
6 Å from the line centre,
although for some of the sharper and weaker He I lines a narrower range
was adopted where this was believed to increase the reliability of
the measurements.
Diagnostic plots (see Fig. 1) were deduced from
synthetic spectra that had been calculated using the non-LTE model
atmosphere codes TLUSTY/SYNSPEC (Hubeny 1988; Hubeny
& Lanz 1995; Hubeny et al. 1998; see also
Ryans et al. 2003). A microturbulent velocity of 5
![]() was adopted, consistent with most of our targets having
spectral types that imply that they are on and/or near the
main sequence (see, for example, Gies & Lambert 1992).
However, as discussed by Dufton et al. (1999), this choice
is not crucial for these broad hydrogen and diffuse helium lines.
Figure 1 shows the variation of the relative strength of
the neutral helium and hydrogen lines (EW(He/H)), and of the mean of the
equivalent width of the hydrogen lines (EW(H)), for the range of
effective temperatures that were available from our
grid of model atmospheres. Note that all measurements of the theoretical
equivalent widths have used the same continuum definitions as for the
observations. For estimating the gravity, the hydrogen lines
provide reliable diagnostics across the entire temperature range.
By contrast the helium line diagnostic flattens out at temperatures >20 000 K, which sets the effective upper limit for which this
method can be used.
was adopted, consistent with most of our targets having
spectral types that imply that they are on and/or near the
main sequence (see, for example, Gies & Lambert 1992).
However, as discussed by Dufton et al. (1999), this choice
is not crucial for these broad hydrogen and diffuse helium lines.
Figure 1 shows the variation of the relative strength of
the neutral helium and hydrogen lines (EW(He/H)), and of the mean of the
equivalent width of the hydrogen lines (EW(H)), for the range of
effective temperatures that were available from our
grid of model atmospheres. Note that all measurements of the theoretical
equivalent widths have used the same continuum definitions as for the
observations. For estimating the gravity, the hydrogen lines
provide reliable diagnostics across the entire temperature range.
By contrast the helium line diagnostic flattens out at temperatures >20 000 K, which sets the effective upper limit for which this
method can be used.
For each star, estimates of the atmospheric parameters were obtained by an iterative procedure, using the diagnostic plots illustrated in Fig. 1. Firstly the observed value EW(He/H) was compared to theoretical predictions for a surface gravity of log g = 4.0 dex (g in cm s-2) to give an initial estimate of the effective temperature (Fig. 1a). The observed value of log(EW(H)) was then compared with theoretical predictions to give an estimate of surface gravity (Fig. 1b). The above procedure was then repeated until convergence was found for both effective temperature and surface gravity.
| Spec. type |
|
Method |
| B0.5 V | 27 000 K | Si III/IV ionization balance (6611-012) |
| B1.0 V | 25 000 K | Si III/IV ionization balance (3293-018; 4755-015; 6611-021 and -033) |
| B1.5 V | 22 500 K | Interpolation between B1 V and B2 V |
| B2.0 V | 20 000 K | Average of the effective temperature estimate for 11 stars based on their helium spectra |
|
21 500 K | Si III/IV ionization balance (3293-003, -007 and -010) |
| B1.5 III | 20 500 K | Interpolation between B1 III and B2 III |
| B2.0 III | 19 500 K | Average of the effective temperature estimate for 2 stars based on their helium spectra |
The neutral helium spectrum is not a useful effective temperature diagnosis
for stars earlier than approximately B2 (
![]()
![]() 20 000 K,
see Fig. 1) and hence for these objects,
the silicon ionization balance was utilized instead. However, atmospheric
parameters could not be estimated for stars with large rotational velocities
where the silicon spectra was poorly observed. Therefore we
only considered narrow-lined stars and adopted their temperature estimates as
representative for other stars with the same spectral type.
20 000 K,
see Fig. 1) and hence for these objects,
the silicon ionization balance was utilized instead. However, atmospheric
parameters could not be estimated for stars with large rotational velocities
where the silicon spectra was poorly observed. Therefore we
only considered narrow-lined stars and adopted their temperature estimates as
representative for other stars with the same spectral type.
By adopting an appropriate surface gravity (4.0 dex for dwarfs and 3.0 dex
for giants) and a microturbulence (5
![]() but see Sect. 3.4
for a discussion of the microturbulence of the supergiant targets)
an initial effective temperature could be estimated using the
relative strengths of the Si III/IV lines and the TLUSTY
(Hubeny 1988; Hubeny & Lanz 1995) non-LTE model
atmosphere grids discussed in Sect. 3.1.1 (see also
Dufton et al. 2005, for details on the calculation of the
silicon spectrum). These temperature estimates
were in turn used to estimate surface gravity by the comparison of
observed and theoretical hydrogen Balmer line profiles.
The new gravity estimate was then used as the starting point in the
next iteration to estimate the effective temperature and the process
was repeated until convergence was obtained.
but see Sect. 3.4
for a discussion of the microturbulence of the supergiant targets)
an initial effective temperature could be estimated using the
relative strengths of the Si III/IV lines and the TLUSTY
(Hubeny 1988; Hubeny & Lanz 1995) non-LTE model
atmosphere grids discussed in Sect. 3.1.1 (see also
Dufton et al. 2005, for details on the calculation of the
silicon spectrum). These temperature estimates
were in turn used to estimate surface gravity by the comparison of
observed and theoretical hydrogen Balmer line profiles.
The new gravity estimate was then used as the starting point in the
next iteration to estimate the effective temperature and the process
was repeated until convergence was obtained.
Narrow-lined stars in the clusters were selected with spectral types
between B0.5 and B1.5 for both dwarfs and giants. For B0.5 V, the target
6611-012 was analyzed, whilst for B1 V, four narrow-lined stars were
available (3293-018, 4755-015, 6611-021 and 6611-033). For B1.5 V, the
spectra of all three targets (4755-011, 4755-017 and 6611-032) only show
Si III lines and the effective temperature for this spectral type
was adopted as the average of those of B1 and B2 type stars.
For B1 III, the effective temperature estimates of three stars
(3293-003, 3293-007 and 3293-010) were averaged. No narrow lined star
was present in our sample with a spectral type B1.5 III. As in
the case of dwarfs, for this spectral type, the effective temperature
was taken to be the average of those for our B1 III
and B2 III stars. In the case of the latter spectral type, the targets
3293-034 and 4755-003 were excluded from the estimation of mean effective
temperature. This was because the former has a peculiar spectrum
(see Paper I), whilst the estimate for the latter (
![]() = 24 000 K)
was beyond the high temperature limit for using the helium spectra
as a reliable diagnostic.
= 24 000 K)
was beyond the high temperature limit for using the helium spectra
as a reliable diagnostic.
These effective temperature estimates are summarized in Table 1 where they have been rounded to the nearest 500 K. They were adopted for all other stars with the same spectral classification but with individual surface gravities being deduced from the hydrogen Balmer line profiles.
The B0 and O-type stars have temperatures at the edge of, or outside, the
range of our TLUSTY grid. In addition many of these objects
show wind features in their optical spectra. For these reasons
the hottest objects in our sample have been analyzed with the unified model
atmosphere code FASTWIND as described in Puls et al. (2005).
In order to reduce convergence times, the theoretical calculations included
only the H and He or the H, He and Si model atoms (depending on the
strength of the Si lines in the spectra and their usefulness as a
![]() diagnostic). However in order to incorporate the line blanketing from
important metals not included in the rate equations an approximate treatment
was invoked (see Puls et al. for details and comparisons with a more
detailed technique used by the model atmosphere code CMFGEN).
The analysis method described below follows closely the iterative
processes outlined in Herrero et al. (2002) and
references therein.
diagnostic). However in order to incorporate the line blanketing from
important metals not included in the rate equations an approximate treatment
was invoked (see Puls et al. for details and comparisons with a more
detailed technique used by the model atmosphere code CMFGEN).
The analysis method described below follows closely the iterative
processes outlined in Herrero et al. (2002) and
references therein.
For the majority of the O-type stars the effective temperature
was determined by profile fitting of the neutral and singly ionized
helium spectra, with more emphasis given to the latter. For the
cooler objects in this subset (i.e. O9-B0), estimates were also
obtained using the silicon ionization equilibrium (Si III/ IV),
with good agreement being obtained between the two approaches.
Profile fitting to the wings of the hydrogen lines was used to determine the
surface gravity. Greater weight was given to the higher order
Balmer lines where the wind has less influence on the core of the lines. The
wind properties were described by the mass-loss rate, the ![]() -parameter
and the terminal velocity, the latter was adopted from the spectral-type -
terminal velocity scale introduced by Kudritzki & Puls (2000). The
-parameter
and the terminal velocity, the latter was adopted from the spectral-type -
terminal velocity scale introduced by Kudritzki & Puls (2000). The
![]() -parameter was initially assumed to be 0.8 and iterated along with
the mass-loss rate to obtain a good fit to the H
-parameter was initially assumed to be 0.8 and iterated along with
the mass-loss rate to obtain a good fit to the H![]() profile.
profile.
Stellar rotational velocities for the B-type stars were determined by comparing observed line profiles to theoretical counterparts that had been convolved with a rotational broadening function (see, for example, Gray 1992). Although the hydrogen lines are well observed throughout our sample, they are intrinsically broad, making it difficult to disentangle effects due to rotation from those due to the atmospheric parameters, whilst there are no metal lines that are usable across all the observed B spectral sub-types. The helium spectrum was a suitable compromise between being well observed whilst not being too intrinsically broad. In particular the He I 4026 Å line was relatively strong and thus measurable in most of the program stars. Its theoretical line shape also appeared to be well calculated when its forbidden components were taken into account. In addition, the line having been already used for the temperature estimation provided an additional consistency in the analysis.
For each program star, a theoretical spectrum was selected at a
matching, or the nearest, point in our grid of non-LTE model
atmospheres to the estimated atmospheric parameters with a
microturbulence of 5
![]() again being adopted. To allow for
any difference in line strength between the model and the observed
spectra, the ratio of their equivalent widths (which was generally
near to unity) was used to scale the model spectrum. We note
that a broader continuum range of
again being adopted. To allow for
any difference in line strength between the model and the observed
spectra, the ratio of their equivalent widths (which was generally
near to unity) was used to scale the model spectrum. We note
that a broader continuum range of ![]() 10 Å from the line
centre was adopted than that used for the estimation of the
atmospheric parameters. This was to ensure the inclusion of the wings
of the profile which were important when estimating the rotational
velocity. The scaled model spectrum was then convolved with various
projected rotational velocity values, and the best fit to
the observation, was obtained through a chi-square minimization test
(see Fig. 2 for an example).
This procedure is a simplified version of that used by
Ryans et al. (2002) to estimate the contribution of rotation and
macroturbulence in the broadening of the spectra of early-type supergiants.
Tests reported by Ryans et al. indicate that the scaling of the equivalent
widths and the values adopted for the atmospheric parameters (including the
microturbulence) are not likely to lead to significant errors for stars with
significant rotational broadening. Figure 3 shows
examples of the optimal fits obtained when estimating the
projected rotational velocity for two stars with relatively
low and high projected rotational velocities, with all the estimates
listed in Tables 7 to 9 having been
rounded to the nearest 5
10 Å from the line
centre was adopted than that used for the estimation of the
atmospheric parameters. This was to ensure the inclusion of the wings
of the profile which were important when estimating the rotational
velocity. The scaled model spectrum was then convolved with various
projected rotational velocity values, and the best fit to
the observation, was obtained through a chi-square minimization test
(see Fig. 2 for an example).
This procedure is a simplified version of that used by
Ryans et al. (2002) to estimate the contribution of rotation and
macroturbulence in the broadening of the spectra of early-type supergiants.
Tests reported by Ryans et al. indicate that the scaling of the equivalent
widths and the values adopted for the atmospheric parameters (including the
microturbulence) are not likely to lead to significant errors for stars with
significant rotational broadening. Figure 3 shows
examples of the optimal fits obtained when estimating the
projected rotational velocity for two stars with relatively
low and high projected rotational velocities, with all the estimates
listed in Tables 7 to 9 having been
rounded to the nearest 5
![]() .
.
We note that the estimates for the very narrow-lined objects may be
unreliable due to the intrinsic width of the He I diffuse lines.
Hence for all stars where
we deduced a v sin i of less than 50
![]() ,
we have undertaken a re-analysis
of the stellar spectra. In these cases the Si III line at 4552 Å in the hotter stars and the Mg II line at 4481 Å in
the cooler objects were considered. A similar methodology as for the
helium lines was adopted with the theoretical profiles again being taken
from our non-LTE grid with a microturbulent velocity of 5
,
we have undertaken a re-analysis
of the stellar spectra. In these cases the Si III line at 4552 Å in the hotter stars and the Mg II line at 4481 Å in
the cooler objects were considered. A similar methodology as for the
helium lines was adopted with the theoretical profiles again being taken
from our non-LTE grid with a microturbulent velocity of 5
![]() being adopted and the doublet splitting for the Mg II line being
explicitly included. In most cases the values obtained from the
helium and metal lines were similar but in some cases they differed by up
to 20
being adopted and the doublet splitting for the Mg II line being
explicitly included. In most cases the values obtained from the
helium and metal lines were similar but in some cases they differed by up
to 20
![]() .
For these narrow lined stars the values listed in Tables 7 to 9 are those estimated from the
metal lines.
.
For these narrow lined stars the values listed in Tables 7 to 9 are those estimated from the
metal lines.
Instrumental broadening has not been included in our analysis and
we have investigated how this might affect our estimates as follows.
Representative theoretical profiles have been convoluted with either just a
rotational broadening function or with a rotational broadening function
and a Gaussian profiles to represent instrumental broadening (with a FWHM
equivalent to the inverse of the spectral resolution). For the FLAMES data,
the profiles only become significantly different for projected rotation
velocities less than 20
![]() ,
with a correspondingly smaller value for the
higher resolution FEROS data. Such small estimates of the projected
rotational velocity have only been found
for two targets in our sample and we have not attempted
to correct these two estimates as they will be subject to additional
uncertainties due to the choice of the intrinsic profiles and in
particular the adopted microturbulence.
,
with a correspondingly smaller value for the
higher resolution FEROS data. Such small estimates of the projected
rotational velocity have only been found
for two targets in our sample and we have not attempted
to correct these two estimates as they will be subject to additional
uncertainties due to the choice of the intrinsic profiles and in
particular the adopted microturbulence.
For the O-type stars in NGC 6611, the projected rotational velocities were determined simultaneously with the atmospheric parameters (see Sect. 3.1.3) using a method similar to the B-type stars. For these stars the N III lines at 4510-4518 Å and the Mg II at 4481 Å line were considered.
![\begin{figure}
\par\includegraphics[angle=90,width=6.8cm]{5392f2.ps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg25.gif) |
Figure 2: An example of the chi-square minimization procedure used to estimate the projected rotational velocity for the star 4755-030. |
![\begin{figure}
\par\includegraphics[angle=270,width=6cm]{5392f3a.ps}\par\vspace*{2mm}
\includegraphics[angle=270,width=6cm]{5392f3b.ps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg26.gif) |
Figure 3:
Observed and rotationally broadened theoretical
helium line profiles. 4755-033 ( upper panel) and
4755-030 ( lower panel) have estimated values of v sin i of 75 and 330
|
![\begin{figure}
\par\includegraphics[angle=90,width=7.5cm]{5392f4.ps}\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg27.gif) |
Figure 4: Initial estimates of atmospheric parameters for targets in NGC 3293, deduced from the hydrogen and helium equivalent widths. |
Figure 4 shows the distribution of our initial estimates of the atmospheric parameters of stars observed in NGC 3293, deduced from the hydrogen and helium line strengths as discussed in Sect. 3.1.1. The distribution of surface gravities is surprising in that there appears to be a significant number of low gravity objects. Given the age of this cluster, it would be expected that main sequence stars would make up the most of the sample for this range of spectral types. In particular forty percent of the stars appear to have surface gravities less than 3.70 dex, which is closer to that expected for giants or supergiants than to main sequence stars. We suspect this may have arisen from the use of a restricted wavelength region when measuring the equivalent widths of the hydrogen and helium lines. Stellar rotation broadens line profiles, and when a line is normalized at a fixed continuum position, the measured EW could be different from its intrinsic value, with the discrepancy increasing with the projected rotational velocity. As we have compared such observational equivalent widths with values measured from theoretical spectra with no rotational broadening, the estimated atmospheric parameters might be incorrect.
To investigate this effect, we have constructed a grid of correction
factors for different projected rotational velocities. Theoretical
spectra have been convolved with rotational broadening functions
and then the equivalent widths of hydrogen and helium lines were
measured. These have been used to deduce atmospheric parameters from
our calibration to estimate how much they deviate from the actual model
parameters. This deviation is indicative of the effects of rotation
on our adopted methodology, and has been used to correct our initial
estimates of the atmospheric parameters. For example,
Fig. 5 illustrates the corrections for a projected
rotational velocity of v sin i = 300
![]() - theoretical spectra
taken from grid points are marked with a diamond (
- theoretical spectra
taken from grid points are marked with a diamond (![]() )
and after
convolution, they imply the set of atmospheric parameters marked with a
plus sign (+). The pairs of numbers next to the latter are the derived
atmospheric parameters, with the amount of deviation presented in
parenthesis. Correction factors were also calculated for projected
rotational velocities from 0 to 360
)
and after
convolution, they imply the set of atmospheric parameters marked with a
plus sign (+). The pairs of numbers next to the latter are the derived
atmospheric parameters, with the amount of deviation presented in
parenthesis. Correction factors were also calculated for projected
rotational velocities from 0 to 360
![]() ,
covering all the v sin i
values of our program stars. The atmospheric parameters of the
program stars were then corrected through a series of linear
interpolations between the nearest grid points in
,
covering all the v sin i
values of our program stars. The atmospheric parameters of the
program stars were then corrected through a series of linear
interpolations between the nearest grid points in
![]() ,
log g
and v sin i and these corrected values are summarized in
Tables 7-9. Tests show that
use of these corrected atmospheric parameters did not lead to any
significant changes in the values previously deduced for the
projected rotational velocities.
,
log g
and v sin i and these corrected values are summarized in
Tables 7-9. Tests show that
use of these corrected atmospheric parameters did not lead to any
significant changes in the values previously deduced for the
projected rotational velocities.
| 3293 | 4755 | 6611 | |
| Binaries | - | 24 | 7, 13, 14, 30, 68 |
| Emission | 11 | 14, 18 | 10, 22, 28 |
| Others | 72, 121 |
Some stars have been excluded from the analysis as the measurements of their hydrogen and helium equivalent widths were either not possible or unreliable. They largely fall into three categories, viz. targets later than B8, binaries or stars with very strong emission feature in their Balmer line profiles and are summarized in Table 2. This leaves 92 out of 126 stars observed in NGC 3293, with the numbers for the other clusters being 87/108 (NGC 4755) and 44/85 (NGC 6611). Some comments on individual stars are given below:
3293-001, -002 and 4755-004: the effective temperature of these supergiants were estimated utilizing the silicon ionization balance. Their microturbulence has been determined to be 20, 14 and 15 km-1, respectively, by minimizing the slope in the abundance estimates from the Si III lines versus their equivalent widths.
3293-027, -029 and -032: the spectral types of these stars remain uncertain due to their very broad line profiles, and they were classified as B0.5-1.5 in Paper I. We assume that they are B1.0 and adopt a "calibrated'' effective temperature of 23 000 K (Table 1).
3293-034: the helium spectrum implies that this B2 IIIh star has an effective temperature of 26 000 K, much higher than the limit of validity for this method and incompatible with its spectral type. We suspect that these inconsistencies arise from its spectral peculiarities.
6611-010 and -022: these Be stars have no useful effective temperature
indicators, making it
difficult to estimate their atmospheric parameters. Theoretical profiles
were fitted to H![]() line to produces loci of possible atmospheric
parameters. For representative parameter pairs, v sin i values
were estimated and their average is presented in Table 9.
line to produces loci of possible atmospheric
parameters. For representative parameter pairs, v sin i values
were estimated and their average is presented in Table 9.
In order to determine stellar luminosities, it is important that we have reliable cluster distances. Several studies have estimated these distances and some of the more recent are summarized in Table 3. We have chosen to list results from wide-field CCD and spectroscopic surveys, which supersede the older photoelectric methods based on less reliable samples.
We have also independently determined a distance to each cluster
from a spectroscopic parallax method, applied to the main-sequence
targets in our clusters. Firstly intrinsic colours (B-V)0
were calculated using standard Johnson BV filter curves and
flux calibrated TLUSTY spectra for a range of effective
temperatures and two gravities. As can be seen from
Table 5 there are relatively small differences
between the values for
![]() and 4.0 dex. Hence we
adopted the former for all stars with
and 4.0 dex. Hence we
adopted the former for all stars with
![]() dex, and the latter
for the higher gravity objects. A standard Galactic reddening law
of
dex, and the latter
for the higher gravity objects. A standard Galactic reddening law
of
![]() E(B-V) was adopted for NGC 3293 and NGC 4755
as this has been found previously to be a suitable value
(Baume et al. 2003). However there is evidence that the
reddening towards NGC 6611 is anomalous and a value of
E(B-V) was adopted for NGC 3293 and NGC 4755
as this has been found previously to be a suitable value
(Baume et al. 2003). However there is evidence that the
reddening towards NGC 6611 is anomalous and a value of
![]() E(B-V) has been found to best match the
optical and infra-red magnitudes of the cluster members when combined
with the colour excesses from stars with known spectral types
(Hillenbrand 1993).
E(B-V) has been found to best match the
optical and infra-red magnitudes of the cluster members when combined
with the colour excesses from stars with known spectral types
(Hillenbrand 1993).
| Cluster | Method | Distance | Age |
| kpc | Myr | ||
| NGC 3293 | |||
| Freyhammer et al. (2005) | Eclipsing Binary | 2.8 |
10-13 |
| Baume et al. (2003) | 2.8 |
6.5-10 | |
| Shobbrook (1983) |
|
2.5 |
- |
| This paper (33 stars) | Spectroscopic parallax | 2.9 |
10-20 |
| Mean of all results | 2.8 |
10 | |
| Mean and SD of |
0.80 |
||
| NGC 4755 | |||
| Sanner et al. (1995) | 2.1 |
8-12 | |
| Balona & Koen (1994) |
|
2.0 |
- |
| Sagar & Cannon (1995) | 2.1 |
10 | |
| This paper (39 stars) | Spectroscopic parallax | 2.3 |
10-15 |
| Mean of all results | 2.1 |
10 | |
| Mean and SD of |
1.15 |
||
| NGC 6611 | |||
| Hillenbrand et al. (1993) | Spectroscopic parallax | 2.0 |
1-3 |
| Belikov et al. (1999) | 2.1 |
- | |
| This paper (24 stars) | Spectroscopic parallax | 1.8 |
2-4 |
| Mean of all results | 2.0 |
2 | |
| Mean and SD of |
2.81 |
From the non-rotating evolutionary tracks of
Schaller et al. (1992) and Meynet et al. (1994)
we have inferred surface gravities and then by interpolating
in the log g-
![]() plane, estimated stellar luminosities.
These have been combined with bolometric corrections and the
E(B-V) values to determine spectroscopic distances for each target.
For
plane, estimated stellar luminosities.
These have been combined with bolometric corrections and the
E(B-V) values to determine spectroscopic distances for each target.
For ![]()
![]() > 4.45, the bolometric corrections
of Vacca et al. (2004) were used, while for lower effective
temperatures, those of Balona (1994) were adopted.
As discussed above, the determination of the surface gravity
in our fastest rotating targets is subject to some uncertainty.
Hence we restricted our sample of stars to those, having
> 4.45, the bolometric corrections
of Vacca et al. (2004) were used, while for lower effective
temperatures, those of Balona (1994) were adopted.
As discussed above, the determination of the surface gravity
in our fastest rotating targets is subject to some uncertainty.
Hence we restricted our sample of stars to those, having
![]() .
Effectively we are estimating
cluster distances by applying a hybrid spectroscopic and evolutionary
parallax method for stars which we are confident are lying close
to the main-sequence and have well determined surface gravities.
The distance estimates are listed in Table 3,
and are in good agreement with those found previously from
other methods. We have adopted a mean value of these estimates
for use in this paper.
.
Effectively we are estimating
cluster distances by applying a hybrid spectroscopic and evolutionary
parallax method for stars which we are confident are lying close
to the main-sequence and have well determined surface gravities.
The distance estimates are listed in Table 3,
and are in good agreement with those found previously from
other methods. We have adopted a mean value of these estimates
for use in this paper.
Using these distances, we have re-determined the luminosity of each star from their V-band magnitude, a bolometric correction (as discussed above) and their E(B-V) value. This allowed stars to be placed on a HR-diagram, and by interpolation between the Geneva evolutionary tracks led to estimates of their evolutionary masses, which are summarized in Tables 7-9.
In order to investigate whether an individual star is a cluster member we
have used two criteria. One is radial velocity (listed in
Tables 7-9 and taken directly from
Paper I) and the other is distance from the cluster centre.
In Table 4, we summarize the mean radial
velocity of the clusters (again as reported in Paper I), together with
the adopted cluster centres and radii (NGC 3293: Baume et al.
2003; NGC 4755: Lynga 1987; NGC 6611: Belikov et al.
1999). The use of radial velocities alone is not a reliable
way to determine cluster membership as stars with discrepant
(but apparently non-variable) radial velocities could be
binaries with periods significantly longer than our sampling
frequency (which for NGC 3293 and NGC 4755 is less than one night).
Hence we have only identified a star as a non-member if its
radial velocity is more than 2![]() away from that of the
mean value and
its distance from the adopted cluster centre (designated
away from that of the
mean value and
its distance from the adopted cluster centre (designated
![]() in Tables 7-9) is more than twice
the cluster radius. Such objects have been identified by a
in Tables 7-9) is more than twice
the cluster radius. Such objects have been identified by a ![]() and we note that they are only a small fraction of our total sample.
In turn this may imply that our rejection criteria may not be sufficiently
stringent but we have found that changing our criteria (e.g. to
radial distances of less than one cluster radius) had little
effect on our sample.
and we note that they are only a small fraction of our total sample.
In turn this may imply that our rejection criteria may not be sufficiently
stringent but we have found that changing our criteria (e.g. to
radial distances of less than one cluster radius) had little
effect on our sample.
| Cluster | Centre | Radius | ||
|
|
RA | Dec | ||
| NGC 3293 |
|
|
4.1 |
|
| NGC 4755 |
|
|
5.0 |
|
| NGC 6611 |
|
|
4.8 |
|
| log g=4.0 | log g=3.0 | |||||
|
|
B-V | U-V | B-V | U-V | ||
| 13 500 | -0.102 | -0.402 | -0.119 | -0.478 | ||
| 15 000 | -0.125 | -0.500 | -0.140 | -0.571 | ||
| 18 000 | -0.161 | -0.649 | -0.174 | -0.724 | ||
| 20 000 | -0.181 | -0.732 | -0.188 | -0.813 | ||
| 23 000 | -0.203 | -0.840 | -0.198 | -0.917 | ||
| 25 000 | -0.212 | -0.899 | -0.209 | -0.958 | ||
| 27 500 | -0.228 | -0.947 | -0.209 | -0.989 | ||
| 30 000 | -0.244 | -0.984 | ||||
| 35 000 | -0.258 | -1.035 | ||||
We have used a variety of methods based on non-LTE model atmosphere techniques to constrain the stellar atmospheric parameters. As discussed in Sect. 3.1.3, the use of different effective temperature criteria for the O and B0-type stars led to excellent agreement. Additionally previous analyzes of the spectra of B-type supergiants using the TLUSTY grid adopted here (Dufton et al. 2005) and the code FASTWIND (Trundle et al. 2005) have also yielded encouraging agreement. Hence we believe that in general our estimates of effective temperature should have an accuracy of typically 5% and should be generally more reliable than those based on the calibrations of broad band colours. Exceptions may occur for the small number of stars that are peculiar (see Sect. 3.4) or where we have adopted effective temperatures based on spectral types.
For our gravity estimates, the situation was complicated by the
corrections required for targets with large projected rotational
velocities (see Sect. 3.3). Whilst the corrections
for the effective temperature estimate are relative small
(typically less than 1000 K), those for the surface
gravity can be significant (see Fig. 5). To
investigate the reliability of these corrections we have considered
how the gravity estimates vary with rotational broadening. Our
procedure has been to divide our targets into two bins - those that
appear to be near to the main sequence (
![]() dex) and
those that may have evolved. For the latter, we have excluded
five supergiants (classified as Ia or Ib in Paper I), as these
targets are clearly evolved. Additionally we have excluded the O-type
stars for NGC 6611 as these were analyzed separately from the B-type
stellar sample and employed detailed fitting of the hydrogen line profiles.
In Table 6, we summarize the mean and standard deviations for
the projected rotational velocities of our two samples for each individual
cluster and for all our targets.
dex) and
those that may have evolved. For the latter, we have excluded
five supergiants (classified as Ia or Ib in Paper I), as these
targets are clearly evolved. Additionally we have excluded the O-type
stars for NGC 6611 as these were analyzed separately from the B-type
stellar sample and employed detailed fitting of the hydrogen line profiles.
In Table 6, we summarize the mean and standard deviations for
the projected rotational velocities of our two samples for each individual
cluster and for all our targets.
| Cluster | High gravity | n | Low gravity | n |
|
|
|
|||
| NGC 3293 | 47 | 41 | ||
| NGC 4755 | 47 | 38 | ||
| NGC 6611 | 22 | 6 | ||
| All targets | 116 | 85 |
For all three clusters (although the sample sizes for NGC 6611 are small), there is a systematic trend in the sense that the low gravity objects have the higher mean projected rotational velocity and this is confirmed when all the targets are considered. This result appears anomalous as if the lower gravity targets had evolved from the main sequence, their rotational velocities might have been expected to decrease due both to the increase in their moment of inertia and to the loss of angular momentum from mass loss. Rather this trend may arise from the estimation of surface gravities for rapidly rotating stars and we have identified two possible causes. Firstly, the correction procedure for the atmospheric parameters discussed in Sect. 3.3 may not have been successful. To test this hypothesis, we have used the atmospheric parameters and projected rotational velocities given in Tables 7-9 to generate theoretical hydrogen line profiles. In effectively all cases these were in good agreement with our observed line profiles and hence we believe that our correction procedure is not the main cause of this discrepancy.
A second explanation is that for stars with large rotational velocities, the effective surface gravity will vary over the stellar surface due to the centrifugal force increasing as one moves from the pole to the equator. To a first order of approximation, our methodology will measure the mean effective surface gravity, which will be smaller than that of an analagous slowly rotating object. Hence the anti-correlation between projected rotational velocity and estimated surface gravity could be a manifestation of such an effect. For example, Howarth & Smith (2001) found a variation of 0.4 dex between the effective surface gravity at the pole and the equator for three rapidly rotating O9-O9.5 type stars.
To test this hypothesis we have computed models and synthetic spectra
for a star with an B spectral type (corresponding to
![]() = 20 000;
log g = 4.0 at the stellar poles) using the methodology discussed by
Townsend (1997) which includes the effects of rotation on the pole to equator temperature
structure and on the stellar radius. The synthetic input spectra were
based on LTE atmospheres, calculated with ATLAS9 (Kurucz 2005)
and LTE line formation, which should be adequate for assessing
the effects of stellar rotation. Further details can be found in
Kaufer et al. (2006).
= 20 000;
log g = 4.0 at the stellar poles) using the methodology discussed by
Townsend (1997) which includes the effects of rotation on the pole to equator temperature
structure and on the stellar radius. The synthetic input spectra were
based on LTE atmospheres, calculated with ATLAS9 (Kurucz 2005)
and LTE line formation, which should be adequate for assessing
the effects of stellar rotation. Further details can be found in
Kaufer et al. (2006).
For models with different rotational velocities, we have measured
the equivalent widths of the features used to estimate atmospheric
parameters such as the He I line at 4026 Å and the hydrogen
Balmer lines. The results are difficult to interpret but
the effects of rotation on these spectral features appear negligible
for equatorial rotational velocities less than 250
![]() .
For faster
rotators, the equivalent width of the He I remains effectively unchanged but the strength of the hydrogen
lines decreases. However the changes are relatively small with
those for the H
.
For faster
rotators, the equivalent width of the He I remains effectively unchanged but the strength of the hydrogen
lines decreases. However the changes are relatively small with
those for the H![]() equivalent width being approximately 10-15%
for equatorial rotational velocities upto 400
equivalent width being approximately 10-15%
for equatorial rotational velocities upto 400
![]() ,
which corresponds
to 80% of the critical equatorial velocity. In turn this would
lead to a change in the estimated surface gravity of 0.2 to 0.3 dex.
,
which corresponds
to 80% of the critical equatorial velocity. In turn this would
lead to a change in the estimated surface gravity of 0.2 to 0.3 dex.
In Sect. 4.5, we estimate the mean equatorial rotational
velocity for the cluster NGC 3293 and NGC 4755 as approximately
225-250
![]() .
Assuming a Gaussian distribution of velocities, the
.
Assuming a Gaussian distribution of velocities, the
![]() width would be approximately 110
width would be approximately 110
![]() .
Hence the number
of targets with equatorial velocities greater than 250
.
Hence the number
of targets with equatorial velocities greater than 250
![]() would be 40-50%, whilst those with a rotational velocity of 400
would be 40-50%, whilst those with a rotational velocity of 400
![]() or more would be of the order of 5-10%. From the above, although
high rotational velocities may contribute to the spread of gravity
estimates found in our two older clusters, it is unclear whether
it can fully explain these variations.
or more would be of the order of 5-10%. From the above, although
high rotational velocities may contribute to the spread of gravity
estimates found in our two older clusters, it is unclear whether
it can fully explain these variations.
In summary, we believe that our effective temperature estimates are secure and find no evidence that our methodology has introduced systematic errors in our gravity determinations. Rather the significant number of relatively low gravity B-type objects may reflect in part a decrease in the effective surface gravity due to centrifugal acceleration.
For all three cluster, we have used the luminosities and effective temperatures listed in Tables 7-9 to construct Hertzsprung-Russell (HR) diagrams and these are presented in Fig. 6. We have used different symbols to distinguish between those targets with estimated logarithmic surface gravities less than and greater than 3.9 dex. These are effectively the same as the samples discussed in Sect. 4.1 but with the supergiants now being included in the former. Also shown are the evolutionary tracks and isochrones of Schaller et al. (1992) and Meynet et al. (1994), taken from the database of the Geneve group (see http://obswww.unige.ch/~mowlavi/evol/stev_database.html; also available from the Centre de Données Astronomiques de Strasbourg, http://cdsweb.u-strasbg.fr/CDS.html) for a metallicity, Z = 0.02.
In general there is a good qualitative agreement between the observed and
theoretical HR diagrams although the observed main sequences appear to be
systematically more luminous than predicted. For the late-B type stars,
where the choice of isochrone is not important, this discrepancy would
appear to be approximately, ![]() log L
log L ![]() 0.4, for the older
clusters. The discrepancy may be larger for NGC 6611 but in this case
the sample size is relatively small. This systematic difference
in luminosity would correspond to an error in our adopted distances
of approximately 60%, which although possible is significantly larger
than the range of values summarized in Table 3.
Slesnick et al. (1992) have undertaken an extensive photometric
and spectroscopic study of the double cluster h and
0.4, for the older
clusters. The discrepancy may be larger for NGC 6611 but in this case
the sample size is relatively small. This systematic difference
in luminosity would correspond to an error in our adopted distances
of approximately 60%, which although possible is significantly larger
than the range of values summarized in Table 3.
Slesnick et al. (1992) have undertaken an extensive photometric
and spectroscopic study of the double cluster h and ![]() Persei,
which is similar in age to those of NGC 3293 and NGC 4755.
Inspection of the HR diagrams (see their Figs. 6 and 7) imply good
agreement between the observed late-B type stars and the theoretical
predictions of Schaller et al. (1992). However, recently,
Strom et al. (2005) have undertaken a study of projected
stellar rotational velocities in h and
Persei,
which is similar in age to those of NGC 3293 and NGC 4755.
Inspection of the HR diagrams (see their Figs. 6 and 7) imply good
agreement between the observed late-B type stars and the theoretical
predictions of Schaller et al. (1992). However, recently,
Strom et al. (2005) have undertaken a study of projected
stellar rotational velocities in h and ![]() Persei and used the
results of Slesnick et al. For this smaller sample, there is again
evidence of a discrepancy (see Fig. 1 of Strom et al.) similar to
that found here for the later B-type spectral types.
Persei and used the
results of Slesnick et al. For this smaller sample, there is again
evidence of a discrepancy (see Fig. 1 of Strom et al.) similar to
that found here for the later B-type spectral types.
In our HR diagrams, we have distinguished between apparently low and high
gravity objects as discussed above. For our two older cluster, the effects of
stars evolving from the main sequence can be seen for our early-B type objects.
However for the later B-spectral types, there is no clear segregation of the
targets as would be expected if the lower gravity objects had evolved
from the main sequence. We have further investigated this by
refining the analysis discussed in Sect. 4.1 to
only consider targets with effective temperatures less than 20 000 K,
where evolutionary effects should be negligible. For all our targets,
the mean projected rotational velocities are
![]() and
and
![]()
![]() for the high and low gravity stars respectively. The former
is similar to that listed in Table 6 for the corresponding
sample, whilst the latter is larger due to the exclusion of hotter evolved
objects. The position of the cool lower gravity objects in the HR diagrams
and their high mean rotational velocities both support the hypothesis that
our gravity estimates are reliable (in the sense that they are measuring the
mean surface gravity) and that their range may reflect the different
contributions of the centrifugal acceleration. An important consequence of
this is that the lower effective gravity has led to many of these objects
being classified as giants (see Tables 7-9)
and hence calibrations based on spectral type of, for example, the luminosity
would led to systematic errors.
for the high and low gravity stars respectively. The former
is similar to that listed in Table 6 for the corresponding
sample, whilst the latter is larger due to the exclusion of hotter evolved
objects. The position of the cool lower gravity objects in the HR diagrams
and their high mean rotational velocities both support the hypothesis that
our gravity estimates are reliable (in the sense that they are measuring the
mean surface gravity) and that their range may reflect the different
contributions of the centrifugal acceleration. An important consequence of
this is that the lower effective gravity has led to many of these objects
being classified as giants (see Tables 7-9)
and hence calibrations based on spectral type of, for example, the luminosity
would led to systematic errors.
From the HR diagrams it was also possible to estimate cluster ages (assuming coeval star formation). For all three clusters the fitting of the isochrones was problematic as discussed below.
NGC 6611: as discussed above, the observed main sequence (which
for this young cluster is still discernible at B0 spectral type)
appears systematically brighter than predicted. There is evidence that the
extinction towards this cluster is anomalous (see, for example, Chini &
Wargau 1990, and references therein) and indeed we adopted a different
value for the ratio of the total extinction to the reddening, R (see Sect. 3.5) than for the other clusters. Hence some of the discrepancy
may arise from uncertainties in the interstellar extinction. We note that
the HR diagram of Hillenbrand et al. (1993; Fig. 8)
implies a similar discrepancy. These authors also considered isochrones for
pre-main sequence evolutionary tracks but for our targets with effective
temperature greater than 20 000 K the timescales for reaching the main
sequence would appear too small to explain this discrepancy - for example 300 000 years at an effective temperature of 20 000 K.
However Hillenbrand et al. also found evidence that some intermediate mass
stars (3-8 solar masses) could be as young as 250 000 years.
If such ages were also present amongst the more massive stars, this
would help explain the enhanced luminosity of our objects.
We find a best fit isochrone for this cluster of approximately 2 Myr, with some evidence for age spread of 1 Myr, consistent
with the results of Hillenbrand et al.
NGC 3293 and NGC 4755: given the similarity in their HR diagrams, these clusters are best considered together. As discussed above, their observed main sequences (for effective temperatures of less than 20 000 K) appear to be more luminous than predicted by evolutionary models. In these cases, this would not appear to be due to anomalous extinction. Also, given the larger cluster ages, it would appear unlikely that we are observing stars evolving to the main sequence, although Sagar & Cannon (1995) identified lower mass pre-main sequence objects with ages between 3-10 million years in NGC 4755. Inspection of their Fig. 7 implies that Sagar & Cannon also found the B-type main sequence to be overluminous compared with the isochrones of Maeder & Maynet (1991). By contrast, Fig. 7 of Baume et al. (2003) implies good agreement between the observed HR diagram of NGC 3293 and the theoretical models of Girardi et al. (2000). However this comparison is complicated by Baume et al. extending the envelope of the predicted B-type main sequence upwards by 0.75 mag corresponding to binary systems with two similar stars. Additionally the published isochrones of Girardi et al. have a minimum age larger than those quoted by Baume et al., who presumably had access to additional unpublished information further complicating any comparisons. A binary population could also help explain our discrepancy but given our use of high dispersion spectroscopy to estimate effective temperatures (compared with Baume et al. who used (B-V)0), we would expect any such contamination to be small. From the position of the main sequence turnoff, both clusters appear to have ages between 10 and 20 million years. The theoretical isochrones fit the giant population reasonably well in NGC 4755 but in NGC 3293, there are a group of stars with an implied evolutionary age greater than 20 million years. Additionally both clusters contain supergiants (the highest luminosity stars in Fig. 6), which if they have evolved as single stars appear to have evolutionary lifetimes of less than 10 million years. Indeed the lower age estimate obtained by Baume et al. may be at least partly influenced by these targets.
In summary, for all three clusters, the agreement between the observed HR diagrams and the theoretical predictions is rather disappointing. This is particularly the case as our effective temperature estimates should be more reliable than other studies that have used photometric colours. Indeed for all three clusters it would appear that there is either non-coeval star formation or the evolution of individual targets is being influenced by other factors. The former is a plausible explanation for NGC 6611 given its youth and the detection by Hillenbrand et al. (1993) of very young pre-main sequence intermediate mass objects. Although the bulk of the star formation for NGC 3293 and NGC 4755 is consistent with ages of 15 Myr, the most massive stars in the cluters have smaller evolutionary ages of approximately 5 Myr. This would imply a very extended period of star formation and hence these discrepancies may be due, at least in part, to other factors such as binarity.
The atmospheric parameters and masses determined in the previous sections allow the mass functions of the three clusters to be re-evaluated with the most extensive data and information to date. As discussed in Paper I, we are not spectroscopically "complete'' in any of the clusters, in the sense that we were not able to place fibres on all stars within a given colour-magnitude range. However in the case of NGC 3293 and NGC 4755 the reddening towards the cluster appears fairly homogeneous and hence we can estimate the effective temperatures and luminosities from the stellar BV photometry. In the case of NGC 6611, which shows a scattered colour-magnitude diagram, such a procedure would not be reliable and we have chosen to increment the Hillenbrand et al. (1993) study with our additional spectroscopy in order to improve the statistical significance of the results.
We have selected all the stars from the colour magnitude diagram
(see Paper I, Fig. 3) for which we do not have spectroscopic data
and which were in the range ![]() and
and
![]() (where (B-V)0 is the intrinsic colour estimated using the
data in Table 3). Effective temperatures were
estimated by fitting a cubic to the
(where (B-V)0 is the intrinsic colour estimated using the
data in Table 3). Effective temperatures were
estimated by fitting a cubic to the
![]() - (B-V)0
results in Table 5 (assuming that
- (B-V)0
results in Table 5 (assuming that
![]() ).
We then calculated bolmetric luminosities and masses using the
method employed in Sect. 3.5. Thirty six stars were
selected, all with masses in the range 3-10
).
We then calculated bolmetric luminosities and masses using the
method employed in Sect. 3.5. Thirty six stars were
selected, all with masses in the range 3-10 ![]() .
There is also one
confirmed red supergiant cluster member of NGC 3293 which must be
included. Feast (1958) gives an M0 Iab classification with
.
There is also one
confirmed red supergiant cluster member of NGC 3293 which must be
included. Feast (1958) gives an M0 Iab classification with
![]() and using the bolometric corrections of Elias et al.
(1985), we have estimated a mass from the Geneva
evolutionary tracks of 15
and using the bolometric corrections of Elias et al.
(1985), we have estimated a mass from the Geneva
evolutionary tracks of 15 ![]() .
.
To determine the IMF, we follow the method of Hillenbrand et al. (1993) and Massey et al. (1995), so that our results can be directly compared to those studies. Stars were divided into mass bins, whose size was chosen to give comparable numbers of objects as far as possible. The number of stars in each bin was normalised to unit logarithmic mass interval and to unit area (kpc2) and the Scalo (1986) notation was adopted. The area sampled was taken from the cluster radius (we used twice the quoted radius, to be consistent with the membership criteria applied above).
In Fig. 7 we plot the present day mass function (PDMF), which
given the relatively small age of NGC 3293 and the fact that the majority
of stars are on the main-sequence, is effectively the IMF. A linear least
squares fit was performed, with each point being weighted by ![]() ,
where N is the number of points in the bin. We find
a slope of
,
where N is the number of points in the bin. We find
a slope of
![]() over the range 2.8-40
over the range 2.8-40 ![]() .
Baume et al.
(2003) estimate
.
Baume et al.
(2003) estimate
![]() for the mass range 1.4-45
for the mass range 1.4-45 ![]() ,
but
find a steeper slope of
,
but
find a steeper slope of
![]() for the higher mass stars in the
range 8-45
for the higher mass stars in the
range 8-45 ![]() .
Our results imply that this steeper value for the high
mass objects extends down to
.
Our results imply that this steeper value for the high
mass objects extends down to ![]() 3
3 ![]() and are consistent with the
range of IMFs found by Massey et al. (1995)
for young clusters in the Northern Milky Way.
and are consistent with the
range of IMFs found by Massey et al. (1995)
for young clusters in the Northern Milky Way.
We have also estimated effective temperatures, luminosities and masses
for likely cluster members in the Hillenbrand et al. sample without
spectral types by calculating Q, and using the
![]() relation
of Massey et al. (1989). None of these targets had masses
above 7
relation
of Massey et al. (1989). None of these targets had masses
above 7 ![]() and hence it
is reasonable to assume that the combination of our spectroscopy and
that of Hillenbrand et al. is virtually complete above 7
and hence it
is reasonable to assume that the combination of our spectroscopy and
that of Hillenbrand et al. is virtually complete above 7 ![]() .
In Fig. 7 we plot the IMF for NGC 6611 and determine a
slope of
.
In Fig. 7 we plot the IMF for NGC 6611 and determine a
slope of
![]() ,
which is slightly steeper than the
value of
,
which is slightly steeper than the
value of
![]() of Hillenbrand et al., but is
consistent with a Salpeter type value and again similar to our other
clusters and those in the Massey et al. (1995)
survey.
of Hillenbrand et al., but is
consistent with a Salpeter type value and again similar to our other
clusters and those in the Massey et al. (1995)
survey.
![\begin{figure}
\par\includegraphics[angle=270,width=15cm]{5392f9.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg85.gif) |
Figure 9:
Cumulative probability function for all targets in
our two older clusters and in h and |
Inspection of Fig. 9 shows that the projected rotational
velocities are systematically higher in the NGC 3293 and
NGC 4755 clusters than in the field populations. This difference has
also been found previously in other studies
(see, for example, Bernacca & Perinotto 1974; Wolff et al.
1982; Keller 2004) and has been interpreted in several ways
including differences in the ages of the field and cluster targets.
However our results are significantly different to the detailed
work by Strom et al. Their CPFs
for the h and ![]() Persei double cluster and the field show a clear
differentiation for group (1) targets, decreasing for groups (2) and (3). Strom et al. discussed this behaviour at length and postulated
that it reflected the star formation environment rather than evolutionary
effects during the stellar lifetimes. Their conclusion that
evolutionary effects were unlikely was based on the fact that the
mean
Persei double cluster and the field show a clear
differentiation for group (1) targets, decreasing for groups (2) and (3). Strom et al. discussed this behaviour at length and postulated
that it reflected the star formation environment rather than evolutionary
effects during the stellar lifetimes. Their conclusion that
evolutionary effects were unlikely was based on the fact that the
mean ![]() of the high mass stars (group 3) was nearly a factor of two higher
than that for the lowest mass objects (group 1).
Meynet & Maeder (2000)
and Heger & Langer (2000) calculations of the rotational
velocity evolution of 12-15
of the high mass stars (group 3) was nearly a factor of two higher
than that for the lowest mass objects (group 1).
Meynet & Maeder (2000)
and Heger & Langer (2000) calculations of the rotational
velocity evolution of 12-15 ![]() stars on the main-sequence suggests a
decrease in velocity of between 25-30% within 10-15 yr. Hence
Strom et al. speculated that the differences
reflected the effects of higher accretion rates that may be characteristic
of star formation in these dense clusters. In particular they suggested
that enhanced aggregation will have three effects, viz. (1) higher initial
rotation speeds, (2) higher initial radii along the stellar birth line (when
deuterium shell burning commences), resulting in greater spin up as the star
evolves to the main sequence and (3) that the higher initial birthline
radii are especially pronounced for mid- to late-B-type stars. This
latter leads naturally to the larger differences with respect
to field stars observed for their group (1) objects in h and
stars on the main-sequence suggests a
decrease in velocity of between 25-30% within 10-15 yr. Hence
Strom et al. speculated that the differences
reflected the effects of higher accretion rates that may be characteristic
of star formation in these dense clusters. In particular they suggested
that enhanced aggregation will have three effects, viz. (1) higher initial
rotation speeds, (2) higher initial radii along the stellar birth line (when
deuterium shell burning commences), resulting in greater spin up as the star
evolves to the main sequence and (3) that the higher initial birthline
radii are especially pronounced for mid- to late-B-type stars. This
latter leads naturally to the larger differences with respect
to field stars observed for their group (1) objects in h and ![]() Persei.
Persei.
In our combined sample for NGC 3293 and NGC 4755, the rotational velocity
distribution of our group (1) objects is essentially the same as that found
by Strom et al. However our group (2) and (3) objects show similar enhanced
projected rotational velocities and in particular do not tend towards those of
the field stars. Hence contrary to the results for h and ![]() Persei, any
effect would appear to be operating throughout our stellar sample.
Huang & Gies (2005) have surveyed 496 OB stars in clusters
within the approximate age range 6-73 Myr, and also find fewer
slower rotators in the cluster stars than in the field. They also present
some evidence for the higher mass stars (late-O to early-B)
spinning slower than the lower mass late B-types, and
suggest that this can be
explained by the spin-down of massive stars through angular momentum
loss via stellar winds e.g. as modelled by
Meynet & Maeder (2000) and Heger & Langer
(2000).
Persei, any
effect would appear to be operating throughout our stellar sample.
Huang & Gies (2005) have surveyed 496 OB stars in clusters
within the approximate age range 6-73 Myr, and also find fewer
slower rotators in the cluster stars than in the field. They also present
some evidence for the higher mass stars (late-O to early-B)
spinning slower than the lower mass late B-types, and
suggest that this can be
explained by the spin-down of massive stars through angular momentum
loss via stellar winds e.g. as modelled by
Meynet & Maeder (2000) and Heger & Langer
(2000).
One possible explanation for the different projected rotational
velocity distributions for groups (2) and (3) in our combined NGC 3293 and NGC 4755 sample and that of Strom et al. (2005)
for h and ![]() Persei is that the clusters have different ages.
Hence we have used the data presented by Strom et al. to construct an
HR diagram similar to those shown in Fig. 6. Our procedure was
to use their absolute visual magnitudes and the bolometric
corrections of Balona (1994) to deduce stellar luminosities
and the HR diagram for h and
Persei is that the clusters have different ages.
Hence we have used the data presented by Strom et al. to construct an
HR diagram similar to those shown in Fig. 6. Our procedure was
to use their absolute visual magnitudes and the bolometric
corrections of Balona (1994) to deduce stellar luminosities
and the HR diagram for h and ![]() Persei is shown in Fig. 10, together with isochrones again taken from the Geneve database.
Persei is shown in Fig. 10, together with isochrones again taken from the Geneve database.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{5392f10.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg87.gif) |
Figure 10:
Hertzsprung-Russell diagrams for the h and |
The observational HR diagram for h and ![]() Persei is qualitatively
similar to those for NGC 3293 and NGC 4755. However for the former the
agreement between observed and theoretical main sequences is better for
the later B-type stars. As for our clusters, the evolved star populations
in h and
Persei is qualitatively
similar to those for NGC 3293 and NGC 4755. However for the former the
agreement between observed and theoretical main sequences is better for
the later B-type stars. As for our clusters, the evolved star populations
in h and ![]() Persei imply a range of ages with an estimate of
approximately 15 million years being reasonable, consistent with the
age of
Persei imply a range of ages with an estimate of
approximately 15 million years being reasonable, consistent with the
age of
![]() million years deduced by Slesnick et al.
(1992) from photometry and moderate resolution spectroscopy.
These estimates are similar to
our adopted ages for NGC 3293 and NGC 4755.
Strom et al. postulate that their projected
rotational velocity distributions were present when the stars were formed.
Hence given that the ages of NGC 3293 and NGC 4755 are comparable with
that of the h and
million years deduced by Slesnick et al.
(1992) from photometry and moderate resolution spectroscopy.
These estimates are similar to
our adopted ages for NGC 3293 and NGC 4755.
Strom et al. postulate that their projected
rotational velocity distributions were present when the stars were formed.
Hence given that the ages of NGC 3293 and NGC 4755 are comparable with
that of the h and ![]() Persei sample, the differences
in projected rotational velocity distributions cannot be explained by
variations in the stellar ages of the samples.
Persei sample, the differences
in projected rotational velocity distributions cannot be explained by
variations in the stellar ages of the samples.
The mean of the v sin i estimates for all the observed stars in our
younger cluster NGC 6611 is 144
![]() ,
which is lower than that for
NGC 3293 and NGC 4755. In NGC 6611 there are
,
which is lower than that for
NGC 3293 and NGC 4755. In NGC 6611 there are ![]() measurements
of 25 stars with masses less than 15
measurements
of 25 stars with masses less than 15 ![]() and 13 stars with masses
between 15-60
and 13 stars with masses
between 15-60 ![]() ,
with mean values of 192 and 116
,
with mean values of 192 and 116
![]() respectively. That for the lower mass group is in good agreement
with those for both NGC 3293 and NGC 4755, where we should be
sampling the same stellar mass range albeit at a different age.
For the massive stars, evolutionary models (Meynet & Maeder
2000; Heger & Langer 2000)
predict that initial rotational velocities of 300
respectively. That for the lower mass group is in good agreement
with those for both NGC 3293 and NGC 4755, where we should be
sampling the same stellar mass range albeit at a different age.
For the massive stars, evolutionary models (Meynet & Maeder
2000; Heger & Langer 2000)
predict that initial rotational velocities of 300
![]() are reduced
to between 60-200
are reduced
to between 60-200
![]() during the main-sequence phase due to angular
momentum loss via their winds, with the most massive luminous objects
showing the most pronounced effect. The fact that we find a lower mean
value of
during the main-sequence phase due to angular
momentum loss via their winds, with the most massive luminous objects
showing the most pronounced effect. The fact that we find a lower mean
value of ![]() for the more massive stars supports the existence
of this effect.
for the more massive stars supports the existence
of this effect.
We can test this hypothesis in a simple and illustrative way. For the 13 stars in the 15-60 ![]() range we assume that they had an initial rotational
velocity of 250
range we assume that they had an initial rotational
velocity of 250
![]() (see Sect. 4.5) and estimate the rotational
velocity for each star after 2 Myr (being our estimated age for
NGC 6611) using the mass dependent evolution of surface equatorial
velocities predicted by Meynet & Maeder (2000)
and Heger & Langer (2000). This gives a mean equatorial
velocity of 166
(see Sect. 4.5) and estimate the rotational
velocity for each star after 2 Myr (being our estimated age for
NGC 6611) using the mass dependent evolution of surface equatorial
velocities predicted by Meynet & Maeder (2000)
and Heger & Langer (2000). This gives a mean equatorial
velocity of 166
![]() ,
and hence a mean v sin i value of 125
,
and hence a mean v sin i value of 125
![]() (assuming that the spin axes are randomly distributed).
This is similar to the observed mean v sin i of 116
(assuming that the spin axes are randomly distributed).
This is similar to the observed mean v sin i of 116
![]() ,
which suggests
that an initial typical equatorial velocity of about 250
,
which suggests
that an initial typical equatorial velocity of about 250
![]() and spin
down according to the evolutionary models is consistent with that observed.
We caution that this is an illustrative and simple comparison as it assumes
a single value for the initial velocity and ignores any macroturbulent
broadening in the atmospheres of the luminous objects.
and spin
down according to the evolutionary models is consistent with that observed.
We caution that this is an illustrative and simple comparison as it assumes
a single value for the initial velocity and ignores any macroturbulent
broadening in the atmospheres of the luminous objects.
The mean v sin i of the stars with masses less than 15 ![]() in each of the
three clusters is consistently around 190
in each of the
three clusters is consistently around 190
![]() ,
which would suggest a mean
equatorial velocity of 240
,
which would suggest a mean
equatorial velocity of 240
![]() (also see Sect. 4.5). The
initial velocity of these objects is then likely to be in the range
250-300
(also see Sect. 4.5). The
initial velocity of these objects is then likely to be in the range
250-300
![]() ,
depending on the evolution of the rotational velocity
over the course of 2-15 Myr. At present this is uncertain for models
less than 12
,
depending on the evolution of the rotational velocity
over the course of 2-15 Myr. At present this is uncertain for models
less than 12 ![]() ,
as there are no detailed published models for
the evolution of the rotational velocity.
For the 12-15
,
as there are no detailed published models for
the evolution of the rotational velocity.
For the 12-15 ![]() models, the rotational velocity does
decrease during the first 1-2 Myr but then remains effectively constant
for the remainder of the main sequence lifetime. Hence it may be reasonable
to compare the lower mass NGC 6611 targets with those in NGC 3293
and NGC 4755.
models, the rotational velocity does
decrease during the first 1-2 Myr but then remains effectively constant
for the remainder of the main sequence lifetime. Hence it may be reasonable
to compare the lower mass NGC 6611 targets with those in NGC 3293
and NGC 4755.
Recently Wolff et al. (2006) have investigated the projected
rotational velocities in a sample of very young stars with masses ranging
from 0.2 to 50 ![]() .
Their principal aim was to investigate the
formation mechanism for high mass stars and in particular if it differed
from that for lower mass stars. For the full range of spectral types
they found
that the ratio of the projected rotational velocity to the equatorial
breakup velocity showed no significant variations. Assuming a random
orientation of rotational axes, this led to a median value for the
ratio of the rotational velocity to the equatorial
breakup velocity, R, of 0.14, with values for B-type stars
(8<M<25
.
Their principal aim was to investigate the
formation mechanism for high mass stars and in particular if it differed
from that for lower mass stars. For the full range of spectral types
they found
that the ratio of the projected rotational velocity to the equatorial
breakup velocity showed no significant variations. Assuming a random
orientation of rotational axes, this led to a median value for the
ratio of the rotational velocity to the equatorial
breakup velocity, R, of 0.14, with values for B-type stars
(8<M<25 ![]() )
of 0.13 and for O-type stars (25<M<90
)
of 0.13 and for O-type stars (25<M<90 ![]() )
of 0.20.
)
of 0.20.
A similar analysis can be undertaken for our samples with the small age
and presence of O-type stars making that for NGC 6611 the most
appropriate. We have again assumed a random orientation of rotational
axes and restricting our sample to stars that appear to be main sequence
with log g ![]() 3.9 and obtain a ratio, R, of 0.22 for 27 targets.
For our 7 O-type stars, the ratio is 0.16, whilst for the 20 B-type
stars the ratio is 0.28. Hence our ratio for O-type stars is in
good agreement with that of Wolff et al. but our B-type value is higher
although given our relatively small sample size this may not be
significant. For our combined B-type sample for older clusters NGC 3293 and NGC 4755, we obtain a far higher median estimate
of 0.61 for 83 targets. The reason
for this higher ratio is unclear, as our targets would not be expected
to have evolved to higher rotational velocities during the clusters'
lifetimes. However it is consistent
with the different mean velocities found for the three clusters and
discussed above.
3.9 and obtain a ratio, R, of 0.22 for 27 targets.
For our 7 O-type stars, the ratio is 0.16, whilst for the 20 B-type
stars the ratio is 0.28. Hence our ratio for O-type stars is in
good agreement with that of Wolff et al. but our B-type value is higher
although given our relatively small sample size this may not be
significant. For our combined B-type sample for older clusters NGC 3293 and NGC 4755, we obtain a far higher median estimate
of 0.61 for 83 targets. The reason
for this higher ratio is unclear, as our targets would not be expected
to have evolved to higher rotational velocities during the clusters'
lifetimes. However it is consistent
with the different mean velocities found for the three clusters and
discussed above.
In summary for our older clusters, we confirm that the cluster stars
show higher projected rotational velocities than their field star
counterparts. However we do not reproduce the results of Strom et al.
for h and ![]() Persei who found that the higher mass stars
tend to rotate significantly more slowly than the lower mass objects.
If their explanation of enhanced accretion causes
the different behaviour between the cluster and field samples, then at
least for NGC 3293 and NGC 4755 this mechanism is present for all
B-type objects. The mean equatorial velocity of the most massive stars
(15-60
Persei who found that the higher mass stars
tend to rotate significantly more slowly than the lower mass objects.
If their explanation of enhanced accretion causes
the different behaviour between the cluster and field samples, then at
least for NGC 3293 and NGC 4755 this mechanism is present for all
B-type objects. The mean equatorial velocity of the most massive stars
(15-60 ![]() )
in NGC 6611 is significantly less than the lower mass stars
in this cluster and those in NGC 4755 and NGC 3293. This could
be due to the more massive stars losing significant angular
momentum through stellar winds during the first 2 Myr of their lifetime
but is also consistent with the rotational velocities
found by Wolff et al. (2006) for very young O-type stars.
)
in NGC 6611 is significantly less than the lower mass stars
in this cluster and those in NGC 4755 and NGC 3293. This could
be due to the more massive stars losing significant angular
momentum through stellar winds during the first 2 Myr of their lifetime
but is also consistent with the rotational velocities
found by Wolff et al. (2006) for very young O-type stars.
The sample of stars for which we have reliable v sin i values is large
enough that we may be able to model the intrinsic rotational velocity
distribution by assuming that the inclination angle i is randomly
distributed in space. Following the formulation of Chandrasekhar &
Münch (1950), which is also discussed in
Brown & Verschueren (1997), we employ the integral
equation which relates the distribution, f(x), of equatorial velocities,
x, for a sample of stars to the corresponding distribution of
projected rotational velocities
![]() .
.
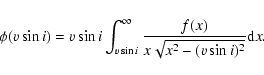 |
(1) |
In order to increase the statistical significance of the model fitting
we have combined the projected rotational velocity distributions for the
samples in NGC 4755 and NGC 3293. These two clusters are very similar
in age, mass function, metallicity and total mass as discussed
above. Hence we should have a sample of stars born in
similar conditions and of a comparable age.
This leads to a combined sample of 178 stars and the histogram of
observed
![]() along with the corresponding CPFs can
be compared with our different predictions for the projected
rotational velocity distribution. We can confidently rule out the
two analytical solutions of the
along with the corresponding CPFs can
be compared with our different predictions for the projected
rotational velocity distribution. We can confidently rule out the
two analytical solutions of the ![]() -function, or the continuous
distribution as they provide clearly inconsistent fits with the
observed histogram and CPF as illustrated in Fig. 11.
In Fig. 12, we show the
predictions for an intrinsic rotational velocity distribution, f(x),
which is a Gaussian function with a peak of 225
-function, or the continuous
distribution as they provide clearly inconsistent fits with the
observed histogram and CPF as illustrated in Fig. 11.
In Fig. 12, we show the
predictions for an intrinsic rotational velocity distribution, f(x),
which is a Gaussian function with a peak of 225
![]() and a
and a
![]() half width,
half width, ![]() ,
of 110
,
of 110
![]() (corresponding to a
full-width-half-maximum, FWHM, of approximately 180
(corresponding to a
full-width-half-maximum, FWHM, of approximately 180
![]() ).
This is the best fit obtainable using a Gaussian profile, both from a
subjective comparison and a
).
This is the best fit obtainable using a Gaussian profile, both from a
subjective comparison and a ![]() test for a grid of possible solutions.
A poorer subjective fit (with significantly higher
test for a grid of possible solutions.
A poorer subjective fit (with significantly higher ![]() )
is found when the peak of the Gaussian profile is changed by
)
is found when the peak of the Gaussian profile is changed by ![]() 25
25
![]() or the width,
or the width, ![]() ,
by
,
by ![]() 20
20
![]() .
As noted
in Sect. 4.2, there are 7 stars which have
evolutionary masses of between 7-40
.
As noted
in Sect. 4.2, there are 7 stars which have
evolutionary masses of between 7-40 ![]() ,
and which have evolved
significantly from the main-sequence. When these are removed from
the sample, we get a slightly higher value of 250
,
and which have evolved
significantly from the main-sequence. When these are removed from
the sample, we get a slightly higher value of 250
![]() for the peak of the distribution and a similar width.
Hence we believe that this is a reasonable solution for the rotational
velocity distribution of stars in the range 3-15
for the peak of the distribution and a similar width.
Hence we believe that this is a reasonable solution for the rotational
velocity distribution of stars in the range 3-15 ![]() at an age of
approximately 15 Myr in these two clusters. However with our methodology
we cannot rule other distributions of a similar nature. For
example Mokiem et al. (2006) show that a Gaussian
function would give a similar model distribution
as a rectangular function of similar width and that a very
large number of observed stars would be required to definitively distinguish
between the two input distributions. Although we
cannot distinguish between such model distributions, or indeed other
distributions of similar form, we can conclude that the underlying
distribution must be a broad function with a centre and width
similar to our best fit Gaussian.
Additionally
we were not able to exclude possible binaries from this sample.
For example Brown & Verschueren (1997) and
Huang & Gies (2005) found that early-type stars
with radial velocity variations on the whole rotated more slowly than the
likely single star sample. Our observational time sampling is not extensive
enough to determine likely binary fractions, although we should be able to
identify binaries in our LMC and SMC clusters (Evans et al. 2006).
at an age of
approximately 15 Myr in these two clusters. However with our methodology
we cannot rule other distributions of a similar nature. For
example Mokiem et al. (2006) show that a Gaussian
function would give a similar model distribution
as a rectangular function of similar width and that a very
large number of observed stars would be required to definitively distinguish
between the two input distributions. Although we
cannot distinguish between such model distributions, or indeed other
distributions of similar form, we can conclude that the underlying
distribution must be a broad function with a centre and width
similar to our best fit Gaussian.
Additionally
we were not able to exclude possible binaries from this sample.
For example Brown & Verschueren (1997) and
Huang & Gies (2005) found that early-type stars
with radial velocity variations on the whole rotated more slowly than the
likely single star sample. Our observational time sampling is not extensive
enough to determine likely binary fractions, although we should be able to
identify binaries in our LMC and SMC clusters (Evans et al. 2006).
In Fig. 12 a similar analysis is shown for NGC 6611.
Only forty four stars were included, which reduces
the significance of the fit considerably. A model with a peak of 175
![]() and
and
![]()
![]() (
(
![]()
![]() )
appears to be the best
fit for a Gaussian distribution of rotational velocities. The mean
rotational velocity is somewhat lower than that for the combined data for
the older clusters, and we note that
previous studies on the rotational velocities of O-type stars in the Galaxy
(Howarth et al. 1997; Penny 1996)
have indicated that rotational velocity distributions are peaked around 100
)
appears to be the best
fit for a Gaussian distribution of rotational velocities. The mean
rotational velocity is somewhat lower than that for the combined data for
the older clusters, and we note that
previous studies on the rotational velocities of O-type stars in the Galaxy
(Howarth et al. 1997; Penny 1996)
have indicated that rotational velocity distributions are peaked around 100
![]() .
Indeed an analogous Gaussian fit to the unevolved sample of
Penny (1996) gives a peak of 155
.
Indeed an analogous Gaussian fit to the unevolved sample of
Penny (1996) gives a peak of 155
![]() and
and
![]()
![]() .
Hence there is a suggestion that the more massive
stars (15-60
.
Hence there is a suggestion that the more massive
stars (15-60 ![]() )
in the Galaxy have typically smaller rotational
velocity distributions than their lower mass counterparts (3-15
)
in the Galaxy have typically smaller rotational
velocity distributions than their lower mass counterparts (3-15 ![]() ).
As discussed in Sect. 4.4 using a simple illustrative
example, this can qualitatively be explained by the models of massive
rotating stars losing significant angular momentum through strong
stellar winds (Meynet & Maeder 2003;
Heger & Langer 2000).
).
As discussed in Sect. 4.4 using a simple illustrative
example, this can qualitatively be explained by the models of massive
rotating stars losing significant angular momentum through strong
stellar winds (Meynet & Maeder 2003;
Heger & Langer 2000).
The rotational velocity distributions found in the previous section
suggest that we should compare our observational HR diagrams to stellar
evolutionary calculations which include rotation. In Fig. 13
we reproduce Fig. 6, but with evolutionary tracks taken from
Meynet & Maeder (2003) which have an initial
rotational velocity on the ZAMS of 300
![]() (we are grateful to Georges
Meynet for providing the lower mass tracks 3-7
(we are grateful to Georges
Meynet for providing the lower mass tracks 3-7 ![]() ;
these are unpublished
at present and are computed without core overshooting).
Meynet & Maeder point out that these models would correspond to average
equatorial rotational velocities of between 180 and 240
;
these are unpublished
at present and are computed without core overshooting).
Meynet & Maeder point out that these models would correspond to average
equatorial rotational velocities of between 180 and 240
![]() during the main sequence phase, which is well matched to
our preferred solutions for the intrinsic rotational velocity distributions.
For the higher mass stars we have truncated the tracks before they move
bluewards towards the WR phase in order to aid clarity in the figures.
The position of the ZAMS in NGC 3293 and NGC 4755 was significantly
below the stellar positions for the non-rotating models as discussed
in Sect. 4.2. The rotating models do provide
somewhat better agreement, as the ZAMS moves towards lower
effective temperature. The width
of the main-sequence phase also increases for a rotating star
which may help to explain the scattering of points
above the ZAMS. However one would still expect the ZAMS to fit through
the middle of the observed distribution rather than the lower envelope
as observed and the cause of this is still unclear. If we were to
use the rotating models to estimate the mass of the stars, we
would obtain different values to those for the non-rotating models,
but not in any simple scalable fashion. However the differences
are at most 10%, and are not likely to influence the PDMF
determinations.
during the main sequence phase, which is well matched to
our preferred solutions for the intrinsic rotational velocity distributions.
For the higher mass stars we have truncated the tracks before they move
bluewards towards the WR phase in order to aid clarity in the figures.
The position of the ZAMS in NGC 3293 and NGC 4755 was significantly
below the stellar positions for the non-rotating models as discussed
in Sect. 4.2. The rotating models do provide
somewhat better agreement, as the ZAMS moves towards lower
effective temperature. The width
of the main-sequence phase also increases for a rotating star
which may help to explain the scattering of points
above the ZAMS. However one would still expect the ZAMS to fit through
the middle of the observed distribution rather than the lower envelope
as observed and the cause of this is still unclear. If we were to
use the rotating models to estimate the mass of the stars, we
would obtain different values to those for the non-rotating models,
but not in any simple scalable fashion. However the differences
are at most 10%, and are not likely to influence the PDMF
determinations.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{5392f13a.eps}\par\vspace*{...
...}\par\vspace*{2mm}
\includegraphics[width=7.8cm,clip]{5392f13c.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg96.gif) |
Figure 13:
Hertzsprung-Russell diagrams for the three clusters together with
rotating stellar evolutionary models from the Geneva group. The symbols are
as in Fig. 6, and all the models have an initial equatorial
rotational velocity of 300
|
Acknowledgements
We thank the referee, Steven Strom, for his valuable and constructive comments on an earlier version of this paper. We are grateful the staff at both Paranal and La Silla for their invaluable assistance with the observational programme. We also thank Jonanthan Smoker and Roheid Mokiem for discussions on rotational velocities and Georges Meynet for access to some of the low mass rotating models in advance of publication. C.J.E. and J.K.L. acknowledge financial support from the UK Particle Physics and Astronomy Research Council (PPARC) under grants PPA/G/S/2001/00131 and PPA/G/O/2001/00473 and IH acknowledges financial support from the Northern Ireland Department of Education and Learning. A.H., C.T. and D.J.L. thank the Spanish Ministerio de Educación y Ciencia for support under project PNAYA 2004-08271-C02-01. S.J.S. acknowledges support from the ESF in the form of a EURYI award. This paper is based in part on observations made with the Isaac Newton and William Herschel telescopes, operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{5392fc6.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg97.gif) |
Figure A.1: VLT-FLAMES targets (open circles) and FEROS targets (open squares) in the NGC 6611 field. |
With the benefit of hindsight on the part of the authors, we now also include finding charts for the targets in the three Galactic clusters reported in Paper I. The NGC 6611 field is shown in Fig. A.1. The cores of NGC 3293 and NGC 4755 are fairly dense, so we show the central 7' of each cluster in Figs. A.2 and A.4, with the full fields shown in Figs. A.3 and A.5.
![\begin{figure}
\par\includegraphics[width=15cm,clip]{5392fc3c.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg98.gif) |
Figure A.2: VLT-FLAMES targets (open circles) and FEROS targets (open squares) in the inner 7' of the NGC 3293 field. |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{5392fc3.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg99.gif) |
Figure A.3: VLT-FLAMES targets (open circles) and FEROS targets (open squares) in the NGC 3293 field. Most of the objects observed in the inner region are shown separately in Fig. A.2. |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{5392fc4c.eps}
\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg100.gif) |
Figure A.4: VLT-FLAMES targets (open circles) and FEROS targets (open squares) in the inner 7' of the NGC 4755 field. |
![\begin{figure}
\par\includegraphics[width=16.8cm,clip]{5392fc4.eps}\end{figure}](/articles/aa/full/2006/37/aa5392-06/Timg101.gif) |
Figure A.5: VLT-FLAMES targets (open circles) and FEROS targets (open squares) in the NGC 4755 field. Most of the objects observed in the inner region are shown separately in Fig. A.4. |