A&A 454, 715 (2006)
DOI: 10.1051/0004-6361:20053557e
Erratum
Probing dark matter caustics with weak lensing![[*]](/icons/foot_motif.gif)
R. Gavazzi1,3 - R. Mohayaee2 - B. Fort2
1 - Laboratoire d'Astrophysique, UMR 5572 CNRS & Université Paul Sabatier, 14 Av. Edouard Belin, 31400 Toulouse, France
2 - Institut d'Astrophysique de Paris, UMR 7095 CNRS & Université Pierre & Marie Curie, 98bis Bd. Arago, 75014 Paris, France
3 -
Oxford University, Astrophysics,
Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
A&A, 445, 43-49 (2006), DOI:10.1051/0004-6361:20053557
Abstract
We correct two errors that were present in the former version of
this paper. First, a factor 1/3 was missing in the expression of
the smooth density profile of the dark matter halo (Eq. (1)) that
propagates into the expression of the projected smooth
density profile (Eq. (9)). Second, the numerical integration of
the caustics' density profile also misses a factor of 2, although the
equations are correct. The former error has no effect on the
analysis but the latter makes the weak lensing signal twice stronger
than previously published. Therefore, the detection of dark matter
caustics through weak lensing is made easier. Instead of a
superposition of about 200 cluster-size halos, one would require
only 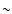 100 such systems for the caustics to show up in
ground-based observations. Similarly, space-based weak lensing data
would achieve the same detection threshold with
100 such systems for the caustics to show up in
ground-based observations. Similarly, space-based weak lensing data
would achieve the same detection threshold with 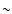 30 galaxy
clusters.
30 galaxy
clusters.
Key words: dark matter - gravitational lensing - errata, addenda
1 Online Material
In Eq. (1) of our original article a factor 1/3 was missing in the
expression of the smooth halo density profile as inferred by the
self-similar model. Equation (1) should instead read
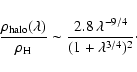 |
(1) |
This factor 1/3 is also missing in the approximation of the projected
halo density profile (Eq. (9) in the previous version). It then reads:
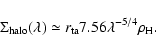 |
(2) |
Therefore the only consequences of this error for the remainder
of the paper is that the smooth black solid curves of Fig. 1
(previous version) should now look like Fig. 1 here
(both are lowered by a factor 1/3).
In addition, when we numerically integrated the density profile of
caustics in order to infer their projected counterpart, an extra
factor 2 was also missing (the leading factor 2 of Eq. (8)
lacking in the numerical integration algorithm). Although all the
remaining equations are correct, the weak lensing signal strength is
thus increased by this extra factor of 2. In this erratum note Figs. 2
and 3 account for this change. Moreover,
we took advantage of this erratum to improve the plotting quality of Fig. 3.
The increased shear signal translates into a gain in the number of
systems that need to be stacked to achieve a significant detection of
dark matter caustics. The signal-to-noise ratio is straightforwardly
changed by the same factor of 2.
Let us first consider the ideal case in which we have perfect knowledge
of the virial (or turnaround) radius of every stacked halo.
The required number of cluster-size halos is lowered to  .
If the dark matter temperature is non zero, with N=100 (resp. 250)
clusters, one could achieve a limit
.
If the dark matter temperature is non zero, with N=100 (resp. 250)
clusters, one could achieve a limit
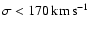 (resp.
(resp.
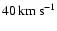 )
at a 95% confidence level. If one considers galaxies instead of cluster-size
haloes, the number of such systems to be stacked is divided by two
in the same way. For space-based weak lensing observations,
the factor of
)
at a 95% confidence level. If one considers galaxies instead of cluster-size
haloes, the number of such systems to be stacked is divided by two
in the same way. For space-based weak lensing observations,
the factor of 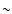 3 gain in sensitivity is conserved.
If we now turn back to the realistic situation in which the virial
radius of individual clusters is known with a
3 gain in sensitivity is conserved.
If we now turn back to the realistic situation in which the virial
radius of individual clusters is known with a
 accuracy,
the results are also changed in the same way. One now needs only
accuracy,
the results are also changed in the same way. One now needs only 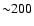 stacked clusters to be observed both in weak lensing and X-ray.
stacked clusters to be observed both in weak lensing and X-ray.
To conclude, the main changes due to the errors present in the previous
version make the possibility of detecting dark matter caustics even
less challenging.
![\begin{figure}
\includegraphics[width=7.8cm,clip]{3557efig1.eps}\hspace*{3mm}
\includegraphics[width=7.8cm,clip]{3557efig2.eps}
\end{figure}](/articles/aa/full/2006/30/aa3557-05e/Timg18.gif) |
Figure 1:
Left panel: tridimensional density profile
for the halo (black), for the caustics in a perfectly cold medium (red)
and for the caustics smoothed out by a warm/hot dark matter with
velocity dispersion
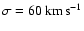 (green). Densities are expressed
in units of the background density
(green). Densities are expressed
in units of the background density
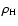 .
Red spikes are all singular with infinite density and
limited here to finite values because of finite resolution.
Right panel: the same colour-coding for the projected 2D
density profiles in units of .
Red spikes are all singular with infinite density and
limited here to finite values because of finite resolution.
Right panel: the same colour-coding for the projected 2D
density profiles in units of
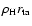 .
When projected,
caustic peaks are smoother and look like a flight of stairs.
Therefore, we expect low lensing magnifications close to
the caustics. .
When projected,
caustic peaks are smoother and look like a flight of stairs.
Therefore, we expect low lensing magnifications close to
the caustics. |
![\begin{figure}
\includegraphics[width=7.6cm,clip]{3557efig3.eps}
\end{figure}](/articles/aa/full/2006/30/aa3557-05e/Timg19.gif) |
Figure 2:
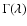 contribution of caustics for two
values of
contribution of caustics for two
values of 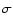 :
cold medium :
cold medium 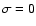 (black curve) and warm medium
(black curve) and warm medium
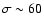 kms-1 (red curve). The green (resp. blue) ``binned''
curve is the noise level for one (resp. 100 stacked) halo(s). kms-1 (red curve). The green (resp. blue) ``binned''
curve is the noise level for one (resp. 100 stacked) halo(s). |
![\begin{figure}
\includegraphics[width=7.6cm,clip]{3557efig4.eps}
\end{figure}](/articles/aa/full/2006/30/aa3557-05e/Timg21.gif) |
Figure 3:
Difference between the
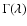 contribution
of cold caustics and the smooth component. We illustrate the blurring
effect of an imperfect knowledge of the turnaround radius of stacked
halos. The solid black line, dashed green line, and dot-dashed
blue line correspond to zero, 3%, and 10% uncertainties, respectively.
As in Fig. 2, the binned curve represents
the noise level achieved with 200 stacked halos. The convolution effect
of error in the assumed/measured value of
contribution
of cold caustics and the smooth component. We illustrate the blurring
effect of an imperfect knowledge of the turnaround radius of stacked
halos. The solid black line, dashed green line, and dot-dashed
blue line correspond to zero, 3%, and 10% uncertainties, respectively.
As in Fig. 2, the binned curve represents
the noise level achieved with 200 stacked halos. The convolution effect
of error in the assumed/measured value of
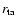 is important and a
significant detection of caustics requires well-determined turnaround
radii (
is important and a
significant detection of caustics requires well-determined turnaround
radii (
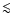 a few percents relative accuracy). The very small-scale
wiggles in the plot are numerical artifacts and ideally the only
sawtooth patterns are those due to caustics. a few percents relative accuracy). The very small-scale
wiggles in the plot are numerical artifacts and ideally the only
sawtooth patterns are those due to caustics. |
Copyright ESO 2006
![]() 100 such systems for the caustics to show up in
ground-based observations. Similarly, space-based weak lensing data
would achieve the same detection threshold with
100 such systems for the caustics to show up in
ground-based observations. Similarly, space-based weak lensing data
would achieve the same detection threshold with ![]() 30 galaxy
clusters.
30 galaxy
clusters.
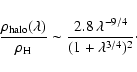
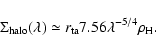
![]() .
If the dark matter temperature is non zero, with N=100 (resp. 250)
clusters, one could achieve a limit
.
If the dark matter temperature is non zero, with N=100 (resp. 250)
clusters, one could achieve a limit
![]() (resp.
(resp.
![]() )
at a 95% confidence level. If one considers galaxies instead of cluster-size
haloes, the number of such systems to be stacked is divided by two
in the same way. For space-based weak lensing observations,
the factor of
)
at a 95% confidence level. If one considers galaxies instead of cluster-size
haloes, the number of such systems to be stacked is divided by two
in the same way. For space-based weak lensing observations,
the factor of ![]() 3 gain in sensitivity is conserved.
If we now turn back to the realistic situation in which the virial
radius of individual clusters is known with a
3 gain in sensitivity is conserved.
If we now turn back to the realistic situation in which the virial
radius of individual clusters is known with a
![]() accuracy,
the results are also changed in the same way. One now needs only
accuracy,
the results are also changed in the same way. One now needs only ![]() stacked clusters to be observed both in weak lensing and X-ray.
stacked clusters to be observed both in weak lensing and X-ray.
![\begin{figure}
\includegraphics[width=7.6cm,clip]{3557efig4.eps}
\end{figure}](/articles/aa/full/2006/30/aa3557-05e/Timg21.gif)