Contents

• On the incidence rate of first overtone Blazhko stars in the Large Magellanic Cloud
• 1 Introduction
• 2 Data and method of analysis
• 3 Spectrum Averaging Method (SAM)
• 4 The phenomenological definition of the BL stars - Separation of the BL and PC variables
• 5 New detections by using SAM
• 6 Conclusions
• References
• 7 Online Material

A&A 454, 257-264 (2006)
DOI: 10.1051/0004-6361:20054538

On the incidence rate of first overtone Blazhko stars in the Large Magellanic Cloud

A. Nagy - G. Kovács

Konkoly Observatory, PO Box 67, 1525 Budapest, Hungary

Received 17 November 2005 / Accepted 29 January 2006

Abstract
Aims. By using the full span of multicolor data on a representative sample of first overtone RR Lyrae stars in the Large Magellanic Cloud (LMC), we revisit the problem of the incidence rate of the amplitude/phase-modulated (Blazhko) stars.
Methods. Multicolor data, obtained by the MAssive Compact Halo Objects (MACHO) project, are utilized through a periodogram averaging method.
Results. The method of analysis enabled us to increase the number of detected multiperiodic variables by 18%, relative to the number obtained by the analysis of the best single color data. We also test the maximum modulation period detectable in the present dataset. We find that variables showing amplitude/phase modulations with periods close to the total time span can still be clearly separated from the class of stars showing period changes. This larger limit on the modulation period, the more efficient data analysis and the longer time span lead to a substantial increase in the incidence rate of the Blazhko stars in comparison to earlier results. We find altogether 99 first overtone Blazhko stars in the full sample of 1332 stars, implying an incidence rate of 7.5%. Although this rate is nearly twice the one derived earlier, it is still significantly lower than that of the fundamental mode stars in the LMC. The by-products of the analysis (e.g. star-by-star comments, distribution functions of various quantities, etc.) are also presented.

Key words: stars: variables: RR Lyrae - stars: fundamental parameters - galaxies: Magellanic Clouds

1 Introduction

Current analyses of the databases of the microlensing projects MACHO and Optical Gravitational Lensing Experiment (OGLE) have led to a substantial increase in our knowledge of the frequency of the amplitude/phase-modulated RR Lyrae (Blazhko [BL]) stars. Moskalik & Poretti (2003) analyzed the OGLE-I data on 215 RR Lyrae stars in the Galactic Bulge. They found incidence rates for the fundamental (RR0) and first overtone (RR1) Blazhko stars of 23% and 5%, respectively. A similar analysis by Mizerski (2003) on a much larger dataset from the OGLE-II database yielded 20% and 7%, respectively. These rates, at least for the RR0 stars, are very similar to the ones suggested some time ago by Szeidl (1988) from the various past analyses of rather limited data on Galactic field and globular cluster stars. One gets smaller rates by analyzing the RR Lyrae stars in the Magellanic Clouds. Based on the OGLE-II observations of a sample of 514 stars in the Small Magellanic Cloud (SMC), in a preliminary study, Soszynski et al. (2002) obtained the same rate of 10% both for the RR0 and RR1 stars. In a similar study, on a very large sample containing 7110 RR Lyrae stars in the LMC, Soszynski et al. (2003) derived 15% and 6% for the RR0 and RR1 stars, respectively. In earlier studies on the same galaxy, based on the observations of the MACHO project, Alcock et al. (2000, 2003, hereafter A00 and A03, respectively) derived rates of 12% and 4% for the above two classes of variables. One may attempt to relate these incidence rates to the metallicities of the various populations (e.g. Moskalik & Poretti 2003), but the relation (if it exists) is certainly not a simple one (Kovács 2005; Smolec 2005).

Except for the SMC, all investigations indicate much lower incidence rates for RR1-BL stars than for RR0-BL ones. It is believed that the cause of this difference is internal, i.e. due to real, physical difference, and cannot be fully accounted for by the potentially smaller modulation amplitudes of the RR1 stars. Since this observation may have important consequences on any future modeling of the BL phenomenon, we decided to re-analyze the MACHO database and utilize all available observations (i.e. full time span two-color data). In Sect. 2, we summarize the basic parameters of the datasets and some details of the analysis. Section 3 describes our method for frequency spectrum averaging. The important question of the longest detectable BL period from the present dataset and the concomitant problem of variable classification are dealt with in Sect. 4. Analysis of the RR1 stars with their resulting classifications are presented in Sect. 5. Finally, in Sect. 6, we summarize our main results with a brief discussion of the current state of the field.

2 Data and method of analysis

For comparative purposes, in the first part of our analysis, we use the same dataset as the one employed by A00. Our final results are based on the full dataset spanning $\sim$7.5 years. Basic properties of these two sets are listed in Table 1. Both sets contain the same 1354 stars and cover the fields #2, 3, 5, 6, 9, 10, 11, 12, 13, 14, 15, 18, 19, 47, 80, 81, and 82, essentially sampling the LMC bar region. Because the selection of the stars was made earlier on simple, preliminary criteria such as period and color, some variables, other than first overtone RR Lyrae stars, were also included. Fortunately, the number of these other variables is only 22, which is small, relative to the full sample.

   

Table 1: Properties of the LMC RR1 datasets analyzed in this paper.

Set	$\langle T_{\rm tot} \rangle$	$\langle N_{\rm d} \rangle$	Colors
#1	6.5	700	"r'', "b''
#2	7.5	900	"r'', "b''

Note: $\langle T_{\rm tot} \rangle =$ average total time span [yr]; $\langle N_{\rm d} \rangle =$ average number of datapoints per variable. Colors: MACHO instrumental magnitudes, see Alcock et al. (1999).

We employed a standard Discrete Fourier Transformation method by following the implementation of Kurtz (1985). All analyses were performed in the [0,6] d^-1 band with 150 000 frequency steps, ensuring an ample sampling of the spectrum line profiles, even for the longest time series. The search for the secondary frequencies was conducted through successive prewhitenings in the time domain. The first step consisted of the subtraction of the main pulsation component together with its harmonics up to order three. In all cases, the frequency of the given component was made more accurate by a direct least squares minimization. When the two colors were used simultaneously, we allowed different amplitudes and phases for each and minimized the harmonic mean of the standard deviations of the respective residuals. Although somewhat arbitrarily, we considered the harmonic mean as a useful function for taking into account differences in the data quality.

For the characterization of the signal-to-noise ratio (SNR) of the frequency spectra, we use the following expression

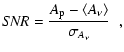$${\it SNR} = {A_{\rm p}-\langle A_{\nu}\rangle\over \sigma_{A_{\nu}}} \hskip 2mm ,$$ (1)

where $A_{\rm p}$ is the amplitude at the highest peak in the spectrum, $\langle A_{\nu}\rangle$ is the average of the spectrum, and  $\sigma_{A_{\nu}}$ is its standard deviation, computed by an iterative $4\sigma$ clipping.

3 Spectrum Averaging Method (SAM)

Unlike OGLE, where measurements are taken mostly in the $I_{\rm c}$ band (e.g. Udalski et al. 1997), the MACHO database has a roughly equal number of measurements in two different colors for the overwhelming majority of the objects (e.g. Alcock et al. 1999). This property of the MACHO database enables us to devise a method that uses both colors to increase the signal detection probability.

It is clear that simple averaging of the time series of the different color bands cannot work because: (i) the two time series are systematically different due to the difference in colors, and (ii) sampling may be different due to the hardware used, the weather, or other reasons. Therefore, we resorted to a spectrum averaging method that uses the frequency spectra of the two time series rather than their directly measured values. Obviously, SAM is also affected by the time series properties mentioned above. However, this effect is a weaker because: (i) we are interested in the positions of the peaks in the spectra and these are the same, regardless of the colors used, and (ii) spectral windows are similar, unless the samplings of the two time series are drastically different. As an example of the fulfilment of this latter condition for the MACHO data, in Fig. 1, we show the spectral windows of the two colors in one representative case.

Figure 1: Example of the similarity of the spectral windows of the MACHO instrumental "r'' and "b'' time series. Close-ups of the main peaks are displayed in the insets. The MACHO identification number of the star analyzed is shown in the upper left corner of the figure.

To optimize noise suppressing, we compute the summed spectrum by weighting the individual spectra by the inverse of their variances

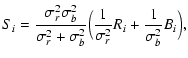$$S_i={\sigma_{r}^2\sigma_{b}^2 \over \sigma_{r}^2+\sigma_{b}^2} \Bigl({1\over \sigma_{r}^2}R_i+{1\over \sigma_{b}^2}B_i\Bigr),$$ (2)

where R_i and B_i are the amplitude spectra of the "r'' and "b'' data and where $\sigma_{r}$ and $\sigma_{b}$ are the standard deviations of the spectra.

Before we discuss the signal detection capability of SAM, it is necessary to give significance levels for periodic signal detection when using the present dataset. Perhaps the simplest way of doing this is to perform a large number of numerical simulations and derive an empirical distribution function of SNR. To achieve this goal, we generated pure Gaussian noise on the observed time base of ten randomly selected stars. For each object, we generated 1000 different realizations and computed the frequency spectra in our standard frequency band of [0,6] d^-1. The empirical distribution function was derived from the 10 000 SNR values computed on these spectra. Figure 2 shows the resulting functions for the single color and SAM spectra. For further reference, the 1% significance levels are at 6.9 and 6.5 for the single color and SAM spectra, respectively. All signals that have lower SNR values than these are considered to be not detected in the given time series. The lower cutoff for the SAM spectra is the result of the averaging of independent spectra, which also results in a greater number of independent points in the SAM spectra and concomitantly, in a slightly different shape of the distribution functions (see also Kovács et al. 2002).

Figure 2: Probability distribution functions of SNRs of the amplitude spectra of pure Gaussian noise. The time series used in the computation of the spectra were generated on the time base of the "r'' data (dotted line), "b'' data (dashed line). The result obtained by SAM is shown by solid line.

We note the following points concerning the signal detection efficiency of SAM. We expect no improvement by applying SAM  at very low SNR because the optimally achievable noise suppression is insufficient for the signal to emerge from the noise. In the other extreme, when the signal is strong, the improvement is expected to be minimal, and secure detection is possible without employing SAM. To verify this scenario, we conducted tests with artificial data. The result of one of these tests is shown in Fig. 3. The test data were generated on the 7.5 year time base given by the variable 10.3434.936. The signal consisted of a simple sinusoidal with a period of 0.278 d and amplitude A, where A was chosen to be the same in both colors and changed in 100 steps between 0.01 and 0.3 to scan different SNR values. At each value of the amplitude, we added Gaussian noise of $\sigma=0.11$ to the signal. This procedure was repeated for 100 different realizations. For each color and amplitude we computed the average and the standard deviation of the SNR values obtained from these 100 realizations. To characterize the gain in SNR by employing SAM, we also computed the ratio of the SNR values ( $R_{\rm SNR}$) as derived from the single color data and by the application of SAM.

Figure 3: Top panel: variation of the ensemble average of $R_{\rm SNR}={\it SNR}_{\rm SAM}/{\it SNR}_{\rm color}$ as a function of the test amplitude. Open circles refer to the "r'' data, crosses to the "b'' data. Middle panel: close-up of the low/mid-SNR region of the top diagram. Error bars show the $1\sigma$ ranges of the values obtained by the various noise realizations. Bottom panel: ensemble average of SNR. The dots are for the SAM values. Short- and long-dashed lines show the 1% noise probability levels at ${\it SNR}=6.9$ and ${\it SNR}=6.5$, corresponding to the single-color and SAM  spectra, respectively.

We see from Fig. 3 that there is a region where the signal has an amplitude that is too low to be detected in the single color data, but that is not low enough to remain hidden in the SAM spectra. This is the most interesting amplitude/noise regime, the one in which the application of SAM results in new discoveries. At higher amplitudes, SAM "only'' leads to an increase in SNR. It is seen that the maximum increase in SNR is at around $\sqrt 2$, as is to be expected from elementary considerations.

To show non-test examples for the signal detection efficiency of SAM, we exhibit the method at work for the observed data of two variables in Figs. 4 and 5. In both cases, the single color data are insufficient for detection, but the combined spectra clearly show the presence of the signal.

Figure 4: Example of the signal detection efficiency of SAM at low SNR levels, when the single color data do not show the presence of the signal. The top and middle panels show the frequency spectra for the "r'' and "b'' data, whereas the bottom one exhibits the SAM result. The MACHO star identification number is shown above the panels, whereas the SNR values are given in the corresponding panels. All spectra are displayed in the same (arbitrary) scale.

Figure 5: Example of the signal detection efficiency of SAM for the case when the signal is at the verge of detection in the single color data and SAM increases the reliability of the detection. Notation is the same as in Fig. 4.

By analyzing all the 1354 variables of Set #1 we can count the number of cases for which significant components are found after the first prewhitening. The result of this exercise is shown in Table 2. We see that there is strong support of the obvious assumption that the application of two-color data significantly increases the detection probability of faint signals. The gain is 18%, relative to the best single color detection rate.

4 The phenomenological definition of the BL stars - Separation of the BL and PC variables

The current loose definition of the BL stars relies purely on the type of the frequency spectra of their light or radial velocity variations. Usually those RR Lyrae stars that exhibit closely spaced peaks in their frequency spectra are called BL variables. Although most of the variables classified as type BL contain only one or two symmetrically spaced peaks at the main pulsation component, complications arise when, after additional prewhitenings, significant components remain, or, when the prewhitening is ambiguous, due to the closeness of the secondary components. There are two basic cases of complication: (i) the remnant components are not well-separated and few successive prewhitenings do not lead to a complete elimination of the secondary components, and (ii) there are several well-defined additional peaks, whose patterns are different from the ones usually associated with the BL phenomenon (single-sided for BL1 and symmetrically spaced for BL2 patterns).

Case (i) can be considered as a consequence of some non-stationarity in the data, leading to a nearly continuous spectral representation, whereas case (ii) can be related to some modulation of a more complicated type than that of the BL phenomenon. To make the phenomenological classification of variable types as clear as possible, we adopt the following definitions, which will be supported by the test presented below:

PC

(period changing stars): close components (i.e. the ones that are close to the main pulsation frequency) cannot be eliminated within three prewhitenening cycles, or, if they can, their separation from the main pulsation component is less than $\sim$1/T, where T is the total time span. Furthermore, except for possible harmonics, there are no other significant components in the spectra.

BL

(Blazhko stars): there is either one close component, or there are two, spaced symmetrically on both sides of the main pulsation frequency. After the second or third prewhitening, except for possible harmonics, no significant pattern remains or the pattern is of type PC.

MC

(stars with closely spaced multiple frequency components): all close components are well-separated (i.e. frequency distances are greater than $\sim$1/T) and, except if there are only two secondary components on one side of the main pulsation frequency, more than three prewhitenings are necessary to eliminate all of them.

We note that the possible appearance of instrumental effects (i.e. peaks at integer d^-1 frequencies) is disregarded in the above classification. Class MC is equivalent to class $\nu$M used in A00 and A03. Here, the new notation is merely aimed at simplifying the old one. Furthermore, in the previous works, variables with "dominantly'' BL2 structures were included in class BL2. Now the above scheme puts them among the MC stars.

Based on the following test, we note that for frequency separations of less than $\sim$1.5/T, distinction among the above types becomes more ambiguous because in the simple prewhitening technique followed in this paper, the result depends on the phase of the modulation.

To substantiate the above definitions, we examine in more detail how we can distinguish between the PC and BL phenomena, based solely on the properties of the prewhitened spectra.

We use the time distribution of arbitrarily selected stars to generate artificial time series with the modulated signal parameters given in Table 3. We see that the chosen types of modulation cover nearly all basic cases in the lowest order approximation (i.e. a single main pulsation component with frequency $\omega_0$, a linear period change, etc.). No noise is added because we are interested in the differences caused by the various non-stationary components in the residual spectrum, after it was prewhitened by the pulsation component. Nevertheless, noise plays an important role at low modulation levels, but a more detailed study of the complicated problem of non-stationary signal classification in the presence of noise is out of the scope of the present work.

   

Table 2: Number of single- and multi-periodic variables in Set #1 of Table 1.

Color	r	b	SAM
N1	978	895	813
N2	376	459	541
N2/(N1+N2)	27.8%	33.9%	40.0%

Note: N₁= number of single-periodic variables; N₂= number of multi-periodic variables.

   

Table 3: Definition of the signals used in the BL/PC variability test.

Type	Time dependence
AM	$A(t) = A\sin~(\Omega t + \Phi)$; $\omega(t)$, $\varphi(t)=$ const.
PM	$\varphi(t) = A_{\varphi}\sin~(\Omega t + \Psi)$; $\omega(t)$, A(t)= const.
FM	$\omega(t) = \omega_0+A_{\omega}\sin~(\Omega t + \Gamma)$; A(t), $\varphi(t)=$ const.
PC	$\omega(t) = \omega_0/(1+\beta t/P_0)$; A(t), $\varphi(t)=$ const.

Note: signal form: $x(t)=(1+A(t))\sin~(\omega(t)t+\varphi(t))$; $\omega_0=2\pi/P_0$; P₀=0.377; $\Omega=2\pi/P_{\rm BL}$; $P_{\rm BL} =$ BL period; AM = amplitude modulation; PM = phase modulation; FM = frequency modulation; PC = secular frequency change; and $\Phi$, $\Psi$, and $\Gamma$ are arbitrary constant phases.

 

 

Table 4: Final classification of the 1354 pre-selected variables.

Classification	Short description	Number	Inc. rate in RR1
RR1-S	Single-periodic overtone RR Lyrae	712	53.5%
RR1-BL1	RR1 with one close component	46	3.5%
RR1-BL2	RR1 with symmetric frequencies	53	4.0%
RR1-MC	RR1 with more close components	13	1.0%
RR1-PC	RR1 with period change	187	14.0%
RR1-D	RR1 with frequencies at integer d-1	137	10.3%
RR1-MI	RR1 with some miscellany	13	1.0%
RR01	FU/FO double-mode RR Lyrae	165	12.4%
RR01-BL1		1	0.1%
RR01-PC		5	0.4%
RR0-S	Fundamental mode RR Lyrae	1	-
RR0-BL1		1	-
RR0-BL2		1	-
MDM	Mysterious double-mode	3	-
BI	Eclipsing binary	16	-

The same pulsation period of 0.377 d is used for ten randomly selected stars. For each star, we scan the modulation frequency $\Omega$ and the rate of period change $\beta$ at fixed values of all the other parameters. Amplitudes are adjusted to get modulation levels that are 20% of the peak of the main pulsation component in the frequency spectra. Parameter $\beta$ is changed in the range of ( $1{-}12)\times 10^{-8}$, yielding modulation levels between 20% and 50%. Each scan is repeated with ten randomly selected phase values. By using the same code for the analysis of these artificial signals as the one employed for the observed data, we get the result shown in Fig. 6. To characterize the efficiency of the prewhitening, we use the ratio A₃/A₁, where A₁ and A₃ denote the peak amplitudes after the first and third prewhitenings, respectively. Although in practice we use the SNR of the frequency spectra to select significant components, here the direct comparison of the amplitudes is more meaningful because for noiseless signals SNR can be high even if the peak amplitude itself is small.

Figure 6: Testing of the various modulated signals given in Table 3. The ratio of the peak amplitudes after the first and third prewhitenings are plotted as a function of the measured frequency distance (in [d-1]) from the main pulsation component. The dashed vertical line shows the position of the 1/T frequency, where T denotes the total time span. Dots of different shades/colors indicate the various modulation types: yellow/light gray, green/gray, red/dark gray, and black are AM, PM, FM, and PC, respectively. The separation of simple amplitude and phase modulations from the more complicated ones (FM and PC) is clearly visible at $\vert\Delta f_1\vert> 2/T$.

It is clear from the figure that PC signals remain difficult to prewhiten, except perhaps near and below 1/T, when any type of signal can be prewhitened due to the proximity of the main pulsation component. Although periodic frequency modulation behaves similarly to secular period change above 1.5/T, it can be prewhitened (and therefore confused) with simple amplitude and phase modulations below this limit. When the secular change or periodic modulation of the pulsation frequency is strong, it is more easily separated from simple modulated signals (of types AM and PM, see Table 3). This happens at measured modulation frequencies greater than $\sim$2/T (see the gap starting at $\sim$0.0008 d^-1). An additional separation between AM and PM signals is observable at modulation frequencies greater than $\sim$5/T , where, as expected, the AM type leaves the weakest trace after the third prewhitening.

We conclude that the standard method of prewhitening used for the analysis of the observed data is capable of signaling distinctions between linear period change and signal modulation, but confusion occurs with periodic frequency modulations under observed modulation frequencies of 1.5/T. Modulation types AM and FM are also difficult to distinguish, except for short modulation periods, when type AM can be prewhitened more easily. These results support our phenomenological classification of variables given at the beginning of this section, even in the case of long modulation periods.

5 New detections by using SAM

Here we readdress the question of the incidence rate of first overtone BL stars by applying the method of analysis and scheme of classification described in the previous sections.

The datasets used in the analysis are described in Sect. 2. The final statistics of classification are shown in Table 4. Additional details of the analysis on a star-by-star basis are given in Table 5. The results presented in Table 4 are based on the analysis of Set #2, which contains all available two-color data. In comparison to the similar summary of A00 (their Table 7), we see that the most striking difference is the increase of the incidence rate of the BL stars by almost a factor of two. This change can be attributed to the following effects:

• The longer time span: +4 stars - from the comparison of the detections in the "r'' data.
• The better quality and higher amplitudes in the "b'' data: +28 stars - from the comparison of the Set #2 "r'' and "b'' data.
• Extending the allowed range of BL periods up to the length of the total time span: +12 stars - based on the SAM statistics of the Set #2 results.
• Employing SAM: +9 stars - from the comparison of the Set #2 "b'' and SAM analyses.
• False detections in A00: -7 stars - due to the higher cutoff employed here for the detection limit and because of the somewhat different classification scheme.

For the above reasons, we also find increases in the number of other types of variables. On the other hand, three stars, classified earlier by A00 as RR12 have been re-classified as MDM, or "mysterious double-mode''. Basic properties of these stars are summarized in Table 6. These objects have been re-classified mostly because of their somewhat extreme position in the color-magnitude diagram. Indeed, if we plot the derived average magnitudes and color indices on the color-magnitude diagram of Alcock et al. (2000a), the three MDM stars fall to the high-luminosity red edge of the region populated by RR1 stars. We recall that in the LMC, $\langle V \rangle = 19.35$ and $\langle V-R \rangle =0.22$, for the RR1 stars, with V-R < 0.3 for most of the variables (see Alcock et al. 2004). Although these objects are about 1 mag fainter than the faintest first/second overtone double-mode Cepheids (see Soszynski et al. 2000), it still may not be excluded that they are faint overtone Cepheids rather than bright and very red overtone RR Lyraes. We also note that there is a narrow overlap in the periods of these two classes of stars. One needs more accurate data to understand the status of these intriguing objects.

A slight change in the statistics of the above classification occurs if we consider double identifications due to field overlaps. We consider a star to be double-identified if the following two conditions are satisfied simultaneously: (i) the simple distance derived from the coordinates is smaller than $2\times 10^{-3}$ degrees, and (ii) the difference between the periods is smaller than 10^-5 d. We find 52 double-identified objects altogether, including 32 RR1-S, 8 RR01, 5 PC, 1 BL1, and 3 BL2. Except for three marginal cases of PC/S ambiguities, the classifications of the double-identified objects are consistent. The multiple identifications lead to the revised incidence rates of 3.5% and 3.9% for the BL1 and BL2 stars, respectively. We see that the changes are insignificant.

 

 

Table 6: Properties of the MDM stars.

MACHO ID	P1	P2/P1	V	V-R
12.10202.285	0.398	0.807	18.99	0.50
12.10443.367	0.337	0.802	18.90	0.45
9.4278.179	0.327	0.805	18.69	0.29

5.1 Properties of the BL and MC stars

The basic data on the 99 BL stars are summarized in Table 7. As was previously mentioned, in the case of BL2 stars, the modulation frequency $f_{\rm BL}$ stands for (f₊+f_-)/2, where f₊ and f_- denote the frequencies of the A₊ and A_- modulation components and f₁ the main pulsation frequency. This type of averaging is justified, in that among the 53 BL2 variables there are only seven with $\delta f=\vert f_{+}+f_{-}-2f_1\vert>0.0001$, four with $\delta f>0.0002$, and only one (star 15.10068.239) with $\delta f=0.00048$. Although this last value might reflect a statistically significant deviation from an equidistant frequency spacing, the majority of the variables are well within the acceptable deviations expected from observational noise (see A00 for numerical tests).

The BL variables have been selected on the basis of the classification scheme described in Sect. 4. In that scheme, MC-type variables (i.e. those with multiple close periods) have been excluded from the class of BL stars. One may wonder if these variables could also be considered as some subclass of the BL variables. We think that without knowing the underlying physics of the BL phenomenon, it is a question of preference whether or not to consider class MC as a subclass BL. Although we opted against this choice here, we note that there are five variables among the MC stars that show symmetric peaks of BL2-type within the multiple peaks. In Fig. 7, we show two representative cases in which the presence of the BL2 structure is obvious.

Figure 7: Examples of type MC variables with BL2 structures. The arrows indicate the position of the (prewhitened) main pulsation component. The spectra are computed by SAM.

Below we give a short description of the frequency spectra of all five stars containing structures of type BL2. In the following explanations we use the notation $\nu_0$ for the main pulsation component.

11.8751.1740 - the frequency spectrum shows a PC-type remnant at $\nu_0$, a symmetric pair of peaks around it, and an additional component further away (see Fig. 7).

14.8376.548 - the frequency spectrum shows a symmetric pair of closely spaced peaks around $\nu_0$ and an additional peak further away (see Fig. 7).

18.2357.757 - this star is classified as BL2 from the SAM analysis of Set #1. From Set #2 we found an additional close component; therefore, the final classification is as MC.

19.4671.684 - the frequency spectrum shows a dominantly BL2 structure, but there are additional peaks spread nearby.

6.6697.1565 - the frequency spectrum shows two superposed BL2 structures, one with large and another one with small frequency separations. The closer pair also has lower amplitudes.

The remaining eight stars from the MC variables show distinct peaks without any apparent BL2-type peak structures. Representative examples of these variables are shown in Fig. 8. We see that these are indeed different from the ones generally classified as type BL.

Figure 8: Examples of type MC variables without symmetric peak structures of type BL2. The arrows indicate the position of the (prewhitened) main pulsation component. Spectra are computed by SAM.

It is interesting to examine the distribution of the size and the position of the modulation components. For comparison, in Fig. 9, we show the distributions of the modulation amplitudes both for the RR1 and RR0 BL stars. It can be seen that in both classes, there are variables with very high modulation amplitudes, exceeding 0.1 mag. This may correspond to $\sim$50% and $\sim$90% relative modulation levels for the RR0 and RR1 stars, respectively. In the other extreme, at low modulation amplitudes, we find cases near 0.01-0.02 mag. From the size of the noise and the number of data points, we expect these amplitudes to be the lowest ones detected in this dataset. It is important to note that current investigations by Jurcsik and co-workers (Jurcsik et al. 2005a) suggest that modulation may occur under 0.01 mag among fundamental mode Galactic field Blazhko stars. It is clear that we need more accurate data to check if these low modulation levels are also common in the LMC.

Figure 9: Upper panel: distribution of the "b'' modulation amplitudes of the 99 RR1 stars shown in Table 7. In the case of BL2 stars, the amplitudes of both side peaks are included. Lower panel: as in the upper panel, but for the "V'' modulation amplitudes of the 731 RR0 stars of A03.

In terms of the relative positions of the modulation components, in Table 8, we show the number of cases obtained in the different datasets with the larger modulation component preceding the main pulsation component. We see that in the case of RR1 stars, there is a nearly 50% probability of this happenning. This result is essentially independent of BL type, color, and the extent of the dataset. We recall that A03 derived 75% for this ratio for the RR0 stars in the LMC.

   

Table 8: Positions of the larger modulation amplitudes.

Type	Color	N+	$N_{\rm tot}$	$N_+/N_{\rm tot}$
BL1	"r''	12	32	0.38
	"b''	18	44	0.41
	"SAM''	21	46	0.46
BL2	"r''	13	22	0.59
	"b''	21	46	0.46
	"SAM''	24	53	0.45

Note: dataset #2 is used; N₊= number of cases when the larger modulation amplitude has a frequency greater than that of the main pulsation component; $N_{\rm tot}=$ total number of BL stars identified in the given color.

The present study has largely extended the range of the BL periods known for RR1 stars. The distributions of the modulation frequencies for the RR1 and RR0 stars are shown in Fig. 10. Although the sample is much smaller for the RR1 stars, it is clear that there are more stars among them with short modulation periods than among the RR0 stars. Nevertheless, we should mention that Jurcsik et al. (2005a,b) also found very short modulation periods among RR0 stars, albeit in the Galactic field (i.e. SS Cnc and RR Gem with $P_{\rm BL}=5.3$ and 7.2 d, respectively). It is also noted that the considerable surplus in the RR1-BL stars with long modulation periods can be attributed only partially to our lower limit set on $f_{\rm BL}$. We find that among the 34 stars contributing to the first bin for the plot of RR1 stars in Fig. 10, there are only eleven with $1.0/T<f_{\rm BL}<1.5/T$ and sixteen with $1.0/T<f_{\rm BL}<2.0/T$. This implies a significant peak in the distribution function for $f_{\rm BL}<0.005$, even with the omission of those objects with very long modulation periods. The lack of such a peak for the RR0 stars might indicate a difference in this respect between the RR0 and RR1 BL stars, but, due to the low sample size for the RR1 stars, we would caution against jumping to this conclusion.

Figure 10: Upper panel: distribution of the modulation frequencies of the 99 RR1 stars shown in Table 7. Lower panel: as in the upper panel, but for the modulation frequencies of the 731 RR0 stars of A03.

5.2 Miscellaneous variables

In Table 9, we list the properties of the variables showing frequency spectra that are difficult to classify. We see that in most cases, the detections are barely above the noise level. Therefore, we cannot exclude that at least some of these variables will turn out to be single-periodic RR1 stars, once more accurate data are available. In the column "Comments'' we show the period ratios in cases in which some sort of double-mode pulsation can be suspected (without suggesting that those variables are indeed of double-mode ones).

   

Table 9: List of miscellaneous stars.

MACHO ID	$\nu_0$	$\nu_{MI}$	SNR	Source	Comments
10.3916.849	3.1389921	1.2070180	6.61	SAM
11.8745.899	3.3176002	4.7867033	6.79	SAM	$\nu_{0}/\nu_{\rm MI}=0.6931$
13.5719.713	3.0220610	3.9155071	6.96	SAM	$\nu_{0}/\nu_{\rm MI}=0.7718$
18.2717.787	2.8643249	4.9297051	6.55	SAM	$\nu_{0}/\nu_{\rm MI}=0.5810$
18.3202.956	2.2855398	5.1908177	6.96	r
19.3575.541	3.3698536	0.5856270	7.91	SAM
3.7451.484	3.3048194	2.7630866	7.85	b	$\nu_{\rm MI}/\nu_{0}=0.8361$
80.6348.2470	2.9571188	1.2069597	6.65	SAM
80.7558.650	2.7828759	0.8240633	6.99	r
81.8519.1395	2.9463890	0.8372214	6.96	r
9.5004.750	3.2877325	0.1604569	7.42	SAM
9.5122.363	3.1033541	4.1679579	6.82	SAM	$\nu_{0}/\nu_{\rm MI}=0.7446$
9.5241.382	3.1777911	1.3826455	6.79	SAM

Note: $\nu_0$ denotes the frequency (in [d^-1]) of the main pulsation component; $\nu_{\rm MI}$ stands for the frequency of the miscellaneous component with the SNR given in the next column. Period ratios, suggesting some forms of double-mode pulsations, are given in the comment lines.

6 Conclusions

This work has been motivated by an earlier result of Alcock et al. (2000) on the low incidence rate of the first overtone Blazhko RR Lyrae (RR1-BL) stars in the LMC. They derived a rate of 4% for these stars, which is a factor of three less than that of the fundamental mode (RR0) stars (see Alcock et al. 2003). Soszynski et al. (2003) obtained a somewhat higher rate of 6% from the OGLE database. However, Alcock et al. (2000) used MACHO "r'' data that have a somewhat lower signal-to-noise ratio for the objects of interest, and, in addition, the data analyzed then spanned a shorter time base than the ones available now. This suggests that the incidence rate could be higher than the one determined earlier. In a full utilization of all available data, we employed a spectrum averaging method that enabled us to increase the detection rate by 18% in comparison to the best single color (i.e. "b'') rates.

The main conclusion of this paper is that the incidence rate of the RR1-BL stars in the LMC is higher than previously derived from nearly the same database. Even though the rate is now determined to be 7.5%, it is still significantly lower than that of the RR0 stars. This latter rate is 12%; we also expect it to increase slightly when the same method as the one used in this paper on RR1 stars is employed on RR0 stars. This means that at least for the LMC, we can treat the conclusion that RR1-BL stars are significantly less frequent than their counterparts among the RR0 stars as a well-established fact. It is also notable that after filtering out the main pulsation component, the highest amplitude peak appears with equal probability at both sides of the frequency of the main pulsation component. We recall that in the case of RR0 stars, there is a 75% preference toward the higher frequency side. The smallest modulation amplitudes detected for RR1 stars are near 0.02 mag. For the larger sample of RR0 stars, this limit goes down to 0.01 mag. The relative size of the modulation may reach 90% for RR1 stars, whereas the same limit is only 50% for the RR0 stars. Furthermore, RR1-BL stars have a relatively large population of short-periodic ( $P_{\rm BL}<20$ d) variables, while this period regime is nearly empty of RR0 stars in the LMC.

Since the underlying physical mechanism of the BL phenomenon is still unknown, it is also unknown whether these (and other) observational facts will put strong (or even any) constraints on future theories. Nevertheless, since these statistics are based on large samples, their significance is high and surely should not be ignored in theoretical discussions. For example, we note that the very existence of BL1 stars puts the present forms of both currently available models (magnetic oblique rotator/pulsator by Shibahashi 2000; non-radial resonant model by Nowakowski & Dziembowski 2001; see however Dziembowski & Mizerski 2004) in jeopardy.

Acknowledgements

This paper utilizes public domain data obtained by the MACHO Project, jointly funded by the US Department of Energy through the University of California, Lawrence Livermore National Laboratory under contract No. W-7405-Eng-48, by the National Science Foundation through the Center for Particle Astrophysics of the University of California under cooperative agreement AST-8809616, and by the Mount Stromlo and Siding Spring Observatory, part of the Australian National University. The support of grant T-038437 of the Hungarian Scientific Research Fund (OTKA) is also acknowledged.

References

 
• Alcock, C., et al., The MACHO Collab. 1999, PASP, 111, 1539  
• Alcock, C., et al., The MACHO Collab. 2000, ApJ, 542, 257 (A00)  
• Alcock, C., et al., The MACHO Collab. 2000a, AJ, 119, 2194  
• Alcock, C., et al., The MACHO Collab. 2003, ApJ, 598, 597 (A03)  
• Alcock, C., et al., The MACHO Collab. 2004, AJ, 127, 334  
• Dziembowski, W. A., & Mizerski, T. 2004, Acta Astr., 54, 363  
• Jurcsik, J., Sódor, Á., Váradi, M., et al. 2005a, A&A, 430, 1049  
• Jurcsik, J., Szeidl, B., Nagy, A., & Sódor, Á. 2005b, Acta Astr., 55, 303  
• Kovács, G. 2005, A&A, 438, 227  
• Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369  
• Kurtz, D. 1985, MNRAS, 213, 773  
• Mizerski, T. 2003, Acta Astron., 53, 307  
• Moskalik, P., & Poretti, E. 2003, A&A, 398, 213  
• Nowakowski, R. M., & Dziembowski, W. A. 2001, Acta Astr., 51, 5  
• Shibahashi, H. 2000, ASP Conf. Ser., 203, 299  
• Smolec, R. 2005, Acta Astron., 55, 59  
• Soszynski, I., Udalski, A., Szymanski, M., et al. 2000, Acta Astron., 50, 451  
• Soszynski, I., Udalski, A., Szymanski, M., et al. 2002, Acta Astron., 52, 369  
• Soszynski, I., Udalski, A., Szymanski, M., et al. 2003, Acta Astron., 53, 93  
• Szeidl, B. 1988, in Multimode Stellar Pulsations, ed. G. Kovács, L. Szabados, & B. Szeidl (Budapest: Konkoly Observatory), 45  
• Szeidl, B., & Kolláth, Z. 2000, ASP Conf. Ser., 203, 281  
• Udalski, A., Szymanski, M., & Kubiak, M. 1997, Acta Astron., 47, 319

 

  
7 Online Material

    

Table 5: Notebook of the analysis.

MACHO ID	Period	Type r	Type r, b	Type r, b	Comments
		(A00)	(SAM)	(SAM)
	[d]	6.5 years		7.5 years
10.3190.501	0.3527946	RR1-S	RR1-S	RR1-S
10.3191.363	0.4060709	RR01	RR01	RR01
10.3193.457	0.2977060	RR1-S	RR1-S	RR1-S	weak peak in r at 0.4477
10.3193.514	0.2762716	RR1-S	RR1-S	RR1-S
10.3310.723	0.3675948	RR1-S	RR1-S	RR1-S
10.3311.612	0.3308571	RR1-S	RR1-S	RR1-S
10.3314.787	0.3575062	RR1-S	RR1-S	RR1-S
10.3314.873	0.3842321	RR1-S	RR1-S	RR1-S
10.3314.916	0.3438987	RR1-S	RR1-S	RR1-S
10.3315.758	0.2755685	RR1-S	RR1-S	RR1-S
10.3432.666	0.3418437	RR1-S	RR1-PC	RR1-PC
10.3434.825	0.2776860	RR1-S	RR1-S	RR1-S
10.3434.936	0.2769524	RR1-S	RR1-S	RR1-S
10.3435.907	0.3295068	RR1-S	RR1-S	RR1-S
10.3550.888	0.3317657	RR1-S	RR1-S	RR1-S
10.3552.745	0.2922940	RR1-BL1	RR1-BL1	RR1-BL1
10.3556.986	0.2961494	RR1-PC	RR1-PC	RR1-PC	$\Delta f=0$.00038
10.3557.1024	0.2947668	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=0$.00043
10.3557.827	0.3933231	RR01	RR01	RR01
10.3559.1080	0.3501022	RR1-S	RR1-S	RR1-S
10.3560.324	0.3387816	RR1-S	RR1-S	RR1-S
10.3673.1018	0.3393109	RR1-S	RR1-S	RR1-S
10.3680.988	0.4138908	RR1-S	RR1-S	RR1-S
10.3797.865	0.3087917	RR1-PC	RR1-PC	RR1-PC
10.3797.923	0.3284057	RR1-S	RR1-S	RR1-S
10.3798.634	0.3247489	RR1-S	RR1-S	RR1-S	2$\nu_0-1$ al. in r
10.3798.927	0.4934297	RR01	RR01	RR01	$\nu_1>\nu_0$
10.3799.828	0.2686594	RR1-S	RR1-S	RR1-S	light curve fuzzy
10.3800.1073	0.2985202	RR1-S	RR1-S	RR1-S
10.3802.446	0.3084910	RR1-S	RR1-PC	RR1-PC
10.3914.645	0.3452763	RR1-S	RR1-S	RR1-S
10.3914.827	0.3554060	RR1-S	RR1-S	RR1-S
10.3916.849	0.3185736	RR1-S	RR1-S	RR1-MI
10.3916.911	0.2731797	RR1-S	RR1-S	RR1-S
10.3920.693	0.3681541	RR1-S	RR1-S	RR1-D	in r
10.3922.1213	0.3456475	RR1-S	RR1-S	RR1-S	peak in r at 1.5282
10.3923.351	0.3339863	RR1-S	RR1-BL1	RR1-S	P(A00) $\ne$ P(SAM)
10.4034.825	0.3470388	RR1-S	RR1-S	RR1-S
10.4035.1095	0.3188217	RR1-S	RR1-BL1	RR1-BL1
10.4035.1299	0.3595035	RR01	RR01	RR01
10.4040.917	0.3673826	RR1-PC	RR1-PC	RR1-PC
10.4041.840	0.3988199	RR01	RR01	RR01
10.4042.1202	0.3703246	RR01	RR01	RR01
10.4043.1392	0.4619426	RR01	RR01	RR01	$\nu_1>\nu_0$
10.4043.939	0.3518691	RR1-S	RR1-D	RR1-S
10.4155.951	0.2907881	RR1-S	RR1-BL1	RR1-S	!!!!
10.4160.1090	0.3674925	RR01	RR01	RR01
10.4160.1109	0.2781280	RR1-S	RR1-S	RR1-S
10.4161.1053	0.2874579	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=.0$940
10.4165.348	0.3505580	RR1-PC	RR1-PC	RR1-PC
10.4275.3059	0.3258438	RR1-S	RR1-PC	RR1-S
10.4276.3455	0.3301617	RR1-S	RR1-S	RR1-S	+strange in b, crossID: 9.4276.488
10.4281.2296	0.3716398	RR1-S	RR1-S	RR1-S
10.4285.2423	0.3480152	RR1-S	RR1-S	RR1-S
10.4397.4675	0.3450608	RR1-S	RR1-S	RR1-S
10.4398.4412	0.3325706	RR1-S	RR1-S	RR1-S	crossID: 9.4398.852
10.4398.4446	0.3048601	RR1-S	RR1-S	RR1-S	crossID: 9.4398.729
10.4400.4594	0.3322339	RR1-S	RR1-S	RR1-S	crossID: 5.4400.1081
10.4400.4733	0.3254609	RR1-S	RR1-S	RR1-S
10.4402.4727	0.3261931	RR1-S	RR1-S	RR1-S	crossID: 5.4402.1009
10.4403.4871	0.4573038	RR01?	RR01+PC	RR01+PC	$\nu_0$ is changing
10.4520.4862	0.2852017	RR1-S	RR1-S	RR1-S	crossID: 9.4520.778
10.4520.5022	0.3365914	RR1-S	RR1-S	RR1-S	crossID: 9.4520.952
10.4522.4058	0.3589834	RR01	RR01	RR01
10.4524.4611	0.3461999	RR1-S	RR01	RR01	crossID: 5.4524.1212
11.8501.543	0.3703048	RR1-S	RR1-S	RR1-S	crossID: 14.8501.3153
11.8501.695	0.3048447	RR1-S	RR1-PC	RR1-PC	crossID: 14.8501.3352
11.8502.742	0.3581869	RR1-S	RR01+PC	RR01
11.8623.942	0.3084204	RR1-S	RR1-S	RR1-S	weak RR1-BL1?
11.8625.1121	0.3442731	RR1-S	RR1-S	RR1-S
11.8626.1188	0.3496315	RR1-S	RR1-S	RR1-S
11.8629.1482	0.3861446	RR01	RR01	RR01
11.8744.658	0.4155896	RR1-PC	RR1-PC	RR1-PC
11.8744.752	0.2809590	RR1-S	RR1-S	RR1-S	crossID: 14.8744.3856
11.8744.924	0.3114378	RR1-S	RR1-D	RR1-S
11.8745.899	0.3014227	RR1-S	RR1-D	RR1-MI	$\nu_0$/$\nu_1=.6$931
11.8750.1672	0.3400457	RR1-S	RR1-S	RR1-D
11.8750.1694	0.3577735	RR01	RR01	RR01
11.8751.1740	0.3577514	RR1-MC	RR1-PC+MC	RR1-PC+MC	symm. pair+$2\Delta f$!
11.8751.2094	0.3160414	RR1-S	RR1-S	RR1-S
11.8863.163	0.3312066	RR1-S	RR1-S	RR1-S	crossID: 14.8863.1362
11.8867.861	0.4131937	RR01	RR01	RR01
11.8867.919	0.3240251	RR1-S	RR1-S	RR1-S
11.8867.970	0.4466407	RR1-PC	RR1-PC	RR1-PC
11.8868.1095	0.3185036	RR1-S	RR1-S	RR1-D	in r
11.8873.1766	0.3277070	RR1-S	RR1-S	RR1-D	in b
11.8985.882	0.3624996	RR01	RR01	RR01
11.8987.1015	0.3341488	RR1-S	RR1-S	RR1-S
11.8987.787	0.3041267	RR1-MC	RR1-MC	RR1-MC
11.8988.974	0.3247708	RR1-S	RR1-S	RR1-S
11.8993.1532	0.3312893	RR1-S	RR1-S	RR1-BL1?	weak
11.8993.1649	0.3477462	RR1-S	RR1-S	RR1-D
11.9107.989	0.2939027	RR1-S	RR1-S	RR1-S
11.9109.1427	0.3611056	RR1-S	RR1-S	RR1-S
11.9110.1410	0.3405182	RR1-S	RR1-S	RR1-S
11.9111.591	0.3145463	RR1-S	RR1-S	RR1-S
11.9112.1035	0.3681675	RR1-S	RR1-S	RR1-S	weak RR1-D
11.9113.1731	0.3664409	RR1-PC	RR1-PC	RR1-PC
11.9116.1382	0.3024869	RR1-PC	RR1-PC	RR1-PC
11.9228.828	0.3179428	RR1-S	RR1-D	RR1-D
11.9230.894	0.2937493	RR1-S	RR1-S	RR1-S
11.9231.545	0.3934738	RR01	RR01	RR01
11.9233.1071	0.3577559	RR1-S	RR1-S	RR1-S
11.9234.960	0.3347677	RR1-S	RR1-PC	RR1-PC	fuzzy light curve
11.9235.1034	0.4175977	RR1-PC	RR1-PC	RR1-PC
11.9349.558	0.4028589	RR1-PC	RR1-PC	RR1-PC
11.9350.903	0.3541080	RR01	RR01	RR01
11.9352.1233	0.3621517	RR1-S	RR1-S	RR1-S	peak in b
11.9355.1235	0.3790599	RR1-PC	RR1-PC	RR1-PC
11.9355.1380	0.2704291	RR1-BL2	RR1-MC	RR1-MC	$\Delta \nu_2=2\Delta\nu_1$
11.9357.1640	0.3503957	RR1-S	RR1-D	RR1-D
11.9470.676	0.3712763	RR01	RR01	RR01
11.9471.1050	0.3542042	RR1-PC	RR1-PC	RR1-PC
11.9471.1172	0.3483401	RR1-S	RR1-S	RR1-S
11.9471.1340	0.2675705	RR1-S	RR1-D	RR1-D
11.9471.659	0.3483822	RR01	RR01	RR01
11.9471.780	0.2859825	RR1-BL1	RR1-BL1	RR1-BL1
11.9472.1070	0.3355736	RR1-S	RR1-S	RR1-S
11.9476.1456	0.3614426	BI	BI	BI	light curve
11.9478.1015	0.3313227	RR1-S	RR1-S	RR1-S
11.9478.774	0.3503890	RR1-S	RR1-S	RR1-S
11.9478.929	0.3522860	RR1-S	RR1-S	RR1-S	weak RR1-D in b
11.9590.1001	0.3600378	RR1-PC	RR1-PC	RR1-PC	crossID: 14.9590.3902
11.9591.1150	0.2523897	RR1-S	RR1-S	RR1-S
11.9591.762	0.3392833	RR1-S	RR1-S	RR1-D	crossID: 14.9591.3539
11.9593.1065	0.3276688	RR1-S	RR1-S	RR1-S
11.9594.880	0.3222766	RR1-PC	RR1-PC	RR1-PC
11.9595.1162	0.4860366	RR01	RR01	RR01	$\nu_1>\nu_0$
11.9597.1164	0.3481222	RR1-S	RR1-S	RR1-S
11.9711.943	0.2950092	RR1-S	RR1-S	RR1-S
11.9714.935	0.3029086	RR1-S	RR1-S	RR1-S	+weak $\nu_1$/ $\nu_0=.7244$
11.9717.1185	0.3365410	RR1-S	RR1-S	RR1-S
11.9717.1404	0.2822904	RR1-S	RR1-S	RR1-S
11.9719.1190	0.3254644	RR1-S	RR1-S	RR1-S
11.9721.989	0.3006416	RR1-S	RR1-S	RR1-S
11.9834.1222	0.3103837	RR1-S	RR1-S	RR1-S
11.9838.1201	0.3523117	RR01	RR01	RR01
11.9838.834	0.3177495	RR1-S	RR1-S	RR1-S
11.9841.828	0.3364250	RR1-S	RR1-S	RR1-S
12.10078.864	0.3940533	RR1-S	RR01	RR01
12.10084.166	0.3390483	RR1-S	RR1-S	RR1-S
12.10196.1046	0.3411752	RR1-S	RR1-S	RR1-S
12.10196.934	0.2856774	RR1-S	RR1-S	RR1-S
12.10197.1341	0.3166097	RR1-S	RR1-S	RR1-S
12.10201.618	0.3801510	RR1-S	RR1-S	RR1-S
12.10202.285	0.3981138	MDM	MDM	MDM	V: 21.22 mag, R: 20.8 mag
12.10203.1158	0.2753769	RR1-S	RR1-S	RR1-S
12.10203.1434	0.2768082	RR1-S	RR1-D	RR1-D
12.10204.1059	0.3573308	RR1-S	RR1-S	RR1-S
12.10204.860	0.3638051	RR1-S	RR1-PC	RR1-S	P(A00) $\ne$ P(SAM)
12.10319.816	0.3437542	RR1-S	RR1-D	RR1-D	.3437486 seems better period?
12.10319.963	0.3364132	RR1-S	RR1-S	RR1-S
12.10320.1544	0.2805502	RR1-S	RR1-S	RR1-S
12.10322.1142	0.3988699	RR1-S	RR1-S	RR1-S
12.10324.1144	0.3361543	RR1-S	RR1-S	RR1-S
12.10324.852	0.3334126	RR1-S	RR1-S	RR1-S
12.10325.1051	0.3016384	RR1-S	RR1-S	RR1-S
12.10437.656	0.3292892	RR1-S	RR1-S	RR1-S
12.10441.1320	0.3466018	RR1-S	RR1-S	RR1-D	+peak in r only
12.10443.367	0.3365587	MDM	MDM	MDM	V: 19.13 mag, R: 17.99 mag
12.10558.1379	0.3503669	RR1-S	RR1-S	RR1-S
12.10560.1841	0.2930150	RR1-S	RR1-S	RR1-S
12.10567.1392	0.2798609	RR1-S	RR1-D	RR1-S
12.10567.1400	0.3366432	RR1-S	RR1-S	RR1-S
12.10679.924	0.3087344	RR1-S	RR1-S	RR1-S
12.10679.968	0.3675864	RR01	RR01	RR01
12.10681.687	0.3507141	RR1-S	RR1-S	RR1-S
12.10682.1050	0.3583923	RR1-S	RR1-S	RR1-S
12.10682.793	0.3636899	RR01	RR01	RR01
12.10685.1084	0.3165502	RR1-S	RR1-S	RR1-S	remnant stuff in b at $\nu_0$
12.10801.843	0.3650891	RR1-PC	RR1-PC	RR1-PC
12.10805.860	0.3411962	RR1-S	RR1-S	RR1-S
12.10807.859	0.4968156	BI	BI	BI	light curve
12.10807.919	0.3119925	RR1-S	RR1-S	RR1-S
12.10808.830	0.3000152	RR1-PC	RR1-PC	RR1-PC
12.10920.615	0.3239811	RR1-D	RR1-D	RR1-D
12.10923.1422	0.3780394	BI	BI	BI	light curve, $\nu_1$/$\nu_0=1/2$
12.10924.961	0.3868628	RR1-PC	RR1-PC	RR1-PC
12.10930.738	0.3596019	RR1-S	RR1-S	RR1-S
12.11042.810	0.3798227	RR1-PC	RR1-PC	RR1-PC
12.11042.884	0.3751375	RR1-S	RR1-S	RR1-S
12.11043.1000	0.2643195	RR1-MI	RR1-D	RR1-D
12.11044.712	0.3516970	RR1-S	RR1-BL1?	RR1-S	weak remnant; period: .3516991?
12.11048.1190	0.2837675	RR1-S	RR1-S	RR1-S
12.11172.776	0.3669065	RR01	RR01	RR01
12.11283.284	0.3403838	RR1-D	RR1-D	RR1-D	+ remnant in r, crossID: 15.11283.1607
12.11284.502	0.2883280	RR1-S	RR1-D	RR1-D
12.9960.1448	0.3086345	RR1-S	RR1-D	RR1-D	+ remnant at $\nu_0$
12.9961.937	0.3208761	RR1-S	RR1-S	RR1-S
12.9962.1341	0.3462807	RR1-S	RR1-S	RR1-S
12.9962.1419	0.3687607	RR01	RR01	RR01
13.5591.31	0.4054494	RR1-S	RR1-S	RR1-S
13.5598.180	0.3030987	RR1-S	RR1-S	RR1-S
13.5599.3267	0.2994202	RR1-S	RR1-S	RR1-PC
13.5601.3249	0.3614176	RR1-S	RR1-S	RR1-PC
13.5712.73	0.3391091	RR1-S	RR1-S	RR1-S
13.5713.590	0.2836353	RR1-BL1	RR1-PC+MC	RR1-BL1+PC	both $\nu_0$ and $\nu_1$ are changing
13.5714.442	0.3168726	RR1-BL1	RR1-BL1	RR1-BL1
13.5714.490	0.3848480	RR1-S	RR1-S	RR1-S	weak BL1 +weak remnant in r
13.5716.523	0.3419968	RR1-S	RR1-S	RR1-S
13.5716.670	0.2934612	RR1-S	RR1-S	RR1-S	aliases in b
13.5717.626	0.2979910	RR1-S	RR1-D	RR1-D
13.5719.650	0.3455553	RR1-S	RR1-S	RR1-S
13.5719.713	0.3309000	RR1-S	RR1-S	RR1-MI	$\nu_0$/ $\nu_1=.7718$
13.5720.572	0.3720968	RR1-S	RR1-PC	RR1-PC
13.5720.646	0.3450355	RR01	RR01	RR01
13.5721.2108	0.3355824	RR1-S	RR1-D	RR1-S	crossID: 6.5721.289
13.5721.2163	0.2974574	RR1-S	RR1-S?	RR1-S	+ peak in b only! crossID: 6.5721.310
13.5721.2180	0.3221557	RR1-PC	RR1-PC	RR1-PC
13.5721.2290	0.3766406	RR01	RR01	RR01
13.5722.3565	0.2944695	RR1-S	RR1-S	RR1-PC	crossID: 6.5722.682
13.5722.4288	0.3902119	RR1-S	RR1-S	BI	$\nu_1$/ $\nu_0=.5000$, light curve.
13.5834.506	0.3538832	RR1-S	RR1-S	RR1-S
13.5836.525	0.3604006	RR01	RR01	RR01
13.5838.497	0.3697960	RR01	RR01	RR01
13.5838.667	0.3425199	RR1-S	RR1-S	RR1-S
13.5839.974	0.3232700	RR1-S	RR1-S	RR1-S	weak RR1-BL1, $\Delta f=-.0$010, aliases
13.5842.2316	0.3604223	RR01	RR01	RR01	crossID: 6.5842.396
13.5842.2468	0.2731424	RR1-S	RR1-S	RR1-BL1
13.5844.3963	0.3702719	RR1-PC	RR1-PC	RR1-PC	crossID: 6.5844.872
13.5955.540	0.2990079	RR1-S	RR1-S	RR1-S
13.5957.647	0.2699266	RR1-S	RR1-S	RR1-S
13.5958.518	0.3712948	RR01	RR01	RR01+PC	$\nu_1$ is changing
13.5959.584	0.3466458	RR1-S	RR1-S	RR1-BL1	$\Delta f=.0010$
13.5960.118	0.4234486	RR1-S	RR1-PC	RR1-PC
13.5960.884	0.3459562	RR1-S	RR1-S	RR1-S
13.5963.2421	0.3033331	RR1-S	RR1-S	RR1-S
13.5963.2479	0.2764699	RR1-S	RR1-S	RR1-S	crossID: 6.5963.363
13.5964.3984	0.2656551	RR1-S	RR1-S	RR1-S
13.5965.3700	0.3669370	RR1-S	RR1-S	RR1-S	crossID: 6.5965.890
13.5965.3725	0.3169630	RR1-S	RR1-D	RR1-D	crossID: 6.5965.835
13.6076.306	0.4270922	RR1-PC	RR1-PC	RR1-PC
13.6076.527	0.3524419	RR1-S	RR1-S	RR1-PC
13.6077.638	0.2906904	RR1-PC	RR1-PC	RR1-PC
13.6079.604	0.3267329	RR1-S	RR1-S	RR1-S
13.6080.541	0.3744790	RR1-PC	RR1-PC	RR1-PC
13.6080.594	0.4047098	RR1-PC	RR1-PC	RR1-PC
13.6080.628	0.4004744	RR1-PC	RR1-PC	RR1-PC
13.6081.990	0.3106862	RR1-S	RR1-S	RR1-S
13.6083.535	0.3440608	RR1-S	RR1-PC?	RR1-PC
13.6084.2519	0.3067479	RR1-S	RR1-S	RR1-S	crossID: 6.6084.462
13.6197.522	0.3572369	RR01	RR01	RR01
13.6198.531	0.3661721	RR1-PC	RR1-PC	RR1-PC
13.6199.567	0.2796456	RR1-S	RR1-S	RR1-S
13.6200.568	0.3432525	RR1-S	RR1-S	RR1-S
13.6200.786	0.3421512	RR1-S	RR1-S	RR1-S
13.6201.670	0.3036885	RR1-S	RR1-S	RR1-S	P(A00) $\ne$ P(SAM)
13.6204.617	0.2931520	RR1-BL1	RR1-S	RR1-S
13.6204.663	0.3531123	RR1-S	RR1-S	RR1-S
13.6318.267	0.3191239	RR1-S	RR1-S	RR1-S
13.6318.304	0.3821733	RR1-S	RR1-S	RR1-S
13.6319.317	0.3254238	RR1-S	RR1-S	RR1-S
13.6322.342	0.2621495	RR1-S	RR1-BL1	RR1-BL1
13.6322.359	0.3239249	RR1-S	RR1-S	RR1-S
13.6323.1244	0.3109691	RR1-S	RR1-S	RR1-PC	whitens out
13.6325.1002	0.2908044	RR1-S	RR1-S	RR1-S	weak RR1-BL1
13.6326.1733	0.2903530	RR1-PC	RR1-PC	RR1-PC
13.6326.2765	0.3304520	RR1-S	RR1-S	RR1-BL1+PC	crossID: 6.6326.424
13.6438.48	0.2936896	RR1-S	RR1-S	RR1-S
13.6439.655	0.3304406	RR1-S	RR1-S	RR1-S
13.6440.550	0.3185115	RR1-S	RR1-S	RR1-S
13.6441.527	0.3435201	RR1-PC	RR1-PC	RR1-PC
13.6441.529	0.4025309	RR1-PC	RR1-PC	RR1-PC
13.6442.574	0.3224344	RR1-S	RR1-S	RR1-D
13.6443.675	0.3792586	RR1-S	RR1-D	RR1-D
13.6444.995	0.2804357	RR1-S	RR1-S	RR1-S	weak (S/N < 6.5) D
13.6445.617	0.3060729	RR1-S	RR1-PC	RR1-PC
13.6445.758	0.3482106	RR1-S	RR1-S	RR1-S
13.6447.3202	0.3501948	RR1-S	RR1-S	RR1-S	crossID: 6.6447.699
13.6448.4137	0.3431569	RR1-S	RR1-BL1	RR1-BL1?	in b only? crossID: 6.6448.801
13.6563.526	0.3625070	RR1-S	RR1-D	RR1-S
13.6567.600	0.4065653	RR1-S	RR1-S	RR1-PC
13.6567.646	0.3482255	RR1-S	RR1-S	RR1-S
13.6567.847	0.3007600	RR1-S	RR1-S	RR1-S
13.6568.3005	0.3380994	RR1-PC	RR1-PC	RR1-PC	crossID: 6.6568.484
13.6569.4088	0.3432541	RR1-S	RR1-S	RR1-S	crossID: 6.6569.980
13.6569.4284	0.3150173	RR1-S	RR1-S	RR1-S	crossID: 6.6569.955
13.6683.524	0.3132242	RR1-S	RR1-S	RR1-S
13.6685.662	0.3293156	RR1-S	RR1-S	RR1-S
13.6688.699	0.3779899	RR1-S	RR1-MI?+PC?	RR1-PC
13.6688.742	0.3413834	RR1-S	RR1-S	RR1-S
13.6689.3055	0.3050575	RR1-S	RR1-S	RR1-S	crossID: 6.6689.563
13.6691.4052	0.4608689	RR01	RR01	RR01	$\nu_1$ > $\nu_0$
13.6802.544	0.3780602	RR01?	RR01+PC	RR01+PC	both $\nu_0$ and $\nu_1$ are changing
13.6804.494	0.3695517	RR01	RR01	RR01
13.6804.515	0.2858770	RR1-S	RR1-S	RR1-D
13.6805.598	0.3364643	RR1-S	RR1-S	RR1-S	+rem.at $\nu_0$/.8221
13.6806.585	0.3202244	RR1-S	RR1-S	RR1-S
13.6806.664	0.3307589	RR1-D	RR1-D	RR1-D
13.6807.1020	0.3191305	RR1-S	RR1-S	RR1-S
13.6807.1093	0.2809988	RR1-S	RR1-S	RR1-S
13.6807.995	0.3256622	RR1-S	RR1-PC	RR1-PC	symmetric, whitens out, $\Delta f=0.0002$
13.6808.1130	0.4154337	BI	BI	BI	light curve
13.6808.718	0.3405710	RR1-S	RR1-S	RR1-S
13.6808.767	0.3382012	RR1-S	RR1-S	RR1-S	strong peak in b only
13.6809.543	0.3574192	RR1-S	RR1-S	RR1-S	weak RR1-D in b
13.6810.2845	0.3814162	RR01	RR01	RR01	crossID: 6.6810.428
13.6810.2981	0.2883863	RR1-S	RR1-PC	RR1-BL2	$\Delta f=.00043$ crossID: 6.6810.616
13.6810.2992	0.2903975	RR1-BL2	RR1-BL2	RR1-BL2+PC	aliases
13.6811.4041	0.3598933	RR01	RR01	RR01	crossID: 6.6811.651
13.6923.613	0.3430536	RR1-S	RR1-S	RR1-S
13.6924.623	0.2951702	RR1-S	RR1-D	RR1-D
13.6925.627	0.3566797	RR01	RR01	RR01
13.6926.490	0.4383823	RR1-PC	RR1-PC	RR1-PC
13.6927.606	0.3631832	RR01	RR01	RR01
13.6927.654	0.3558534	RR1-S	RR1-S	RR1-S
13.6928.978	0.3617956	RR1-S	RR1-MC+PC?	RR1-PC	PERIOD? 0.36179008r; 0.36179099b
13.6929.784	0.3549622	RR1-S	RR1-PC	RR1-PC
13.6930.802	0.3200681	RR1-S	RR1-S	RR1-S
13.6930.870	0.3270085	RR1-S	RR1-S	RR1-S
13.6931.3165	0.3590473	RR1-S	RR1-S	RR1-S	crossID: 6.6931.704
13.6931.3219	0.3154412	RR1-S	RR1-S	RR1-D	crossID: 6.6931.655
13.6931.3278	0.3228077	RR1-S	RR1-S	RR1-S	crossID: 6.6931.649
13.6933.3973	0.3228538	RR1-S	RR1-PC	RR1-PC
13.7048.418	0.3490157	RR01	RR01	RR01
13.7050.432	0.3347571	RR1-S	RR1-S	RR1-S
13.7051.372	0.3373318	RR1-S	RR1-S	RR1-S
13.7051.448	0.3657709	RR1-S	RR1-MC	RR1-PC
13.7051.459	0.3251078	RR1-S	RR1-PC	RR1-PC
13.7052.2231	0.2929019	RR1-S	RR1-S	RR1-S
13.7054.3006	0.3129400	RR1-S	RR1-S	RR1-S	crossID: 6.7054.710
14.8252.301	0.3424035	RR1-S	RR1-BL1	RR1-D
14.8376.498	0.2901747	RR1-S	RR1-D	RR1-D
14.8376.548	0.2915711	RR1-MC	RR1-MC	RR1-MC	$\Delta f=\pm$.0036(37), $\nu_3-\nu_0=-$.0371
14.8380.776	0.3208658	RR1-S	RR1-S	RR1-S	weak RR1-D in b
14.8493.641	0.2804552	RR1-S	RR1-S	RR1-S
14.8493.841	0.3377429	RR1-S	RR1-S	RR1-S
14.8495.582	0.2971105	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=0.0441$
14.8497.534	0.2893001	RR1-PC	RR1-PC	RR1-PC
14.8498.847	0.3368901	RR1-S	RR1-S	RR1-S
14.8499.544	0.3214172	RR1-S	RR1-S	RR1-S
14.8500.1226	0.3507788	RR1-S	RR1-S	RR1-S	P(A00) $\ne$ P(SAM)
14.8501.3153	0.3703045	RR1-S	RR1-D	RR1-D	P(A00) $\ne$ P(SAM) crossID: 11.8501.543
14.8501.3352	0.3048425	RR1-S	RR1-S	RR1-PC	crossID: 11.8501.695
14.8613.787	0.3525904	RR1-S	RR1-MI	RR0-S	S/N = 6 rem at $\nu_0$/.73
14.8616.635	0.2676608	RR1-S	RR1-S	RR1-S
14.8616.709	0.3538649	RR1-S	RR1-S	RR1-S	rem at $\nu_0$/.7322
14.8618.603	0.3399275	RR1-S	RR1-S	RR1-S	+ weak RR1-D
14.8619.816	0.2652884	RR1-S	RR1-S	RR1-S
14.8734.678	0.2958678	RR1-S	RR1-S	RR1-S
14.8737.685	0.3450778	RR1-S	RR1-S	RR1-S	+weak RR1-D
14.8737.823	0.3329859	RR1-S	RR1-S	RR1-S
14.8739.801	0.2815096	RR1-S	RR1-D	RR1-D	in b
14.8744.3716	0.4156945	RR1-PC	RR1-PC	RR1-PC
14.8744.3856	0.2809577	RR1-S	RR1-S	RR1-S	crossID: 11.8744.752
14.8854.199	0.3390661	RR1-D	RR1-PC+?	RR1-PC
14.8859.663	0.3103481	RR1-S	RR1-S	RR1-S
14.8863.1362	0.3312052	RR1-S	RR1-S	RR1-S	+weak $\nu_0$/ $\nu_1=.8104$ crossID: 11.8863.163
14.8977.1739	0.3432359	RR1-S	RR1-S	RR1-S
14.8977.283	0.3134319	RR1-S	RR1-S	RR1-S
14.8982.1963	0.3676332	RR01	RR01	RR01
14.9099.710	0.2820734	RR1-S	RR1-S	RR1-D	weak
14.9101.877	0.4361277	RR1-S	BI	BI	$\nu_1$/ $\nu_0=.5000$, lc maybe
14.9220.799	0.3438955	RR01	RR01	RR01
14.9223.737	0.3098789	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0316$
14.9225.776	0.3551288	RR1-BL1	RR1-BL1+PC?	RR1-BL1	+weak $\nu_2/\nu_1=.7477$
14.9338.255	0.2676678	RR1-S	RR1-S	RR1-S
14.9340.686	0.3403248	RR1-S	RR1-S	RR1-S	+weak peak at 0.92
14.9342.919	0.3424704	RR1-S	RR1-S	RR1-D	in r
14.9344.714	0.3473183	RR1-S	RR1-S	RR1-S
14.9346.412	0.3434954	RR1-PC	RR1-PC	RR1-PC
14.9463.846	0.2749961	RR1-S	RR1-BL1	RR1-BL1	+ peak at $\approx\nu_0+1$
14.9465.585	0.3547704	RR1-S	RR1-S	RR1-D
14.9465.589	0.3287855	RR1-S	RR1-S	RR1-S
14.9467.864	0.3465627	RR01	RR01	RR01
14.9582.717	0.2835774	RR1-S	RR1-S	RR1-S
14.9583.1037	0.4060893	BI	BI	BI	light curve
14.9587.828	0.3512629	RR01	RR01	RR01
14.9588.864	0.3716179	RR1-S	RR1-S	RR1-S	weak RR1-D in b
14.9589.1469	0.3020927	RR1-S	RR1-S	RR1-S	peak in b at $\approx$1.9
14.9590.3902	0.3600392	RR1-PC	RR1-PC	RR1-PC	crossID: 11.9590.1001
14.9591.3539	0.3392787	RR1-S	RR1-S	RR1-S	crossID: 11.9591.762
14.9702.401	0.2754043	RR1-BL1	RR1-BL1	RR1-BL1	+ weak RR1-D
14.9703.450	0.3522143	RR01	RR01	RR01
14.9703.651	0.3566657	RR1-S	RR1-S	RR1-S
15.10064.662	0.3162848	RR1-S	RR1-S	RR1-S
15.10066.781	0.3497410	RR1-S	RR1-S	RR1-S
15.10068.239	0.2976949	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0334$
15.10069.680	0.3745080	RR1-PC	RR1-S	RR1-PC
15.10071.765	0.3528949	RR01	RR01	RR01
15.10071.888	0.3521986	RR01	RR01	RR01
15.10072.818	0.2834267	RR1-S	RR1-S	RR1-S	RR1-D in b
15.10072.918	0.2930774	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-.0369$
15.10194.3317	0.3353776	RR1-S	RR1-S	RR1-S
15.10307.549	0.3306027	RR1-S	RR1-S	RR1-S
15.10308.620	0.3535518	RR1-PC	RR1-PC	RR1-PC
15.10309.843	0.2984189	RR1-S	RR1-S	RR1-S
15.10311.782	0.3482903	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0010$
15.10313.606	0.2925053	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0644$
15.10427.514	0.3485194	RR1-S	RR1-D	RR1-D
15.10433.787	0.3394885	RR1-PC	RR1-PC	RR1-PC
15.10550.374	0.3077982	RR1-S	RR1-S	RR1-S
15.10550.495	0.3471121	RR1-S	RR1-S	RR1-S
15.10557.2836	0.3541081	RR1-S	RR01	RR01
15.10557.2954	0.3644224	RR01	RR01	RR01
15.10670.583	0.2999786	RR1-S	RR1-S	RR1-S	+strange rem.
15.10671.500	0.4062024	RR01	RR01	RR01
15.10678.3345	0.3344386	RR1-S	RR1-S	RR1-S
15.10795.916	0.3074573	RR1-PC	RR1-PC	RR1-PC
15.10797.871	0.3485675	RR01	RR01	RR01
15.10911.457	0.3408487	RR1-S	RR1-D	RR1-S
15.10912.514	0.3723185	RR1-S	RR1-S	RR1-S
15.10914.663	0.3670500	RR1-PC	RR1-PC	RR1-PC
15.10920.3094	0.3239824	RR1-S	RR1-D	RR1-D
15.11036.255	0.2869357	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=+0$.0782
15.11037.690	0.3611758	RR1-S	RR1-S	RR1-S	+very weak RR1-PC
15.11040.667	0.3555267	RR1-S	RR1-S	RR1-S
15.11040.828	0.3319008	RR1-S	RR1-S	RR1-S
15.11154.325	0.3381630	RR1-S	RR1-S	RR1-S
15.11155.469	0.2894198	RR1-S	RR1-S	RR1-S
15.11156.431	0.3735111	RR1-S	RR1-S	RR1-S	aliases
15.11157.243	0.3359253	RR1-S	RR1-S	RR1-S
15.11276.323	0.3508712	RR1-S	RR1-S	RR1-S	in b
15.11280.663	0.3299770	RR1-S	RR1-S	RR1-BL1
15.11283.1607	0.3403839	RR1-S	RR1-S	RR1-S	weak RR1-D in b, crossID: 12.11283.284
15.9830.183	0.2806755	RR1-S	RR1-D	RR1-D
15.9942.675	0.2850893	RR1-S	RR1-S	RR1-S
15.9943.714	0.3433162	RR1-S	RR1-S	RR1-S
15.9944.822	0.3358499	RR1-S	RR1-S	RR1-S
15.9947.338	0.2882211	RR1-MC	RR1-MC	RR1-MC	$\Delta \nu_1=-.0350,\Delta \nu_2=-$.0482
15.9948.593	0.3091553	RR1-S	RR1-S	RR1-S	weak RR1-D in b
15.9950.876	0.2905768	RR1-S	RR1-S	RR1-S
15.9952.3389	0.3541299	RR1-S	RR1-S	RR1-S
15.9952.3454	0.2615364	RR1-S	RR1-D	RR1-D
18.2234.1176	0.3537102	RR01	RR01	RR01
18.2357.757	0.3938249	RR1-S	RR1-BL2	RR1-MC	$\Delta f=\pm$0.0247, $\Delta\nu_2=0$.0539
18.2361.870	0.3254790	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0$.0298
18.2364.968	0.3563781	RR1-S	RR1-S	RR1-S
18.2476.903	0.2623399	RR1-S	RR1-S	RR1-S
18.2479.655	0.3187457	RR1-S	RR1-S	RR1-S
18.2482.790	0.3991355	RR1-S	RR1-S	RR1-S
18.2483.800	0.3342781	RR1-S	RR1-S	RR1-D
18.2597.765	0.3579695	RR1-PC	RR1-PC+MC?	RR1-PC
18.2597.933	0.2898306	RR1-S	RR1-S	RR1-S	peak at 1.2 in b
18.2598.715	0.3167194	RR1-S	RR1-S	RR1-S
18.2601.439	0.3676446	RR01	RR01	RR01
18.2717.787	0.3491224	RR1-S	RR1-S	RR1-MI	$\nu_{MI}=\nu_0$/.581
18.2717.812	0.3506581	RR01	RR01	RR01
18.2719.645	0.3557849	RR01	RR01	RR01
18.2723.888	0.3487799	RR1-S	RR1-D	RR1-D
18.2727.794	0.3407561	RR1-S	RR1-S	RR1-S
18.2839.754	0.3603664	RR1-S	RR01	RR01
18.2843.2547	0.3523502	RR01	RR01	RR01
18.2848.544	0.3538016	RR1-S	RR1-S	RR1-S
18.2961.764	0.3368673	RR1-S	RR1-S	RR1-S
18.2962.667	0.3642834	RR1-S	RR1-S	RR1-S
18.2962.942	0.3283045	RR1-S	RR1-S	RR1-S
18.3082.1147	0.3083016	RR1-S	RR1-S	RR1-S
18.3084.852	0.3514798	RR1-S	RR1-S	RR1-S
18.3085.1997	0.2913733	RR1-S	RR1-S	RR1-S
18.3086.1308	0.3049418	RR1-PC	RR1-PC	RR1-PC
18.3089.963	0.3292058	RR1-S	RR1-S	RR1-S
18.3090.696	0.2850000	RR1-S	RR1-S	RR1-S
18.3090.736	0.3401601	RR1-S	RR1-S	RR1-S	peak at 1.2 in b
18.3202.956	0.4375334	RR1-S	RR1-S	RR1-MI
18.3207.1039	0.2803413	RR1-S	RR1-S	RR1-S
18.3211.679	0.3577120	RR1-S	RR1-S	RR1-S
18.3326.1039	0.3120644	RR1-S	RR1-D	RR1-D
18.3327.434	0.2676823	RR1-S	RR1-S	RR1-BL1?	$\Delta f=+.1217$, in r
18.3444.5297	0.2919160	RR1-S	RR1-D	RR1-D	+ strange stuff in r
18.3445.5324	0.3193574	RR1-S	RR1-S	RR1-S
18.3449.4292	0.3975811	RR1-S	RR1-S	RR1-S
19.3575.541	0.2967488	RR1-S	RR1-S	RR1-MI	$\nu_{\rm MI}=0.5856$
19.3575.690	0.3237353	RR1-S	RR1-S	RR1-S
19.3580.465	0.3553299	RR01	RR01	RR01
19.3581.468	0.3564439	RR01	RR01	RR01
19.3695.1013	0.3184404	RR1-S	RR1-S	RR1-S
19.3700.930	0.3597382	RR1-S	RR1-S	RR1-S	double peak. at $\approx$1.1 in b
19.3702.545	0.3587570	RR01	RR01	RR01
19.3702.861	0.2782078	RR1-S	RR1-S	RR1-S
19.3815.835	0.3434257	RR1-S	RR1-S	RR1-S
19.3818.902	0.3419316	RR1-S	RR1-S	RR1-S
19.3819.806	0.3419088	RR1-S	RR1-S	RR1-S
19.3821.759	0.3575546	RR1-S	RR1-S	RR1-S
19.3821.794	0.3176546	RR1-S	RR1-PC	RR1-PC
19.3823.473	0.4089799	RR1-PC	RR1-PC	RR1-PC
19.3823.546	0.3379297	RR1-PC	RR1-PC	RR1-PC	P(A00) $\ne$ P(SAM) .3380507
19.3940.956	0.2575013	RR1-S	RR1-S	RR1-S
19.3942.690	0.2586072	RR1-S	RR1-S	RR1-S	+peak in r at $\nu_0\cdot0.6913$
19.3942.803	0.3430451	RR1-S	RR1-S	RR1-S
19.3943.856	0.3454221	RR1-S	RR1-PC	RR1-S
19.3943.871	0.3218319	RR1-S	RR1-S	RR1-S
19.4057.1115	0.3589699	RR01	RR01	RR01	no f0+f1 and f0-f1
19.4061.855	0.3418551	RR1-S	RR1-D	RR1-D	in r
19.4062.1230	0.2775809	RR1-S	RR1-S	RR1-S	S/N = 6.4 peak in b at 1.4769
19.4066.807	0.3005532	RR1-S	RR1-S	RR1-S
19.4182.345	0.4016251	RR01	RR01	RR01
19.4184.1390	0.3569192	RR1-S	RR1-D	RR1-D
19.4185.239	0.2773293	RR1-S	RR1-S	RR1-S
19.4187.1316	0.3457721	RR1-S	RR1-S	RR1-S
19.4188.1264	0.3702574	RR1-BL2	RR1-PC+BL2	RR1-PC+BL2
19.4188.1317	0.3347047	RR1-S	RR1-D	RR1-D
19.4188.1333	0.2855346	RR1-S	RR1-S	RR1-S
19.4188.195	0.2828193	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0121$
19.4299.1724	0.2915693	RR1-S	RR1-S	RR1-S
19.4299.1932	0.2774828	RR1-S	RR1-S	RR1-S
19.4303.852	0.2616854	RR1-S	RR1-S	RR1-S
19.4308.880	0.3583355	RR01	RR01	RR01
19.4420.1511	0.3417203	RR1-S	RR1-MI?	RR1-S
19.4427.769	0.3493883	RR1-S	RR1-S	RR1-S
19.4429.678	0.3775181	RR1-PC	RR1-PC	RR1-PC
19.4429.703	0.3581288	RR01	RR01	RR01
19.4541.1357	0.3618792	RR01	RR01	RR01
19.4543.1583	0.4111521	RR1-S	RR1-S	RR1-S
19.4545.1503	0.3194264	RR1-S	RR1-S	RR1-S
19.4547.725	0.3317246	RR1-S	RR1-S	RR1-S
19.4662.4346	0.3287573	RR1-S	RR1-S	RR1-S
19.4668.2769	0.3842229	RR01	RR01	RR01	crossID: 2.4668.539
19.4669.2905	0.3119589	RR1-PC	RR1-PC	RR1-PC	crossID: 2.4669.545
19.4671.684	0.3787444	RR1-MC	RR1-MC	RR1-MC	d$\nu_1=\pm$.00125 (and more)
19.4784.5754	0.3517982	RR1-PC	RR1-PC	RR1-PC
19.4785.5170	0.4286302	RR01	RR01	RR01
19.4785.5287	0.3440254	RR1-S	RR1-S	RR1-S	crossID: 2.4785.1203
19.4786.4838	0.3393137	RR1-S	RR1-D	RR1-D
19.4787.4455	0.3411946	RR1-S	RR1-PC	RR1-PC	$\nu_1=\nu_0+1$ (alias) crossID: 2.4787.1072
19.4789.4086	0.3824050	RR1-S	RR01	RR01	+ peak near "-'' crossID: 2.4789.1029
19.4789.4120	0.3269113	RR1-S	RR1-S	RR1-S	weak RR1-D crossID: 2.4789.946
19.4792.584	0.3290488	RR1-S	RR1-S	RR1-D
2.4661.4689	0.3627190	RR1-S	RR1-S	RR1-S
2.4661.4727	0.3384451	RR1-S	RR1-S	RR1-S
2.4662.795	0.3461673	RR1-S	RR1-S	RR1-S
2.4663.775	0.3902756	RR1-S	RR1-MI	RR1-PC	aliases
2.4663.944	0.3552641	RR1-PC	RR1-PC	RR1-PC	whitens out
2.4667.659	0.3243990	RR1-S	RR1-S	RR1-D
2.4668.539	0.3842213	RR01	RR01	RR01	crossID: 19.4668.2769
2.4669.545	0.3119586	RR1-PC	RR1-PC	RR1-PC	crossID: 19.4669.2905
2.4785.1121	0.3385838	RR1-S	RR1-S	RR1-S
2.4785.1203	0.3440255	RR1-S	RR1-S	RR1-S	weak RR1-D, crossID: 19.4785.5287
2.4787.1072	0.3411926	RR1-S	RR1-S	RR1-S	crossID: 19.4787.4455
2.4787.770	0.3357061	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=.0$005, symm, 2 $\nu_0\pm\Delta f$
2.4787.904	0.2758016	RR1-S	RR1-S	RR1-S
2.4789.1029	0.3824081	RR01	RR01	RR01	crossID: 19.4789.4086
2.4789.946	0.3269118	RR1-S	RR1-S	RR1-S	weak peak at 1.35 in b, crossID: 19.4789.4120
2.4790.736	0.2719880	RR1-S	RR1-S	RR1-D
2.4791.631	0.8358569	BI	BI	BI	light curve
2.4904.1425	0.3455885	RR1-S	RR01	RR01	no f0+f1
2.4904.1651	0.3503548	RR01	RR01	RR01	no f0-f1
2.4906.826	0.3857453	RR1-S	RR01	RR01	no $f_0\pm f_1$, changing?
2.4908.1321	0.3440402	RR01	RR01	RR01
2.4908.826	0.3765790	RR1-PC	RR1-PC	RR1-PC
2.5023.5787	0.3245356	RR1-MC	RR1-MC	RR1-MC	$\Delta \nu_1=.01$29, $\Delta \nu_2=.0$080
2.5023.6558	0.2674391	RR1-S	RR1-S	RR1-S
2.5024.3210	0.3675679	RR1-S	RR1-S	RR01
2.5028.411	0.2809399	RR1-S	RR1-S	RR1-S
2.5031.701	0.2763638	RR1-S	RR1-S	RR1-S
2.5031.766	0.2935514	RR1-S	RR1-S	RR1-S
2.5032.703	0.3077973	RR1-S	RR1-PC?	RR1-BL1
2.5033.535	0.2627292	RR1-S	RR1-D	RR1-D
2.5145.3578	0.3375009	RR1-S	RR1-S	RR1-S
2.5147.1527	0.3353089	RR1-S	RR1-S	RR1-S
2.5148.1207	0.2946848	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0353
2.5148.713	0.3212517	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=.0$007, whitens out
2.5149.515	0.2804797	RR1-S	RR1-S	RR1-S
2.5149.551	0.2993013	RR1-S	RR1-BL1	RR1-S
2.5150.896	0.3371211	RR1-S	RR1-S	RR1-S
2.5151.924	0.3146242	RR1-PC	RR1-PC	RR1-PC
2.5151.939	0.2959491	RR1-S	RR1-S	RR1-S
2.5151.955	0.3837021	RR1-S	RR1-S	RR1-S	+ very weak RR1-PC-like rem.
2.5151.982	0.3445221	RR1-S	RR1-S	RR1-S
2.5152.635	0.3347839	RR1-S	RR1-S	RR1-S
2.5152.763	0.3246989	RR1-S	RR1-S	RR1-D	$\nu_2=1.9773$ strong in b
2.5266.3857	0.3408903	RR1-S	RR1-S	RR1-S
2.5266.3864	0.2793840	RR1-BL1	RR1-BL1	RR1-BL1	+RR1-PC RR1-BL1 changes
2.5269.422	0.3181246	RR1-S	RR1-S	RR1-S	peak at 5.4496??
2.5271.1466	0.3182645	RR1-S	RR1-D	RR1-D
2.5271.1540	0.4394383	RR1-PC	RR1-PC	RR1-PC
2.5271.255	0.4347510	RR1-BL2	RR1-BL2+PC	RR1-BL2+PC	$\Delta f=\pm$0.0012
2.5272.1445	0.3137556	RR1-S	RR1-S	RR1-S
2.5272.1454	0.3171863	RR1-S	RR1-S	RR1-S
2.5272.238	0.3581800	RR01	RR01	RR01
2.5273.1267	0.4208925	RR1-PC	RR1-PC	RR1-PC	wide, $\Delta f\approx\pm$0.0017
2.5273.1356	0.3578176	RR1-S	RR1-S	RR1-S
2.5274.1140	0.3437471	RR1-S	RR1-S	RR1-S
2.5274.1185	0.3550667	RR01	RR01	RR01
2.5388.1150	0.3885822	RR1-PC	RR1-PC	RR1-PC	wide
2.5389.1138	0.3641254	RR01	RR01	RR01
2.5389.1478	0.2505581	RR1-PC	RR1-PC	RR1-PC	$\Delta f=.00$038, symm., whitens out
2.5390.844	0.3163344	RR1-S	RR1-S	RR1-S
2.5391.1359	0.3512177	RR1-S	RR1-S	RR1-S
2.5394.801	0.2870105	RR1-S	RR1-S?	RR1-S
2.5395.855	0.2790402	RR1-S	RR1-BL1	RR1-PC
2.5507.6257	0.3679040	RR1-S	RR1-S	RR1-S
2.5510.1080	0.3543775	RR1-S	RR1-MI?	RR1-S
2.5511.772	0.3029241	RR1-S	RR1-S	RR1-S
2.5513.821	0.3505221	RR1-S	RR1-S	RR1-S
2.5514.660	0.3153734	RR1-PC	RR1-PC	RR1-PC
2.5516.783	0.2615758	RR1-S	RR1-S	RR1-S
2.5628.6071	0.2812632	RR1-S	RR1-S	RR1-S
2.5630.1156	0.3123141	RR1-PC	RR1-PC	RR1-BL2?	$\Delta f=.0004$, whitens out
2.5632.1001	0.2771319	RR1-S	RR1-S	RR1-S
2.5632.931	0.2861475	RR1-S	RR1-S	RR1-S
2.5633.1275	0.2959713	RR1-S	RR1-S	RR1-S
2.5633.1369	0.2937634	RR1-S	RR1-S	RR1-S	peak at $\approx$2$\nu_0-2$
2.5634.989	0.3432276	RR1-S	RR1-S	RR1-S
2.5749.6175	0.3255826	RR1-S	RR1-S	RR1-S
2.5750.3309	0.3117014	RR1-S	RR1-S	RR1-S
2.5751.1094	0.3407763	RR1-S	RR1-S	RR1-S
2.5751.923	0.3233653	RR1-S	RR1-PC	RR1-PC
2.5752.387	0.4592303	RR1-S	RR1-S	RR1-S	peak at $\approx$4.6 in r only
2.5755.839	0.3240553	RR1-S	RR1-S	RR1-S
2.5755.874	0.3080512	RR1-S	RR1-S	RR1-S
2.5758.661	0.2663870	RR1-S	RR1-S	RR1-S	peak at $\approx$1.3 in r only
2.5870.4598	0.3523722	RR1-PC	RR1-PC	RR1-PC	very wide
2.5871.3052	0.3144845	RR1-S	RR1-S	RR1-D
2.5872.1272	0.3626709	RR1-PC	RR1-PC	RR1-PC
2.5873.332	0.2964994	RR1-S	RR1-S	RR1-S
2.5875.1085	0.3418996	RR1-S	RR1-S	RR1-S
2.5875.250	0.3190485	RR1-S	RR1-D	RR1-S
2.5876.444	0.3966802	RR1-PC	RR1-PC	RR1-PC	very wide
2.5876.741	0.2859854	RR1-S	RR1-BL1	RR1-BL1	$\Delta f=-0$.0722
3.6233.503	0.3402755	RR1-S	RR1-S	RR1-S
3.6236.690	0.4356755	RR1-PC	RR1-PC	RR1-PC
3.6238.647	0.3389355	RR1-S	RR1-S	RR1-S
3.6240.450	0.3836371	RR1-BL2	RR1-BL2	RR1-BL2	+RR1-PC $\Delta f=\pm$0.0012
3.6240.470	0.3349953	RR1-PC	RR1-PC	RR1-PC
3.6242.544	0.2709690	RR1-S	RR1-S	RR1-S
3.6243.353	0.2838777	RR1-S	RR1-S	RR1-S
3.6243.404	0.2708506	RR1-D	RR1-D	RR1-D
3.6354.459	0.3600521	RR1-S	RR1-S	RR1-S	+weak RR1-D in r crossID: 80.6354.3448
3.6356.1136	0.3494046	RR1-S	RR1-S	RR1-S
3.6358.619	0.3685809	RR1-S	RR1-S	RR1-S
3.6358.924	0.2849506	RR1-S	RR1-S	RR1-S	peak at $\approx$1.65 in b only
3.6359.900	0.3110378	RR1-S	RR1-S	RR1-S
3.6360.656	0.3545480	RR1-PC	RR1-PC	RR1-PC
3.6362.689	0.3573751	RR1-PC	RR1-PC	RR1-PC
3.6362.753	0.3584007	RR1-S	RR1-MI?	RR1-S
3.6362.766	0.3297486	RR1-S	RR1-S	RR1-S
3.6363.700	0.3403633	RR1-S	RR1-S	RR1-S
3.6364.606	0.3419252	RR1-S	RR1-S	RR1-S
3.6364.637	0.3623667	RR1-S	RR1-S	RR1-S	RR1-MC in b only!!!!
3.6481.718	0.2745777	RR1-S	RR1-S	RR1-S
3.6482.728	0.2954001	RR1-S	RR1-S	RR1-S
3.6597.1167	0.3004253	RR1-S	RR1-S	RR1-S
3.6597.756	0.3086451	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=0.0$0095 crossID: 80.6597.4435
3.6598.939	0.3678199	RR1-PC	RR1-PC	RR1-PC	$\Delta f=\pm$0.0003
3.6602.677	0.3454810	RR1-S	RR1-S	RR1-S
3.6602.827	0.3298892	RR1-S	RR1-S	RR1-S
3.6603.595	0.3439608	RR1-S	RR1-S	RR1-S
3.6603.795	0.2765073	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-0$.0173
3.6717.628	0.3484935	RR1-S	RR1-S	RR1-S
3.6723.769	0.3692349	RR1-PC	RR1-PC	RR1-PC
3.6724.676	0.3413850	RR1-S	RR1-S	RR1-S
3.6725.468	0.3333831	RR1-S	RR1-S	RR1-S
3.6725.519	0.3567805	RR01	RR01	RR01
3.6838.1298	0.3583389	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=\pm$.0004 crossID: 80.6838.2884
3.6839.2073	0.3451022	RR1-S	RR1-S	RR1-S
3.6839.2292	0.3043062	RR1-S	RR1-S	RR1-S	crossID: 80.6839.4533
3.6840.1964	0.3332806	RR1-S	RR1-S	RR1-S
3.6840.330	0.2803475	RR1-S	RR1-S	RR1-S
3.6841.1739	0.3013309	RR1-S	RR1-S	RR1-S
3.6846.1385	0.3324324	RR1-S	RR1-S	RR1-S
3.6847.1380	0.2772299	RR1-S	RR1-BL1?	RR1-S	+peak in b
3.6848.1045	0.2799079	RR1-S	RR1-S	RR1-S
3.6961.824	0.3098935	RR1-D	RR1-D	RR1-D
3.6963.574	0.3580682	RR01	RR01	RR01
3.6964.448	0.3300737	RR1-S	RR1-S	RR1-S
3.6964.499	0.4028749	RR1-S	RR1-S	RR1-S
3.6964.590	0.3820309	RR1-S	RR1-S	RR1-S	RR1-D in b
3.6964.602	0.3347313	RR1-S	RR1-S	RR1-S
3.6965.609	0.3261702	RR1-S	RR1-S	RR1-S
3.6966.427	0.2972764	RR1-S	RR1-BL1	RR1-BL1
3.6966.557	0.3334606	RR1-S	RR1-S	RR1-S
3.7082.957	0.3574617	RR01	RR01	RR01
3.7083.609	0.3247032	RR1-S	RR1-S	RR1-S
3.7088.623	0.3244180	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=\pm$.0006, rem.
3.7089.446	0.3446722	RR1-S	RR1-S	RR1-S
3.7201.504	0.3191092	RR1-S	RR1-S	RR1-S	crossID: 80.7201.3035
3.7202.916	0.3571132	RR01	RR01	RR01	crossID: 80.7202.4678
3.7203.866	0.3669407	RR01	RR01	RR01
3.7205.727	0.3812379	RR1-PC	RR1-PC	RR1-PC
3.7208.477	0.3645413	RR01	RR01	RR01
3.7322.614	0.3180069	RR1-S	RR1-S	RR1-S	crossID: 80.7322.3124
3.7326.897	0.2724766	RR1-S	RR1-S	RR1-S
3.7329.399	0.3725990	RR1-S	RR1-S	RR1-S
3.7331.413	0.2767823	RR1-S	RR1-S	RR1-S
3.7331.467	0.3559271	RR01	RR01	RR01
3.7332.492	0.3495740	RR1-S	RR1-S	RR1-S
3.7444.744	0.3419769	RR1-S	RR1-S	RR1-S
3.7444.782	0.3174510	RR1-PC	RR1-PC	RR1-PC
3.7447.739	0.3490642	RR01	RR01	RR01
3.7448.428	0.3485081	RR01	RR01	RR01
3.7449.447	0.3392843	RR1-S	RR1-S	RR1-S
3.7450.214	0.3919072	RR1-PC	RR1-PC	RR1-PC
3.7451.484	0.3025884	RR1-S	RR1-S	RR1-MI	$\nu_{\rm MI}=0.8361\cdot\nu_0$, in b only
3.7452.501	0.3837212	RR1-S	RR1-S	RR1-S
3.7452.536	0.3432080	RR1-S	RR1-S	RR1-S
3.7453.433	0.3402314	RR1-S	RR1-S	RR1-S
47.1401.225	0.2825295	RR1-S	RR1-S	RR1-D	in b
47.1521.589	0.3587236	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0423
47.1526.209	0.3490908	RR01	RR01	RR01
47.1528.169	0.6626505	RR1-S	RR1-PC	RR1-PC
47.1529.356	0.2723754	RR1-S	RR1-S	RR1-S
47.1529.379	0.3181970	RR1-S	RR1-S	RR1-S
47.1530.341	0.3530136	RR1-S	RR1-S	RR1-S
47.1531.207	0.3347459	RR1-S	RR1-S	RR1-S
47.1643.373	0.3402277	RR1-S	RR1-S	RR1-S
47.1645.407	0.3191876	RR1-S	RR1-S	RR1-PC	alias
47.1647.290	0.3496320	RR01	RR01	RR01
47.1771.401	0.3070320	RR1-S	RR1-S	RR1-S
47.1772.308	0.3262692	RR1-S	RR1-S	RR1-PC	one peak, whitens out, at the $\approx$1/T lim.
47.1883.161	0.3526035	RR1-S	RR1-S	RR1-S
47.2006.1210	0.3474766	RR1-S	RR1-S	RR1-S
47.2013.132	0.2881477	RR1-S	RR1-S	RR1-S
47.2126.530	0.3588453	RR1-S	RR1-S	RR1-S
47.2130.520	0.4049867	RR1-S	RR1-S	RR1-S	alias at $\nu_0+2$
47.2133.446	0.3262074	RR1-S	RR1-S	RR1-S
47.2134.462	0.3276747	RR1-S	RR1-S	RR1-S
47.2247.648	0.3920761	RR01	RR01	RR01
47.2254.504	0.2794452	RR1-S	RR1-S	RR1-S	peak at $\approx$3.1 in b only
47.2368.572	0.3360793	RR1-S	RR1-S	RR1-D	in b
47.2609.56	0.3573236	RR1-BL1	RR01+BL1	RR01+BL1
47.2610.799	0.2811866	RR1-S	RR1-S	RR1-D
47.2611.1088	0.3520640	RR1-S	RR1-S	RR1-D
47.2611.1176	0.3446541	RR1-S	RR1-S	RR1-S
47.2613.1137	0.3619210	RR1-S	RR1-S	RR1-S
47.2619.1486	0.3658715	RR01	RR01	RR01
5.4287.1797	0.3434526	RR1-S	RR1-S	RR1-S
5.4400.1081	0.3322317	RR1-S	RR1-S	RR1-S	crossID: 10.4400.4594
5.4401.1018	0.2685325	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0$047
5.4401.868	0.3530038	RR01	RR01	RR01
5.4402.1009	0.3261942	RR1-S	RR1-S	RR1-S	crossID: 10.4402.4727
5.4407.1348	0.3399189	RR1-S	RR1-S	RR1-S
5.4409.5680	0.3521620	RR1-S	RR1-S	RR1-S
5.4409.5985	0.3296998	RR1-S	RR1-S	RR1-S
5.4521.1005	0.3591018	RR1-S	RR1-S	RR1-S
5.4521.1330	0.3337677	RR1-S	RR1-S	RR1-S
5.4522.1059	0.3589848	RR01	RR01	RR01
5.4524.1212	0.3461996	RR01	RR01	RR01	crossID: 10.4524.4611
5.4524.972	0.3742322	RR1-PC	RR1-PC	RR1-PC
5.4526.966	0.2813246	RR1-S	RR1-S	RR1-S
5.4528.1555	0.2752904	RR1-S	RR1-BL1	RR1-BL1
5.4530.5228	0.3448424	RR1-S	RR1-S	RR1-S
5.4531.4873	0.2914121	RR1-S	RR1-S	RR1-S
5.4642.1017	0.2989019	RR1-S	RR1-BL1?	RR1-S	weak RR1-D
5.4642.902	0.3641288	RR1-S	RR1-S?	RR1-S
5.4645.1196	0.3982278	RR1-S	RR1-S	RR1-S
5.4646.1080	0.2938281	RR1-S	RR1-S	RR1-S
5.4646.1198	0.3220916	RR1-S	RR1-S	RR1-D	+peak at $\approx$4.25 in b only
5.4649.1029	0.3252660	RR1-D	RR1-D	RR1-D
5.4649.1307	0.3293101	RR1-S	RR1-S	RR1-S
5.4765.1125	0.2817559	RR1-S	RR1-S	RR1-S
5.4766.1109	0.3324650	RR1-PC	RR1-PC	RR1-PC
5.4766.1302	0.2736351	RR1-S	RR1-S	RR1-S
5.4766.918	0.3610716	RR1-PC	RR1-PC	RR1-PC
5.4767.1388	0.3078064	RR1-PC	RR1-PC	RR1-PC
5.4767.952	0.3811693	RR01	RR01	RR01
5.4767.962	0.3630248	RR01	RR01	RR01
5.4768.1122	0.3356274	RR1-S	RR1-S	RR1-S
5.4769.1287	0.3442608	RR1-S	RR1-S	RR1-S
5.4769.1363	0.3785277	RR1-PC	RR1-PC	RR1-PC
5.4771.2743	0.4003445	RR1-S	RR1-S	RR1-S
5.4772.5496	0.3420781	RR1-S	RR1-S	RR1-S
5.4885.1316	0.3253087	RR1-S	RR1-BL1	RR1-S
5.4888.796	0.3552391	RR1-S	RR1-S	RR1-S
5.4889.1060	0.2815683	RR1-S	RR1-BL1	RR1-BL1	in b
5.4889.1102	0.4627494	RR01	RR01	RR01
5.4889.921	0.3447723	RR01	RR01	RR01
5.4891.1617	0.3217797	RR1-PC	RR1-PC	RR1-PC
5.4892.3500	0.3581734	RR01	RR01	RR01
5.4893.6682	0.2927763	RR1-S	DD1-D	RR1-S	weak RR1-D
5.5008.1556	0.3866424	RR1-S	RR1-S	RR1-PC
5.5008.1902	0.3774283	RR1-PC	RR1-PC+BL1	RR1-PC+BL1
5.5011.1801	0.2946025	RR1-S	RR1-S	RR1-S	weak RR1-D
5.5013.3494	0.3504694	RR01	RR01	RR01
5.5126.1055	0.3388227	RR1-S	RR1-S	RR1-S
5.5128.1262	0.4279750	RR1-MC	RR1-MC	RR1-MC	$\Delta f_1=\Delta f_2=-.00$10
5.5128.1322	0.3821018	RR1-S	RR1-S	RR1-S
5.5129.1381	0.2687570	RR1-S	RR1-S	RR1-S
5.5129.1451	0.2899344	RR1-S	RR1-S	RR1-D
5.5130.1099	0.3004342	RR1-S	RR1-S	RR1-S
5.5131.1076	0.3227172	RR1-S	RR1-S	RR1-S
5.5131.1128	0.3154071	RR1-S	RR1-S	RR1-S
5.5131.954	0.3576141	RR1-S	RR1-S	RR1-S	+ peak in r only at $\approx$1.2
5.5132.2100	0.3370932	RR1-S	RR1-S	RR1-S
5.5134.3483	0.3473474	RR1-S	RR1-S	RR1-S
5.5134.3773	0.3309423	RR1-S	RR1-S	RR1-S
5.5136.5295	0.3678665	RR01	RR01	RR01
5.5247.894	0.3732139	RR01	RR01	RR01
5.5249.1034	0.3393207	RR1-S	RR1-D	RR1-D
5.5250.1199	0.3574901	RR1-S	RR1-S	RR1-S
5.5250.1501	0.3551757	RR1-PC	RR1-PC	RR1-BL2	symm. $\Delta f =\pm.0005$, whitens out
5.5251.1187	0.3414968	RR1-S	RR1-S	RR1-S
5.5251.1298	0.3171333	RR1-S	RR1-S	RR1-S
5.5251.1676	0.3375434	RR1-S	RR1-S	RR1-S
5.5252.708	0.3663170	RR1-S	RR1-S	RR1-PC
5.5252.890	0.3555672	RR1-S	RR1-S	RR1-S
5.5253.953	0.2853174	RR1-S	RR1-S	RR1-S
5.5254.1692	0.3453603	RR01	RR01	RR01
5.5367.3432	0.2854189	RR1-S	RR1-MC	RR1-BL2	$\Delta f=\pm$0.0296 (no $\Delta\nu_2$)
5.5368.1201	0.3365130	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0056
5.5369.1184	0.3837979	RR01	RR01	RR01
5.5370.1059	0.3522415	RR1-S	RR1-S	RR1-S
5.5371.1247	0.3111854	RR1-S	RR1-S	RR1-D
5.5371.1493	0.3114060	RR1-S	RR1-S	RR1-D	in r
5.5372.1172	0.3322713	RR1-S	RR1-S	RR1-S	weak RR1-D
5.5372.1429	0.3471178	RR01	RR01	RR01
5.5374.1149	0.3177985	RR1-S	RR1-S	RR1-S
5.5375.1852	0.3130981	RR1-S	RR1-S	RR1-S
5.5489.1125	0.3898567	RR1-PC	RR1-PC	RR1-PC
5.5489.1188	0.2920376	RR1-S	RR1-PC	RR1-PC
5.5489.1289	0.3619541	RR01	RR01	RR01
5.5489.1397	0.2899676	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-0$.0478
5.5490.1390	0.2935354	RR1-S	RR1-S	RR1-S
5.5492.1293	0.3943940	RR01	RR01	RR01
5.5492.1482	0.3337507	RR1-S	RR1-S	RR1-S
5.5492.1489	0.3506307	RR1-S	RR1-S	RR1-D
5.5492.1619	0.2661855	RR1-S	RR1-D	RR1-S
5.5493.1455	0.2964112	RR1-S	RR1-S	RR1-S
5.5495.1326	0.3687091	RR1-S	RR1-S	RR1-S
5.5496.1582	0.3454742	RR1-S	RR1-S	RR1-S
5.5496.2445	0.2885515	RR1-S	RR1-S	RR1-S
5.5497.3874	0.2680527	RR1-S	RR1-BL1	RR1-BL1	"+'' is very weak
5.5610.2922	0.3259662	RR1-S	RR1-D	RR1-D	mostly in b
5.5611.2835	0.2944371	RR1-S	RR1-PC	RR1-PC
5.5612.2886	0.3159385	RR1-S	RR1-S	RR1-S
5.5614.3014	0.3327409	RR1-S	RR1-S	RR1-S
6.5721.289	0.3355822	RR1-S	RR1-S	RR1-S	crossID: 13.5721.2108
6.5721.310	0.2974560	RR1-S	RR1-S	RR1-S	crossID: 13.5721.2163
6.5721.352	0.3766420	RR01	RR01	RR01	crossID: 13.5721.2290
6.5722.682	0.2944694	RR1-S	RR1-S	RR1-S	crossID: 13.5722.3565
6.5724.620	0.3829355	RR1-PC	RR1-PC	RR1-PC
6.5724.869	0.3340855	RR1-S	RR1-S	RR1-S
6.5724.887	0.3019672	RR1-S	RR1-S	RR1-S
6.5727.790	0.2684920	RR1-S	RR1-S	RR1-D
6.5728.1012	0.3413199	RR1-S	RR1-S	RR1-S
6.5728.873	0.2709565	RR1-S	RR1-S	RR1-S
6.5729.1008	0.3501063	RR1-PC	RR1-PC	RR1-PC
6.5729.958	0.2778179	RR1-BL1	RR1-BL1+MI	RR1-BL1	$\Delta f=+0$.0742
6.5730.3852	0.3986377	RR1-S	RR1-S	RR1-S
6.5730.3869	0.3551622	RR01	RR01	RR01
6.5730.4053	0.3463310	RR1-S	RR1-S	RR1-S
6.5730.4057	0.2763214	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=+0.$0776
6.5731.4354	0.2412002	RR1-S	RR1-S	RR1-S
6.5732.3906	0.3523542	RR01	RR01	RR01
6.5842.396	0.3604255	RR01	RR01	RR01	crossID: 13.5842.2316
6.5844.872	0.3702682	RR1-PC	RR1-PC	RR1-PC	crossID: 13.5844.3963
6.5846.967	0.3394754	RR1-S	RR1-S	RR1-S	peak in r at $\approx$2$\nu_0$
6.5847.252	0.2890379	RR1-S	RR1-D	RR1-D
6.5848.1122	0.3591429	RR1-PC	RR1-PC	RR1-PC
6.5849.1114	0.2553474	RR1-S	RR1-S	RR1-S
6.5849.1135	0.3132256	RR1-S	RR1-PC	RR1-PC
6.5850.1081	0.3335893	RR1-S	RR1-S	RR1-BL1	$\Delta f=-0$.2283
6.5850.1195	0.3315815	RR1-S	RR1-S	RR1-S
6.5850.1436	0.2720254	RR1-S	RR1-S	RR1-S
6.5850.933	0.3730655	RR01	RR01	RR01
6.5851.3773	0.3209512	RR1-S	RR1-S	RR1-S
6.5852.4852	0.3431204	RR1-S	RR1-S	RR1-S	peak in b at $\approx$2$\nu_0$
6.5852.4915	0.3562610	RR1-S	RR1-S	RR1-S
6.5852.5312	0.3057469	RR1-S	RR1-S	RR1-S
6.5853.3986	0.3554134	RR01	RR01	RR01
6.5963.363	0.2764715	RR1-S	RR1-S	RR1-S	crossID: 13.5963.2479
6.5965.835	0.3169592	RR1-S	RR1-S	RR1-S	crossID: 13.5965.3725
6.5965.890	0.3669381	RR1-S	RR1-S	RR1-D	mostly in b; crossID: 13.5965.3700
6.5966.757	0.3132610	RR1-S	RR1-S	RR1-S
6.5966.886	0.3393764	RR1-S	RR1-S	RR1-S
6.5968.1603	0.3851853	RR1-S	RR1-S	RR1-S
6.5971.1194	0.4009782	RR1-PC	RR1-PC	RR1-PC
6.5971.1233	0.2877179	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0735 + al.2$\nu_0$ + fm
6.5971.1408	0.3712570	RR01	RR01	RR01
6.5972.5021	0.2826945	RR1-S	RR1-S	RR1-S
6.5974.3945	0.3725992	RR1-S	RR1-S	RR1-D	+strange stuff in b
6.6084.462	0.3067477	RR1-S	RR1-S	RR1-S	crossID: 13.6084.2519
6.6085.884	0.3195912	RR1-S	RR1-S	RR1-S
6.6086.792	0.3480795	RR01	RR01	RR01
6.6087.966	0.2831662	RR1-S	RR1-S	RR1-PC
6.6089.1661	0.3591991	RR01	RR01	RR01
6.6089.1737	0.3477483	RR1-S	RR1-S	RR1-S
6.6091.1198	0.2668322	RR1-S	RR1-BL1	RR1-BL1	$\Delta f=\pm$0.0754, "+'' is weak
6.6091.1245	0.3474788	RR1-S	RR1-S	RR1-S	+strange peak in r
6.6091.877	0.3206106	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-0$.0385
6.6092.1311	0.3547291	RR1-S	RR1-S	RR1-S	+ strange stuff in b
6.6093.5030	0.2653642	RR1-D	RR1-D	RR1-D	P(A00)$\ne$P(SAM)
6.6094.5331	0.3356851	RR1-PC	RR1-PC	RR1-PC
6.6094.5406	0.2851642	RR1-PC	RR1-PC	RR1-PC
6.6094.5606	0.3393854	RR1-PC	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0012? (+very weak RR1-PC)
6.6208.869	0.3321579	RR1-S	RR1-S	RR1-S	peak in r at $\approx$1.82
6.6209.727	0.2718806	RR1-S	RR1-S	RR1-S
6.6210.1695	0.3391681	RR1-S	RR1-S	RR1-S
6.6210.1712	0.3189901	RR1-S	RR1-S	RR1-S	weak RR1-D in r
6.6212.1063	0.3602799	RR01	RR01	RR01
6.6212.1142	0.3732319	RR1-PC	RR1-PC	RR1-PC
6.6212.1454	0.2820694	RR1-S	RR1-S	RR1-S
6.6213.1506	0.3374679	RR1-S	RR1-S	RR1-S
6.6213.1520	0.3156754	RR1-S	RR1-S	RR1-S	RR1-D in b
6.6213.1685	0.3050434	RR1-S	RR1-S	RR1-S
6.6214.4637	0.3491769	RR01	RR01	RR01
6.6214.5338	0.2819035	RR1-S	RR1-S	RR1-S
6.6215.5777	0.2848354	RR1-S	RR1-S	RR1-S
6.6215.6520	0.2787094	RR1-S	RR1-S	RR1-S
6.6326.424	0.3304519	RR1-BL1	RR1-BL1	RR1-BL1+PC	$\Delta f=-0$.0726, crossID: 13.6326.2765
6.6329.884	0.3597879	RR01	RR01	RR01
6.6331.238	0.3448059	RR1-S	RR1-S	RR1-S
6.6333.912	0.3483025	RR1-S	RR1-S	RR1-S
6.6335.5311	0.3377354	RR1-S	RR1-S	RR1-S
6.6336.6017	0.3565227	RR1-S	RR1-S	RR1-S
6.6447.699	0.3501959	RR1-S	RR1-S	RR1-PC	alias, crossID: 13.6447.3202
6.6448.801	0.3431581	RR1-S	RR1-S	RR1-S	stuff at 1.54, crossID: 13.6448.4137
6.6450.888	0.3437111	RR1-S	RR1-D	RR1-D	in b
6.6451.919	0.4020766	RR1-PC	RR1-PC+MC?	RR1-PC	wide
6.6452.2394	0.3348319	RR1-PC	RR1-PC	RR1-PC
6.6452.704	0.3540965	RR01	RR01	RR01
6.6452.811	0.3617118	BI	BI	BI	light curve $\approx$sinusoidal, $\nu_1$/$\nu_0=1/2$
6.6453.1387	0.2819384	RR1-S	RR1-S	RR1-PC
6.6455.1326	0.3356315	RR1-PC	RR1-PC	RR1-PC
6.6455.1877	0.2962379	RR1-S	RR1-D	RR1-D
6.6456.5690	0.2941663	RR1-S	RR1-S	RR1-S
6.6457.6650	0.3186543	RR1-S	RR1-D	RR1-D	in r
6.6568.484	0.3380989	RR1-PC	RR1-PC	RR1-PC	crossID: 13.6568.3005
6.6569.955	0.3150184	RR1-S	RR1-S	RR1-S	crossID: 13.6569.4284
6.6569.980	0.3432539	RR1-S	RR1-D	RR1-D	in b, crossID: 13.6569.4088
6.6570.751	0.3502577	RR1-S	RR1-S	RR1-S
6.6571.851	0.2717850	RR1-S	RR1-S	RR1-S
6.6572.919	0.3756908	RR01	RR01	RR01
6.6574.1353	0.3585347	RR01	RR01	RR01
6.6576.1701	0.3082586	RR1-S	RR1-S	RR1-S
6.6576.558	0.2692476	RR1-S	RR1-D	RR1-D
6.6689.563	0.3050574	RR1-S	RR1-S	RR1-D	weak $\nu_2$ in b, crossID: 13.6689.3055
6.6690.945	0.3417750	RR1-S	RR1-S	RR1-D
6.6692.937	0.3568799	RR1-PC	RR1-PC	RR1-PC
6.6693.1075	0.2963217	RR1-S	RR1-S	RR1-S
6.6697.1361	0.3973327	RR1-PC	RR1-PC	RR1-PC	very wide
6.6697.1565	0.4334935	RR1-MC	RR1-MC	RR1-MC	$\Delta\nu_1\pm=.00$124, $\Delta \nu_2=\pm$.0005
6.6697.1859	0.3072472	RR1-S	RR1-S	RR1-S
6.6699.5598	0.3526863	RR1-D	RR1-D	RR1-D
6.6699.5619	0.3304007	RR1-S	RR1-S	RR1-S
6.6699.6734	0.2915436	RR1-S	RR1-S	RR1-S
6.6810.428	0.3814159	RR01	RR01	RR01	crossID: 13.6810.2845
6.6810.616	0.2883850	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=\pm$.0004, wh., crossID: 13.6810.2981
6.6811.481	0.3559612	RR1-S	RR1-S	RR1-S
6.6811.651	0.3598909	RR01	RR01	RR01	crossID: 13.6811.4041
6.6812.1063	0.3165557	RR1-S	RR1-S	RR1-S
6.6812.923	0.3547845	RR1-PC	RR1-PC	RR1-MC
6.6812.929	0.3212383	RR1-S	RR1-S	RR1-S	+weak RR1-D
6.6813.699	0.3825721	RR1-PC	RR1-PC	RR1-PC
6.6813.807	0.2688031	RR1-S	RR1-S	RR1-S
6.6814.901	0.2999740	RR1-S	RR1-S	RR1-S
6.6815.747	0.2920236	RR1-D	RR1-D	RR1-D
6.6815.788	0.3260021	RR1-S	RR1-S	RR1-S
6.6819.6629	0.3393739	RR1-S	RR1-S	RR1-S
6.6819.6763	0.2843131	RR1-S	RR1-PC	RR1-PC
6.6819.7278	0.2845135	RR1-S	RR1-D	RR1-D
6.6820.7288	0.2882788	RR1-S	RR1-S	RR1-S
6.6820.7412	0.2948450	RR1-S	RR1-S	RR1-S
6.6820.7594	0.3178720	RR1-S	RR1-S	RR1-S
6.6931.649	0.3228060	RR1-D	RR1-D	RR1-D	crossID: 13.6931.3278
6.6931.655	0.3154455	RR1-S	RR1-S	RR1-S	+weak RR1-D in b, crossID: 13.6931.3219
6.6931.704	0.3590484	RR1-S	RR1-S	RR1-S	crossID: 13.6931.3165
6.6933.1043	0.3228416	RR1-PC	RR1-PC	RR1-PC
6.6933.939	0.3454407	RR01	RR01	RR01
6.6934.1056	0.3376670	RR1-S	RR1-S	RR1-S
6.6936.2825	0.2737831	RR1-S	RR1-S	RR1-S
6.6937.1264	0.3655773	RR1-S	RR1-S	RR1-S
6.6937.1923	0.3348225	RR1-S	RR1-S	RR1-S
6.6938.1574	0.3219262	RR1-S	RR1-S	RR1-S
6.6938.1698	0.3392113	RR1-S	RR1-D	RR1-D
6.6938.1809	0.3432712	RR1-S	RR1-S	RR1-S
6.7054.710	0.3129435	RR1-S	RR1-S	RR1-S	crossID: 13.7054.3006
6.7054.713	0.4404073	RR1-BL2	RR1-BL2	RR1-BL2+PC	$\Delta f=\pm$0.0016
6.7055.814	0.3506573	RR1-S	RR1-S	RR1-S
6.7056.785	0.3492702	RR1-S	RR1-S	RR1-S
6.7056.836	0.4476160	RR1-S	RR1-D	RR1-BL2	$\Delta f=\pm$0.0011, + weak RR1-D
6.7056.952	0.3344727	RR1-S	RR1-S	RR1-S
6.7058.1128	0.3244414	RR1-S	RR1-S	RR1-S
6.7059.995	0.3156189	RR1-S	RR1-S	RR1-S
80.6231.667	0.3557524	RR1-S	RR1-S	RR1-S
80.6233.2102	0.2673977	RR1-S	RR1-D	RR1-D	in b, +peak at .4017 in b
80.6345.7307	0.2941656	RR1-S	RR1-D	RR1-D	$\nu_1=2.$00
80.6346.2144	0.4649030	RR01	RR01	RR01	$\nu_1>\nu_0$
80.6348.1413	0.3046775	RR1-S	RR1-D?	RR1-D	in b
80.6348.1828	0.3564758	RR1-S	RR1-S	RR1-S
80.6348.2470	0.3381670	RR1-S	RR1-S	RR1-MI	peak in b at 1.2
80.6349.2365	0.3394050	RR1-S	RR1-S	RR1-S	double peak at $\approx$2$\nu_0$
80.6350.1072	0.3346674	RR1-S	RR1-D	RR1-D
80.6350.3508	0.3900628	RR1-PC	RR1-PC	RR1-PC
80.6351.2358	0.3393575	RR1-S	RR1-S	RR1-S
80.6352.1495	0.3079889	RR1-BL1	RR1-BL1	RR1-BL1+PC	both are changing
80.6353.1048	0.3071428	RR1-S	RR1-S	RR1-D	in b
80.6353.1458	0.2753242	RR1-D	RR1-D	RR1-D
80.6354.3448	0.3600498	RR1-S	RR1-S	RR1-D	crossID: 3.6354.459
80.6354.3658	0.3242243	RR1-S	RR1-BL1?	RR1-S
80.6355.5162	0.3444493	RR1-S	RR1-S	RR1-S
80.6468.1883	0.3346678	RR1-S	RR1-S	RR1-S
80.6468.2765	0.3493692	RR1-PC	RR1-PC	RR1-PC	wide
80.6469.2447	0.3314219	RR1-S	RR1-D	RR1-D	in b
80.6470.2000	0.3706713	RR1-S	RR1-PC	RR1-BL2
80.6472.1694	0.3284227	RR1-S	RR1-S	RR1-S
80.6475.3548	0.3266714	RR1-S	RR1-S	RR1-S
80.6589.1879	0.2499859	RR1-S	RR1-D	RR1-S	weak RR1-D in b
80.6589.2425	0.3497221	RR1-S	RR1-S	RR1-S
80.6590.1844	0.3511759	RR01	RR01	RR01
80.6590.1980	0.3453431	RR1-S	RR1-S	RR1-S
80.6590.2058	0.3138516	RR1-S	RR1-S	RR1-S
80.6591.2357	0.3345161	RR1-S	RR1-S	RR1-S
80.6595.1558	0.3412933	RR1-S	RR1-S	RR1-S
80.6595.1599	0.3323705	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=\pm$0.0368
80.6596.3127	0.2965595	RR1-S	RR1-S	RR1-PC
80.6597.4435	0.3086445	RR1-PC	RR1-BL1	RR1-BL2	crossID: 3.6597.756
80.6597.4461	0.2635343	RR1-S	RR1-S	RR1-S
80.6597.4703	0.3001928	RR1-S	RR1-PC	RR1-S
80.6708.6771	0.2860939	RR1-D	RR1-D	RR1-D
80.6708.6879	0.3139923	RR1-S	RR1-D	RR1-D
80.6709.2322	0.3325378	RR1-D	RR1-D	RR1-S	weak RR1-D in r
80.6710.2075	0.3478087	RR1-S	RR1-D	RR1-S
80.6712.1521	0.3038647	RR1-S	RR1-S	RR1-S	weak RR1-D in r
80.6712.1806	0.3365525	RR1-S	RR1-S	RR1-S
80.6830.2303	0.3676399	RR01	RR01	RR01
80.6832.2030	0.2843896	RR1-S	RR1-S	RR1-S
80.6835.1144	0.3410573	RR1-S	RR1-S	RR1-D
80.6835.1220	0.3502291	RR1-PC	RR1-PC	RR1-PC
80.6835.1442	0.3651713	RR1-S	RR1-S	RR1-PC?	weak
80.6836.1492	0.3720830	RR01	RR01	RR01
80.6837.1444	0.3257803	RR1-S	RR1-D	RR1-D	in r
80.6838.2884	0.3583390	RR1-PC	RR1-PC	RR1-BL2	symmetric, crossID: 3.6838.1298
80.6839.4533	0.3043054	RR1-S	RR1-S	RR1-S	crossID: 3.6839.2292
80.6950.6196	0.3021638	RR1-S	RR1-D	RR1-D
80.6950.6414	0.3384454	RR1-PC	RR1-PC	RR1-PC
80.6950.6751	0.2778871	RR1-S	RR1-S	RR1-D	in r
80.6951.2395	0.3114197	RR1-PC	RR1-PC	RR1-BL2	symmetric
80.6953.1499	0.3061991	RR1-S	RR1-D	RR1-D
80.6953.1590	0.4061294	RR1-PC	RR1-PC	RR1-PC
80.6953.1751	0.3517135	RR1-BL2	RR1-BL2	RR1-BL2+PC	$\Delta f=0.0$280
80.6954.1181	0.2863514	RR1-S	RR1-S	RR1-D	in r
80.6954.1386	0.3015044	RR1-S	RR1-S	RR1-S
80.6957.409	0.4078831	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=.00$08, not exactly symm.
80.6958.1037	0.2752632	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=.03$43
80.6959.3673	0.3311194	RR1-S	RR1-S	RR1-S
80.7071.5289	0.3572094	RR01	RR01	RR01
80.7072.1233	0.3677101	RR01	RR01	RR01
80.7072.1545	0.3583444	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=\pm$0.0013
80.7072.2154	0.3608532	RR01	RR01	RR01
80.7072.2280	0.2786360	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-0$.0472
80.7073.1658	0.3478323	RR01	RR01	RR01
80.7073.2115	0.3524070	RR1-S	RR1-S	RR1-S	weak RR1-D in r
80.7074.1175	0.3059442	RR1-S	RR1-D	RR1-D	in b + peak at 1.2 in b
80.7075.1977	0.3284916	RR1-S	RR1-S	RR1-D	in r
80.7077.750	0.4043715	RR1-S	RR1-S	RR1-S
80.7192.3592	0.4059588	RR1-PC	RR1-PC	RR1-PC	wide, asymm. P = 0.40599526?
80.7192.4319	0.3495739	RR1-S	RR1-S	RR1-D	in b
80.7192.4927	0.3162052	RR1-S	RR1-S	RR1-S
80.7193.1485	0.3288181	RR01	RR01	RR01	$\nu_1=3.04$,$\nu_0=2.2$6
80.7195.1166	0.3107549	RR1-PC	RR1-PC	RR1-PC
80.7200.1403	0.2615610	RR1-S	RR1-S	RR1-S	+ rem at $\nu_0$ in r
80.7200.997	0.3092638	RR1-S	RR1-S	RR1-S
80.7201.3035	0.3191099	RR1-S	RR1-S	RR1-S	crossID: 3.7201.504
80.7202.4678	0.3571148	RR01	RR01	RR01	crossID: 3.7202.916
80.7313.3932	0.3406024	RR1-S	RR1-D	RR1-D	$\nu_1=4.0$08
80.7313.4672	0.3681655	RR01	RR01	RR01
80.7314.1485	0.3081994	RR1-S	RR1-S	RR1-S
80.7315.1237	0.3191161	RR1-S	RR1-PC	RR1-PC
80.7315.1538	0.3533676	RR01	RR01	RR01
80.7316.1285	0.3655236	RR01	RR01	RR01
80.7319.1287	0.2978598	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=.0$009
80.7320.1224	0.3397082	RR1-S	RR1-S	RR1-S
80.7321.1365	0.3706183	RR01	RR01	RR01
80.7322.3124	0.3180059	RR1-S	RR1-S	RR1-S	crossID: 3.7322.614
80.7434.4258	0.3357009	RR1-S	RR1-S	RR1-S
80.7436.1309	0.3692421	RR1-S	RR1-S	RR1-PC
80.7436.1463	0.3025085	RR1-PC	RR1-PC	RR1-PC
80.7436.1633	0.3304713	RR1-PC	RR1-PC	RR1-PC
80.7437.1665	0.3377207	RR1-S	RR1-S	RR1-S
80.7437.1678	0.2781401	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=-.0$889, weak RR1-MC too
80.7439.1826	0.3943811	RR01	RR01	RR01
80.7439.1836	0.4622122	RR01	RR01	RR01	$\nu_1>\nu_0$
80.7440.1192	0.3430250	RR1-PC	RR1-PC	RR1-BL2
80.7441.933	0.2733126	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=.0$480
80.7441.960	0.3689460	RR01	RR01	RR01
80.7444.3505	0.3174408	RR1-PC	RR1-PC	RR1-PC
80.7556.850	0.3413911	RR1-S	RR1-S	RR1-PC	weak
80.7558.650	0.3593405	RR1-S	RR1-S	RR1-MI	MI in r
80.7563.516	0.3420220	RR1-S	RR1-PC	RR1-PC	symm., $\Delta f=.0$0045
81.8396.1664	0.3507728	RR1-S	RR1-S	RR1-S
81.8398.799	0.3265745	RR1-S	RR1-S	RR1-S
81.8400.901	0.2739736	RR1-S	RR1-BL1	RR1-BL1
81.8401.496	0.2883848	RR1-S	RR1-S	RR1-S
81.8515.2414	0.3496134	RR1-S	RR1-S	RR1-S	+weak RR1-D
81.8515.3056	0.3352154	RR1-S	RR1-S	RR1-S
81.8518.1621	0.4106231	RR1-PC	RR1-PC	RR1-PC
81.8518.970	0.3085487	RR1-S	RR1-BL1	RR1-BL1+PC	both PC, $\Delta f=-0.0$150
81.8519.1395	0.3393985	RR1-D	RR1-D	RR1-MI	peak at 0.8372 only in r
81.8520.1634	0.3132956	RR1-S	RR1-PC	RR1-PC
81.8521.1454	0.3094402	RR1-D	RR1-D	RR1-D	in r
81.8635.2066	0.3388585	RR1-S	RR1-S	RR1-S
81.8635.2229	0.3172088	RR1-S	RR1-MI	RR1-S	strange peak at $\nu_0\cdot0.6$965
81.8636.1973	0.3696486	RR1-S	RR1-S	RR1-S
81.8638.2973	0.3185128	RR1-S	RR1-S	RR1-S
81.8639.1450	0.3352574	RR01	RR01	RR01
81.8639.1749	0.3759094	RR1-BL2	RR1-PC+BL2	RR1-PC+BL2	$\Delta f=.0$448, $\Delta f=.0$005
81.8639.662	0.2852523	RR1-S	RR1-S	RR1-S
81.8640.1359	0.3250148	RR1-S	RR1-S	RR1-D	+ peak at 2.3 in r
81.8641.1339	0.2969103	RR1-S	RR1-D	RR1-D	in b
81.8642.1238	0.3674166	RR1-S	RR1-S	RR1-S
81.8642.1384	0.3407948	RR1-S	RR1-S	RR1-S
81.8643.1218	0.2927151	BI	RR1-S?	RR1-S	p. in r at 5.01 RR1-D?
81.8758.1447	0.4562457	RR1-BL2	RR1-BL2	RR0-BL2	$\Delta f=.0$298, 2 $\nu_0-\Delta f$ too, lc.
81.8759.832	0.3038356	RR1-S	RR1-S	RR1-BL1	$\Delta f=+0$.0744
81.8760.1697	0.3964948	RR1-S	RR1-S	RR1-S
81.8761.2328	0.3909220	RR1-S	RR0-S	RR0-BL1	$\Delta f=.0$007, 2 $\nu_0-\Delta f$ too, lc.
81.8762.1416	0.3400559	RR1-S	RR1-S	RR1-S
81.8764.909	0.2966042	RR1-S	RR1-S	RR1-S
81.8875.2038	0.4057937	RR1-PC	RR1-PC	RR1-PC
81.8876.2820	0.3511419	RR1-S	RR1-S	RR1-S
81.8879.1869	0.2975649	RR1-PC	RR1-PC	RR1-BL2	$\Delta f=\pm$0.0008
81.8879.2137	0.3264594	RR1-S	RR1-D	RR1-S	+weak RR1-D
81.8881.1370	0.4093554	RR1-S	RR1-S	RR1-S	alias in b
81.8882.1067	0.3491217	RR01	RR01	RR01
81.8882.1422	0.3353903	RR1-S	RR1-S	RR1-S
81.8884.1212	0.3703148	RR1-S	RR1-S	RR1-S
81.8885.1203	0.2817928	RR1-S	RR1-S	RR1-S	weak RR1-D in r,+ stuff in b
81.9001.2673	0.3558753	RR1-S	RR1-S	RR1-S
81.9004.1177	0.3180302	RR1-PC	RR1-PC	RR1-PC
81.9117.1184	0.3295384	RR1-S	RR1-D	RR1-D
81.9118.1794	0.3501430	RR01	RR01	RR01
81.9120.1324	0.3350516	RR1-S	RR1-S	RR1-S
81.9121.1477	0.3001045	RR1-S	RR1-S	RR1-S
81.9123.806	0.3853143	RR1-PC	RR1-PC	RR1-PC
81.9247.1035	0.2910902	RR1-S	RR1-S	RR1-S
81.9247.1164	0.3268370	RR1-S	RR1-S	RR1-S
81.9247.1293	0.3928922	RR1-S	RR1-S	RR1-S
81.9248.1307	0.3235209	RR1-S	RR1-S	RR1-S
81.9366.1335	0.3098233	RR1-S	RR1-S	RR1-D	in b
81.9368.944	0.3381468	RR1-S	RR1-S	RR1-S
81.9481.624	0.3967379	BI	BI	BI	light curve
81.9482.1608	0.3502312	RR1-S	RR1-S	RR1-S
81.9484.1382	0.2713864	RR1-S	RR1-S	RR1-S
81.9486.734	0.3008852	RR1-S	RR1-PC	RR1-PC	alias
81.9601.1319	0.3241070	RR1-S	RR1-S	RR1-S	peak in r at $\approx$3.85
81.9603.1133	0.3397803	RR1-S	RR1-S	RR1-S
81.9604.1054	0.2801471	RR1-S	RR1-S	RR1-S
81.9611.399	0.4005153	RR1-S	RR1-PC	RR1-PC
81.9723.796	0.3369516	RR1-PC	RR1-PC	RR1-PC	wide
81.9723.894	0.3886024	RR1-PC	RR1-PC	RR1-PC	+ very weak RR1-BL1
81.9724.295	0.3538641	RR1-PC	RR1-PC	RR1-PC	wide
82.7920.1074	0.3386711	RR1-S	RR1-S	RR1-BL1	weak
82.7921.759	0.3564993	RR1-S	RR1-S	RR1-D	mostly in b
82.7921.822	0.3497370	RR1-S	RR1-S	RR1-S
82.7921.827	0.3281433	RR1-S	RR1-S	RR1-S
82.7922.520	0.3635551	RR01	RR01	RR01
82.7922.838	0.3253781	RR1-S	RR1-S	RR1-S
82.7924.1100	0.3090396	RR1-S	RR1-S	RR1-S	weak p. in r at $\approx$2$\nu_0-1$
82.7928.580	0.3521369	RR1-S	RR1-S	RR1-D
82.8040.1189	0.2979495	RR1-S	RR1-D	RR1-D	in b
82.8041.1029	0.4067153	RR1-PC	RR1-PC	RR1-PC
82.8042.1304	0.2885570	RR1-S	RR1-S	RR1-S
82.8043.1209	0.3339364	RR1-S	RR1-S	RR1-PC
82.8043.1438	0.3055072	RR1-S	RR1-S	RR1-S
82.8046.1235	0.3144617	RR1-S	RR1-S	RR1-S	weak RR1-D
82.8047.999	0.3409796	RR1-S	RR1-S	RR1-S
82.8048.806	0.3462522	RR1-S	RR1-D	RR1-D	peak in b at $\approx$2$\nu_0$
82.8049.746	0.2987354	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=.07$20, 2 $\nu_0-\Delta f$ too
82.8049.898	0.3662099	RR01	RR01	RR01
82.8160.3605	0.2756421	RR1-S	RR1-S	RR1-S	P(A00)$\ne$P(SAM)
82.8161.1231	0.4045666	RR1-S	RR1-PC	RR1-PC	strong aliasing
82.8163.1039	0.3677745	RR01	RR01	RR01
82.8163.1275	0.2637632	RR1-S	RR1-S	RR1-S
82.8164.932	0.2781573	RR1-S	RR1-S	RR1-S
82.8167.864	0.3933491	RR1-S	RR1-BL1?	RR1-PC	around 2$\nu_0$ too
82.8168.1006	0.3531867	RR1-S	RR1-S	RR1-S
82.8168.1014	0.3709171	RR1-S	RR1-S	RR1-S
82.8168.1144	0.3335168	RR1-S	RR1-S	RR1-D	weak, P(A00)$\ne$P(SAM)
82.8169.1038	0.2954577	RR1-S	RR1-S	RR1-S
82.8169.654	0.3539979	RR01	RR01	RR01
82.8282.1019	0.3271100	RR1-PC	RR1-PC	RR1-PC
82.8283.1040	0.3700767	RR1-PC	RR1-PC	RR1-PC
82.8284.1105	0.3421157	RR1-S	RR1-S	RR1-S
82.8285.733	0.3505385	RR1-S	RR1-S	RR1-S
82.8285.967	0.3923695	RR1-S	RR1-S	RR1-S
82.8286.1733	0.3403737	RR1-S	RR1-S	RR1-S
82.8286.1784	0.3285773	RR1-S	RR1-PC	RR1-BL1	one peak, whitens out
82.8288.869	0.3740560	RR1-PC	RR1-PC	RR1-PC
82.8289.887	0.2829623	RR1-BL1	RR1-BL1	RR1-MC	$\Delta\nu_1=-.1896$ $\Delta\nu_2=\Delta\nu_1$/2
82.8289.894	0.2765946	RR1-S	RR1-S?	RR1-S
82.8289.975	0.3191820	RR1-S	RR1-S	RR1-S
82.8291.748	0.3453027	RR1-S	RR1-S	RR1-S
82.8403.1229	0.3638096	RR1-S	RR1-S	RR1-D
82.8403.1251	0.2821401	RR1-S	RR1-D	RR1-D	mostly in r
82.8406.1180	0.3738827	RR1-PC	RR1-PC	RR1-PC
82.8407.1628	0.3761618	RR1-S	RR1-S	RR1-S
82.8407.312	0.3563439	RR1-S	RR1-D	RR1-BL1	$\Delta f=.0$008
82.8408.1002	0.2962930	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=.0$354
82.8410.986	0.3483861	RR01	RR01	RR01
82.8411.841	0.3394055	RR1-S	RR1-S	RR1-S
82.8525.1778	0.3518382	RR1-S	RR1-S	RR1-S
82.8525.1980	0.2833982	RR1-MI	RR1-S	RR1-BL1	$\Delta f=0.0$841
82.8526.1176	0.3238862	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.1$270
82.8527.1433	0.3384423	RR1-S	RR1-S	RR1-S
82.8530.1009	0.4020850	RR1-S	RR1-S	RR1-PC	in r
82.8533.1307	0.2806150	RR1-S	RR1-D	RR1-D
82.8646.1074	0.3456339	RR1-S	RR1-S	RR1-S
82.8646.1162	0.3446226	RR1-S	RR1-S	RR1-S
82.8652.908	0.3729295	RR1-S	RR1-S	RR1-S
82.8765.1250	0.3049238	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=0.0$490,+weak RR1-PC
82.8766.1305	0.2592516	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=.0$031
82.8886.1146	0.3570008	RR01	RR01	RR01
82.8889.452	0.3601860	RR01	RR01	RR01
82.8890.449	0.4400493	RR1-PC	RR1-PC	RR1-PC	aliases
82.8894.808	0.3412773	RR1-S	RR1-S	RR1-S
82.9015.1092	0.3013519	RR1-S	RR1-S	RR1-S
82.9016.731	0.3041599	RR1-S	RR1-S	RR1-S
82.9017.426	0.3222430	RR1-S	RR1-PC	RR1-PC
82.9130.408	0.3490416	RR1-S	RR01?	RR1-S
82.9138.552	0.3516634	RR1-S	RR1-PC	RR1-S
9.4270.541	0.3193464	RR1-S	RR1-S	RR1-S
9.4270.685	0.2773749	RR1-S	RR1-S	RR1-S
9.4273.1378	0.3606228	RR1-S	RR1-S	RR1-S
9.4274.644	0.2636423	RR1-S	RR1-S	RR1-BL1	$\Delta f=\pm$.1230, "+'' is weak, in b
9.4275.536	0.3530716	RR01	RR01	RR01
9.4276.488	0.3301639	RR1-S	RR1-S	RR1-S	crossID: 10.4276.3455
9.4278.179	0.3268162	MDM	MDM	MDM	V18.92 R18.01
9.4390.560	0.4110355	RR1-PC	RR1-PC	RR1-PC
9.4392.625	0.3445635	RR1-S	RR1-PC	RR1-PC
9.4392.833	0.3034402	RR1-PC	RR1-PC	RR1-PC
9.4393.761	0.2755079	RR1-S	RR1-S	RR1-S
9.4394.386	0.2907779	RR1-PC	RR1-PC	RR1-PC	aliases
9.4398.729	0.3048604	RR1-S	RR1-S	RR1-S	crossID: 10.4398.4446
9.4398.852	0.3325725	RR1-S	RR1-S	RR1-S	crossID: 10.4398.4412
9.4512.701	0.3446228	RR1-S	RR1-S	RR1-S	weak p. in b at $\approx$.9
9.4513.866	0.2852547	RR1-S	RR1-S	RR1-S
9.4514.979	0.3574786	RR01	RR01	RR01
9.4516.965	0.3125994	RR1-S	RR1-S	RR1-D	double peak
9.4516.980	0.2741678	RR1-S	RR1-D	RR1-D	in b
9.4520.778	0.2852016	RR1-S	RR1-D	RR1-D	in b, crossID: 10.4520.4862
9.4520.952	0.3365915	RR1-S	RR1-S	RR1-S	+ stuff in b, crossID: 10.4520.5022
9.4632.592	0.2802225	RR1-S	RR1-S	RR1-S	+weak RR1-D in r
9.4632.731	0.2775501	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=0.0$0668
9.4632.793	0.3406884	RR1-S	RR1-S	RR1-S	+ weak peak in r at $\approx$2.2
9.4634.863	0.3981110	RR1-PC	RR1-PC	RR1-PC	+very weak RR1-BL1, 6.21, +.0963
9.4635.790	0.3607762	RR1-S	RR1-S	RR1-D	in b
9.4635.878	0.3463833	RR01	RR01	RR01
9.4636.1979	0.3933065	RR1-S	RR1-PC?	RR1-BL1	$\Delta f=.0$005, whitens out
9.4638.870	0.3307464	RR1-S	RR1-S	RR1-S	+str. in b at $\nu_0$/$\nu_1=.7$013
9.4639.933	0.3314458	RR1-S	RR1-S	RR1-S	+ weak RR1-D in b
9.4640.1003	0.2995329	RR1-S	RR1-S	RR1-S	+ weak rem. at $\nu_0$
9.4753.921	0.3704734	BI	BI	BI	$\nu_1$/$\nu_0$, light curve
9.4755.739	0.3368453	RR1-S	RR1-S	RR1-S
9.4758.925	0.3173162	RR1-S	RR1-S	RR1-S
9.4759.891	0.3694758	RR1-S	RR1-D	RR1-S	weak RR1-D in b
9.4760.1004	0.3102123	RR1-S	RR1-D	RR1-D	in b
9.4760.861	0.2996671	RR1-PC	RR1-PC	RR1-PC
9.4760.945	0.3248036	RR1-S	RR1-S	RR1-S
9.4761.1258	0.3009386	RR1-PC	RR1-PC	RR1-PC
9.4761.966	0.3395877	RR1-S	RR1-S	RR1-S	weak RR1-D
9.4762.1015	0.3454185	RR1-S	RR1-S	RR1-S
9.4762.1072	0.3105078	RR1-S	RR1-S	RR1-S
9.4873.497	0.3586208	RR1-PC	RR1-PC	RR1-PC
9.4873.519	0.3512584	RR01	RR01	RR01
9.4875.697	0.3206464	RR1-PC	RR1-PC	RR1-PC
9.4875.852	0.3130636	RR1-S	RR1-S	RR1-D	in b
9.4877.802	0.3420082	RR1-S	RR1-S	RR1-S
9.4878.2126	0.3375846	RR1-S	RR1-BL1	RR1-PC
9.4879.502	0.3982046	RR1-PC	RR1-PC	RR1-PC
9.4879.550	0.3791640	RR1-S	RR1-S	RR1-PC
9.4880.858	0.3537984	RR1-S	RR1-S	RR1-D
9.4881.635	0.3663045	RR01	RR01	RR01
9.4882.1059	0.2763814	RR1-S	RR1-S	RR1-S
9.4883.1241	0.3602522	RR1-S	RR1-S	RR1-S
9.4994.491	0.3664183	RR1-PC	RR1-PC	RR1-PC
9.4995.551	0.3266079	RR1-S	RR1-S	RR1-S
9.4998.709	0.3942098	BI	BI	BI	$\nu_1$/$\nu_0$, light curve
9.4998.725	0.2971509	RR1-S	RR1-MI	RR1-D	peak at .1163 in b only
9.4999.1530	0.2869667	RR1-S	RR1-S	RR1-D	in b
9.4999.1762	0.3194617	RR1-S	RR1-MI?	BI	$\nu_1$/$\nu_0$, light curve rather eclipse
9.5001.708	0.3383914	RR1-S	RR1-S	RR1-S
9.5001.841	0.3400434	RR1-S	RR1-S	RR1-S
9.5002.709	0.3014034	RR1-S	RR1-S	RR1-S
9.5003.684	0.2862712	RR1-S	RR1-S	RR1-S	weak RR1-D in b
9.5003.978	0.3597825	RR1-S	RR1-S	RR1-S
9.5004.750	0.3041610	RR1-D	RR1-D	RR1-MI	$\nu_2=.16$05
9.5115.785	0.3485641	BI	BI	BI	$\nu_1$/$\nu_0$, light curve
9.5117.617	0.3601338	RR1-S	RR1-PC	RR1-BL2	symm, $\Delta f=.00$05, whitens out
9.5117.696	0.3466028	RR1-S	RR1-S	RR1-S	+ rem at $\nu_0$
9.5117.814	0.2760081	RR1-S	RR1-S	RR1-S
9.5119.644	0.3565925	RR01	RR01	RR01
9.5121.767	0.3530495	RR1-S	RR1-S	RR1-S
9.5121.827	0.3518164	RR01	RR01	RR01
9.5122.363	0.3222320	RR1-D	RR1-D	RR1-MI	$\nu_0/\nu_2=.7$446
9.5123.1127	0.2982710	RR1-S	RR1-S	RR1-S
9.5123.284	0.2995174	RR1-S	RR1-S	RR1-S
9.5123.633	0.2677299	RR1-MI	RR1-MI	RR01
9.5123.713	0.3702883	RR1-S	RR1-S	RR1-S
9.5124.1174	0.3535816	RR01	RR01	RR01
9.5124.850	0.3051548	RR1-S	RR1-S	RR1-S
9.5125.1018	0.2598093	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=.0$052, in r
9.5236.587	0.3616035	RR1-S	RR1-S	RR1-S
9.5236.675	0.3430403	RR1-S	RR1-D	RR1-S
9.5238.724	0.2948677	RR1-S	RR1-S	RR1-S
9.5238.784	0.3311550	RR1-S	RR1-S	RR1-S
9.5238.804	0.3655498	RR01	RR01	RR01
9.5239.1141	0.3633337	NC	RR1-PC	RR1-PC	(RRc) P(A00)$\ne$P(SAM) RR1-D in r
9.5239.728	0.3530979	RR1-S	RR1-S	RR1-S
9.5240.750	0.3187437	RR1-S	RR1-S	RR1-S
9.5241.1725	0.2911409	RR1-S	RR1-S	RR1-S
9.5241.1868	0.3594974	RR1-S	RR1-S	RR1-S	+weak RR1-D in r
9.5241.382	0.3416840	RR1-S	RR1-S	RR1-MI	peak at 2.35 in b
9.5242.1032	0.2858950	RR1-BL1	RR1-BL1	RR1-BL1	$\Delta f=+0$.0375
9.5242.974	0.3194565	RR1-S	RR1-S	RR1-S
9.5243.1131	0.3293029	RR1-S	RR1-S	RR1-S
9.5243.955	0.3595260	RR1-S	RR1-S	RR1-S
9.5245.1046	0.3217844	RR1-S	RR1-D	RR1-D	in r
9.5245.1190	0.3506518	RR1-S	RR1-D	RR1-D	in r
9.5246.989	0.3135361	RR1-S	RR1-D	RR1-D
9.5358.566	0.3710141	RR01	RR01	RR01
9.5359.671	0.2893691	RR1-S	RR1-D	RR1-D	in b
9.5359.714	0.3537696	RR1-S	RR1-S	RR1-S
9.5360.768	0.3375177	RR1-D	RR1-D	RR1-D
9.5360.773	0.3615600	RR1-S	RR1-D	RR1-D
9.5360.782	0.3075059	RR1-S	RR1-S	RR1-S
9.5360.853	0.3390032	RR1-S	RR1-S	RR1-S	peak in r at detection limit
9.5360.903	0.4138971	RR1-PC	RR1-PC	RR1-PC	+ weak RR1-D
9.5361.694	0.3125844	RR1-S	RR1-S	RR1-D	in r
9.5361.900	0.3576700	RR1-S	RR1-S	RR1-S	rem. at $\nu_0+1$; P(A00)$\ne$P(SAM)
9.5362.1886	0.3423878	RR1-S	RR1-S	RR1-S
9.5362.314	0.3975989	RR1-S	RR1-S	RR1-S
9.5362.324	0.3447272	RR1-S	RR1-S	RR1-S
9.5363.899	0.3640478	RR1-PC	RR1-PC	RR1-PC
9.5364.886	0.3987656	RR1-PC	RR1-PC	RR1-MC
9.5365.878	0.3149004	RR1-S	RR1-D	RR1-D
9.5365.907	0.3172517	RR1-S	RR1-S	RR1-S
9.5367.1206	0.3226902	RR1-S	RR1-S	BI	$\nu_1$/$\nu_0$, light curve rather eclipse
9.5367.959	0.3399758	RR1-S	RR1-S	RR1-S
9.5478.719	0.3074701	RR1-S	RR1-PC	RR1-PC	whitens out
9.5478.786	0.2833626	RR1-S	RR1-S	RR1-S
9.5479.1190	0.2793167	RR1-S	RR1-BL1	RR1-S	S/N was 6.67, it is 5.92 now...!!!
9.5479.751	0.3464845	RR1-S	RR1-S?	RR1-S	+ peak at 1.1971 in r
9.5479.852	0.3217303	RR1-BL2	RR1-BL2	RR1-BL2	$\Delta f=\pm$.0008, rem.
9.5481.746	0.3581725	RR1-S	RR1-PC	RR1-BL2	$\Delta f=\pm$.0005, wh. Aliases!
9.5481.871	0.3513143	RR1-S	RR1-S	RR1-S	weak rem. at $\nu_0$; P(A00)$\ne$P(SAM)
9.5481.965	0.3244519	RR1-S	RR1-D?	RR1-D	in r
9.5482.1335	0.3813366	RR1-S	RR1-S	RR1-S
9.5482.824	0.2996470	RR1-S	RR1-S	RR1-PC
9.5482.883	0.2724089	RR1-S	RR1-S?	RR1-S	weak stuff
9.5482.933	0.3339844	RR1-S	RR1-D?	RR1-S
9.5482.957	0.3405742	RR01	RR01	RR01
9.5483.1857	0.3672216	RR01	RR01	RR01
9.5483.1931	0.3409496	RR1-S	RR1-S	RR1-S
9.5484.705	0.3316851	RR1-S	RR1-S	RR1-S
9.5484.829	0.3577133	RR1-S	RR1-S	RR1-D
9.5486.777	0.2982475	RR1-S	RR1-S	RR1-S
9.5487.1048	0.3615973	RR1-S	RR1-MI?	RR1-S
9.5487.584	0.3692732	RR1-S	RR1-PC	RR1-PC	alias
9.5487.736	0.3506117	RR01	RR01	RR01
9.5599.617	0.2782061	RR1-D	RR1-D	RR1-D
9.5599.682	0.4102560	BI	BI	BI	$\nu_1$/$\nu_0$, light curve sin.
9.5599.762	0.2994160	RR1-PC	RR1-PC	RR1-PC
9.5600.566	0.3313306	RR1-PC	RR1-PC	RR1-PC	rem. at 2$\nu_0$ too
9.5600.609	0.3046859	RR1-S	RR1-S	RR1-S
9.5602.813	0.3163610	RR1-S	RR1-S	RR1-S
9.5602.987	0.2975537	RR1-S	RR1-S	RR1-S
9.5606.348	0.2909644	RR1-S	RR1-BL2	RR1-BL2	$\Delta f=.0712$
9.5606.829	0.3563769	RR1-S	RR1-S	RR1-S
9.5606.838	0.3530134	RR1-S	RR1-S	RR1-S
9.5606.882	0.2647507	RR1-S	RR1-S	RR1-S
9.5606.884	0.3096000	RR1-S	RR1-S	RR1-S
9.5609.856	0.2848128	RR1-S	RR1-S	RR1-D	stuff in b at 1.6329
9.5609.956	0.2707240	RR1-S	RR1-S	RR1-D	in b

Notes: Additional data (positions, magnitudes, etc.) can be found at the MACHO on-line database (http://wwwmacho.mcmaster.ca/Data/MachoData.html). Comments are intended to draw attention to the given variable rather than supply detailed description of the peculiarities found.

   

Table 7: Data on the first overtone Blazhko stars.

MACHO ID.	P1	$f_{\rm BL}$	A+	A0	A-	MACHO ID.	P1	$f_{\rm BL}$	A+	A0	A-
10.3552.745	0.2922940	0.037408	0.0666	0.1280	-	6.5729.958	0.2778179	0.074254	0.1045	0.1641	-
10.3557.1024	0.2947668	0.000426	0.1000	0.2643	0.0941	6.5730.4057	0.2763214	0.077598	0.0662	0.1249	-
10.4035.1095	0.3188217	0.080780	0.0496	0.2239	-	6.5850.1081	0.3335893	-0.118341	-	0.1617	0.0326
10.4161.1053	0.2874579	0.094288	0.0769	0.1443	-	6.5971.1233	0.2877179	-0.073476	0.0380	0.1868	0.0666
11.9471.780	0.2859825	-0.113512	-	0.2076	0.0764	6.6091.1198	0.2668322	-0.075389	-	0.1654	0.0307
13.5713.590	0.2836353	0.100165	0.0636	0.0870	-	6.6091.877	0.3206106	-0.038525	-	0.1046	0.0642
13.5714.442	0.3168726	0.109252	0.0547	0.1008	-	6.6094.5606	0.3393854	-0.001244	0.0593	0.2476	0.0637
13.5842.2468	0.2731424	-0.084060	-	0.2060	0.0355	6.6326.424	0.3304519	-0.072633	-	0.2353	0.0504
13.5959.584	0.3466458	0.000993	0.0286	0.2629	-	6.6810.616	0.2883850	-0.000403	0.0552	0.2113	0.0704
13.6322.342	0.2621495	0.180083	0.0385	0.1166	-	6.7054.713	0.4404073	-0.001674	0.0445	0.2110	0.0478
13.6326.2765	0.3304520	-0.072702	-	0.2387	0.0334	6.7056.836	0.4476160	0.001120	0.0317	0.1781	0.0252
13.6810.2981	0.2883863	0.000419	0.0691	0.2050	0.0659	80.6352.1495	0.3079889	-0.071798	-	0.0937	0.0682
13.6810.2992	0.2903975	-0.041503	0.0909	0.2153	0.1318	80.6470.2000	0.3706713	0.000564	0.0492	0.2016	0.0472
14.8495.582	0.2971105	0.044128	0.0696	0.2236	0.0364	80.6595.1599	0.3323705	-0.036844	0.0326	0.1977	0.0812
14.9223.737	0.3098789	0.031590	0.0941	0.2270	0.1075	80.6597.4435	0.3086445	-0.000950	0.0368	0.1503	0.0519
14.9225.776	0.3551288	-0.054055	-	0.2589	0.0903	80.6838.2884	0.3583390	0.000478	0.0707	0.2950	0.0599
14.9463.846	0.2749961	0.070745	0.0470	0.1293	-	80.6951.2395	0.3114197	-0.000583	0.0487	0.1821	0.0597
14.9702.401	0.2754043	-0.184006	-	0.2349	0.0469	80.6953.1751	0.3517135	-0.028083	0.0677	0.2699	0.0709
15.10068.239	0.2976949	-0.033619	0.0325	0.1769	0.0398	80.6957.409	0.4078831	0.000793	0.0537	0.1470	0.0452
15.10072.918	0.2930774	-0.036838	-	0.2971	0.0649	80.6958.1037	0.2752632	-0.034210	0.0355	0.2141	0.0392
15.10311.782	0.3482903	0.001036	0.0440	0.2308	0.0450	80.7072.1545	0.3583444	-0.001338	0.0268	0.1236	0.0263
15.10313.606	0.2925053	0.064385	0.0806	0.1861	0.0597	80.7072.2280	0.2786360	-0.047201	-	0.1486	0.0359
15.11036.255	0.2869357	0.078243	0.1029	0.1030	-	80.7319.1287	0.2978598	0.000852	0.0973	0.2210	0.0761
15.11280.663	0.3299770	-0.000580	-	0.2853	0.0393	80.7437.1678	0.2781401	-0.088902	-	0.1858	0.1289
18.2361.870	0.3254790	0.029733	0.0661	0.2112	0.0650	80.7440.1192	0.3430250	-0.001029	0.0582	0.1660	0.0663
19.4188.1264	0.3702574	0.000911	0.0945	0.1690	0.0678	80.7441.933	0.2733126	0.047918	0.0551	0.1684	0.0420
19.4188.195	0.2828193	0.012127	0.0683	0.1752	0.0665	81.8400.901	0.2739736	0.006469	0.0404	0.1651	-
2.4787.770	0.3357061	-0.000461	0.0617	0.2749	0.0620	81.8518.970	0.3085487	-0.014972	-	0.1192	0.0264
2.5032.703	0.3077973	-0.006788	-	0.1864	0.0344	81.8639.1749	0.3759094	0.044767	0.0459	0.2201	0.0363
2.5148.1207	0.2946848	-0.035316	0.0611	0.1824	0.0664	81.8759.832	0.3038356	0.074458	0.0377	0.2144	-
2.5148.713	0.3212517	-0.000684	0.0318	0.1651	0.0333	81.8879.1869	0.2975649	-0.000735	0.0614	0.1871	0.0660
2.5266.3864	0.2793840	0.065535	0.0705	0.1768	-	82.7920.1074	0.3386711	0.038043	0.0470	0.2152	-
2.5271.255	0.4347510	0.001169	0.0658	0.1821	0.0541	82.8049.746	0.2987354	0.071957	0.0675	0.2256	0.0482
2.5876.741	0.2859854	-0.072205	-	0.2184	0.0347	82.8286.1784	0.3285773	-0.000494	-	0.1893	0.0357
3.6240.450	0.3836371	-0.001203	0.0641	0.2129	0.0583	82.8407.312	0.3563439	0.000804	0.0371	0.2317	-
3.6597.756	0.3086451	-0.000950	0.0304	0.1378	0.0367	82.8408.1002	0.2962930	0.035408	0.0694	0.2299	0.0503
3.6603.795	0.2765073	-0.017362	-	0.2527	0.0369	82.8525.1980	0.2833982	0.081435	0.0355	0.2378	-
3.6838.1298	0.3583389	0.000466	0.0646	0.3078	0.0563	82.8526.1176	0.3238862	0.127004	0.0321	0.1293	0.0312
3.6966.427	0.2972764	0.078251	0.0272	0.2148	-	82.8765.1250	0.3049238	-0.048999	0.0422	0.2267	0.0538
3.7088.623	0.3244180	-0.000642	0.0530	0.2485	0.0676	82.8766.1305	0.2592516	-0.003018	-	0.0936	0.0518
47.1521.589	0.3587236	-0.042303	0.0575	0.2303	0.0634	9.4274.644	0.2636423	-0.122986	-	0.1529	0.0343
5.4401.1018	0.2685325	-0.004754	0.0761	0.0830	0.0802	9.4632.731	0.2775501	-0.006687	0.0310	0.1220	0.1233
5.4528.1555	0.2752904	-0.010273	-	0.0908	0.0212	9.4636.1979	0.3933065	0.000434	0.0254	0.2201	-
5.4889.1060	0.2815683	-0.097085	-	0.1052	0.0309	9.5117.617	0.3601338	-0.000491	0.0265	0.2328	0.0341
5.5008.1902	0.3774283	0.073639	0.0436	0.1327	-	9.5125.1018	0.2598093	-0.005181	0.0376	0.1075	0.0572
5.5250.1501	0.3551757	-0.000513	0.0378	0.2143	0.0433	9.5242.1032	0.2858950	0.037524	0.0879	0.1245	-
5.5367.3432	0.2854189	0.029594	0.0370	0.1800	0.0367	9.5479.852	0.3217303	0.000755	0.1144	0.1728	0.0827
5.5368.1201	0.3365130	-0.005552	0.0287	0.2049	0.0554	9.5481.746	0.3581725	-0.000506	0.0234	0.2063	0.0345
5.5489.1397	0.2899676	-0.047824	-	0.1849	0.0719	9.5606.348	0.2909644	0.071233	0.0226	0.1168	0.0209
5.5497.3874	0.2680527	-0.018829	-	0.1566	0.0381

Note: the amplitude of the main pulsation component is denoted by A₀. The modulation amplitudes are A₊ and A_-, corresponding to the larger and smaller frequencies, respectively. Amplitudes are given in MACHO instrumental "b'' magnitudes and the frequencies in [d^-1]. The sign of the modulation frequency $f_{\rm BL}$ is positive, if A_-<A₊, and negative, if A_->A₊. For BL2 stars, $f_{\rm BL}$ stands for the average of the two modulation frequencies. This table also appears at the CDS (http://cdsweb.u-strasbg.fr).