A&A 452, 1113-1120 (2006)
DOI: 10.1051/0004-6361:20054744
C. E. Hudson - K. L. Bell
School of Mathematics and Physics, The Queens University of Belfast, Belfast BT7 1NN, Northern Ireland, UK
Received 21 December 2005 / Accepted 15 February 2006
Abstract
Context. S V emission lines have been observed in solar flares, solar upper atmospheres, quiet sun regions and broad band absorption line quasars, with particular lines being used as diagnostics for electron temperature and density. Accurate atomic data are needed to analyse the observational data and to date the best available calculations for this ion have not included contributions from resonances.
Aims. To calculate fine structure effective collision strengths for the electron impact excitation of S V using a method which incorporates resonances.
Methods. A 14-state R-matrix calculation has been performed. The target states are represented by configuration interaction wavefunctions and consist of the 14 lowest LS states, having configurations (2p6)3s2, 3s3p, 3p2, 3s3d, 3s4s, 3p3d. These target states give rise to 26 fine structure levels and 325 possible transitions. The fine structure collision strengths were obtained by transforming to a jj-coupling scheme using the JAJOM program of Saraph and have been determined at a sufficiently fine energy mesh to delineate properly the resonance structure. The effective collision strengths were calculated by averaging the electron collision strengths over a Maxwellian distribution of velocities.
Results. Tabulations of the non-zero effective collision strengths for transitions between both the LS states and the fine structure levels are given for electron temperatures (![]() )
in the range
)
in the range
![]() .
Comparisons are made with previous R-matrix and distorted-wave calculations.
.
Comparisons are made with previous R-matrix and distorted-wave calculations.
Key words: atomic processes - line: formation - methods: analytical
S V emission lines have been observed in solar flares, solar upper atmospheres, quiet sun regions and in the broad band absorption line quasar 0226-1024. Curdt et al. (1997) note that the 3s3p 1P1 - 3s3d 1D2 and 3s2 1S0 - 3s3p 1P1 lines near 696 and 780 Å can be used for temperature diagnostics. Laming et al. (1997) use the 3s2 1S0 - 3s3p 3P2 and 3s2 1S0 - 3s3p 3P1 lines at 1188 and 1199 Å for density diagnostics.
These observational data require accurate atomic data in the form of effective collision strengths for analysis and interpretation. The most recent theoretical investigations providing collisional data for this ion are the R-matrix calculation of Dufton & Kingston (1984) and the work of Pradhan (1988) which uses the collision strengths from the distorted-wave approximation of Christensen et al. (1986).
Christensen et al. (1986) carried out a calculation in LS coupling using the distorted-wave approximation with ten LS states, to produce fine structure collision strengths for transitions between the first sixteen j-levels. These collision strengths were produced at six energy points but results are noted only for three energies which the authors claim are sufficient to show the general trend in the collision strength. From these collision strengths, Pradhan (1988) has obtained the fine structure effective collision strengths for the 120 transitions involving these 16 levels.
The earlier R-matrix calculation of Dufton & Kingston (1984) obtained the effective collision strengths between the eight lowest LS target states in S V in the electron temperature range
![]() .
Thus the calculation of Pradhan provides fine structure data for a larger set of transitions and for a greater temperature range
.
Thus the calculation of Pradhan provides fine structure data for a larger set of transitions and for a greater temperature range
![]() .
Pradhan (1988) finds agreement of 20-30% with the work of Dufton & Kingston (1984) for most transitions, but states that for some transitions there are more severe discrepancies.
.
Pradhan (1988) finds agreement of 20-30% with the work of Dufton & Kingston (1984) for most transitions, but states that for some transitions there are more severe discrepancies.
These discrepancies are likely to be due to the fact that the distorted-wave approximation neglects the resonance contributions in the collision strengths. In fact, Pradhan (1988) suggests that the effective collision strength for the 3s2 1S0 - 3s3p 3P1 may be underestimated by a factor of two due to neglect of the contributions from resonances. Feldman et al. (1981) also note that for this transition they believe their distorted-wave evaluations to be underestimated by a factor of 5 for the same reason, having compared to observational data.
Doschek et al. (1999) have also used the results of Pradhan (1988) to compare with observed line intensity ratios. For the 786.48 Å/1199.13 Å ratio i.e. (3s2 1S0-3s3p 1P1)/(3s2 1S0-3s3p 3P1), they find that distorted-wave theory predicts an intensity ratio which is a factor of five larger than the observed ratio.
Therefore, in order to provide accurate fine-structure effective collision strengths for transitions in S V using a method which incorporates resonances we have carried out a more sophisticated R-matrix calculation. The 14 lowest LS levels have been employed as target states, giving rise to 26 j-levels and a total of 325 fine structure transitions.
Wavefunctions were constructed for the 14 lowest LS target states of S V using the configuration interaction code CIV3 (Hibbert 1975). Each target-state wavefunction ![]() is represented by a linear combination of single-configuration functions
is represented by a linear combination of single-configuration functions ![]() ,
each of which has the same total
,
each of which has the same total ![]() symmetry as the target-state wavefunction
symmetry as the target-state wavefunction
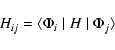 |
(2) |
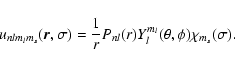 |
(3) |
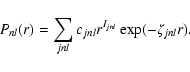 |
(4) |
Table 1:
The Hartree-Fock orbital parameters (c, I, ![]() )
of the radial wavefunctions for the 1s, 2s, 3s and 2p orbitals.
)
of the radial wavefunctions for the 1s, 2s, 3s and 2p orbitals.
We used the Hartree-Fock orbital parameters of Clementi & Roetti (1974) for the 1s, 2s, 2p and 3s orbitals, and these are noted in Table 1. For the remainder of the real orbitals, the CIV3 code was employed to determine the cjnl, Ijnl and
![]() parameters and the values obtained are given in Table 2.
parameters and the values obtained are given in Table 2.
For the optimisations of the real orbitals, we note that: the 3p orbital was optimised on the energy of the 3s3p 3P![]() state using this single configuration; the 3d was optimised on the 3s3d 1D state using the 3s3d and 3p2 configurations; the 4s was optimised on the energy of the 3s4s 3S state using this single configuration; the 4p was optimised on the 3s4p 3P
state using this single configuration; the 3d was optimised on the 3s3d 1D state using the 3s3d and 3p2 configurations; the 4s was optimised on the energy of the 3s4s 3S state using this single configuration; the 4p was optimised on the 3s4p 3P![]() energy using the four configurations - 3p3d, 3s3p, 3s4p and 3p4s.
energy using the four configurations - 3p3d, 3s3p, 3s4p and 3p4s.
Table 2:
The optimised c, I and ![]() parameters of the non-Hartree-Fock orbitals.
parameters of the non-Hartree-Fock orbitals.
The pseudo-orbitals were optimised in the following way: a
![]() orbital was optimised on the energy of the 3p3d 3F
orbital was optimised on the energy of the 3p3d 3F![]() state using the 3s
state using the 3s
![]() ,
3p3d and 3p
,
3p3d and 3p
![]() configurations, this acts as a corrector to the 3d orbital; a
configurations, this acts as a corrector to the 3d orbital; a
![]() orbital was also optimised on the energy of the 3p3d 3F
orbital was also optimised on the energy of the 3p3d 3F![]() state using the 3s
state using the 3s
![]() ,
3p3d and 3p
,
3p3d and 3p
![]() configurations which allows for 3p3d
configurations which allows for 3p3d
![]() 3s
3s
![]() correlation; the
correlation; the
![]() orbital acts as a corrector to the 3s orbital and was optimised on the 3s4s 3S state using the 3s4s, 3p4p, 3d
orbital acts as a corrector to the 3s orbital and was optimised on the 3s4s 3S state using the 3s4s, 3p4p, 3d
![]() and 4s
and 4s
![]() configurations; the
configurations; the
![]() orbital allows for 3s4s
orbital allows for 3s4s
![]() 3pnp correlation and was optimised on the 3s4s 3S state using the 3s4s, 3p4p, 3p
3pnp correlation and was optimised on the 3s4s 3S state using the 3s4s, 3p4p, 3p
![]() and 4p
and 4p
![]() configurations. The orbital parameters resulting from these optimisations are also shown in Table 2.
configurations. The orbital parameters resulting from these optimisations are also shown in Table 2.
Wavefunctions for the 14 S V target states were constructed according to equation (1) using the orbitals from Tables 1 and 2 to define a set of single-configuration functions generated by a two electron replacement on the 1s22s22p63s2 basis configuration, with the 1s, 2s and 2p shells being kept closed, and allowing at most one electron in the 4f shell. Using the 10 symmetries involved in the target state set, this generation leads to a total of 123 configurations - 15 ![]() 1S, 18
1S, 18 ![]() 1D, 17
1D, 17 ![]() 1P
1P![]() ,
8
,
8 ![]() 1D
1D![]() ,
7
,
7 ![]() 3S, 9
3S, 9 ![]() 3P, 13
3P, 13 ![]() 3D, 17
3D, 17 ![]() 3P
3P![]() ,
8
,
8 ![]() 3D
3D![]() ,
11
,
11 ![]() 3F
3F![]() .
.
In Table 3, we compare the calculated LS target state energies in Rydbergs (1
![]() J) for S V relative to the 2s22p63s2 1S ground state with values from the NIST database available at http://www.physics.nist.gov (data quoted from Martin et al. (1990) and references therein). We also tabulate the energy levels calculated by the Opacity Project (Butler et al. 1992) along with those from the calculations of Christensen et al. (1986) and Dufton & Kingston (1984). For each of the calculations we display the energy levels and note the difference of these from the observed values of NIST in parentheses. Such a comparison between the calculated values and the observed data provides a useful test of the wavefunctions. From Table 3, we note that the values from the current calculation
differ on average by 0.016 Ryd from the NIST values. For the Opacity Project (Butler et al. 1992) the values differ on average by 0.0086 Ryd, for the calculation of Christensen et al. (1986) the average difference is 0.0113 Ryd and for the work of Dufton & Kingston (1984) this difference is 0.0204 Ryd. Thus the current calculation achieves energy levels which are improved from the earlier R-matrix calculation of Dufton & Kingston (1984).
J) for S V relative to the 2s22p63s2 1S ground state with values from the NIST database available at http://www.physics.nist.gov (data quoted from Martin et al. (1990) and references therein). We also tabulate the energy levels calculated by the Opacity Project (Butler et al. 1992) along with those from the calculations of Christensen et al. (1986) and Dufton & Kingston (1984). For each of the calculations we display the energy levels and note the difference of these from the observed values of NIST in parentheses. Such a comparison between the calculated values and the observed data provides a useful test of the wavefunctions. From Table 3, we note that the values from the current calculation
differ on average by 0.016 Ryd from the NIST values. For the Opacity Project (Butler et al. 1992) the values differ on average by 0.0086 Ryd, for the calculation of Christensen et al. (1986) the average difference is 0.0113 Ryd and for the work of Dufton & Kingston (1984) this difference is 0.0204 Ryd. Thus the current calculation achieves energy levels which are improved from the earlier R-matrix calculation of Dufton & Kingston (1984).
Table 3:
Energy levels in Rydbergs for the 14 LS target states included in the calculation, relative to the S V 2p63s2 1S![]() ground state. Values are shown for the experimental data of NIST along with the values obtained from the current calculation, as well as data from the calculations of the Opacity Project (Butler et al. 1992)[OP], Christensen et al.(1986)[C et al.] and Dufton & Kingston (1984)[D&K]. The differences between the observed values of NIST and the data from each of the three calculations are given in parentheses.
ground state. Values are shown for the experimental data of NIST along with the values obtained from the current calculation, as well as data from the calculations of the Opacity Project (Butler et al. 1992)[OP], Christensen et al.(1986)[C et al.] and Dufton & Kingston (1984)[D&K]. The differences between the observed values of NIST and the data from each of the three calculations are given in parentheses.
As an additional check on the quality of the wavefunctions for the target-states, we also examine the oscillator strengths produced using our set of wavefunctions. Oscillator strengths for the allowed transitions between the 14 LS target states are given in Table 4. Comparisons are made in Table 4 with oscillator strengths from several other sources: the Opacity Project (Butler et al. 1992), Gupta & Msezane (2000) and Christensen et al. (1986). The calculation of Gupta & Msezane (2000) is a large scale relativistic calculation, calculating oscillator strengths between the fine structure levels using the CIV3 code of Hibbert (1975) and using 24 LS configurations.
Table 4: Oscillator strengths for the allowed transitions between the 14 LS target states included in the current calculation. Values are given for the length and velocity forms of the oscillator strength (fl and fv) and are compared, where available, to values from the Opacity Project (Butler et al. 1992)[OP], Gupta & Msezane (2000)[G&M] and Christensen et al. (1986)[C et al.]
For the 16 transitions noted in Table 4, we find that the length form of our oscillator strengths agree with the Opacity Project data to within 7% when we neglect the 3s4s 3S![]() - 3p3d 3P
- 3p3d 3P![]() transition (transition 16 in Table 4), and we find that 13 of the transitions agree to within 4%. Compared with the values of Gupta & Msezane (2000), we have agreement to within 6% for 14 of the transitions, transition 16 exhibiting the worst agreement. With the 8 values of Christensen et al. (1986), we find overall agreement to within 9%, and on neglecting the 3s3p 1P
transition (transition 16 in Table 4), and we find that 13 of the transitions agree to within 4%. Compared with the values of Gupta & Msezane (2000), we have agreement to within 6% for 14 of the transitions, transition 16 exhibiting the worst agreement. With the 8 values of Christensen et al. (1986), we find overall agreement to within 9%, and on neglecting the 3s3p 1P![]() - 3p2 1D
- 3p2 1D![]() transition (transition 5 in Table 4), the agreement is to within 5%.
transition (transition 5 in Table 4), the agreement is to within 5%.
When we consider a comparison between the length and velocity forms of the oscillator strengths, we find that the current values agree to within 10% and better for 13 out of the 16 transitions. The transitions outside this range of agreement are 3s3p 1P![]() - 3p2 1D
- 3p2 1D![]() ,
3s3d 1D
,
3s3d 1D![]() - 3p3d 1D
- 3p3d 1D![]() and 3s4s 3S
and 3s4s 3S![]() - 3p3d 3P
- 3p3d 3P![]() (transitions 5, 15 and 16 in Table 4). We also note that the current values show better length and velocity agreement for 11 out of 16 transitions when compared with the values of Gupta & Msezane (2000), with the above transitions (5, 15 and 16) achieving better agreement in the current calculation. Of the five transitions where the length and velocity agreement is poorer in this calculation, the agreement is still within the 10%, and only marginally differs from the agreement of Gupta & Msezane (2000) for three of these transitions: 3s3p 3P
(transitions 5, 15 and 16 in Table 4). We also note that the current values show better length and velocity agreement for 11 out of 16 transitions when compared with the values of Gupta & Msezane (2000), with the above transitions (5, 15 and 16) achieving better agreement in the current calculation. Of the five transitions where the length and velocity agreement is poorer in this calculation, the agreement is still within the 10%, and only marginally differs from the agreement of Gupta & Msezane (2000) for three of these transitions: 3s3p 3P![]() - 3s3d 3D
- 3s3d 3D![]() ;
3p2 3P
;
3p2 3P![]() - 3p3d 3P
- 3p3d 3P![]() and 3p2 3P
and 3p2 3P![]() - 3p3d 3D
- 3p3d 3D![]() (transitions 3, 10 and 11 in Table 4). For the transitions 3s3p 3P
(transitions 3, 10 and 11 in Table 4). For the transitions 3s3p 3P![]() - 3s4s 3S
- 3s4s 3S![]() and 3s3d 3D
and 3s3d 3D![]() - 3p3d 3F
- 3p3d 3F![]() (4 and 14 in Table 4), although the current calculation shows greater disagreement than Gupta & Msezane (2000), the current values are still within 10% of each other.
(4 and 14 in Table 4), although the current calculation shows greater disagreement than Gupta & Msezane (2000), the current values are still within 10% of each other.
All of this analysis of the energy levels and oscillator strengths generated using the current set of target state wavefunctions leads us to be confident that we have an accurate representation of the target system. Using these target state wavefunctions, the (N+1) "ion-plus-electron'' system is described using the R-matrix method outlined by
Burke & Robb (1975), using the associated computer codes detailed by Berrington et al. (1987). Configurations describing the (N+1)-electron symmetries were generated through the addition of one electron from the orbital set to those configurations generated above by the two-electron replacement on the basis configuration. The R-matrix radius was calculated to be 11 atomic units and for each orbital angular momentum, 20 Schmidt-orthogonalized continuum orbitals were included, ensuring that a converged collision strength was
obtained up to an incident electron energy of 16 Rydbergs (1
![]() J). The correct positioning
of resonances relative to the target states included in the
calculation was ensured by adjusting our theoretical energies to
the values of NIST, prior to diagonalization of the Hamiltonian
matrix.
J). The correct positioning
of resonances relative to the target states included in the
calculation was ensured by adjusting our theoretical energies to
the values of NIST, prior to diagonalization of the Hamiltonian
matrix.
In forming the (N+1) symmetries, we consider all total angular momenta
![]() .
Adding an electron to the target state symmetries, which are singlets and triplets, means that for the (N+1) symmetries we now include both even and odd parities for doublet and quartet multiplicities. For dipole-allowed transitions,
however, it is necessary to consider the effect of higher partial
waves with L>12 because they have a significant effect upon the
collision strengths. The contributions from these higher partial waves is approximated by assuming the partial collision strengths
form a geometric series expansion, with a geometric scaling factor
given by the ratio of two adjacent terms. This "topping-up''
procedure has been used successfully in similar calculations of
Bell & Ramsbottom (2000), and Ramsbottom et al.
(2001).
.
Adding an electron to the target state symmetries, which are singlets and triplets, means that for the (N+1) symmetries we now include both even and odd parities for doublet and quartet multiplicities. For dipole-allowed transitions,
however, it is necessary to consider the effect of higher partial
waves with L>12 because they have a significant effect upon the
collision strengths. The contributions from these higher partial waves is approximated by assuming the partial collision strengths
form a geometric series expansion, with a geometric scaling factor
given by the ratio of two adjacent terms. This "topping-up''
procedure has been used successfully in similar calculations of
Bell & Ramsbottom (2000), and Ramsbottom et al.
(2001).
For small energy intervals between fine structure levels, it is possible to recouple the matrices obtained from non-relativistic calculations in LS coupling to obtain the electron collision strengths between these levels. Above all the thresholds the effects of intermediate coupling in the target can be included by using this method. In the current work, the program of Saraph (1978) is used to carry out this recoupling procedure. Further details of the coupling scheme are given by Bell & Ramsbottom (2000).
Effective collision strengths
![]() for a particular
electron temperature
for a particular
electron temperature ![]() (in Kelvin) were obtained by averaging
the electron collision strengths
(in Kelvin) were obtained by averaging
the electron collision strengths
![]() over a Maxwellian
distribution of velocities, so that
over a Maxwellian
distribution of velocities, so that
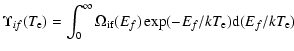 |
(5) |
Table 5: J-levels.
Table 6:
Effective collision strengths for the fine structure transitions from the 3s2 1S0 ground state to levels 2-14 of S V, for electron temperatures ranging from
![]() to 6.0 in steps of 0.2 dex. A superscript indicates the power of 10 with which the number must be multiplied i.e.,
to 6.0 in steps of 0.2 dex. A superscript indicates the power of 10 with which the number must be multiplied i.e.,
![]() ,
i and j denote the initial and final levels of the transition (see Table 5).
,
i and j denote the initial and final levels of the transition (see Table 5).
The collision strengths calculated in this work have been evaluated for a fine mesh of incident impact energies. An energy interval of 0.0008 rydbergs (0.00005 in z-scaled rydbergs) was used in the region containing the target states (0-3.1715 Ryd), and in the region beyond this, an interval of 0.032 Ryd (0.002 in z-scaled rydbergs) was employed. This fine mesh in the target region ensured that the autoionizing resonances which converge to the target state thresholds were fully delineated.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4744fig1.eps}\par\vspace*{2mm}
\hspace*{3mm}\includegraphics[width=8cm,clip]{4744fig2.eps}\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg42.gif) |
Figure 1:
Upper graph - Effective collision strengths for the fine structure transition 3s2 1S0-3s3p 3P
|
| Open with DEXTER | |
The inclusion of the 14 LS target states leads to 26 j-levels and a total of 325 transitions. The j-levels are noted in Table 5, and are listed in ascending order according to the J-value. For the three 3p3d 3P![]() levels arising from the thirteenth target state, we note however that this is not the order of the energy levels. In terms of the observed energy, the order of these levels is reversed with the J=2 level having the lowest energy and the J=0 level having the largest energy. All the other levels increase in energy along with an increasing J-value. In Table 6 we give the current effective collision strengths for a selection of 13 transitions, namely those from the ground state 3s2 1S0 to j-levels 2-14, for a range of electron temperatures [
levels arising from the thirteenth target state, we note however that this is not the order of the energy levels. In terms of the observed energy, the order of these levels is reversed with the J=2 level having the lowest energy and the J=0 level having the largest energy. All the other levels increase in energy along with an increasing J-value. In Table 6 we give the current effective collision strengths for a selection of 13 transitions, namely those from the ground state 3s2 1S0 to j-levels 2-14, for a range of electron temperatures [
![]() (K
)= 4.0-6.0] suitable for application in plasma and astronomical diagnostics. The complete set of 325 transitions is given in Table 7, available at CDS, and contains the following information: Col. 1 lists the transitions between fine-structure states indicated as initial-final according to the index assigned to each fine-structure levels noted in the accompanying table. For example, 3-17 denotes the transition 3s3p 3P
(K
)= 4.0-6.0] suitable for application in plasma and astronomical diagnostics. The complete set of 325 transitions is given in Table 7, available at CDS, and contains the following information: Col. 1 lists the transitions between fine-structure states indicated as initial-final according to the index assigned to each fine-structure levels noted in the accompanying table. For example, 3-17 denotes the transition 3s3p 3P
![]() - 3p3d 3F
- 3p3d 3F
![]() .
The remaining columns list the effective collision strengths for each transition at logarithmic electron temperatures
.
The remaining columns list the effective collision strengths for each transition at logarithmic electron temperatures
![]() (K
)=4.0-6.0 in steps of 0.1 dex.
(K
)=4.0-6.0 in steps of 0.1 dex.
We present below several plots to illustrate how our collision strengths and effective collision strengths compare to the previous works of Christensen et al. (1986), Pradhan (1988) and Dufton & Kingston (1984). In general we see good agreement for higher temperatures but in some cases quite severe differences at low temperatures, which we believe arise from the inclusion in our calculation or the neglect in other calculations of the resonance contributions.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4744fig3.eps}
\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg44.gif) |
Figure 2:
Effective collision strengths for the LS transition 3s2 1S-3s3p 3P |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4744fig4.eps}\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{4744fig5.eps}\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg45.gif) |
Figure 3:
Upper graph - Effective collision strengths for the fine structure transition 3s2 1S0-3p2 3P1 of S V as a function of the electron temperature (in K): |
| Open with DEXTER | |
Figure 1 shows the collision strength and effective collision strength for the 3s2 1S0 - 3s3p 3P
![]() fine structure transition, i.e. one of the fine structure transitions which contribute to the LS transition 3s2 1S - 3s3p 3P
fine structure transition, i.e. one of the fine structure transitions which contribute to the LS transition 3s2 1S - 3s3p 3P![]() .
The upper graph in Fig. 1 shows the effective collision strength from the current calculation along with values from the distorted-wave evaluations of Pradhan (1988). The lower graph in Fig. 1 shows the current collision strength as the solid black line, and the three values given for the collision strength in the work of Christensen et al. (1986). For the effective collision strength, the current values are almost 70% higher than the distorted-wave approximation at the low temperature extremity. This is discussed by Pradhan (1988) who notes that the distorted-wave evaluations for this transition may be underestimated by a factor of 2 due to the neglect of the resonance contributions.
.
The upper graph in Fig. 1 shows the effective collision strength from the current calculation along with values from the distorted-wave evaluations of Pradhan (1988). The lower graph in Fig. 1 shows the current collision strength as the solid black line, and the three values given for the collision strength in the work of Christensen et al. (1986). For the effective collision strength, the current values are almost 70% higher than the distorted-wave approximation at the low temperature extremity. This is discussed by Pradhan (1988) who notes that the distorted-wave evaluations for this transition may be underestimated by a factor of 2 due to the neglect of the resonance contributions.
In Fig. 2 we show the data for the LS transition, in order to compare with the values of Dufton & Kingston (1984). The LS transition 3s2 1S - 3s3p 3P![]() involves the fine structure transitions (see Table 5) 1-2, 1-3 and 1-4. Thus we simply sum over the effective collision strengths from these three transitions to obtain the LS transition values. Figure 2 shows good agreement between the current calculation and the earlier R-matrix calculation of Dufton & Kingston (1984).
involves the fine structure transitions (see Table 5) 1-2, 1-3 and 1-4. Thus we simply sum over the effective collision strengths from these three transitions to obtain the LS transition values. Figure 2 shows good agreement between the current calculation and the earlier R-matrix calculation of Dufton & Kingston (1984).
In Fig. 3, we show the effective collision strength and collision strength for the 3s2 1S0-3p2 3P1 transition. In the upper graph we compare with the data of Pradhan (1988) for the effective collision strength and in the lower graph we compare our collision strength with the values from Christensen et al. (1986). Here again we can see the the impact including the resonance structure from the collision strength makes to the Maxwellian-average effective collision strength.
Figure 4 shows the LS data for the 3s2 1S-3p2 3P transition. Here we again sum over the j-levels involved i.e. transitions 1-7, 1-8 and 1-9. On this graph we include the effective collision strength from the 8-state R-matrix LS-coupling calculation of Dufton & Kingston. There appears to be reasonable agreement between the earlier R-matrix calculation (Dufton & Kingston 1984) and the distorted-wave approximation. The earlier R-matrix calculation does include some resonance contributions. This calculation only incorporated 8 target states which means that resonances were obtained up to the energy of the last target state - the 3s3d 1D at 2.5632 Ryd. In the current R-matrix calculation we have used 14 target states which means we obtain resonance structure up to the energy of the 3p3d 3D![]() level at 3.1715 Ryd. The resonances we obtain in the 2.5632-3.1717 Ryd region due to the larger target set, are substantial in height and so these will enhance the effective collision strength leading to values larger than those from the earlier R-matrix calculation. We also note that the current calculation uses a finer energy mesh than Dufton & Kingston (1984) to resolve the resonances. This too will mean that additional resonance structure is detected.
level at 3.1715 Ryd. The resonances we obtain in the 2.5632-3.1717 Ryd region due to the larger target set, are substantial in height and so these will enhance the effective collision strength leading to values larger than those from the earlier R-matrix calculation. We also note that the current calculation uses a finer energy mesh than Dufton & Kingston (1984) to resolve the resonances. This too will mean that additional resonance structure is detected.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4744fig6.eps}\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg46.gif) |
Figure 4:
Effective collision strengths for the LS transition 3s2 1S-3p2 3P of S V as a function of the electron temperature (in K): |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4744fig7.eps}\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{4744fig8.eps}
\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg47.gif) |
Figure 5:
Upper graph - Effective collision strengths for the fine structure transition 3s2 1S0-3s3p 1P
|
| Open with DEXTER | |
The data for the 3s2 1S0-3s3p 1P
![]() transition are shown in Fig. 5. We find that the current values are slightly lower than both the distorted-wave approximation (Pradhan 1988) and the earlier R-matrix calculation (Dufton & Kingston 1984). The current calculation is 6-14% lower than the Dufton & Kingston evaluations and 14-26% lower than the distorted-wave approximation. In the lower graph of Fig. 5, we compare the collision strength from the current calculation along with the values from the distorted-wave data of Christensen et al. (1986). Whilst there is good agreement with the current calculation at the three energies given by Christensen et al., we note that in this case the resonant structure does not dominate the collision strength and so perhaps in extrapolating down to lower energies the distorted-wave approximation may over-estimate the collision strength and therefore in turn over-estimate the effective collision strength. The lesser differences between the current calculation and the earlier work of Dufton & Kingston are most likely due to the change in resolution of the energy mesh used.
transition are shown in Fig. 5. We find that the current values are slightly lower than both the distorted-wave approximation (Pradhan 1988) and the earlier R-matrix calculation (Dufton & Kingston 1984). The current calculation is 6-14% lower than the Dufton & Kingston evaluations and 14-26% lower than the distorted-wave approximation. In the lower graph of Fig. 5, we compare the collision strength from the current calculation along with the values from the distorted-wave data of Christensen et al. (1986). Whilst there is good agreement with the current calculation at the three energies given by Christensen et al., we note that in this case the resonant structure does not dominate the collision strength and so perhaps in extrapolating down to lower energies the distorted-wave approximation may over-estimate the collision strength and therefore in turn over-estimate the effective collision strength. The lesser differences between the current calculation and the earlier work of Dufton & Kingston are most likely due to the change in resolution of the energy mesh used.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4744fig9.eps}\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{4744fg10.eps}
\end{figure}](/articles/aa/full/2006/24/aa4744-05/Timg48.gif) |
Figure 6:
Upper graph - Effective collision strengths for the fine structure transition 3s2 1S0-3s3d 1D2 of S V as a function of the electron temperature (in K): |
| Open with DEXTER | |
In Fig. 6, we show the effective collision strength and collision strength for the 3s2 1S0-3s3d 1D2 transition. From the lower plot we see that the resonance structure here does dominate the collision strength which leads to the larger values for the effective collision strength than those obtained from the distorted-wave approximation. In fact the current calculation is almost a factor of three larger than the Pradhan (1988) data at low temperatures, but the two do coincide at the high temperature extremity. The agreement with the effective collision strength of Dufton & Kingston (1984) is very good over the entire temperature range. We note that for this transition, Christensen et al. (1986) included contributions from higher partial waves up to l=50 since there is a strong quadrupole moment associated with the transition. In our calculation we account for the higher partial waves by applying the "topping-up'' procedure (described in Sect. 2). The effect of the "top-up'' on the collision strength can be seen in the lower graph in Fig. 6 where the dashed line represents the collision strength before "top-up'' and the solid line shows the "topped-up'' values. Clearly better accord is found with the values obtained by Christensen et al. We find that this "topped-up'' collision strength alters the effective collision strength only slightly at the high temperature extremity. The "topped-up'' and the "non-topped-up'' values are identical up to
![]() (K)= 5.2 where they begin to deviate, with the "topped-up'' data being 12% higher at
(K)= 5.2 where they begin to deviate, with the "topped-up'' data being 12% higher at
![]() (K)= 6.0.
(K)= 6.0.
In this paper we present effective collision strengths for the electron impact excitation of the S V ion. These astrophysically important atomic data are evaluated for the electron temperature range
![]() (K
)= 4.0-6.0 and for all transitions among the lowest 14 LS states of S V, corresponding to 26 fine structure levels and 325 individual fine structure transitions. We have compared our results to an earlier R-matrix calculation and a distorted-wave approximation between which there were discrepancies.
(K
)= 4.0-6.0 and for all transitions among the lowest 14 LS states of S V, corresponding to 26 fine structure levels and 325 individual fine structure transitions. We have compared our results to an earlier R-matrix calculation and a distorted-wave approximation between which there were discrepancies.
The present calculation is certainly the most sophisticated so far. The target state representations, and consequently the (N+1) "ion-plus-electron'' system representations, judged by the target state energies and oscillator strengths, are highly accurate and so the present effective collision strengths should also be of high accuracy.
The fine structure transitions noted in Figs. 1 and 5, i.e. 3s2 1S0-3s3p 3P
![]() and 3s2 1S0-3s3p 1P
and 3s2 1S0-3s3p 1P
![]() ,
are the transitions used as a diagnostic by Doschek et al. (1999), for which these authors find a factor of 5 discrepancy between the predicted and observed line ratios. It is hoped that the results provided by this new calculation will go some way to resolving this situation and other similar discrepancies.
,
are the transitions used as a diagnostic by Doschek et al. (1999), for which these authors find a factor of 5 discrepancy between the predicted and observed line ratios. It is hoped that the results provided by this new calculation will go some way to resolving this situation and other similar discrepancies.
All the effective collision strength data for the LS and fine structure transitions over the temperature range
![]() (K
)= 4.0-6.0 (in steps of 0.1 dex) are available, along with the electron collision strengths, by contacting the authors or via the website www.am.qub.ac.uk/apa
(K
)= 4.0-6.0 (in steps of 0.1 dex) are available, along with the electron collision strengths, by contacting the authors or via the website www.am.qub.ac.uk/apa
Acknowledgements
This work has been supported by PPARC, under the auspices of a Rolling Grant. The calculations were carried out on the ENIGMA supercomputer at the HiPerSPACE Computing Centre, UCL, which is funded by the UK Particle Physics and Astronomy Research Council.