All Tables

Table 1: Basic data and parameters for the star HE 0338-3945.
Table 3: Assigned average values of 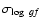$\sigma_{\log~gf}$ for each element.
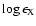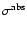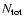Table 4: Derived elemental abundances for HE 0338-3945. For each element X the LTE abundance is presented as $\log\epsilon_{{\rm X}}$ and [X/Fe], together with their relative, $\sigma ^{{\rm rel}}$ , and absolute, $\sigma ^{{\rm abs}}$ , rms error estimates (see text). $N_{\rm tot}$ gives the number of lines of the element used for abundance determination for each element, and 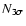$N_{{\rm 3}\sigma }$ gives the number of those features classified as 3 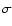$\sigma$ detections.
Table 5: The change in the logarithmic abundances due to a change of the fundamental parameters by amounts corresponding approximately to their uncertainties.
Table 6: Estimated effects of NLTE and 3D on abundances from literature and adapted to the parameters of HE 0338-3945. The numbers are in many cases highly uncertain; see text for further discussion.
Table 7: Comparison of the mean abundances relative to Fe, for normal Population II stars of Paper II in the metallicity range $-2.6 < {\rm [Fe/H]} < -2.2$ , with those for HE 0338-3945. For each element we report the number of measurements N available from Paper II, the mean value of [X/Fe], and the standard deviation of [X/Fe] for the sample, the abundance for HE 0338-3945 ${\rm [X/Fe]}_\star$ , and the difference ${\rm [X/Fe]}_\star - \langle {\rm [X/Fe]} \rangle$ .
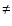Table 8: Data for stars of different classes. For r-I stars and stars not n-enhanced, see Paper II, Burris et al. (2000), and Fulbright (2000), although data are presented for some outliers of interest from Burris et al. When several investigations exist, either the most reliable source or the mean of recent data has been taken. The mean of abundance ratios ${\rm [X/Y]}$ , Y $\ne$ Fe, was calculated from the mean of the abundances relative to Fe, and not from individual measurements of ${\rm [X/Y]}$ . (:) indicates an insecure measurement, and such cases are not considered when calculating the means. References: (1) This work, (2) Aoki et al. (2001), (3) Aoki et al. (2002), (4) Barbuy et al. (2005), (5) Paper II, (6) Unpublished preliminary result obtained in Paper II, (7) Burris et al. (2000), (8) Cohen et al. (2003), (9) Hill et al. (2000), (10) Hill et al. (2002) and Plez et al. (2004), (11) Honda et al. (2004a), (12) Ivans et al. (2005), (13) Johnson & Bolte (2002), (14) Johnson & Bolte (2004), (15) Jonsell et al. (2005), (16) Lucatello et al. (2003), (17) Preston & Sneden (2001), (18) Sivarani et al. (2004), (19) Sneden et al. (2003a), (20) Van Eck et al. (2003), (21) Zacs et al. (1998), (22) mean of presented data, (23) mean of (4) and (17).
Table 9: Definition of classes for n-capture-rich stars. In this article we define stars not falling under any of these classes as "normal''.
Table 2: Line data and abundances from an analysis of the r- and s-process enhanced star HE0338-3945. Each column gives: 1) Definition of the line: d=dummy line for defining the wavelength and region, h=hyperfine structure (hfs) line, i=isotopic splitting (isot) line, b=blending line. 2) The element or molecule producing the line, including isotopic information if necessary. 3) Ionic stage: 1=neutral, 2=singly ionised. 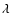4) $\lambda$ , the central air wavelength in Ångströms. 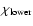5) $\chi _{\rm lower}$ , the lower transition level excitation energy. 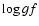6) $\log gf$ , the oscillator strength multiplied with the statistical weight, all in logarithm. 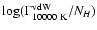7) $\log(\Gamma^{\rm vdW}_{\rm 10000~K}/N_H)$ , the van der Waals damping constant. If the value is < 0 then it is the log of the FWHM per perturber at 10000 K in the reported units. If the value = 0 (blanks in the table) then the classical Unsöld recipe is used with an enhancement factor of 2. If the value is > 0 then the data are from the broadening theory of Anstee, Barklem & O'Mara. 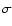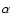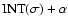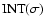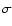The broadening cross section ( $\sigma$ ) for a collision speed 10000 m/s, and the velocity parameter ( $\alpha$ ) are packed into a single parameter given by ${\rm INT}(\sigma )+\alpha$ , such that ${\rm INT}(\sigma )$ is the nearest integer to $\sigma$ . 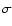For example, if the value is 207.345, then $\sigma$ is 207 au. 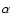and $\alpha$ is 0.345. 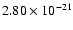The broadening cross section is in atomic units ( $2.80\times 10^{-21}$ m²). The velocity parameter is dimensionless. See Anstee & O'Mara (1995; MNRAS 276, 859) for details of how to compute the line width. 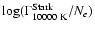8) $\log(\Gamma^{\rm Stark}_{\rm 10000~K}/N_e)$ , the Stark broadening constant, the log of the FWHM per perturber at 10000K. 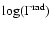9) $\log(\Gamma^{\rm rad})$ , Radiation damping constant, the log of the FWHM. 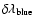10) $\delta \lambda _{\rm blue}$ , the range from central wavelength to blue end of spectral window, in milliÅngström. 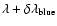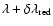The spectral window employed for the line is $\lambda + \delta \lambda _{\rm blue}$ to $\lambda + \delta \lambda _{\rm red}$ . 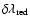11) $\delta \lambda _{\rm red}$ , the range from central wavelength to red end of spectral window, in milliÅngström. 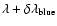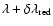The spectral window employed for the line is $\lambda + \delta \lambda _{\rm blue}$ to $\lambda + \delta \lambda _{\rm red}$ . 12) References and notes for the line data.