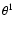Based on observations obtained using the MuSiCoS spectropolarimeter at the Pic du Midi observatory, France.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

Credible quantitative models invoking contemporaneous dynamos operating in the convective core have also been proposed (e.g. Charbonneau & MacGregor 2001), but these models generally have significant difficulty explaining the intensities and topologies of the observed fields, their diversity, lack of correlation of field with angular velocity, as well as the young ages of many magnetic stars.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... days

See, e.g., Fullerton (2003) for a recent review of the characteristics of variability in hot-stars winds.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Cranmer & Owocki 1996)

Magnetic fields are also seen by some investigators as an ingredient necessary to explain intrinsic X-ray fluxes and non-thermal radio emission from massive stars.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... variability

Recently, Donati et al. (2005) reported the detection of a 1.5 kG dipolar magnetic field in the O-type spectrum variable HD 191612 [Of?p], which exhibits stellar wind variations with a period of 538 days. They suggested that HD 191612 represents an evolved version of 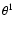$\theta ^1$ Ori C.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... paper

Although all available evidence points to the adopted inclination, we have performed additional modelling to explore the sensitivity of more extreme inclination angles on the derived magnetic field geometry. For inclinations as small as 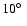$10\hbox{$^\circ$ }$ and as large as 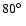$80\hbox{$^\circ$ }$ , we find that the conclusions of this paper are not qualitatively affected.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... level

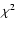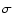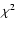Confidence intervals were obtained using $\chi ^2$ probability tables from Bevington (1969). According to these tables, the 2 $\sigma$ (95%) confidence interval, considering each model parameter independently, corresponds to an increase in total $\chi ^2$ of 3.84.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.