- ... scenario
![[*]](/icons/foot_motif.gif)
- Appendix A is only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Fellow of CONICET, and IALP
CONICET/FCAG-UNLP, Argentina.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Member
of the Carrera del Investigador Científico y
Tecnológico and IALP, CONICET/FCAG-UNLP, Argentina.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- Fellow of
CONICET, and IALP CONICET/FCAG-UNLP, Argentina.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... account
![[*]](/icons/foot_motif.gif)
- For example Stancliffe et al. (2004) find much stronger He burning luminosities during the thermal pulses at the AGB if structural and composition equations are solved
simultaneously.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model
![[*]](/icons/foot_motif.gif)
- Also it is expected that the
H-driven expansion may depend on the mass of the model. Explicitly,
the authors have found that in a 0.664
 model the H-driven
expansion stops at log
model the H-driven
expansion stops at log
 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sequence
![[*]](/icons/foot_motif.gif)
- Comparing the predictions of the two sequences we have to keep in mind that the stellar masses of the remnants are not strictly the same.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... choice
![[*]](/icons/foot_motif.gif)
- We note that for our best
model the energy liberated by proton burning is in the range of
expected values from the following rough estimation: If the whole
H-mass (6.3
 10-5
10-5  )
were burned only through the
chain
)
were burned only through the
chain
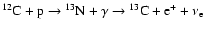 (in which each burned proton liberates
3.4573 Mev, as it happens initially) then
(in which each burned proton liberates
3.4573 Mev, as it happens initially) then
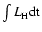 = 4.15
= 4.15  1047 erg. While if the complete H-mass were burned through the two important reactions (the previous one and
also
1047 erg. While if the complete H-mass were burned through the two important reactions (the previous one and
also
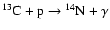 )
working
at the same rate (in this case 5.504 Mev are liberated per burned
proton) then
)
working
at the same rate (in this case 5.504 Mev are liberated per burned
proton) then
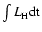 = 6.6
= 6.6  1047 erg.
1047 erg.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...v
![[*]](/icons/foot_motif.gif)
- In the previous work by Althaus et al. (2005) the relation used was D= l
 v and that is (mainly) why they find greater
born again times than in the present work.
v and that is (mainly) why they find greater
born again times than in the present work.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1985)
![[*]](/icons/foot_motif.gif)
- We have also performed some simulations using the expresion for D derived from Cox & Giuli (1968)
![$\left(D=\alpha^{4/3}
H_{\rm P} \left[\frac{c}{\kappa \rho} (1-\beta) \nabla_{\rm ad} (\nabla_{\rm
rad}-\nabla)\right]^{1/3}\right)$](/articles/aa/full/2006/13/aa3804-05/img84.gif) .
We find that no significant difference
arises from this change.
.
We find that no significant difference
arises from this change.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
larger
![[*]](/icons/foot_motif.gif)
- Because of the very short time during which this
process takes place, the H distribution is not homogeneous.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... discussion
![[*]](/icons/foot_motif.gif)
- Changing the
efficiency of overshooting during the thermally pulsing phase is
expected to modify the amount of 16O in the intershell region
below the helium buffer (Herwig 2000).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.