A&A 447, 797-812 (2006)
DOI: 10.1051/0004-6361:20053915
Z. Meliani
1,2,![]() - C. Sauty1 - N. Vlahakis3 - K. Tsinganos3 - E. Trussoni4
- C. Sauty1 - N. Vlahakis3 - K. Tsinganos3 - E. Trussoni4
1 - Observatoire de Paris, LUTh, 92190 Meudon, France
2 - Université de Paris 7, APC, 2 place Jussieu, 75005 Paris, France
3 - Section of Astrophysics, Astronomy & Mechanics, Department
of Physics and IASA, University of Athens,
Panepistimiopolis, 157 84 Zografos, Athens, Greece
4 - Istituto Nazionale di Astrofisica (INAF) - Osservatorio Astronomico
di Torino, Strada Osservatorio 20, 10025 Pino Torinese (TO), Italy
Received 26 July 2005 / Accepted 10 October 2005
Abstract
Steady axisymmetric outflows originating at the hot coronal
magnetosphere of a Schwarzschild black hole and surrounding
accretion disk are studied in the framework of general
relativistic magnetohydrodynamics (GRMHD). The assumption of
meridional self-similarity is adopted for the construction of
semi-analytical solutions of the GRMHD equations describing
outflows close to the polar axis. In addition, it is assumed that
relativistic effects related to the rotation of the black hole and
the plasma are negligible compared to the gravitational and other
energetic terms. The constructed model allows us to extend
previous MHD studies for coronal winds from young stars to spine
jets from Active Galactic Nuclei surrounded by disk-driven
outflows. The outflows are thermally driven and magnetically or
thermally collimated. The collimation depends critically on an
energetic integral measuring the efficiency of the magnetic
rotator, similarly to the non relativistic case. It is also shown
that relativistic effects quantitatively affect the depth of the
gravitational well and the coronal temperature distribution in the
launching region of the outflow. Similarly to previous analytical
and numerical studies, relativistic effects tend to increase the
efficiency of the thermal driving but reduce the effect of
magnetic self-collimation.
Key words: stars: winds, outflows - acceleration of particles - stars: mass-loss - galaxies: jets - magnetohydrodynamics (MHD) - relativity
The formation of relativistic jets around compact objects and
Active Galactic Nuclei (AGNs) is one of the most intriguing and
yet not fully understood astrophysical phenomena
(Ferrari 1998; Mirabel & Rodríguez 1998; Mirabel 2003).
In those jets, velocities reach a fraction of the speed of light
with the corresponding Lorentz factor ranging from values
![]() in Seyfert Galaxies and radio loud AGNs (Piner et
al. 2003; Urry & Padovani 1995) up to the inferred values
in Seyfert Galaxies and radio loud AGNs (Piner et
al. 2003; Urry & Padovani 1995) up to the inferred values
![]() in GRBs; AGN jets are also characterized by the
rather narrow opening angles of a few degrees
(Biretta et al. 2002; Tsinganos & Bogovalov 2005).
in GRBs; AGN jets are also characterized by the
rather narrow opening angles of a few degrees
(Biretta et al. 2002; Tsinganos & Bogovalov 2005).
MHD models for coronal or disk-jets rely on the basic idea that the gravitational energy of the central object is transferred to the accreting plasma which via a collimation mechanism then produces the jet. This energy released by accretion increases with the mass of the central object, a fact which may explain the wide variety of the powerful jets observed. Several analytical and numerical efforts have been invested to investigate the mechanisms of jet acceleration and collimation. The formation of collimated jets seems to be closely related to the presence of large scale magnetic fields (e.g., Gabuzda 2003) and the existence of a gaseous disk and/or a hot corona around the central object (Königl & Pudritz 2000; Livio 2002).
For the energy source of jets, it is usually assumed that at their base they are powered either by a spinning black hole (Blandford & Znajek 1977; Rees et al. 1982; Begelman et al. 1984), or, by the surrounding accretion disk (Miller & Stone 2000). Furthermore, they are plausibly Poynting flux dominated (Sikora et al. 2005) with their central spine hydrodynamically dominated (Meliani et al. 2004) and their plasma composed by protons-electrons or by electron-positron pairs.
The collimation of the outflow, this is likely to be due mainly to the hoop stress resulting from the toroidal magnetic field generated by the rotation of the source (Bogovalov 1995). Recent VLBI observations suggest that the direction of the magnetic field vectors is transverse to the jet axis. This is the case in BL Lac objects, e.g., in Mrk 501 (Gabuzda 2003), or/in quasars where the central faster part of the jet is characterized by toroidal magnetic fields (Asada et al. 2002). Magnetic self-collimation has been shown to be efficient in the non relativistic context (Heyvaerts & Norman 1989, 2003; Livio 2002; Honda & Honda 2002; Tsinganos & Bogovalov 2002). In the relativistic limit however it is slower due to the decollimating effect of the electric force and the higher inertia of the flow, but still possible (Vlahakis & Königl 2003, 2004). Alternatively, collimation in relativistic jets may be due to the external pressure of a surrounding slower and easily collimated disk wind, Bogovalov & Tsinganos (2005).
Magnetized no relativistic jets from extended accretion disks
were first modelled analytically by Blandford & Payne (1982),
wherein the plasma acceleration relies on the magnetic extraction
of angular momentum and rotational energy from the underlying cold
Keplerian disk. This energy is channeled along the large-scale
open magnetic fieldlines anchored in the corona or the rotating
disk. The ionized fluid is forced to follow the fieldlines and to
rotate with them while it is magnetocentrifugally accelerated if
the angle between the poloidal magnetic field and the disk is less
than
![]() .
Cao & Spruit (1994) showed that in the relativistic
case this condition is less severe and that close to the black
hole the magnetocentrifugal acceleration may be efficient even at
higher angles. Analytical, radially self-similar disk-wind
solutions were extended to special relativistic cold winds in Li
et al. (1992), and Contopoulos (1994), by neglecting gravity to
allow the separation of the variables. Thermal effects were
introduced into these relativistic models by Vlahakis & Königl
(2003) to analyze the formation of a relativistic flow from hot
magnetized plasmas, showing that such solutions could be applied
to Gamma Ray Bursts wherein the flow is thermally driven at the
base. However, most of the acceleration is of magnetic origin and
there is an efficient conversion of Poynting to kinetic flux of
the order of 50%. They also applied this disk wind solution to
AGN jets (Vlahakis & Königl 2004) showing that they could trace
the observed parsec scale expansion of the wind. Another approach
to solve the relativistic MHD equations for outflows around black
holes is to solve numerically the transfield equation in the
force-free limit (Camenzind 1986a),
a study further developed in GRMHD by using first a Schwarzschild
metric and then extending it to a Kerr metric (Fendt 1997).
.
Cao & Spruit (1994) showed that in the relativistic
case this condition is less severe and that close to the black
hole the magnetocentrifugal acceleration may be efficient even at
higher angles. Analytical, radially self-similar disk-wind
solutions were extended to special relativistic cold winds in Li
et al. (1992), and Contopoulos (1994), by neglecting gravity to
allow the separation of the variables. Thermal effects were
introduced into these relativistic models by Vlahakis & Königl
(2003) to analyze the formation of a relativistic flow from hot
magnetized plasmas, showing that such solutions could be applied
to Gamma Ray Bursts wherein the flow is thermally driven at the
base. However, most of the acceleration is of magnetic origin and
there is an efficient conversion of Poynting to kinetic flux of
the order of 50%. They also applied this disk wind solution to
AGN jets (Vlahakis & Königl 2004) showing that they could trace
the observed parsec scale expansion of the wind. Another approach
to solve the relativistic MHD equations for outflows around black
holes is to solve numerically the transfield equation in the
force-free limit (Camenzind 1986a),
a study further developed in GRMHD by using first a Schwarzschild
metric and then extending it to a Kerr metric (Fendt 1997).
Radial self-similarity is usually used in disk-wind models due to the complexity of the non linear system of MHD equations. However, such solutions cannot describe the flow close to the rotational axis where they become singular. On the other hand, meridional self-similarity provides a better alternative to study the outflow close to the symmetry and rotation axis of the central corona. In the central part where the thermal energy is rather high, the wind may be thermally driven. Spherically symmetric relativistic hydrodynamical models have been proposed to study the formation of such outflows (Michel 1972; Das 1999; Meliani et al. 2004). Those models are restricted to the case where the magnetic effects in the acceleration are negligible. In these models, a wind forms in the hot corona because of the internal shock maintained by the centrifugal barrier (Chakrabarti 1989; Das 2001), or by the pressure induced via a first order Fermi mechanism (Das 1999).
An important alternative to analytical models are numerical simulations. In the special relativistic domain, simulations have been presented for coronal winds (Bogovalov & Tsinganos 1999; Tsinganos & Bogovalov 2002), and in the general relativistic domain for disk winds (e.g. Koide et al. 1999, 2001) to model the formation and collimation of relativistic outflows in the vicinity of black holes. The difficulty for relativistic outflows in a single-component model to be collimated led Bogovalov & Tsinganos (2005) to propose a two-component model wherein a relativistic central wind is collimated by a surrounding non relativistic disk-wind. Shocks may also develop as the disk-wind collides and collimates the inner relativistic wind. Note that all such simulations are performed by using time-dependent codes. Analytical models conversely have presented more sophisticated steady solutions of outflows to be used as initial conditions in more complex simulations, albeit sacrificing freedom on the chosen boundary conditions.
In this article we present an extension of the non relativistic meridionally self-similar solutions (Sauty & Tsinganos 1994, hereafter ST94) to the case of relativistic jets emerging from a spherical corona surrounding the central part of a Schwarzschild black hole and its inner accretion disk.
We will not discuss here the origin of the plasma, assuming that it can come from, e.g., the accretion disk or pair creation. Furthermore, only the outflow process is considered, with the base of the corona placed at a few Schwarzschild radii, just above the so called separating surface (Takahashi et al. 1990).
Attention is also given to the contribution of the different mechanisms, hydrodynamic and magnetic, to the acceleration and collimation of the outflow, as in previous papers of this series (Sauty et al. 1999, 2002, 2004, hereafter STT99, STT02 and STT04). This is also a way to extend to 2D outflows, thermally driven, spherically symmetric (1D) wind models (Price et al. 2003; Meliani et al. 2004).
In the following two sections, the basic steady axisymmetric GRMHD equations are presented using a 3+1 formalism (Sect. 2), together with their integrals. The assumptions leading to the self-similar model are presented in Sect. 3. In Sect. 4, the analytical expressions of the model together with the derivation of an extra free integral controlling the efficiency of the magnetic rotator, as in STT99, are given. In Sect. 5, an asymptotic analysis of the solutions is performed as well as the link to the boundary conditions in the source. Section 6 is devoted to a parametric study of various solutions to emphasize the main difference obtained with relativistic flows. We discuss the acceleration and collimation of these new solutions (Sect. 7) and compare them with the non relativistic model in Sect. 8. In the last Sect. 9 we summarize our results and shortly outline their main astrophysical implications. The confrontation of the present model with observed jets from radio loud extragalactic jets, such as those associated with FRI and FRII sources, is postponed to a following paper, as it involves special techniques for constraining the parameters by using observational data and a specific iterative scheme to use the model.
The gravitational potential due to the matter outside the black
hole is assumed to be negligible. In Schwarzschild coordinates
(ct, r, ![]() ,
,
![]() )
the background metric is written
as,
)
the background metric is written
as,
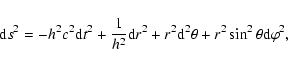 |
(1) |
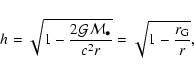 |
(2) |
In the following we find convenient to use a 3+1 split of space-time, following the usual approach of MHD flow treatment in general relativity (Thorne & McDonald 1982; Thorne et al. 1986; Mobarry & Lovelace 1986; Camenzind 1986a). The 3+1 approach allows to obtain equations similar to the familiar classical equations. We write all quantities in the FIDucial Observer frame of reference, known as FIDO, which corresponds to observers in free fall around the Schwarzschild black hole. For the FIDO, space time is locally flat.
The equation of conservation of particles
(n ua);a = 0 in the 3+1 formalism is
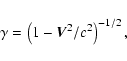 |
(4) |
Maxwell's equations written in the 3+1 formulation (Thorne &
MacDonald 1982; Breitmoser & Camenzind 2000) are![]()
Euler's equation is obtained by projecting the conservation of the
energy-momentum tensor,
Ta b;b =0, onto the spatial
coordinates (a=1,2,3) and combined with Maxwell's equations
(see Breitmoser & Camenzind 2000; or, for an expression closer
to ours, albeit restricted to special relativity Goldreich &
Julian 1970; Appl & Camenzind 1993; Heyvaerts & Norman 2003),
The first law of thermodynamics is obtained by projecting the
conservation of the energy-momentum tensor along the fluid
four-velocity,
ua T;bab=0. In fact, for ideal MHD fluid
the corresponding contribution of the electromagnetic field is
null due to the assumed infinite conductivity. Thus, only the
thermal energy affects the variation of the proper enthalpy of the
fluid,
Assuming axisymmetry of the plasma flow allows us to reduce the number of differential equations by integrating some of them and thus obtaining conserved quantities along the streamlines. We follow the notations of Tsinganos (1982).
From Eqs. (6) and (3) we can introduce a magnetic
flux function A,
From Eq. (7), we can define an electric potential associated to the
electric field,
![]() .
Thus, the previous
equation and axisymmetry imply
.
Thus, the previous
equation and axisymmetry imply
![]() .
In addition from the flux freezing condition
(Eq. (9)) and Eqs. (12) and (13)
we get that
.
In addition from the flux freezing condition
(Eq. (9)) and Eqs. (12) and (13)
we get that ![]() is constant on surfaces of
constant A on which the corresponding streamlines and fieldlines are
roped,
is constant on surfaces of
constant A on which the corresponding streamlines and fieldlines are
roped,
![]() .
It follows that
.
It follows that
![]() is a function of A and we can write
is a function of A and we can write
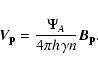 |
(14) |
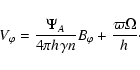 |
(15) |
The azimuthal component of the momentum equation yields the
conservation of the total specific angular momentum,
We have obtained the usual four integrals of motion ![]() ,
,
![]() ,
,
![]() ,
L (Heyvaerts & Norman 2003) that are
constant along a fieldline for a stationary and axisymmetric
plasma. They can be used to find algebraic relations between the
Lorentz factor, the toroidal velocity and the toroidal magnetic
field. Defining the poloidal "Alfvenic'' number M(Michel 1969; Camenzind 1986b;
Breitmoser & Camenzind 2000)
,
L (Heyvaerts & Norman 2003) that are
constant along a fieldline for a stationary and axisymmetric
plasma. They can be used to find algebraic relations between the
Lorentz factor, the toroidal velocity and the toroidal magnetic
field. Defining the poloidal "Alfvenic'' number M(Michel 1969; Camenzind 1986b;
Breitmoser & Camenzind 2000)
The MHD equations possess a well known singularity at the Alfvén
surface where the denominator of Eqs. (20)-(22) vanishes. Then, the numerators should vanish
simultaneously to ensure a regular behavior, implying at the
Alfvén point,
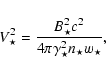 |
(26) |
In the Newtonian limit, Eqs. (23) and (24) give
![]() where m=w/c2 is the
particle mass.
where m=w/c2 is the
particle mass.
Our goal in this section is to find semi-analytical solutions of the
r- and ![]() components of the Euler Eq. (10), by
means of separating the variables r and
components of the Euler Eq. (10), by
means of separating the variables r and ![]() .
In order to facilitate the analysis it is convenient to use dimensionless
quantities normalizing at the Alfvén radius along the polar axis.
Using the notations introduced in ST94 we define a dimensionless
radius R and magnetic flux function
.
In order to facilitate the analysis it is convenient to use dimensionless
quantities normalizing at the Alfvén radius along the polar axis.
Using the notations introduced in ST94 we define a dimensionless
radius R and magnetic flux function ![]() ,
,
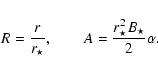 |
(27) |
Combining Eqs. (28) and (29) we get a condition that
restrict the parametric space to
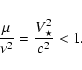 |
(30) |
As ![]() on the rotational axis and we are interested on the
central component of the jet, we assume that the cross section area of a
given magnetic flux tube can be expanded to first order in
on the rotational axis and we are interested on the
central component of the jet, we assume that the cross section area of a
given magnetic flux tube can be expanded to first order in ![]() ,
,
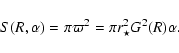 |
(31) |
This is equivalent to assume, as in ST94, that the magnetic flux
function
![]() has a dipolar latitudinal dependence,
has a dipolar latitudinal dependence,
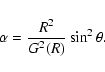 |
(32) |
The pressure dependence is obtained by making a first order expansion in ![]()
Combining Eqs. (18) and (34) we deduce that
Similarly we expand ![]()
Finally we choose for ![]() a form similar to the
one in ST94
a form similar to the
one in ST94
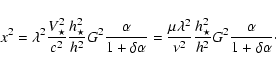 |
(40) |
Conversely to the non relativistic limit, we cannot neglect the
charge separation and the presence of the electric field. From the
previous assumptions, we can calculate the electric force
![]() which has the following two components
which has the following two components
Contrary to the non relativistic case and in order to separate the
variables
![]() in the r- and
in the r- and ![]() components of
the Euler Eq. (10) we need some further assumptions.
Basically we expand these equations with respect to
components of
the Euler Eq. (10) we need some further assumptions.
Basically we expand these equations with respect to ![]() .
.
We suppose that the rotational speed of the fluid remains always
subrelativistic. In other words, we focus on streamlines
that never cross the
light cylinder such that the later does not affect the dynamics
(![]() ,
which implies
,
which implies
![]() ). Of course this reduces
the domain of validity of the solutions to the vicinity of the
rotational axis because
). Of course this reduces
the domain of validity of the solutions to the vicinity of the
rotational axis because
![]() as it is given by Eq. (41)
is sufficiently small only for relatively small
as it is given by Eq. (41)
is sufficiently small only for relatively small ![]() .
The
region of validity of our model depends on how small the parameter
.
The
region of validity of our model depends on how small the parameter
![]() is, though. The
requirement that the light cylinder lies further away from the
Alfvénic surface
is, though. The
requirement that the light cylinder lies further away from the
Alfvénic surface
![]() constrains the parametric space
to
constrains the parametric space
to
![]() .
On the other hand, there is a
possibility that all streamlines never cross the light cylinder. This
happens when the equation
.
On the other hand, there is a
possibility that all streamlines never cross the light cylinder. This
happens when the equation
A consequence of this is that the jet is thermally driven. Indeed the ratio
between the Poynting flux and the matter energy flux is,
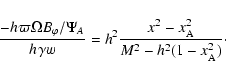 |
(46) |
More generally, after expanding with respect to
![]() ,
we
neglect terms of the order
,
we
neglect terms of the order
![]() or higher.
This is also consistent with our previous assumption of keeping
terms only up to
or higher.
This is also consistent with our previous assumption of keeping
terms only up to ![]() in the integrals. For example, the
expression of the azimuthal magnetic field, Eq. (21),
becomes
in the integrals. For example, the
expression of the azimuthal magnetic field, Eq. (21),
becomes
As another example, the approximate form of the electric force is
Note that in the very vicinity of the black hole
![]() and since the factor h x does not vanish (see Eq. (19)),
x becomes larger than unity,
as expected by the presence of the second light cylinder close to the horizon
(e.g., Takahashi et al. 1990).
However, it is enough that the coronal base is at a distance of a few
gravitational radii (
and since the factor h x does not vanish (see Eq. (19)),
x becomes larger than unity,
as expected by the presence of the second light cylinder close to the horizon
(e.g., Takahashi et al. 1990).
However, it is enough that the coronal base is at a distance of a few
gravitational radii (
![]() )
to guarantee that
)
to guarantee that ![]() at the base of the outflow (this condition is fulfilled in our
solutions).
at the base of the outflow (this condition is fulfilled in our
solutions).
The velocity and magnetic fields can now be written exclusively in terms of
unknown functions of R. For later convenience, as in ST94, we shall denote by
NB, NV and D the following quantities that appear in various
components of the fields,
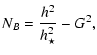 |
(50) | ||
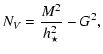 |
(51) | ||
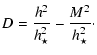 |
(52) |
Similarly, the enthalpy and the particle number density are given by
There are three equations given in Appendix A
that determine the three unknown functions ![]() ,
F(R) and
M2(R). We recall that G2 is related to F through Eq. (33).
Before discussing in detail the results of the parametric study
we outline the method for the numerical integration
of Eq. (33) and Eqs. (A.1)-(A.3).
We start integrating the equations from the Alfvén critical
surface. In order to calculate the toroidal components of the fields, i.e.
NB/D and
NV/D=NB/D-1, we apply L'Hôpital's rule,
,
F(R) and
M2(R). We recall that G2 is related to F through Eq. (33).
Before discussing in detail the results of the parametric study
we outline the method for the numerical integration
of Eq. (33) and Eqs. (A.1)-(A.3).
We start integrating the equations from the Alfvén critical
surface. In order to calculate the toroidal components of the fields, i.e.
NB/D and
NV/D=NB/D-1, we apply L'Hôpital's rule,
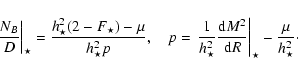 |
(61) |
| C3 p3+C2 p2+C1 p+ C0 = 0 , | (62) |
| C0 | = | 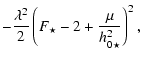 |
(63) |
| C1 | = | 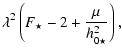 |
(64) |
| C2 | = | 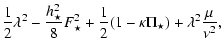 |
(65) |
| C3 | = | (66) |
It is worth noticing that the shape of the streamlines ![]() at R=1 is determined by
the regular crossing of the slow magnetosonic surface. We point out further
that, besides the free parameters listed at the beginning of the section,
solutions depend also on
at R=1 is determined by
the regular crossing of the slow magnetosonic surface. We point out further
that, besides the free parameters listed at the beginning of the section,
solutions depend also on
![]() ,
i.e. the pressure at the Alfvén
surface. As in the classical case its value has been chosen such that the gas pressure is always
positive. More details on the numerical technique can be found in ST94 and STT02.
,
i.e. the pressure at the Alfvén
surface. As in the classical case its value has been chosen such that the gas pressure is always
positive. More details on the numerical technique can be found in ST94 and STT02.
As in ST94, it is possible to find a constant ![]() for all fieldlines.
This parameter
for all fieldlines.
This parameter ![]() has been used in ST94 and in the following papers
to classify the various solutions. We shall use a similar technique to
construct such a constant in the present model.
has been used in ST94 and in the following papers
to classify the various solutions. We shall use a similar technique to
construct such a constant in the present model.
Equation (11), after substituting n from
Eq. (18) and using
![]() (derivative keeping
(derivative keeping ![]() constant),
can be re-written as
constant),
can be re-written as
By writing the term
| |
= | 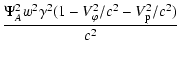 |
|
| = | 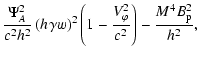 |
(68) |
| |
= | ![$\displaystyle \frac{\Psi_A^2 {\cal E}^2}{c^2 h_{}^2}
\left[ \frac{M^2-h_{}^2(1-x_{\rm A}^2)}{M^2-h_{}^2(1-x^2)} \right]^2$](/articles/aa/full/2006/09/aa3915-05/img193.gif) |
|
![$\displaystyle -\frac{\Psi_A^2 {\cal E}^2}{c^2 h_{}^2}
\left[ \frac{M^2 x_{\rm A...
..._{\rm A}^2)}{M^2-h_{}^2(1-x^2)} \right]^2
-\frac{M^4 B_{\rm p}^2}{h_{}^2}
\cdot$](/articles/aa/full/2006/09/aa3915-05/img194.gif) |
(69) |
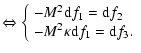 |
(70) |
Similarly to what was done in ST99, we can calculate this constant at
the base of the flow Roassuming the poloidal velocity is negligible there [
![]() ]. Let's express
]. Let's express
![]() in terms of
the conditions at the source boundary,
in terms of
the conditions at the source boundary,
 |
(72) |
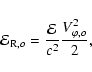 |
(73) |
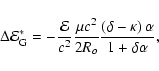 |
(74) |
In the region far from the base where the jet attains its
asymptotic velocity, assuming it becomes cylindrical, the forces
in the radial direction become negligible, since the jet is no
longer accelerated. In the transverse direction, the following
four forces balance each other: the transverse pressure gradient,
![]() ,
the total magnetic stress (magnetic pinching plus
magnetic pressure gradient) of the toroidal magnetic field
component,
,
the total magnetic stress (magnetic pinching plus
magnetic pressure gradient) of the toroidal magnetic field
component,
![]() ,
the centrifugal force,
,
the centrifugal force,
![]() and the charge separation electric force,
and the charge separation electric force,
![]() ,
,
Combining Eq. (75) with Eqs. (76)-(79) we obtain,
At the base of the wind the Alfvén number vanishes,
![]() ,
while the opening of the jet is weak,
,
while the opening of the jet is weak,
![]() .
We can use this criterion to define the distance
Ro where the outflow starts. Namely from the expression of
.
We can use this criterion to define the distance
Ro where the outflow starts. Namely from the expression of
![]() ,
Eq. (71), we get,
,
Eq. (71), we get,
Note that the definition of Ro coincide with the so called separating surface (see e.g. Takahashi et al. 1990, for a cold plasma in a Kerr metric). Above this surface the plasma is outflowing. Below this surface other critical surfaces exist (e.g., Beskin & Kuznetsova 2000) but remain out of our consideration. If the plasma is created via pair production this may constrain the boundary conditions at the base of the flow. However we do not discuss the origin of the coronal plasma in this paper.
![\begin{figure}
\par\includegraphics[height=5.8cm,width=8cm,clip]{3915Fig1a.eps}\...
...e*{3mm}
\includegraphics[height=5.8cm,width=8cm,clip]{3915Fig1b.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg245.gif) |
Figure 1:
Variation of the velocity vs. r/r* for
different values of |
As as first step of the numerical analysis we have performed a
study of the effects on the solution of the free parameters of
the model ![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() .
With
respect to the classical case, the relativistic effects are ruled
by the new parameter
.
With
respect to the classical case, the relativistic effects are ruled
by the new parameter ![]() .
.
The parameters ![]() and
and ![]() denote the escape speed in units of
the light and Alfvén speed, respectively. However similar they
look, they have opposite effects on the initial acceleration and
the terminal speed. In the super-Alfvénic region the
acceleration is not strongly affected by different values of
denote the escape speed in units of
the light and Alfvén speed, respectively. However similar they
look, they have opposite effects on the initial acceleration and
the terminal speed. In the super-Alfvénic region the
acceleration is not strongly affected by different values of ![]() for
for
![]() ;
in fact, the effect of relativistic gravity is
negligible after
;
in fact, the effect of relativistic gravity is
negligible after
![]() (Fig. 1). So
the effects we are discussing now refer to the base of the flow,
in the subAlfvénic regime.
(Fig. 1). So
the effects we are discussing now refer to the base of the flow,
in the subAlfvénic regime.
The parameter ![]() ,
the ratio between the Schwarzschild and the
Alfvénic radius, representing also the escape speed at the
Alfvèn radius in units of c, is related to the relativistic
effects of gravity in this model. Basically
,
the ratio between the Schwarzschild and the
Alfvénic radius, representing also the escape speed at the
Alfvèn radius in units of c, is related to the relativistic
effects of gravity in this model. Basically ![]() controls the
extension of the corona and the acceleration of the flow in the
sub-Alfvénic region. Increasing
controls the
extension of the corona and the acceleration of the flow in the
sub-Alfvénic region. Increasing ![]() increases also the
asymptotic velocity, as it can be seen in Fig. 1a. A simple physical interpretation may
be given to this behaviour. When the Alfvénic surface approaches
the Schwarzschild surface, gravity in the sub-Alfvénic region,
and thus in the corona, increases. Consequently, to support
gravity the thermal energy increases too. This larger amount of
thermal energy in the corona will be transformed in turn largely
into kinetic energy along the flow. In other words, the increase
of
increases also the
asymptotic velocity, as it can be seen in Fig. 1a. A simple physical interpretation may
be given to this behaviour. When the Alfvénic surface approaches
the Schwarzschild surface, gravity in the sub-Alfvénic region,
and thus in the corona, increases. Consequently, to support
gravity the thermal energy increases too. This larger amount of
thermal energy in the corona will be transformed in turn largely
into kinetic energy along the flow. In other words, the increase
of ![]() implies a stronger density gradient of the flow in the
sub-Alfvénic region, increasing the radial pressure gradient
implies a stronger density gradient of the flow in the
sub-Alfvénic region, increasing the radial pressure gradient
![]() and leading to a stronger expansion and
acceleration.
and leading to a stronger expansion and
acceleration.
This behaviour can be also understood considering that larger
values of ![]() imply a larger space curvature, increasing also
the expansion of the streamlines and thence the efficiency of the
acceleration, as it has been shown in the study of the
relativistic Parker wind (see Meliani et al. 2004).
imply a larger space curvature, increasing also
the expansion of the streamlines and thence the efficiency of the
acceleration, as it has been shown in the study of the
relativistic Parker wind (see Meliani et al. 2004).
Conversely, increasing ![]() decreases the asymptotic velocity as
well, since it reduces the size of the corona, keeping
decreases the asymptotic velocity as
well, since it reduces the size of the corona, keeping ![]() constant, that is the distance of the Alfvén surface to the
Black Hole (see Fig. 1b). This figure
shows that the base of the flow gets closer to the Alfvén radius
and farther from the Schwarzschild radius. As in the non
relativistic case the parameter
constant, that is the distance of the Alfvén surface to the
Black Hole (see Fig. 1b). This figure
shows that the base of the flow gets closer to the Alfvén radius
and farther from the Schwarzschild radius. As in the non
relativistic case the parameter ![]() is the ratio of
gravitational to kinetic energy at the Alfvén surface, Eq. (28). An increase of
is the ratio of
gravitational to kinetic energy at the Alfvén surface, Eq. (28). An increase of ![]() reduces the fluid velocity at
the Alfvén radius with respect to escape speed needed to get out
of the black hole's attraction. The reduction of the size of the
corona is also consistent with the reduction of the velocity. The
behaviour is as expected from the solutions in the classical
regime (ST94, STT02, STT04): the higher is the value of
reduces the fluid velocity at
the Alfvén radius with respect to escape speed needed to get out
of the black hole's attraction. The reduction of the size of the
corona is also consistent with the reduction of the velocity. The
behaviour is as expected from the solutions in the classical
regime (ST94, STT02, STT04): the higher is the value of ![]() the
lower is the asymptotic velocity, although we didn't show it
explicitly, as in the present Fig. 1b.
There is also a minimum value of
the
lower is the asymptotic velocity, although we didn't show it
explicitly, as in the present Fig. 1b.
There is also a minimum value of ![]() to have mass ejection,
below that value the thermal energy cannot support gravity (see
STT02).
to have mass ejection,
below that value the thermal energy cannot support gravity (see
STT02).
The parameter ![]() is related to the rotation of the flow and to the
axial electric current (Fig. 2b).
As for non relativistic outflows (ST94, STT02) it rules the jet dynamics
through the Lorentz force, collimating asymptotically the jet via the toroidal
magnetic field, while the centrifugal force has instead a decollimating
effect. We have checked that the behaviour of the solutions is similar to the
classical case. The increase of
is related to the rotation of the flow and to the
axial electric current (Fig. 2b).
As for non relativistic outflows (ST94, STT02) it rules the jet dynamics
through the Lorentz force, collimating asymptotically the jet via the toroidal
magnetic field, while the centrifugal force has instead a decollimating
effect. We have checked that the behaviour of the solutions is similar to the
classical case. The increase of ![]() leads to more collimated and slower
jets (Fig. 2a). This can be understood as follows.
Increasing
leads to more collimated and slower
jets (Fig. 2a). This can be understood as follows.
Increasing ![]() increases the axial current (Fig. 2b) which increases the toroidal
magnetic pinching. In order to preserve equilibrium the flows reacts by increasing the centrifugal
force and thus its rotational speed by reducing its cross section. The reduction of the expansion
factor reduces as usual the pressure gradient and the thermal driving efficiency thus reducing the
asymptotic speed.
increases the axial current (Fig. 2b) which increases the toroidal
magnetic pinching. In order to preserve equilibrium the flows reacts by increasing the centrifugal
force and thus its rotational speed by reducing its cross section. The reduction of the expansion
factor reduces as usual the pressure gradient and the thermal driving efficiency thus reducing the
asymptotic speed.
![\begin{figure}
\par\includegraphics[height=7.8cm,width=7.2cm,clip]{3915Fig3a.eps...
...{8mm}
\includegraphics[height=7.8cm,width=7.2cm,clip]{3915Fig3b.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg251.gif) |
Figure 3:
Morphology in the poloidal plane of the streamlines of the
two solutions of the previous figure and their light cylinders for
|
In addition we must take into account that ![]() is related to
the electric potential
is related to
the electric potential ![]() .
Consequently it controls the
charge separation and the corresponding electric
force
.
Consequently it controls the
charge separation and the corresponding electric
force
![]() .
This force becomes dominant where the jet rotation speed becomes
relativistic
.
This force becomes dominant where the jet rotation speed becomes
relativistic
![]() .
In other words the higher is
.
In other words the higher is
![]() the larger the effects of the light cylinder
(Fig. 3).
the larger the effects of the light cylinder
(Fig. 3).
The physical meaning of ![]() remains the same as in non
relativistic flows. For
remains the same as in non
relativistic flows. For ![]() positive or negative the gas
pressure increases or decreases with colatitude, respectively.
Then in the first case the gas contributes to the thermal
confinement of the flow (underpressured jets), while in the second
to its thermal support (overpressured jets). We have limited
ourselves to present here the study of underpressured flows. The
behaviour of the relativistic solutions with
positive or negative the gas
pressure increases or decreases with colatitude, respectively.
Then in the first case the gas contributes to the thermal
confinement of the flow (underpressured jets), while in the second
to its thermal support (overpressured jets). We have limited
ourselves to present here the study of underpressured flows. The
behaviour of the relativistic solutions with ![]() is
analogous to that of classical flows. For higher
is
analogous to that of classical flows. For higher ![]() both
the asymptotic velocity and jet cross sections decrease (see STT99;
and STT02 for details).
both
the asymptotic velocity and jet cross sections decrease (see STT99;
and STT02 for details).
In the present model the parameter ![]() controls the variation of the ratio n/w with
colatitude, or equivalently in the direction perpendicular to the rotational axis.
This is a relativistic generalization of the classical solutions where it
governs the transverse profile of the mass density. As a result,
the effects are similar to those found for non relativistic solutions.
A larger
controls the variation of the ratio n/w with
colatitude, or equivalently in the direction perpendicular to the rotational axis.
This is a relativistic generalization of the classical solutions where it
governs the transverse profile of the mass density. As a result,
the effects are similar to those found for non relativistic solutions.
A larger ![]() means a larger gravitational potential of
the external streamlines with respect to the axis, where the acceleration is more efficient. Then
the asymptotic velocity increases with
means a larger gravitational potential of
the external streamlines with respect to the axis, where the acceleration is more efficient. Then
the asymptotic velocity increases with ![]() (ST94; STT02).
(ST94; STT02).
![\begin{figure}
\par\includegraphics[height=7.3cm,width=7.3cm,clip]{3915Fig4a.eps...
...{8mm}
\includegraphics[height=7.3cm,width=7.3cm,clip]{3915Fig4b.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg255.gif) |
Figure 4:
Morphology of the poloidal streamlines for two solutions
corresponding to an Inefficient Magnetic Rotator (IMR,
|
![\begin{figure}
\par\includegraphics[height=4.4cm,width=8cm,clip]{3915Fig5a.eps}\...
...e*{3mm}
\includegraphics[height=4.4cm,width=8cm,clip]{3915Fig5b.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg256.gif) |
Figure 5:
Variation of the energy flux normalized to the mass
energy, along the external streamline for the IMR solution in a)
and the EMR solution in b) of the previous figure. The Poynting
energy is |
![\begin{figure}
\par\includegraphics[height=4.4cm,width=7.8cm,clip]{3915Fig6a.eps...
...6mm}
\includegraphics[height=4.4cm,width=7.8cm,clip]{3915Fig6b.eps}
\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg257.gif) |
Figure 6: Plot of the transverse forces for the relativistic IMR a) and EMR b). Forces are normalized by their maximum value, usually reached at the base of the flow. The parameters are the same as in Fig. 4. |
We will address now the question of the process of acceleration
and collimation of the jet in the case of EMRs and IMRs. Keeping
fixed ![]() we have displayed the results for an IMR
solution with
we have displayed the results for an IMR
solution with
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() (
(
![]() )
in Fig. 4a (see also Figs. 5a and 6a), and an EMR with
)
in Fig. 4a (see also Figs. 5a and 6a), and an EMR with
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() (
(
![]() )
in Fig. 4b (see also Figs. 5b
and 6b).
)
in Fig. 4b (see also Figs. 5b
and 6b).
We see that the shape of the streamlines in the two cases (Figs. 4) looks similar to the corresponding non relativistic case (STT02; see later Figs. 7). IMRs show a fast expansion in an intermediate region, while far from the base the collimated streamlines show strong oscillations. EMRs show conversely a continuous expansion with relatively mild oscillations, or even no oscillations at all when pressures are lower. We also display for the two solutions the energies along a given streamline (Fig. 5) and the forces perpendicular to the flow (Fig. 6).
By construction of this model, the wind is basically
thermally driven. At the lowest order we have
![]() ,
while the first order term corresponds to the Poynting flux which remains
however of
the same order than the thermal terms in the transverse direction.
This supposes that there is a high temperature corona around the black hole
as proposed
by Chakrabarti (1989) and Das (1999, 2000). The latest has shown that the
stronger is the thermal
energy, the more stable is the corona.
,
while the first order term corresponds to the Poynting flux which remains
however of
the same order than the thermal terms in the transverse direction.
This supposes that there is a high temperature corona around the black hole
as proposed
by Chakrabarti (1989) and Das (1999, 2000). The latest has shown that the
stronger is the thermal
energy, the more stable is the corona.
We can study the acceleration of the jet analysing the
contribution of the different energies and their conversion from
one to the other along the streamlines. The dominating energy at
the base of the outflow is the enthalpy. Part of it is used to
balance gravity and the remaining part is converted into kinetic
energy in the region of expansion of the jet and stops when the
streamlines collimate (compare Figs. 4 and 5). In fact, during the expansion of the
jet, the plasma density decreases which also induces a decrease of
the enthalpy. In turn, it creates a strong pressure gradient
![]() that accelerates the jet. For
the parameters we have chosen, we see that the EMR solution has a
larger expansion factor than the IMR one (Figs. 4), because of the thermal driving. This is
correlated to the larger Lorentz factor of the EMR solution
(
that accelerates the jet. For
the parameters we have chosen, we see that the EMR solution has a
larger expansion factor than the IMR one (Figs. 4), because of the thermal driving. This is
correlated to the larger Lorentz factor of the EMR solution
(
![]() )
as compared to the IMR one (
)
as compared to the IMR one (
![]() ).
This result is not related to the nature of the magnetic rotator. For
other parameters, we would get different results but the
asymptotic Lorentz factor always increases with the increase of
the expansion factor because of the thermal driving. We verified
that the Poynting flux in the two solutions is negligible,
representing at maximum only
).
This result is not related to the nature of the magnetic rotator. For
other parameters, we would get different results but the
asymptotic Lorentz factor always increases with the increase of
the expansion factor because of the thermal driving. We verified
that the Poynting flux in the two solutions is negligible,
representing at maximum only ![]() of the enthalpy at the basis
of the flow.
of the enthalpy at the basis
of the flow.
![\begin{figure}
\par\includegraphics[height=7.2cm,width=7.3cm,clip]{3915Fig7a.eps...
...6mm}
\includegraphics[height=7.2cm,width=7.25cm,clip]{3915Fig7b.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg264.gif) |
Figure 7:
Morphology of the poloidal streamlines for non
relativistic IMR a) and EMR b): the parameters are the same as in Fig. 4. with
|
The IMR solution undergoes a strong expansion in this region
until a distance of
![]() and then recollimates and
consequently decelerates because of the compression. On the other
hand, the EMR solution collimates already at a distance of
approximately
and then recollimates and
consequently decelerates because of the compression. On the other
hand, the EMR solution collimates already at a distance of
approximately
![]() and accelerates all the way
downwind. In other words, the nature of the collimation affects
obviously the velocity profile.
and accelerates all the way
downwind. In other words, the nature of the collimation affects
obviously the velocity profile.
The collimation of the flow is controlled by different types of forces that depend on the morphology of the streamlines in the jet. We have plotted for the two solutions the forces perpendicular to the streamlines in Fig. 6. Asymptotically the centrifugal force is the dominant term which supports the wind against either the magnetic confinement in EMR or the pressure gradient in IMR.
The behaviour of the other forces depends on the shape of the streamlines
(Fig. 6) and they play a relevant role
in the intermediate region before collimation is fully achieved.
In particular, the stress tensor from the poloidal magnetic field
and the gravity favor deviation from radial expansion while the
thermal pressure
gradient initially tends to maintain the radial expansion. In the region of
formation of the jet, the strong gravity along the polar axis generates a
strong pressure gradient.
As density and pressure increase with colatitude (
![]() ), it also
generates a total force
), it also
generates a total force
![]() which further out in the jet provides the
thermal confinement.
which further out in the jet provides the
thermal confinement.
In an IMR, neither the pressure gradient nor the pinching force
from the toroidal magnetic field can brake the expansion of the
flow, and the recollimation occurs where the curvature of the
poloidal streamlines becomes relevant. In the asymptotic region,
the collimation is mainly provided by the transverse pressure
gradient,
![]() ,
which balances the centrifugal force. The
pressure confined jets undergo strong oscillations similarly to
the non relativistic case (STT94; STT99).
,
which balances the centrifugal force. The
pressure confined jets undergo strong oscillations similarly to
the non relativistic case (STT94; STT99).
In an EMR, conversely, the pinching force of the toroidal magnetic field provides collimation all along the flow. The pressure gradient may help this collimation as for the present solution or be completely negligible for other sets of parameters. The magnetic pinching force is balanced asymptotically mainly by the centrifugal force which tends to decollimate the jet. We must notice also that, as expected in the relativistic case, the electric force is always positive and its effect in decollimating the jet may be comparable with the centrifugal force, differently from IMRs (see Fig. 6).
![\begin{figure}
\par\includegraphics[height=6cm,width=7.8cm,clip]{3915Fig8a.eps}\...
...*{4mm}
\includegraphics[height=6cm,width=7.8cm,clip]{3915Fig8b.eps}
\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg270.gif) |
Figure 8:
Plot of the transverse forces for the non relativistic IMR
a) and EMR b). We assumed
|
We analyse here in more detail the main differences between the
relativistic and non relativistic solutions already discussed
in previous Sect. 6. By increasing
the value of ![]() we increase the depth of the potential well. In our calculations we have assumed
we increase the depth of the potential well. In our calculations we have assumed
![]() for the relativistic solutions and this can be justified as follows.
for the relativistic solutions and this can be justified as follows.
We supposed that the Alfvén surface is roughly at a distance of
10ro from the central object. This typical distance is usually chosen
because it corresponds to the case where the wind
carries away all the accreted angular momentum, provided about 10% of
the accreted mass goes to the jet (Livio 1999). This is of course arbitrary but
allows us to compare our solutions to other models.
In the case of young stellar jets, the star has a mass of the order of
![]() .
The corresponding Schwarzschild radius is approximately
.
The corresponding Schwarzschild radius is approximately
![]() km. Therefore, space curvature
at the Alfvén surface corresponds to a value of
km. Therefore, space curvature
at the Alfvén surface corresponds to a value of
![]() .
Conversely, for
AGN jets, with a central super massive black hole of
.
Conversely, for
AGN jets, with a central super massive black hole of
![]() ,
we have
,
we have
![]() which corresponds to the value we have chosen
which corresponds to the value we have chosen
![]() .
.
We have drawn the corresponding morphologies of two non relativistic solutions associated with an IMR and an EMR in Figs. 7, keeping the other parameters as in Fig. 4. We also plotted the corresponding transverse forces for the non relativistic solutions in Figs. 8.
Let's first turn our attention to the solution from an IMR. The morphologies of classical and relativistic jets show indeed small differences. The relativistic jet, though, undergoes an expansion slightly more important in the intermediate region (Fig. 4a) than in the classical case (Fig. 7a). This expansion induces a slight relative increase of the curvature forces (inertial and magnetic) compared to other forces. In the asymptotic region, the relativistic jet recollimation is comparable to the non relativistic one (Fig. 9a).
Note also that in the asymptotic region, the relativistic jet pinching by the toroidal magnetic field is almost null, while in the non relativistic solution this force is of the order of the pressure gradient (Figs. 6a and 8a). This behaviour is a consequence of the decrease of the collimation efficiency in relativistic jets.
Last, we know that in the relativistic solutions, there is
an extra electric force,
![]() ,
due to the non negligible
charge separation, which also decollimates. In IMRs,
its influence remains however weak because of the low
magnetic field.
,
due to the non negligible
charge separation, which also decollimates. In IMRs,
its influence remains however weak because of the low
magnetic field.
In the jet solution associated with an EMR, the solution is effectively magnetically collimated because of the toroidal magnetic field pinching force. This solution clearly shows the role of the magnetic field in collimating the jet but also the contribution of the charge separation to the electric field and then to the decollimation.
The morphology of EMR jets is more affected by relativistic effects than the one of IMR jets. This can be seen by comparing Figs. 4b and 7b. In particular, the jet radius, or equivalently the expansion factor, asymptotically becomes more important in relativistic jets because of the increase of the centrifugal and electric forces (Figs. 6b and 8b). Simultaneously, the magnitude of the Lorentz force decreases and the thermal acceleration increases.
We can give a simple explanation to this relativistic effect. An
increase of gravity at the base of the jet induces a decrease of
the normalized electric current in the jet because
![]() where
where
![]() .
We have plotted the dimensionless electric current in Fig. 10 for the two EMR
solutions. The electric current
.
We have plotted the dimensionless electric current in Fig. 10 for the two EMR
solutions. The electric current ![]() flows through a given
cross sectional area
flows through a given
cross sectional area
![]() of the classical and
relativistic solutions. We use the normalized electric current
because of the different scaling of the classical and the
relativistic solutions. The decrease of the current goes with a
decrease of the toroidal magnetic field and with an increase of
the expansion of the jet as explained in Sect. 6.2
and, consequently, with an increase of the poloidal velocity.
Note that this increase of the velocity corresponds to the
increase of the relativistic gravity as we already discussed. The new point
is that, conversely
to hydrodynamical models, it also decollimates the flow.
On the other hand, the magnetocentrifugal driving of the Poynting flux
becomes weaker in
relativistic thermally driven winds, as expected.
Thus, as the rest mass increases, the
Poynting flux is getting weaker relatively to the other energies,
of the classical and
relativistic solutions. We use the normalized electric current
because of the different scaling of the classical and the
relativistic solutions. The decrease of the current goes with a
decrease of the toroidal magnetic field and with an increase of
the expansion of the jet as explained in Sect. 6.2
and, consequently, with an increase of the poloidal velocity.
Note that this increase of the velocity corresponds to the
increase of the relativistic gravity as we already discussed. The new point
is that, conversely
to hydrodynamical models, it also decollimates the flow.
On the other hand, the magnetocentrifugal driving of the Poynting flux
becomes weaker in
relativistic thermally driven winds, as expected.
Thus, as the rest mass increases, the
Poynting flux is getting weaker relatively to the other energies,
![]() ,
while, the thermal
energy becomes relativistic and comparable to the rest mass
,
while, the thermal
energy becomes relativistic and comparable to the rest mass
![]() .
.
![\begin{figure}
\par\includegraphics[height=4.5cm,width=8cm,clip]{3915Fig10.eps}
\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg286.gif) |
Figure 10:
Density of the electric current normalized
|
The relativistic effects on the jet acceleration become remarkable only
for a distance between the Alfvén surface and the Schwarzschild surface
smaller than 100 (i.e. ![]() ,
see Fig. 11a). For
,
see Fig. 11a). For ![]() ,
using this model, we see that outflows from a
star with mass
,
using this model, we see that outflows from a
star with mass
![]() and starting at
and starting at
![]() are simply scaling with
are simply scaling with ![]() (Figs. 11b and 11c). Similarly the ratio between the
energetics of the two jets are simply proportional to
(Figs. 11b and 11c). Similarly the ratio between the
energetics of the two jets are simply proportional to ![]() .
The scaling
just reflects the linear growth of the flow formation region with
gravity, i.e. with
.
The scaling
just reflects the linear growth of the flow formation region with
gravity, i.e. with ![]() .
.
Conversely, for ![]() ,
the jet is formed at a distance smaller than
,
the jet is formed at a distance smaller than
![]() ,
this linear scaling with
,
this linear scaling with ![]() of the dynamics and the energetics
does not hold any longer because of non linear relativistic effects.
The thermal energy converts more efficiently into kinetic energy
(Fig. 11a) as in the spherical case
(Meliani et al. 2004). It increases even more because of the stronger
expansion of the
relativistic jet in the super-Alfvénic region. In fact, in
the relativistic solution displayed in Fig. 11a,
collimation starts at 50 Alfvén radii, while, in
the non relativistic solution, Fig. 11c,
collimation occurs only at 10 Alfvén radii.
of the dynamics and the energetics
does not hold any longer because of non linear relativistic effects.
The thermal energy converts more efficiently into kinetic energy
(Fig. 11a) as in the spherical case
(Meliani et al. 2004). It increases even more because of the stronger
expansion of the
relativistic jet in the super-Alfvénic region. In fact, in
the relativistic solution displayed in Fig. 11a,
collimation starts at 50 Alfvén radii, while, in
the non relativistic solution, Fig. 11c,
collimation occurs only at 10 Alfvén radii.
![\begin{figure}
\par\includegraphics[height=4.5cm,width=8cm,clip]{3915Fig11a.eps}...
...mm}\includegraphics[height=4.65cm,width=7.65cm,clip]{3915Fig11d.eps}\end{figure}](/articles/aa/full/2006/09/aa3915-05/Timg292.gif) |
Figure 11:
Plot of the energies normalized by the parameter |
As we have seen, solutions obtained with this model are essentially thermally driven winds but collimation is either thermal (pressure confinement) or magnetic (toroidal magnetic pinching). However, conversely to the non relativistic case an extra decollimating force exists which is the electric force, despite that we neglect the light cylinder effects.
The strength of the electric field results from the induction term
![]() and it is higher for higher magnetic fields. As
a matter of fact it gets more important when magnetic effects are important
and when the light cylinder is closer to the streamlines.
In relativistic flows where the poloidal velocity is of the order
of the light velocity, the contribution in the transverse direction
of this force increases in the super-Alfvénic domain.
and it is higher for higher magnetic fields. As
a matter of fact it gets more important when magnetic effects are important
and when the light cylinder is closer to the streamlines.
In relativistic flows where the poloidal velocity is of the order
of the light velocity, the contribution in the transverse direction
of this force increases in the super-Alfvénic domain.
Therefore, the contribution of this force, in relativistic jets
from EMRs, is of the order of the pinching force and the
centrifugal force. Conversely, in the non relativistic limit, the
poloidal velocity remains largely subrelativistic,
![]() ,
and the electric field remains weak (
,
and the electric field remains weak (
![]() ;
see for
comparison Figs. 6b and 8b). The electric field does not
affect the collimation of the non relativistic jet and the charge
separation can be neglected.
;
see for
comparison Figs. 6b and 8b). The electric field does not
affect the collimation of the non relativistic jet and the charge
separation can be neglected.
Conversely, the effects of the electric force are negligible in
pressure confined jets from IMRs as the magnetic effects
themselves are very weak or completely negligible,
![]() .
.
Parallely, the effects of the electric force on the acceleration of the jet are very weak even for EMRs. The correction introduced on the asymptotic speed is negligible. This is because the electric force is perpendicular to the streamlines and, so, it affects mainly the morphology of the jet.
In this paper, we have investigated the problem of the formation
and collimation of relativistic jets. We have explored these
problems by means of a semi-analytical model, which is the first
meridional self-similar model of relativistic jets, including
general relativistic effects. We constructed it on the basis of
the classical model developed in ST94 to study jets from young
stars. We have made an extension of this model for a black hole
characterized by weak angular momentum,
![]() .
Therefore, we treated the problem of
GRMHD outflows in a Schwarzschild metric. Moreover, we
concentrated our efforts on modelling the jet close to its polar
axis. In the construction of this model, we were limited to
describing jets possessing a weak rotation velocity compared to the
speed of light and we neglected the effects of the light cylinder.
Thus, we restricted our study to thermally accelerated jets with
a weak contribution of the Poynting flux.
However, in the collimation of the jet, both electric and magnetic
terms are comparable to the inertial and pressure gradient ones.
We have also studied the collimation effects by magnetic and
thermal forces and the decollimation effect of centrifugal and
electric forces.
Our model is restricted to outflow solutions only, and we do not
address to the problem of the origin of the hot coronal plasma.
.
Therefore, we treated the problem of
GRMHD outflows in a Schwarzschild metric. Moreover, we
concentrated our efforts on modelling the jet close to its polar
axis. In the construction of this model, we were limited to
describing jets possessing a weak rotation velocity compared to the
speed of light and we neglected the effects of the light cylinder.
Thus, we restricted our study to thermally accelerated jets with
a weak contribution of the Poynting flux.
However, in the collimation of the jet, both electric and magnetic
terms are comparable to the inertial and pressure gradient ones.
We have also studied the collimation effects by magnetic and
thermal forces and the decollimation effect of centrifugal and
electric forces.
Our model is restricted to outflow solutions only, and we do not
address to the problem of the origin of the hot coronal plasma.
We found that the influence of the electric force and the charge
separation in the
jet depends on the collimation regime. In the case of EMRs
where jets are magnetically collimated, the electric decollimating force
plays an important role. This force is of the order of the magnitude
of the centrifugal force and of the magnetic pinching.
Therefore, relativistic jets from EMRs are less collimated than
their non relativistic counterparts.
Conversely, jets from IMRs,
where collimation is mainly of thermal origin, are not very sensitive
to the electric decollimation.
In this type of jets, the contribution of
![]() is balanced
by the increase of the external pressure.
is balanced
by the increase of the external pressure.
We have also used the model to compare classical jets to
relativistic jets. We undertook this comparative study by changing
the free parameter ![]() .
In fact, this new parameter gives in the
relativistic model the space curvature which is induced by gravity
near the central object. We used typical values of
.
In fact, this new parameter gives in the
relativistic model the space curvature which is induced by gravity
near the central object. We used typical values of ![]() from
from
![]() for Jets from Young Stellar Objects to
for Jets from Young Stellar Objects to
![]() for jets from compact sources. We found that the difference
between these two types of jets is only a scaling effect on
for jets from compact sources. We found that the difference
between these two types of jets is only a scaling effect on ![]() for
for
![]() .
In this case, the spatial dimensions and
energies are linear functions of
.
In this case, the spatial dimensions and
energies are linear functions of ![]() .
For
.
For
![]() ,
the
relativistic effects increase together with the thermal
acceleration of the jet. Simultaneously, strongly relativistic
effects tend to decollimate the jets because of the decrease of
the electric current density.
,
the
relativistic effects increase together with the thermal
acceleration of the jet. Simultaneously, strongly relativistic
effects tend to decollimate the jets because of the decrease of
the electric current density.
To conclude we have seen that relativistic effects and particularly relativistic gravity tend to enhance the thermal acceleration (as in Meliani et al. 2004) and reduce the magnetic collimation of the jet (as in Bogovalov & Tsinganos 2005). Still collimation can be obtained either by thermal or magnetic means but relativistic effects lower the efficiency of the magnetic rotator. This means that despite quantitative changes, we can use this generalized model to verify, for the classification of AGN jets, the conjectures given in Sauty et al. (2001) using the non relativistic model. Mainly we see that the observed types of jets from radio loud galaxies can be connected to the efficiency of their magnetic rotator and to the environment of the host galaxy. By using the present model, a more precise and quantitative analysis of the observed jets will be presented in a following paper.
Acknowledgements
We acknowledge financial support for our visits from the French Foreign Office and the Greek General Secretariat of Research and Technology (Program PLATON), from the European RTN JETSET (MRTN-CT-2004-005592) and the Observatoire de Paris. E.T. acknowledges financial support by the Italian Ministry for Education, University and Research (MIUR) under the grant Cofin 2003/027534-002. Part of this work has been supported by the European RTN ENIGMA (HPRN-CY-2002-00231).
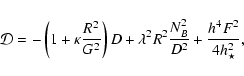 |
(A.4) |
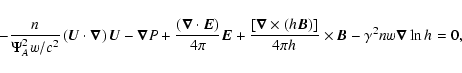 |
(B.1) |
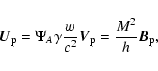 |
(B.2) |
![\begin{displaymath}U_\varphi = \Psi_A \gamma \frac{w}{c^2} V_\varphi
= \lambda h...
...{}^2-h_{}^2 + G^2 h_{\star}^2 x_{\rm A}^2}\right]
\sin\theta .
\end{displaymath}](/articles/aa/full/2006/09/aa3915-05/img320.gif) |
(B.3) |
| |
= | 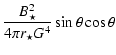 |
|
![$\displaystyle \times\left[ \frac{F}{2} \frac{{\rm d} M^2}{{\rm d} R} + \frac{M^...
... F}{{\rm d} R}
+ \frac{\lambda^2 h_{\star}^2 R}{M^2} \frac{N_{V}^2}{D^2}\right]$](/articles/aa/full/2006/09/aa3915-05/img326.gif) |
(B.5) |
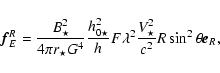 |
(B.8) |
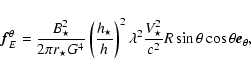 |
(B.9) |
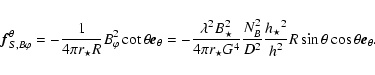 |
(B.11) |