a Spectral types from Table 1.
(B-V)0 adopted from Fitzpatrick (1988) for LMC supergiants of corresponding optical spectral type.
Intrinsic colour for WR/WN/WC stars from Smith et al. (1990): (B-V)
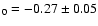 .
b .
b
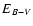
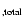 = (B-V) = (B-V)
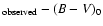 .
c .
c
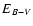
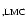 = =
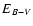
 -
-
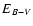
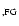 .
The foreground reddening .
The foreground reddening
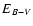
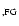 (=MW + VC reddening) towards the LMC lines of sight was estimated by applying the relation
N(Na I) =
(=MW + VC reddening) towards the LMC lines of sight was estimated by applying the relation
N(Na I) =
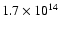
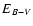 1.8 (Hobbs 1974b),
to the observed Na I column densities.
d 1.8 (Hobbs 1974b),
to the observed Na I column densities.
d
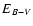
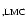 = =
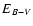
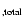 -
-
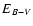
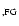 ,
with ,
with
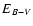
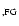 = =
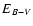
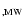 + +
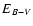
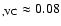 mag. mag.
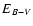
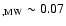 mag, estimated from the Galactic extinction map by Drimmel et al. (2003), mag, estimated from the Galactic extinction map by Drimmel et al. (2003),
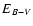
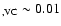 mag, derived via N(Na I).
The foreground reddening map based on H I by Staveley-Smith gives a similar value of mag, derived via N(Na I).
The foreground reddening map based on H I by Staveley-Smith gives a similar value of
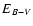
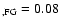 mag. mag.
|