A&A 447, 31-48 (2006)
DOI: 10.1051/0004-6361:20054185
P. Astier1 - J. Guy1 - N. Regnault1 - R. Pain1 - E. Aubourg2,3 - D. Balam4 - S. Basa5 - R. G. Carlberg6 - S. Fabbro7 - D. Fouchez8 - I. M. Hook9 - D. A. Howell6 - H. Lafoux3 - J. D. Neill4 - N. Palanque-Delabrouille3 - K. Perrett6 - C. J. Pritchet4 - J. Rich3 - M. Sullivan6 - R. Taillet1,10 - G. Aldering11 - P. Antilogus1 - V. Arsenijevic7 - C. Balland1,2 - S. Baumont1,12 - J. Bronder9 - H. Courtois13 - R. S. Ellis14 - M. Filiol5 - A. C. Gonçalves15 - A. Goobar16 - D. Guide1 - D. Hardin1 - V. Lusset3 - C. Lidman12 - R. McMahon17 - M. Mouchet15,2 - A. Mourao7 - S. Perlmutter11,18 - P. Ripoche8 - C. Tao8 - N. Walton17
1 - LPNHE, CNRS-IN2P3 and Universités Paris VI & VII, 4 place Jussieu,
75252 Paris Cedex 05, France;
2 - APC, Collège de France, 11 place Marcellin Berthelot, 75005 Paris,
France
3 - DSM/DAPNIA, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
4 - Department of Physics and Astronomy, University of Victoria,
PO Box 3055, Victoria, BC VSW 3P6, Canada
5 - LAM, CNRS, BP8, Traverse du Siphon, 13376 Marseille Cedex 12, France
6 - Department of Astronomy and Astrophysics, University of Toronto,
60 St. George Street, Toronto, ON M5S 3H8, Canada
7 - CENTRA-Centro M. de Astrofisica and Department of Physics, IST, Lisbon,
Portugal
8 - CPPM, CNRS-IN2P3 and Université Aix-Marseille II, Case 907,
13288 Marseille Cedex 9, France
9 - University of Oxford Astrophysics, Denys Wilkinson Building, Keble Road,
Oxford OX1 3RH, UK
10 - Université de Savoie, 73000 Chambery, France
11 - LBNL, 1 Cyclotron Rd, Berkeley, CA 94720, USA
12 - ESO, Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
13 - CRAL, 9 avenue Charles André, 69561 Saint-Genis-Laval cedex, France
14 - California Institute of Technology, Pasadena, California, USA
15 - LUTH, UMR 8102, CNRS and Observatoire de Paris, 92195 Meudon, France
16 - Department of Physics, Stockholm University, Sweden
17 - IoA, University of Cambridge, Madingley Road,
Cambridge CB3 0EZ, UK
18 - Department of Physics, University of California Berkeley, Berkeley, CA 94720, USA
Received 9 September 2005 / Accepted 11 October 2005
Abstract
We present distance measurements to 71 high redshift type
Ia supernovae discovered during the first year of the 5-year
Supernova Legacy Survey (SNLS). These events were detected and their
multi-color light-curves measured using the MegaPrime/MegaCam instrument at
the Canada-France-Hawaii Telescope (CFHT), by repeatedly imaging four one-square degree fields in
four bands, as part of the CFHT Legacy Survey (CFHTLS). Follow-up spectroscopy was performed at
the VLT, Gemini and Keck telescopes to confirm the nature of the
supernovae and to measure their redshift. With this data set, we
have built a Hubble diagram extending to z=1, with all distance
measurements involving at least two bands. Systematic uncertainties
are evaluated making use of the multi-band photometry obtained
at CFHT. Cosmological fits to this first year SNLS
Hubble diagram give the following results:
![]() for a flat
for a flat ![]() CDM model; and
CDM model; and
![]() for a flat cosmology with
constant equation of state w when combined with the
constraint from the recent Sloan Digital Sky Survey measurement of
baryon acoustic oscillations.
for a flat cosmology with
constant equation of state w when combined with the
constraint from the recent Sloan Digital Sky Survey measurement of
baryon acoustic oscillations.
Key words: supernovae: general - cosmology: observations - cosmological parameters
The discovery of the acceleration of the Universe stands as a major breakthrough of observational cosmology. Surveys of cosmologically distant Type Ia supernovae (SNe Ia; Riess et al. 1998; Perlmutter et al. 1999) indicated the presence of a new, unaccounted-for "dark energy'' that opposes the self-attraction of matter and causes the expansion of the Universe to accelerate. When combined with indirect measurements using cosmic microwave background (CMB) anisotropies, cosmic shear and studies of galaxy clusters, a cosmological world model has emerged that describes the Universe as flat, with about 70% of its energy contained in the form of this cosmic dark energy (see for example Seljak et al. 2005).
Current projects aim at directly probing the nature of the dark energy
via a determination of
its equation of state parameter - the pressure to energy-density ratio -
![]() ,
which
also defines the time dependence of the dark energy density:
,
which
also defines the time dependence of the dark energy density:
![]() ,
where a is the scale factor.
Recent constraints on w (Knop et al. 2003; Barris et al. 2004; Riess et al. 2004; Tonry et al. 2003) are
consistent with a very wide range of Dark Energy models. Among them,
the historical cosmological constant (w=-1) is 10120 to
1060 smaller than plausible vacuum energies predicted by fundamental
particle theories. It also cannot explain why matter and dark energy
have comparable densities today. "Dynamical
,
where a is the scale factor.
Recent constraints on w (Knop et al. 2003; Barris et al. 2004; Riess et al. 2004; Tonry et al. 2003) are
consistent with a very wide range of Dark Energy models. Among them,
the historical cosmological constant (w=-1) is 10120 to
1060 smaller than plausible vacuum energies predicted by fundamental
particle theories. It also cannot explain why matter and dark energy
have comparable densities today. "Dynamical ![]() '' models have
been proposed (quintessence, k-essence) based on speculative field
models, and some predict values of w above -0.8 - significantly
different from -1. Measuring the average value of w with a
precision better than 0.1 will permit a discrimination between the
null hypothesis (pure cosmological constant, w=-1)
and some dynamical dark energy models.
'' models have
been proposed (quintessence, k-essence) based on speculative field
models, and some predict values of w above -0.8 - significantly
different from -1. Measuring the average value of w with a
precision better than 0.1 will permit a discrimination between the
null hypothesis (pure cosmological constant, w=-1)
and some dynamical dark energy models.
Improving significantly over current SN constraints on the dark energy requires a ten-fold larger sample (i.e. o(1000) at 0.2<z<1., where w is best measured), in order to significantly improve on statistical errors but also, most importantly, on systematic uncertainties. The traditional method of measuring distances to SNe Ia involves different types of observations at about 10 different epochs spread over nearly 3 months: discovery via image subtraction, spectroscopic identification, and photometric follow-up, usually on several telescopes. Many objects are lost or poorly measured in this process due to the effects of inclement weather during the follow-up observations, and the analysis often subject to largely unknown systematic uncertainties due to the use of various instruments and telescopes.
The Supernova Legacy Survey (SNLS)![]() was designed to improve
significantly over the traditional strategy as follows: 1) discovery
and photometric follow-up are performed with a wide field imager used
in "rolling search'' mode, where a given field is observed every
third to fourth night as long as it remains visible; 2) service
observing is exploited for both spectroscopy and imaging, reducing the
impact of bad weather. Using a single imaging instrument to observe
the same fields reduces photometric systematic
uncertainties; service observing optimizes both the yield of spectroscopic
observing time, and the light-curve sampling.
was designed to improve
significantly over the traditional strategy as follows: 1) discovery
and photometric follow-up are performed with a wide field imager used
in "rolling search'' mode, where a given field is observed every
third to fourth night as long as it remains visible; 2) service
observing is exploited for both spectroscopy and imaging, reducing the
impact of bad weather. Using a single imaging instrument to observe
the same fields reduces photometric systematic
uncertainties; service observing optimizes both the yield of spectroscopic
observing time, and the light-curve sampling.
In this paper we report the progress made, and the cosmological results obtained, from analyzing the first year of the SNLS. We present the data collected, the precision achieved both from improved statistics and better control of systematics, and the potential of the project to further reduce and control systematic uncertainties on cosmological parameters. Section 2 describes the imaging and spectroscopic surveys and their current status. Sections 3 and 4 present the data reduction and photometric calibration. The light-curve fitting method, the SNe samples and the cosmological analysis are discussed in Sect. 5. A comparison of the nearby and distant samples used in the cosmological analysis is performed in Sect. 6 and the systematic uncertainties are discussed in Sect. 7.
The Supernova Legacy Survey is comprised of two components: an imaging survey to detect SNe and monitor their light-curves, and a spectroscopic program to confirm the nature of the candidates and measure their redshift.
The imaging is taken as part of the deep component of the CFHT Legacy
Survey (CFHTLS 2002) using the one square degree imager,
MegaCam (Boulade et al. 2003). In total, CFHTLS has been allocated
474 nights
over 5 years and consists of 3 surveys: a very wide shallow survey
(1300 square degrees), a wide survey (120 square degrees) and a deep
survey (4 square degrees). The 4 pointings of the deep survey
are evenly distributed in right ascension
(Table 1). The observations for the deep survey
are sequenced in a way suitable for detecting supernovae and measuring
their light-curves: in every lunation in which a field is visible,
it is imaged at five equally spaced epochs during a MegaCam run
(which lasts about 18 nights). Observations are taken in a combination of ![]() ,
, ![]() plus
plus ![]() or
or ![]() filters (the MegaCam filter set;
see Sect. 4) depending on the phase of
the moon. Each field is observed for 5 to 7 consecutive lunations.
Epochs lost to weather on any one night remain in the queue until the
next clear observing opportunity, or until a new observation in the
same filter is scheduled.
filters (the MegaCam filter set;
see Sect. 4) depending on the phase of
the moon. Each field is observed for 5 to 7 consecutive lunations.
Epochs lost to weather on any one night remain in the queue until the
next clear observing opportunity, or until a new observation in the
same filter is scheduled.
During the first year of the survey, the observing efficiency was
lower than expected and the nominal observation plan could not always
be fulfilled. The scheduled ![]() exposures (
exposures (
![]() s plus
s plus
![]() s per lunation)
and
s per lunation)
and ![]() exposures (5 epochs
exposures (5 epochs ![]() 1500 s) were usually
acquired. Assigned a lower priority,
1500 s) were usually
acquired. Assigned a lower priority, ![]() and
and ![]() received less
time than originally planned: on average only 2.2 epochs of 1050 s
were collected per lunation in
received less
time than originally planned: on average only 2.2 epochs of 1050 s
were collected per lunation in ![]() ,
and 2 epochs of 2700 s in
,
and 2 epochs of 2700 s in ![]() ;
for the latter, the average ignores the D2 field and the D3 field in 2003, for which only fragmentary observations were
obtained in
;
for the latter, the average ignores the D2 field and the D3 field in 2003, for which only fragmentary observations were
obtained in ![]() .
With efficiency
ramping up,
.
With efficiency
ramping up, ![]() and
and ![]() approached their nominal rate in May 2004, and since then
the nominal observation plan (detailed in Sullivan et al. 2005) is
usually completed.
approached their nominal rate in May 2004, and since then
the nominal observation plan (detailed in Sullivan et al. 2005) is
usually completed.
Table 1: Coordinates and average Milky Way extinction (from Schlegel et al. 1998) of fields observed by the Deep/SN component of the CFHTLS.
Observations and real-time pre-processing are performed by the CFHT
staff using the Elixir reduction pipeline (Magnier & Cuillandre 2004), with the
data products immediately available to the SN search teams. We have
set up two independent real-time pipelines which analyze
these pre-processed images. The detection of new candidates is
performed by subtracting a "past" image to the current images,
where the past-image is constructed by stacking previous
observations of the same field. The key element of these pipelines is
matching the point spread function of a new exposure to the
past-image. This is done using the Alard algorithm (Alard & Lupton 1998; Alard 2000)
for one of the pipelines, and using a non-parametric approach for the
other.
New candidates are detected and measured on the subtraction images;
detections are matched to other
detections in the field, if any.
One of the pipelines processes all bands on an equal footing, the
other detects in the ![]() band (which is deep enough for trigger
purposes) and measures fluxes in the other bands.
The two candidate lists are merged after each epoch and typically have
an overlap greater than 90% for
band (which is deep enough for trigger
purposes) and measures fluxes in the other bands.
The two candidate lists are merged after each epoch and typically have
an overlap greater than 90% for
![]() after two epochs in a
dark run.
The reasons for one candidate being found by only one
pipeline are usually traced to different masking strategies or
different handling of the CCD overlap regions.
after two epochs in a
dark run.
The reasons for one candidate being found by only one
pipeline are usually traced to different masking strategies or
different handling of the CCD overlap regions.
Spectroscopy is vital in order to obtain SN redshifts, and to
determine the nature of each SN candidate. This requires observations
on 8-10 m class telescopes due to the faintness of these distant
supernovae. Spectroscopic follow-up time for the candidates presented
in this paper was obtained at a variety of telescopes during the
Spring and Fall semesters of 2003 and the Spring semester of 2004.
The principle spectroscopic allocations were at the European Southern
Observatory Very Large Telescope (program ID ![]() 171.A-0486
171.A-0486![]() ;
60 h per semester), and at Gemini-North and South (Program-IDs:
GN-2004A-Q-19, GS-2004A-Q-11, GN-2003B-Q-9, and GS-2003B-Q-8; 60 h per semester).
Spectroscopic time was also obtained at Keck-I and Keck-II (3 nights during each Spring semester) as the D3 field
cannot be seen by VLT or Gemini-South. Further complementary
spectroscopic follow-up observations were also obtained at Keck-I (4 nights in each of 2003A, 2003B and 2004A) as part of a detailed study
of the intermediate redshift SNe in our sample
(Ellis et al., in prep.).
;
60 h per semester), and at Gemini-North and South (Program-IDs:
GN-2004A-Q-19, GS-2004A-Q-11, GN-2003B-Q-9, and GS-2003B-Q-8; 60 h per semester).
Spectroscopic time was also obtained at Keck-I and Keck-II (3 nights during each Spring semester) as the D3 field
cannot be seen by VLT or Gemini-South. Further complementary
spectroscopic follow-up observations were also obtained at Keck-I (4 nights in each of 2003A, 2003B and 2004A) as part of a detailed study
of the intermediate redshift SNe in our sample
(Ellis et al., in prep.).
Most of the observations are performed in long-slit mode. The detailed spectroscopic classification of these candidates is discussed elsewhere (see Howell et al. 2005 and Basa et al., in prep.). In summary, we consider two classes of events (see Howell et al. 2005 for the exact definitions): secure SNe Ia events ("SN Ia''), and probable Ia events ("SN Ia*''), for which the spectrum matches a SN Ia better than any other type, but does not completely rule out other possible interpretations. All other events which were not spectroscopically identified as SN Ia or SN Ia* were ignored in this analysis.
The imaging survey still delivers more variable candidates than can actually be observed spectroscopically. Hence, an accurate ranking of these candidates for further observations is essential. This ranking is performed to optimize the SN Ia yield of our allocations. Our method uses both a photometric selection tool (discussed in Sullivan et al. 2005) which performs real-time light-curve fits to reduce the contamination of core-collapse SNe, and a database of every variable object ever detected by our pipelines to remove AGN and variable stars which are seen to vary repeatedly in long-timescale data sets (more than one year).
SN Ia candidates fainter than
![]() (likely at z>1) and
those with very low percentage increases over their host galaxies
(where identification is extremely difficult - see
Howell et al. 2005) are usually not observed. With the real-time
light-curve fit technique, approximately 70% of our candidates turned out to
be SNe Ia. The possible biases associated with this selection were
studied in Sullivan et al. (2005) and found to be negligible.
(likely at z>1) and
those with very low percentage increases over their host galaxies
(where identification is extremely difficult - see
Howell et al. 2005) are usually not observed. With the real-time
light-curve fit technique, approximately 70% of our candidates turned out to
be SNe Ia. The possible biases associated with this selection were
studied in Sullivan et al. (2005) and found to be negligible.
The imaging survey started in August 2003 after a few months of MegaCam commissioning. (Some SN candidates presented here were detected during the commissioning period.) This paper considers candidates with maximum light up to July 15th 2004, corresponding approximatively to a full year of operation. During this time frame, which includes the ramping-up period of the CFHTLS, about 400 transients were detected, 142 spectra were acquired: 20 events were identified as Type II supernovae, 9 as AGN/QSO, 4 as SN Ib/c, and 91 events were classified as SN Ia or SN Ia*. The 18 remaining events have inconclusive spectra. Table 7 gives the 91 objects identified as SN Ia or SN Ia* during our first year of operation.
At the end of each MegaCam run, the images are pre-processed again at CFHT using the Elixir pipeline (Magnier & Cuillandre 2004). This differs from the real-time reduction process described in Sect. 2.1, in that master flat-field images and fringe-correction frames are constructed from all available data from the entire MegaCam run (including PI data). The Elixir process consists of flat-fielding and fringe subtraction, with an approximate astrometric solution also derived. Elixir provides reduced data which has a uniform photometric response across the mosaic (at the expense of a non-uniform sky background). This "photometric flat-field'' correction is constructed using exposures with large dithers obtained on dense stellar fields.
The SNLS pipelines then associate a weight map with each Elixir-processed image (i.e. each CCD from a given exposure) from the flat-field frames and the sky background variations. Bad pixels (as identified by Elixir), cosmic rays (detected using the Laplacian filter of van Dokkum 2001), satellite trails, and saturated areas are set to zero in the weight maps. An object catalog is then produced using SExtractor (Bertin & Arnouts 1996), and point-like objects are used to derive an image quality (IQ) estimate. The sky background map computed by SExtractor is then subtracted from the image. We additionally perform aperture photometry on the objects of the SExtractor catalog for the purpose of photometric calibration (see Sect. 4).
For each supernova candidate, the image with the best IQ (subsequently called "reference'') is identified, and all other images (both science images and their weight maps) are resampled to the pixel grid defined by this reference. The variations of the Jacobian of the geometrical transformations, which translate into photometric non-uniformities in the re-sampled images, are sufficiently small (below the millimag level) to be ignored. We then derive the convolution kernels that would match the PSF (modeled using the DAOPHOT package Stetson 1987) of the reference image to the PSF of the other resampled science images, but we do not perform the convolutions. These convolution kernels not only match the PSFs, but also contain the photometric ratios of each image to the reference. We ensure that these photometric ratios are spatially uniform by imposing a spatially uniform kernel integral, but allow for spatial kernel shape variations as the images may have spatially varying PSFs. Following Alard (2000), the kernel is fit on several hundred objects selected for their high, though unsaturated, peak flux. The kernel fit is made more robust by excluding objects with large residuals and iterating.
Our approach to the differential flux measurement of a SN is
to simultaneously fit all images in a given filter
with a model that includes (i) a spatially variable galaxy (constant
with time), and (ii) a time-variable point source (the supernova).
The model is described in detail in Fabbro (2001).
The shape of the galaxy and positions of both
galaxy and supernova are fit globally. The intensity Di,p in a
pixel p of image i is modeled as:
The fit parameters are: the supernova position
and the galaxy pixel values (common to all images), the supernova
fluxes, and a constant sky background (different for each
image). In some images in the series, the supernova flux is known to
be absent or negligible; these frames enter the fit as "zero flux
images'' and are thus used to determine the values of the galaxy pixels.
The least-squares photometric fit minimizes:
Note that this method does not involve any real image convolution: the
fitted model possesses the PSF of the reference image, and it is the model
that is convolved to
match the PSF of every other image.
We typically fit
![]() galaxy pixels and several hundred images, and
each SN fit usually has 2000 to 3000 parameters. The fit is run once,
5
galaxy pixels and several hundred images, and
each SN fit usually has 2000 to 3000 parameters. The fit is run once,
5![]() outlier pixels are removed, and the fit is run again.
outlier pixels are removed, and the fit is run again.
The photometric fit yields values of the fit parameters along with a covariance matrix. There are obvious correlations between SN fluxes and galaxy brightness, between these two parameters and the background level, and between the SN position and the flux, for any given image. More importantly, the uncertainty in the SN position and the galaxy brightness introduces correlations between fluxes at different epochs that have to be taken into account when analyzing the light-curves. Note that flux variances and the correlations between fluxes decrease when adding more "zero flux images'' into the fit. It will therefore be possible to derive an improved photometry for most of the events presented in this paper, when the fields are observed again and more images without SN light are available.
Once the photometric fit has converged, the parameter covariance matrix (including flux variances and covariances) is derived. This Section addresses the accuracy of these uncertainties, in particular the flux variances and covariances, which are used as inputs to the subsequent light-curve fit.
The normalization of the
parameter covariance matrix directly reflects the normalization of
image weights. We checked that the weights are on average properly
normalized because the minimum ![]() per degree of freedom is very
close to 1 (we find 1.05 on average). However, this does not imply
mathematically that the flux uncertainties are properly normalized,
because Eq. (2) neglects the correlations
between neighboring pixels introduced by image re-sampling. We
considered accounting for these correlations; however, this would make
the fitting code intolerably slow, as the resulting
per degree of freedom is very
close to 1 (we find 1.05 on average). However, this does not imply
mathematically that the flux uncertainties are properly normalized,
because Eq. (2) neglects the correlations
between neighboring pixels introduced by image re-sampling. We
considered accounting for these correlations; however, this would make
the fitting code intolerably slow, as the resulting ![]() would be
non-diagonal.
Using approximate errors in least squares (such as ignoring
correlations) increases the actual variance of the estimators, but in
the case considered here, the loss in photometric accuracy is below 1%.
The real drawback of ignoring pixel correlations is that
parameter uncertainties extracted from the fit are underestimated
(since pixel correlations are positive); this is a product of any photometry
method that assumes uncorrelated pixels on re-sampled or convolved
images. Our geometric alignment technique, used to align images prior
to the flux measurement as described in
Sect. 3.2, uses a
would be
non-diagonal.
Using approximate errors in least squares (such as ignoring
correlations) increases the actual variance of the estimators, but in
the case considered here, the loss in photometric accuracy is below 1%.
The real drawback of ignoring pixel correlations is that
parameter uncertainties extracted from the fit are underestimated
(since pixel correlations are positive); this is a product of any photometry
method that assumes uncorrelated pixels on re-sampled or convolved
images. Our geometric alignment technique, used to align images prior
to the flux measurement as described in
Sect. 3.2, uses a ![]() pixel quadratic
re-sampling kernel,
which
produces output pixels with an average variance of 80% of the input
pixel variance, where the remaining 20% contributes to covariance in nearby pixels.
We checked that flux variances (and covariances)
computed assuming independent pixels are also underestimated by the
same amount: on average, a 25% increase is required.
pixel quadratic
re-sampling kernel,
which
produces output pixels with an average variance of 80% of the input
pixel variance, where the remaining 20% contributes to covariance in nearby pixels.
We checked that flux variances (and covariances)
computed assuming independent pixels are also underestimated by the
same amount: on average, a 25% increase is required.
In order to derive accurate
uncertainties, we used the fact that for
each epoch, several images are available which measure the same
object flux. Estimating fluxes on individual exposures rather than on
stacks per night preserves the photometric precision since a common
position is fit using all images. It also allows a check on the
consistency of fluxes measured within a night. We therefore fit a
common flux per night to the fluxes measured on each individual image
by minimizing a
![]() (where n stands for nights); this matrix is
non-diagonal because the differential photometry produces correlated
fluxes. The
(where n stands for nights); this matrix is
non-diagonal because the differential photometry produces correlated
fluxes. The
![]() contribution of every individual image is
evaluated, and outliers >
contribution of every individual image is
evaluated, and outliers >![]() (due to, for
example, unidentified cosmic rays) are discarded; this cut
eliminates 1.4% of the measurements on average. The covariance of
the per-night fluxes is then extracted, and normalized so that the minimum
(due to, for
example, unidentified cosmic rays) are discarded; this cut
eliminates 1.4% of the measurements on average. The covariance of
the per-night fluxes is then extracted, and normalized so that the minimum ![]() per degree of freedom is 1.
This translates into an "effective'' flux uncertainty derived from
the scatter of repeated observations rather than from first
principles. If the only source of noise (beyond photon statistics) were
pixel correlations introduced by image resampling, we would expect an
average
per degree of freedom is 1.
This translates into an "effective'' flux uncertainty derived from
the scatter of repeated observations rather than from first
principles. If the only source of noise (beyond photon statistics) were
pixel correlations introduced by image resampling, we would expect an
average
![]() of 1.25, as all flux variances are on
average under-estimated by 25%. Our average value is 1.55; hence we
conclude that our photometric uncertainties are only
of 1.25, as all flux variances are on
average under-estimated by 25%. Our average value is 1.55; hence we
conclude that our photometric uncertainties are only ![]() 12%
(
12%
(
![]() )
larger than photon statistics,
leaving little margin for drastic improvement.
)
larger than photon statistics,
leaving little margin for drastic improvement.
Table 2
summarizes the statistics of the differential photometry fits in each
filter. The larger values of
![]() in
in ![]() and
and ![]() probably indicate contributions from residual fringes. Examples of SNe Ia
light-curves points are presented in
Figs. 1 and 2
showing SNe at z=0.358 and z=0.91 respectively.
Also shown on these figures are the results of the light-curves fits
described in Sect. 5.1.
probably indicate contributions from residual fringes. Examples of SNe Ia
light-curves points are presented in
Figs. 1 and 2
showing SNe at z=0.358 and z=0.91 respectively.
Also shown on these figures are the results of the light-curves fits
described in Sect. 5.1.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f1_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg43.gif) |
Figure 1:
Observed light-curves points
of the SN Ia SNLS-04D3fk in |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f2_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg46.gif) |
Figure 2:
Observed light-curves points of the SN Ia SNLS-04D3gx at z=0.91.
With a SN redshift of 0.91, only two of the measured pass-bands
lie in the wavelength range of the light-curve model,
defined by rest-frame U to R bands, and are therefore used in the fit (shown
as solid lines).
Note the excellent quality of the
photometry at this high redshift value. Note
also the clear signal observed in |
| Open with DEXTER | |
Table 2:
Average number of images and nights per band for
each SNLS light-curve. Note that there is less data in ![]() and
and ![]() .
The
.
The ![]() column refers to the last fit that imposes equal
fluxes on a given night. The expected value is 1.25 (due to pixel correlations),
so we face a moderate scatter excess of about 12% over photon statistics.
The larger values in
column refers to the last fit that imposes equal
fluxes on a given night. The expected value is 1.25 (due to pixel correlations),
so we face a moderate scatter excess of about 12% over photon statistics.
The larger values in ![]() and
and ![]() indicate that fringes play a role in this excess. The last column displays the average wavelength of the effective
filters in Å.
indicate that fringes play a role in this excess. The last column displays the average wavelength of the effective
filters in Å.
The next section discusses how accurately the SN fluxes can be extracted from the science frames relative to nearby field stars, i.e. how well the method assigns magnitudes to SNe, given magnitudes of the field stars which are used for photometric calibration, called tertiary standards hereafter.
The SN flux measurement technique of Sect. 3.2 delivers SN fluxes on the same photometric scale as the reference image. In this Section, we discuss how we measure ratios of the SN fluxes to those of the tertiary standards (namely stars in the SNLS fields). The absolute flux calibration of the tertiary standards themselves is discussed in Sect. 4.
The image model that we use to measure the SN fluxes (Eq. (1)) can also be adapted to fit the tertiary standards by setting the "underlying galaxy model'' to zero. We measure the fluxes of field stars by running the same simultaneous fit to the images used for the supernovae, but without the "zero-flux'' images, and without an underlying galaxy. As this fitting technique matches that used for the SNe as closely as possible, most of the systematics involved (such as astrometric alignment residuals, PSF model uncertainties, and the convolution kernel modeling) cancel in the flux ratios.
For each tertiary standard (around 50 per CCD), we obtain one flux for each image (as done for the SNe), expressed in the same units. From the magnitudes of these fitted stars, we can extract a photometric zero point for the PSF photometry for every star on every image, which should be identical within measurement uncertainties. Several systematic checks were performed to search for trends in the fitted zero-points as a function of several variables (including image number, star magnitude, and star color); no significant trends were detected. As zero-points are obtained from single measurements on single images, the individual measurements are both numerous and noisy, with a typical rms of 0.03 mag; however since they have the same expectation value, we averaged them using a robust fit to the distribution peak to obtain a single zero-point per observed filter.
To test how accurately the ratio of SN flux to tertiary standard stars is retrieved by our technique, we tested the method on simulated SNe. For each artificial supernova, we selected a random host galaxy, a neighboring bright star (the model star), and a down-scale ratio (r). For half of the images that enter the fit, we superimposed a scaled-down copy (by a factor r) of the model on the host galaxy. We rounded the artificial position at an integer pixel offset from the model star to avoid re-sampling. We then performed the full SN fit (i.e. one that allows for an underlying galaxy model and "zero flux images'') at the position of the artificial object, and performed the calibration star fit (i.e. one with no galaxy mode and no "zero-flux images'') at the original position of the model star. This matches exactly the technique used for the measurement and calibration of a real SN. We then compared the recovered flux ratio to the (known) down-scale ratio.
We found no significant bias as a function of SN flux or galaxy
brightness at the level of 1%, except at signal-to-noise (S/N) ratios
(integrated over the whole light-curve) below 10. At a
S/N ratio of 10, fluxes are on average
underestimated by less than 1%; this bias rises to about 3% at a S/N
ratio of 7. This small flux bias disappears when the fitted object position
is fixed, as expected because the fit is then linear. For this
reason, when fitting ![]() light-curves of objects at
z>0.7, for which the S/N is expected to be low, we use the fixed SN
position from that obtained from the
light-curves of objects at
z>0.7, for which the S/N is expected to be low, we use the fixed SN
position from that obtained from the ![]() and
and ![]() fits.
fits.
Given the statistics of our simulations, the systematic uncertainty of SN fluxes due to the photometric method employed is less than 1% across the range of S/N we encounter in real data, and the observed scatter of the retrieved "fake SNe'' fluxes behaves in the same way as that for real SNe. Over a limited range of S/N (more than 100 integrated over the whole light-curve), we can exclude biases at the 0.002 mag level. Our upper limits for a flux bias have a negligible impact on the cosmological conclusions drawn from the sample described here, and will likely be improved with further detailed simulations.
The supernova light-curves produced by the techniques described in Sect. 3.2 are calibrated relative to nearby field stars (the tertiary standards). Our next step is to place these instrumental fluxes onto a photometric calibration system using observations of stars of known magnitudes.
Several standard star calibration catalogs are available in the
literature, such as the Landolt (1992b,1983) Johnson-Cousins
(Vega-based) ![]() system, or the Smith et al. (2002)
u'g'r'i'z'AB-magnitude system which is used to calibrate the
Sloan Digital Sky Survey (SDSS). However, there are systematic errors
affecting the transformations between the Smith et al. (2002) system and the widely used
Landolt system. As discussed in Fukugita et al. (1996), these errors arise
from various sources, for example uncertainties in the
cross-calibration of the spectral energy distributions of the AB
fundamental standard stars relative to that of Vega. Since the nearby
SNe used in our cosmological fits were extracted from the literature
and are typically calibrated using the standard star catalogs of
Landolt (1992b), we adopted the same calibration source for our
high-redshift sample. This avoids introducing additional systematic
uncertainties between the distant and nearby SN fluxes, which
are used to determine the cosmological parameters.
To eliminate uncertainties associated with color corrections, we
derive magnitudes in the natural MegaCam filter system.
system, or the Smith et al. (2002)
u'g'r'i'z'AB-magnitude system which is used to calibrate the
Sloan Digital Sky Survey (SDSS). However, there are systematic errors
affecting the transformations between the Smith et al. (2002) system and the widely used
Landolt system. As discussed in Fukugita et al. (1996), these errors arise
from various sources, for example uncertainties in the
cross-calibration of the spectral energy distributions of the AB
fundamental standard stars relative to that of Vega. Since the nearby
SNe used in our cosmological fits were extracted from the literature
and are typically calibrated using the standard star catalogs of
Landolt (1992b), we adopted the same calibration source for our
high-redshift sample. This avoids introducing additional systematic
uncertainties between the distant and nearby SN fluxes, which
are used to determine the cosmological parameters.
To eliminate uncertainties associated with color corrections, we
derive magnitudes in the natural MegaCam filter system.
Both standard and science fields were repeatedly observed over a
period of about 18 months. Photometric nights were selected using the
CFHT "Skyprobe'' instrument (Cuillandre 2003), which monitors
atmospheric transparency in the direction that the telescope is pointing. Only
the 50% of nights with the smallest scatter in transparency were
considered. For each night, stars were selected in the science fields
and their aperture fluxes measured and corrected to an
airmass of 1 using the average atmospheric extinction of Mauna Kea.
These aperture fluxes were then averaged, allowing for photometric
ratios between exposures. Stable observing conditions were indicated
by a very small scatter in these photometric ratios (typically 0.2%); again the averaging was robust, with 5-![]() deviations
rejected. Observations of the Landolt standard star fields were
processed in the same manner, though their fluxes were not averaged.
The apertures were chosen sufficiently large (about 6
deviations
rejected. Observations of the Landolt standard star fields were
processed in the same manner, though their fluxes were not averaged.
The apertures were chosen sufficiently large (about 6
![]() in
diameter) to bring the variations of aperture corrections across the
mosaic below 0.005 mag. However, since fluxes are measured in the same
way and in the same apertures in science images and standard star
fields, we did not apply any aperture correction.
in
diameter) to bring the variations of aperture corrections across the
mosaic below 0.005 mag. However, since fluxes are measured in the same
way and in the same apertures in science images and standard star
fields, we did not apply any aperture correction.
Using standard star observations, we first determined zero-points
by fitting linear color transformations and zero-points to each night
and filter, however with color slopes common to all nights.
In order to account for possible non-linearities in the
Landolt to MegaCam color relations,
the observed color-color relations were then compared to
synthetic ones derived from spectrophotometric standards. This led
to shifts of roughly 0.01 in all bands other than ![]() ,
for which the
shift was 0.03 due to the nontrivial relation to B and V.
,
for which the
shift was 0.03 due to the nontrivial relation to B and V.
We then applied the zero-points appropriate for each night to the
catalog of science field stars of that same night. These magnitudes were
averaged
robustly, rejecting 5-![]() outliers, and the average standard star
observations were merged.
Figure 3 shows the dispersion of the
calibration residuals in the
outliers, and the average standard star
observations were merged.
Figure 3 shows the dispersion of the
calibration residuals in the ![]() ,
, ![]() ,
, ![]() and
and ![]() bands.
The observed standard deviation, which sets the upper bound to the
repeatability of the photometric measurements, is about or below 0.01 mag in
bands.
The observed standard deviation, which sets the upper bound to the
repeatability of the photometric measurements, is about or below 0.01 mag in
![]() ,
, ![]() and
and ![]() ,
and about 0.016 mag in
,
and about 0.016 mag in ![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f3_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg49.gif) |
Figure 3:
The calibration residuals - i.e. the residuals around
the mean
magnitude of each Deep field tertiary
standard - in the bands |
| Open with DEXTER | |
For each of the four SNLS fields, a catalog of tertiary standards was
produced using the procedure described above. These catalogs were
then used to calibrate the supernova fluxes, as described in
Sect. 3.4. The dominant uncertainty in
the photometric scale of these catalogs comes from the determination
of the color-color relations of the standard star measurements. For
the ![]() ,
, ![]() and
and ![]() bands, a zero-point offset of 0.01 mag
would easily be detected; hence we took this value as a conservative
uncertainty estimate. The
bands, a zero-point offset of 0.01 mag
would easily be detected; hence we took this value as a conservative
uncertainty estimate. The ![]() band is affected by a larger
measurement noise, and it is calibrated with respect to I and R-ILandolt measurements. We therefore attributed to it a larger zero
point uncertainty of 0.03 mag.
band is affected by a larger
measurement noise, and it is calibrated with respect to I and R-ILandolt measurements. We therefore attributed to it a larger zero
point uncertainty of 0.03 mag.
The MegaCam shutter is designed to preserve the mosaic illumination uniformity. Nevertheless, the shutter precision is a potential source of systematic uncertainties, given (1) the possible non uniformities due to the shutter motion and (2) the exposure time differences between the calibration images (a few seconds) and the science images (hundreds of seconds). For MegaCam, the actual exposure time is measured and reported for each exposure, using dedicated sensors. The shutter precision was investigated by Cuillandre (2005) and it was shown that the non-uniformity due to the shutter is less than 0.3% across the mosaic. Short and long exposures of the same fields were also compared. The systematic flux differences between the exposures were found to be below 1% (rms).
As the supernova fluxes are measured in the instrumental filter system, the MegaCam transmission functions (up to an arbitrary constant) are needed in order to correctly interpret the SN photometry. Similarly, for the published nearby supernovae which are reported in Landolt magnitudes, the filter responses of the Landolt system are required.
For the MegaCam filters, we used the measurements provided by the manufacturer, multiplied by the CCD quantum efficiency, the MegaPrime wide-field corrector transmission function, the CFHT primary mirror reflectivity, and the average atmospheric transmission at Mauna Kea. As an additional check, we computed synthetic MegaCam-SDSS color terms using the synthetic transmissions of the SDSS 2.5-m telescope (SDSS 2004b) and spectrophotometric standards taken from Pickles (1998) and Gunn & Stryker (1983). Since the SDSS science catalog (Raddick 2002; SDSS 2004a; Finkbeiner et al. 2004) shares thousands of objects with two of the four fields repeatedly observed with MegaCam, we were able to compare these synthetic color transformations with the observed transformations. We found a good agreement, with uncertainties at the 1% level. This constrains the central wavelengths of the MegaCam band passes to within 10 to 15 Å with respect to the SDSS 2.5m band passes.
The choice of filter band passes to use for Landolt-based observations is not unique. Most previous supernova cosmology works assumed that the determinations of Bessell (1990) describe the effective Landolt system well, although the author himself questions this fact, explicitly warning that the Landolt system "is not a good match to the standard system'' - i.e. the historical Johnsons-Cousins system. Fortunately, Hamuy et al. (1992,1994) provide spectrophotometric measurements of a few objects measured in Landolt (1992a); this enabled us to compare synthetic magnitudes computed using Bessell transmissions with Landolt measurements of the same objects. This comparison reveals small residual color terms which vanish if the B, V, R and I Bessell filters are blue-shifted by 41, 27, 21 and 25 Å respectively. Furthermore, if one were to assume that the Bessell filters describe the Landolt system, this would lead to synthetic MegaCam-Landolt color terms significantly different from the measured ones; the blue shifts determined above bring them into excellent agreement. We therefore assumed that the Landolt catalog magnitudes refer to blue-shifted Bessell filters, with a typical central wavelength uncertainty of 10 to 15 Å, corresponding roughly to a 0.01 accuracy for the color terms.
Given the variations with time of the cosmological scale factor a(t), one can predict the evolution with redshift of the observed flux of classes of objects of reproducible luminosity though not necessarily known. This is why the cosmological conclusions that can be drawn from flux measurements rely on flux ratios of distant to nearby SNe, preferably measured in similar rest-frame pass-bands. The measured SNe magnitudes must therefore be converted to fluxes at some point in the analysis.
The flux in an imaginary rest-frame band of
transmission
![]() for a SN at redshift z is deduced from the
magnitude
for a SN at redshift z is deduced from the
magnitude
![]() measured in an observer band of transmission
measured in an observer band of transmission
![]() via:
via:
Inspecting Eq. (3), we first note that the normalizations
of
![]() and
and
![]() cancel.
The width of
cancel.
The width of
![]() is a second order effect.
When forming the ratio of two such quantities for two different SN,
the normalization of
is a second order effect.
When forming the ratio of two such quantities for two different SN,
the normalization of
![]() does not matter, nor the normalization
of
does not matter, nor the normalization
of
![]() ,
provided the same
,
provided the same
![]() is chosen for both objects. The width of
is chosen for both objects. The width of
![]() matters only at the second order. The factors
that do enter as first order effects are:
matters only at the second order. The factors
that do enter as first order effects are:
A possible shortcut consists in relying on spectrophotometric standards (Hamuy et al. 1992,1994) which also have magnitudes on the Landolt system (Landolt 1992a). When we compare synthetic Vega magnitudes of these objects with the photometric measurements, we find excellent matching of colors (at better than the 1% level), indicating that choosing Vega or spectrophotometric fluxes as the reference makes little practical difference.
We constructed catalogs of tertiary standard stars in the SNLS fields,
expressed in MegaCam natural magnitudes, and defined on the Landolt
standard system. The repeatability of measurements of a single star
on a given epoch (including measurement noise) is about or below 0.01 mag
rms in ![]() ,
, ![]() and
and ![]() ,
and about 0.016 mag in
,
and about 0.016 mag in ![]() .
From
standard star observations, we set conservative uncertainties of the
overall scales of 0.01 mag in
.
From
standard star observations, we set conservative uncertainties of the
overall scales of 0.01 mag in ![]() ,
, ![]() and
and ![]() and 0.03 in
and 0.03 in ![]() .
The MegaCam central wavelengths are constrained by color
terms with respect to both the SDSS 2.5 m telescope and the Landolt
catalog to
within 10 to 15 Å. The central wavelengths of the band passes of
the Landolt catalog are found slightly offset with respect to
Bessell (1990), using spectrophotometric measurements of a subsample
of this catalog.
.
The MegaCam central wavelengths are constrained by color
terms with respect to both the SDSS 2.5 m telescope and the Landolt
catalog to
within 10 to 15 Å. The central wavelengths of the band passes of
the Landolt catalog are found slightly offset with respect to
Bessell (1990), using spectrophotometric measurements of a subsample
of this catalog.
To derive the brightness, light-curve shape and SN color estimates required for the cosmological analysis, the time sequence of photometric measurements for each SN was fit using a SN light-curve model. This procedure is discussed in this section together with the nearby and distant SN Ia samples selection and the cosmological analysis.
We fit the SN Ia light-curves in two or more bands using the
SALT light-curve model (Guy et al. 2005) which returns
the supernova rest-frame B-band magnitude m*B,
a single shape parameter s and a single color parameter c.
The supernova rest-frame B-band magnitude at the date
of its maximum luminosity in B is defined as:
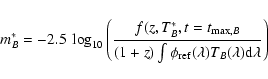
The light-curve model was trained on very nearby supernovae
(mostly at z<0.015) published
in the literature (see Guy et al. 2005 for the selection of these
objects).
Note that these training objects were not used
in the Hubble diagram described in this paper.
The SALT light-curve model
generates light-curves in the observed bands at a given redshift,
SALT also incorporates corrections for the Milky Way extinction,
using the dust maps of Schlegel et al. (1998) coupled with
the extinction law of Cardelli et al. (1989).
The rest-frame coverage of SALT extends from 3460 to 6500 Å (i.e. slightly
bluewards from U to R).
We require that photometry is available in at least 2 measured
bands with central wavelengths within this wavelength range to
consider a SN for the
cosmological analysis. Light curves in the ![]() band become essential for z>0.80, since at these redshifts,
band become essential for z>0.80, since at these redshifts, ![]() corresponds to rest-frame
corresponds to rest-frame
![]() .
All observed bands are fitted simultaneously,
with common stretch and color parameters,
global intensity and date of B-band maximum light.
Making use of U-, B- and V-band measurements of nearby SNe Ia
from the literature (mostly from Riess et al. 1999; Jha 2002; Hamuy et al. 1996),
Guy et al. (2005) have constructed
a distance estimator using either U- and B-band data or B- and V-band
which shows a dispersion of 0.16 mag
around the Hubble line.
The fitted global intensity is then translated into a rest-frame-B observed
magnitude at maximum light (mB*)
which does not include any correction for brighter-slower or
brighter-bluer relations.
.
All observed bands are fitted simultaneously,
with common stretch and color parameters,
global intensity and date of B-band maximum light.
Making use of U-, B- and V-band measurements of nearby SNe Ia
from the literature (mostly from Riess et al. 1999; Jha 2002; Hamuy et al. 1996),
Guy et al. (2005) have constructed
a distance estimator using either U- and B-band data or B- and V-band
which shows a dispersion of 0.16 mag
around the Hubble line.
The fitted global intensity is then translated into a rest-frame-B observed
magnitude at maximum light (mB*)
which does not include any correction for brighter-slower or
brighter-bluer relations.
The light-curve fit is carried out in two steps. The first fit uses all photometric data points to obtain a date of maximum light in the B-band. All points outside the range [-15,+35] rest-frame days from maximum are then rejected, and the data refit. This restriction avoids the dangers of comparing light-curve parameters derived from data with different phase coverage: nearby SNe usually have photometric data after maximum light, but not always before maximum when the SN is rising, and almost never before -15 days. By contrast, SNLS objects have photometric sampling that is essentially independent of the phase of the light-curve because of the rolling-search observing mode, though late-time data (in the exponential tail) often has a poor S/N, or is absent due to field visibility.
The cosmological analysis requires assembling a sample of nearby and distant SNe Ia.
We assembled a nearby SN Ia sample from the literature. Events with redshifts below z=0.015 were rejected to limit the influence of peculiar velocities. We further retained only objects whose first photometric point was no more than 5 days after maximum light. To check for possible biases that this latter procedure might have introduced, we fitted subsets of data from objects with pre-maximum photometry. Our distance estimator (see Sect. 5.4) was found to be unaffected if the data started up to 7 days after maximum light. A sample of 44 nearby SNe Ia matched our requirements. Table 8 gives the SN name, redshift and filters used in the light-curve fits, as well as fitted rest-frame B-band magnitude and values of the parameters s and c.
For this paper, we considered only distant SNe Ia that were discovered and followed during the first year of SNLS since this data set already constitutes the largest well controlled homogeneous sample of distant SN Ia. As discussed in Sect. 2.3, 91 objects were spectroscopically identified as "Ia'' or "Ia*'', with a date of maximum light before July 15, 2004. Ten of these are not yet analyzed: 5 because images uncontaminated by SN light were not available at the time of this analysis, and 5 due to a limitation of our reduction pipeline which does not yet handle field regions observed with different CCDs. Six SNe have incomplete data due to either instrument failures, or persistent bad weather and two SNe, SNLS-03D3bb and SNLS-03D4cj, which happen to be spectroscopically peculiar (see Ellis et al., in prep.) have photometric data incompatible with the light-curve model.
The resulting fit parameters of the remaining 73 "Ia''+''Ia*'' SNe are given in Table 9 and examples of light-curves measured in the four MegaCam bands are shown in Figs. 1 and 2, together with the result of the light-curve fit.
There is no consensus on how to correct for host galaxy extinction affecting high redshift SNe Ia. The pioneering SN cosmology papers (Riess et al. 1998; Perlmutter et al. 1999) typically observed in only one or two filters, and so had little or no color information with which to perform extinction corrections. Subsequent papers either selected low-extinction subsamples based on host galaxy diagnostics (Sullivan et al. 2003), or used multicolor information together with an assumed color of an unreddened SN to make extinction corrections on a subset of the data (Knop et al. 2003; Tonry et al. 2003).
These techniques have their drawbacks: the intrinsic color of
SNe Ia has some dispersion, and measured colors often have large
statistical errors in high-redshift data sets. When these two color
uncertainties are multiplied by the ratio of total to selective
absorption,
![]() ,
the resulting error can be very large.
To circumvent this, some studies
used Bayesian priors
(e.g. Barris et al. 2004; Riess et al. 1998,2004; Tonry et al. 2003). Other authors
argue that this biases the results (e.g. Knop et al. 2003; Perlmutter et al. 1999).
,
the resulting error can be very large.
To circumvent this, some studies
used Bayesian priors
(e.g. Barris et al. 2004; Riess et al. 1998,2004; Tonry et al. 2003). Other authors
argue that this biases the results (e.g. Knop et al. 2003; Perlmutter et al. 1999).
Here we employ a technique that makes use of color information to empirically improve distance estimates to SNe Ia. We exploit the fact that the SN color acts in the same direction as reddening due to dust - i.e. redder SNe are intrinsically dimmer, brighter SNe are intrinsically bluer (Tripp & Branch 1999). By treating the correction between color and brightness empirically, we avoid model-dependent assumptions that can both artificially inflate the errors and potentially lead to biases in the determination of cosmological parameters. Because we have more than one well-measured color for several SNe, we can perform consistency checks on this technique - distances from multiple colors should, and do, agree to a remarkable degree of precision (Sect. 6.3).
From the fits to the light-curves
(Sect. 5.1),
we computed a rest-frame-Bmagnitude, which, for perfect standard candles, should vary with
redshift according to the luminosity distance. This rest-frame-Bmagnitude refers to observed brightness, and therefore does
not account for
brighter-slower and brighter-bluer correlations (see Guy et al. 2005 and
references therein). As a distance estimator, we use:
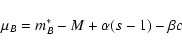
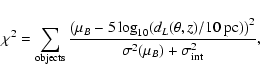
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f4_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg81.gif) |
Figure 4:
Hubble diagram of SNLS and nearby SNe Ia, with various
cosmologies superimposed. The bottom plot shows the residuals for
the best fit to a flat |
| Open with DEXTER | |
The
best-fitting values of ![]() and
and ![]() are
are
![]() and
and
![]() ,
comparable with previous works using
similar distance estimators (see for example Tripp 1998).
As discussed by several authors (see Guy et al. (2005) and references therein),
the value of
,
comparable with previous works using
similar distance estimators (see for example Tripp 1998).
As discussed by several authors (see Guy et al. (2005) and references therein),
the value of ![]() does differ considerably from RB=4, the value expected if
color were only affected by dust reddening.
This discrepancy may be an indicator of intrinsic color variations in the
SN sample (e.g. Nobili et al. 2003), and/or variations in RB. For the
absolute magnitude M, we obtain
does differ considerably from RB=4, the value expected if
color were only affected by dust reddening.
This discrepancy may be an indicator of intrinsic color variations in the
SN sample (e.g. Nobili et al. 2003), and/or variations in RB. For the
absolute magnitude M, we obtain
![]() .
.
The parameters ![]() ,
, ![]() and M are nuisance
parameters in the cosmological fit, and their
uncertainties must be accounted for in the cosmological error analysis.
The resulting confidence contours are shown in
Figs. 5 and 6, together
with the product of these confidence estimates with
the probability distribution from baryon acoustic
oscillations (BAO) measured in the SDSS (Eq. (4) in Eisenstein et al. 2005).
We impose w=-1 for the
and M are nuisance
parameters in the cosmological fit, and their
uncertainties must be accounted for in the cosmological error analysis.
The resulting confidence contours are shown in
Figs. 5 and 6, together
with the product of these confidence estimates with
the probability distribution from baryon acoustic
oscillations (BAO) measured in the SDSS (Eq. (4) in Eisenstein et al. 2005).
We impose w=-1 for the
![]() contours, and
contours, and
![]() for the
for the
![]() contours. Note that the constraints from BAO and SNe Ia are
quite complementary. The best-fitting cosmologies are given in
Table 3.
contours. Note that the constraints from BAO and SNe Ia are
quite complementary. The best-fitting cosmologies are given in
Table 3.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{f5_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg86.gif) |
Figure 5:
Contours at 68.3%, 95.5% and 99.7% confidence levels for
the fit to an
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{f6_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg87.gif) |
Figure 6:
Contours at 68.3%, 95.5% and 99.7% confidence levels
for the fit to a flat
|
| Open with DEXTER | |
Table 3: Cosmological parameters and statistical errors of Hubble diagram fits, with the BAO prior where applicable.
Using Monte Carlo realizations of our SN sample, we checked that our
estimators of the cosmological parameters are unbiased (at the level
of 0.1![]() ), and that the quoted uncertainties match the observed
scatter.
We also checked the field-to-field variation of the cosmological
analysis. The four
), and that the quoted uncertainties match the observed
scatter.
We also checked the field-to-field variation of the cosmological
analysis. The four
![]() values (one for each field, assuming
values (one for each field, assuming
![]() )
are compatible at 37% confidence level. We also fitted separately the Ia and Ia* SNLS samples and found results compatible at the 75% confidence level.
)
are compatible at 37% confidence level. We also fitted separately the Ia and Ia* SNLS samples and found results compatible at the 75% confidence level.
We derive an intrinsic dispersion,
![]() ,
appreciably
smaller than previously measured (Riess et al. 1998; Barris et al. 2004; Perlmutter et al. 1999; Riess et al. 2004; Tonry et al. 2003).
The intrinsic dispersions of nearby only (
,
appreciably
smaller than previously measured (Riess et al. 1998; Barris et al. 2004; Perlmutter et al. 1999; Riess et al. 2004; Tonry et al. 2003).
The intrinsic dispersions of nearby only (
![]() )
and SNLS only (
)
and SNLS only (
![]() )
events are statistically consistent although
SNLS events show a bit less dispersion.
)
events are statistically consistent although
SNLS events show a bit less dispersion.
A notable feature of Fig. 4 is that the error bars
increase significantly beyond z=0.8, where the ![]() photometry is
needed to measure rest-frame B-V colors.
The
photometry is
needed to measure rest-frame B-V colors.
The ![]() data is affected by a low signal-to-noise ratio
because of low quantum efficiency and high sky background.
For z > 0.8,
data is affected by a low signal-to-noise ratio
because of low quantum efficiency and high sky background.
For z > 0.8,
![]() ,
because the lever arm between the central wavelengths of
,
because the lever arm between the central wavelengths of
![]() and
and ![]() is about 1.6 times lower than for B and V. Furthermore, errors in rest-frame color are
scaled by a further factor of
is about 1.6 times lower than for B and V. Furthermore, errors in rest-frame color are
scaled by a further factor of
![]() in the distance
modulus estimate. With a typical measurement uncertainty
in the distance
modulus estimate. With a typical measurement uncertainty
![]() ,
we have a distance modulus uncertainty
,
we have a distance modulus uncertainty
![]() .
Since the fall 2004 semester, we now acquire about three
times more
.
Since the fall 2004 semester, we now acquire about three
times more ![]() data than for the data
in the current paper, and this will improve the accuracy of future cosmological
analyses.
data than for the data
in the current paper, and this will improve the accuracy of future cosmological
analyses.
The distance model we use is linear in stretch and color. Excluding
events at z>0.8, where the color uncertainty is larger than the
natural color dispersion, we checked that adding quadratic terms in stretch
or color to the distance estimator decreases the minimum ![]() by less
than 1. We hence conclude that the linear distance estimator accurately
describes our sample.
by less
than 1. We hence conclude that the linear distance estimator accurately
describes our sample.
Since the distance estimator we use depends on the color parameter c, residuals to the Hubble Diagram are statistically correlated to c. The correlation becomes very apparent when the c measurement uncertainty dominates the distance uncertainty budget, as happens in our sample when z>0.8. We checked that the measurement uncertainties can account for the observed residual-c correlation at z>0.8. Because of this correlation, color selected sub-samples mechanically lead to biased estimations of cosmological parameters.
The distributions of the shape and color parameters - s and c
as defined in Sect. 5.1 -
are compared in Figs. 7 and 8 for nearby objects
and for SNLS supernovae at z < 0.8 for which c
is accurately measured.
These distributions look very similar, both in central value
and shape. The average values for the two samples differ by about ![]() in stretch and
in stretch and ![]() in color: we find that
distant supernovae are on average slightly bluer and slower than nearby ones.
The statistical significance of the differences is low and
the differences can easily be interpreted in terms of selection effects
rather than evolution.
The evolution of average s and c parameters
with redshift is shown in Sect. 7.4;
stretch is not monotonic, and color seems to drift towards the blue
with increasing redshift. We show in
Sect. 7.4 that the bulk of this effect
can be reproduced
by selection effects applied to an unevolving population.
in color: we find that
distant supernovae are on average slightly bluer and slower than nearby ones.
The statistical significance of the differences is low and
the differences can easily be interpreted in terms of selection effects
rather than evolution.
The evolution of average s and c parameters
with redshift is shown in Sect. 7.4;
stretch is not monotonic, and color seems to drift towards the blue
with increasing redshift. We show in
Sect. 7.4 that the bulk of this effect
can be reproduced
by selection effects applied to an unevolving population.
| |
Figure 7:
The stretch (s parameter) distributions
of nearby (hashed blue) and distant (thick black with filled symbols)
SNLS SNe with z<0.8. These distributions are
very similar with averages
of
|
| Open with DEXTER | |
| |
Figure 8:
The color (c parameter) distributions for
nearby (hashed blue) and distant (thick black with filled symbols)
SNe with z<0.8. These distributions are very similar, with
averages of
|
| Open with DEXTER | |
Figures 9 and 10 compare the nearby and distant samples in the stretch-magnitude and color-magnitude planes. There is no significant difference between these samples.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f9_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg106.gif) |
Figure 9:
Residuals in the Hubble diagram as a function of
stretch (s parameter), for nearby (blue open
symbols) and distant (z<0.8, black filled symbols). This diagram
computes distance
modulus |
| Open with DEXTER | |
In Fig. 8,
two of the SNLS events (SNLS-04D1ag and SNLS-04D3oe) have a color value, c,
smaller than -0.1. These supernovae are both classified as secure Ia.
There are no SNe Ia in the nearby sample that are this blue.
Figure 10 shows that these events lie on the
derived brighter-bluer relation.
Although they are brighter than average, fitting with or without these
two events changes the cosmological results by less than 0.1![]() .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f10_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg107.gif) |
Figure 10:
Residuals in the Hubble diagram as a function of
color (c parameter), for nearby (blue open
symbols) and distant (z<0.8, black filled symbols).
This diagram computes distance
modulus |
| Open with DEXTER | |
The measurement of distances to high redshift SNLS SNe involves the
rest-frame Uband. The MegaCam ![]() band shifts from rest-frame B at z=0.5 to rest-frame U at z=0.8. Within this redshift range,
distances are estimated mainly using
band shifts from rest-frame B at z=0.5 to rest-frame U at z=0.8. Within this redshift range,
distances are estimated mainly using ![]() and
and ![]() ,
the weight of
,
the weight of ![]() being affected by high photometric noise;
the (
being affected by high photometric noise;
the (
![]() )
pair roughly changes from rest-frame (B, V) to rest-frame
(U, B).
)
pair roughly changes from rest-frame (B, V) to rest-frame
(U, B).
Our cosmological conclusions rely on having a consistent distance estimate when using rest-frame BV and UB. This property is tested in Guy et al. (2005). However, it can be tested further on the subset of SNLS data having at least three usable photometric bands. The test proceeds as follows:
There are 10 SNLS "intermediate'' redshift events at
0.25<z<0.4,
where
![]() sample the
UBV rest-frame region, and 17 "distant'' events at
0.55<z<0.8,
where UBVshifts to the
sample the
UBV rest-frame region, and 17 "distant'' events at
0.55<z<0.8,
where UBVshifts to the
![]() triplet. We also have at our disposal
a sample of 28 "nearby''
objects measured in UBV, both from the nearby sample described in
Table 8, and also from the light-curve model
training sample which consists mainly of very nearby
objects (see Guy et al. 2005).
Figure 11 displays the value
of
triplet. We also have at our disposal
a sample of 28 "nearby''
objects measured in UBV, both from the nearby sample described in
Table 8, and also from the light-curve model
training sample which consists mainly of very nearby
objects (see Guy et al. 2005).
Figure 11 displays the value
of
![]() as a function of redshift and Table 4
summarizes the averages and dispersions. A very small scatter
(about 0.033) is found for the intermediate redshift sample.
The nearby and
distant samples exhibit larger scatters; the nearby sample is probably
affected by the practical difficulties in calibrating U observations,
and our distant sample is affected by the poor S/N in the
as a function of redshift and Table 4
summarizes the averages and dispersions. A very small scatter
(about 0.033) is found for the intermediate redshift sample.
The nearby and
distant samples exhibit larger scatters; the nearby sample is probably
affected by the practical difficulties in calibrating U observations,
and our distant sample is affected by the poor S/N in the ![]() band.
We conclude from this study that our light curves model accurately describes
the relations between the supernovae colors.
Note that this
band.
We conclude from this study that our light curves model accurately describes
the relations between the supernovae colors.
Note that this
![]() indicator is a
promising tool for photometric classification of SNe Ia, provided its
scatter remains comparable to that found for the intermediate redshift
sample.
indicator is a
promising tool for photometric classification of SNe Ia, provided its
scatter remains comparable to that found for the intermediate redshift
sample.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f11_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg113.gif) |
Figure 11:
|
| Open with DEXTER | |
Table 4: Statistics of the 3 samples displayed in Fig. 11.
The same exercise can be done without imposing identical stretch and date of maximum light on the two fits. Rather than testing the light curves model, one then tests for potential biases in color estimates (leading to biases in distance estimates). The conclusions are the same as with fixed parameters: the samples have averages consistent with 0, and the dispersion of the central sample increases from 0.033 to 0.036.
We present, in this section, estimates of the systematic uncertainties possibly affecting our cosmological parameter measurements.
We simulated a zero-point shift by varying the magnitudes of
the light-curve points, one band at a time. Table 5
gives the resulting shifts in the derived cosmological parameters from
the calibration errors derived in
Sect. 4.1.
We assume that
errors in the
![]() zero-points are independent,
and propagate these 4 errors quadratically to obtain the total effect on cosmology.
zero-points are independent,
and propagate these 4 errors quadratically to obtain the total effect on cosmology.
Table 5: Influence of a photometric calibration error on the cosmological parameters.
We rely on the spectrum of one object, Vega (![]() Lyrae), to transform magnitudes into
fluxes; the broadband flux errors for Vega are about 1% (Hayes (1985) and
Sect. 4.3). To take
into account the Vega flux and broadband color uncertainties,
we simulated a flux error linear in wavelength that would
offset the Vega (B-R) color by 0.01. The impact on
Lyrae), to transform magnitudes into
fluxes; the broadband flux errors for Vega are about 1% (Hayes (1985) and
Sect. 4.3). To take
into account the Vega flux and broadband color uncertainties,
we simulated a flux error linear in wavelength that would
offset the Vega (B-R) color by 0.01. The impact on
![]() is
is ![]() 0.012.
0.012.
Uncertainties in the filter bandpasses affect the determination of
supernovae brightnesses; the first-order effect is from errors in the central
wavelengths. In the color-color relations (Landolt/MegaCam and
SDSS/MegaCam - Sect. 4.2),
we were able to detect shifts of 10 Å (corresponding
roughly to a change of 0.01 in the color term). The effect of this
shift is in fact very small: only the ![]() filter has a sizable
impact of
filter has a sizable
impact of ![]() 0.007 on
0.007 on
![]() .
.
If the light-curve model fails to properly describe the true light-curve shape, the result would be a bias in the light-curve parameters, and possibly in the cosmological parameters if the bias depends on redshift. We have already discussed two possible causes of such a bias: the influence of the first measurement date (Sect. 5.2), and the choice of rest-frame bands used to measure brightness and color (Sect. 6.3). Both have very small effects. However, given only 10 intermediate redshift SNLS events, each with an uncertainty of 0.033, the precision with which we can define the average (U-B) color at given (B-V) is limited to about 0.01 mag by our sample size.
Uncertainties in the k-corrections (due to SNe Ia spectral variability at fixed color) contribute directly to the observed scatter. The redshift range of the intermediate redshift sample of Sect. 6.3 corresponds to a rest-frame wavelength span of about 400 Å, in a region where SNe Ia spectra are highly structured. Since we observe compatible intrinsic dispersions for nearby and SNLS events (indeed, slightly lower for SNLS), we find no evidence that k-correction uncertainties add significantly to the intrinsic dispersion.
Nevertheless, since the measured scatter of the intermediate redshift sample
appears surprisingly small and, since the sample size is small,
we used a more conservative value of 0.02 for the light-curve model
error, to account for both the errors in the colors and from k-corrections.
A shift of the U-band light-curve model of 0.02 mag results in a
change in
![]() of 0.018. This is to be added to the statistical
uncertainty.
of 0.018. This is to be added to the statistical
uncertainty.
Concerns have been expressed regarding the use
of rest-frame U-band fluxes to measure luminosity
distances (e.g. Jha 2002 and Nugent et al. 2002),
motivated by the apparent large variability of the U-band
luminosity of SNe Ia. Such variability seems also to be present
at intermediate redshifts although there seems to be little obvious
evolution to z=0.5 of the overall UV SED
(Ellis et al., in prep.).
Note that Guy et al. (2005) have succeeded in
constructing a distance estimator using U- and B-band data
which shows a dispersion of only 0.16 mag around the Hubble line,
comparable to that found for distances derived using B- and V-band data.
Note also that the quantity
![]() appears to be independent of
redshift, implying that if the average luminosity of SNe Ia evolves with
redshift, this evolution must preserve the UBV rest-frame color relations.
Lentz et al. (2000) predict a strong
dependence of the UV flux from the progenitor metallicity
(at fixed B-V color), which
should have been visible if metallicity evolution were indeed present.
appears to be independent of
redshift, implying that if the average luminosity of SNe Ia evolves with
redshift, this evolution must preserve the UBV rest-frame color relations.
Lentz et al. (2000) predict a strong
dependence of the UV flux from the progenitor metallicity
(at fixed B-V color), which
should have been visible if metallicity evolution were indeed present.
The Malmquist bias may affect the cosmological conclusions by altering the average brightness of measured SNe in a redshift dependent way. The mechanism is however not exactly straightforward since the reconstructed distance depends on stretch and color, and not only on the brightness. We have conducted simulations, both of nearby SN searches and of the SNLS survey, to investigate the effects on the derivation of cosmological parameters.
We simulated light-curves of nearby SNe Ia ( 0.02<z<0.1) with random explosion date, stretch and color, using the observed brighter-slower and brighter-bluer correlations. We then simulated a brightness cut at a fixed date. Although the number of "detected'' events and their average redshift strongly depends on the brightness cut, the average distance bias of the survivors is found to change by less than 10%, when varying both the value and the sharpness of the brightness cut. The bias is also essentially independent of the discovery phase, although the peak brightness is not. We find a distance modulus bias of 0.027 (similar in B, V and R), sensitive at the 10% level to the unknown details of nearby searches. Note that the redshift dependence of the distance bias of the nearby sample has no impact on the cosmological measurements: only the average bias matters.
The crude simulation we conducted applies only to flux limited
searches, which applies to about half of the sample.
We compute an average bias value for our nearby sample as the simulation result
(0.027 mag) times the fraction of events to which it applies.
Assuming that both
factors suffer from an uncertainty of 50%, we find an average nearby
sample bias value of
![]() mag. A global increase of all
nearby distances by 0.017(
mag. A global increase of all
nearby distances by 0.017(![]() ) mag increases
) mag increases
![]() (flat universe) by 0.019 (
(flat universe) by 0.019 (![]() ).
).
For the distant SNLS sample, which is flux limited,
we simulated supernovae at a rate per co-moving volume
independent of redshift, accounted for the
brighter-slower and brighter-bluer correlations, and adjusted the
position and smoothness of the limiting magnitude cut in order to reproduce the
redshift and peak magnitude distributions. In contrast with nearby SN simulations, here we have many observed distributions for a single search,
and the key parameters that enter the simulation are highly constrained.
The best match to SNLS data is shown in
Fig. 12,
and Fig. 13
shows the expected biases as a function of redshift in the shape
and color parameters, and for our distance estimator.
The distance modulus bias is about 0.02 mag at
z=0.8, increasing to 0.05 at z=1. Correcting for the computed
bias decreases
![]() (flat Universe) by 0.02. We assumed that the
uncertainty in this bias correction is 50% of its value.
(flat Universe) by 0.02. We assumed that the
uncertainty in this bias correction is 50% of its value.
To summarize: we find that the differential bias between nearby and
distant samples almost exactly cancels, and estimate an overall
uncertainty of 0.016 in
![]() (flat Universe). Since applying the
Malmquist bias corrections changes the cosmological results by less than 0.1
(flat Universe). Since applying the
Malmquist bias corrections changes the cosmological results by less than 0.1![]() ,
the corrections have not been applied. However, in the future,
when the SNLS sample size increases, modeling and applying the
Malmquist bias correction will assume a greater importance. The same
applies to the
nearby sample, where having a more controlled and homogeneous sample,
discovered by
a single search (e.g. SN Factory, Aldering et al. 2002)
will be essential to reduce the associated systematic uncertainty.
,
the corrections have not been applied. However, in the future,
when the SNLS sample size increases, modeling and applying the
Malmquist bias correction will assume a greater importance. The same
applies to the
nearby sample, where having a more controlled and homogeneous sample,
discovered by
a single search (e.g. SN Factory, Aldering et al. 2002)
will be essential to reduce the associated systematic uncertainty.
![\begin{figure}
\par\mbox{\includegraphics[width=4.3cm,clip]{f12_4185.eps}\hspace...
...s}\hspace*{2mm}
\includegraphics[width=4.3cm,clip]{f15_4185.eps} }\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg122.gif) |
Figure 12:
Distributions of redshifts, peak |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{f16_4185.eps}\par\vspace*{...
...}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{f18_4185.eps}
\end{figure}](/articles/aa/full/2006/07/aa4185-05/Timg123.gif) |
Figure 13: Stretch, color and Hubble diagram residuals as a function of redshift for SNLS supernovae (gray dots). The black points correspond to average values in redshift bins. The red solid (dashed) lines represent the average (one standard deviation) values obtained with SNe simulations as described in Sect. 7.4. At large redshifts, since only bright SNe are identified, the average stretch factor is larger and the average color bluer. The average distance modulus is less affected by the selection (see text for details). |
| Open with DEXTER | |
All supernovae used here were spectroscopically identified as SN Ia, but we have labeled the least secure identifications as SN Ia* (Sect. 2.2, Howell et al. 2005). These 15 events are probable SN Ia but for this class a small amount of contamination by SNe Ib or SNe Ic (SNe Ib/c) is possible. We have checked that cosmological fits done with or without these events lead to the same cosmological conclusions (Sect. 5.4).
We also looked at estimating the SN Ib/c contamination in our sample. SNe Ib/c have an intrinsic luminosity distribution which is wider than SNe Ia (cf. dispersion 0.45 mag for SNe Ia, vs. 1.2 mag for SNe Ib/c; Richardson et al. 2002; Homeier 2005). After correcting for the SNe Ia brighter-slower and brighter-bluer correlations, a conservative estimate is that the SNe Ib/c scatter around the SNe Ia Hubble line with a dispersion 3 to 4 times larger than for SNe Ia. The first clue of SN Ib/c contamination would be the presence of objects with large residuals around the Hubble line; these contaminants should on average be fainter than SNe Ia at the same redshift. We have rejected two objects from the Hubble diagram (Sect. 5.4). Even if we consider both of these events to be SN Ib/c events, and assume that the dispersion of the SN Ia distribution about the Hubble line is 4 times smaller than for SNe Ib/c, we expect on average only 0.5 Ib/c interloper within the fitted sample.
For these reasons, we estimate the potential bias arising from the presence of non Ia events in our sample to be negligible.
Whereas the average flux is conserved in the case of weak lensing,
part of the SN light is lost when strong lensing produces multiple
images among which some escape detection. Multiple images of distant
radio sources have been systematically searched by the CLASS
survey (Myers et al. 2003) and have proved to be rare: the occurrence
of multiple images separated by more than
![]() and with flux
ratio below 10:1 was found to be of 1 out of 690with 1.44 secondary image on average,
with inefficiencies due to the
separation and flux ratio cuts of 13% and 37%
respectively (Browne et al. 2003).
Multiple images with a smaller separation are not
resolved in the SNLS, and their time delay is much smaller than the
typical duration of a SN light curve
and with flux
ratio below 10:1 was found to be of 1 out of 690with 1.44 secondary image on average,
with inefficiencies due to the
separation and flux ratio cuts of 13% and 37%
respectively (Browne et al. 2003).
Multiple images with a smaller separation are not
resolved in the SNLS, and their time delay is much smaller than the
typical duration of a SN light curve![]() so that no flux is
lost for such events. Hence CLASS results provide us with an upper
limit for the number of (resolved) strong lensing cases in the SNLS
supernova sample, given the fact that CLASS sources are globally more
distant (see Chae 2003). Assuming (pessimistically) that for each
strongly lensed SN, we see only one image, the flux bias is smaller than
so that no flux is
lost for such events. Hence CLASS results provide us with an upper
limit for the number of (resolved) strong lensing cases in the SNLS
supernova sample, given the fact that CLASS sources are globally more
distant (see Chae 2003). Assuming (pessimistically) that for each
strongly lensed SN, we see only one image, the flux bias is smaller than
![]() at z=1.
at z=1.
Gravitational lensing also broadens asymmetrically the brightness
distribution of SNe at large redshifts (Bergström et al. 2000). As a
consequence, a cosmological fit using SNe magnitudes (instead of
fluxes) is biased. Holz & Linder (2004) found a dispersion of
![]() (note that Bergström et al. 2000 find a value of
(note that Bergström et al. 2000 find a value of ![]() 0.04 at z=1for smooth halo profiles in flat
0.04 at z=1for smooth halo profiles in flat ![]() CDM), which translates into a bias
of the average magnitude of
CDM), which translates into a bias
of the average magnitude of ![]()
![]() .
The broadening of
the brightness distribution also affects the cosmological parameters
uncertainties. In the cosmological fit, we have derived a constant
"intrinsic'' dispersion which includes the average dispersion due to lensing.
Neglecting its redshift dependence has no significant impact on the
accuracy of the errors derived for the cosmological parameters.
.
The broadening of
the brightness distribution also affects the cosmological parameters
uncertainties. In the cosmological fit, we have derived a constant
"intrinsic'' dispersion which includes the average dispersion due to lensing.
Neglecting its redshift dependence has no significant impact on the
accuracy of the errors derived for the cosmological parameters.
In summary, the total effect of lensing on cosmological parameters is
very small. We find that
![]() for a flat
for a flat ![]() CDM cosmology
and the equation of state for a flat
universe with BAO constraints, are shifted
by at most -0.005 and -0.01 respectively. We
therefore did not apply any correction to our results.
CDM cosmology
and the equation of state for a flat
universe with BAO constraints, are shifted
by at most -0.005 and -0.01 respectively. We
therefore did not apply any correction to our results.
The possibility that SNe Ia could be dimmed by intergalactic grey dust
(i.e. with weak extinction variation over the optical wavelengths)
has been suggested by Aguirre (1999b,a) as an astrophysical
alternative to the dark energy hypothesis. Some simple dust scenarios
without a cosmological constant could be excluded by Riess et al. (2004)
using SNe Ia data. Studying the colors of a large sample of quasars,
Östman & Mörtsell (2005) were able to set limits on the light absorption length
as a function of RV, but these limits can only be translated into an
upper bound of supernovae dimming. Conservatively assuming RV = 12,
using the SNOC program (Goobar et al. 2002), we computed an upper
limit in the dimming of supernovae which translates into
a shift of -0.025 in
![]() for a
for a ![]() CDM cosmology, and a shift
of -0.048 in w for a flat cosmology with constant equation of state when
combined with SDSS BAO results.
Note that these are upper limits and that a scenario without any intergalactic
dust cannot be excluded. We therefore did not apply any correction to our
results.
CDM cosmology, and a shift
of -0.048 in w for a flat cosmology with constant equation of state when
combined with SDSS BAO results.
Note that these are upper limits and that a scenario without any intergalactic
dust cannot be excluded. We therefore did not apply any correction to our
results.
Table 6 summarizes the uncertainties affecting
our cosmological parameter measurements. The table includes the impact of
uncertainties in several parameter directions: the
![]() direction for a flat
direction for a flat
![]() (i.e. w=-1) cosmology, the
(i.e. w=-1) cosmology, the
![]() direction for a general
direction for a general
![]() cosmology, and the w direction at fixed
cosmology, and the w direction at fixed
![]() for a
for a
![]() cosmology. We also report here the observed shifts when the BAO prior
is applied to a flat
cosmology. We also report here the observed shifts when the BAO prior
is applied to a flat
![]() cosmology.
Note that measurement and isolation of systematic errors is a
major goal of the SNLS. Some of these uncertainties will decrease as more
data is acquired and future papers will examine a wider range of issues,
using our growing dataset.
cosmology.
Note that measurement and isolation of systematic errors is a
major goal of the SNLS. Some of these uncertainties will decrease as more
data is acquired and future papers will examine a wider range of issues,
using our growing dataset.
Combining Tables 3
and 6, we obtain the following results:
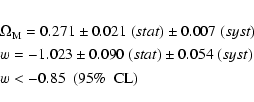
These results agree well with previous works, both from
SNe Ia, and also from other sources. For example Seljak et al. (2005) finds
very similar results combining CMB, LSS and Ly![]() constraints.
The dominant systematic uncertainties arise from the nearby
sample and from the photometric calibration of the
constraints.
The dominant systematic uncertainties arise from the nearby
sample and from the photometric calibration of the ![]() band; both will be
improved in the future. The multi-band light-curves allow us to study
color relations as a function of redshift; these data are expected to be
sensitive indicators of evolution. We observed a surprisingly narrow
correlation between (U-B) and (B-V) (using the
band; both will be
improved in the future. The multi-band light-curves allow us to study
color relations as a function of redshift; these data are expected to be
sensitive indicators of evolution. We observed a surprisingly narrow
correlation between (U-B) and (B-V) (using the
![]() indicator),
indicating that the dispersion in U-band properties is well correlated with
measurements in redder bands.
indicator),
indicating that the dispersion in U-band properties is well correlated with
measurements in redder bands.
Table 6:
Summary of uncertainties in the derived cosmological parameters. The dominant
systematic uncertainty arises from the photometric calibration, itself
dominated by the ![]() and
and ![]() band contributions.
band contributions.
From the first year of SNLS data, we placed 71 distant events on the
Hubble Diagram, with 10 more from the same period to be added later.
(Our full first year statistics would have been around 100 SNe Ia with
spectroscopic confirmation had we not lost Feb. 2004 to an instrument
failure.) Our time sampling, filter coverage, and image quality have
now significantly improved since early 2004,
and we now regularly acquire 2-3 times as much data in ![]() .
A precise photometric calibration is essential, and we are
now working with the CFHTLS community in refining
the photometric calibration of the MegaCam instrument. We have
embarked on the process of calibrating tertiary standards in our
fields, from Sloan secondary and primary standards. This will allow us
to cross-check the Vega/Landolt zero-points, and
more accurately calibrate
.
A precise photometric calibration is essential, and we are
now working with the CFHTLS community in refining
the photometric calibration of the MegaCam instrument. We have
embarked on the process of calibrating tertiary standards in our
fields, from Sloan secondary and primary standards. This will allow us
to cross-check the Vega/Landolt zero-points, and
more accurately calibrate ![]() band observations.
band observations.
After only two years of operation, the SNLS has already demonstrated its advantages over all previous ground-based supernova surveys. The "rolling search'' technique is robust to weather and instrument-related problems, and the technical characteristics of the survey are now well understood. The average rate of spectroscopically-confirmed SNe Ia is currently about 10 per lunation and continues to increase. Up until July 2005, the SNLS sample includes more than 200 spectroscopically identified SNe Ia, most with excellent photometric temporal and filter coverage. An extrapolation of the current rate to the end of the survey indicates that we should reach our goal of building a Hubble diagram with about 700 spectroscopically identified well-measured SN Ia events. The SNLS already has the largest-ever sample of high-z SNe discovered by a single telescope, and will eventually produce a homogeneous, high-quality sample that is an order of magnitude larger still.
High statistical accuracy benefits the control of systematics. With our
unmatched SN statistics, by year 5
we will be able to populate each ![]() 0.1 redshift bin
with
0.1 redshift bin
with ![]() 100 SNe Ia,
thus filling the brightness, decline-rate, and
color 3-dimensional parameter space. This will enable us to detect possible
drifts in "SNe Ia demographics'', and control Malmquist bias.
Moreover, the rolling-search observing mode produces many
events at low to intermediate redshift with superb photometric
accuracy, because integration times are
tailored for the faintest objects. These relatively bright events
permit demanding internal consistency tests,
and may lead to improvements in distance estimation.
100 SNe Ia,
thus filling the brightness, decline-rate, and
color 3-dimensional parameter space. This will enable us to detect possible
drifts in "SNe Ia demographics'', and control Malmquist bias.
Moreover, the rolling-search observing mode produces many
events at low to intermediate redshift with superb photometric
accuracy, because integration times are
tailored for the faintest objects. These relatively bright events
permit demanding internal consistency tests,
and may lead to improvements in distance estimation.
Acknowledgements
The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. We gratefully acknowledge the assistance of the CFHT Queued Service Observing Team, led by P. Martin (CFHT). We heavily rely on the dedication of the CFHT staff and particularly J.-C. Cuillandre for continuous improvement of the instrument performance. The real-time pipelines for supernovae detection run on computers integrated in the CFHT computing system, and are very efficiently installed, maintained and monitored by K. Withington (CFHT). We also heavily rely on the real-time Elixir pipeline which is operated and monitored by J-C. Cuillandre, E. Magnier and K. Withington. We are grateful to L. Simard (CADC) for setting up the image delivery system and his kind and efficient responses to our suggestions for improvements. The French collaboration members carry out the data reductions using the CCIN2P3. Canadian collaboration members acknowledge support from NSERC and CIAR; French collaboration members from CNRS/IN2P3, CNRS/INSU, PNC and CEA. This work was supported in part by the Director, Office of Science, Office of High Energy and Nuclear Physics, of the US Department of Energy. The France-Berkeley Fund provided additional collaboration support. CENTRA members were supported by Fundação para a Ciência e Tecnologia (FCT), Portugal under POCTI/FNU/43423. S. Fabbro and C. Gonçalves acknowledge support from FCT under grants no SFRH/BPD/14682/2003 and SFRH/BPD/11641/2002 respectively.
Table 7: Transients from the first year sample identified as SNIa or SNIa*.
Table 8: Nearby type Ia supernovae.
Table 9: SNLS type Ia supernovae.