A&A 447, 157-172 (2006)
DOI: 10.1051/0004-6361:20054024
T. Nagao1,2 - A. Marconi1 - R. Maiolino1
1 -
INAF - Osservatorio Astrofisico di Arcetri,
Largo Enrico Fermi 5, 50125 Firenze, Italy
2 -
National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka, Tokyo 151-8588, Japan
Received 9 August 2005 / Accepted 6 October 2005
Abstract
Based on 5344 quasar spectra taken from the SDSS Data Release 2,
the dependences of various emission-line flux ratios on redshift
and quasar luminosity are investigated in the ranges
![]() and
and
![]() .
We show that the emission lines in the composite spectra are
fitted better with power-law profiles than with double Gaussian
or modified Lorentzian profiles, and in particular we show that
the power-law profiles are more appropriate
to measure broad emission-line fluxes than other methods.
The composite spectra show that there are statistically
significant correlations between quasar luminosity and various
emission-line flux ratios, such as N V/C IV and
N V/He II, while there are only marginal correlations
between quasar redshift and emission-line flux ratios.
We obtain detailed photoionization models to interpret the
observed line ratios. The correlation of line ratios with
luminosity is interpreted in terms of higher gas metallicity in
more luminous quasars. For a given quasar luminosity, there is
no metallicity evolution for the redshift range
.
We show that the emission lines in the composite spectra are
fitted better with power-law profiles than with double Gaussian
or modified Lorentzian profiles, and in particular we show that
the power-law profiles are more appropriate
to measure broad emission-line fluxes than other methods.
The composite spectra show that there are statistically
significant correlations between quasar luminosity and various
emission-line flux ratios, such as N V/C IV and
N V/He II, while there are only marginal correlations
between quasar redshift and emission-line flux ratios.
We obtain detailed photoionization models to interpret the
observed line ratios. The correlation of line ratios with
luminosity is interpreted in terms of higher gas metallicity in
more luminous quasars. For a given quasar luminosity, there is
no metallicity evolution for the redshift range
![]() .
The typical metallicity of BLR gas clouds
is estimated to be
.
The typical metallicity of BLR gas clouds
is estimated to be
![]() ,
although the inferred
metallicity depends on the assumed BLR cloud properties, such as
their density distribution function and their radial distribution.
The absence of a metallicity evolution up to
,
although the inferred
metallicity depends on the assumed BLR cloud properties, such as
their density distribution function and their radial distribution.
The absence of a metallicity evolution up to
![]() implies that the active star-formation epoch of quasar host
galaxies occurred at
implies that the active star-formation epoch of quasar host
galaxies occurred at ![]() .
.
Key words: galaxies: active - galaxies: evolution - galaxies: nuclei - galaxies: quasars: emission lines - galaxies: quasars: general
Quasars are among the most luminous objects in the universe and therefore they can be detected and investigated in detail even at very high redshifts, up to z>6 (Fan et al. 2001, 2003, 2004). As a consequence, they have been frequently used as a tool to pursue the exploration of the distant universe, such as the investigation of the intergalactic matter (see, e.g., Rauch 1998 for a review), the cosmic re-ionization history (e.g., Fan et al. 2002; Gnedin 2004) and the metal-enrichment history in the universe. Since the gas in the broad-line region (BLR) of quasars is most likely photoionized, as suggested by reverberation mapping observations (e.g., Peterson 1993), it is possible to investigate the chemical composition of gas clouds in BLRs by comparing spectroscopic data with photoionization model calculations. The gas-phase elemental abundances are determined by the star-formation history of the galaxies, therefore studies on the metallicity of BLR in distant quasars are highly insightful of the metal-enrichment history and the galaxy formation in the very early universe (e.g., Matteucci & Padovani 1993; Hamann & Ferland 1993, 1999; Venkatesan et al. 2004). Note that the analysis on the gas metallicity of high-zgalaxies not hosting AGN are extremely difficult and time-consuming, because even the brightest galaxies are much fainter than quasars at the same redshift (but see, e.g., Teplitz et al. 2000; Kobulnicky & Koo 2000; Pettini et al. 2001).
It has been often claimed that the gas metallicity of the BLR
in quasars is higher than solar (e.g., Baldwin
& Netzer 1978; Hamann & Ferland 1992; Ferland et al. 1996;
Dietrich et al. 1999, 2003). The inferred metallicity is
sometimes very high, several times solar, and for the most
extreme case QSO 0353-383 it reaches as much as
![]() (Baldwin et al. 2003).
Since such high metallicities require
deep gravitational potentials and intense star-forming activity
in the host galaxies, they provide strong constraints on the
evolutionary scenarios of quasar host galaxies
(e.g., Hamann & Ferland 1993, 1999; Di Matteo et al. 2004).
Another surprising result is that the BLR metallicity does not
appear to decrease at the highest redshift proved so far
(e.g., Pentericci et al. 2002;
Dietrich et al. 2003; Maiolino et al. 2003).
This finding gives tight constraints on the
first epoch of star formation in the host galaxies,
especially when the minimum timescale required for the
enrichment of some metals (C, Si, Fe and so on) is taken
into account. On the other hand, some observations suggest that
quasars at higher-z show higher metallicity than
lower-z quasars (e.g., Hamann & Ferland 1992, 1993, 1999).
It is also recognized that the BLR metallicity tends to be
higher in more luminous quasars (e.g., Hamann & Ferland
1993, 1999). This trend may suggest a connection between the
BLR metallicity of quasars and evolutionary processes of the
host galaxies. However, since higher-luminosity quasars tend
to be selectively observed at higher-z, it is not clear
how the BLR metallicity depends on the luminosity and
redshift, individually.
(Baldwin et al. 2003).
Since such high metallicities require
deep gravitational potentials and intense star-forming activity
in the host galaxies, they provide strong constraints on the
evolutionary scenarios of quasar host galaxies
(e.g., Hamann & Ferland 1993, 1999; Di Matteo et al. 2004).
Another surprising result is that the BLR metallicity does not
appear to decrease at the highest redshift proved so far
(e.g., Pentericci et al. 2002;
Dietrich et al. 2003; Maiolino et al. 2003).
This finding gives tight constraints on the
first epoch of star formation in the host galaxies,
especially when the minimum timescale required for the
enrichment of some metals (C, Si, Fe and so on) is taken
into account. On the other hand, some observations suggest that
quasars at higher-z show higher metallicity than
lower-z quasars (e.g., Hamann & Ferland 1992, 1993, 1999).
It is also recognized that the BLR metallicity tends to be
higher in more luminous quasars (e.g., Hamann & Ferland
1993, 1999). This trend may suggest a connection between the
BLR metallicity of quasars and evolutionary processes of the
host galaxies. However, since higher-luminosity quasars tend
to be selectively observed at higher-z, it is not clear
how the BLR metallicity depends on the luminosity and
redshift, individually.
To investigate the BLR metallicity and understand the
chemical evolution of quasars and their host galaxies,
it is thus necessary to observe a large number of
quasars with sufficiently large ranges of luminosity and
redshift. Francis & Koratkar (1995) compared the rest-UV
spectra of quasars at the local universe observed with IUE
with those at
1.7 < z < 3.3 obtained by
Large Bright Quasar Survey (LBQS; Foltz et al. 1987)
and found little redshift evolution of the UV
spectra. Dietrich et al. (2002) investigated the
spectra of a larger sample of quasars at 0 < z < 5spanning 6 orders of magnitude in luminosity, based on
the data compilation of various observations that were
performed with IUE, HST, and some ground-based
observatories. However, to avoid possible systematic
uncertainties, it is crucially important to use large
homogeneous samples of quasars obtained by the same
instrument and manner. Thanks to the public data
release of the Sloan Digital Sky Survey (SDSS) project
(York et al. 2000), spectra of more than a few thousands quasars
are now available,
and therefore a systematic examination of BLR properties
becomes feasible. Although the signal-to-noise ratio of
each spectrum in the SDSS database is not high enough to
measure emission-line fluxes accurately,
higher quality spectra can be obtained by the "composite'' of
numerous individual spectra. Composite spectra are a very
efficient tool not only to increase the data quality, but also
to minimize effects due to individual characteristics of each
quasars. Note that the datasets of the 2dF and 6dF QSO Redshift
Surveys (e.g., Croom et al. 2004) are also available to examine
various statistical properties of quasars
(e.g., Croom et al. 2002); however, most quasars
found by these surveys are only at z<3 and the spectra are not
calibrated in (relative) flux, making it difficult to obtain
accurate emission-line flux ratios.
By using composite SDSS spectra, various
spectroscopic properties of quasars have already been
investigated, such as the spectral energy distribution
(SED) (Vanden Berk et al. 2001) and
broad absorption line (BAL) objects (Reichard et al. 2003a).
The purpose of this paper is to use composite spectra of SDSS
quasars to derive the dependences of BLR
emission-line spectra on redshift and luminosity in wide ranges,
although the luminosity range is narrower for
high-redshift quasars due to the limited spectroscopic
sensitivity of the SDSS dataset.
|
|
|
|
|
|
Total | |
|
|
643 | 50 | 1 | 0 | 0 | 694 |
|
|
1497 | 284 | 332 | 153 | 25 | 2291 |
|
|
917 | 385 | 323 | 222 | 120 | 1967 |
|
|
105 | 71 | 76 | 53 | 45 | 350 |
|
|
5 | 11 | 16 | 5 | 3 | 40 |
|
|
0 | 1 | 1 | 0 | 0 | 2 |
| total | 3167 | 802 | 749 | 433 | 193 | 5344 |
In this paper, we present our making of the composite spectra
of SDSS quasars for various redshift and luminosity intervals.
The measured emission-line flux ratios and other spectroscopic
properties are discussed in detail.
By combining these observational results with new extensive
photoionization models, we investigate the metallicity and other
spectroscopic properties
of the BLRs. Throughout this paper, we adopt a cosmology with
(
![]() ,
,
![]() ,
,
![]() ) = (1.0, 0.3, 0.7) and
H0 = 70 km s-1 Mpc-1 .
) = (1.0, 0.3, 0.7) and
H0 = 70 km s-1 Mpc-1 .
The spectroscopic data of SDSS quasars (Richards et al. 2002a)
were obtained from the SDSS archive, Data Release 2
(DR2; Abazajian et al. 2004)![]() .
The spectral resolution of
the SDSS spectroscopic data is
.
The spectral resolution of
the SDSS spectroscopic data is ![]() 2000, that corresponds
to
2000, that corresponds
to
![]() km s-1, which is high enough
for our scientific purposes. Only quasars at
km s-1, which is high enough
for our scientific purposes. Only quasars at
![]() are considered in this paper, because
in this redshift range the wavelength coverage of the SDSS
spectroscopic data
(
are considered in this paper, because
in this redshift range the wavelength coverage of the SDSS
spectroscopic data
(
![]() )
includes at least the rest frame wavelength interval from
Ly
)
includes at least the rest frame wavelength interval from
Ly![]()
![]() 1216 to He II
1216 to He II ![]() 1640.
There are 6181 quasars
1640.
There are 6181 quasars![]() within this redshift
range and with a redshift confidence level of zConf
within this redshift
range and with a redshift confidence level of zConf ![]() 0.75 in the DR2 archive; while 311 objects are excluded
because not matching this zConf criterion. 109 objects are removed from the 6181 quasars:
84 spectra of them suffer from bad focusing of
the spectrograph collimator and 25 spectra suffer from
leaking light from a LED (see Abazajian et al.
2004 for more details). Therefore the number of usable
quasar spectra is 6072. Note however that this sample is
not a complete one in
any sense, because the spectroscopic targets are selected
heterogeneously: some of them are selected through their
SDSS photometric properties, and others are
selected by cross-identification with radio or X-ray
sources.
0.75 in the DR2 archive; while 311 objects are excluded
because not matching this zConf criterion. 109 objects are removed from the 6181 quasars:
84 spectra of them suffer from bad focusing of
the spectrograph collimator and 25 spectra suffer from
leaking light from a LED (see Abazajian et al.
2004 for more details). Therefore the number of usable
quasar spectra is 6072. Note however that this sample is
not a complete one in
any sense, because the spectroscopic targets are selected
heterogeneously: some of them are selected through their
SDSS photometric properties, and others are
selected by cross-identification with radio or X-ray
sources.
The SDSS quasar selection algorithm picks up not only
"normal'' quasars, but also
broad absorption line (BAL) quasars (Richards et al. 2002a).
Indeed Reichard et al. (2003b) found 224 BAL quasars among
3814 quasars in the SDSS early data release
(EDR; Stoughton et al. 2002). BAL quasars
should be removed because the BAL features affect
fluxes and profiles of broad emission lines in the composite
spectra, therefore we
removed BAL quasars from our sample. Here we did not adopt
the standard "Balnicity Index (BI)'' (Weymann et al. 1991) to
identify BAL quasars. This is because BI does not identify
quasars with a strong absorption line close to the
systemic velocity of the quasar
(
![]() km s-1),
by definition. For our purpose, however, quasars with such
associated absorption lines (see, e.g., Foltz et al. 1986)
should be also removed to investigate the BLR emission-line
properties correctly. We checked all of the 6072 quasars by eye
and identified 724 quasars with strong absorption features,
which were removed from our quasar sample.
km s-1),
by definition. For our purpose, however, quasars with such
associated absorption lines (see, e.g., Foltz et al. 1986)
should be also removed to investigate the BLR emission-line
properties correctly. We checked all of the 6072 quasars by eye
and identified 724 quasars with strong absorption features,
which were removed from our quasar sample.
Each spectrum was then corrected for Galactic reddening
with the reddening curve of Cardelli et al. (1989),
even though the effect is very small in most cases because
the SDSS survey area is at high Galactic latitude,
i.e.
E(B-V)<0.05 mag for ![]()
![]() and
E(B-V)<0.10 mag for
and
E(B-V)<0.10 mag for ![]()
![]() of our sample
[the median value is
E(B-V)=0.029 mag]. Note that the
spectroscopic data in the EDR archive and the DR1 archive are
already corrected for the Galactic reddening, which is different
from the spectroscopic data in the DR2 archive.
The k-correction for each quasar was applied for calculating
the absolute B magnitude. For this purpose, a
simple power-law SED with a power-law index of
of our sample
[the median value is
E(B-V)=0.029 mag]. Note that the
spectroscopic data in the EDR archive and the DR1 archive are
already corrected for the Galactic reddening, which is different
from the spectroscopic data in the DR2 archive.
The k-correction for each quasar was applied for calculating
the absolute B magnitude. For this purpose, a
simple power-law SED with a power-law index of
![]() (where
(where
![]() )
is assumed for the
intrinsic spectral shape of quasars, following other
studies on SDSS quasars (e.g., Schneider et al. 2002, 2003).
This assumption seems valid at least at
)
is assumed for the
intrinsic spectral shape of quasars, following other
studies on SDSS quasars (e.g., Schneider et al. 2002, 2003).
This assumption seems valid at least at
![]() ,
based on the composite spectrum of the whole SDSS quasar sample
(Vanden Berk et al. 2001).
In this study, the absolute magnitude of quasars was calculated
from the
,
based on the composite spectrum of the whole SDSS quasar sample
(Vanden Berk et al. 2001).
In this study, the absolute magnitude of quasars was calculated
from the
![]() magnitude, because an
magnitude, because an
![]() -band flux is not affected by the Lyman-break
for quasars at
-band flux is not affected by the Lyman-break
for quasars at
![]() .
.
For most of the quasars in our sample, the signal-to-noise ratio
of the individual spectra is not high enough to
measure the properties of the broad emission lines accurately.
However, as mentioned above, we can investigate the BLR
properties as a function of redshift and quasar luminosity by
constructing composite spectra of quasars in certain parameters
ranges and by examining the BLR properties in such composite
spectra. As discussed by Vanden Berk et al. (2001), there are
mainly two methods to combine the spectroscopic data. One is
the arithmetic mean method, which preserves the relative fluxes
of emission features. The other is the geometric mean method,
which preserves global continuum shapes. Since we are interested
mainly in broad emission-line properties and not in global
continuum SED, we adopt the former strategy to combine the
quasar spectra. However, the choice of the composite
method does not affect results and discussion significantly:
the measured emission-line fluxes vary
less than 10% if we adopt the geometric mean instead of
the arithmetic mean. The spectral composition was
performed by using the IRAF![]() task, scombine, adopting a 5
task, scombine, adopting a 5![]() clipping rejection
criterion to remove bad pixels.
Before combining the spectral data, it is necessary to shift
the data from the observed frame to the quasar rest frame.
However, the accurate determination of quasar redshifts is
not an easy task, because broad emission lines tend to be
shifted blueward or redward compared to the quasar rest frame
(e.g., Gaskell 1982; Richards et al. 2002b).
Although narrow emission lines are sometimes used as a measure
of systemic recession velocities of quasars (e.g.,
Vanden Berk et al. 2001), we cannot use
narrow emission lines because only the rest-frame ultraviolet
spectral region (which lacks of narrow lines) is available due
to the redshift range of the sample. Despite this uncertainty,
we simply adopted the redshift assigned by the SDSS reduction
pipeline. This choice is acceptable for us because
we are mainly interested in the broad emission-line flux ratios,
but it should be kept in mind that a consequence may be
non-negligible uncertainties in the velocity profiles of
emission lines in the composite spectra.
We will discuss this issue briefly in Sect. 4.1.
After shifting the spectra to the quasar rest frame, the data
were re-binned to a common dispersion of 1
clipping rejection
criterion to remove bad pixels.
Before combining the spectral data, it is necessary to shift
the data from the observed frame to the quasar rest frame.
However, the accurate determination of quasar redshifts is
not an easy task, because broad emission lines tend to be
shifted blueward or redward compared to the quasar rest frame
(e.g., Gaskell 1982; Richards et al. 2002b).
Although narrow emission lines are sometimes used as a measure
of systemic recession velocities of quasars (e.g.,
Vanden Berk et al. 2001), we cannot use
narrow emission lines because only the rest-frame ultraviolet
spectral region (which lacks of narrow lines) is available due
to the redshift range of the sample. Despite this uncertainty,
we simply adopted the redshift assigned by the SDSS reduction
pipeline. This choice is acceptable for us because
we are mainly interested in the broad emission-line flux ratios,
but it should be kept in mind that a consequence may be
non-negligible uncertainties in the velocity profiles of
emission lines in the composite spectra.
We will discuss this issue briefly in Sect. 4.1.
After shifting the spectra to the quasar rest frame, the data
were re-binned to a common dispersion of 1 ![]() .
Then each individual spectrum was normalized to the mean flux
density at
.
Then each individual spectrum was normalized to the mean flux
density at
![]() .
In this normalization process, 4 objects were removed from the
5348 objects because their spectra show significant problems in
the wavelength range of
.
In this normalization process, 4 objects were removed from the
5348 objects because their spectra show significant problems in
the wavelength range of
![]() .
As a consequence the number of quasars used in the following
analysis is 5344.
Then the quasars are divided into redshift and luminosity bins
with the intervals of
.
As a consequence the number of quasars used in the following
analysis is 5344.
Then the quasars are divided into redshift and luminosity bins
with the intervals of
![]() and
and
![]() mag.
In Table 1 the final number of objects used in our analysis is
given for each redshift and luminosity bin. Among the
composite spectra, we analyze only those which were created
by at least 5 individual spectra.
The resulting composite spectra are shown in Figs. 1-21.
mag.
In Table 1 the final number of objects used in our analysis is
given for each redshift and luminosity bin. Among the
composite spectra, we analyze only those which were created
by at least 5 individual spectra.
The resulting composite spectra are shown in Figs. 1-21.
The measurement of emission-line fluxes in quasar spectra is
a complicated issue, both because some adjoining emission-line
such as "Ly![]() and N V
and N V![]() 1240'' and
"Al III
1240'' and
"Al III![]() 1857, Si III]
1857, Si III]![]() 1892 and
C III]
1892 and
C III]![]() 1909'' are heavily blended, and also because
the continuum level is often not easy to estimate.
There are two methods which have been employed mostly.
One is by fitting the detected emission-line feature by some
appropriate function, and the other is by defining a "local''
continuum level for each emission line and integrating the
flux above the adopted continuum level. Zheng et al. (1997)
adopted the former method to measure emission-line fluxes
in the composite HST quasar spectrum through
multiple Gaussian fitting (see also, e.g., Laor et al. 1994).
Vanden Berk et al. (2001) adopted
the latter strategy and measured line fluxes in the composite
spectrum of 2204 SDSS quasars spanning a wide luminosity and
redshift range by summing up the line
flux above a defined local continuum level.
Here it should be kept in mind that both methods
have serious difficulties to measure accurate emission-line
fluxes.
As for the profile-fitting method, it is crucial to
choose appropriate functions to fit emission lines.
A simple Gaussian or
Lorentzian profile does not work since the broad emission
lines of quasars generally show asymmetric velocity profiles
(e.g., Corbin 1997; Vanden Berk et al. 2001;
Baskin & Laor 2005).
Although the multi-Gaussian method can achieve
reasonably sufficient profile fit, it requires
many free parameters.
It is also reported that the best-fit profile function may
depend on the velocity width and other AGN properties
(e.g., Sulentic et al. 2002).
As for the local-continuum method, on the other hand,
it is not clear whether the adopted continuum level is
appropriate or not; this uncertainty may be crucial especially
when blended emission lines are concerned.
1909'' are heavily blended, and also because
the continuum level is often not easy to estimate.
There are two methods which have been employed mostly.
One is by fitting the detected emission-line feature by some
appropriate function, and the other is by defining a "local''
continuum level for each emission line and integrating the
flux above the adopted continuum level. Zheng et al. (1997)
adopted the former method to measure emission-line fluxes
in the composite HST quasar spectrum through
multiple Gaussian fitting (see also, e.g., Laor et al. 1994).
Vanden Berk et al. (2001) adopted
the latter strategy and measured line fluxes in the composite
spectrum of 2204 SDSS quasars spanning a wide luminosity and
redshift range by summing up the line
flux above a defined local continuum level.
Here it should be kept in mind that both methods
have serious difficulties to measure accurate emission-line
fluxes.
As for the profile-fitting method, it is crucial to
choose appropriate functions to fit emission lines.
A simple Gaussian or
Lorentzian profile does not work since the broad emission
lines of quasars generally show asymmetric velocity profiles
(e.g., Corbin 1997; Vanden Berk et al. 2001;
Baskin & Laor 2005).
Although the multi-Gaussian method can achieve
reasonably sufficient profile fit, it requires
many free parameters.
It is also reported that the best-fit profile function may
depend on the velocity width and other AGN properties
(e.g., Sulentic et al. 2002).
As for the local-continuum method, on the other hand,
it is not clear whether the adopted continuum level is
appropriate or not; this uncertainty may be crucial especially
when blended emission lines are concerned.
In this work, we adopt the profile-fitting method because
we are interested in the fluxes of emission lines including
heavily blended ones, such as N V![]() 1240, which is
generally regarded as an important metallicity diagnostic
(e.g., Hamann & Ferland 1993; Hamann et al. 2002).
The following function is adopted to fit the line profiles:
1240, which is
generally regarded as an important metallicity diagnostic
(e.g., Hamann & Ferland 1993; Hamann et al. 2002).
The following function is adopted to fit the line profiles:
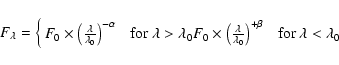 |
(1) |
| Ion | Ionization potential | Ionization potential | Classification |
| lower (eV) | upper (eV) | ||
| O I | 0.0 | 13.6 | LIL |
| Al II | 5.9 | 18.8 | LIL |
| Si II | 8.1 | 16.3 | LIL |
| C II | 11.3 | 24.4 | LIL |
| Si III | 16.3 | 33.5 | LIL |
| Al III | 18.8 | 28.4 | LIL |
| C III | 24.4 | 47.9 | LIL |
| He II | 24.6 | 54.4 | HIL
|
| Si IV | 33.5 | 45.1 | LIL |
| O III | 35.1 | 54.9 | LIL |
| N IV | 47.4 | 77.4 | HIL |
| C IV | 47.9 | 64.5 | HIL |
| O IV | 54.9 | 77.4 | HIL |
| N V | 77.4 | 97.9 | HIL |
|
ionization potential is important rather than the lower ionization potential. |
The O I+Si II composite at 1305 ![]() and
C II
and
C II![]() 1335 is measured simply by summing up all of
flux above the continuum level for each line
(
1335 is measured simply by summing up all of
flux above the continuum level for each line
(
![]() for the
O I+Si II composite and
for the
O I+Si II composite and
![]() for C II
for C II![]() 1335), because their
velocity profiles are different from both HILs and LILs.
We also measure the flux of a "1600
1335), because their
velocity profiles are different from both HILs and LILs.
We also measure the flux of a "1600![]() bump'',
which is clearly seen in the residual spectra (see lower panels
in Figs. 1-21). We simply sum up the flux above the continuum
level (
bump'',
which is clearly seen in the residual spectra (see lower panels
in Figs. 1-21). We simply sum up the flux above the continuum
level (
![]() )
also for this unidentified spectral feature.
The nature of the 1600
)
also for this unidentified spectral feature.
The nature of the 1600![]() bump will be discussed in
Sect. 4.2.
All these spectral regions (O I+Si II
bump will be discussed in
Sect. 4.2.
All these spectral regions (O I+Si II ![]() 1305,
C II
1305,
C II![]() 1335, and "1600
1335, and "1600 ![]() bump'') are
excluded from the fit.
Also, the wavelength region
at
bump'') are
excluded from the fit.
Also, the wavelength region
at
![]() is excluded from
the fitting process because there are heavily blended emission
lines such as N IV
is excluded from
the fitting process because there are heavily blended emission
lines such as N IV![]() 1719, Al II
1719, Al II![]() 1722,
N III]
1722,
N III]![]() 1750 and Fe II multiplets.
1750 and Fe II multiplets.
![\begin{figure}
\par\includegraphics[angle=-90,width=16.5cm,clip]{4024f22.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg63.gif) |
Figure 22:
Measured flux ratios as a function of redshift. Open circles,
squares, triangles, pluses, and stars denote the composite
spectra for
|
The fitting results are shown in Figs. 1-21.
The measured emission-line fluxes, normalized to the
C IV![]() 1549 flux, are given in Tables 3-7.
Here the errors given in Tables 3-7 contain only
the statistical errors, which are estimated from
the covariance matrix in the standard way.
The measured profile parameters, i.e., the velocity shifts
from the systemic velocity, the
1549 flux, are given in Tables 3-7.
Here the errors given in Tables 3-7 contain only
the statistical errors, which are estimated from
the covariance matrix in the standard way.
The measured profile parameters, i.e., the velocity shifts
from the systemic velocity, the ![]() and
and ![]() parameters, and the velocity widths in FWHM, are given in
Table 8. To see how the BLR emission-line properties depend on
redshift and luminosity, some measured emission-line flux
ratios are plotted as a function of redshift and absolute
B magnitude in Figs. 22 and 23.
For Si IV
parameters, and the velocity widths in FWHM, are given in
Table 8. To see how the BLR emission-line properties depend on
redshift and luminosity, some measured emission-line flux
ratios are plotted as a function of redshift and absolute
B magnitude in Figs. 22 and 23.
For Si IV![]() 1397 and
O IV]
1397 and
O IV]![]() 1402 only the sum of their flux is considered,
because the wavelength separation
of those two lines is so small that the fitting process
can hardly deblend them for some composite spectra
(in Table 3 the measured O IV]
1402 only the sum of their flux is considered,
because the wavelength separation
of those two lines is so small that the fitting process
can hardly deblend them for some composite spectra
(in Table 3 the measured O IV]![]() 1402 flux is
nearly zero only for the brightest case while the
Si IV flux increases suddenly at this luminosity).
For the same reason, only the sum of the O III]
1402 flux is
nearly zero only for the brightest case while the
Si IV flux increases suddenly at this luminosity).
For the same reason, only the sum of the O III]![]() 1663
and the Al II
1663
and the Al II![]() 1671 is plotted in Figs. 22 and 23.
As shown in Fig. 22, there are no apparent redshift
dependences in the major emission-line ratios, although
the highest-redshift data may deviate from the lower-redshift
trend in some flux ratios such as
Si II
1671 is plotted in Figs. 22 and 23.
As shown in Fig. 22, there are no apparent redshift
dependences in the major emission-line ratios, although
the highest-redshift data may deviate from the lower-redshift
trend in some flux ratios such as
Si II![]() 1263/C IV
1263/C IV![]() 1549,
(O I
1549,
(O I![]() 1304+Si II
1304+Si II![]() 1307)/C
IV
1307)/C
IV![]() 1549, and (O III]
1549, and (O III]![]() 1663+Al
II
1663+Al
II![]() 1671)/C IV
1671)/C IV![]() 1549.
Figure 22 shows that systematic differences in the
emission-line flux ratios at different
luminosities are present. This tendency is
more clear in Fig. 23, where significant
correlations between some flux ratios and luminosity are seen.
1549.
Figure 22 shows that systematic differences in the
emission-line flux ratios at different
luminosities are present. This tendency is
more clear in Fig. 23, where significant
correlations between some flux ratios and luminosity are seen.
In order to examine more quantitatively the significance
of the correlation of emission-line flux ratios with
redshift and luminosity, in Figs. 24 and 25 we show the flux ratios normalized to the values
measured from the composite spectra at
![]() or
or
![]() .
For these normalized flux ratios,
we apply a linear fit, whose results are also shown
in Figs. 24 and 25. The slopes of the best-fit results are
given in Table 9. We also examine whether the flux ratios
are correlated with redshift or absolute B magnitude with a
statistical significance, by applying the Spearman rank-order
test. The derived Spearman rank-order correlation
coefficients (
.
For these normalized flux ratios,
we apply a linear fit, whose results are also shown
in Figs. 24 and 25. The slopes of the best-fit results are
given in Table 9. We also examine whether the flux ratios
are correlated with redshift or absolute B magnitude with a
statistical significance, by applying the Spearman rank-order
test. The derived Spearman rank-order correlation
coefficients (![]() )
and their statistical significance
)
and their statistical significance
![]() ,
which is the probability of the data being
consistent with the null hypothesis that the flux ratio is
not correlated with redshift or absolute B magnitude,
are also given in Table 9. The results of the Spearman
rank-order test are summarized as follows:
,
which is the probability of the data being
consistent with the null hypothesis that the flux ratio is
not correlated with redshift or absolute B magnitude,
are also given in Table 9. The results of the Spearman
rank-order test are summarized as follows:
We also examine the dependences of emission-line shifts and
FWHMs on
redshift and absolute B magnitude. However, as mentioned
in Sect. 2.1, the shape of the emission lines
may be inaccurate due to the uncertainty in redshift of individual
quasars. Therefore we focus on the relative velocity difference
between HILs and LILs, which is less affected by uncertainties
in the absolute velocity determinations.
The relative differences of HILs and LILs in emission-line
peaks (
![]() )
and FWHMs of HILs
and LILs are plotted in Fig. 26, as a function of redshift and
absolute B magnitude. These profile parameters appear to be
strongly correlated with absolute B magnitude while not correlated
with redshift. The Spearman rank-order test results in
probabilities of the uncorrelation between redshift and
emission-line shift, FWHM of HILs and LILs of 0.46, 0.11 and 0.45 respectively,
while those between absolute B magnitude
and emission-line shift, FWHM of HILs and LILs are
)
and FWHMs of HILs
and LILs are plotted in Fig. 26, as a function of redshift and
absolute B magnitude. These profile parameters appear to be
strongly correlated with absolute B magnitude while not correlated
with redshift. The Spearman rank-order test results in
probabilities of the uncorrelation between redshift and
emission-line shift, FWHM of HILs and LILs of 0.46, 0.11 and 0.45 respectively,
while those between absolute B magnitude
and emission-line shift, FWHM of HILs and LILs are
![]() ,
,
![]() and
and
![]() .
These results indicate that the correlations between absolute B
magnitude and emission-line shift and FWHM of HILs are
statistically significant while those between redshift and
emission-line shift, FWHM of HILs and LILs are statistically
uncorrelated.
The relations between FWHMs, redshift, and
absolute B magnitude are interesting issues since they
contains information on the growth of supermassive black holes
(SMBHs).
We do not discuss this issue further since this topic is
beyond the scope of this paper.
.
These results indicate that the correlations between absolute B
magnitude and emission-line shift and FWHM of HILs are
statistically significant while those between redshift and
emission-line shift, FWHM of HILs and LILs are statistically
uncorrelated.
The relations between FWHMs, redshift, and
absolute B magnitude are interesting issues since they
contains information on the growth of supermassive black holes
(SMBHs).
We do not discuss this issue further since this topic is
beyond the scope of this paper.
To interpret these results quantitatively, it is very useful to compare emission-line flux ratios with photoionization models. However, it is well known that simple one-zone photoionization models cannot properly describe BLRs because gas clouds in BLRs span wide ranges in densities and/or ionization degrees in general (e.g., Davidson 1977; Collin-Souffrin et al. 1982). To investigate the physical properties of gas clouds in the BLRs of quasars, Baldwin et al. (1995) proposed the locally optimally emitting cloud (LOC) model, which is a multi-zone photoionization model. In this model, gas clouds with a wide range of physical conditions are present at a wide range of distances, and thus the net emission-line spectra can be calculated by integrating in the parameter space of gas density and radius, assuming some distribution functions. This model can predict fluxes of both low-ionization emission lines and high-ionization emission lines consistently and simultaneously, and thus it has been sometimes used to investigate physical and/or chemical properties of ionized gas clouds in BLRs (e.g., Korista et al. 1998; Korista & Goad 2000; Hamann et al. 2002).
Adopting this LOC model, we carried out photoionization model
calculations by using the photoionization code Cloudyversion 94.00 (Ferland 1997). For simplification, we assume
a plane-parallel geometry and a constant gas density for each
gas cloud. Dust grains are not included in our calculations
because gas clouds in BLRs are thought to be in a dust-free
region (e.g., Netzer & Laor 1993)
and we have verified that the physical conditions in our grid
of models imply dust sublimation in most cases. Those few cases
which allow dust survival were excluded from the final
calculation, as briefly mentioned also in Sect. 3.2.
Our assumption for the chemical composition is the same as that
of Hamann et al. (2002), in which the relative metal abundances
scale by keeping solar relative values except for nitrogen, which
scales as the square power of other metal abundances (see
Table 3 of Hamann et al. 2002). Here the solar elemental
abundances are taken from Grevesse & Anders (1989) with
extensions by Grevesse & Noels (1993).
As for the SED of the ionizing photons, two types of SED
are adopted to see possible SED effects on the results:
one is a SED with a strong UV thermal bump which matches the
quasar template of Scott et al. (2004), and the other is with a
weak UV thermal bump which matches the HST quasar templates
(Zheng et al. 1998; Telfer et al. 2002; see also Marconi
et al. 2004 for more details). Both SEDs have the same
optical to X-ray ratio
![]() (Zamorani et al. 1981;
Ferland 1997), i.e.,
(Zamorani et al. 1981;
Ferland 1997), i.e.,
![]() ,
but different
slopes in the energy range of
,
but different
slopes in the energy range of
![]() .
See Fig. 27 for a
graphical representation of the two SEDs (see also Nagao et al.
2006). The calculation for each cloud is stopped
when the cloud thickness reaches 1023 cm-2 or
when the cloud temperature drops below 3000 K.
We performed model runs for gas clouds with
a gas density (n) in the range of 107-14 cm-3with a 0.2 dex step, with a flux of ionizing photons (
.
See Fig. 27 for a
graphical representation of the two SEDs (see also Nagao et al.
2006). The calculation for each cloud is stopped
when the cloud thickness reaches 1023 cm-2 or
when the cloud temperature drops below 3000 K.
We performed model runs for gas clouds with
a gas density (n) in the range of 107-14 cm-3with a 0.2 dex step, with a flux of ionizing photons (![]() )
in
the range
1017 - 1024 cm-2 s-1 also with a 0.2 dex step, and with metallicities of
)
in
the range
1017 - 1024 cm-2 s-1 also with a 0.2 dex step, and with metallicities of
![]() ,
0.5, 1.0, 2.0, 5.0 and 10.0.
Therefore the number of the performed model runs is 1296 for each metallicity and SED, giving a total number of
15552 runs.
,
0.5, 1.0, 2.0, 5.0 and 10.0.
Therefore the number of the performed model runs is 1296 for each metallicity and SED, giving a total number of
15552 runs.
Once the calculations are completed, we can obtain the net emission-line
flux by integrating the line emissivity of all clouds; i.e.,
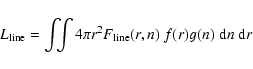 |
(2) |
In Fig. 28, we present some examples of calculated line
emissivities as a function of gas density and ionizing photon
flux. Contours indicate the predicted equivalent widths
for full geometrical coverage referred to the incident continuum
at
![]() ,
for models with ionizing
SED with a large UV thermal bump and a metallicity
of
,
for models with ionizing
SED with a large UV thermal bump and a metallicity
of
![]() .
It should be mentioned that the model calculations for
some clouds with certain pair of (n,
.
It should be mentioned that the model calculations for
some clouds with certain pair of (n, ![]() )
fail
because of a thermal instability effect of the ionized gas
(see Ferland 1997 for details of this problem). This problem is
more serious when high metallicity gas clouds are examined.
However even for the highest-metallicity cases (i.e.,
)
fail
because of a thermal instability effect of the ionized gas
(see Ferland 1997 for details of this problem). This problem is
more serious when high metallicity gas clouds are examined.
However even for the highest-metallicity cases (i.e.,
![]() ), the fraction of the crashed runs is less
than 6% of the 1296 model runs.
The line emissivities for the crashed cases are
estimated by simple interpolations on the n-
), the fraction of the crashed runs is less
than 6% of the 1296 model runs.
The line emissivities for the crashed cases are
estimated by simple interpolations on the n-![]() plane
using the results of the neighboring uncrashed models.
plane
using the results of the neighboring uncrashed models.
In Fig. 29, the net emission-line flux ratios are presented
as a function of gas metallicity, which are obtained by
the integrations as given in the Eq. (2).
Here we adopt
![]() and
and
![]() ,
i.e.,
,
i.e.,
![]() and
and
![]() .
In the integration procedure, gas clouds with a gas density of
n < 108 cm-3 are excluded because such low-density
clouds are thought to be implausible for BLRs, which is
inferred by the absence of broad [O III]
.
In the integration procedure, gas clouds with a gas density of
n < 108 cm-3 are excluded because such low-density
clouds are thought to be implausible for BLRs, which is
inferred by the absence of broad [O III]![]() 4363
emission lines in spectra of AGNs (note that the critical
density of the [O III]
4363
emission lines in spectra of AGNs (note that the critical
density of the [O III]![]() 4363 transition is
4363 transition is
![]() cm-3). Gas clouds with an
ionizing photon flux of
cm-3). Gas clouds with an
ionizing photon flux of
![]() cm-2 s-1are also excluded, because the energy density temperature of
the incident continuum emission for clouds with such a small
cm-2 s-1are also excluded, because the energy density temperature of
the incident continuum emission for clouds with such a small ![]() falls below 1000 K for our
adopted SEDs, at such temperature dust grains may survive
and absorb most of the ionizing photons (as well as most
of any UV line flux which may be produced;
Netzer & Laor 1993).
The adopted integration range is thus
falls below 1000 K for our
adopted SEDs, at such temperature dust grains may survive
and absorb most of the ionizing photons (as well as most
of any UV line flux which may be produced;
Netzer & Laor 1993).
The adopted integration range is thus
![]() and
and
![]() .
The predicted net emission-line flux ratios are also given
in Table 10.
.
The predicted net emission-line flux ratios are also given
in Table 10.
As apparent in Fig. 29, most of emission-line fluxes
normalized to the flux of C IV![]() 1549 are positively
correlated with the gas metallicity. This is mainly because
the C IV
1549 are positively
correlated with the gas metallicity. This is mainly because
the C IV![]() 1549 transition is an important coolant.
This is especially true in metal-poor environments where the cooling
by other metal lines is less effective, making
C IV
1549 transition is an important coolant.
This is especially true in metal-poor environments where the cooling
by other metal lines is less effective, making
C IV![]() 1549 emission become stronger when the
gas metallicity is lower. The effects of ionizing continuum
SED on the resultant predictions are very small,
generally far less than a factor of 2.
Note that some of the predicted flux ratios are sensitive
to the adopted weighting functions, f(r) and g(n),
especially when lines with a different ionization degree are
concerned (e.g., C II/C IV). We discuss the effect
of this dependence on our results in Sect. 4.2.
Note that Hamann et al. (2002) also presented the
results of the LOC photoionization model calculations
with the same assumption on the relative elemental
abundance ratios. Our results are almost consistent
with those of Hamann et al. (2002). The small
differences may be due to the differences in the
adopted SEDs, to the integration ranges of n and
1549 emission become stronger when the
gas metallicity is lower. The effects of ionizing continuum
SED on the resultant predictions are very small,
generally far less than a factor of 2.
Note that some of the predicted flux ratios are sensitive
to the adopted weighting functions, f(r) and g(n),
especially when lines with a different ionization degree are
concerned (e.g., C II/C IV). We discuss the effect
of this dependence on our results in Sect. 4.2.
Note that Hamann et al. (2002) also presented the
results of the LOC photoionization model calculations
with the same assumption on the relative elemental
abundance ratios. Our results are almost consistent
with those of Hamann et al. (2002). The small
differences may be due to the differences in the
adopted SEDs, to the integration ranges of n and ![]() ,
to the version of Cloudy, and to the column density of
clouds.
,
to the version of Cloudy, and to the column density of
clouds.
Before comparing the results of photoionization model
calculations with the measured emission-line flux ratios
of SDSS DR2 quasars, we should discuss whether our
measurement method is appropriate or not. Our adopted
formula for measuring emission lines (Eq. (1)) is
different from the widely adopted formulae such as
multi-Gaussian and (modified) Lorentzian. In Fig. 30,
we compare the fitting results by adopting Eq. (1),
double Gaussian (allowing the different central velocity
for the two Gaussian components), and modified Lorentzian
that is described by the following formula;
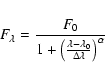 |
(3) |
However, since the power-law formula is not a conventional one to describe the BLR emission-line profiles, we should be careful to judge whether the power-law formula is a really representative for the BLR emission. In order to investigate whether the power-law emission-line profiles of our quasar composite spectra are due to some artificial effect, rather than resulting from the intrinsic kinematic properties of the BLR, some individual spectra of SDSS quasars with a high S/N are also fitted by using the power-law formula in the same way as for the composite spectra. The fitting results are shown in Figs. 31-33, where SDSS J085417.6+532735 (z=2.42, MB = -28.6), SDSS J080342.0+302254 (z=2.03, MB = -28.9), and SDSS J154359.4+535903 (z=2.37, MB = -28.5) are investigated. It is clear that the power-law formula describes properly individual spectra of quasars, and not only quasar composite spectra. This suggests that the power-law profile is really representative of the BLR emission and it should be insightful to investigate kinematic properties and the geometrical configuration of gas clouds in BLRs. We do not discuss these issues further because these are beyond the scope of this paper.
In Sect. 2.1, it was mentioned that possible uncertainties
in the redshift assigned to each object may introduce
artifacts in the emission-line profiles of composite spectra.
To check how much this effect might be significant,
we investigate the difference in redshift determined by a
specific emission line and the redshift assigned for each
object by the SDSS pipeline (i.e., the average of various
spectral features).
What really matters is not the absolute redshift difference
between a specific line and the average redshift from
other line, but the dispersion of such a difference.
As for the C IV![]() 1549 emission of quasars with
1549 emission of quasars with
![]() at
at
![]() ,
the average difference
,
the average difference
![]() and its standard deviation are
and its standard deviation are
![]() .
This standard deviation
(
.
This standard deviation
(
![]() )
corresponds to a velocity dispersion
of
)
corresponds to a velocity dispersion
of ![]() 1800 km s-1. Therefore we should be aware that
velocity structures on scales less than this velocity interval
of the C IV
1800 km s-1. Therefore we should be aware that
velocity structures on scales less than this velocity interval
of the C IV![]() 1549 emission-line profile
in the composite spectra may be affected by some artificial
effects; more global velocity structures are thought to be
free from such effects.
1549 emission-line profile
in the composite spectra may be affected by some artificial
effects; more global velocity structures are thought to be
free from such effects.
As mentioned in Sect. 2.2, there is another measurement method
which has often been adopted, that is the local-continuum
method. It is useful to compare the results of our
measurements with the values measured by adopting local
continuum levels, as in Vanden Berk et al. (2001).
In Fig. 34, we show the estimated local continuum levels
for the wavelength regions around N V![]() 1240,
C IV
1240,
C IV![]() 1549 and C III]
1549 and C III]![]() 1909. Here
we adopt roughly the same
1909. Here
we adopt roughly the same
![]() and
and
![]() as those defined by Vanden Berk et al.
(2001). The local continuum is linear for the wavelength
region around C IV
as those defined by Vanden Berk et al.
(2001). The local continuum is linear for the wavelength
region around C IV![]() 1549, while for the
wavelength regions around N V
1549, while for the
wavelength regions around N V![]() 1240 and
C III]
1240 and
C III]![]() 1909 the local continua are determined
by third polynomial fitting by using the wavelength parts
outside the emission lines. For this comparison, the
composite quasar spectrum at
1909 the local continua are determined
by third polynomial fitting by using the wavelength parts
outside the emission lines. For this comparison, the
composite quasar spectrum at
![]() and
and
![]() is used, because most of quasars
used by Vanden Berk et al. (2001) are at lower redshift and
are less luminous than ours. The flux measurement results
are presented in Table 11 and compared with the values of
Vanden Berk et al. (2001) and with the results of our
method in Sect. 2.2. The fluxes reported by Vanden Berk et al.
(2001) are similar to the values measured by us by adopting
the local-continuum method, but are very different from the
values given in Table 3a obtained by fitting with Eq. (1). This indicates that the flux measurement for several
of the BLR emission lines highly depends on the adopted
measurement method. Which method is more appropriate? To
tackle this problem, emission-line profiles are very
useful, because emission lines with similar ionization
potentials are thought to arise in similar regions in BLRs,
and therefore should have similar emission-line profiles.
In our fitting method, HILs (N V
is used, because most of quasars
used by Vanden Berk et al. (2001) are at lower redshift and
are less luminous than ours. The flux measurement results
are presented in Table 11 and compared with the values of
Vanden Berk et al. (2001) and with the results of our
method in Sect. 2.2. The fluxes reported by Vanden Berk et al.
(2001) are similar to the values measured by us by adopting
the local-continuum method, but are very different from the
values given in Table 3a obtained by fitting with Eq. (1). This indicates that the flux measurement for several
of the BLR emission lines highly depends on the adopted
measurement method. Which method is more appropriate? To
tackle this problem, emission-line profiles are very
useful, because emission lines with similar ionization
potentials are thought to arise in similar regions in BLRs,
and therefore should have similar emission-line profiles.
In our fitting method, HILs (N V![]() 1240,
C IV
1240,
C IV![]() 1549 and He II
1549 and He II![]() 1640) have
the same velocity profile and the same velocity shift from
the systemic velocity by definition. The emission-line
width and skewness for each line reported by
Vanden Berk et al. (2001) are, on the other hand, very
different among these three emission lines; the reported
width and skewness are (
1640) have
the same velocity profile and the same velocity shift from
the systemic velocity by definition. The emission-line
width and skewness for each line reported by
Vanden Berk et al. (2001) are, on the other hand, very
different among these three emission lines; the reported
width and skewness are (![]() ,
Skew) =
(2.71
,
Skew) =
(2.71 ![]() ,
-0.21), (14.33
,
-0.21), (14.33 ![]() ,
-0.04) and
(4.43
,
-0.04) and
(4.43 ![]() ,
-0.22) for N V
,
-0.22) for N V![]() 1240,
C IV
1240,
C IV![]() 1549 and He II
1549 and He II![]() 1640,
respectively. The difference of the line skewness should
correspond to the difference in the kinematic status of the
line-emitting clouds, implying a strong segregation of the
line emitting regions among HILs. These line widths
correspond to the velocity widths of 655 km s-1,
2779 km s-1 and 810 km s-1, respectively.
The difference of a factor of 3-4 in the velocity width
corresponds to the difference of a factor of
1640,
respectively. The difference of the line skewness should
correspond to the difference in the kinematic status of the
line-emitting clouds, implying a strong segregation of the
line emitting regions among HILs. These line widths
correspond to the velocity widths of 655 km s-1,
2779 km s-1 and 810 km s-1, respectively.
The difference of a factor of 3-4 in the velocity width
corresponds to the difference of a factor of ![]() 10 in
the radius from the nucleus, if the BLR motions are
dominated by the gravitational potential of the SMBH.
As presented in Fig. 28, the photoionization model
suggests that the emitting region of
N V
10 in
the radius from the nucleus, if the BLR motions are
dominated by the gravitational potential of the SMBH.
As presented in Fig. 28, the photoionization model
suggests that the emitting region of
N V![]() 1240 and C IV
1240 and C IV![]() 1549 are not
segregated with a factor of 10 in radius from the nucleus.
Reverberation mapping observations also suggest that HILs
arise from a similar region, and actually
He II
1549 are not
segregated with a factor of 10 in radius from the nucleus.
Reverberation mapping observations also suggest that HILs
arise from a similar region, and actually
He II![]() 1640 sometimes shows even more rapid
time variations than C IV
1640 sometimes shows even more rapid
time variations than C IV![]() 1549 (e.g.,
Clavel et al. 1991; Korista et al. 1995;
Peterson & Wandel 1999). Taking all of the above matters
into account, we conclude that our measurement method is
better than the local continuum method to measure the
emission-line fluxes accurately.
1549 (e.g.,
Clavel et al. 1991; Korista et al. 1995;
Peterson & Wandel 1999). Taking all of the above matters
into account, we conclude that our measurement method is
better than the local continuum method to measure the
emission-line fluxes accurately.
Our analysis on the SDSS DR2 composite spectra clearly indicates that some emission-line flux ratios (N V/C IV, Si II/C IV, (Si IV+O IV)/C IV, Al III/C IV and N V/He II) positively correlate with absolute B magnitude with a high statistical significance, but are independent of redshift. As presented in Sect. 3.2, photoionization models suggest that these flux ratios positively correlate with the gas metallicity. This means that the dependences of emission line ratios on absolute B magnitude are caused by the dependence of the BLR gas metallicity on the luminosity. In other words, the BLR gas metallicity positively depends on the quasar luminosity, but independent of the quasar redshift. This conclusion is also suggested by some earlier studies. As for Seyfert 1 galaxies at the local universe, the C III]/C IV flux ratio depends strongly on the luminosity (Véron-Cetty et al. 1983), which suggests the dependence of the gas metallicity on the luminosity. The correlation of the BLR metallciity with the quasar luminosity has been reported by, e.g., Hamann & Ferland (1999), Warner et al. (2004), and Shemmer et al. (2004). Warner et al. (2004) also reported the correlation of the BLR metallciity with the mass of SMBHs (see also Shemmer et al. 2004).
The dependence of the gas metallicity on the quasar luminosity
is expected, since (1) the quasar luminosity
should positively correlate with the mass of SMBHs for a
given Eddington accretion ratio, (2) a good correlation between
mass of SMBHs and mass of the host galaxies, exists at least
in the local universe (e.g., Gebhardt et al. 2000;
Ferrarese & Merritt 2000; Marconi & Hunt 2003), and (3) more massive
galaxies tend to have higher metallicity gas and stars due to
their deeper gravitational potential (e.g., Pagel & Edmunds 1981;
Arimoto & Yoshii 1987; Matteucci & Tornambè 1987;
Tremonti et al. 2004). The results presented in
this paper indicate the existence of close relation between
mass of SMBHs and host galaxies, and that the galaxy mass-metallicity
relation holds also at high redshift, up to
![]() .
We should mention that the independence of
broad emission-line flux ratios from redshift may be due to some
selection effects. For instance, quasars with low metallicity
may be dust-enshrouded in their young phase and thus very
difficult to detect (see, e.g., Kawakatu et al. 2003).
Hard X-ray deep and wide surveys are required to examine this
possibility.
.
We should mention that the independence of
broad emission-line flux ratios from redshift may be due to some
selection effects. For instance, quasars with low metallicity
may be dust-enshrouded in their young phase and thus very
difficult to detect (see, e.g., Kawakatu et al. 2003).
Hard X-ray deep and wide surveys are required to examine this
possibility.
However, by comparing the measured flux ratios with the results
of the photoionization model calculations with fixed
weighting functions (![]() and
and ![]() in Sect. 3), the inferred
gas metallicity is apparently different depending on the
adopted flux ratio. For instance, the observed
ratios of N V/C IV,
(Si IV+O IV)/C IV, Al III/C IV and
N V/He II suggest gas metallicities of
in Sect. 3), the inferred
gas metallicity is apparently different depending on the
adopted flux ratio. For instance, the observed
ratios of N V/C IV,
(Si IV+O IV)/C IV, Al III/C IV and
N V/He II suggest gas metallicities of
![]() ,
while the ratios of C II/C IV,
(O III]+Al II)/C IV, Si III]/C IV and
C III]/C IV suggest
,
while the ratios of C II/C IV,
(O III]+Al II)/C IV, Si III]/C IV and
C III]/C IV suggest
![]() (Fig. 29).
The ratio of He II/C IV is also not reproduced in most
cases. This is consistent with earlier works that the estimates
of the BLR metallicity using only the N V/C IV
and/or N V/He II flux ratios alone might be quite
uncertain (see Hamann et al. 2002).
As for the ratio of Si II/C IV, the observed
value deviates completely from the range of model predictions.
The deviation of Si II/C IV may be due to
the contamination of other emission lines into the Si II.
Indeed, we find that the flux of S II
(Fig. 29).
The ratio of He II/C IV is also not reproduced in most
cases. This is consistent with earlier works that the estimates
of the BLR metallicity using only the N V/C IV
and/or N V/He II flux ratios alone might be quite
uncertain (see Hamann et al. 2002).
As for the ratio of Si II/C IV, the observed
value deviates completely from the range of model predictions.
The deviation of Si II/C IV may be due to
the contamination of other emission lines into the Si II.
Indeed, we find that the flux of S II![]() 1256 becomes
high under some physical conditions. In Fig. 35, we show
the predicted flux ratio of S II/Si II for
1256 becomes
high under some physical conditions. In Fig. 35, we show
the predicted flux ratio of S II/Si II for
![]() and 5.0, and
U = 10-2.5 and 10-3.5as a function of gas metallicity, adopting the ionizing continuum
SED with a large UV thermal bump. The S II/Si II ratio
exceeds 0.2 and reaches
and 5.0, and
U = 10-2.5 and 10-3.5as a function of gas metallicity, adopting the ionizing continuum
SED with a large UV thermal bump. The S II/Si II ratio
exceeds 0.2 and reaches ![]() 1 for models with high
gas densities. Apparently the contribution of the S II
flux makes the deviation of the measured Si II/C IV
ratio from the theoretically predicted range.
Apart from the Si II deviation issue, what causes the
discrepancies among the inferred metallicity from different
line ratios?
SED effects are an implausible explanation of this
problem, because we have already
seen in Fig. 29 that the predicted line flux ratios do not vary
so significantly by changing the adopted SED.
Since the SEDs adopted in this paper (Fig. 27) are thought to
be extreme, opposite cases for the
actual ionizing continuum of quasars,
the SED effects on the flux ratios should be smaller than those
presented in Fig. 29.
1 for models with high
gas densities. Apparently the contribution of the S II
flux makes the deviation of the measured Si II/C IV
ratio from the theoretically predicted range.
Apart from the Si II deviation issue, what causes the
discrepancies among the inferred metallicity from different
line ratios?
SED effects are an implausible explanation of this
problem, because we have already
seen in Fig. 29 that the predicted line flux ratios do not vary
so significantly by changing the adopted SED.
Since the SEDs adopted in this paper (Fig. 27) are thought to
be extreme, opposite cases for the
actual ionizing continuum of quasars,
the SED effects on the flux ratios should be smaller than those
presented in Fig. 29.
One possibility which can cause the discrepancies of the
inferred metallicities from various emission-line flux ratios
is that the assumption on the weighting functions ![]() and
and ![]() is an oversimplification.
To examine this possibility quantitatively,
we investigate the dependence of the theoretical predictions
of some emission-line flux ratios on the adopted
is an oversimplification.
To examine this possibility quantitatively,
we investigate the dependence of the theoretical predictions
of some emission-line flux ratios on the adopted ![]() and
and ![]() parameters, as shown in Fig. 36.
It is clear that various predicted emission-line
flux ratios are highly dependent on the adopted values of
parameters, as shown in Fig. 36.
It is clear that various predicted emission-line
flux ratios are highly dependent on the adopted values of ![]() and
and ![]() .
Since the theoretical flux ratios
presented in Fig. 29
are predicted by adopting
.
Since the theoretical flux ratios
presented in Fig. 29
are predicted by adopting
![]() and
and
![]() (as in many other studies), other assumptions on
(as in many other studies), other assumptions on ![]() and
and ![]() result in other predictions and thus
the metallicity inferred by each one of the observed
emission-line flux ratios would change accordingly.
result in other predictions and thus
the metallicity inferred by each one of the observed
emission-line flux ratios would change accordingly.
| |
Figure 38:
Estimated metallicities from our composite spectra, averaged
in the luminosity range
-25.5 > MB > -28.5, as a function of
redshift. The estimation of the metallicity given in this figure
is derived from the fit with the varying |
| |
Figure 39:
Estimated metallicities from our composite spectra, averaged
in the redshift range
|
In order to illustrate our results on the metallicity trends
in a graphical way, for the reader's convenience, Fig. 38
shows the metallicity, averaged in luminosity, as a function
of redshift. Here we use the metallicities derived by the fit
with varying ![]() and
and ![]() given in Tables 12-16.
To avoid biases when calculating the average metallicity, we
have only used the luminosity bins for which a metallicity
determination is available at all redshifts. This
limits the range of usable luminosities to
-25.5 > MB > -28.5, where the averaged metallicity are
calculated. The errorbars are the estimated errors on the
mean obtained by combining the uncertainty in the metallicity
determination for each luminosity bin. The resulting plot
shows what was already clear from Tables 12-16 and from our
earlier discussion, i.e., there is no significant evolution
of the metallicity as a function of redshift. Figure 39 shows
the complementary diagram, i.e., the metallicity, averaged in
redshift, as a function of luminosity. Again, to avoid biases
when calculating the averaged metallicity, we have only used
the redshift bins for which a metallicity determination is
available at all luminosities, which limits the range
of usable redshifts to 2<z<3. The resulting diagram shows
that the averaged metallicity increases significantly with
absolute magnitude, as already inferred from the individual
results in Tables 12-16.
given in Tables 12-16.
To avoid biases when calculating the average metallicity, we
have only used the luminosity bins for which a metallicity
determination is available at all redshifts. This
limits the range of usable luminosities to
-25.5 > MB > -28.5, where the averaged metallicity are
calculated. The errorbars are the estimated errors on the
mean obtained by combining the uncertainty in the metallicity
determination for each luminosity bin. The resulting plot
shows what was already clear from Tables 12-16 and from our
earlier discussion, i.e., there is no significant evolution
of the metallicity as a function of redshift. Figure 39 shows
the complementary diagram, i.e., the metallicity, averaged in
redshift, as a function of luminosity. Again, to avoid biases
when calculating the averaged metallicity, we have only used
the redshift bins for which a metallicity determination is
available at all luminosities, which limits the range
of usable redshifts to 2<z<3. The resulting diagram shows
that the averaged metallicity increases significantly with
absolute magnitude, as already inferred from the individual
results in Tables 12-16.
Another possibility which may cause the discrepancies among the gas metallicities inferred from each emission-line flux ratio is the elemental abundance ratios. In our model, the relative elemental abundances are assumed to scale proportionally to solar, except for nitrogen which is assumed to scale as the square of other metal abundances. However these assumptions are an oversimplification. In more realistic metallicity evolutionary scenarios abundances never scale linearly with the global metallicity (e.g., Pipino & Matteucci 2004). The inclusion of more realistic abundance pattern in our photoionization models will be presented in a forthcoming paper.
Our analysis on the composite spectra shows that there is no
apparent dependence of emission-line flux ratios on redshift
up to
![]() ,
which is consistent with the results of
Dietrich et al. (2002). This suggests that the chemical
composition of the gas clouds in BLRs does not change
significantly up to
,
which is consistent with the results of
Dietrich et al. (2002). This suggests that the chemical
composition of the gas clouds in BLRs does not change
significantly up to
![]() .
Although the
.
Although the ![]() elements, such as oxygen, can be
enriched on a very short timescale (
elements, such as oxygen, can be
enriched on a very short timescale (![]() 1 Gyr) owing to
type II supernovae, the enrichment of carbon and silicon
require longer timescales (
1 Gyr) owing to
type II supernovae, the enrichment of carbon and silicon
require longer timescales (![]() 0.5-1 Gyr) since they are
produced mainly by the low-mass or intermediate-mass evolved
stars. Therefore, if the elemental abundance ratios in BLRs
remain constant up to high redshift, this gives a strong
constraint on the first epoch of active star-formation
in quasar host galaxies. In particular, constant elemental
abundance ratios up to z=4.5 suggest that the main
star-formation epoch in the host galaxies occurred at
0.5-1 Gyr) since they are
produced mainly by the low-mass or intermediate-mass evolved
stars. Therefore, if the elemental abundance ratios in BLRs
remain constant up to high redshift, this gives a strong
constraint on the first epoch of active star-formation
in quasar host galaxies. In particular, constant elemental
abundance ratios up to z=4.5 suggest that the main
star-formation epoch in the host galaxies occurred at
![]() ,
when minimum timescale to enrich C and Si is
taken into account. However this kind of discussion
requires a detailed theoretical predictions of the metal
enrichment history based on galaxy chemical evolutionary
models. Theoretical studies on the BLR evolution coupled
with galaxy evolutionary models are thus crucial to
understand the quasar formation and evolution.
Here we mention that possible variations of the
emission-line spectra beyond z=4 might be present in
Fig. 23, though the statistical significance is not high
enough. Further spectroscopic observations of
quasars in this redshift range or even at higher redshifts, for
sizeable samples of quasars, would be
highly insightful to examine the quasar evolutionary scenarios.
,
when minimum timescale to enrich C and Si is
taken into account. However this kind of discussion
requires a detailed theoretical predictions of the metal
enrichment history based on galaxy chemical evolutionary
models. Theoretical studies on the BLR evolution coupled
with galaxy evolutionary models are thus crucial to
understand the quasar formation and evolution.
Here we mention that possible variations of the
emission-line spectra beyond z=4 might be present in
Fig. 23, though the statistical significance is not high
enough. Further spectroscopic observations of
quasars in this redshift range or even at higher redshifts, for
sizeable samples of quasars, would be
highly insightful to examine the quasar evolutionary scenarios.
Similarly to some emission-line flux ratios, the velocity shift of HILs relative to LILs also correlates with the quasar luminosity and is independent of quasar redshift, as presented in Fig. 26. The velocity difference between HILs and LILs has been analyzed for a long time to investigate various kinematic/geometrical models for BLRs (e.g., Gaskell 1982; Wilkes 1984, 1986; Espey et al. 1989; Corbin 1990; Vanden Berk et al. 2001). The correlation between this velocity difference and the quasar luminosity has been reported also by other studies (e.g., Corbin 1990; Richards et al. 2002b). Our results confirm those previous works and reveal their independence of redshift.
Finally we discuss the nature of the "1600 ![]() bump''. This unidentified emission feature has been noted in
earlier studies, e.g., Wilkes (1984) and Boyle (1990). Our
analysis on the composite spectra clarifies that the
1600
bump''. This unidentified emission feature has been noted in
earlier studies, e.g., Wilkes (1984) and Boyle (1990). Our
analysis on the composite spectra clarifies that the
1600 ![]() bump is universally seen in spectra of
quasars. Laor et al. (1994) clearly presented this emission
feature in some low-redshift quasars. The 1600
bump is universally seen in spectra of
quasars. Laor et al. (1994) clearly presented this emission
feature in some low-redshift quasars. The 1600 ![]() bump of the sample of Laor et al. (1994) is characterized by
bump of the sample of Laor et al. (1994) is characterized by
![]() -24 000 km s-1 and
-24 000 km s-1 and
![]() km s-1 if it is one of
C IV
km s-1 if it is one of
C IV![]() 1549 components. They also found a very
redshifted broad component for Ly
1549 components. They also found a very
redshifted broad component for Ly![]() and
O VI
and
O VI![]() 1034 (see Table 4 of Laor et al. 1994),
which appears to support the interpretation that the
1600
1034 (see Table 4 of Laor et al. 1994),
which appears to support the interpretation that the
1600 ![]() bump is one of C IV
bump is one of C IV![]() 1549
components. If this is the case, a slight negative
correlation between the flux ratio of the 1600
1549
components. If this is the case, a slight negative
correlation between the flux ratio of the 1600 ![]() bump to C IV
bump to C IV![]() 1549 and the quasar luminosity
(Fig. 25) may be due to some luminosity dependence of the
structure of the C IV
1549 and the quasar luminosity
(Fig. 25) may be due to some luminosity dependence of the
structure of the C IV![]() 1549-emitting region in
the BLR.
The 1600
1549-emitting region in
the BLR.
The 1600 ![]() bump may be, otherwise, a blueshifted
component of the He II
bump may be, otherwise, a blueshifted
component of the He II![]() 1640 emission. This
interpretation is inferred by the negative correlation of
the flux ratio of the 1600
1640 emission. This
interpretation is inferred by the negative correlation of
the flux ratio of the 1600 ![]() bump to
C IV
bump to
C IV![]() 1549 with the quasar luminosity, because
the He II/C IV ratio also shows the similar
negative correlation with the quasar luminosity (Fig. 25).
However similar blueshifted spectral profile should appear
for the emission lines with a similar ionization degree
such as C IV
1549 with the quasar luminosity, because
the He II/C IV ratio also shows the similar
negative correlation with the quasar luminosity (Fig. 25).
However similar blueshifted spectral profile should appear
for the emission lines with a similar ionization degree
such as C IV![]() 1549, which is not the case for
our composite quasar spectra. One possibility might be the
presence of outflowing very dense gas clouds with a low
ionization parameter. As shown in Fig. 28, gas clouds
with low
1549, which is not the case for
our composite quasar spectra. One possibility might be the
presence of outflowing very dense gas clouds with a low
ionization parameter. As shown in Fig. 28, gas clouds
with low ![]() and high n radiate He II
and high n radiate He II![]() 1640
emission, but do not radiate the C IV
1640
emission, but do not radiate the C IV![]() 1549
emission. This idea could be tested by examining velocity
profiles of the other transition of He II. Although the
He II Fowler lines (
1549
emission. This idea could be tested by examining velocity
profiles of the other transition of He II. Although the
He II Fowler lines (![]() 4686,
4686, ![]() 3203, ...) may be
difficult to investigate due to their blending with the strong
Fe II multiplet emission, the He II Pickering lines,
especially He II
3203, ...) may be
difficult to investigate due to their blending with the strong
Fe II multiplet emission, the He II Pickering lines,
especially He II![]() 10124 may be useful to perform
this test.
Alternatively, the 1600
10124 may be useful to perform
this test.
Alternatively, the 1600 ![]() bump may be caused by the
UV Fe II multiplet emission. Sometimes at
bump may be caused by the
UV Fe II multiplet emission. Sometimes at
![]()
![]() ,
the Fe II feature is seen in
emission in quasars (e.g., Marziani et al. 1996;
Vestergaard & Wilkes 2001; Vestergaard & Peterson 2005) or in
absorption in low-ionization BALs (e.g., Hall et al. 2002).
As for the sample of Laor et al. (1994), the quasars with a
stronger UV Fe II multiplet emission appear to show also
stronger 1600
,
the Fe II feature is seen in
emission in quasars (e.g., Marziani et al. 1996;
Vestergaard & Wilkes 2001; Vestergaard & Peterson 2005) or in
absorption in low-ionization BALs (e.g., Hall et al. 2002).
As for the sample of Laor et al. (1994), the quasars with a
stronger UV Fe II multiplet emission appear to show also
stronger 1600 ![]() bump, which may support the
interpretation that the 1600
bump, which may support the
interpretation that the 1600 ![]() bump is also a
part of the UV Fe II multiplet emission.
The only problem with the Fe II scenario is the
interpretation of the anti-correlation of
(1600
bump is also a
part of the UV Fe II multiplet emission.
The only problem with the Fe II scenario is the
interpretation of the anti-correlation of
(1600 ![]() bump)/C IV with luminosity, which is not
seen in other low-ionization lines.
bump)/C IV with luminosity, which is not
seen in other low-ionization lines.
In order to investigate the properties of BLR gas clouds as a
function of quasar luminosity and redshift, we made
composite spectra of the SDSS DR2 quasars in the ranges of
![]() and
and
![]() for
each luminosity and redshift bin with
for
each luminosity and redshift bin with
![]() mag
and
mag
and
![]() .
By analyzing these composite spectra, we obtained the
following results.
.
By analyzing these composite spectra, we obtained the
following results.
Acknowledgements
Funding for the creation and distribution of the SDSS Archive has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the U.S. Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Korean Scientist Group, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, University of Pittsburgh, Princeton University, the United States Naval Observatory, and the University of Washington. We thank Gary Ferland for providing his excellent photoionization code Cloudy to the public. We also acknowledge the anonymous referee and M. Vestergaard for their useful comments. The numerical calculations in this work were performed partly with computer facilities in Astronomical Institute, Tohoku University. TN acknowledges financial support from the Japan Society for the Promotion of Science (JSPS) through JSPS Research Fellowships for Young Scientists. RM acknowledges financial support from MIUR under grant PRIN-03-02-23.
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f02.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg125.gif) |
Figure 2:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f03.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg126.gif) |
Figure 3:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f04.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg127.gif) |
Figure 4:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f05.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg128.gif) |
Figure 5:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f06.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg129.gif) |
Figure 6:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f07.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg130.gif) |
Figure 7:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f08.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg131.gif) |
Figure 8:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f09.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg132.gif) |
Figure 9:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f10.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg133.gif) |
Figure 10:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f11.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg134.gif) |
Figure 11:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f12.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg135.gif) |
Figure 12:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f13.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg136.gif) |
Figure 13:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f14.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg137.gif) |
Figure 14:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm]{4024f15.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg138.gif) |
Figure 15:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f16.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg139.gif) |
Figure 16:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f17.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg140.gif) |
Figure 17:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f18.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg141.gif) |
Figure 18:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f19.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg142.gif) |
Figure 19:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f20.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg143.gif) |
Figure 20:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{4024f21.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg144.gif) |
Figure 21:
Same as Fig. 1 but for the composite spectrum of
quasars with
|
![\begin{figure}
\par\includegraphics[angle=-90,width=16.5cm,clip]{4024f23.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg145.gif) |
Figure 23:
Measured flux ratios as a function of absolute B magnitude.
Open circles, squares, triangles, pluses, and stars denote the
composite spectra for
|
![\begin{figure}
\par\includegraphics[angle=-90,width=15.5cm,clip]{4024f24.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg146.gif) |
Figure 24:
Flux ratios normalized by the value measured on
composite spectra at
|
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{4024f25.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg147.gif) |
Figure 25:
Flux ratios normalized by the value measured on
composite spectra at
|
![\begin{figure}
\par\includegraphics[angle=90,width=14.4cm,clip]{4024f31.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg148.gif) |
Figure 31: Same as Fig. 1 but for the individual spectrum of SDSS J085417.6+532735 (z=2.42, MB = -28.6), not for quasar composite spectrum. |
![\begin{figure}
\par\includegraphics[angle=90,width=14.4cm,clip]{4024f32.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg149.gif) |
Figure 32: Same as Fig. 31 but for SDSS J080342.0+302254 (z=2.03, MB = -28.9). |
![\begin{figure}
\par\includegraphics[angle=90,width=14.5cm,clip]{4024f33.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg150.gif) |
Figure 33: Same as Fig. 31 but for SDSS J154359.4+535903 (z=2.37, MB = -28.5). |
![\begin{figure}
\par\includegraphics[angle=-90,width=16.5cm,clip]{4024f34.eps}
\end{figure}](/articles/aa/full/2006/07/aa4024-05/Timg151.gif) |
Figure 34:
Examples of the estimated local continuum (dotted lines) for
a few lines. The composite spectrum used here is
for quasars at
|
| Line |
|
|
|
|
|
| N V |
0.506 |
0.717 |
0.887 |
0.983 |
1.144 |
| Si II |
0.089 |
0.126 |
0.140 |
0.176 |
0.222 |
| O I Si II |
0.061 |
0.081 |
0.086 |
0.085 |
0.145 |
| C II |
0.033 |
0.047 |
0.052 |
0.050 |
0.089 |
| Si IV |
0.111 |
0.027 |
0.001 |
0.033 |
-- |
| O IV] |
0.145 |
0.308 |
0.374 |
0.365 |
0.419 |
| N IV] |
0.017 |
0.013 |
0.015 |
0.020 |
-- |
| C IV |
1.000 |
1.000 |
1.000 |
1.000 |
1.000 |
| 1600 Å bump | 0.112 |
0.106 |
0.098 |
0.097 |
0.060 |
| He II |
0.147 |
0.152 |
0.149 |
0.140 |
0.133 |
| O III] |
0.077 |
0.083 |
0.072 |
0.083 |
0.104 |
| Al II |
0.010 |
0.010 |
0.022 |
0.018 |
-- |
| Al III |
0.064 |
0.092 |
0.105 |
0.124 |
0.146 |
| Si III] |
0.093 |
0.118 |
0.127 |
0.129 |
0.110 |
| C III] |
0.285 |
0.326 |
0.326 |
0.348 |
0.395 |
| Line |
|
|
|
|
|
| N V |
0.561 |
0.578 |
0.858 |
1.004 |
1.248 |
| Si II |
0.160 |
0.117 |
0.149 |
0.194 |
0.210 |
| O I + Si II |
0.121 |
0.089 |
0.095 |
0.119 |
0.112 |
| C II |
0.065 |
0.037 |
0.055 |
0.059 |
0.074 |
| Si IV |
0.052 |
0.160 |
-- | -- | -- |
| O IV] |
0.202 |
0.092 |
0.360 |
0.401 |
0.462 |
| N IV] |
0.021 |
0.029 |
0.022 |
0.019 |
0.012 |
| C IV |
1.000 |
1.000 |
1.000 |
1.000 |
1.000 |
| 1600 Å bump | 0.125 |
0.111 |
0.103 |
0.092 |
0.100 |
| He II |
0.151 |
0.146 |
0.151 |
0.143 |
0.125 |
| O III] |
0.087 |
0.083 |
0.093 |
0.086 |
0.096 |
| Al II |
-- | 0.015 |
0.013 |
0.017 |
-- |
| Al III |
0.078 |
0.071 |
0.102 |
0.109 |
0.165 |
| Si III] |
0.070 |
0.063 |
0.108 |
0.152 |
0.204 |
| C III] |
0.375 |
0.351 |
0.354 |
0.328 |
0.331 |
| Line |
|
|
|
|
| N V |
0.635 |
0.819 |
1.034 |
0.979 |
| Si II |
0.126 |
0.161 |
0.183 |
0.198 |
| O I + Si II |
0.090 |
0.095 |
0.109 |
0.094 |
| C II |
0.050 |
0.049 |
0.055 |
0.039 |
| Si IV |
0.102 |
0.043 |
0.075 |
-- |
| O IV] |
0.176 |
0.286 |
0.327 |
0.370 |
| N IV] |
0.030 |
0.023 |
0.019 |
0.045 |
| C IV |
1.000 |
1.000 |
1.000 |
1.000 |
| 1600 Å bump | 0.117 |
0.117 |
0.099 |
0.083 |
| He II |
0.148 |
0.148 |
0.148 |
0.102 |
| O III] |
0.084 |
0.092 |
0.078 |
0.088 |
| Al II |
0.027 |
0.019 |
0.030 |
0.012 |
| Al III |
0.072 |
0.109 |
0.126 |
0.117 |
| Si III] |
0.068 |
0.112 |
0.105 |
0.134 |
| C III] |
0.337 |
0.321 |
0.379 |
0.281 |
| Line |
|
|
|
|
| N V |
0.617 |
0.856 |
1.062 |
1.001 |
| Si II |
0.129 |
0.156 |
0.194 |
0.083 |
| O I + Si II |
0.098 |
0.105 |
0.115 |
0.180 |
| C II |
0.030 |
0.051 |
0.062 |
0.105 |
| Si IV |
0.196 |
-- | -- | 0.024 |
| O IV] |
0.065 |
0.347 |
0.395 |
0.398 |
| N IV] |
0.038 |
0.025 |
0.016 |
0.031 |
| C IV |
1.000 |
1.000 |
1.000 |
1.000 |
| 1600 Å bump | 0.106 |
0.113 |
0.100 |
0.032 |
| He II |
0.153 |
0.145 |
0.128 |
0.108 |
| O III] |
0.081 |
0.083 |
0.089 |
0.056 |
| Al II |
0.016 |
0.017 |
-- | -- |
| Al III |
0.084 |
0.098 |
0.121 |
0.124 |
| Si III] |
0.066 |
0.122 |
0.186 |
0.193 |
| C III] |
0.355 |
0.332 |
0.343 |
0.426 |
| Line |
|
|
|
| N V |
0.724 |
0.933 |
1.075 |
| Si II |
0.251 |
0.249 |
0.217 |
| O I + Si II |
0.148 |
0.146 |
0.134 |
| C II |
0.067 |
0.068 |
0.064 |
| Si IV |
0.205 |
0.379 |
0.055 |
| O IV] |
0.144 |
0.004 |
0.354 |
| N IV] |
0.019 |
0.010 |
0.007 |
| C IV |
1.000 |
1.000 |
1.000 |
| 1600 Å bump | 0.075 |
0.070 |
0.061 |
| He II |
0.132 |
0.095 |
0.095 |
| O III] |
0.048 |
0.064 |
0.029 |
| Al II |
0.000 |
-- | 0.046 |
| Redshift | Magnitude | Line | Velocity Shift | Profile Parameter |
|
|
| (km s-1) | (km s-1) | |||||
|
|
|
HIL | -464.9 |
117.30 |
99.37 |
3858 |
| LIL | -83.4 |
114.49 |
119.60 |
3550 | ||
|
|
HIL | -495.6 |
112.90 |
85.50 |
4264 | |
| LIL | +111.5 |
106.01 |
110.53 |
3838 | ||
|
|
HIL | -446.5 |
110.31 |
79.98 |
4474 | |
| LIL | +308.1 |
106.49 |
109.75 |
3842 | ||
|
|
HIL | -327.0 |
114.32 |
77.77 |
4480 | |
| LIL | +484.8 |
101.64 |
104.12 |
4038 | ||
|
|
HIL | -583.7 |
106.74 |
80.08 |
4535 | |
| LIL | +153.3 |
93.17 |
105.50 |
4199 | ||
|
|
|
HIL | -390.6 |
128.57 |
117.31 |
3384 |
| LIL | -170.7 |
115.80 |
125.72 |
3445 | ||
|
|
HIL | -354.7 |
127.48 |
106.94 |
3568 | |
| LIL | +4.6 |
125.05 |
116.90 |
3436 | ||
|
|
HIL | -371.4 |
112.18 |
82.69 |
4358 | |
| LIL | +259.9 |
101.31 |
103.77 |
4051 | ||
|
|
HIL | -451.1 |
109.93 |
74.99 |
4653 | |
| LIL | +571.5 |
109.82 |
102.59 |
3914 | ||
|
|
HIL | -535.5 |
108.21 |
73.18 |
4751 | |
| LIL | +737.3 |
104.08 |
95.22 |
4175 | ||
|
|
|
HIL | -507.0 |
122.96 |
98.43 |
3795 |
| LIL | -186.5 |
119.09 |
111.70 |
3602 | ||
|
|
HIL | -576.9 |
119.72 |
89.27 |
4056 | |
| LIL | -20.1 |
106.02 |
119.36 |
3699 | ||
|
|
HIL | -549.8 |
118.15 |
74.78 |
4528 | |
| LIL | +16.9 |
110.84 |
102.22 |
3904 | ||
|
|
HIL | -298.9 |
126.01 |
80.60 |
4218 | |
| LIL | +763.3 |
110.34 |
103.28 |
3891 | ||
|
|
|
HIL | -644.7 |
126.18 |
110.47 |
3524 |
| LIL | -350.6 |
124.67 |
124.82 |
3329 | ||
|
|
HIL | -588.7 |
116.88 |
85.67 |
4196 | |
| LIL | +263.9 |
111.61 |
103.73 |
3861 | ||
|
|
HIL | -507.8 |
120.30 |
76.28 |
4441 | |
| LIL | +433.2 |
99.75 |
114.15 |
3902 | ||
|
|
HIL | -5.3 |
109.58 |
88.25 |
4245 | |
| LIL | +553.2 |
116.68 |
115.84 |
3572 | ||
|
|
|
HIL | -625.7 |
133.03 |
137.22 |
3073 |
| LIL | -145.0 |
89.42 |
86.79 |
4716 | ||
|
|
HIL | -634.4 |
116.43 |
91.71 |
4044 | |
| LIL | +169.8 |
123.05 |
76.44 |
4397 | ||
|
|
HIL | -262.2 |
115.83 |
78.54 |
4431 | |
| LIL | -287.4 |
111.97 |
91.26 |
4127 | ||
a Instrumental broadening was corrected by assuming that the instrumental width of 150 km s-1.
| Line Ratio | slope |
|
|
| vs. redshift | |||
| N V/C IV | -0.000 |
+0.05 |
|
| Si II/C IV | +0.042 |
+0.47 |
|
| (O I+Si II)/C IV | +0.086 |
+0.66 |
|
| C II/C IV | +0.028 |
+0.34 |
|
| (Si IV+O IV)/C IV | -0.003 |
+0.12 |
|
| (1600 |
-0.076 |
-0.20 |
|
| He II/C IV | -0.057 |
-0.59 |
|
| (O III]+Al II)/C II | -0.085 |
-0.31 |
|
| Al III/C IV | -0.030 |
-0.37 |
|
| Si III]/C IV | +0.007 |
-0.07 |
|
| C III]/C IV | +0.002 |
+0.19 |
|
| N V/He II | +0.057 |
+0.32 |
|
| vs. absolute B magnitude | |||
| N V/C IV | +0.082 |
+0.95 |
|
| Si II/C IV | +0.039 |
+0.53 |
|
| (O I+Si II)/C IV | +0.039 |
+0.48 |
|
| C II/C IV | +0.059 |
+0.50 |
|
| (Si IV+O IV)/C IV | +0.059 |
+0.95 |
|
| (1600 |
-0.068 |
-0.88 |
|
| He II/C IV | -0.031 |
-0.70 |
|
| (O III]+Al II)/C II | -0.001 |
+0.10 |
|
| Al III/C IV | +0.076 |
+0.95 |
|
| Si III]/C IV | +0.088 |
+0.77 |
|
| C III]/C IV | +0.009 |
+0.16 |
|
| N V/He II | +0.113 |
+0.97 |
|
|
a
Spearman rank-order correlation coefficient. b Probability of the data being consistent with the null hypothesis that the flux ratio is not correlated with redshift or absolute B magnitude. |
| Line Ratio |
|
|
|
|
|
|
| SED with a large UV thermal bump | ||||||
| N V/C IV | 0.019 | 0.044 | 0.092 | 0.199 | 0.439 | 0.712 |
| Si II/C IV | 0.001 | 0.002 | 0.003 | 0.005 | 0.010 | 0.017 |
| C II/C IV | 0.021 | 0.034 | 0.056 | 0.105 | 0.224 | 0.364 |
| Si IV/C IV | 0.056 | 0.075 | 0.104 | 0.158 | 0.248 | 0.329 |
| O IV]/C IV | 0.050 | 0.043 | 0.045 | 0.058 | 0.088 | 0.115 |
| He II/C IV | 0.198 | 0.176 | 0.183 | 0.211 | 0.235 | 0.231 |
| O III]/C IV | 0.059 | 0.085 | 0.124 | 0.193 | 0.290 | 0.353 |
| Al II/C IV | 0.003 | 0.005 | 0.008 | 0.014 | 0.029 | 0.049 |
| Al III/C IV | 0.010 | 0.016 | 0.027 | 0.048 | 0.095 | 0.152 |
| Si III]/C IV | 0.037 | 0.059 | 0.090 | 0.149 | 0.252 | 0.349 |
| C III]/C IV | 0.038 | 0.068 | 0.157 | 0.361 | 0.562 | 0.604 |
| SED with a small UV thermal bump | ||||||
| N V/C IV | 0.024 | 0.054 | 0.108 | 0.222 | 0.499 | 0.837 |
| Si II/C IV | 0.002 | 0.002 | 0.003 | 0.005 | 0.010 | 0.017 |
| C II/C IV | 0.024 | 0.037 | 0.060 | 0.103 | 0.199 | 0.317 |
| Si IV/C IV | 0.059 | 0.078 | 0.111 | 0.159 | 0.243 | 0.320 |
| O IV]/C IV | 0.057 | 0.047 | 0.048 | 0.056 | 0.080 | 0.106 |
| He II/C IV | 0.189 | 0.164 | 0.170 | 0.181 | 0.186 | 0.178 |
| O III]/C IV | 0.064 | 0.088 | 0.127 | 0.182 | 0.259 | 0.322 |
| Al II/C IV | 0.004 | 0.005 | 0.009 | 0.015 | 0.030 | 0.051 |
| Al III/C IV | 0.012 | 0.019 | 0.031 | 0.052 | 0.101 | 0.168 |
| Si III]/C IV | 0.042 | 0.064 | 0.100 | 0.157 | 0.266 | 0.375 |
| C III]/C IV | 0.045 | 0.081 | 0.185 | 0.330 | 0.474 | 0.534 |
| Line Ratio | our compositea | Vanden Berk et al. (2001) | |
| local cont. | Eq. (1)b | local cont. | |
| N V/C IV | 0.097 |
0.506 |
0.097 |
| Si II/C IV | 0.012 |
0.089 |
0.012 |
| He II/C IV | 0.027 |
0.147 |
0.021 |
| Al III/C IV | 0.016 |
0.064 |
0.013 |
| Si III]/C IV | 0.006 |
0.093 |
0.006 |
| C III]/C IV | 0.424 |
0.285 |
0.630 |
|
a The quasar composite spectrum for
b The given values are the same as those in Table 3. |
| Parameter | Obs. | Err.a | Modelsb | |
|
|
||||
| 2.0 | 2.0 | |||
| -1.00 | -1.17 | |||
| -1.00 | -1.66 | |||
| N V/C IV | 0.506 | 0.025 | 0.222 | 0.420 |
| (O I+Si II)/C IV | 0.061 | 0.010 | 0.091 | 0.041 |
| C II/C IV | 0.033 | 0.010 | 0.103 | 0.087 |
| (Si IV+O IV])/C IV | 0.256 | 0.013 | 0.215 | 0.252 |
| N IV]/C IV | 0.016 | 0.010 | 0.062 | 0.066 |
| He II/C IV | 0.147 | 0.010 | 0.181 | 0.203 |
| (O III]+Al II)/C IV | 0.088 | 0.010 | 0.196 | 0.176 |
| Al III/C IV | 0.064 | 0.010 | 0.052 | 0.046 |
| Si III]/C IV | 0.093 | 0.010 | 0.157 | 0.085 |
| C III]/C IV | 0.285 | 0.014 | 0.330 | 0.249 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.08 | |||
| -1.00 | -1.51 | |||
| N V/C IV | 0.717 | 0.036 | 0.499 | 0.776 |
| (O I+Si II)/C IV | 0.081 | 0.010 | 0.163 | 0.089 |
| C II/C IV | 0.047 | 0.010 | 0.199 | 0.187 |
| (Si IV+O IV])/C IV | 0.334 | 0.017 | 0.322 | 0.409 |
| N IV]/C IV | 0.013 | 0.010 | 0.152 | 0.148 |
| He II/C IV | 0.152 | 0.010 | 0.186 | 0.197 |
| (O III]+Al II)/C IV | 0.093 | 0.010 | 0.289 | 0.275 |
| Al III/C IV | 0.092 | 0.010 | 0.101 | 0.101 |
| Si III]/C IV | 0.117 | 0.010 | 0.266 | 0.163 |
| C III]/C IV | 0.326 | 0.016 | 0.474 | 0.332 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.10 | |||
| -1.00 | -1.61 | |||
| N V/C IV | 0.887 | 0.044 | 0.499 | 0.843 |
| (O I+Si II)/C IV | 0.086 | 0.010 | 0.163 | 0.078 |
| C II/C IV | 0.052 | 0.010 | 0.199 | 0.184 |
| (Si IV+O IV])/C IV | 0.375 | 0.019 | 0.322 | 0.424 |
| N IV]/C IV | 0.015 | 0.010 | 0.152 | 0.150 |
| He II/C IV | 0.149 | 0.010 | 0.186 | 0.200 |
| (O III]+Al II)/C IV | 0.094 | 0.010 | 0.289 | 0.274 |
| Al III/C IV | 0.105 | 0.010 | 0.101 | 0.099 |
| Si III]/C IV | 0.127 | 0.010 | 0.266 | 0.148 |
| C III]/C IV | 0.326 | 0.016 | 0.474 | 0.314 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.11 | |||
| -1.00 | -1.63 | |||
| N V/C IV | 0.983 | 0.049 | 0.499 | 0.858 |
| (O I+Si II)/C IV | 0.085 | 0.010 | 0.163 | 0.076 |
| C II/C IV | 0.050 | 0.010 | 0.199 | 0.184 |
| (Si IV+O IV])/C IV | 0.398 | 0.020 | 0.322 | 0.427 |
| N IV]/C IV | 0.020 | 0.010 | 0.152 | 0.150 |
| He II/C IV | 0.140 | 0.010 | 0.186 | 0.201 |
| (O III]+Al II)/C IV | 0.101 | 0.010 | 0.289 | 0.275 |
| Al III/C IV | 0.124 | 0.010 | 0.101 | 0.098 |
| Si III]/C IV | 0.130 | 0.010 | 0.266 | 0.145 |
| C III]/C IV | 0.348 | 0.017 | 0.474 | 0.311 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.06 | |||
| -1.00 | -1.50 | |||
| N V/C IV | 1.145 | 0.057 | 0.499 | 0.770 |
| (O I+Si II)/C IV | 0.145 | 0.010 | 0.163 | 0.091 |
| C II/C IV | 0.089 | 0.010 | 0.199 | 0.189 |
| (Si IV+O IV])/C IV | 0.419 | 0.021 | 0.322 | 0.413 |
| N IV]/C IV | 0.000 | 0.010 | 0.152 | 0.144 |
| He II/C IV | 0.133 | 0.010 | 0.186 | 0.198 |
| (O III]+Al II)/C IV | 0.104 | 0.010 | 0.289 | 0.272 |
| Al III/C IV | 0.146 | 0.010 | 0.101 | 0.105 |
| Si III]/C IV | 0.110 | 0.010 | 0.266 | 0.163 |
| C III]/C IV | 0.395 | 0.020 | 0.474 | 0.318 |
|
a Errors adopted for carrying out model fittings.
Values are changed from those presented in
Table 3; see text for details. b Model predictions with fixed |
| Parameter | Obs. | Err.a | Modelsb | |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.04 | |||
| -1.00 | -1.23 | |||
| N V/C IV | 0.561 | 0.028 | 0.499 | 0.608 |
| (O I+Si II)/C IV | 0.121 | 0.010 | 0.163 | 0.122 |
| C II/C IV | 0.065 | 0.010 | 0.199 | 0.190 |
| (Si IV+O IV])/C IV | 0.254 | 0.013 | 0.322 | 0.355 |
| N IV]/C IV | 0.021 | 0.010 | 0.152 | 0.152 |
| He II/C IV | 0.151 | 0.010 | 0.186 | 0.187 |
| (O III]+Al II)/C IV | 0.087 | 0.010 | 0.289 | 0.285 |
| Al III/C IV | 0.078 | 0.010 | 0.101 | 0.099 |
| Si III]/C IV | 0.070 | 0.010 | 0.266 | 0.219 |
| C III]/C IV | 0.375 | 0.019 | 0.474 | 0.423 |
|
|
||||
| 5.0 | 2.0 | |||
| -1.00 | -1.17 | |||
| -1.00 | -1.64 | |||
| N V/C IV | 0.578 | 0.029 | 0.499 | 0.407 |
| (O I+Si II)/C IV | 0.089 | 0.010 | 0.163 | 0.041 |
| C II/C IV | 0.037 | 0.010 | 0.199 | 0.086 |
| (Si IV+O IV])/C IV | 0.252 | 0.013 | 0.322 | 0.248 |
| N IV]/C IV | 0.029 | 0.010 | 0.152 | 0.067 |
| He II/C IV | 0.147 | 0.010 | 0.186 | 0.200 |
| (O III]+Al II)/C IV | 0.098 | 0.010 | 0.289 | 0.178 |
| Al III/C IV | 0.071 | 0.010 | 0.101 | 0.045 |
| Si III]/C IV | 0.063 | 0.010 | 0.266 | 0.087 |
| C III]/C IV | 0.351 | 0.018 | 0.474 | 0.258 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.11 | |||
| -1.00 | -1.58 | |||
| N V/C IV | 0.858 | 0.043 | 0.499 | 0.820 |
| (O I+Si II)/C IV | 0.095 | 0.010 | 0.163 | 0.081 |
| C II/C IV | 0.055 | 0.010 | 0.199 | 0.183 |
| (Si IV+O IV])/C IV | 0.360 | 0.018 | 0.322 | 0.413 |
| N IV]/C IV | 0.022 | 0.010 | 0.152 | 0.153 |
| He II/C IV | 0.151 | 0.010 | 0.289 | 0.278 |
| (O III]+Al II)/C IV | 0.106 | 0.010 | 0.289 | 0.278 |
| Al III/C IV | 0.101 | 0.010 | 0.101 | 0.096 |
| Si III]/C IV | 0.108 | 0.010 | 0.266 | 0.155 |
| C III]/C IV | 0.354 | 0.018 | 0.474 | 0.335 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.07 | |||
| -1.00 | -1.54 | |||
| N V/C IV | 1.004 | 0.050 | 0.499 | 0.800 |
| (O I+Si II)/C IV | 0.119 | 0.010 | 0.163 | 0.086 |
| C II/C IV | 0.059 | 0.010 | 0.199 | 0.188 |
| (Si IV+O IV])/C IV | 0.401 | 0.020 | 0.322 | 0.421 |
| N IV]/C IV | 0.019 | 0.010 | 0.152 | 0.144 |
| He II/C IV | 0.143 | 0.010 | 0.186 | 0.199 |
| (O III]+Al II)/C IV | 0.104 | 0.010 | 0.289 | 0.271 |
| Al III/C IV | 0.109 | 0.010 | 0.101 | 0.104 |
| Si III]/C IV | 0.152 | 0.010 | 0.266 | 0.155 |
| C III]/C IV | 0.328 | 0.016 | 0.474 | 0.309 |
|
|
||||
| 10.0 | 10.0 | |||
| -1.00 | -1.03 | |||
| -1.00 | -1.53 | |||
| N V/C IV | 1.248 | 0.062 | 0.837 | 1.191 |
| (O I+Si II)/C IV | 0.112 | 0.010 | 0.250 | 0.122 |
| C II/C IV | 0.074 | 0.010 | 0.317 | 0.290 |
| (Si IV+O IV])/C IV | 0.462 | 0.023 | 0.426 | 0.586 |
| N IV]/C IV | 0.012 | 0.010 | 0.298 | 0.251 |
| He II/C IV | 0.125 | 0.010 | 0.178 | 0.180 |
| (O III]+Al II)/C IV | 0.096 | 0.010 | 0.373 | 0.370 |
| Al III/C IV | 0.165 | 0.010 | 0.168 | 0.175 |
| Si III]/C IV | 0.204 | 0.010 | 0.375 | 0.211 |
| C III]/C IV | 0.331 | 0.017 | 0.534 | 0.323 |
|
a
Errors adopted for carrying out model fittings.
Values are changed from those presented in
Table 4; see text for details. b Model predictions with fixed |
| Parameter | Obs. | Err.a | Modelsb | |
|
|
||||
| 5.0 | 2.0 | |||
| -1.00 | -1.17 | |||
| -1.00 | -1.68 | |||
| N V/C IV | 0.635 | 0.032 | 0.499 | 0.433 |
| (O I+Si II)/C IV | 0.090 | 0.010 | 0.163 | 0.040 |
| C II/C IV | 0.050 | 0.010 | 0.199 | 0.089 |
| (Si IV+O IV])/C IV | 0.279 | 0.014 | 0.322 | 0.257 |
| N IV]/C IV | 0.030 | 0.010 | 0.152 | 0.066 |
| He II/C IV | 0.148 | 0.010 | 0.186 | 0.206 |
| (O III]+Al II)/C IV | 0.111 | 0.010 | 0.289 | 0.174 |
| Al III/C IV | 0.072 | 0.010 | 0.101 | 0.047 |
| Si III]/C IV | 0.068 | 0.010 | 0.266 | 0.083 |
| C III]/C IV | 0.336 | 0.017 | 0.474 | 0.240 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.07 | |||
| -1.00 | -1.54 | |||
| N V/C IV | 0.819 | 0.041 | 0.499 | 0.795 |
| (O I+Si II)/C IV | 0.095 | 0.010 | 0.163 | 0.086 |
| C II/C IV | 0.049 | 0.010 | 0.199 | 0.188 |
| (Si IV+O IV])/C IV | 0.329 | 0.016 | 0.322 | 0.418 |
| N IV]/C IV | 0.023 | 0.010 | 0.152 | 0.145 |
| He II/C IV | 0.148 | 0.010 | 0.186 | 0.199 |
| (O III]+Al II)/C IV | 0.111 | 0.010 | 0.289 | 0.272 |
| Al III/C IV | 0.108 | 0.010 | 0.101 | 0.103 |
| Si III]/C IV | 0.112 | 0.010 | 0.266 | 0.157 |
| C III]/C IV | 0.321 | 0.016 | 0.474 | 0.314 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.11 | |||
| -1.00 | -1.61 | |||
| N V/C IV | 1.034 | 0.052 | 0.499 | 0.840 |
| (O I+Si II)/C IV | 0.109 | 0.010 | 0.163 | 0.078 |
| C II/C IV | 0.055 | 0.010 | 0.199 | 0.183 |
| (Si IV+O IV])/C IV | 0.402 | 0.020 | 0.322 | 0.420 |
| N IV]/C IV | 0.019 | 0.010 | 0.152 | 0.152 |
| He II/C IV | 0.148 | 0.010 | 0.186 | 0.200 |
| (O III]+Al II)/C IV | 0.108 | 0.010 | 0.289 | 0.277 |
| Al III/C IV | 0.126 | 0.010 | 0.101 | 0.097 |
| Si III]/C IV | 0.105 | 0.010 | 0.266 | 0.149 |
| C III]/C IV | 0.379 | 0.019 | 0.474 | 0.323 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.06 | |||
| -1.00 | -1.61 | |||
| N V/C IV | 0.979 | 0.049 | 0.499 | 0.846 |
| (O I+Si II)/C IV | 0.094 | 0.010 | 0.163 | 0.080 |
| C II/C IV | 0.039 | 0.010 | 0.199 | 0.191 |
| (Si IV+O IV])/C IV | 0.370 | 0.018 | 0.322 | 0.443 |
| N IV]/C IV | 0.045 | 0.010 | 0.152 | 0.138 |
| He II/C IV | 0.102 | 0.010 | 0.186 | 0.203 |
| (O III]+Al II)/C IV | 0.100 | 0.010 | 0.289 | 0.263 |
| Al III/C IV | 0.117 | 0.010 | 0.101 | 0.109 |
| Si III]/C IV | 0.134 | 0.010 | 0.266 | 0.141 |
| C III]/C IV | 0.281 | 0.014 | 0.474 | 0.269 |
|
a
Errors adopted for carrying out model fittings.
Values are changed from those presented in
Table 5; see text for details. b Model predictions with fixed |
| Parameter | Obs. | Err.a | Modelsb | |
|
|
||||
| 5.0 | 2.0 | |||
| -1.00 | -1.13 | |||
| -1.00 | -1.60 | |||
| N V/C IV | 0.618 | 0.031 | 0.499 | 0.406 |
| (O I+Si II)/C IV | 0.098 | 0.010 | 0.163 | 0.045 |
| C II/C IV | 0.030 | 0.010 | 0.199 | 0.091 |
| (Si IV+O IV])/C IV | 0.261 | 0.013 | 0.322 | 0.255 |
| N IV]/C IV | 0.038 | 0.010 | 0.152 | 0.064 |
| He II/C IV | 0.153 | 0.010 | 0.186 | 0.202 |
| (O III]+Al II)/C IV | 0.097 | 0.010 | 0.289 | 0.175 |
| Al III/C IV | 0.084 | 0.010 | 0.101 | 0.049 |
| Si III]/C IV | 0.066 | 0.010 | 0.266 | 0.090 |
| C III]/C IV | 0.355 | 0.018 | 0.474 | 0.243 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.08 | |||
| -1.00 | -1.54 | |||
| N V/C IV | 0.856 | 0.043 | 0.499 | 0.796 |
| (O I+Si II)/C IV | 0.105 | 0.010 | 0.163 | 0.086 |
| C II/C IV | 0.051 | 0.010 | 0.199 | 0.186 |
| (Si IV+O IV])/C IV | 0.347 | 0.017 | 0.322 | 0.415 |
| N IV]/C IV | 0.025 | 0.010 | 0.152 | 0.148 |
| He II/C IV | 0.145 | 0.010 | 0.186 | 0.198 |
| (O III]+Al II)/C IV | 0.101 | 0.010 | 0.289 | 0.274 |
| Al III/C IV | 0.098 | 0.010 | 0.101 | 0.101 |
| Si III]/C IV | 0.122 | 0.010 | 0.266 | 0.158 |
| C III]/C IV | 0.332 | 0.017 | 0.474 | 0.323 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.07 | |||
| -1.00 | -1.50 | |||
| N V/C IV | 1.062 | 0.053 | 0.499 | 0.773 |
| (O I+Si II)/C IV | 0.115 | 0.010 | 0.163 | 0.089 |
| C II/C IV | 0.062 | 0.010 | 0.199 | 0.187 |
| (Si IV+O IV])/C IV | 0.395 | 0.020 | 0.322 | 0.410 |
| N IV]/C IV | 0.016 | 0.010 | 0.152 | 0.147 |
| He II/C IV | 0.128 | 0.010 | 0.186 | 0.197 |
| (O III]+Al II)/C IV | 0.089 | 0.010 | 0.289 | 0.274 |
| Al III/C IV | 0.122 | 0.010 | 0.101 | 0.102 |
| Si III]/C IV | 0.186 | 0.010 | 0.266 | 0.164 |
| C III]/C IV | 0.343 | 0.017 | 0.474 | 0.329 |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.02 | |||
| -1.00 | -1.28 | |||
| N V/C IV | 1.006 | 0.050 | 0.499 | 0.639 |
| (O I+Si II)/C IV | 0.180 | 0.010 | 0.163 | 0.118 |
| C II/C IV | 0.105 | 0.010 | 0.199 | 0.194 |
| (Si IV+O IV])/C IV | 0.421 | 0.021 | 0.322 | 0.377 |
| N IV]/C IV | 0.031 | 0.010 | 0.152 | 0.143 |
| He II/C IV | 0.108 | 0.010 | 0.186 | 0.194 |
| (O III]+Al II)/C IV | 0.056 | 0.010 | 0.289 | 0.276 |
| Al III/C IV | 0.124 | 0.010 | 0.101 | 0.107 |
| Si III]/C IV | 0.193 | 0.010 | 0.266 | 0.203 |
| C III]/C IV | 0.426 | 0.021 | 0.474 | 0.369 |
|
a Errors adopted for carrying out model fittings.
Values are changed from those presented in
Table 6; see text for details. b Model predictions with fixed |
| Parameter | Obs. | Err.a | Modelsb | |
|
|
||||
| 5.0 | 5.0 | |||
| -1.00 | -1.06 | |||
| -1.00 | -1.24 | |||
| N V/C IV | 0.724 | 0.036 | 0.499 | 0.614 |
| (O I+Si II)/C IV | 0.148 | 0.010 | 0.163 | 0.119 |
| C II/C IV | 0.067 | 0.010 | 0.199 | 0.188 |
| (Si IV+O IV])/C IV | 0.349 | 0.017 | 0.322 | 0.352 |
| N IV]/C IV | 0.019 | 0.010 | 0.152 | 0.155 |
| He II/C IV | 0.132 | 0.010 | 0.186 | 0.185 |
| (O III]+Al II)/C IV | 0.049 | 0.010 | 0.289 | 0.288 |
|
|
||||
| 10.0 | 5.0 | |||
| -1.00 | -1.03 | |||
| -1.00 | -1.40 | |||
| N V/C IV | 0.933 | 0.047 | 0.837 | 0.709 |
| (O I+Si II)/C IV | 0.146 | 0.010 | 0.250 | 0.103 |
| C II/C IV | 0.068 | 0.010 | 0.317 | 0.194 |
| (Si IV+O IV])/C IV | 0.383 | 0.019 | 0.426 | 0.404 |
| N IV]/C IV | 0.010 | 0.010 | 0.298 | 0.139 |
| He II/C IV | 0.095 | 0.010 | 0.178 | 0.198 |
| (O III]+Al II)/C IV | 0.064 | 0.010 | 0.373 | 0.269 |
|
|
||||
| 10.0 | 5.0 | |||
| -1.00 | -1.02 | |||
| -1.00 | -1.54 | |||
| N V/C IV | 1.075 | 0.054 | 0.837 | 0.805 |
| (O I+Si II)/C IV | 0.133 | 0.010 | 0.250 | 0.088 |
| C II/C IV | 0.064 | 0.010 | 0.317 | 0.197 |
| (Si IV+O IV])/C IV | 0.409 | 0.020 | 0.426 | 0.445 |
| N IV]/C IV | 0.007 | 0.010 | 0.298 | 0.130 |
| He II/C IV | 0.095 | 0.010 | 0.178 | 0.204 |
| (O III]+Al II)/C IV | 0.075 | 0.010 | 0.373 | 0.257 |
|
a Errors adopted for carrying out model fittings.
Values are changed from those presented in
Table 7; see text for details. b Model predictions with fixed |