A&A 443, 863-881 (2005)
DOI: 10.1051/0004-6361:20053115
M. Perucho1 - J. M. Martí1 - M. Hanasz2
1 - Departament d'Astronomia i Astrofísica,
Universitat de València, 46100 Burjassot, Spain
2 - Torun Centre for
Astronomy, Nicholas Copernicus University, 97-148
Piwnice k.Torunia, Poland
Received 22 March 2005 / Accepted 15 June 2005
Abstract
The linear and non-linear stability of sheared, relativistic
planar jets is studied by means of linear stability analysis and
numerical hydrodynamical simulations. Our results extend the previous
Kelvin-Hemlholtz stability studies for relativistic, planar jets in
the vortex sheet approximation performed by Perucho et al. (2004a, A&A, 427, 415; 2004b, A&A, 427, 431)
by including a shear layer between the jet and the external medium and
more general perturbations. The models considered span a wide range of
Lorentz factors (2.5-20) and internal energies
(
0.08 c2-60 c2) and are classified into three classes
according to the main characteristics of their long-term, non-linear
evolution. We observe a clear separation of these three groups in a
relativistic Mach-number Lorentz-factor plane. Jets with a low Lorentz
factor and small relativistic Mach number are disrupted after
saturation. Those with a large Lorentz factor and large relativistic
Mach number are the stablest, due to the appearance of short
wavelength resonant modes which generate local mixing and heating in
the shear layer around a fast, unmixed core, giving a plausible
solution for the problem of the long-term stability of relativistic
jets. A third group is present between them, including jets with
intermediate values of Lorentz factor and relativistic Mach number,
which are disrupted by a slow process of mixing favored by an
efficient and continuous conversion of kinetic into internal
energy. In the long term, all the models develop a distinct
transversal structure (shear/transition layers) as a consequence of KH
perturbation growth, depending on the class they belong to. The
properties of these shear layers are analyzed in connection with the
parameters of the original jet models.
Key words: galaxies: jets - hydrodynamics - instabilities
Transversal structure in extragalactic jets could be the natural consequence of current formation mechanisms (see, e.g., Sol et al. 1989; Celotti & Blandford 2000), in which an ultrarelativistic presumably electron/positron outflow from the high latitude region close to the spinning black hole (and powered by, e.g., the extraction of energy from the hole) is surrounded by a mildly relativistic, electron/proton, hydromagnetic outflow launched from the outer parts of the accretion disk. Recent numerical simulations of jet formation from black hole magnetospheres (Koide et al. 1997) also lead to outflows with two-layered shell structure consisting of inner, fast gas pressure driven jets surrounded by slower, magnetically dominated winds. On larger scales, shear layers (with distinct kinematical properties and magnetic field configurations) have been invoked in the past by several authors (Komissarov 1990; Laing 1996; Laing & Bridle 2002a,b) in order to account for a number of the observational characteristics of FR I radio sources. The model of De Young (1993) to explain the FRI/FRII morphological dichotomy is based on deceleration of the jet flow at the inner galactic core and the subsequent formation of turbulent shear layers in FRIs. Recently, Swain et al. (1998) found evidence of shear layers in FR II radio galaxies (3C 353), and Attridge et al. (1999) have inferred a two-component structure in the parsec-scale jet of the source 1055+018. On the other hand, first simulations of radio emission from three-dimensional relativistic jets with shear layers (Aloy et al. 2000) allowed several observational trends in parsec and kiloparsec jets to be interpreted: inhomogeneous distributions of apparent speeds within radio knots (Biretta et al. 1995); rails of low polarization along jets (as in 3C 353; Swain et al. 1998); top/down jet emission asymmetries in the blazar 1055+018 (Attridge et al. 1999). Stawarz & Ostrowski (2002) have studied the contribution to the radiative jet output from turbulent shear layers in large-scale jets.
Given all the pieces of theoretical and observational evidence
concerning the ubiquity of shear layers in extragalactic jets, it
appears natural to analyze their influence on the
dynamics and stability of relativistic jets. An attempt to investigate
the growth of the Kelvin-Helmholtz (KH) instability in some particular
class of sheared, cylindrical relativistic jets was pursued by
Birkinshaw (1991). However, this study is limited to the ordinary and
low-order reflection modes, and the domain of jet parameters
considered involves only marginally relativistic flows (beam flow
velocities ![]() 0.1 c; c is the speed of light) and
non-relativistic (jet, ambient) sound speeds (
0.1 c; c is the speed of light) and
non-relativistic (jet, ambient) sound speeds (![]() 0.01c). Other
approaches to linear analysis of the stability of relativistic
stratified jets (Hanasz & Sol 1996; Hardee & Hughes 2003) and
sheared, ultrarelativistic jets (Urpin 2002) have also been taken.
Several recent works combine linear analysis and hydrodynamical
simulations in the context of both relativistic jets (Rosen et al. 1999; Hardee 2000, 2001) and GRBs (Aloy et al. 2002).
0.01c). Other
approaches to linear analysis of the stability of relativistic
stratified jets (Hanasz & Sol 1996; Hardee & Hughes 2003) and
sheared, ultrarelativistic jets (Urpin 2002) have also been taken.
Several recent works combine linear analysis and hydrodynamical
simulations in the context of both relativistic jets (Rosen et al. 1999; Hardee 2000, 2001) and GRBs (Aloy et al. 2002).
In this paper, we focus on the study of the evolution of
relativistic (planar) flows with shear layers through the linear and
non-linear regimes relying on both linear, analytical stability
analysis and hydrodynamical numerical simulations. The present work
complements the one presented in Perucho et al. (2004a,b; hereafter,
Papers I and II, respectively), in which we characterized the effects of
relativistic dynamics and thermodynamics in the development of KH
instabilities in planar, relativistic jets in the vortex sheet
approximation. We used a more general setup for simulations with the
inclusion of a set of symmetric (pinching) and antisymmetric (helical)
sinusoidal perturbations in two dimensional slab jets and a thicker
shear layer (![]() 0.2 Rj) than that used to mimic vortex sheet
evolution. The use of slab jets allows for inclusion of helical
perturbations, which are known to be present in extragalactic
jets. Moreover, two dimensional simulations provide the possibility of
a much larger resolution than three dimensional ones. The aim of this
work is to study the stability properties of jets depending on their
initial parameters and the effect of shear layers in those
properties. We used the temporal approach, which allows for larger
resolution, and fixed two different grid sizes, depending on the
thermodynamical properties of jets, which are neither directly related nor
coupled to the wavelength of a specific mode, as was the case in
Papers I and II. Jet parameters are based on those of previous papers
for direct comparison. We generalized our results with simulations
where only one antisymmetric mode is perturbed (similar to
simulations in Paper I), and simulations of cylindrical jets, where several
modes are perturbed (as in simulations presented in this paper).
0.2 Rj) than that used to mimic vortex sheet
evolution. The use of slab jets allows for inclusion of helical
perturbations, which are known to be present in extragalactic
jets. Moreover, two dimensional simulations provide the possibility of
a much larger resolution than three dimensional ones. The aim of this
work is to study the stability properties of jets depending on their
initial parameters and the effect of shear layers in those
properties. We used the temporal approach, which allows for larger
resolution, and fixed two different grid sizes, depending on the
thermodynamical properties of jets, which are neither directly related nor
coupled to the wavelength of a specific mode, as was the case in
Papers I and II. Jet parameters are based on those of previous papers
for direct comparison. We generalized our results with simulations
where only one antisymmetric mode is perturbed (similar to
simulations in Paper I), and simulations of cylindrical jets, where several
modes are perturbed (as in simulations presented in this paper).
The plan of this paper is as follows. In Sect. 2 we describe the numerical simulations and present the parameters used in this paper. In Sect. 3 we describe our results concerning linear and nonlinear regimes of new simulations; we discuss them in Sect. 4 and present our conclusions in Sect. 5.
 |
The equations governing the evolution of a
relativistic perfect-fluid jet (see Paper I) are
The steady initial flow is 2D-planar and symmetric with respect to
the x=0 plane. The flow moves in the positive z direction. Our
simulations were performed in the so-called temporal approach, as in
Papers I and II. In this approach, the evolution of perturbations in a
periodical slice of an infinite jet is followed along the time. In
order to study the effects of shearing in the development of the
instability, we assumed a continuous transition between the jet and the
ambient (the same as the one considered by Ferrari et al. 1982). The
profiles of the axial velocity and proper rest-mass density across
this transition layer, vz(x) and ![]() ,
respectively, are given by
,
respectively, are given by
Following conclusions given in the Appendices of both
Papers I and II, the numerical resolution used was
![]() in the transversal direction times
in the transversal direction times
![]() in the axial direction. Note that we reduced the
transversal resolution with respect to the simulations in Papers I and
II. One reason for that were computational time limitations, as now our
grids are twice as large in the transversal direction as those used in
Paper I, since we are now combining symmetric and antisymmetric
structures. However, in the present simulations, transversal
resolution is not as critical as in the previous works, since we are
not interested in mimicking the evolution of instability in the
vortex sheet limit and therefore do not have steep shear
layers. The saving in transversal resolution allowed us to double
axial resolution, which affects the non-linear results (see Appendix
in Paper II). The physical sizes of grids are 8 Rj axially times
6 Rj transversally for hot jets (models D, see Table 1) and 16 Rj axially times 6 Rj transversally
for cold jets (models A and B in Table 1). The different axial
size is due to hot models having shorter unstable modes; see Sect. 3.1, where we show linear problem solutions for one cold
and one hot jet.
in the axial direction. Note that we reduced the
transversal resolution with respect to the simulations in Papers I and
II. One reason for that were computational time limitations, as now our
grids are twice as large in the transversal direction as those used in
Paper I, since we are now combining symmetric and antisymmetric
structures. However, in the present simulations, transversal
resolution is not as critical as in the previous works, since we are
not interested in mimicking the evolution of instability in the
vortex sheet limit and therefore do not have steep shear
layers. The saving in transversal resolution allowed us to double
axial resolution, which affects the non-linear results (see Appendix
in Paper II). The physical sizes of grids are 8 Rj axially times
6 Rj transversally for hot jets (models D, see Table 1) and 16 Rj axially times 6 Rj transversally
for cold jets (models A and B in Table 1). The different axial
size is due to hot models having shorter unstable modes; see Sect. 3.1, where we show linear problem solutions for one cold
and one hot jet.
Previous to these simulations, we performed several representative runs (B05, D05, B20, D20) with the aim of studying the evolution of models under single eigenmode perturbations in planar antisymmetric geometry, exciting the first reflection antisymmetric mode at its peak growth rate. These simulations were used to check the consistency of the numerical results in the linear phase with the linear stability analysis for relativistic, sheared flows. Discussion of the evolution of these models through the non-linear regime can be found in Appendix A. Tests were also performed in order to assess the difference in the evolution of linear and non-linear regimes using a general sinusoidal perturbation (to be used in this paper) and a superposition of eigenmodes, as done with the first body mode alone in Paper I. Results showed that structures and qualitative properties of the resulting flow were basically the same. This fact confirms that general perturbations excite eigenmodes of the system.
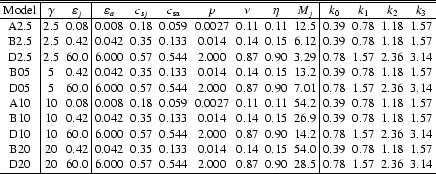
The parameters used in the simulations are shown in Table 1. We swept a wide range in Lorentz factors (from 2.5 to 20) and in specific internal jet energies (from 0.08 c2 to 60
c2) in order to obtain a global view of the response of different
initial data sets to perturbations. All the models correspond to a
single-component ideal gas with adiabatic exponent
![]() .
These parameters were chosen in order to study the stability regions
found in Paper II: Class I for cold and slow models, which were deeply
mixed and mass loaded; Class II for hot and fast jets, which were
slowly mixed in the nonlinear regime, progressively losing their
axial momentum; Class III for hot and slow jets, with properties
between Classes I and II, and Class IV for cold/warm and fast models,
which were the stablest in the nonlinear regime. We performed
simulations for models B05
.
These parameters were chosen in order to study the stability regions
found in Paper II: Class I for cold and slow models, which were deeply
mixed and mass loaded; Class II for hot and fast jets, which were
slowly mixed in the nonlinear regime, progressively losing their
axial momentum; Class III for hot and slow jets, with properties
between Classes I and II, and Class IV for cold/warm and fast models,
which were the stablest in the nonlinear regime. We performed
simulations for models B05![]() , B10, B20, D05,
D10, and D20 of Paper II, and added A2.5 (same thermodynamical properties as A05 in Paper II),
A10, B2.5, and D2.5. Models A2.5,
B2.5, and B05 correspond to regions of Class I
jets. Models D10 and D20 correspond to Class II,
D2.5 and D05 to Class III, and
A10, B10 and B20 belong to Class IV.
, B10, B20, D05,
D10, and D20 of Paper II, and added A2.5 (same thermodynamical properties as A05 in Paper II),
A10, B2.5, and D2.5. Models A2.5,
B2.5, and B05 correspond to regions of Class I
jets. Models D10 and D20 correspond to Class II,
D2.5 and D05 to Class III, and
A10, B10 and B20 belong to Class IV.
Perturbations we applied adding the following sinusoidal form to
transversal velocity, vx(x,z):
Numerical simulations were performed using a finite-difference code based on a high-resolution shock-capturing scheme which solves the equations of relativistic hydrodynamics written in conservation form (Martí et al. 1997, and references therein). Before performing the simulations, several improvements were made in the numerical code. In particular, the relativistic PPM routines (Martí & Müller 1996) were properly symmetrized. The code was recently parallelized using OMP directives. Simulations were performed with 4 processors on SGI 2000 and SGI Altix 3000 machines.
We introduced an adiabatic perturbation of the form ![]()
![]() to the flow Eqs. (1)-(3),
to the flow Eqs. (1)-(3), ![]() and kz (kx) being the
frequency and wavenumber of the perturbation along (across) the jet
flow. We followed the temporal approach, in which perturbations
grow in time, with real wavenumbers and complex frequencies, with the
imaginary part being the growth rate. By linearizing the equations
and eliminating the perturbations of rest mass density and flow
velocity, a second-order ordinary differential equation for the
pressure perturbation P1, is obtained (Birkinshaw 1991; Aloy et al. 2002)
and kz (kx) being the
frequency and wavenumber of the perturbation along (across) the jet
flow. We followed the temporal approach, in which perturbations
grow in time, with real wavenumbers and complex frequencies, with the
imaginary part being the growth rate. By linearizing the equations
and eliminating the perturbations of rest mass density and flow
velocity, a second-order ordinary differential equation for the
pressure perturbation P1, is obtained (Birkinshaw 1991; Aloy et al. 2002)
Linear stability analysis was performed for all models presented in Sect. 2, in the symmetric and antisymmetric cases. Figure 1 shows examples of solutions for the linear problem for sheared jets in models B05 and D20. Top panels in Fig. 1 show the (real part of) frequency as a function of wavenumber, and bottom panels show the imaginary part of frequency or growth rate, defined as the inverse of the time needed by a given mode to e-fold its amplitude, also as a function of wavenumber. Each mode is defined by its wavelength, frequency and growth rate.
From these results, we note that the individual reflection mode
solutions of the shear problem present lower growth rates for most
wavenumbers, especially in the large wavenumber limit, than do the
corresponding solutions in the vortex sheet case. This behaviour was
noticed for the first time by Ferrari et al. (1982) for the
first and second reflection modes in the non-relativistic limit. The
growth rate curves corresponding to a single nxth reflection mode
consists of a broad maximum at higher wavenumbers and a local peak
which is placed in the low wavenumber limit, near the marginal
stability point of a chosen reflection mode. Regarding the
relativistic case, while in the vortex-sheet limit the small
wavenumber peaks for individual modes are relatively unimportant
(since the maximum growth rates at these peaks are lower than those of
other unstable modes), while in the presence of the shear-layer they display
high growth rates for high order body modes. Therefore we shall call
these peaks the shear layer resonances. In
Fig. 2 we show the solution for four specific modes of
model D20, from
Fig. 1.
Low order body modes do not show high peaks
at maximum unstable wavelengths, whereas high order body modes
show peaks (shear layer resonances) at this maximum wavelength
and do not present broad maxima.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3115f2.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg69.gif) |
Figure 2: Specific modes of solutions shown in Fig. 1, symmetric solution for model D20. Dotted line: first body mode; dashed: second body mode; dash-dot: twentieth body mode; dash-triple dot: twenty-fifth body mode. Arows point to both the broad maxima and the small wavenumber peaks present in every single mode. Low wavenumber peaks of high order body modes show higher growth rates and are thus defined as (shear layer) resonances. |
| Model | wi,k0 | wi,k1 | wi,k2 | wi,k3 | Dominant | wi |
| Symm. |
Symm. |
Symm. |
Symm. |
|||
| A2.5 | 0.036 |
0.038 |
0.034 |
0.031 |
k0 | 0.030 |
| B2.5 | 0.042 |
0.070 |
0.066 |
0.073 |
k1, k2 | 0.070 |
| D2.5 | 0.046 |
0.131 |
0.210 |
0.142 |
k2, k1 | 0.200 |
| B05 | 0.037 |
0.037 |
0.036 |
0.034 |
k0, k1 | 0.035 |
| D05 | 0.068 |
0.085 |
0.100 |
0.068 |
k1, k2, k0 | 0.080 |
| A10 | 0.009 |
0.006 |
0.005 |
0.006 |
k0* | 0.004 (0.005) |
| B10 | 0.022 |
0.019 |
0.018 |
0.013 |
k0 | 0.020 |
| D10 | 0.034 |
0.041 |
0.044 |
0.051 |
k1, k2 | 0.040 |
| B20 | 0.011 |
0.009 |
0.007 |
0.009 |
k0* | 0.006 (0.008) |
| D20 | 0.018 |
0.020 |
0.022 |
0.027 |
k1, k0 | 0.016 |
From Eq. (7) we see that radial structure of perturbations depends on physical parameters of the flow, as well as on the given frequency and axial wavenumber of a given perturbation. Resonances are determined by this transversal structure, and therefore we should expect changes in their characteristics depending on the properties of the shear layer and physical parameters: i) a decrease of the jet Lorentz factor reduces the dominance of the growth rates of resonant modes with respect to ordinary and low order reflection modes; ii) a decrease in the specific internal energy of the jet causes resonances to appear at longer wavelengths; iii) further widening of the shear layer reduces the growth rates and the dominance of the shear-layer resonances, suggesting that there is an optimal width of the shear layer that maximizes the effect for a given set of jet parameters; the largest growth rate of resonant modes moves to smaller wavenumbers and lower order reflection modes; iv) perturbations with wavenumber higher than some limiting value (that decreases with the shear layer width) are significantly diminished (short-wavelength cut-off), consistent with previous non-relativistic results (Ferrari et al. 1982). The discovery of the shear layer resonances and their potential role in the long-term stability of relativistic jets is reported in Perucho et al. (2005).
Table 2 summarizes the properties of the linear phase in our simulations. The left part of the table (Cols. 2-9) gives the theoretical growth rates of the perturbed wavelengths, taken at the vertical lines in Fig. 1. The last column gives the values of the growth rate corresponding to the dominant wavelength as deduced from Fourier analysis of the transversal profiles of the rest mass density distribution in the jet. Note, however, that Fourier analysis can only give us information about wavelengths, but cannot distinguish between symmetric and antisymmetric modes. The growths of pressure, axial, and transversal velocity perturbations along the simulations are shown in Fig. 3.
Comparison of the evolution through the linear phase of the different models in the numerical simulations and from the linear stability analysis is summarized as follows:
Models A10 and B20, marked with an asterisk in Table 2, have fitted growth rates in the first part of the linear regime below the predicted values. Note that these models have the lower growth rates. After this initial phase, short harmonics start dominating the linear growth.
We have observed the appearance of fast growing, very short modes in models A10, B20, and D20, which are clearly associated to the resonant modes presented above in the previous section and which could have been excited as harmonics of the initially perturbed wavelengths. The same kind of resonant mode might have developed in model C20 of Paper II and caused the irregular linear growth found with respect to the rest of models. These modes generate a rich internal structure in the jet due to their large perpendicular wavenumber or, equivalently, short perpendicular wavelengths (characteristic of high order body modes). A direct comparison between the structure generated by these resonant modes in the numerical simulations and that coming from linear stability analysis can be seen in Fig. 4. In this figure, we display one snapshot from model D20 and the theoretical counterpart using one of those resonant modes. The upper plots correspond to the numerical simulation in the linear regime, where the signature of the initial perturbations (k0,k1,k2 and k3) are the oblique waves seen outside the jet. As seen in these plots, resonant modes grow to amplitudes larger than those of the long waves, as indicated by the black/white scale saturating precisely on the interface. The lower plots represent the theoretical structure that we would find if we had only excited a resonant mode and that is fairly similar to the one appearing in the shear layer of the simulated jet. Let us point out, however, that it is difficult to identify the exact mode in the simulation, as the resonant modes overlap so much (see Fig. 1) and it may happen that what we see is the structure resulting from a combination of competing resonant modes.
According to the linear stability analysis, resonant modes have the
highest growth rates in high Lorentz factor jets and, among them, in
colder jets. This could be the reason why they only appear in
simulations of models A10, B20, and D20. Table 3 collects the models which present
maximum growth rate for all resonant modes (i.e., at any wavelength),
found in the solutions to the linear problem, above the growth rates
of the perturbed modes. Maximum growth rates for resonant modes in
those models where they have been found, along with the fitted growth
rates in the simulation, are listed. Typically, the growth rates from
the numerical simulations are about 1.4-2.0 times higher. This
difference remains unexplained, but it could be caused by second-order
effects, like interaction between modes.
| Model |
|
|
|
| B05 | 0.052 | - | - |
| D05 | 0.11 | - | - |
| A10 | 0.013 | 0.017 | 0.009 |
| B10 | 0.035 | - | - |
| D10 | 0.057 | - | - |
| B20 | 0.026 | 0.036 | 0.036 |
| D20 | 0.035 | 0.070 | 0.047 |
Summarizing, two kinds of linear growth are found in these simulations, one dominated by longer modes typical of slower jets and another one where short, fast modes appear. This difference is important, for the transition to the non-linear evolution depends critically on the dominant modes at the end of the linear regime.
Table 4 shows the times at which linear phase
ends. As the end of the linear regime we selected the moment
when one of the variables (usually axial velocity) changes its slope
(departs from the linear growth, see definitions in Paper I). On the
other hand, we noticed that the longitudinal velocity perturbation
grows linearly up to values close to the speed of light and then beyond
the sound speed. This means that shocks should form at the end of
linear phase, as it is the case; see Fig. 3 in Paper I, where we
observe weak shocks starting to appear as conical structures. We
could have selected the end of the linear regime as the moment
when these shocks start to appear. This would relate the end of the
linear regime directly to the internal sound
speed. We see that colder jets have longer linear phases than hot
ones, due to smaller typical growth rates in the former.
![]() times are larger than those in Paper I, as growth rates are reduced by
the presence of the shear layer. Model A10 presents the
longest linear phase.
times are larger than those in Paper I, as growth rates are reduced by
the presence of the shear layer. Model A10 presents the
longest linear phase.
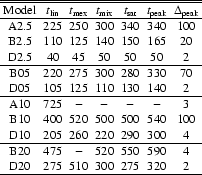 |
Saturation of perturbations is reached (see Paper I) when
perpendicular velocity cannot grow further in the jet reference frame
due to the speed of light limit. Saturation times
![]() for
the different models are listed in Table 4. In this
phase, structures generated by dominating modes become visible in the
deformations of the jet. In Fig. 5 we show snapshots of
three models (B2.5, D05, and D10) at
saturation time where mode competition derived from Fourier analysis
is clearly observed. Asymmetric structures appear as a result of
several symmetric and antisymmetric modes with large amplitudes.
for
the different models are listed in Table 4. In this
phase, structures generated by dominating modes become visible in the
deformations of the jet. In Fig. 5 we show snapshots of
three models (B2.5, D05, and D10) at
saturation time where mode competition derived from Fourier analysis
is clearly observed. Asymmetric structures appear as a result of
several symmetric and antisymmetric modes with large amplitudes.
The parallel and perpendicular wavelengths of the shear-layer
resonant modes, ![]() and
and ![]() ,
respectively, are both
small (
,
respectively, are both
small (
![]() )
with
)
with
![]() .
Therefore
their wavevectors are almost perpendicular to the jet axis so the
waves propagate from the shear layer towards the jet axis. On the
other hand, the resonant modes have high growth rates, exceeding the
growth rate of other modes, so they start to dominate in the
evolution. Subsequently, the resonant modes saturate as soon as the
flow velocity oscillation amplitude approaches the speed of light. As
the maximum amplitude is reached, the sound waves steepen while
travelling towards the jet axis and form shock fronts on the leading
edges of wave profiles Dissipation of the oscillation energy of
resonant modes in shocks changes the background flow, so that the
amplification conditions of the longer wavelength modes change during
the course of time, reducing the value of
.
Therefore
their wavevectors are almost perpendicular to the jet axis so the
waves propagate from the shear layer towards the jet axis. On the
other hand, the resonant modes have high growth rates, exceeding the
growth rate of other modes, so they start to dominate in the
evolution. Subsequently, the resonant modes saturate as soon as the
flow velocity oscillation amplitude approaches the speed of light. As
the maximum amplitude is reached, the sound waves steepen while
travelling towards the jet axis and form shock fronts on the leading
edges of wave profiles Dissipation of the oscillation energy of
resonant modes in shocks changes the background flow, so that the
amplification conditions of the longer wavelength modes change during
the course of time, reducing the value of
![]() and
preventing the formation of a strong shock.
and
preventing the formation of a strong shock.
Finally, as found in Paper II, the generation of the shock
wave at the jet/ambient interface is imprinted in the evolution of the
maxima of the transversal Mach number of the jet with respect to the
unperturbed ambient medium. This quantity is defined as
![]() ,
with
,
with
![]() and
and
![]() the Lorentz factors
associated to
the Lorentz factors
associated to
![]() and
and
![]() ,
respectively. A value
significantly larger than 1 around
,
respectively. A value
significantly larger than 1 around
![]() points towards a
supersonic expansion of the jet at the end of the saturation
phase. This magnitude is shown in Fig. 6. We observe a
clear inverse tendency of the peak value of this magnitude from colder
to hotter and from slower to faster jets, with the exception of A10 with respect to B10 and D10, due to the
presence of the resonant stabilizing modes preventing the formation of
a strong shock.
points towards a
supersonic expansion of the jet at the end of the saturation
phase. This magnitude is shown in Fig. 6. We observe a
clear inverse tendency of the peak value of this magnitude from colder
to hotter and from slower to faster jets, with the exception of A10 with respect to B10 and D10, due to the
presence of the resonant stabilizing modes preventing the formation of
a strong shock.
It is important to note that models with
![]() (A2.5, B2.5, B05, and B10) coincide
with those developing larger transversal Mach numbers, see top panels
of Fig. 5 for model B2.5, where pressure maxima
are observed at the jet center and in the interaction of the growing
wave with the ambient.
(A2.5, B2.5, B05, and B10) coincide
with those developing larger transversal Mach numbers, see top panels
of Fig. 5 for model B2.5, where pressure maxima
are observed at the jet center and in the interaction of the growing
wave with the ambient.
In Paper II, the non-linear evolution of the instability in the
different models was characterized through the processes of
jet/ambient mixing and momentum transfer. In Fig. 7 we show
the width of the mixing layer as a function of time for all the
models. The times at which mixing starts in the different models
![]() appear listed in Table 4. In all cases
these times are around
appear listed in Table 4. In all cases
these times are around
![]() .
Generally, models developing
wider shear layers are also more mixed; i.e., the amount of mass in
zones with jet mass fraction strictly different from 0 and 1, is
higher. We observe that those models with larger values of
.
Generally, models developing
wider shear layers are also more mixed; i.e., the amount of mass in
zones with jet mass fraction strictly different from 0 and 1, is
higher. We observe that those models with larger values of
![]() (lower Lorentz factor and colder jets) develop wider
layers (>5Rj) soon after saturation due to turbulent mixing
induced by the shock, while those models where resonant modes appear
do not show strong mixing with the ambient. Models B10 and D10 undergo a mixing process, though slower than the former.
(lower Lorentz factor and colder jets) develop wider
layers (>5Rj) soon after saturation due to turbulent mixing
induced by the shock, while those models where resonant modes appear
do not show strong mixing with the ambient. Models B10 and D10 undergo a mixing process, though slower than the former.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{3115f7.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg92.gif) |
Figure 7: Evolution of the mean width of the jet/ambient mixing layer (for tracer values between 0.05 and 0.95) with time for all simulations. Lines represent the same models as in Fig. 6. A value of 5 Rj for the width of the mixing layer (horizontal dashed line) serves to classify the evolution of the different models. |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3115f8.ps}
\par\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg93.gif) |
Figure 8: Evolution of the normalized total longitudinal momentum in the jet as a function of time. Lines represent the same models as in Fig. 6. The long-dashed horizontal line identifies those models transferring more than 50% of the initial jet momentum to the ambient. |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3115f9.ps}
\par\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg94.gif) |
Figure 9: Evolution of the normalized total transversal momentum in the jet as a function of time for all the simulations. Lines represent the same models as in Fig. 6. |
Figure 8 shows the fraction of initial axial momentum
kept by the jet as a function of time. Axial momentum is lost first
through sound waves forming the linear perturbations and
second, but more important, through shocks themselves and by
subsequent mixing, which implies sharing of momentum with the ambient
medium. Correlation with Fig. 7 is remarkable. Models
developing wide mixing layers coincide with those losing more than ![]() of their initial axial momentum just after saturation; models B10 and D10 share their momentum with the ambient
medium continuously in the non-linear regime; and models where
resonant modes dominate saturation keep almost all their initial
momentum by the end of the simulations. Results derived from
Fig. 8 are corroborated by Fig. 9. In the latter
we plot the total transversal momentum in the jets normalized to the
corresponding longitudinal momentum. Transversal momentum in the jet
(initially zero) is generated through turbulent motions and continuous
conversion of kinetic into internal energy. The value of the
normalized transversal momentum at a given time is an indication of
how far from equilibrium the jet is. We observe that colder and lower
Lorentz factor models present strong peaks at
of their initial axial momentum just after saturation; models B10 and D10 share their momentum with the ambient
medium continuously in the non-linear regime; and models where
resonant modes dominate saturation keep almost all their initial
momentum by the end of the simulations. Results derived from
Fig. 8 are corroborated by Fig. 9. In the latter
we plot the total transversal momentum in the jets normalized to the
corresponding longitudinal momentum. Transversal momentum in the jet
(initially zero) is generated through turbulent motions and continuous
conversion of kinetic into internal energy. The value of the
normalized transversal momentum at a given time is an indication of
how far from equilibrium the jet is. We observe that colder and lower
Lorentz factor models present strong peaks at
![]() ,
coincident with the triggering of the shock and the sudden transfer of
longitudinal momentum seen in the previous plot: Those models where
resonant modes appear barely generate any transversal momentum, and
models B10 and D10 do not present strong peaks at
saturation but display a steady transmission of the transversal momentum
through the non-linear regime (see Fig. 9), implying continuous
loss of energy.
,
coincident with the triggering of the shock and the sudden transfer of
longitudinal momentum seen in the previous plot: Those models where
resonant modes appear barely generate any transversal momentum, and
models B10 and D10 do not present strong peaks at
saturation but display a steady transmission of the transversal momentum
through the non-linear regime (see Fig. 9), implying continuous
loss of energy.
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f10.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg96.gif) |
Figure 10: Snapshot at the last frame of the simulation of logarithmic maps of pressure, jet mass fraction and specific internal energy and non-logarithmic Lorentz factor for model A2.5. |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f11.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg97.gif) |
Figure 11: Same as Fig. 10 for model B2.5. |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f12.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg98.gif) |
Figure 12: Same as Fig. 10 for model D2.5. |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f13.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg99.gif) |
Figure 13: Same as Fig. 10 for model B05. |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f14.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg101.gif) |
Figure 14: Same as Fig. 10 for model D05. |
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{3115f15.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg102.gif) |
Figure 15: Same as Fig. 10 for model A10. |
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3115f16.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg103.gif) |
Figure 16: Same as Fig. 10 for model B10. |
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3115f17.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg104.gif) |
Figure 17: Same as Fig. 10 for model D10. |
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{3115f18.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg105.gif) |
Figure 18: Same as Fig. 10 for model B20. |
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{3115f19.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg106.gif) |
Figure 19: Same as Fig. 10 for model D20. |
Simulations presented in Papers I and II, performed for the most
unstable first reflection mode of the corresponding models, confirmed
the general trends resulting from the linear stability analysis: the
faster (larger Lorentz factor) and colder jets have smaller growth
rates in the linear regime. In Paper II, the non-linear evolution of
the instability in the different models was characterized through the
processes of jet/ambient mixing and momentum transfer. The models were
then classified into four classes (I to IV) according to the
particular nature of these processes in each of the models. Class I
models (corresponding to cold and slow jets) were deeply mixed and
mass-loaded by the end of the simulation. Models in Class II (hot and
fast jets) were slowly mixed in the nonlinear regime, progressively
losing their longitudinal momentum. Models in Class III (hot and slow
jets) have properties between Classes I and II. Finally, Class IV
(containing cold/warm and fast models) appeared as the most stable in
the nonlinear regime. Shear layers formed in all the models as a
result of the non-linear evolution. Models in Classes I/II developed
broad shear layers and appeared totally mixed, cooled, and slowed
down. In contrast, models in Classes III/IV have an inner core
surrounded by thinner layers and keep a larger amount of their initial
longitudinal momentum. We performed a number of additional simulations
keeping the properties of the ambient medium fixed and changing the
rest-mass density of the jet and the Lorentz factor. Results confirmed
that these models behave like previous simulations, and are naturally
placed in the classification already defined.
The stability classes considered in Paper II were defined according to the jet response to single modes. In this paper we revisit this classification scheme in the light of the present results based on more general perturbations. From the analysis of Figs. 7-9, we classified jets depending on their nonlinear behaviour in three different groups:
Model A2.5 shows a totally mixed, mass-loaded flow with averaged maximum speed 0.4c, i.e., barely relativistic, as these jets are efficiently slowed down by mass entrainment after the disruption. The mass loading is inferred from the low values in the tracer profile (f<0.3), which imply a large fraction of ambient medium material inside the jet. The efficient conversion of kinetic energy into internal energy enhanced by the shock triggered in the early post-linear phase causes the jet to increase its specific internal energy.
UST2 jets undergo a slower process of mixing, so they still keep a larger fraction of axial velocity and Lorentz factor by the end of the simulation, even though they appear to be totally mixed (f<0.7everywhere). However, as we have mentioned in the previous section, the mixing and slowing process is still going on in B10 and D10, so it is clear that if the simulation had continued, the longitudinal velocity and Lorentz factor values would be smaller than those found. We also observe that the more mass-loaded parts of the jet (i.e., the region with -10 Rj<x<0) are consistently colder.
Finally, the jet in model B20 remains very thin. The
velocity profile of the model has widened by 2-3 Rj by the end of the
simulation, coinciding with the generation of a hot shear layer. This
layer is seen in the figure as an overheated and underdense
(![]() )
region shielding the unmixed core (f=1.), which keeps
almost all its initial axial momentum and Lorentz factor. The core has
a rich internal structure (see the pressure panel in
Fig. 18) that also manifests in the spiky structure of the
shows longitudinal momentum profile.
)
region shielding the unmixed core (f=1.), which keeps
almost all its initial axial momentum and Lorentz factor. The core has
a rich internal structure (see the pressure panel in
Fig. 18) that also manifests in the spiky structure of the
shows longitudinal momentum profile.
A comparison of the present non-linear evolution classification scheme and that of Paper II (classes I-IV) allows us to conclude that, in general, models in Classes I and III fall into UST1, whereas models in Class II corresponds to UST2 and those in Class IV to ST. The reason models D2.5 and D05 (belonging formerly to Class III) move to UST1 may be the inclusion of longer wavelength perturbations, along with the antisymmetric modes, which are more disruptive than the symmetric first reflection mode used in the previous work, and the lack of axial resolution in the latter, as discussed in the appendix of Paper II. This can be seen by comparing structures and evolution of model D05 here and in Paper II, in particular the evolution of the mixing and momentum transfer.
Regarding UST2 here compared to former class II, B10 and D10 undergo a very similar slow process of momentum transfer to the external medium to that observed for D10 and D20 in Paper II, although their temperatures are very different and the shock in B10 is much stronger than in D10 (see Table 4). The reason for this slow momentum exchange may be the same as proposed in Paper II for models D10 and D20, i.e., a continuous conversion of kinetic into internal energy due to the large initial Lorentz factor, which acts as a source of transversal momentum favoring the process of mixing and mass-loading. Model B10 changes from Class I in Paper II to UST2 here, meaning that disruption occurs by slow mixing in the new simulation, compared to sudden disruption in the previous one.
Models in Class IV were characterized by a rich internal-structure jet preserving a large fraction of initial momentum and Lorentz factor. ST models share these features, but now we are able to clearly associate them to with the growth of resonant modes, which could be the reason for the breaking of the linear slope in model C20 in Paper I (see Fig. 2 there). Steepening of short wavelength perturbations at the shear layer generates small shocks which favor local mixing and an efficient conversion of kinetic into internal energy. As a result of this process, the shear layer heats up and the jet expands to form a hot and underdense layer around the jet core (see Fig. 20). It is remarkable that model A10 is largely asymmetric by the end of the simulation (see Fig. 15). This is a consequence of the resonant modes only growing on one side of the jet during the linear regime, and it is understood on the basis of asymmetry resulting from mixture of symmetric and antisymmetric modes. This effect, though much less evident, is also observed in model B20. Finally, model D20 has moved from class II in Paper II to ST here, clearly due to the appearance of resonant modes. This fact allows us to conclude that the fate of ST models would be exactly the same as those in UST2, if it were not for the growth of resonant modes; hence, their importance in the long term stability of these jets.
We classified jets depending on their nonlinear behaviour in
three different groups, which are clearly separated in a relativistic
internal jet Mach number vs. jet Lorentz factor plot
(Fig. 21). In this plot, we also include models from
Paper II, in order to show the general character of our results and to
note that this division of the stability properties of jets is more
accurate than in Paper II, with the jet-to-ambient enthalpy ratio
instead of the relativistic Mach number. A clear correlation between
the two plotted parameters and the non-linear stability properties of
the jets is observed. Models B10 and D20 are
represented with two different symbols to show the change of nonlinear
behaviour from Paper II. These are placed in transition regions of the
plot, either in Lorentz factor (B10) or in relativistic Mach
number (D20). This fact could explain differences in the
non-linear behaviour as caused by changes in the initial jet profiles,
what is quite evident in the case of D20, for resonant modes
appear due to the presence of the shear layer. As in the previous
discussion, we have given the same symbols (crosses) as for UST1 jets
here to models in Class III of Paper II, as we do not consider that
they have different non-linear behaviour in both
simulations. Figure 21 can be considered as the
relativistic counterpart of the ![]() (Mach number-density ratio)
diagram in Bodo et al. (1994); note that the density ratio,
(Mach number-density ratio)
diagram in Bodo et al. (1994); note that the density ratio,
![]() ,
is inverted with respect to ours. In our case
the Mach number is relativistic; and the density ratio, which stands
for the inertia of the flow, is replaced by the Lorentz factor
here, as relativistic momentum is
,
is inverted with respect to ours. In our case
the Mach number is relativistic; and the density ratio, which stands
for the inertia of the flow, is replaced by the Lorentz factor
here, as relativistic momentum is ![]()
![]() ,
so it dominates
the inertia of relativistic jets. Our conclusions are similar to
theirs, for denser (higher Lorentz factor) and highly supersonic jets
(high relativistic Mach number) are the stablest. However, in our
case, we found a higher degree of stability due to the growth of
resonant, stabilizing modes.
,
so it dominates
the inertia of relativistic jets. Our conclusions are similar to
theirs, for denser (higher Lorentz factor) and highly supersonic jets
(high relativistic Mach number) are the stablest. However, in our
case, we found a higher degree of stability due to the growth of
resonant, stabilizing modes.
This result agrees with the conclusion of Hardee (2000), where linear stability arguments show that distortions induced by instabilities are smaller for higher Lorentz factor flows, although they were not associated to the shear resonances reported by us.
Finally, simulations discussed in Appendices A (single antisymmetric mode in planar geometry) and B (single symmetric mode in cylindrical geometry) have confirmed general trends of the present clasification scheme, generalizing our results.
One of the current open problems in extragalactic jet research is to understand the morphological dichotomy between FRI and FRII jets. Several possible explanations have been proposed which mainly fall in one of these two general possibilities: either (i) FRI and FRII sources are intrinsically the same, and the morphology and jet evolution depend mainly on the ISM in which they are embedded in the first kiloparsecs, or (ii) they depend on intrinsic differences stemming from the jet formation process (black hole rotation, Blandford 1994; accretion rate, Baum et al. 1995; black hole mass, Ghisellini & Celotti 2001; the so-called magnetic switch, Meier et al. 1998), or (iii) a combination of both (e.g., Snellen & Best 2003). Of course, all the mechanisms could come into play with differing effects and significance depending on the source.
Leaving the basis of the morphological dichotomy aside, current
models (Laing & Bridle 2002a,b and references therein) interpret FRI
morphologies as the result of a smooth deceleration from relativistic
(
![]() ,
Pearson 1996) to non-relativistic transonic speeds
(
,
Pearson 1996) to non-relativistic transonic speeds
(![]() 0.1 c) on kpc scales. On the contrary, flux asymmetries
between jets and counter-jets in the most powerful radio galaxies and
quasars indicate that relativistic motion (
0.1 c) on kpc scales. On the contrary, flux asymmetries
between jets and counter-jets in the most powerful radio galaxies and
quasars indicate that relativistic motion (
![]() )
extends
up to kpc scales in these sources, although with smaller values of the
overall bulk speeds (
)
extends
up to kpc scales in these sources, although with smaller values of the
overall bulk speeds (
![]() ,
Bridle et al. 1994). Current
models for high energy emission from powerful jets at kpc scales
(e.g., Celotti et al. 2001) offer additional support to the hypothesis
of relativistic bulk speeds on these scales.
,
Bridle et al. 1994). Current
models for high energy emission from powerful jets at kpc scales
(e.g., Celotti et al. 2001) offer additional support to the hypothesis
of relativistic bulk speeds on these scales.
The results concerning the long-term evolution of relativistic jets
presented in this paper and summarized in Fig. 20
confirm that slower and smaller Mach number jets (UST1) are entrained
by ambient material and slowed down to v<0.5 c after becoming
overpressured (due to conversion of kinetic into internal energy) and
being disrupted by nonlinear instabilities effects which cause flaring
and rapid expansion of the mixing flow. UST2 jets undergo a smooth
slowing down; and though by the end of the simulation jet velocity is
![]() 0.9 c, this process is continuous, and eventual loss of
velocity to mildly relativistic values is to be expected. Finally, ST
jets keep their initial highly relativistic velocities, and their
steadiness by the end of simulations makes them firm candidates for
remaining collimated over long distances. Hence our results would
point to a high Lorentz factor, highly supersonic jets as forming FRII
Class, whereas FRI jets would be found in the opposite corner of the
diagram (slow, small Mach number jets). The validity of our results
extends to models with different jet-to-ambient-density ratios and
specific internal energies as seen in Paper II.
0.9 c, this process is continuous, and eventual loss of
velocity to mildly relativistic values is to be expected. Finally, ST
jets keep their initial highly relativistic velocities, and their
steadiness by the end of simulations makes them firm candidates for
remaining collimated over long distances. Hence our results would
point to a high Lorentz factor, highly supersonic jets as forming FRII
Class, whereas FRI jets would be found in the opposite corner of the
diagram (slow, small Mach number jets). The validity of our results
extends to models with different jet-to-ambient-density ratios and
specific internal energies as seen in Paper II.
Our conclusions point to an important contribution by intrinsic properties of the source to the morphological dichotomy. Nevertheless, the importance of the ambient medium cannot be ruled out on the basis of our simulations, since we consider an infinite jet in pressure equilibrium flowing in an already open funnel and surrounded by a homogeneous ambient medium. Thus our approach does not take into account the consequences of the interaction of the jet with the ambient in order to penetrate it or the effects of a spatially varying atmosphere. Simulations following the spatial approach (perturbations grow with distance) for jets propagating in different ISM profiles and using a more realistic microphysics (allowing for a local mixture of electron, positron, and proton Boltzmann gases) will be performed in order to clarify these points.
As dicussed in the introduction of this paper, there are plenty of
arguments indicating the existence of transversal structure in
extragalactic jets at all scales. In the simulations presented here,
the initial states were defined with a continuous transition layer of
thickness ![]() 0.2 Rj. As discussed in the previous paragraphs,
this shear layer has played an important role in the long-term
stability of the jet flow. Besides this, thicker shear layers have
been generated in the course of the non-linear evolution. Relatively
thin (
0.2 Rj. As discussed in the previous paragraphs,
this shear layer has played an important role in the long-term
stability of the jet flow. Besides this, thicker shear layers have
been generated in the course of the non-linear evolution. Relatively
thin (![]() 2 Rj), hot shear layers are found in present ST
models (the physically meaningful counterparts of the layers found in
the three-dimensional, low-resolution simulations of Aloy et al. 1999,
2000), which could explain several observational trends in powerful
jets at both parsec and kiloparsec scales (see Aloy et al. 2000 and
references therein). Conversely and according to our simulations,
these transition layers could be responsible for the stability of
fast, highly supersonic jets, preventing the mass-loading and
subsequent disruption. Finally, the type of shear layers developed by
models UST1/2 could mimic the transition layers invoked in models of
FRIs (Laing & Bridle 2002a,b).
2 Rj), hot shear layers are found in present ST
models (the physically meaningful counterparts of the layers found in
the three-dimensional, low-resolution simulations of Aloy et al. 1999,
2000), which could explain several observational trends in powerful
jets at both parsec and kiloparsec scales (see Aloy et al. 2000 and
references therein). Conversely and according to our simulations,
these transition layers could be responsible for the stability of
fast, highly supersonic jets, preventing the mass-loading and
subsequent disruption. Finally, the type of shear layers developed by
models UST1/2 could mimic the transition layers invoked in models of
FRIs (Laing & Bridle 2002a,b).
We performed a number of simulations spanning a wide range of parameters, such as Lorentz factor and specific internal energy, for a general setup where a slab-sheared jet is perturbed with a set of symmetric and antisymmetric sinusoidal perturbations, in order to characterize the stability properties of relativistic jets.
The most remarkable feature regarding the linear evolution of instabilities is the finding of resonant modes in our simulations, which were later confirmed by applying linear stability theory to sheared flows. These modes are important for the long-term stability properties of some jets (ST), for they remain collimated and unmixed, thereby keeping a large amount of initial axial momentum. Jets in which these modes do not grow fast enough with respect to longer modes are disrupted either after a shock or by slow momentum transfer and mixing.
We classified jets depending on their nonlinear behaviour in three different classes, which are clearly separated in a relativistic internal Mach number vs. Lorentz factor plot (Fig. 21). UST1 models are disrupted after a shock forms in the early post-linear phase, and ambient gas penetrates deep into the jet stream, decelerating and cooling the initial flow down. UST2 models are slowly decelerated by an efficient conversion of kinetic energy into internal energy, which causes momentum transfer and mixing. Finally, ST models present little expansion, but remain collimated and isolated from the ambient by a hot shear layer. ST models would fall into UST2, if resonant modes were not present, as occurs for model D20 in Paper II.
Our simulations admit a clear interpretation in the context of the morphological dichotomy of radio jets. Results presented here could point to high Lorentz factor, highly supersonic jets as forming FRII Class, whereas FRI jets would be related to slow, small Mach number jets. In the former, the generation of a hot shear layer surrounding a stable core could be related to the transversal structure observed in several powerful jets.
Acknowledgements
The authors want to thank J.A. Miralles for clarifying discussions during the development of this work. Calculations were performed on the SGI Altix 3000 computer CERCA at the Servei d'Informàtica de la Universitat de València. This work was supported in part by the Spanish Dirección General de Enseñanza Superior under grant AYA-2001-3490-C02 and by the Polish Committee for Scientific Research (KBN) under grant PB 0656/P03/2004/26. M.H. acknowledges financial support from the visitor program of the Universitat de València. M.P. benefited from a predoctoral fellowship of the Universitat de València (V Segles program).
Previous to simulations presented in this paper, we performed
simulations following the same perturbation setup as in Paper I, but
using the first antisymmetric reflection mode, instead, for models
B05, B20, D05 and D20, representing the four stability regions found
in Paper II. Numerical setup in these simulations is the same as that
used for the corresponding simulation in this paper, excepting the box
size, which was adapted to the wavelength of the least stable first
body wavelength (![]() 7 Rj for model B05,
7 Rj for model B05, ![]() 1.8 Rj for D05,
1.8 Rj for D05,
![]() 9 Rj for B20 and
9 Rj for B20 and ![]() 3 Rj for D20). Results showed the
same tendencies found for the combination of modes presented here (see
Fig. A.1) with slight changes. Model B05 has the same
behaviour as those jets of UST1 (loss of momentum and development of
wide mixing layers and disruption), whereas D05 presents the same
features as UST2 models (slower loss of momentum in the nonlinear
regime).
Finally, models B20 and D20 show the development of resonant
modes and undergo the same nonlinear evolution as ST jets; short modes
excited as harmonics of the perturbed first reflection mode grow fast
and change nonlinear evolution, stabilizing the jet. Model D05
changes from UST1 in the paper to UST2 here, maybe due to the much
shorter mode used (
3 Rj for D20). Results showed the
same tendencies found for the combination of modes presented here (see
Fig. A.1) with slight changes. Model B05 has the same
behaviour as those jets of UST1 (loss of momentum and development of
wide mixing layers and disruption), whereas D05 presents the same
features as UST2 models (slower loss of momentum in the nonlinear
regime).
Finally, models B20 and D20 show the development of resonant
modes and undergo the same nonlinear evolution as ST jets; short modes
excited as harmonics of the perturbed first reflection mode grow fast
and change nonlinear evolution, stabilizing the jet. Model D05
changes from UST1 in the paper to UST2 here, maybe due to the much
shorter mode used (![]() 1.8 Rj versus 8 Rj) which avoids the
development of a strong shock after saturation. In
Figs. A.2-A.5 we show panels at the
last frame of the simulations, for jet mass fraction and Lorentz
factor.
1.8 Rj versus 8 Rj) which avoids the
development of a strong shock after saturation. In
Figs. A.2-A.5 we show panels at the
last frame of the simulations, for jet mass fraction and Lorentz
factor.
![\begin{figure}
\par\includegraphics[width=6.4cm,clip]{3115fA1a.ps}\hspace*{3mm}
\includegraphics[width=6.4cm,clip]{3115fA1b.ps}
\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg117.gif) |
Figure A.1:
Left panel: evolution of the mean width of the jet/ambient
mixing layer (for tracer values between 0.05 and 0.95) with time.
Right panel: evolution of the normalized total longitudinal momentum
in the jet as a function of time. As in Fig. 6, dotted
lines stand for |
| |
Figure A.2: Snapshot at the last frame of the simulation of jet mass fraction ( left panel) and Lorentz factor ( right panel) for model B05. |
| |
Figure A.3: Model D05. Same as Fig. A.2. |
| |
Figure A.4: Model B20. Same as Fig. A.2. |
| |
Figure A.5: Model D20. Same as Fig. A.2. |
Simulations corresponding to models B05, D05, B20 and D20 were also performed using cylindrical coordinates. In this case, resolution was 128 cells/Rj axially and 256 cells/Rj radially, shear layer width is the same as in planar coordinates, and we applied several symmetric (i.e., pinching) sinusoidal perturbations. Reflection boundary conditions were applied in the jet axis. Again, the same evolutionary patterns are found, and models B05 and D05 are disrupted in the early post-linear phase (UST1), whereas models B20 and D20 are stabilized by short resonant modes. The most remarkable features in this case include the very low axial momentum kept by the jet in models B05 and D05 and the stronger mixing and mass loading (see Fig. B.1). This may be due to geometric effects, as the surface of the interface grows radially in cylindrical coordinates, resulting in a more efficient transference of momentum to the ambient medium. However, results show the generalized character of conclusions presented in this paper. In Figs. B.2-B.5 we show panels at the last frame of the simulations for jets mass fraction and Lorentz factor.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3115fB1a.ps}\hspace*{4mm}
\includegraphics[width=6.5cm,clip]{3115fB1b.ps}
\par\end{figure}](/articles/aa/full/2005/45/aa3115-05/Timg122.gif) |
Figure B.1: Left panel: evolution of the mean width of the jet/ambient mixing layer (for tracer values between 0.05 and 0.95) with time. Right panel: evolution of the normalized total longitudinal momentum in the jet as a function of time. Lines represent the same models as in Fig. A.1. |
| |
Figure B.2: Model B05. Same as Fig. A.2. |
| |
Figure B.3: Model D05. Same as Fig. A.2. |
| |
Figure B.4: Model B20. Same as Fig. A.2. |
| |
Figure B.5: Model D20. Same as Fig. A.2. |