The subscript E indicates the statistical estimator of 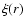$\xi(r)$ in a given sample.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

We remark that in nature any fractal distribution has a lower and an upper cut-off between which the characteristic scaling proprieties are manifested: the infinite volume limit is, of course, simply a useful mathematical idealization. In particular the hypothesis that the galaxy distribution manifests fractal scaling always refers implicitly to some finite range of (observable) scales.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... scales

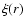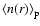Note that we are discussing here the results of measures of $\xi(r)$ and ${\langle n(r)\rangle}_{\rm p}$ in redshift space. Such studies (e.g. Park et al. 1994; Benoist et al. 1996) have consistently reported a dimension D=1.2- 1.5. Note also that finite size effects perturb the estimations of the correlation exponent differently for the correlation function and the power spectrum (see Sylos Labini & Amendola 1996 for more details).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... size

We remark, in particular, that in HEB3GS the density in each sphere is not actually calculated by dividing the number of points by its volume. Instead the division is by the number of points in the same volume in an artificial catalog, which is constructed to correct for effects leading to incompleteness of the sample. This actually involves building in the assumption of homogeneity at large scales. It is stated that the sample is sufficiently complete that this is "essentially equivalent'' to dividing by the volume. The dependence of the results on this difference should however be quantified carefully and controlled for in future analyses.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...h

The paper actually follows what has become a standard practice in the last few years: results are given only for the "projected real space'' correlation function, rather than the redshift space correlation function, which we have considered here. This makes it much more difficult to compare the results for the estimated dimension, and so we will not focus on this point here.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...h

This value (in redshift space) can be inferred from the data given in Table 2 of Zehavi et al. (2005b).

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.