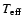**Table 6:** Final Li abundances as derived by using different sets of ${T}_{\rm eff}$ .
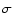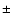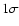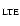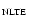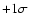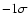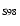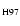HIP	Bin	[Fe/H]	$\sigma$ (Fe)	logg	EW	$\pm$ $1\sigma$	A(Li) $_{\rm LTE}$	A(Li) $_{\rm NLTE}$	$+1\sigma$	$-1\sigma$	A(Li) $_{\rm S98}$	A(Li) $_{\rm H97}$
		dex	dex	cm s^-1	mÅ	mÅ	dex	dex	dex	dex	dex	dex

Sample #1: the clean sample
911	s	-1.84	0.150	4.50	30.8	3.5	2.117	2.112	0.042	0.067	2.200	2.191
3026	x	-1.25	0.070	3.85	45.0	6.0	2.428	2.418	0.078	0.086	2.573	2.567
3446		-3.50	0.100	4.50	27.0	3.9	1.973	1.986	0.074	0.076	2.045	2.048
3564		-1.27	0.150	3.50	35.2	3.5	2.011	2.054	0.056	0.076	2.244	2.008
8572		-2.51	0.010	3.85	27.0	1.4	2.257	2.236	0.026	0.027	2.239	2.257
10140		-1.00	0.150	4.20	14.0	3.0	1.479	1.536	0.092	0.113	1.861	1.551
11952		-1.85	0.170	4.50	28.0	2.6	2.183	2.162	0.052	0.048	2.247	2.196
12529	*	-2.25	0.070	3.85	34.0	1.5	2.227	2.222	0.046	0.024	2.227	2.237
14594	v	-2.06	0.060	4.50	37.5	3.5	2.178	2.177	0.052	0.075	2.178	2.224
16072		-1.35	0.150	4.50	44.2	3.5	2.315	2.308	0.047	0.049	2.341	2.274
18082		-1.97	0.270	3.50	47.7	3.0	2.376	2.364	0.038	0.040	2.386	2.255
18802		-1.06	0.100	3.50	23.0	2.0	1.853	1.894	0.042	0.045	1.903	1.915
19797	x	-1.58	0.050	4.00	27.9	2.8	2.139	2.131	0.079	0.054	2.133	2.211
22632		-1.40	0.100	4.50	35.0	3.5	2.165	2.169	0.056	0.077	2.290	2.215
23344	?	-2.77	0.080	4.00	20.5	1.1	2.155	2.134	0.026	0.026	2.291	2.199
24316		-1.61	0.090	4.50	32.3	2.9	1.982	2.005	0.066	0.047	2.086	2.036
28887		-1.67	0.030	3.00	18.0	2.0	1.418	1.511	0.051	0.057	1.418	1.693
29759	?	-2.03	0.170	3.50	13.7	2.1	1.370	1.443	0.067	0.078	1.370	1.435
30098		-1.98	0.150	3.20	16.0	3.0	1.308	1.407	0.083	0.100	1.308	1.698
32567		-1.46	0.030	3.85	34.5:	2.4	2.321:	2.310:	0.040	0.065	2.548:	2.641:
34630	*	-2.53	0.240	4.20	30.0	2.9	2.128	2.124	0.049	0.052	2.385	...
36174		-1.56	0.090	4.20	35.8:	2.7	2.342:	2.325:	0.044	0.070	2.504:	2.410:
36430	x	-2.10	0.210	3.50	44.0	3.0	2.356	2.352	0.040	0.042	2.474	2.609
36513	?	-2.65	0.060	3.85	24.0	4.0	2.159	2.145	0.078	0.094	2.410	2.571
37671	s	-1.48	0.150	3.85	37.6	3.3	2.398	2.380	0.051	0.082	2.548	2.352
38541	?	-1.77	0.050	4.50	12.0	2.0	1.206	1.274	0.072	0.084	1.347	1.079
40778		-1.60	0.100	4.50	31.0	3.5	2.118	2.118	0.055	0.061	2.297	2.201
42592		-1.96	0.100	4.00	23.6	1.5	2.142	2.124	0.030	0.032	2.372	2.249
44605		-2.09	0.160	5.00	38.0	3.4	2.091	2.106	0.086	0.075	2.177	2.149
44716		-1.02	0.100	2.50	<3.5	...	<0.314	...	...	...	<0.353	<0.310
46516		-2.88	0.040	3.85	19.3	1.3	2.181	2.155	0.031	0.033	2.287	2.096
47480	s	-2.79	0.290	3.85	19.6	2.6	2.147	2.172	0.061	0.061	2.598	2.193
48152	?	-2.28	0.170	3.85	24.6	1.2	2.281	2.249	0.027	0.029	2.836	2.654
52771	x	-1.82	0.030	5.00	45.0	6.9	2.145	2.163	0.084	0.095	2.255	2.181
53070	?	-1.55	0.080	4.20	35.8	1.6	2.209	2.211	0.026	0.050	2.319	2.222
55022	*	-1.29	0.130	3.85	<3.0	...	<1.332	<1.313	...	...	<1.544	<2.391
59109		-2.23	0.280	4.00	25.3	1.0	2.304	2.268	0.059	0.057	2.410	2.292
59376		-2.20	0.120	4.20	29.0	3.1	2.117	2.114	0.020	0.019	2.226	2.174
60632	x	-1.82	0.210	4.00	31.7	1.3	2.204	2.212	0.020	0.021	2.294	2.280
61361	?	-2.63	0.040	4.20	36.0	2.1	2.253	2.249	0.027	0.063	2.411	2.308
61545	*	-2.23	0.070	4.00	27.0	3.5	2.159	2.147	0.062	0.075	2.235	2.182
61802		-1.22	0.150	3.50	13.6	3.5	1.310	1.393	0.108	0.140	1.366	1.309
62747		-1.34	0.150	3.00	17.2	3.5	1.268	1.381	0.091	0.109	1.166	1.040
63559		-0.93	0.100	4.20	37.0	2.0	2.119	2.142	0.031	0.033	2.375	2.005
66354	*	-1.43	0.100	4.50	8.0	2.0	1.008	1.088	0.101	0.129	1.082	1.022
66673	?	-3.38	0.130	3.85	25.8	4.0	2.347	2.316	0.074	0.089	2.292	2.219
67655		-1.03	0.100	4.50	<6.0	...	<1.167	<1.245	...	...	<1.167	<1.193
67863		-0.88	0.100	3.50	<5.0	...	<1.283	<1.338	...	...	<1.657	<1.368
68321	x	-2.34	0.050	3.85	23.0	1.5	2.172	2.151	0.031	0.033	2.221	2.218
68464		-1.93	0.100	3.85	40.0	2.0	2.414	2.390	0.029	0.031	2.677	2.945
68592		-2.96	0.360	3.85	16.2	4.0	2.077	2.057	0.105	0.133	2.146	2.029
71458		-2.32	0.150	3.50	11.4	3.5	1.206	1.289	0.130	0.159	1.277	...
72461	*	-2.52	0.230	4.50	30.0	3.6	2.240	2.220	0.059	0.066	2.258	2.158
72561	*	-1.66	0.150	4.50	<6.3	...	<1.672	<1.639	...	...	<1.758	<1.590
72920		-2.84	0.040	4.00	21.3	2.9	2.209	2.183	0.068	0.070	2.142	2.047
73385	v	-1.62	0.180	3.50	53.0	3.5	2.376	2.383	0.042	0.043	2.593	2.219
74079		-1.60	0.150	3.50	44.0	3.5	2.221	2.243	0.047	0.049	2.379	2.245
76059		-1.70	0.070	3.50	53.7	4.5	2.212	2.248	0.051	0.054	2.212	2.074
76976	v	-2.48	0.080	3.50	47.2	1.8	2.260	2.278	0.024	0.024	2.260	2.228
78640		-1.56	0.080	4.00	28.0	4.8	2.081	2.089	0.081	0.094	2.131	2.177
81276	*	-1.50	0.150	3.85	<6.0	...	<1.740	<1.705	...	...	<1.808	<1.876
86443	x	-2.32	0.210	4.50	32.7	1.3	2.065	2.070	0.021	0.021	2.065	2.324
86694		-1.76	0.160	3.85	41.0	2.1	2.565	2.522	0.031	0.032	2.565	2.465
87101		-1.38	0.150	4.00	43.5	1.5	2.121	2.156	0.020	0.021	2.121	1.783
87467		-2.57	0.040	4.00	25.5	3.0	2.274	2.246	0.057	0.067	2.348	2.268
87693	x	-2.09	0.120	4.00	27.5	2.2	2.221	2.201	0.045	0.041	2.602	2.424
88010		-1.36	0.120	4.00	22.1	2.1	1.599	1.668	0.041	0.046	1.599	1.702
88827		-2.40	0.100	4.00	21.5	2.2	2.350	2.307	0.048	0.052	2.350	2.420
89554		-1.60	0.150	4.20	40.0	3.8	2.442	2.419	0.054	0.060	2.890	2.516
95333		-1.70	0.300	4.50	40.6	4.5	2.242	2.241	0.076	0.085	2.620	2.285
96115	x	-2.42	0.180	3.85	25.3	1.1	2.248	2.223	0.021	0.028	2.248	2.473
98020	x	-1.73	0.090	5.00	18.8	3.4	1.576	1.609	0.082	0.100	1.576	1.607
98532		-1.30	0.150	3.50	42.0	1.6	2.113	2.152	0.022	0.023	2.113	2.243
98989		-1.71	0.080	4.00	29.8	2.6	2.092	2.102	0.043	0.046	2.088	2.357
99423		-1.54	0.070	3.50	79.2	2.0	2.643	2.620	0.020	0.021	2.643	2.751
100568		-1.15	0.100	4.20	28.8	3.4	1.872	1.915	0.055	0.061	2.098	2.085
100682	?	-2.83	0.030	4.50	<2.0	...	<1.108	<1.088	...	...	<1.108	<1.249
100792		-1.45	0.110	4.00	28.8	0.9	2.001	2.021	0.015	0.015	2.487	1.685
102337		-2.06	0.030	4.00	29.3	3.1	2.326	2.295	0.053	0.062	2.524	2.294
102718	s	-1.80	0.100	3.85	29.0	7.9	1.972	1.995	0.154	0.158	2.350	2.237
104660	x	-0.80	0.150	3.50	5.0	3.3	1.038	1.098	0.227	0.477	2.364	1.946
104658		-1.28	0.100	4.20	25.2	0.6	1.886	1.912	0.013	0.012	1.038	1.211
106468		-2.63	0.150	4.00	29.8	1.4	2.259	2.243	0.024	0.025	2.480	2.294
109558	*	-1.73	0.200	4.00	28.1	2.2	2.103	2.101	0.038	0.041	2.350	2.260
110140		-1.25	0.070	3.85	37.0	7.4	2.219	2.229	0.115	0.138	2.509	2.315
111195	*	-1.39	0.090	4.50	35.0	2.6	2.158	2.163	0.043	0.064	2.389	2.160
111372		-2.08	0.300	3.50	31.0	4.5	2.297	2.279	0.096	0.086	2.314	2.331
114271		-1.83	0.130	4.00	29.0	1.4	2.351	2.316	0.024	0.026	2.393	2.306
114962	?	-1.52	0.100	3.85	39.1	1.3	2.231	2.245	0.019	0.020	2.364	2.277
115167		-1.81	0.310	3.85	30.5	3.5	2.178	2.173	0.058	0.068	2.392	2.231
115704	*	-2.00	0.060	4.50	29.0	2.1	2.163	2.146	0.041	0.038	2.163	2.399
Sample #2: the 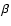$\beta$ sample
484		-1.23	0.150	3.00	12.1	3.5	0.953	1.101	...	...	0.949	...
3554		-2.87	0.150	3.00	17.7	3.5	1.018	1.153	0.087	0.104	1.044	1.238
4343		-2.08	0.150	3.00	9.1	3.5	0.766	0.912	0.150	0.219	0.878	0.680
8314	?	-1.68	0.090	4.00	27.0	3.0	2.378	2.337	0.053	0.058	2.262	2.523
13749		-1.62	0.150	3.00	14.6	3.5	0.876	1.039	0.102	0.128	0.901	0.870
17001		-2.70	0.150	3.00	12.6	3.5	1.054	1.171	0.115	0.150	1.058	0.926
21609	s	-1.60	0.005	4.50	21.0:	3.0	1.348:	1.434:	0.065	0.074	1.465:	1.357:
25659	v	-2.00	0.100	4.50	43.9	6.4	2.249	2.245	0.082	0.092	2.248	2.243
30668		-1.40	0.110	3.00	9.9	3.5	1.154	1.253	0.141	0.199	1.079	1.167
49371		-1.75	0.150	3.00	24.5	3.5	1.328	1.457	0.068	0.076	1.294	1.354
57244	*	-2.80	0.100	5.00	34.0	2.2	1.864	1.901	0.019	0.039	1.961	1.825
57983		-2.29	0.150	3.00	10.2	3.5	0.994	1.121	0.138	0.186	1.104	0.835
58357		-1.71	0.150	3.00	<4.0	...	<0.237	...	...	...	<0.248	<0.301
60719		-2.32	0.150	3.00	<4.0	...	<0.687	<0.789	...	...	<0.791	<0.638
63385		-1.83	0.150	3.00	21.3	3.5	1.074	1.234	0.076	0.088	1.194	1.065
65206	*	-2.60	0.100	3.50	30.0	2.9	2.050	2.070	0.048	0.057	2.048	2.024
92775		-2.18	0.150	3.50	20.7	4.2	1.759	1.799	0.090	0.109	1.773	1.148
99267		-2.12	0.020	4.50	45.0	4.5	2.269	2.265	0.058	0.062	2.226	2.261
114502		-1.87	0.150	3.00	12.1	3.5	0.911	1.060	0.119	0.158	1.033	0.853
117522	*	-2.40	0.100	5.00	28.0	2.9	1.834	1.865	0.048	0.053	2.150	1.889
Sample #3: the ubvy sample
12807		-2.87	0.220	4.50	22.9	3.0	1.918	1.929	0.066	0.068	2.676	1.940
83320		-2.56	0.150	3.50	<5.0	...	<1.265	1.287	...	...	<1.603	<1.167
87062		-1.67	0.230	4.50	31.5	4.0	2.109	2.111	0.088	0.069	2.109	2.106
91129	*	-2.96	0.100	4.50	27.3	2.5	2.208	2.191	0.045	0.054	2.899	2.224
103337		-2.07	0.150	3.00	25.8	3.5	1.025	1.197	0.069	0.072	1.179	0.877
104191		-2.99	0.120	3.00	9.0	1.7	0.959	1.070	0.084	0.100	0.840	1.435

[?] Identifies a suspected binary (Latham et al. 2002; Carney et al. 1994, 2003).
* Identifies a confirmed single- or double-lined binary (from Latham et al. 2002; Carney et al. 1994, 2003).

Source LaTeX | All tables | In the text

	1 The lithium paradigm
	2 The "Lithium plateau debate''?
	3 Sample selection: a critical analysis of the literature
	4 Stellar parameters: I. Gravity, metallicity, and microturbulence
	5 Stellar parameters. II. The temperature scale and its weaknesses
	6 Our final choice: temperature and data-sample(s)
	7 The lithium abundance
	8 Preliminary results on the mean lithium abundance and the dispersion
	9 Evolutionary status of the stars
	10 The lithium abundance along the plateau for the dwarf stars
	11 The lithium abundance in evolved stars
	12 Duplicity and variability
	13 Stars with extreme Li abundances
	14 Implications for stellar structure and evolution
	15 Summary and conclusions
	References
	Online Material