A&A 439, 1215-1227 (2005)
DOI: 10.1051/0004-6361:20053057
K. M. Aggarwal - F. P. Keenan
Department of Physics and Astronomy, Queen's University, Belfast BT7 1NN, Northern Ireland, UK
Received 14 March 2005 / Accepted 10 May 2005
Abstract
Collision strengths for 4005 transitions among the lowest 90 levels of the (1s22s22p6) 3s23p5, 3s3p6, 3s23p43d, 3s3p53d and 3s23p33d2
configurations of Fe X have been calculated using the Dirac Atomic R-matrix Code (DARC) of Norrington & Grant (2005, Comput. Phys. Commun., in preparation), over a wide energy range up to 210 Ryd.
Resonances have been resolved in the threshold region, and effective collision strengths have been obtained over a wide temperature range up to 107 K. The present calculations
should represent a significant improvement (in both range and accuracy) over the earlier available results of Bhatia & Doschek (1995, At. Data Nucl. Data Tables, 60, 97), Tayal (2001, ApJS, 132, 117) and Pelan &
Berrington (2001, A&A, 365, 258). Based on several comparisons, the accuracy of our data is assessed to be better than 20%, for a majority of transitions.
Key words: atomic data - atomic processes
In a recent paper, we (Aggarwal & Keenan 2004b) reported calculations of energy levels and radiative rates for transitions among the lowest 54 levels of the
(1s22s22p6) 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations of Fe X, and in this paper we present our results for collision
strengths (![]() )
and effective collision strengths (
)
and effective collision strengths (![]() )
for transitions among the lowest 90 levels of the 3s23p5, 3s3p6, 3s23p43d,
3s3p53d and 3s23p33d2 configurations.
)
for transitions among the lowest 90 levels of the 3s23p5, 3s3p6, 3s23p43d,
3s3p53d and 3s23p33d2 configurations.
Iron is an abundant element in solar and fusion plasmas, and its emission lines are observed over almost all ionization stages. To analyse the vast amount of observational
data available from space missions such as SOHO, Chandra and XMM Newton, theoretical atomic data for Fe ions are required, because there is
paucity of desired experimental results. To this end we have also reported atomic data (namely, energy levels, radiative rates, collision strengths and excitation rate
coefficients) for Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004a, 2005), Fe XV (Aggarwal et al. 2000,
2001, 2003a), Fe XVII (Aggarwal et al. 2003b, 2004), Fe XVIII (Jonauskas et al. 2004),
Fe XXI (Aggarwal & Keenan 2001), and Fe XXIV (McKeown et al. 2004), and in this paper we present our results of ![]() and
and ![]() for transitions in Fe X.
for transitions in Fe X.
Emission lines of Cl-like Fe X in the EUV (150-900 ![]() )
and UV (900-2000
)
and UV (900-2000 ![]() )
ranges have been observed in the spectra of the solar atmosphere (Brosius et al. 1998)
and late-type stars (Drake et al. 1995a,b), and have proved to be useful plasma diagnostics (Foster et al. 1996).
A famous visible transition of Fe X is the red line at
)
ranges have been observed in the spectra of the solar atmosphere (Brosius et al. 1998)
and late-type stars (Drake et al. 1995a,b), and have proved to be useful plasma diagnostics (Foster et al. 1996).
A famous visible transition of Fe X is the red line at ![]() 6375
6375 ![]() belonging to the (3s23p5) 2P
belonging to the (3s23p5) 2P
![]() P
P
![]() magnetic dipole (M1) transition. Therefore, realising the importance of Fe X, a number of workers, particularly in the past decade, have performed a variety of calculations to compute various
atomic parameters. The most notable among the available data, particularly for
magnetic dipole (M1) transition. Therefore, realising the importance of Fe X, a number of workers, particularly in the past decade, have performed a variety of calculations to compute various
atomic parameters. The most notable among the available data, particularly for ![]() and
and ![]() ,
are the calculations of Bhatia & Doschek (1995, henceforth BD),
Tayal (2000, 2001) and Pelan & Berrington (2001). However, we find that there is scope for improvement as well as an
extension of the available data. We discuss this below.
,
are the calculations of Bhatia & Doschek (1995, henceforth BD),
Tayal (2000, 2001) and Pelan & Berrington (2001). However, we find that there is scope for improvement as well as an
extension of the available data. We discuss this below.
BD have reported results for energy levels, radiative rates (A-values) and collision strengths for all transitions among 54 levels of the
3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations. They have adopted the SuperStructure (SS) code of Eissner et al. (1974) for the generation of
wavefunctions, and the Distorted-Wave (DW) code of Eissner & Seaton (1972) for the computation of ![]() .
Their calculations are basically in LS coupling,
and results for transitions in intermediate coupling (
.
Their calculations are basically in LS coupling,
and results for transitions in intermediate coupling (![]() )
were obtained through an algebraic transformation using the
)
were obtained through an algebraic transformation using the
![]() program of Saraph (1972). One-body
relativistic effects were included in the calculations through term coupling coefficients. However, their calculations are limited mainly for two reasons. Firstly, their
wavefunctions are not accurate, because many of their energy levels differ with experimental and other theoretical results by
program of Saraph (1972). One-body
relativistic effects were included in the calculations through term coupling coefficients. However, their calculations are limited mainly for two reasons. Firstly, their
wavefunctions are not accurate, because many of their energy levels differ with experimental and other theoretical results by ![]() 5%, and some by up to 11% - see Table 1
of Aggarwal & Keenan (2004b). This has a direct effect on the subsequent calculations of radiative rates and collision strengths, which may easily vary by a factor of
5%, and some by up to 11% - see Table 1
of Aggarwal & Keenan (2004b). This has a direct effect on the subsequent calculations of radiative rates and collision strengths, which may easily vary by a factor of ![]() 2 for strong transitions, and by larger factors for weaker transitions - see, for example, Tables 3 and 4 of Tayal (2001). The main reason for this inaccuracy is
the neglect
of configuration interaction (CI) with additional configurations, as CI is very important for Fe X. This is in spite of it being a moderately heavy ion (Z = 26), as already
explained and demonstrated in our earlier paper (Aggarwal & Keenan 2004b). Secondly, and more importantly, BD have reported values of
2 for strong transitions, and by larger factors for weaker transitions - see, for example, Tables 3 and 4 of Tayal (2001). The main reason for this inaccuracy is
the neglect
of configuration interaction (CI) with additional configurations, as CI is very important for Fe X. This is in spite of it being a moderately heavy ion (Z = 26), as already
explained and demonstrated in our earlier paper (Aggarwal & Keenan 2004b). Secondly, and more importantly, BD have reported values of ![]() at only 5 energies (9-45 Ryd) above thresholds, and have not resolved resonances in the thresholds region. Therefore, any results obtained for
at only 5 energies (9-45 Ryd) above thresholds, and have not resolved resonances in the thresholds region. Therefore, any results obtained for ![]() from their limited data of
from their limited data of ![]() will
be highly underestimated, especially for the forbidden transitions, because resonances may enhance values of
will
be highly underestimated, especially for the forbidden transitions, because resonances may enhance values of ![]() up to an order of magnitude, depending on the
transition and the temperature.
up to an order of magnitude, depending on the
transition and the temperature.
Tayal (2001, henceforth SST) attempted to remove both the limitations of the calculations by BD. For the generation of wavefunctions, he included additional CI (mainly
with the 4![]() orbitals), and resolved
resonances in order to improve the accuracy of the
orbitals), and resolved
resonances in order to improve the accuracy of the ![]() results. Furthermore, he adopted an independent approach by employing the CIV3 program of Hibbert (1975) for
the generation of wavefunctions, and the R-matrix code of Berrington et al. (1995) for the computation of
results. Furthermore, he adopted an independent approach by employing the CIV3 program of Hibbert (1975) for
the generation of wavefunctions, and the R-matrix code of Berrington et al. (1995) for the computation of ![]() .
His calculations were performed in
.
His calculations were performed in ![]() coupling, and one-body relativistic effects were included through the Breit-Pauli approximation. However, his calculations are also limited for three main reasons. Firstly,
his lowest 24 energy levels are the highest among all the available theoretical results, and are higher by up to 8% in comparison with the experimental ones - see,
for example, levels 19 and 20 in Table 1 of SST. Additionally, the orderings of his energy levels agree neither with the experimental ones nor with any of the CI calculations of
Pelan & Berrington (2001), Deb et al. (2002), or Aggarwal & Keenan (2004b). Secondly, SST
excluded 10 levels, namely 3s23p4(1D)3d 2G
7/2,9/2, 3s3p5(3P)3d 4F
coupling, and one-body relativistic effects were included through the Breit-Pauli approximation. However, his calculations are also limited for three main reasons. Firstly,
his lowest 24 energy levels are the highest among all the available theoretical results, and are higher by up to 8% in comparison with the experimental ones - see,
for example, levels 19 and 20 in Table 1 of SST. Additionally, the orderings of his energy levels agree neither with the experimental ones nor with any of the CI calculations of
Pelan & Berrington (2001), Deb et al. (2002), or Aggarwal & Keenan (2004b). Secondly, SST
excluded 10 levels, namely 3s23p4(1D)3d 2G
7/2,9/2, 3s3p5(3P)3d 4F
![]() ,
3s3p5(3P)3d 2F
,
3s3p5(3P)3d 2F
![]() and 3s3p5(1P)3d
2F
and 3s3p5(1P)3d
2F
![]() .
These metastable levels are spectroscopically important (Del Zanna et al. 2004), and therefore results for transitions involving these
levels are not only required but their omissions also affect the resonance patterns in the thresholds region, and subsequently their contributions in the determination of
.
These metastable levels are spectroscopically important (Del Zanna et al. 2004), and therefore results for transitions involving these
levels are not only required but their omissions also affect the resonance patterns in the thresholds region, and subsequently their contributions in the determination of ![]() values. Finally, and most importantly, he reported results of
values. Finally, and most importantly, he reported results of ![]() only for transitions from the lowest three levels to higher excited levels. However,
results for all transitions are required for a diagnostic or modelling calculation, and this has been clearly emphasized and demonstrated by Del Zanna et al. - see
particularly their Fig. 2 and Table 6.
only for transitions from the lowest three levels to higher excited levels. However,
results for all transitions are required for a diagnostic or modelling calculation, and this has been clearly emphasized and demonstrated by Del Zanna et al. - see
particularly their Fig. 2 and Table 6.
Finally, there are calculations by Pelan & Berrington (2001, henceforth PB), who have adopted a similar approach to SST, i.e. they too have performed their
calculations in ![]() coupling through the Breit-Pauli approximation, and have employed the CIV3 and R-matrix programs for the generation of wavefunctions and computations
of
coupling through the Breit-Pauli approximation, and have employed the CIV3 and R-matrix programs for the generation of wavefunctions and computations
of ![]() ,
respectively. They have included extensive CI in the generation of wavefunctions, which is clearly reflected by the excellent agreement their energy levels have,
not only in magnitude but also in ordering, with the experimental ones and with other theoretical results of Deb et al. (2002) and Aggarwal & Keenan
(2004b). Additionally, they too have resolved resonances in a fine energy mesh, and hence their results for all atomic parameters should be
comparatively more accurate than those of BD or SST. However, their results are limited to transitions from the lowest three levels to higher excited levels, but in
a recent paper (Del Zanna et al. 2004) they have widened the range by also reporting results for the remaining 378 transitions. Nevertheless, their
results for
,
respectively. They have included extensive CI in the generation of wavefunctions, which is clearly reflected by the excellent agreement their energy levels have,
not only in magnitude but also in ordering, with the experimental ones and with other theoretical results of Deb et al. (2002) and Aggarwal & Keenan
(2004b). Additionally, they too have resolved resonances in a fine energy mesh, and hence their results for all atomic parameters should be
comparatively more accurate than those of BD or SST. However, their results are limited to transitions from the lowest three levels to higher excited levels, but in
a recent paper (Del Zanna et al. 2004) they have widened the range by also reporting results for the remaining 378 transitions. Nevertheless, their
results for ![]() are still confined to the lowest 31 levels of the 3s23p5, 3s3p6 and 3s23p43d configurations,
whereas corresponding results for transitions involving the additional 23 levels of the 3s3p53d configuration are also required, as has been emphasized by Del Zanna et al.,
because transitions involving these levels have already been observed in solar plasmas. Apart from this limitation of their work, there is some concern about the accuracy of
their results, which we discuss below.
are still confined to the lowest 31 levels of the 3s23p5, 3s3p6 and 3s23p43d configurations,
whereas corresponding results for transitions involving the additional 23 levels of the 3s3p53d configuration are also required, as has been emphasized by Del Zanna et al.,
because transitions involving these levels have already been observed in solar plasmas. Apart from this limitation of their work, there is some concern about the accuracy of
their results, which we discuss below.
The PB results for ![]() differ
with those of SST by a factor of two for many transitions, such as 2-3, 4, 5, 6, 7 - see Table 1 for level indices. These substantial differences are not confined to any particular
range of temperature, but are noticeable for the entire range (
differ
with those of SST by a factor of two for many transitions, such as 2-3, 4, 5, 6, 7 - see Table 1 for level indices. These substantial differences are not confined to any particular
range of temperature, but are noticeable for the entire range (
![]() (K
(K![]() )
for some of the transitions, such as 2-4 and 2-5. Similarly, their values of
)
for some of the transitions, such as 2-4 and 2-5. Similarly, their values of ![]() differ by a factor of two for some of the allowed transitions, such as 1-3 and 2-3. This is in spite of the fact that the transition energies and oscillator strengths
(f-values) are comparable in both calculations. Since both of these calculations (of SST and PB) are contemporary, are of comparable accuracy, and adopt the same methodology
(of using the R-matrix code in the Breit-Pauli approximation), such large differences for many transitions of importance are not expected. Therefore, our aim is to assess the
accuracy of the available data for
differ by a factor of two for some of the allowed transitions, such as 1-3 and 2-3. This is in spite of the fact that the transition energies and oscillator strengths
(f-values) are comparable in both calculations. Since both of these calculations (of SST and PB) are contemporary, are of comparable accuracy, and adopt the same methodology
(of using the R-matrix code in the Breit-Pauli approximation), such large differences for many transitions of importance are not expected. Therefore, our aim is to assess the
accuracy of the available data for ![]() and
and ![]() ,
as well as to extend the
range of transitions. We achieve this aim by performing a calculation by an independent approach. Contrary to the already available calculations, our approach is fully
relativistic as we employ the GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989) for the generation of wavefunctions, and the Dirac
Atomic R-matrix Code (DARC) of Norrington & Grant (2005) for the computations of
,
as well as to extend the
range of transitions. We achieve this aim by performing a calculation by an independent approach. Contrary to the already available calculations, our approach is fully
relativistic as we employ the GRASP (General purpose Relativistic Atomic Structure Package) code of Dyall et al. (1989) for the generation of wavefunctions, and the Dirac
Atomic R-matrix Code (DARC) of Norrington & Grant (2005) for the computations of ![]() ,
and subsequently of
,
and subsequently of ![]() .
.
The 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations of Fe X give rise to 54 fine-structure levels. However, energy levels obtained with CI among these four
configurations alone differ by up to 5% when compared with the corresponding experimental results compiled by NIST (http://physics.nist.gov/PhysRefData) - see Table 1
of Aggarwal & Keenan (2004b). Since experimental energies for the higher levels of the 3s23p33d2 configuration are not yet available, no direct comparisons
can be made to assess
the accuracy of the theoretical results. However, the importance of the inclusion of larger CI in the accurate determination of energy levels has already been emphasized and
demonstrated by Pelan & Berrington (2001), Deb et al. (2002), and Aggarwal & Keenan (2004b). Energy levels obtained with limited CI (among the above stated
4 configurations) may differ by up to 11% in comparison with those obtained with extensive CI - see Table 1 of Aggarwal & Keenan. Therefore, based on several test calculations,
we concluded in our earlier paper (Aggarwal & Keenan 2004b) that to achieve reasonable accuracy in energy levels and radiative rates, CI among 8 configurations (namely,
3s23p5, 3s3p6, 3s23p43d, 3s3p53d, 3p63d, 3s3p43d2, 3s23p33d2 and 3s23p23d3) is necessary. However, these
configurations give rise to 669 levels, with which a scattering calculation cannot be performed with the resources available to us. Therefore, a compromise has to be made. Since
36 levels of the 3s23p33d2 configuration lie below the highest level 2P
![]() of the 3s3p53d configuration, their inclusion in the scattering
calculation becomes necessary. Therefore, in the present work we have included the lowest 90 levels of the 3s23p5, 3s3p6, 3s23p43d, 3s3p53d and 3s23p33d2 configurations of Fe X. The inclusion of additional levels will not only improve the results for effective collision strengths,
but may also be beneficial to spectral modelling.
of the 3s3p53d configuration, their inclusion in the scattering
calculation becomes necessary. Therefore, in the present work we have included the lowest 90 levels of the 3s23p5, 3s3p6, 3s23p43d, 3s3p53d and 3s23p33d2 configurations of Fe X. The inclusion of additional levels will not only improve the results for effective collision strengths,
but may also be beneficial to spectral modelling.
To generate the wavefunctions, we have used the fully relativistic GRASP code of Dyall et al. (1989) with the option of extended average level (EAL), in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. Our calculations are in the jj coupling scheme, and Breit and QED corrections have been included. CI has been included among the above stated eight configurations, and energy levels obtained are the same as reported in Table 1 of Aggarwal & Keenan (2004b) under the column GRASP8. However, in that paper we reported energies for the 54 levels of the lowest four configurations only, and here in Table 1 we list energies for the lowest 90 levels among the 3s23p5, 3s3p6, 3s23p43d, 3s3p53d and 3s23p33d2 configurations. Since an elaborate comparison has already been made of our energies with other available theoretical and experimental results, and no corresponding data are available in the literature for the additional higher lying 36 levels now included, we do not discuss our energy levels any further. However, based on several comparisons, the accuracy of our energy levels is assessed to be better than 3%. Similarly, in our earlier paper we reported A-values for (E1, E2, M1 and M2) transitions among the 54 levels of the 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations, and corresponding results involving the higher levels of the 3s23p33d2 configuration can be obtained on request from one of the authors (K.Aggarwal@qub.ac.uk).
| Index | Configuration | Level | GRASPa | GRASPb | Index | Configuration | Level | GRASPa | GRASPb |
| 1...... | 3s23p5 | 2P
|
0.0000 | 0.0000 | 46...... | 3s3p5(3P)3d | 2D
|
7.0780 | 7.0664 |
| 2...... | 3s23p5 | 2P
|
0.1461 | 0.1426 | 47...... | 3s3p5(1P)3d | 2P
|
7.1552 | 7.1458 |
| 3...... | 3s3p6 | 2S1/2 | 2.6066 | 2.6024 | 48...... | 3s3p5(1P)3d | 2P
|
7.2331 | 7.2206 |
| 4...... | 3s23p4 (3P)3d | 4D5/2 | 3.5545 | 3.5473 | 49...... | 3s23p3(4S)3d2(3F) | 6F
|
7.2842 | 7.2722 |
| 3s23p4 (3P)3d | 4D7/2 | 3.5550 | 3.5468 | 50...... | 3s23p3(4S)3d2(3F) | 6F
|
7.2859 | 7.2736 | |
| 6...... | 3s23p4 (3P)3d | 4D3/2 | 3.5653 | 3.5587 | 51...... | 3s23p3(4S)3d2(3F) | 6F
|
7.2892 | 7.2762 |
| 7...... | 3s23p4 (3P)3d | 4D1/2 | 3.5791 | 3.5724 | 52...... | 3s23p3(4S)3d2(3F) | 6F
|
7.2942 | 7.2803 |
| 8...... | 3s23p4 (3P)3d | 4F9/2 | 3.8485 | 3.8407 | 53...... | 3s23p3(4S)3d2(3F) | 6F
|
7.3012 | 7.2862 |
| 9...... | 3s23p4 (1D)3d | 2P1/2 | 3.8673 | 3.8608 | 54...... | 3s23p3(4S)3d2(3F) | 6F
|
7.3101 | 7.2935 |
| 10...... | 3s23p4 (3P)3d | 4F7/2 | 3.8954 | 3.8876 | 55...... | 3s3p5(1P)3d | 2F
|
7.4346 | 7.4237 |
| 11...... | 3s23p4 (3P)3d | 4F5/2 | 3.9301 | 3.9220 | 56...... | 3s3p5(1P)3d | 2F
|
7.4756 | 7.4626 |
| 12...... | 3s23p4 (3P)3d | 4F3/2 | 3.9421 | 3.9345 | 57...... | 3s23p3(4S)3d2(3P) | 6P
|
7.5391 | 7.5263 |
| 13...... | 3s23p4 (1D)3d | 2P3/2 | 3.9451 | 3.9375 | 58...... | 3s23p3(4S)3d2(3P) | 6P
|
7.5427 | 7.5295 |
| 14...... | 3s23p4 (1D)3d | 2D3/2 | 4.0010 | 3.9942 | 59...... | 3s23p3(4S)3d2(3P) | 6P
|
7.5470 | 7.5323 |
| 15...... | 3s23p4 (3P)3d | 4P1/2 | 4.0050 | 3.9992 | 60...... | 3s3p5(1P)3d | 2D
|
7.6883 | 7.6777 |
| 16...... | 3s23p4 (3P)3d | 4P3/2 | 4.0516 | 4.0435 | 61...... | 3s3p5(1P)3d | 2D
|
7.7055 | 7.6931 |
| 17...... | 3s23p4 (3P)3d | 4P5/2 | 4.0700 | 4.0615 | 62...... | 3s23p3(4S)3d2(1D) | 4D
|
7.7747 | 7.7604 |
| 18...... | 3s23p4 (3P)3d | 2F7/2 | 4.0785 | 4.0716 | 63...... | 3s23p3(4S)3d2(1D) | 4D
|
7.7815 | 7.7680 |
| 19...... | 3s23p4 (1D)3d | 2D5/2 | 4.0932 | 4.0836 | 64...... | 3s23p3(4S)3d2(1D) | 4D
|
7.7860 | 7.7734 |
| 20...... | 3s23p4 (1D)3d | 2G9/2 | 4.1716 | 4.1612 | 65...... | 3s23p3(4S)3d2(1D) | 4D
|
7.7977 | 7.7850 |
| 21...... | 3s23p4 (1D)3d | 2G7/2 | 4.1750 | 4.1660 | 66...... | 3s23p3(2D)3d2(3F) | 4G
|
7.8071 | 7.7946 |
| 22...... | 3s23p4 (3P)3d | 2F5/2 | 4.2027 | 4.1935 | 67...... | 3s23p3(2D)3d2(3P) | 4P
|
7.8082 | 7.7951 |
| 23...... | 3s23p4 (1D)3d | 2F5/2 | 4.4736 | 4.4664 | 68...... | 3s23p3(2D)3d2(3F) | 4G
|
7.8179 | 7.8046 |
| 24...... | 3s23p4 (1D)3d | 2F7/2 | 4.5114 | 4.5020 | 69...... | 3s23p3(2D)3d2(3P) | 4F
|
7.8248 | 7.8127 |
| 25...... | 3s23p4 (1S)3d | 2D3/2 | 4.7315 | 4.7243 | 70...... | 3s23p3(2D)3d2(3F) | 4G
|
7.8380 | 7.8230 |
| 26...... | 3s23p4 (1S)3d | 2D5/2 | 4.7715 | 4.7618 | 71...... | 3s23p3(2D)3d2(3P) | 4P
|
7.8407 | 7.8272 |
| 27...... | 3s23p4 (1D)3d | 2S1/2 | 5.0297 | 5.0228 | 72...... | 3s23p3(2D)3d2(3P) | 4F
|
7.8590 | 7.8452 |
| 28...... | 3s23p4 (3P)3d | 2P3/2 | 5.2800 | 5.2727 | 3s23p3(2D)3d2(3F) | 4G
|
7.8593 | 7.8426 | |
| 29...... | 3s23p4 (3P)3d | 2P1/2 | 5.3332 | 5.3243 | 74...... | 3s23p3(2D)3d2(3P) | 4P
|
7.8736 | 7.8591 |
| 30...... | 3s23p4 (3P)3d | 2D5/2 | 5.3503 | 5.3428 | 75...... | 3s23p3(2D)3d2(3P) | 4F
|
7.8963 | 7.8813 |
| 31...... | 3s23p4 (3P)3d | 2D3/2 | 5.4739 | 5.4633 | 76...... | 3s23p3(2D)3d2(3P) | 4F
|
7.9270 | 7.9102 |
| 32...... | 3s3p5(3P)3d | 4P
|
6.2330 | 6.2252 | 77...... | 3s23p3(2D)3d2(3F) | 4H
|
7.9866 | 7.9746 |
| 33...... | 3s3p5(3P)3d | 4P
|
6.2578 | 6.2485 | 78...... | 3s23p3(2D)3d2(3F) | 4H
|
7.9968 | 7.9833 |
| 34...... | 3s3p5(3P)3d | 4P
|
6.3016 | 6.2905 | 79...... | 3s23p3(2D)3d2(3F) | 4H
|
8.0118 | 7.9964 |
| 35...... | 3s3p5(3P)3d | 4F
|
6.5623 | 6.5516 | 80...... | 3s23p3(2D)3d2(3F) | 4H
|
8.0378 | 8.0197 |
| 36...... | 3s3p5(3P)3d | 4F
|
6.5873 | 6.5771 | 81...... | 3s23p3(2D)3d2(1D) | 2F
|
8.0691 | 8.0553 |
| 37...... | 3s3p5(3P)3d | 4F
|
6.6145 | 6.6044 | 82...... | 3s23p3(2D)3d2(3F) | 2H
|
8.1123 | 8.0983 |
| 38...... | 3s3p5(3P)3d | 4F
|
6.6395 | 6.6293 | 83...... | 3s23p3(2D)3d2(1D) | 2F
|
8.1176 | 8.1038 |
| 39...... | 3s3p5(3P)3d | 4D
|
6.8612 | 6.8504 | 84...... | 3s23p3(2D)3d2(1D) | 2D
|
8.1333 | 8.1211 |
| 40...... | 3s3p5(3P)3d | 4D
|
6.8721 | 6.8630 | 3s23p3(2D)3d2(3F) | 2H
|
8.1336 | 8.1180 | |
| 41...... | 3s3p5(3P)3d | 4D
|
6.8767 | 6.8662 | 86...... | 3s23p3(2P)3d2(3F) | 4G
|
8.1999 | 8.1863 |
| 42...... | 3s3p5(3P)3d | 4D
|
6.8777 | 6.8678 | 87...... | 3s23p3(2P)3d2(3F) | 4G
|
8.2122 | 8.1983 |
| 43...... | 3s3p5(3P)3d | 2F
|
6.9369 | 6.9268 | 88...... | 3s3p5(3P)3d | 2P
|
8.2169 | 8.2058 |
| 44...... | 3s3p5(3P)3d | 2F
|
6.9965 | 6.9859 | 3s23p3(2D)3d2(3F) | 2D
|
8.2186 | 8.2031 | |
| 45...... | 3s3p5(3P)3d | 2D
|
7.0612 | 7.0510 | 90...... | 3s3p5(3P)3d | 2P
|
8.2235 | 8.2119 |

For the computations of collision strengths, we have employed the DARC program of Norrington & Grant (2005). This
program includes the relativistic effects in a systematic way, in both the target description and the scattering model. It is based on the jj coupling scheme,
and uses the Dirac-Coulomb Hamiltonian in the R-matrix approach. However, because of the inclusion of fine-structure in the definition of channel coupling, the
matrix size of the Hamiltonian increases substantially, making the calculations computationally more expensive. The R-matrix radius has been adopted to be 3.28 au,
and 21 continuum orbitals have been included for each
channel angular momentum for the expansion of the wavefunction. This allows us to compute ![]() up to an energy of 210 Ryd. The maximum number of channels for a
partial wave is 538, and the corresponding size of the Hamiltonian matrix is 11 340. In order to obtain convergence of
up to an energy of 210 Ryd. The maximum number of channels for a
partial wave is 538, and the corresponding size of the Hamiltonian matrix is 11 340. In order to obtain convergence of ![]() for all transitions and at all energies,
we have included all partial waves with angular momentum
for all transitions and at all energies,
we have included all partial waves with angular momentum ![]() ,
although a higher range would have been preferable for the convergence of allowed transitions,
especially at higher energies. However, given the resources available to us, this was not possible. Nevertheless, to account for the inclusion of
higher neglected partial waves, we have included a top-up, based on the Coulomb-Bethe approximation for allowed transitions and geometric series for
forbidden transitions. We will further elaborate about it later in this section.
,
although a higher range would have been preferable for the convergence of allowed transitions,
especially at higher energies. However, given the resources available to us, this was not possible. Nevertheless, to account for the inclusion of
higher neglected partial waves, we have included a top-up, based on the Coulomb-Bethe approximation for allowed transitions and geometric series for
forbidden transitions. We will further elaborate about it later in this section.
In Figs. 1a, 2a and 3a we show the variation of ![]() with angular momentum J at three energies of 10, 30 and 50 Ryd, and for three transitions, namely 1-2
(3s23p5 2P
with angular momentum J at three energies of 10, 30 and 50 Ryd, and for three transitions, namely 1-2
(3s23p5 2P
![]() s23p5 2P
s23p5 2P
![]() ), 1-3 (3s23p5 2P
), 1-3 (3s23p5 2P
![]() s3p6 2S1/2) and 3-26 (3s3p6 2S
1/2-3s23p4(1S)3d 2D5/2), which are parity forbidden, allowed, and forbidden, respectively. The corresponding results
at three higher energies of 100, 150 and 200 Ryd are shown in Figs. 1b, 2b and 3b, respectively. For the forbidden transitions, such as 1-2 and 3-26 shown in Figs. 1 (a and b)
and 3 (a and b),
s3p6 2S1/2) and 3-26 (3s3p6 2S
1/2-3s23p4(1S)3d 2D5/2), which are parity forbidden, allowed, and forbidden, respectively. The corresponding results
at three higher energies of 100, 150 and 200 Ryd are shown in Figs. 1b, 2b and 3b, respectively. For the forbidden transitions, such as 1-2 and 3-26 shown in Figs. 1 (a and b)
and 3 (a and b), ![]() have (almost) fully converged at all energies, including the highest energy of our calculations, i.e. 210 Ryd. For allowed transitions, such as 1-3 shown in Fig. 2 (a and b),
have (almost) fully converged at all energies, including the highest energy of our calculations, i.e. 210 Ryd. For allowed transitions, such as 1-3 shown in Fig. 2 (a and b), ![]() have converged within our range of partial waves only at lower energies (below 50 Ryd), and a top-up is required for its convergence at
higher energies. Additionally, for some
transitions such as 1-3, the values of
have converged within our range of partial waves only at lower energies (below 50 Ryd), and a top-up is required for its convergence at
higher energies. Additionally, for some
transitions such as 1-3, the values of ![]() show an unphysical oscillation for two partial waves. This is due to the fact that the long-range potentials have been omitted
for these partial waves and only Coulomb functions have been used. This is performed automatically by the program in DSTGF whenever there is a numerical problem in the
convergence of the wavefunction in the outer region of the R-matrix. The solution to this problem is to increase the number of integration points. In the present calculations,
we have restricted this number to 2000, and increasing it further makes the program more computationally demanding. This is not currently feasible keeping in view our
resources, and the fact that
show an unphysical oscillation for two partial waves. This is due to the fact that the long-range potentials have been omitted
for these partial waves and only Coulomb functions have been used. This is performed automatically by the program in DSTGF whenever there is a numerical problem in the
convergence of the wavefunction in the outer region of the R-matrix. The solution to this problem is to increase the number of integration points. In the present calculations,
we have restricted this number to 2000, and increasing it further makes the program more computationally demanding. This is not currently feasible keeping in view our
resources, and the fact that ![]() have to be computed at a large number of energies. However, as a result of this,
have to be computed at a large number of energies. However, as a result of this, ![]() is up to
is up to ![]() 20% lower than what it should
be with the inclusion of long-range potentials. Since it happens for only two partial waves, the net effect on
20% lower than what it should
be with the inclusion of long-range potentials. Since it happens for only two partial waves, the net effect on
![]() is negligible. For example, for the transition
shown in Fig. 2b,
is negligible. For example, for the transition
shown in Fig. 2b, ![]() values are affected (and are lower) by less than 1%, which is much lower than the accuracy estimates of the calculations.
values are affected (and are lower) by less than 1%, which is much lower than the accuracy estimates of the calculations.
In Table 2 we present our results of ![]() for transitions from the lowest 3 levels to higher excited levels, and in
a wider energy range up to 200 Ryd. The indices adopted to represent a transition are already given in Table 1. These results of
for transitions from the lowest 3 levels to higher excited levels, and in
a wider energy range up to 200 Ryd. The indices adopted to represent a transition are already given in Table 1. These results of ![]() are not directly applicable in any
diagnostic or modelling work, but are very useful in assessing the accuracy of a calculation, and will be helpful for future comparisons. The only significant corresponding data
for
are not directly applicable in any
diagnostic or modelling work, but are very useful in assessing the accuracy of a calculation, and will be helpful for future comparisons. The only significant corresponding data
for ![]() available in the literature are of BD, who have reported their results from the DW code, at 5 energies in the range
available in the literature are of BD, who have reported their results from the DW code, at 5 energies in the range
![]() Ryd. Since their
wavefunctions are different from ours (as stated in Sect. 1), disagreements in the values of
Ryd. Since their
wavefunctions are different from ours (as stated in Sect. 1), disagreements in the values of ![]() are not unexpected. However, for most of the allowed transitions,
differences in the two sets of
are not unexpected. However, for most of the allowed transitions,
differences in the two sets of ![]() are in accordance with their corresponding f-values, which indicates that there is no unexpected discrepancy. Since the inaccuracy of
the BD data has already been highlighted in Sect. 1 (and earlier by PB and SST), our main focus is on comparisons with the other available calculations of PB and SST.
Unfortunately, both of these papers have listed values of
are in accordance with their corresponding f-values, which indicates that there is no unexpected discrepancy. Since the inaccuracy of
the BD data has already been highlighted in Sect. 1 (and earlier by PB and SST), our main focus is on comparisons with the other available calculations of PB and SST.
Unfortunately, both of these papers have listed values of ![]() at four energies (18, 27, 36 and 45 Ryd), and only for a few transitions. Nevertheless, in Table 3 we compare
all four sets of
at four energies (18, 27, 36 and 45 Ryd), and only for a few transitions. Nevertheless, in Table 3 we compare
all four sets of ![]() (and f-values for allowed transitions) for some of the common transitions, which will serve our purpose of making an assessment of the accuracy of
the calculations.
(and f-values for allowed transitions) for some of the common transitions, which will serve our purpose of making an assessment of the accuracy of
the calculations.
| Transition | Bhatia & Doschek (1995) | Tayal (2001) | |||||||||
| i | j | f | 18.0 | 27.0 | 36.0 | 45.0 | f | 18.0 | 27.0 | 36.0 | 45.0 Ryd |
| 1 | 2 | 2.358-1 | 2.251-1 | 2.188-1 | 2.143-1 | 0.368 | 0.345 | 0.328 | 0.318 | ||
| 1 | 3 | 0.0179 | 4.212-1 | 4.414-1 | 4.610-1 | 4.791-1 | 0.028 | 0.607 | 0.669 | 0.714 | 0.754 |
| 1 | 4 | 1.78-5 | 3.915-2 | 2.552-2 | 1.787-2 | 1.325-2 | 0.044 | 0.029 | 0.020 | 0.015 | |
| 1 | 5 | 5.929-2 | 3.834-2 | 2.651-2 | 1.933-2 | 0.066 | 0.043 | 0.030 | 0.022 | ||
| 2 | 3 | 0.0183 | 2.255-1 | 2.394-1 | 2.515-1 | 2.622-1 | 0.028 | 0.327 | 0.360 | 0.383 | 0.404 |
| 2 | 4 | 1.200-2 | 7.893-3 | 5.582-3 | 4.179-3 | 0.013 | 0.009 | 0.006 | 0.005 | ||
| 2 | 5 | 7.918-3 | 5.047-3 | 3.470-3 | 2.524-3 | 0.009 | 0.006 | 0.004 | 0.003 | ||
| 3 | 4 | 1.999-3 | 1.3-1-3 | 9.220-4 | 6.940-4 | ||||||
| 3 | 5 | 2.621-3 | 1.672-3 | 1.158-3 | 8.490-4 | ||||||
| Transition | Pelan & Berrington (2001) | Present results | |||||||||
| i | j | f | 18.0 | 27.0 | 36.0 | 45.0 | f | 18.0 | 27.0 | 36.0 | 45.0 Ryd |
| 1 | 2 | 0.2111 | 0.2057 | 0.2031 | 0.2018 | ||||||
| 1 | 3 | 0.0257 | 0.356 | 0.363 | 0.361 | 0.361 | 0.0273 | 0.5961 | 0.6520 | 0.6952 | 0.7300 |
| 1 | 4 | 5.20-5 | 0.044 | 0.028 | 0.020 | 0.015 | 1.00-4 | 4.55-2 | 3.00-2 | 2.13-2 | 1.61-2 |
| 1 | 5 | 0.0662 | 0.0423 | 0.0293 | 0.0213 | 6.71-2 | 4.31-2 | 2.97-2 | 2.16-2 | ||
| 2 | 3 | 0.0257 | 0.186 | 0.188 | 0.188 | 0.188 | 0.0267 | 0.3164 | 0.3464 | 0.3692 | 0.3875 |
| 2 | 4 | 0.0140 | 0.0085 | 0.0060 | 0.0045 | 1.34-2 | 8.79-3 | 6.20-3 | 4.64-3 | ||
| 2 | 5 | 9.05-3 | 5.75-3 | 3.94-3 | 2.85-3 | ||||||
| 3 | 4 | 0.0020 | 0.0013 | 0.0010 | 0.0008 | 2.09-3 | 1.41-3 | 1.03-3 | 8.00-4 | ||
| 3 | 5 | 2.69-3 | 1.74-3 | 1.22-3 | 9.03-4 | ||||||
As stated earlier, for allowed transitions (such as 1-3 and 2-3) the ![]() values of BD differ with those of ours or of SST by
values of BD differ with those of ours or of SST by ![]() 50% over the entire energy range. However,
these differences are clearly understandable because the corresponding f-values also differ by the same amount. Among the forbidden transitions, noticeable differences
are for the 1-2 transition, for which ours and the BD values of
50% over the entire energy range. However,
these differences are clearly understandable because the corresponding f-values also differ by the same amount. Among the forbidden transitions, noticeable differences
are for the 1-2 transition, for which ours and the BD values of ![]() are comparable, but those of SST are higher by
are comparable, but those of SST are higher by ![]() 50%. For this transition, PB have not
reported their results, but in general their values of
50%. For this transition, PB have not
reported their results, but in general their values of ![]() for forbidden transitions are in agreement with all other calculations. However, their results for the allowed
transitions are in complete contrast with other work. In spite of their f-values for the 1-3 and 2-3 transitions being comparable with those of ours or of SST, the PB values of
for forbidden transitions are in agreement with all other calculations. However, their results for the allowed
transitions are in complete contrast with other work. In spite of their f-values for the 1-3 and 2-3 transitions being comparable with those of ours or of SST, the PB values of ![]() are lower by a factor of two, and are not in accordance with the expected behaviour. Similarly, in spite of their f-values being higher than those of BD, their values of
are lower by a factor of two, and are not in accordance with the expected behaviour. Similarly, in spite of their f-values being higher than those of BD, their values of ![]() are the lowest. In the absence of much detail about their calculations, it is not straightforward to identify the exact source of this obvious
discrepancy in the PB data for allowed transitions. However, based on our experience on a number of Fe ions, and similar discrepancies observed earlier among different
calculations for some of these ions, such as Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004a, 2005), and Fe XV (Aggarwal
et al. 2000, 2001, 2003a), we make an attempt to understand this discrepancy.
are the lowest. In the absence of much detail about their calculations, it is not straightforward to identify the exact source of this obvious
discrepancy in the PB data for allowed transitions. However, based on our experience on a number of Fe ions, and similar discrepancies observed earlier among different
calculations for some of these ions, such as Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004a, 2005), and Fe XV (Aggarwal
et al. 2000, 2001, 2003a), we make an attempt to understand this discrepancy.
Since the ![]() values of PB are (nearly) constant for the 1-3 and 2-3 allowed transitions, in the entire energy range of 18-45 Ryd, it gives us an impression that for at
least these energies, their results are not converged. Since they claim to have included all partial waves with angular momentum
values of PB are (nearly) constant for the 1-3 and 2-3 allowed transitions, in the entire energy range of 18-45 Ryd, it gives us an impression that for at
least these energies, their results are not converged. Since they claim to have included all partial waves with angular momentum ![]() ,
the results for
,
the results for ![]() must have
converged, as is apparent from Fig. 2a for the 1-3 transition. Additionally, values of
must have
converged, as is apparent from Fig. 2a for the 1-3 transition. Additionally, values of ![]() for allowed transitions generally increase with increasing energy, and this is
also the trend confirmed by the other three calculations of BD, SST and ours. To elaborate further, in Fig. 4 we show the variation of
for allowed transitions generally increase with increasing energy, and this is
also the trend confirmed by the other three calculations of BD, SST and ours. To elaborate further, in Fig. 4 we show the variation of ![]() with the increasing addition of
partial waves, for the 1-3 transition at three energies of 18, 27 and 45 Ryd. It is clear from this figure that
with the increasing addition of
partial waves, for the 1-3 transition at three energies of 18, 27 and 45 Ryd. It is clear from this figure that ![]() have (nearly) converged in the partial waves range with
have (nearly) converged in the partial waves range with ![]() ,
at all three energies. It also clearly shows the cross-over from the contributions of lower partial waves to the higher ones. Up to a certain range (below J =
20 in the present case) the lower partial waves dominate, which means that if only
,
at all three energies. It also clearly shows the cross-over from the contributions of lower partial waves to the higher ones. Up to a certain range (below J =
20 in the present case) the lower partial waves dominate, which means that if only ![]() are included,
are included,
![]() will decrease with increasing energy.
However, as the contribution of higher partial waves is included, the reverse becomes true, i.e.
will decrease with increasing energy.
However, as the contribution of higher partial waves is included, the reverse becomes true, i.e.
![]() becomes higher at higher energies.
In the past, due to a scarcity of computational resources, it was a general practice to gradually increase the contribution of partial
waves with increasing electron energy. Therefore, we suspect that PB might have included all partial waves with
becomes higher at higher energies.
In the past, due to a scarcity of computational resources, it was a general practice to gradually increase the contribution of partial
waves with increasing electron energy. Therefore, we suspect that PB might have included all partial waves with ![]() for energies towards
the higher end of their calculations of
for energies towards
the higher end of their calculations of ![]() ,
but a limited range of partial waves was probably included for the calculations of
,
but a limited range of partial waves was probably included for the calculations of ![]() at energies below
at energies below ![]() 50 Ryd.
A detailed comparison of our calculations, for both 1-3 and 2-3 transitions, with their results listed in Table 3, indicates that they probably included
50 Ryd.
A detailed comparison of our calculations, for both 1-3 and 2-3 transitions, with their results listed in Table 3, indicates that they probably included ![]() ,
,
![]() and
and ![]() for calculating values of
for calculating values of ![]() at E = 18, 27 and 45 Ryd, respectively. Furthermore, apart from what is shown in Figs. 2a and 4, our above analysis is
based on exactly the same discrepancy observed in the Breit-Pauli calculations of Eissner et al. (1999) for allowed transitions in Fe XV - see particularly Fig. 5 of
Aggarwal et al. (2000) and note the step-wise increase in the
at E = 18, 27 and 45 Ryd, respectively. Furthermore, apart from what is shown in Figs. 2a and 4, our above analysis is
based on exactly the same discrepancy observed in the Breit-Pauli calculations of Eissner et al. (1999) for allowed transitions in Fe XV - see particularly Fig. 5 of
Aggarwal et al. (2000) and note the step-wise increase in the ![]() values of Eissner et al., and Figs. 1-4 of Aggarwal et al. (2001). Furthermore, in a recent
paper on Fe XXIII, Chidichimo et al. (2005) have also noted the non-inclusion of higher partial waves at lower energies in their earlier work (Chidichimo et al.
1999).
values of Eissner et al., and Figs. 1-4 of Aggarwal et al. (2001). Furthermore, in a recent
paper on Fe XXIII, Chidichimo et al. (2005) have also noted the non-inclusion of higher partial waves at lower energies in their earlier work (Chidichimo et al.
1999).
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{3057fig4.ps}
\end{figure}](/articles/aa/full/2005/33/aa3057-05/Timg41.gif) |
Figure 4:
Partial sums of collision strengths for the 3s23p5 2P
|
To conclude, we can state with confidence that for allowed transitions, and at least at energies below ![]() 50 Ryd, the
50 Ryd, the ![]() values of Pelan & Berrington (2001)
are not converged, due to the inclusion of a limited range of partial waves. Since this energy region is very important for the calculations of
values of Pelan & Berrington (2001)
are not converged, due to the inclusion of a limited range of partial waves. Since this energy region is very important for the calculations of ![]() at temperatures below
at temperatures below
![]() K (
K (![]()
![]() K), the reported results of PB for the effective collision strengths are expected to be underestimated, especially for the
allowed transitions, in the entire temperature range of their calculations. Some of the forbidden transitions will also be affected (see Figs. 1a and 3a for the 1-2 and 3-26),
but not to the same extent as the allowed ones. We discuss this further in Sect. 4.
K), the reported results of PB for the effective collision strengths are expected to be underestimated, especially for the
allowed transitions, in the entire temperature range of their calculations. Some of the forbidden transitions will also be affected (see Figs. 1a and 3a for the 1-2 and 3-26),
but not to the same extent as the allowed ones. We discuss this further in Sect. 4.
Finally, in Table 4 we demonstrate the effect of top-up for two forbidden (namely, 1-2 and 5-16) and two allowed (namely, 1-28 and 2-3) transitions, at three energies of 100,
150 and 200 Ryd. It is clear from this table that partial waves with ![]() are inadequate for accurate determination of
are inadequate for accurate determination of ![]() for both types of transitions. Similarly,
partial waves with
for both types of transitions. Similarly,
partial waves with ![]() may result up to 20% underestimation in the values of
may result up to 20% underestimation in the values of ![]() ,
especially for the allowed transitions. However, further addition of 10 more
partial waves provides results with comparable accuracy as achieved within our range of calculations with
,
especially for the allowed transitions. However, further addition of 10 more
partial waves provides results with comparable accuracy as achieved within our range of calculations with ![]() .
Therefore, based on this comparison and the behaviour of
partial
.
Therefore, based on this comparison and the behaviour of
partial ![]() s shown earlier in Figs. 1-4, we can state with confidence that the accuracy of our
s shown earlier in Figs. 1-4, we can state with confidence that the accuracy of our ![]() values is better than 10%, at all energies and for all transitions.
values is better than 10%, at all energies and for all transitions.
| (a) Forbidden transitions. | ||||||
| Transition | 1-2 | 5-16 | ||||
| Partial waves | 100 | 150 | 200 | 100 | 150 | 200 Ryd |
| 1.20-1 | 9.87-2 | 8.43-2 | 1.20-1 | 9.92-2 | 8.46-2 | |
| + top-up | 2.21-1 | 4.76-1 | 8.74-1 | 2.04-1 | 2.43-1 | 3.22-1 |
| 1.82-1 | 1.72-1 | 1.62-1 | 1.83-1 | 1.74-1 | 1.64-1 | |
| + top-up | 1.90-1 | 1.85-1 | 1.81-1 | 1.97-1 | 1.98-1 | 1.98-1 |
| 1.95-1 | 1.91-1 | 1.87-1 | 1.96-1 | 1.93-1 | 1.89-1 | |
| + top-up | 1.98-1 | 1.96-1 | 1.96-1 | 2.02-1 | 2.02-1 | 2.07-1 |
| 1.99-1 | 1.98-1 | 1.96-1 | 2.00-1 | 1.99-1 | 1.97-1 | |
| + top-up | 2.01-1 | 2.00-1 | 1.99-1 | 2.03-1 | 2.04-1 | 2.04-1 |
| (b) Allowed transitions. | ||||||
| Transition | 1-28 | 2-3 | ||||
| Partial waves | 100 | 150 | 200 | 100 | 150 | 200 Ryd |
| 1.83+0 | 1.23-0 | 8.78-1 | 7.43-2 | 4.92-2 | 3.48-2 | |
| + top-up | 6.49+0 | 6.35+0 | 6.32+0 | 2.97-1 | 2.90-1 | 2.88-1 |
| 4.80+0 | 4.13+0 | 3.55+0 | 1.98-1 | 1.68-1 | 1.45-1 | |
| + top-up | 9.45+0 | 9.25+0 | 8.99+0 | 4.20-1 | 4.09-1 | 3.98-1 |
| 6.30+0 | 5.82+0 | 5.32+0 | 2.71-1 | 2.40-1 | 2.17-1 | |
| + top-up | 1.00+1 | 1.07+1 | 1.08+1 | 4.46-1 | 4.68-1 | 4.71-1 |
| 7.09+0 | 6.89+0 | 6.53+0 | 3.21-1 | 2.92-1 | 2.70-1 | |
| + top-up | 1.00+1 | 1.07+1 | 1.12+0 | 4.46-1 | 4.68-1 | 4.88-1 |
Effective collision strengths ![]() are obtained after integrating
are obtained after integrating ![]() over a Maxwellian distribution of electron velocities, i.e.
over a Maxwellian distribution of electron velocities, i.e.
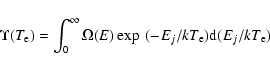 |
(1) |
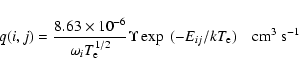 |
(2) |
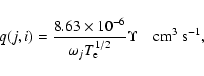 |
(3) |
Since the threshold energy region is dominated by numerous resonances, ![]() must be computed at a large number of energies in order to delineate these resonances.
We have performed our calculations of
must be computed at a large number of energies in order to delineate these resonances.
We have performed our calculations of ![]() at over 5400 energies in the threshold region. Close to thresholds (
at over 5400 energies in the threshold region. Close to thresholds (![]() 0.1 Ryd above a threshold)
the energy mesh is 0.001 Ryd, and away from thresholds is 0.002 Ryd. Thus care has been taken to include as many resonances as possible, and with as fine a resolution as is
computationally feasible. The values of
0.1 Ryd above a threshold)
the energy mesh is 0.001 Ryd, and away from thresholds is 0.002 Ryd. Thus care has been taken to include as many resonances as possible, and with as fine a resolution as is
computationally feasible. The values of ![]() so computed are listed in Table 5 at a series of electron temperatures in the range
so computed are listed in Table 5 at a series of electron temperatures in the range
![]() K, which is
fully sufficient for the application of the data to solar, astrophysical and fusion plasmas.
K, which is
fully sufficient for the application of the data to solar, astrophysical and fusion plasmas.
Before we compare our ![]() values, we would like to mention that the energy range of our calculations (i.e. 210 Ryd) is fully sufficient to determine results up to
values, we would like to mention that the energy range of our calculations (i.e. 210 Ryd) is fully sufficient to determine results up to
![]() K, which corresponds to
K, which corresponds to ![]() 63 Ryd in energy units. Hence, our included energy range is more than three times the highest temperature considered in the
calculations. To assess the
effect of various energy ranges, we have performed an exercise at a temperature of 106 K, including energies up to 15, 21, 27, 33 and 40 Ryd, which are up to 5 times this
temperature of
63 Ryd in energy units. Hence, our included energy range is more than three times the highest temperature considered in the
calculations. To assess the
effect of various energy ranges, we have performed an exercise at a temperature of 106 K, including energies up to 15, 21, 27, 33 and 40 Ryd, which are up to 5 times this
temperature of ![]() 6.3 Ryd, including the highest threshold energy of
6.3 Ryd, including the highest threshold energy of ![]() 8 Ryd. Results for resonance transitions obtained with up to one and two times the
8 Ryd. Results for resonance transitions obtained with up to one and two times the ![]() energies
differ up to 35%, whereas the corresponding differences with up to two and three times the
energies
differ up to 35%, whereas the corresponding differences with up to two and three times the ![]() energies are within 11%. Extension of the energy range up to four times
yields the
energies are within 11%. Extension of the energy range up to four times
yields the ![]() values within 4%, which further converge within 2% with the inclusion of higher energies up to five times the
values within 4%, which further converge within 2% with the inclusion of higher energies up to five times the ![]() .
Therefore, we see no need to
extrapolate our values of
.
Therefore, we see no need to
extrapolate our values of ![]() to determine results for
to determine results for ![]() .
.
| Transition | Tayal (2001) | Pelan & Berrington (2001) | Present results | |||||||
| Temperature (log |
Temperature (log |
Temperature (log |
||||||||
| i | j | 5.40 | 6.00 | 6.60 | 5.40 | 6.00 | 6.60 | 5.40 | 6.00 | 6.60 |
| 1 | 2 | 2.232 | 1.130 | 0.494 | 2.970-0 | 1.790-0 | 7.300-1 | 3.118-0 | 1.813-0 | 7.392-1 |
| 1 | 3 | 0.753 | 0.647 | 0.667 | 7.939-1 | 5.133-1 | 4.008-1 | 1.202-0 | 8.902-1 | 7.444-1 |
| 1 | 4 | 0.368 | 0.162 | 0.067 | 1.742-1 | 1.045-1 | 5.222-2 | 5.863-1 | 2.293-1 | 8.620-2 |
| 1 | 5 | 0.475 | 0.218 | 0.093 | 2.389-1 | 1.468-1 | 7.492-2 | 9.143-1 | 3.424-1 | 1.263-1 |
| 1 | 6 | 0.234 | 0.100 | 0.040 | 9.933-2 | 5.968-2 | 2.979-2 | 2.943-1 | 1.148-1 | 4.448-2 |
| 1 | 7 | 0.103 | 0.044 | 0.017 | 4.176-2 | 2.500-2 | 1.215-2 | 1.967-1 | 7.060-2 | 2.430-2 |
| 1 | 9 | 0.143 | 0.064 | 0.026 | 1.702-1 | 1.036-1 | 5.142-2 | 4.370-1 | 2.224-1 | 8.621-2 |
| 1 | 8 | 0.273 | 0.129 | 0.053 | 7.151-2 | 4.285-2 | 2.321-2 | 1.505-1 | 7.076-2 | 2.873-2 |
| 1 | 10 | 0.219 | 0.098 | 0.039 | 1.281-1 | 7.439-2 | 3.679-2 | 2.176-1 | 1.071-1 | 4.622-2 |
| 1 | 11 | 0.156 | 0.071 | 0.031 | 8.460-2 | 4.880-2 | 2.392-2 | 1.343-1 | 6.965-2 | 3.282-2 |
| 1 | 12 | 0.118 | 0.055 | 0.025 | 1.132-1 | 7.286-2 | 4.108-2 | 2.316-1 | 1.242-1 | 5.329-2 |
| 1 | 13 | 0.253 | 0.124 | 0.066 | 6.973-2 | 4.195-2 | 1.989-2 | 3.655-1 | 1.997-1 | 8.948-2 |
| 1 | 14 | 0.213 | 0.117 | 0.075 | 7.923-2 | 5.739-2 | 2.952-2 | 3.221-1 | 1.802-1 | 9.809-2 |
| 1 | 15 | 0.070 | 0.036 | 0.023 | 9.438-2 | 5.733-2 | 3.106-2 | 6.069-2 | 3.666-2 | 2.312-2 |
| 1 | 16 | 0.131 | 0.058 | 0.024 | 5.434-2 | 3.293-2 | 2.400-2 | 1.338-1 | 6.642-2 | 2.565-2 |
| 1 | 17 | 0.230 | 0.117 | 0.062 | 1.343-1 | 9.302-2 | 6.585-2 | 6.413-1 | 3.457-1 | 1.418-1 |
| 1 | 18 | 0.387 | 0.167 | 0.081 | 1.351-1 | 9.067-2 | 6.485-2 | 6.437-1 | 2.965-1 | 1.316-1 |
| 1 | 19 | 0.267 | 0.135 | 0.118 | 1.619-1 | 9.527-2 | 6.761-2 | 3.754-1 | 1.914-1 | 7.929-2 |
| 1 | 20 | 1.627-1 | 1.100-1 | 8.230-2 | 5.610-1 | 2.523-1 | 1.218-1 | |||
| 1 | 21 | 1.177-1 | 6.502-2 | 2.889-2 | 2.794-1 | 1.210-1 | 4.433-2 | |||
| 1 | 22 | 0.197 | 0.088 | 0.044 | 1.101-1 | 6.217-2 | 3.300-2 | 3.002-1 | 1.321-1 | 5.597-2 |
| 1 | 23 | 0.236 | 0.102 | 0.057 | 1.045-1 | 6.480-2 | 4.470-2 | 1.804-1 | 9.901-2 | 6.153-2 |
| 1 | 24 | 0.288 | 0.126 | 0.073 | 1.288-1 | 8.221-2 | 6.221-2 | 2.194-1 | 1.040-1 | 6.415-2 |
| 1 | 25 | 0.152 | 0.080 | 0.063 | 5.803-2 | 4.534-2 | 3.937-2 | 2.045-1 | 9.789-2 | 6.087-2 |
| 1 | 26 | 0.217 | 0.092 | 0.054 | 5.941-2 | 4.350-2 | 4.242-2 | 1.326-1 | 6.780-2 | 4.115-2 |
| 1 | 27 | 1.709 | 2.003 | 2.763 | 1.908-0 | 1.933-0 | 1.950-0 | 1.887-0 | 2.080-0 | 2.649-0 |
| 1 | 28 | 3.360 | 3.847 | 5.286 | 3.856-0 | 3.934-0 | 4.018-0 | 4.081-0 | 4.224-0 | 5.337-0 |
| 1 | 29 | 0.494 | 0.511 | 0.681 | 4.783-1 | 4.924-1 | 5.608-1 | 5.618-1 | 5.518-1 | 6.788-1 |
| 1 | 30 | 5.628 | 6.650 | 9.217 | 6.805-0 | 7.032-0 | 7.171-0 | 6.476-0 | 7.259-0 | 9.355-0 |
| 1 | 31 | 0.322 | 0.292 | 0.363 | 2.161-1 | 2.274-1 | 2.690-1 | 1.909-1 | 1.987-1 | 2.406-1 |
| 2 | 3 | 0.380 | 0.340 | 0.356 | 3.508-1 | 2.481-1 | 2.039-1 | 5.769-1 | 4.661-1 | 3.953-1 |
| 2 | 4 | 0.164 | 0.066 | 0.025 | 5.955-2 | 3.416-2 | 1.662-2 | 4.003-1 | 1.305-1 | 4.159-2 |
| 2 | 5 | 0.160 | 0.062 | 0.022 | 5.393-2 | 2.842-2 | 1.270-2 | 1.808-1 | 6.708-2 | 2.292-2 |
| 2 | 6 | 0.125 | 0.054 | 0.022 | 5.324-2 | 3.237-2 | 1.627-2 | 1.319-1 | 5.434-2 | 2.181-2 |
| 2 | 7 | 0.067 | 0.031 | 0.013 | 3.206-2 | 2.058-2 | 1.077-2 | 8.254-2 | 3.457-2 | 1.445-2 |
| 2 | 8 | 0.087 | 0.039 | 0.016 | 2.919-2 | 1.508-2 | 6.590-3 | 4.530-2 | 1.960-2 | 7.596-3 |
| 2 | 9 | 0.074 | 0.036 | 0.021 | 3.117-2 | 2.159-2 | 1.185-2 | 6.843-2 | 3.856-2 | 2.489-2 |
| 2 | 10 | 0.102 | 0.048 | 0.020 | 4.983-2 | 2.856-2 | 1.362-2 | 7.923-2 | 3.996-2 | 1.648-2 |
| 2 | 11 | 0.084 | 0.041 | 0.017 | 5.393-2 | 3.136-2 | 1.508-2 | 7.515-2 | 3.934-2 | 1.724-2 |
| 2 | 12 | 0.059 | 0.028 | 0.011 | 7.865-2 | 4.837-2 | 2.264-2 | 1.955-1 | 9.893-2 | 4.189-2 |
| 2 | 13 | 0.140 | 0.070 | 0.035 | 4.683-2 | 2.706-2 | 1.835-2 | 2.194-1 | 1.108-1 | 4.292-2 |
| 2 | 14 | 0.099 | 0.049 | 0.031 | 3.081-2 | 1.936-2 | 9.344-3 | 2.018-1 | 9.542-2 | 3.901-2 |
| 2 | 15 | 0.035 | 0.018 | 0.010 | 3.601-2 | 2.157-2 | 1.060-2 | 2.118-2 | 1.356-2 | 8.386-3 |
| 2 | 16 | 0.090 | 0.045 | 0.020 | 5.164-2 | 3.272-2 | 2.405-2 | 1.598-1 | 7.657-2 | 2.840-2 |
| 2 | 17 | 0.081 | 0.035 | 0.015 | 4.712-2 | 2.662-2 | 1.277-2 | 1.053-1 | 5.557-2 | 2.432-2 |
| 2 | 18 | 0.118 | 0.053 | 0.027 | 8.664-2 | 4.518-2 | 2.053-2 | 1.398-1 | 5.981-2 | 2.052-2 |
| 2 | 19 | 0.171 | 0.093 | 0.050 | 7.566-2 | 5.034-2 | 3.169-2 | 1.537-1 | 8.785-2 | 4.327-2 |
| 2 | 20 | 9.240-2 | 5.633-2 | 2.808-2 | 3.740-1 | 1.291-1 | 4.635-2 | |||
| 2 | 21 | 1.118-1 | 7.448-2 | 5.606-2 | 1.966-1 | 1.058-1 | 6.798-2 | |||
| 2 | 22 | 0.152 | 0.066 | 0.032 | 8.446-2 | 5.010-2 | 2.847-2 | 2.931-1 | 1.551-1 | 6.390-2 |
| 2 | 23 | 0.122 | 0.053 | 0.033 | 6.416-2 | 3.916-2 | 3.245-2 | 1.223-1 | 6.197-2 | 3.494-2 |
| 2 | 24 | 0.125 | 0.054 | 0.029 | 6.110-2 | 4.136-2 | 3.164-2 | 7.865-2 | 4.544-2 | 2.991-2 |
| 2 | 25 | 0.093 | 0.036 | 0.016 | 3.808-2 | 2.613-2 | 1.251-2 | 3.966-2 | 2.529-2 | 1.879-2 |
| 2 | 26 | 0.122 | 0.054 | 0.028 | 4.474-2 | 3.155-2 | 2.069-2 | 1.486-1 | 6.576-2 | 3.106-2 |
| 2 | 27 | 0.624 | 0.715 | 0.958 | 6.641-1 | 6.714-1 | 7.446-1 | 6.783-1 | 7.521-1 | 9.556-1 |
| 2 | 28 | 0.274 | 0.224 | 0.263 | 1.400-1 | 1.393-1 | 1.828-1 | 1.552-1 | 1.291-1 | 1.438-1 |
| 2 | 29 | 1.337 | 1.550 | 2.136 | 1.520-0 | 1.548-0 | 1.549-0 | 1.418-0 | 1.610-0 | 2.080-0 |
| 2 | 30 | 0.130 | 0.053 | 0.024 | 2.923-2 | 2.191-2 | 1.624-2 | 6.315-2 | 3.047-2 | 1.874-2 |
| 2 | 31 | 3.545 | 4.185 | 5.811 | 4.289-0 | 4.431-0 | 4.500-0 | 4.056-0 | 4.625-0 | 5.977-0 |
| 3 | 4 | 0.082 | 0.031 | 0.010 | 7.320-2 | 3.511-2 | 1.180-2 | 1.352-1 | 5.156-2 | 1.576-2 |
| 3 | 5 | 0.095 | 0.036 | 0.011 | 7.490-2 | 3.613-2 | 1.232-2 | 1.206-1 | 4.800-2 | 1.508-2 |
| 3 | 6 | 0.062 | 0.023 | 0.007 | 5.718-2 | 2.846-2 | 9.616-3 | 1.059-1 | 3.802-2 | 1.137-2 |
| 3 | 7 | 0.032 | 0.013 | 0.004 | 3.368-2 | 1.877-2 | 6.472-3 | 5.473-2 | 2.008-2 | 5.993-3 |
| 3 | 8 | 0.024 | 0.008 | 0.002 | 4.523-2 | 1.926-2 | 5.966-3 | 4.152-2 | 1.754-2 | 5.298-3 |
| 3 | 9 | 0.076 | 0.031 | 0.009 | 1.418-1 | 7.953-2 | 2.662-2 | 6.101-2 | 2.742-2 | 8.571-3 |
| 3 | 10 | 0.020 | 0.008 | 0.002 | 4.355-2 | 1.893-2 | 5.838-3 | 4.211-2 | 1.767-2 | 5.250-3 |
| 3 | 11 | 0.016 | 0.007 | 0.003 | 3.996-2 | 1.757-2 | 5.655-3 | 3.980-2 | 1.753-2 | 5.573-3 |
| 3 | 12 | 0.020 | 0.010 | 0.006 | 1.864-1 | 1.074-1 | 3.684-2 | 6.341-2 | 3.089-2 | 1.059-2 |
| 3 | 13 | 0.119 | 0.050 | 0.015 | 5.186-2 | 2.452-2 | 8.010-3 | 7.875-2 | 3.642-2 | 1.196-2 |
| 3 | 14 | 0.069 | 0.034 | 0.016 | 6.553-2 | 3.666-2 | 1.323-2 | 9.052-2 | 4.928-2 | 2.107-2 |
| 3 | 15 | 0.023 | 0.010 | 0.003 | 7.676-2 | 3.946-2 | 1.414-2 | 1.522-2 | 6.707-3 | 2.063-3 |
| 3 | 16 | 0.046 | 0.020 | 0.007 | 5.784-2 | 3.379-2 | 1.321-2 | 4.264-2 | 2.001-2 | 6.523-3 |
| 3 | 17 | 0.055 | 0.026 | 0.012 | 8.582-2 | 4.626-2 | 1.927-2 | 1.141-1 | 5.648-2 | 2.378-2 |
| 3 | 18 | 0.036 | 0.014 | 0.005 | 8.799-2 | 4.168-2 | 1.433-2 | 7.205-2 | 3.081-2 | 9.763-3 |
| 3 | 19 | 0.105 | 0.050 | 0.023 | 9.557-2 | 5.065-2 | 2.401-2 | 1.121-1 | 5.432-2 | 2.078-2 |
| 3 | 20 | 7.761-2 | 3.980-2 | 1.469-2 | 1.031-1 | 4.112-2 | 1.391-2 | |||
| 3 | 21 | 7.417-2 | 3.427-2 | 1.175-2 | 5.712-2 | 2.624-2 | 8.977-3 | |||
| 3 | 22 | 0.035 | 0.014 | 0.005 | 6.696-2 | 3.221-2 | 1.028-2 | 5.259-2 | 2.188-2 | 6.572-3 |
| 3 | 23 | 0.139 | 0.045 | 0.013 | 4.850-2 | 2.454-2 | 8.389-3 | 5.118-2 | 2.366-2 | 7.633-3 |
| 3 | 24 | 0.188 | 0.058 | 0.016 | 4.806-2 | 2.592-2 | 9.892-3 | 4.211-2 | 1.795-2 | 5.938-3 |
| 3 | 25 | 0.077 | 0.035 | 0.020 | 4.152-2 | 2.820-2 | 1.836-2 | 6.774-2 | 3.585-2 | 2.196-2 |
| 3 | 26 | 0.090 | 0.046 | 0.030 | 5.213-2 | 3.718-2 | 2.734-2 | 6.841-2 | 4.240-2 | 3.173-2 |
| 3 | 27 | 0.087 | 0.039 | 0.015 | 2.772-1 | 1.819-1 | 6.321-2 | 6.568-2 | 2.808-2 | 1.056-2 |
| 3 | 28 | 0.149 | 0.069 | 0.023 | 1.967-1 | 1.057-1 | 3.508-2 | 1.574-1 | 6.616-2 | 2.190-2 |
| 3 | 29 | 0.081 | 0.037 | 0.012 | 1.179-1 | 6.294-2 | 2.079-2 | 9.328-2 | 3.978-2 | 1.293-2 |
| 3 | 30 | 0.203 | 0.092 | 0.034 | 1.712-1 | 7.721-2 | 2.835-2 | 2.324-1 | 9.731-2 | 3.474-2 |
| 3 | 31 | 0.138 | 0.060 | 0.023 | 1.199-1 | 5.453-2 | 2.051-2 | 1.166-1 | 5.706-2 | 2.243-2 |
In Table 6 we compare our results of ![]() with those of SST and PB for common transitions, from the lowest three levels to higher excited levels, at three common
temperatures of
with those of SST and PB for common transitions, from the lowest three levels to higher excited levels, at three common
temperatures of
![]() ,
6.0 and 6.6 K. Although all three sets of calculations are based on the R-matrix method, included CI and relativistic effects in the
generation of wavefunctions, and have resolved resonances in thershold region, the values of
,
6.0 and 6.6 K. Although all three sets of calculations are based on the R-matrix method, included CI and relativistic effects in the
generation of wavefunctions, and have resolved resonances in thershold region, the values of ![]() show poor agreement for a majority of transitions. Different sets of
results differ by up to a factor of two. For example, the
show poor agreement for a majority of transitions. Different sets of
results differ by up to a factor of two. For example, the ![]() values of SST and PB differ for the 1-4 and 2-4 transitions, SST and ours for the 1-5 and 1-9, and PB and ours for the 1-3 and 1-5 transitions. However, such large differences among different calculations are fully understandable, but before we explain this we would like to
first mention the specific differences between our calculations and those of SST and PB. Firstly, our calculations are fully relativistic and in jj coupling, which
not only properly accounts for the relativistic effects, but also shows comparatively more resonances because of the inclusion of fine-structure in the definition of channel
coupling. In contrast, the calculations of SST and PB are semi-relativistic in the
values of SST and PB differ for the 1-4 and 2-4 transitions, SST and ours for the 1-5 and 1-9, and PB and ours for the 1-3 and 1-5 transitions. However, such large differences among different calculations are fully understandable, but before we explain this we would like to
first mention the specific differences between our calculations and those of SST and PB. Firstly, our calculations are fully relativistic and in jj coupling, which
not only properly accounts for the relativistic effects, but also shows comparatively more resonances because of the inclusion of fine-structure in the definition of channel
coupling. In contrast, the calculations of SST and PB are semi-relativistic in the ![]() coupling scheme, and do not account for the two-body relativistic operators. Secondly,
for the generation of wavefunctions our calculations include larger CI than those of SST or PB, which improves the accuracy of the energy levels and radiative rates, and
subsequently of
coupling scheme, and do not account for the two-body relativistic operators. Secondly,
for the generation of wavefunctions our calculations include larger CI than those of SST or PB, which improves the accuracy of the energy levels and radiative rates, and
subsequently of ![]() and
and ![]() .
Thirdly, our calculations include a larger range of partial waves (
.
Thirdly, our calculations include a larger range of partial waves (![]() 39) than those of SST (
39) than those of SST (![]() )
or of PB (see
Sect. 3).
This improves the accuracy of the
)
or of PB (see
Sect. 3).
This improves the accuracy of the ![]() values, not only for the allowed transitions but for the forbidden ones also, as already discussed in Sect. 3. Similarly, our
calculations cover a wider range of energy, i.e.
values, not only for the allowed transitions but for the forbidden ones also, as already discussed in Sect. 3. Similarly, our
calculations cover a wider range of energy, i.e. ![]() Ryd in comparison to
Ryd in comparison to
![]() Ryd of SST. PB have included a higher energy range, but to no additional advantage, because to calculate values of
Ryd of SST. PB have included a higher energy range, but to no additional advantage, because to calculate values of ![]() up to
up to
![]() K,
K, ![]() Ryd is more than sufficient, as discussed above. Finally, our calculations include 90 levels, whereas those of SST and PB include 54 and 31 levels, respectively.
The energy mesh of our calculations and those of PB
are comparable (
Ryd is more than sufficient, as discussed above. Finally, our calculations include 90 levels, whereas those of SST and PB include 54 and 31 levels, respectively.
The energy mesh of our calculations and those of PB
are comparable (
![]() Ryd), whereas that of SST is comparatively coarse, i.e.
Ryd), whereas that of SST is comparatively coarse, i.e.
![]() Ryd. In summary, the calculations of PB or ours
are comparatively more sophisticated than those of SST, yet there is a better agreement of our
Ryd. In summary, the calculations of PB or ours
are comparatively more sophisticated than those of SST, yet there is a better agreement of our ![]() results with those of SST than of PB. We explain this below.
results with those of SST than of PB. We explain this below.
In Figs. 5-7 we show our values of ![]() in the threshold region for the 1-2, 1-3 and 2-3 transitions, respectively. SST has shown his results for these transitions in his
Figs. 1-3 (Tayal 2000), and PB have shown their results for the 1-3 and 2-3 transitions in their Fig. 2. A comparison of these figures clearly shows that resonances in our
calculations are
denser, because of the reasons explained above. Therefore, it is no surprise that our results of
in the threshold region for the 1-2, 1-3 and 2-3 transitions, respectively. SST has shown his results for these transitions in his
Figs. 1-3 (Tayal 2000), and PB have shown their results for the 1-3 and 2-3 transitions in their Fig. 2. A comparison of these figures clearly shows that resonances in our
calculations are
denser, because of the reasons explained above. Therefore, it is no surprise that our results of ![]() are higher than those of SST, especially for the forbidden
transitions, such as 1-2, 2-4 and 3-5. For some of the allowed transitions (such as 1-9, 1-12 and 2-28), part of the differences between our results and his are probably
because of the similar differences in the corresponding f-values, although it cannot be verified because he has not reported his results for oscillator strengths and/or
the radiative rates. On the other hand, the corresponding results of PB for the allowed transitions, such as 1-3 and 2-3, are lower. This is in spite of the fact that the f-values for both of these transitions are comparable in all three calculations. A closer comparison of our Figs. 6 and 7 with the corresponding figures of SST shows that the
background
are higher than those of SST, especially for the forbidden
transitions, such as 1-2, 2-4 and 3-5. For some of the allowed transitions (such as 1-9, 1-12 and 2-28), part of the differences between our results and his are probably
because of the similar differences in the corresponding f-values, although it cannot be verified because he has not reported his results for oscillator strengths and/or
the radiative rates. On the other hand, the corresponding results of PB for the allowed transitions, such as 1-3 and 2-3, are lower. This is in spite of the fact that the f-values for both of these transitions are comparable in all three calculations. A closer comparison of our Figs. 6 and 7 with the corresponding figures of SST shows that the
background ![]() are also comparable, whereas those of PB (shown in their Fig. 2 for the same transitions) are lower by
are also comparable, whereas those of PB (shown in their Fig. 2 for the same transitions) are lower by ![]() 30%. This is because their values of
30%. This is because their values of ![]() have not converged at lower energies, as explained in Sect. 3. For the same reason, the discrepancy between their results and ours or those of SST increases with
increasing temperature, because the PB
have not converged at lower energies, as explained in Sect. 3. For the same reason, the discrepancy between their results and ours or those of SST increases with
increasing temperature, because the PB ![]() values decrease with increasing temperature for (almost) all transitions, including the allowed ones. This limitation to their
work becomes more apparent for some of the strong allowed transitions, such as 1-27, 1-28, 1-30, 2-29 and 2-31. For all of these transitions, the
values decrease with increasing temperature for (almost) all transitions, including the allowed ones. This limitation to their
work becomes more apparent for some of the strong allowed transitions, such as 1-27, 1-28, 1-30, 2-29 and 2-31. For all of these transitions, the ![]() results of PB remain
nearly constant (within 10%) in the temperature range of
results of PB remain
nearly constant (within 10%) in the temperature range of
![]() K, whereas those of us or SST increase by
K, whereas those of us or SST increase by ![]() 50% in the same range of
temperature. Since the temperature of maximum Fe X abundance in ionization equilibrium is around 106 K, the temperature range discussed above is highly important. It is
clear from the comparisons shown in Table 6 that the
50% in the same range of
temperature. Since the temperature of maximum Fe X abundance in ionization equilibrium is around 106 K, the temperature range discussed above is highly important. It is
clear from the comparisons shown in Table 6 that the ![]() results of PB are underestimated by up to a factor of two, mostly for the
allowed transitions, such as 1-3 and 2-3. Their corresponding results for some of the forbidden transitions are also underestimated, particularly towards the higher end of the
temperature range, and examples of these are the 1-21, 2-20, 3-4 and 3-26 transitions. It may also be noted that the temperature of
results of PB are underestimated by up to a factor of two, mostly for the
allowed transitions, such as 1-3 and 2-3. Their corresponding results for some of the forbidden transitions are also underestimated, particularly towards the higher end of the
temperature range, and examples of these are the 1-21, 2-20, 3-4 and 3-26 transitions. It may also be noted that the temperature of ![]() 106 K is only important in
solar plasmas, and higher temperatures (of the order of 107 K) may be required for diagnostics of fusion plasmas. At such high temperatures, the
106 K is only important in
solar plasmas, and higher temperatures (of the order of 107 K) may be required for diagnostics of fusion plasmas. At such high temperatures, the ![]() results of PB
are clearly underestimated, and are likely to be unsuitable for applications.
results of PB
are clearly underestimated, and are likely to be unsuitable for applications.
Finally, in Figs. 8-11 we show resonances in ![]() for the 1-4, 1-5, 3-4 and 3-5 transitions, because similar resonances have also been shown by PB in their Figs. 3 and 4. It
is interesting to note two clear differences for all the 4 transitions. Firstly, close to the thresholds the background values of
for the 1-4, 1-5, 3-4 and 3-5 transitions, because similar resonances have also been shown by PB in their Figs. 3 and 4. It
is interesting to note two clear differences for all the 4 transitions. Firstly, close to the thresholds the background values of ![]() are higher in the PB work than
in our calculations. This is perhaps a direct consequence of the difference in the coupling schemes adopted in the two calculations. Secondly, at energies above
are higher in the PB work than
in our calculations. This is perhaps a direct consequence of the difference in the coupling schemes adopted in the two calculations. Secondly, at energies above ![]() 5 Ryd
there is a dense group of resonances in the calculations of PB, which is missing from our work. This is most likely because of the inclusion of all the 141 levels of the
3s23p33d2 configuration in the PB work (for a limited range of partial waves only), whereas only 36 of these levels are included in our calculations, as stated in
Sect. 2. Due to the limitations of our computational resources, a larger calculation with all the levels could not be performed at present, but it clearly emphasizes the
need for including the additional levels. Nevertheless, in spite of the higher
5 Ryd
there is a dense group of resonances in the calculations of PB, which is missing from our work. This is most likely because of the inclusion of all the 141 levels of the
3s23p33d2 configuration in the PB work (for a limited range of partial waves only), whereas only 36 of these levels are included in our calculations, as stated in
Sect. 2. Due to the limitations of our computational resources, a larger calculation with all the levels could not be performed at present, but it clearly emphasizes the
need for including the additional levels. Nevertheless, in spite of the higher ![]() background at lower energies and denser resonances in the wider energy range, the
background at lower energies and denser resonances in the wider energy range, the
![]() values of PB are still lower than ours. This is because of the denser and higher resonances we observe at energies close to the threshold, which have arisen
due to the inclusion of fine-structure in the definition of channel coupling.
values of PB are still lower than ours. This is because of the denser and higher resonances we observe at energies close to the threshold, which have arisen
due to the inclusion of fine-structure in the definition of channel coupling.
![\begin{figure}\par\includegraphics[angle=-90,width=8.5cm,clip]{3057fig12.ps}
\end{figure}](/articles/aa/full/2005/33/aa3057-05/Timg65.gif) |
Figure 12:
Cross sections for the (2s23p5) 2P
|
| Level | Index | Wang & Griem (1983) | Mason (1975) | Mann (1983) | ||||||
| Temperature (eV) | 45 | 75 | 95 | 45 | 75 | 95 | 45 | 75 | 95 | |
| 3p4(1D)3d 2S1/2 | 27 | 2.0 | 2.4 | 3.3 | 1.4 | 2.0 | 2.2 | 1.5 | 2.3 | 2.6 |
| 3p4(3P)3d 2P3/2 | 28 | 2.3 | 2.6 | 3.0 | 1.8 | 2.6 | 2.8 | 2.0 | 3.1 | 3.4 |
| 3p4(3P)3d 2P1/2 | 29 | .96 | 1.2 | 2.2 | .93 | 1.4 | 1.5 | 1.0 | 1.6 | 1.7 |
| 3p4(3P)3d 2D5/2 | 30 | 3.9 | 4.8 | 6.6 | 3.2 | 4.8 | 5.2 | 3.8 | 5.8 | 6.4 |
| 3p4(3P)3d 2D3/2 | 31 | 2.3 | 2.8 | 4.2 | 2.2 | 3.1 | 3.4 | 2.5 | 3.8 | 4.2 |
| Level | Index | Tayal (2001) | Pelan & Berrington (2001) | Present results | ||||||
| Temperature (eV) | 45 | 75 | 95 | 45 | 75 | 95 | 45 | 75 | 95 | |
| 3p4(1D)3d 2S1/2 | 27 | 1.08 | 1.64 | 1.83 | 1.14 | 1.63 | 1.76 | 1.17 | 1.74 | 1.92 |
| 3p4(3P)3d 2P3/2 | 28 | 1.49 | 2.31 | 2.66 | 1.62 | 2.40 | 2.69 | 1.69 | 2.55 | 2.91 |
| 3p4(3P)3d 2P1/2 | 29 | .775 | 1.18 | 1.33 | .804 | 1.20 | 1.30 | .833 | 1.27 | 1.42 |
| 3p4(3P)3d 2D5/2 | 30 | 2.39 | 3.79 | 4.26 | 2.74 | 4.10 | 4.49 | 2.69 | 4.19 | 4.70 |
| 3p4(3P)3d 2D3/2 | 31 | 1.67 | 2.61 | 2.95 | 1.83 | 2.75 | 3.02 | 1.78 | 2.78 | 3.15 |
Wang & Griem (1983) have measured statistically averaged excitation rates from the ground state 2p5 2P![]() to higher excited levels of the 2p43d configuration,
at three electron temperatures of 45, 75 and 95 eV. Their results are compared in Table 7 with our corresponding theoretical rates. Also included in this table are the earlier
results from the work of Mason (1975) and Mann (1983). Both of them have adopted the DW code for the computations of
to higher excited levels of the 2p43d configuration,
at three electron temperatures of 45, 75 and 95 eV. Their results are compared in Table 7 with our corresponding theoretical rates. Also included in this table are the earlier
results from the work of Mason (1975) and Mann (1983). Both of them have adopted the DW code for the computations of ![]() ,
have employed limited CI in the
generation of wavefunctions, and have not resolved resonances in thresholds region. As a result of these limitations, their rates are not only comparable with each other
(within 20%), but also agree with the measurements. However, later calculations of Pelan & Berrington (2001) and Tayal (2001) are comparatively more sophisticated
as already discussed in Sect. 1. The excitation rates obtained from their
,
have employed limited CI in the
generation of wavefunctions, and have not resolved resonances in thresholds region. As a result of these limitations, their rates are not only comparable with each other
(within 20%), but also agree with the measurements. However, later calculations of Pelan & Berrington (2001) and Tayal (2001) are comparatively more sophisticated
as already discussed in Sect. 1. The excitation rates obtained from their ![]() values are also listed in Table 7 to provide a ready comparison. Both sets of these rates
compare excellently with each other, at all temperatures and for all transitions listed in Table 7, and also agree within 10% with our present results. However, in comparison
to all the three R-matrix calculations, which employ better wavefunctions and include resonances in the determination of rates (or
values are also listed in Table 7 to provide a ready comparison. Both sets of these rates
compare excellently with each other, at all temperatures and for all transitions listed in Table 7, and also agree within 10% with our present results. However, in comparison
to all the three R-matrix calculations, which employ better wavefunctions and include resonances in the determination of rates (or ![]() ), the experimental results of
Wang & Griem are clearly overestimated by up to 50% for almost all transitions and at all temperatures. Nevertheless, their estimated errors are up to 60%, depending
on the transition and the temperature of measurement. Taking these error estimates into consideration, we may state that theory and experiment agree well at high temperatures.
), the experimental results of
Wang & Griem are clearly overestimated by up to 50% for almost all transitions and at all temperatures. Nevertheless, their estimated errors are up to 60%, depending
on the transition and the temperature of measurement. Taking these error estimates into consideration, we may state that theory and experiment agree well at high temperatures.
In the present work, collision strengths and effective collision strengths for transitions among 90 fine-structure levels of Fe X are computed
using the fully relativistic DARC code of Norrington & Grant (2005). Results for both of these parameters are reported over a wide range of energy/temperature, suitable
for applications in a variety of plasmas. Together with our earlier results for energy levels and radiative rates (Aggarwal & Keenan 2004b), the present work reports a
consistent set of results for many atomic parameters, and for a wider range of levels/transitions than hitherto available in the literature. Additionally, the present work is a
clear improvement over the earlier results of BD, SST and PB. This has become possible due to the availability of better computational resources to us, which were perhaps not
available to earlier workers. In comparison to the work of BD, our calculations have significantly improved the accuracy of energy levels,
radiative rates and collision strengths, by including extensive CI and performing the calculations in the jj coupling. Furthermore, the levels/transitions range of their work
has been increased by almost a factor of two, and the energy range by over a factor of four. In comparison to the work of SST, an overall improvement has been made by: (i) including additional CI in the generation of wavefunctions, and thus improving the accuracy of energy levels; (ii) extending the range of levels from 54 to 90, and hence
including many of the desired levels among which the transitions have already been observed; (iii) improving the accuracy of ![]() values, by extending the range of partial
waves (from 20 to 39) and the energy range (from 90 Ryd to 210 Ryd); (iv) improving the
values, by extending the range of partial
waves (from 20 to 39) and the energy range (from 90 Ryd to 210 Ryd); (iv) improving the ![]() values by resolving resonances in a finer energy mesh and by including
additional resonances; (v) performing the calculations in the jj coupling instead of the SST semi-relativistic approach in the
values by resolving resonances in a finer energy mesh and by including
additional resonances; (v) performing the calculations in the jj coupling instead of the SST semi-relativistic approach in the ![]() coupling scheme; and finally (vi) reporting
the results for all transitions, instead of only a few. Similarly, the present work is an improvement over the work of PB mainly by extending the range of levels
(transitions) from 31 (465) to 90 (4005), and by achieving convergence in values of
coupling scheme; and finally (vi) reporting
the results for all transitions, instead of only a few. Similarly, the present work is an improvement over the work of PB mainly by extending the range of levels
(transitions) from 31 (465) to 90 (4005), and by achieving convergence in values of ![]() at all energies. The latter factor in particular has shown that the
earlier reported results of
at all energies. The latter factor in particular has shown that the
earlier reported results of ![]() by PB are underestimated up to a factor of two, for many transitions and in a wider range of temperature.
by PB are underestimated up to a factor of two, for many transitions and in a wider range of temperature.
Based on the available experimental data for energy levels and life-times, and on comparisons with several sets of calculations, we assessed the accuracy of our energy
levels and radiative rates to be better than 3% and 20%, respectively (Aggarwal & Keenan 2004b). Experimental values of collision cross sections are confined to a
single transition (1-2), and that too for a very limited energy range below 6 eV. Unfortunately, our theoretical results disagree with the experimental ones for this
limited data. However, statistically averaged excitation rates are available from the plasma experiments for a few levels, and at three temperatures of 45, 75 and 95 eV. For
these common levels there is satisfactory agreement among various sophisticated theoretical results, but the experimental values are assessed to be overestimated by up to 50%.
Nevertheless, this overestimation of experimental data are within the estimated error limits. Furthermore, based on several comparisons made with the
earlier available results and our experience of similar calculations on a wide range of ions, we estimate the accuracy of our ![]() and
and ![]() data to be better than 20%
for a majority of transitions. However, due to the presence of dense resonances in the threshold region, the results for
data to be better than 20%
for a majority of transitions. However, due to the presence of dense resonances in the threshold region, the results for ![]() become more variable particularly towards the
lower end of the temperature range. This particularly affects those transitions for which near-threshold resonances are dense as well as high. Similarly, radiative damping may
reduce the resonance effect, which needs to be explored in future work. Furthermore, scope also remains for an
improvement for transitions with higher upper levels, by including resonances from the higher lying levels of the neglected configurations, as highlighted in Sect. 4.
However, this will significantly increase the range of levels and the calculations for which may be possible in future. Until then the present set of results for a range of
atomic parameters should be highly useful for diagnostics and modelling applications.
become more variable particularly towards the
lower end of the temperature range. This particularly affects those transitions for which near-threshold resonances are dense as well as high. Similarly, radiative damping may
reduce the resonance effect, which needs to be explored in future work. Furthermore, scope also remains for an
improvement for transitions with higher upper levels, by including resonances from the higher lying levels of the neglected configurations, as highlighted in Sect. 4.
However, this will significantly increase the range of levels and the calculations for which may be possible in future. Until then the present set of results for a range of
atomic parameters should be highly useful for diagnostics and modelling applications.
Finally, it is unfortunate that in a recent elaborate "benchmarking'' exercise Del Zanna et al. (2004) have adopted the atomic data of Pelan &
Berrington (2001), which have been shown to be deficient. Without performing a calculation it is difficult to assess the impact of our data on their derived results of
wavelengths and intensities for many transitions of importance. The five brightest lines of Fe X (in decreasing order of intensity) are from the 1-30, 1-2, 1-28, 1-27 and 1-5 transitions - see Table 7 of Del Zanna et al. Only for the 1-2 transition, do our and the PB values of ![]() agree closely in the entire temperature range (see Table 6).
Their
agree closely in the entire temperature range (see Table 6).
Their ![]() results for the 1-27, 1-28 and 1-30 transitions are lower by up to 30%, particularly towards the higher end of the temperature range, whereas their results
for the 1-5 transition are lower between a factor of 4 and 2, depending on the temperature. Therefore, it will be interesting to see the effect of our new data in a fresh
calculation. We hope to perform such an exercise in the near future.
results for the 1-27, 1-28 and 1-30 transitions are lower by up to 30%, particularly towards the higher end of the temperature range, whereas their results
for the 1-5 transition are lower between a factor of 4 and 2, depending on the temperature. Therefore, it will be interesting to see the effect of our new data in a fresh
calculation. We hope to perform such an exercise in the near future.
Acknowledgements
This work has been financed by the Engineering and Physical Sciences and Particle Physics and Astronomy Research Councils of the UK. We would like to thank Dr. Patrick Norrington for providing his DARC code prior to publication, and FPK is grateful to AWE Aldermaston for the award of a William Penny Fellowship. Finally, we thank an anonymous referee whose careful reading of the earlier version and constructive criticism have been helpful in improving the overall presentation of our work.