- ... short-range
![[*]](/icons/foot_motif.gif)
- Due to the power-law relation between flux density and
frequency, the influence of the flux density variability on the spectral index
decreases with increasing frequency interval.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... relativity
![[*]](/icons/foot_motif.gif)
- If
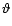 is the angle enclosed by the
line of sight and the direction of motion and if
is the angle enclosed by the
line of sight and the direction of motion and if 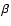 is the intrinsic
velocity, one finds
is the intrinsic
velocity, one finds
 .
The minimal
intrinsic velocity
.
The minimal
intrinsic velocity
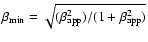 implies an
angle
implies an
angle
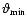 fulfilling:
fulfilling:
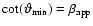 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dominant
![[*]](/icons/foot_motif.gif)
- E.g. at the last epoch the
extended components show flux densities of 20% of the central flux
density.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... factor
![[*]](/icons/foot_motif.gif)
- With the terms of
footnote 2 it is
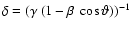 with
with
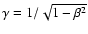 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
estimate
![[*]](/icons/foot_motif.gif)
- If much more (spectral and multi-epoch) data are available
as e.g. in the case of the quasar 3C 345, inhomogeneities in the particle
number density can also be estimated. Lobanov & Zensus (1999) used more
detailed analyzis to explain the observed flux density
variations quantitatively with time of 3C 345.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.