A&A 438, 341-348 (2005)
DOI: 10.1051/0004-6361:20052712
A. A. Kuznetsov
Institute of Solar-Terrestrial Physics, Irkutsk, Russia
Received 17 January 2005 / Accepted 16 March 2005
Abstract
The processes of generation and nonlinear interaction of
Bernstein modes are investigated. The physical conditions considered
correspond here to the sources of microwave bursts with a zebra pattern.
It is shown that the simultaneous generation of plasma waves corresponding
to several cyclotron harmonics is possible under these conditions.
Nonlinear coupling of plasma waves results in formation of a zebra
pattern with a frequency separation between the adjacent stripes close to
the electron cyclotron frequency. The emission is confined in the
narrow angle interval near the transversal (relative to the magnetic
field) propagation direction. Polarization of emission in this process
corresponds to the extraordinary wave, and the polarization degree reaches 100%.
Key words: radiation mechanisms: non-thermal - Sun: flares - Sun: radio radiation
Using the Siberian Solar Radiotelescope (SSRT) and the spectropolarimeters of the National Astronomical Observatories of China (NAOC), we at the first time managed to detect a zebra pattern in the microwave range (near 5.6 GHz) with high spatial resolution (down to 10''). This event is described in detail in the article by Altyntsev et al. (2005). Figure 1 shows the dynamic spectrum and the emission temporal profiles of the burst with zebra pattern. This zebra pattern was observed both by the SSRT and by the NAOC spectropolarimeters in the emission with right circular polarization only, which suggests high (up to 100%) circular polarization degree.
A comparison with the magnetogram shows that the emission source is situated above the region with the northern polarity magnetic field; thus the polarization sign corresponds to the extraordinary wave (X-mode) emission. This is quite an unexpected conclusion, so we investigated the possibility of polarization reversal. The observed polarization sign can differ from the polarization in the source if the emission crosses regions of quasi-transversal magnetic field or neutral current sheets during propagation from the source to the Earth (Zheleznyakov 1997). But reconstruction of the magnetic field structure from the magnetogram (Rudenko 2001) shows that in this event the observed zebra pattern emission does not cross the regions where polarization reversal can take place; therefore the high polarization degree, corresponding to the X-mode, is formed in the emission source.
Direct measurements with the SSRT show that the emission source size is less than 10'' and the sources of different zebra stripes spatially coincide. But the dynamic spectrum properties suggest even an stricter limitation on the source size. Indeed, the different zebra stripes have a very similar temporal evolution (including the simultaneous sudden onset of the frequency drift seen in Fig. 1), which requires a simultaneous change of source parameters, such as plasma density and magnetic field, in all parts of the source. The observed time delay of the frequency drift onset of different zebra stripes is not more than 50 ms; multiplying this value by the Alfven velocity, that is, the velocity of the fastest disturbances affecting the magnetic field and plasma density in the magnetized plasma, results in a source size not more than one thousand km even for the upper estimations of the Alfven velocity.
Among the mechanisms that were proposed for interpreting zebra
patterns, the compact source and mainly extraordinary wave can be explained
by the process of nonlinear coupling of Bernstein modes harmonics
(Zheleznyakov & Zlotnik 1975b; Mollwo & Sauer 1977).
The most complete investigation of this process has been done in the works of
Willes & Robinson (1996) and Willes (1999), but with
application to relatively low cyclotron harmonics. At the same time, in the
microwave zebra pattern (Fig. 1) the ratio of frequency interval
between the adjacent zebra stripes to the emission frequency is
![]() ,
which corresponds to the coalescence of
Bernstein mode harmonics with numbers around 17-18.
,
which corresponds to the coalescence of
Bernstein mode harmonics with numbers around 17-18.
The purpose of this work is to investigate the processes of generation and nonlinear interaction of Bernstein modes with application to conditions typical of the source of the microwave zebra pattern (Altyntsev et al. 2005).
The dispersion equation for the longitudinal plasma waves propagating
perpendicular (or almost perpendicular) to the ambient magnetic
field has the form (Zheleznyakov & Zlotnik 1975a; Zheleznyakov
1997)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_02.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg23.gif) |
Figure 2:
Dispersion curves of longitudinal plasma waves. The parameters
of plasma and magnetic field are given in Table 1.
The dashed line shows the dispersion curve of upper-hybrid waves -
the oscillation branch with normal dispersion law
|
Equation (1) was obtained under the nonrelativistic
approximation that is not valid within narrow frequency intervals
![]() below harmonics of cyclotron frequency
below harmonics of cyclotron frequency
![]() ,
,
![]() .
It will be shown below that
under these conditions the frequency of generated Bernstein modes
differs sufficiently from the integer harmonics of cyclotron frequency,
so the dispersion Eq. (1) is valid. In addition, the
condition
.
It will be shown below that
under these conditions the frequency of generated Bernstein modes
differs sufficiently from the integer harmonics of cyclotron frequency,
so the dispersion Eq. (1) is valid. In addition, the
condition
| Plasma density: |
n0=1011
|
| Plasma temperature: | T0=107 K |
| Plasma frequency: |
|
| Magnetic field strength: | B=50 G |
| Cyclotron frequency: |
|
|
|
|
| Accelerated particles distribution: | Dory-Guest-Harris |
| Accelerated particles temperature: |
|
| Accelerated particles concentration: |
|
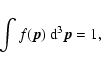 |
(5) |
For the positive growth rate of plasma waves the presence of a region with
positive slope on the distribution function (
![]() )
is necessary. Let the distribution
function be in the form
)
is necessary. Let the distribution
function be in the form
Calculations show that the generation of high harmonics of Bernstein modes
by the electron distribution of loss-cone type is ineffective. In this
case the resonance curve passes through the region of positive slope on the
distribution function (see Fig. 3) only for the waves that
have essentially a nonzero longitudinal component of wave vector ![]() .
For these waves condition (2) is not satisfied and Landau
damping becomes important; in other words, other resonance curves make too
strong a negative contribution to the sum over harmonics of cyclotron
frequency.
.
For these waves condition (2) is not satisfied and Landau
damping becomes important; in other words, other resonance curves make too
strong a negative contribution to the sum over harmonics of cyclotron
frequency.
The more effective source of Bernstein modes is the so-called ring beam
with maximum at
![]() (Fig. 3).
This distribution can be simulated by the formula (Dory et al.
1965)
(Fig. 3).
This distribution can be simulated by the formula (Dory et al.
1965)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_04.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg68.gif) |
Figure 4:
Necessary conditions of Bernstein modes generation.
The curve marked
|
Another condition arises from the properties of the Bessel function that is
contained in expression (4). The parameter
![]() (the argument of Bessel function) in
the resonance region must coincide with a maximum for function
(the argument of Bessel function) in
the resonance region must coincide with a maximum for function
![]() ,
otherwise corresponding regions will not make a significant contribution to
the growth rate. For sufficiently high harmonics (
,
otherwise corresponding regions will not make a significant contribution to
the growth rate. For sufficiently high harmonics (
![]() )
this requirement is reduced to
)
this requirement is reduced to
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_05.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg75.gif) |
Figure 5:
Necessary conditions of Bernstein modes generation: the
dependence of the typical wave vector on the harmonic number for the
different values of the accelerated electrons temperature. The parameters of
plasma and magnetic field are given in Table 1.
The dashed line, corresponding to the minimal possible value of the
wave vector (9), is drawn for
|
Figure 5 shows the typical values of wave vectors of the Bernstein
modes that are generated by electrons with different energy. When
analysing the generation of zebra pattern, the question is important:
which modes of plasma waves will be predominantly generated under the
given conditions? It is seen from Fig. 2 that for the formation
of zebra pattern the generation of several harmonics of waves with
anomalous dispersion law is necessary. At the same time, the upper-hybrid
waves (the waves with normal dispersion law) have a much higher
growth rate (Zheleznyakov & Zlotnik 1975a). It then follows from Fig. 5 that at electron energy ![]() about 108 K and
background plasma temperature
T0=107 K the condition of generation (9) is not satisfied for the upper-hybrid waves. Therefore the
energy of the unstable electron distribution will be distributed among the
harmonics of plasma waves with an anomalous dispersion law.
about 108 K and
background plasma temperature
T0=107 K the condition of generation (9) is not satisfied for the upper-hybrid waves. Therefore the
energy of the unstable electron distribution will be distributed among the
harmonics of plasma waves with an anomalous dispersion law.
In Fig. 6 the maximal growth rates of plasma waves for different
harmonics s are shown. With an increase of harmonic number, the growth
rate decreases; nevertheless the growth rates of different harmonics are
comparable. The frequency interval between the waves of adjacent harmonics
is close to the electron cyclotron frequency
![]() .
Note in
addition that the frequencies of plasma waves can significantly differ from
the integer harmonics of cyclotron frequency
.
Note in
addition that the frequencies of plasma waves can significantly differ from
the integer harmonics of cyclotron frequency
![]() ;
the
difference is about
;
the
difference is about
![]() ,
where
,
where
![]() is the typical velocity
of electrons generating those waves.
is the typical velocity
of electrons generating those waves.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_06.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg81.gif) |
Figure 6: Dependence of the growth rate of Bernstein modes on frequency for the transversal propagation. The parameters of plasma and magnetic field are given in Table 1. |
In Fig. 7 the dependence of the growth rate on the wave parameters
is shown in detail; here ![]() is the angle between the wave vector
and the magnetic field. The complicated shape of the dependence
is the angle between the wave vector
and the magnetic field. The complicated shape of the dependence
![]() arises from the oscillating behaviour of function
arises from the oscillating behaviour of function
![]() in the resonance region. Note in
addition that the plasma waves are confined in the narrow angular interval,
less than
in the resonance region. Note in
addition that the plasma waves are confined in the narrow angular interval,
less than
![]() ,
which agrees with condition (2). This
peculiarity causes the narrow angular spectrum of the generated
radioemission.
,
which agrees with condition (2). This
peculiarity causes the narrow angular spectrum of the generated
radioemission.
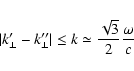 |
(11) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2712_07.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg94.gif) |
Figure 7: The dependence of the growth rate of Bernstein modes on the wave vector and the propagation direction for the harmonic s=19. |
Second, for the longitudinal (parallel to the magnetic field)
components of the wave vectors of the interacting waves the relation
![]() is satisfied, where
is satisfied, where
![]() and
and
![]() are the longitudinal components of wave vectors of Bernstein
modes which correspond to the largest possible deviation from the
transversal propagation. This results in the limitation of the angular
spectrum width of the generated radio emission:
are the longitudinal components of wave vectors of Bernstein
modes which correspond to the largest possible deviation from the
transversal propagation. This results in the limitation of the angular
spectrum width of the generated radio emission:
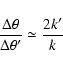 |
(12) |
The spectral intensity of the radioemission, observed at the Earth,
under the optically thin source approximation is
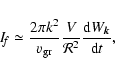 |
(16) |
We consider the case of weakly anisotropic plasma, and also it is assumed that the emission frequency significantly exceeds the extraordinary wave cutoff point. Under these conditions the dispersion properties of ordinary and extraordinary electromagnetic waves are similar, and the appearance of the high polarization degree is hard to expect. An exception is the case of quasi-transversal propagation, when the polarization of electromagnetic waves becomes linear; in the ordinary wave the electric field vector is parallel to the ambient magnetic field, and in the extraordinary wave the electric field vector is perpendicular to the ambient magnetic field.
Let us consider the situation when all of the interacting waves, including
both the Bernstein modes and the electromagnetic wave, propagate exactly
across the magnetic field. Bernstein modes are almost longitudinal waves;
therefore in the coordinate system with axis z parallel to the ambient
magnetic field ![]() (Fig. B.1), the components a'z and a''z of the polarization vectors of the interacting plasma waves equal
zero. The polarization vector of the ordinary electromagnetic wave
propagating perpendicular to the magnetic field has the form
(Fig. B.1), the components a'z and a''z of the polarization vectors of the interacting plasma waves equal
zero. The polarization vector of the ordinary electromagnetic wave
propagating perpendicular to the magnetic field has the form
![]() ,
|az|=1; for the extraordinary wave
one obtains
,
|az|=1; for the extraordinary wave
one obtains
![]() ,
|ax|2+|ay|2=1.
In the considered coordinate system the components of the plasma nonlinear
conductivity tensor
,
|ax|2+|ay|2=1.
In the considered coordinate system the components of the plasma nonlinear
conductivity tensor
![]() ,
as the
perpendicular to the magnetic field components of the electric field do not
affect the electron motion in the direction parallel to the magnetic field.
It is easy to see that under these conditions the convolution S (15) and, consequently, the three-wave process probability for
the ordinary wave equal zero; on the contrary, for the extraordinary wave
the three-wave process probability has nonzero values. Thus for the
quasi-transversal propagation the generation conditions for the extraordinary
wave are much more favorable than for the ordinary one, and the degree of
polarization can reach 100%.
,
as the
perpendicular to the magnetic field components of the electric field do not
affect the electron motion in the direction parallel to the magnetic field.
It is easy to see that under these conditions the convolution S (15) and, consequently, the three-wave process probability for
the ordinary wave equal zero; on the contrary, for the extraordinary wave
the three-wave process probability has nonzero values. Thus for the
quasi-transversal propagation the generation conditions for the extraordinary
wave are much more favorable than for the ordinary one, and the degree of
polarization can reach 100%.
In the weakly anisotropic plasma the quasi-transversal approximation for the electromagnetic waves propagation is valid only within a very narrow angle interval (Zheleznyakov 1997). Therefore for the plasma waves with a relatively broad angular distribution the effect above described can be neglected (Stepanov et al. 1999). On the contrary, it has been shown above that for the interaction of Bernstein modes the kinematic conditions of coupling (10) are satisfied only for the angular interval of emission propagation where the quasi-transversal approximation is valid.
For more accurate estimation of the radio emission parameters we use expression (C.1) for the plasma nonlinear conductivity tensor (Trakhtengerts 1970). This expression was obtained under the quasi-hydrodynamic approximation, and it is applicable for the weakly-damped oscillations of various types in the anisotropic medium.
The energy density distribution of Bernstein modes in the space of wave
vectors is described by the following model:
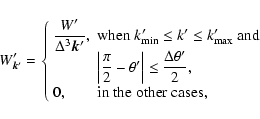 |
(17) |
![\begin{displaymath}\begin{array}{l}
k'_{\min}\simeq 0.389s-0.458~{\rm cm}^{-1},\\ [5pt]
k'_{\max}\simeq 0.433s-0.360~{\rm cm}^{-1}.
\end{array}\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img127.gif)
The numerical simulation results for the process of Bernstein modes nonlinear
interaction are shown in Figs. 8-11. In Fig. 8 the maximal transformation coefficient of plasma waves energy
into electromagnetic waves
![]() for
the different harmonics is shown. The energy transformation efficiency
increases with an increase of the harmonic number. Note in addition that
the efficiency of emission generation due to coalescence of the adjacent
harmonics of Bernstein modes (
s''=s'+1) is comparable with the efficiency
of emission generation in the case of coalescence of waves with the same
harmonic number (s''=s'). Thus the frequency interval between the adjacent
stripes in the zebra pattern will be close to the electron cyclotron
frequency. The simulations show that the efficiency of emission generation
decreases sharply for the case
s''=s'+2.
for
the different harmonics is shown. The energy transformation efficiency
increases with an increase of the harmonic number. Note in addition that
the efficiency of emission generation due to coalescence of the adjacent
harmonics of Bernstein modes (
s''=s'+1) is comparable with the efficiency
of emission generation in the case of coalescence of waves with the same
harmonic number (s''=s'). Thus the frequency interval between the adjacent
stripes in the zebra pattern will be close to the electron cyclotron
frequency. The simulations show that the efficiency of emission generation
decreases sharply for the case
s''=s'+2.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_10.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg133.gif) |
Figure 10:
The same as in Fig. 9, but for the harmonics
s'=s''=19;
W'=0.002
|
Examples of calculation of the intensity observed at the Earth of
radio emission of different modes, where the possible damping and scattering
during propagation are not taken into account, are shown in Figs. 9
and 10. Based on observations, the size of emission source is
assumed to be about one thousand km; the required energy density of Bernstein
modes in this case is
10-3-10-2
![]() .
These values are rather small in comparison to the energy density
of the background plasma or of the accelerated electrons:
.
These values are rather small in comparison to the energy density
of the background plasma or of the accelerated electrons:
![]() ;
;
![]() .
.
It has been already noted that emission in the generation region is confined within the narrow angle interval, and the intensity maximum corresponds to the transversal to the magnetic field propagation direction. It is seen from the figures that the coalescence of Bernstein modes results in generation of a mainly extraordinary wave, and the polarization degree equals 100% for the transversal propagation direction. With deviation from the transversal propagation the polarization degree decreases somewhat; nevertheless it remains high for most of the angular interval of generation.
The frequency spectrum of emission (Fig. 11) that is generated due
to coalescence of Bernstein modes is rather narrowband:
![]() at the level
at the level ![]() of the maximal intensity. The observed spectral width of the microwave zebra
pattern stripes is somewhat larger, possibly caused by inhomogeneities
of the magnetic field and plasma in the emission source.
of the maximal intensity. The observed spectral width of the microwave zebra
pattern stripes is somewhat larger, possibly caused by inhomogeneities
of the magnetic field and plasma in the emission source.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2712_11.eps}
\end{figure}](/articles/aa/full/2005/28/aa2712-05/Timg137.gif) |
Figure 11: Frequency dependence of the radio emission intensity for the same parameters as in Fig. 10. The maximal intensity is shown, which corresponds to the transversal emission propagation and extraordinary wave. |
The transformation coefficient of the energy of Bernstein modes into
electromagnetic waves increases with an increase in harmonic number (Fig. 8). This effect can limit the frequency of the observed stripes of
zebra pattern from below; besides, the conditions of escape of the emission
from plasma set the limitation
![]() .
On the other hand,
the generation efficiency of Bernstein modes decreases with an increase
in harmonic number (Fig. 6). This effect limits the frequency of
zebra pattern stripes from above. The estimations show that even for the
saturated generation regime, when the plasma wave energy density is
proportional to the growth rate, the influence of the last effect is more
essential; so one can expect generation of emission at the intermediate
frequencies: slightly above the plasma frequency
.
On the other hand,
the generation efficiency of Bernstein modes decreases with an increase
in harmonic number (Fig. 6). This effect limits the frequency of
zebra pattern stripes from above. The estimations show that even for the
saturated generation regime, when the plasma wave energy density is
proportional to the growth rate, the influence of the last effect is more
essential; so one can expect generation of emission at the intermediate
frequencies: slightly above the plasma frequency
![]() ,
but
considerably below the double plasma frequency
,
but
considerably below the double plasma frequency
![]() .
In the
event of January 5, 2003 the interval favorable for generation contains 2-3 harmonics of Bernstein modes which correspond to 3-4 stripes of the zebra
pattern. Note in addition that the bursts with zebra pattern in the meter and
decimeter ranges sometimes contain up to several tens of stripes;
interpretation of these events using the mechanism considered is difficult
and, probably, they have a different origin (Aurass et al. 2003;
Zlotnik et al. 2003).
.
In the
event of January 5, 2003 the interval favorable for generation contains 2-3 harmonics of Bernstein modes which correspond to 3-4 stripes of the zebra
pattern. Note in addition that the bursts with zebra pattern in the meter and
decimeter ranges sometimes contain up to several tens of stripes;
interpretation of these events using the mechanism considered is difficult
and, probably, they have a different origin (Aurass et al. 2003;
Zlotnik et al. 2003).
Under reasonable assumptions about the source size the energy density of
individual harmonics of Bernstein modes, which is required for generation
of a microwave zebra pattern with the observed intensity, is about
10-3-10-2
![]() .
By assuming that the fraction of
energy that corresponds to each harmonic is proportional to the growth rate,
the so-called saturated generation regime, we found that the total energy
density of all harmonics under these conditions does not exceed 2-3% of the energy density of accelerated particles. This estimation
includes the harmonics with number
.
By assuming that the fraction of
energy that corresponds to each harmonic is proportional to the growth rate,
the so-called saturated generation regime, we found that the total energy
density of all harmonics under these conditions does not exceed 2-3% of the energy density of accelerated particles. This estimation
includes the harmonics with number ![]() ,
which are not involved in
generation of the observed emission and for which the growth rate
reaches
,
which are not involved in
generation of the observed emission and for which the growth rate
reaches
![]()
![]() .
In the non-saturated regime of
plasma waves generation, the formation of zebra pattern requires
additional mechanisms that limit the amplification of harmonics with
numbers
.
In the non-saturated regime of
plasma waves generation, the formation of zebra pattern requires
additional mechanisms that limit the amplification of harmonics with
numbers ![]() .
.
The emission generated due to interaction of Bernstein modes has high
directivity that decreases the probability of its observation on Earth.
However, one can expect that scattering on the small-scale plasma
inhomogeneities (with scale about radio emission wave length) during
propagation of emission from the source will result both in broadening of the
beam angular width and in averaging of the polarization degree.
In this case the polarization degree of the observed emission
can be estimated as
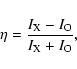 |
(18) |
Acknowledgements
This work was supported by the RFBR (grant numbers 02-02-39030, 04-02-39003 and 03-02-16229) and by the Russian Department of Education (grant number E02-3.2-489).
 |
(A.1) |
 |
(A.2) |
![\begin{displaymath}\frac{\partial\psi}{\partial\rho}=
\Gamma\left\{\frac{\Gamma ...
...ert}-v_0)+
v_{\bot}^2\right]-k_{\Vert}(v_{\Vert}-v_0)\right\}.
\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img158.gif) |
(A.4) |
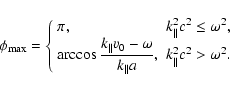 |
(A.5) |
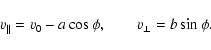 |
(A.6) |
The parameter
![]() is determined by (Melrose & Sy 1972;
Willes & Robinson 1996)
is determined by (Melrose & Sy 1972;
Willes & Robinson 1996)
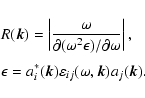 |
(B.2) |
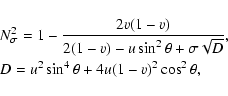 |
(B.3) |
We consider the coordinate system (Fig. B.1) where (i) z axis is
directed along the magnetic field; (ii) x axis is perpendicular to the
magnetic field and lies in the same plane with the magnetic field vector ![]() and the wave vector of the electromagnetic wave
and the wave vector of the electromagnetic wave ![]() ;
and (iii) y axis is perpendicular to the vectors
;
and (iii) y axis is perpendicular to the vectors ![]() and
and ![]() .
In this system the wave vector of the electromagnetic wave takes the form
.
In this system the wave vector of the electromagnetic wave takes the form
![]() ,
and the polarization vector of
the electromagnetic wave equals
,
and the polarization vector of
the electromagnetic wave equals
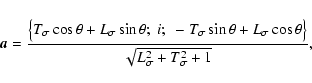 |
(B.4) |
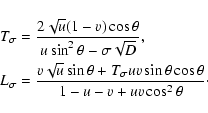 |
(B.5) |
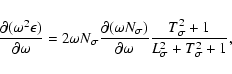 |
(B.6) |
![$\displaystyle \displaystyle N_{\sigma}\frac{\partial(\omega N_{\sigma})}{\parti...
...ta)^2}
\left[1+
\frac{(1+v)(1-T_{\sigma}^2)}{(1-v)(1+T_{\sigma}^2)}\right]\cdot$](/articles/aa/full/2005/28/aa2712-05/img180.gif) |
(B.7) |
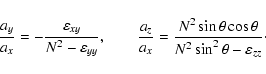 |
(B.8) |
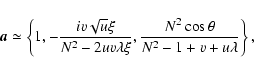 |
(B.9) |
![\begin{displaymath}\xi=
\displaystyle -2\omega^2{\rm e}^{-\lambda}\sum\limits_{r...
..._r(\lambda)-I'_r(\lambda)]}{\omega^2-r^2\omega_{\rm B}^2}\cdot
\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img188.gif) |
(B.10) |
If the azimuthal angle ![]() is nonzero, then the above-mentioned
wave vector and polarization vector should be multiplied by the rotation
matrix:
is nonzero, then the above-mentioned
wave vector and polarization vector should be multiplied by the rotation
matrix:
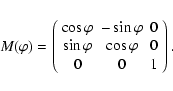 |
(B.11) |
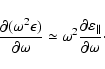 |
(B.13) |
The tensor of plasma nonlinear conductivity used in this paper has the
following form (Trakhtengerts 1970):
![\begin{displaymath}\sigma_{ij}(\omega, \vec{k})=
\frac{\omega}{4\pi i}[\varepsilon_{ij}(\omega, \vec{k})-\delta_{ij}],
\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img202.gif) |
(C.2) |
By using the relations (B.1), the convolution S (15) can be
transformed to the form:
| S | = | 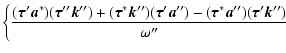 |
|
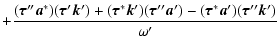 |
|||
![$\displaystyle \left.\left.-\frac{4\pi i}{\omega_{\rm p}^2}
\left[(\vec{\tau}^*\...
...+
(\vec{\tau}^*\vec{\tau}')(\vec{\tau}''\vec{k}')\right]\right\}
\right/(en_0).$](/articles/aa/full/2005/28/aa2712-05/img205.gif) |
(C.3) |
![\begin{displaymath}\begin{array}{l}
\displaystyle
\tau^*_j=
\frac{c^2}{4\pi i\om...
...2}{c^2}\right]a'_i-
(\vec{k}'\vec{a}')k'_i\right\}.
\end{array}\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img208.gif) |
(C.4) |
By using the properties of delta-function the integral (13) can be
reduced to the integral over the direction angles of the wave vector ![]() :
:
| (C.6) |
![\begin{displaymath}\frac{\partial w}{\partial k'}=-\frac{\partial\omega'}{\parti...
...ial k''}\right]\right\vert _{\vec{k}''=
\vec{k}-\vec{k}'}\cdot
\end{displaymath}](/articles/aa/full/2005/28/aa2712-05/img219.gif) |
(C.7) |