A&A 436, 895-915 (2005)
DOI: 10.1051/0004-6361:20042352
L. Girardi1 - M. A. T. Groenewegen2 - E. Hatziminaoglou3,4 - L. da Costa3
1 -
Osservatorio Astronomico di Trieste, INAF,
via Tiepolo 11, 34131 Trieste, Italy
2 -
PACS ICC-team, Instituut voor Sterrenkunde, Celestijnenlaan 200B,
3001 Leuven, Belgium
3 -
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85740 Garching bei München, Germany
4 -
Instituto de Astrofísica de Canarias, C/ vía Láctea s/n,
38200 La Laguna, Spain
Received 10 November 2004 / Accepted 15 March 2005
Abstract
We describe TRILEGAL, a new populations synthesis code for
simulating the stellar photometry of any Galaxy field.
The code attempts to improve upon several technical aspects
of star count models, by:
dealing with very complete input libraries of evolutionary tracks;
using a stellar spectral library to simulate the photometry in
virtually any broad-band system; being very versatile allowing
easy changes in the input libraries and in the description of
all of its ingredients - like the star formation rate,
age-metallicity relation, initial mass function, and geometry of
Galaxy components. In a previous paper (Groenewegen et al. 2002,
Paper I), the code was first applied to describe the very deep
star counts of the CDFS stellar catalogue. Here, we briefly describe
its initial calibration using EIS-deep and DMS star
counts, which, as we show, are adequate samples to probe both the
halo and the disc components of largest scale heights (oldest ages).
We then present the changes in the calibration that were necessary
to cope with some improvements in the model input data, and the
use of more extensive photometry datasets:
now the code is shown to successfully simulate also
the relatively shallower 2MASS catalogue, which probes
mostly the disc at intermediate ages, and the immediate solar
neighbourhood as sampled by Hipparcos - in particular
its absolute magnitude versus colour diagram -, which contains
a somewhat larger fraction of younger stars than deeper surveys.
Remarkably, the same model calibration can
reproduce well the star counts in all the above-mentioned
data sets, that span from the very deep magnitudes of CDFS
(16<R<23) to the very shallow ones of Hipparcos (V<8).
Significant deviations (above 50 percent in number counts)
are found just for fields close to the Galactic Center
(since no bulge component was included) and Plane,
and for a single set of South Galactic Pole data.
The TRILEGAL code is ready to use for the variety of
wide-angle surveys in the optical/infrared that will become available
in the coming years.
Key words: stars: luminosity function, mass function - stars: Hertzsprung-Russell (HR) and C-M diagrams - surveys - Galaxy: stellar content - Galaxy: structure
The number counts of Galactic stars in a given
bin of apparent magnitude
![]() - where
- where ![]() stands for a passband - and towards an element of
galactic coordinates
stands for a passband - and towards an element of
galactic coordinates ![]() and solid angle
and solid angle
![]() ,
is given
by the fundamental equation of stellar statistics (see Bahcall 1986,
for a review)
,
is given
by the fundamental equation of stellar statistics (see Bahcall 1986,
for a review)
To describe the stellar densities
![]() for the
largest possible volume, and to a lesser extent
also
for the
largest possible volume, and to a lesser extent
also
![]() ,
is the ultimate task of the
so-called Galaxy star count models. To achieve these goals,
the usual way is
to assume the functional forms of
,
is the ultimate task of the
so-called Galaxy star count models. To achieve these goals,
the usual way is
to assume the functional forms of ![]() and
and ![]() ,
and then
compare the results of Eq. (1) to observed
number counts in several Galaxy fields. A number of assumptions help
in simplifying the task. The first one is to
recognize that the Galaxy can be separated in a few distinct components,
such as the disc, halo, and bulge:
,
and then
compare the results of Eq. (1) to observed
number counts in several Galaxy fields. A number of assumptions help
in simplifying the task. The first one is to
recognize that the Galaxy can be separated in a few distinct components,
such as the disc, halo, and bulge:
| (2) |
The recipes for ![]() can be of two types. Either one
(1) assumes an empirical
can be of two types. Either one
(1) assumes an empirical ![]() ,
derived from e.g. star counts
in globular clusters or in the Solar Neighbourhood; or
(2) assumes a theoretical
,
derived from e.g. star counts
in globular clusters or in the Solar Neighbourhood; or
(2) assumes a theoretical ![]() ,
derived from a set of
evolutionary tracks together with suitable distributions
of stellar masses, ages, and metallicities.
,
derived from a set of
evolutionary tracks together with suitable distributions
of stellar masses, ages, and metallicities.
Option (1) was the preferred one in the past,
and the one adopted in some of the most successful Galaxy models.
Despite their success in reproducing several sorts of data,
it is not difficult to find points of inconsistency
in many of such models.
A common approximation, for instance, has been that disc
stars of different absolute magnitude present different
scale heights (and hence
![]() ):
Bahcall & Soneira (1980, 1984; and many authors later on)
assigned the scale height of 325 pc for MV>5.1,
of 90 pc for MV<2.3 dwarfs,
and linearly interpolated in between. This separation
was interpreted as a coarse separation into
"young'' and "old'' populations. Red giants instead
were assigned 250 pc. Gilmore & Reid (1983)
adopt similar approximations for main sequence stars.
Méndez & van Altena (1996, 1998) do the same, and
moreover assume a unique scale height for all evolved stars
(subgiants, giants, and white dwarfs).
From the point of view of stellar and
population synthesis theories, these approximations are
clearly not justified, for a series of reasons:
(a) Most coeval stellar populations
contain both red and blue stars characterized by
initial mass values which are, at least for the most luminous objects,
very much the same; it is then very unlikely that the spatial
distribution of these red and blue stars
could be different. (b) Similarly, young stellar populations
contain both bright and faint main sequence stars, whose relative
scale heights cannot change that dramatically in time-scales of less
than one Gyr. (c) Moreover, it is remarkable that population synthesis
theory indicate that in star-forming galaxy components (e.g. in
the thin disc), red giants are
relatively young - most having less than say 2 Gyr
(see Girardi & Salaris 2001) - and not old objects;
applying the largest scale heights to all giants
is then simply wrong.
):
Bahcall & Soneira (1980, 1984; and many authors later on)
assigned the scale height of 325 pc for MV>5.1,
of 90 pc for MV<2.3 dwarfs,
and linearly interpolated in between. This separation
was interpreted as a coarse separation into
"young'' and "old'' populations. Red giants instead
were assigned 250 pc. Gilmore & Reid (1983)
adopt similar approximations for main sequence stars.
Méndez & van Altena (1996, 1998) do the same, and
moreover assume a unique scale height for all evolved stars
(subgiants, giants, and white dwarfs).
From the point of view of stellar and
population synthesis theories, these approximations are
clearly not justified, for a series of reasons:
(a) Most coeval stellar populations
contain both red and blue stars characterized by
initial mass values which are, at least for the most luminous objects,
very much the same; it is then very unlikely that the spatial
distribution of these red and blue stars
could be different. (b) Similarly, young stellar populations
contain both bright and faint main sequence stars, whose relative
scale heights cannot change that dramatically in time-scales of less
than one Gyr. (c) Moreover, it is remarkable that population synthesis
theory indicate that in star-forming galaxy components (e.g. in
the thin disc), red giants are
relatively young - most having less than say 2 Gyr
(see Girardi & Salaris 2001) - and not old objects;
applying the largest scale heights to all giants
is then simply wrong.
Although this sort of inconsistency is not inherent to method (1),
they are completely removed by the use of method (2).
In the latter, at any ![]() the relative numbers of stars with
different colours and absolute magnitude strictly obey the constraints
settled by stellar evolution and population synthesis theories;
hence,
the relative numbers of stars with
different colours and absolute magnitude strictly obey the constraints
settled by stellar evolution and population synthesis theories;
hence,
![]() cannot be arbitrarily changed
as a function of absolute magnitude. On the other hand,
method (2) allows
cannot be arbitrarily changed
as a function of absolute magnitude. On the other hand,
method (2) allows
![]() to be easily expressed
as a function of other stellar parameters, such as
age and metallicity - something not possible with method (1)
where individual stellar ages and metallicities
are not available - then allowing the simulation of important
effects like metallicity gradients, scale lengths increasing
with age, etc. This turns out to be a significant advantage
of method (2) over (1).
to be easily expressed
as a function of other stellar parameters, such as
age and metallicity - something not possible with method (1)
where individual stellar ages and metallicities
are not available - then allowing the simulation of important
effects like metallicity gradients, scale lengths increasing
with age, etc. This turns out to be a significant advantage
of method (2) over (1).
Models that follow method (2) may be put under the generic name of "population synthesis Galaxy star count models'', and have been developed in the last decades by e.g. Robin & Crézé (1986), Haywood (1994), Ng et al. (1995), Castellani et al. (2002), and Robin et al. (2003). These works benefit from the releases of extended databases of stellar evolutionary tracks to predict the properties of stars of given mass, age, and metallicity. Some assumptions then are necessary to give the distributions of these stellar parameters. Such distributions may be derived, for instance, starting from an initial mass function (IMF), an age-metallicity relation (AMR), and a law for the star formation rate (SFR) as a function of Galaxy age.
In the present paper, we will describe a Galaxy model developed according to the population synthesis approach, taking particular care in the consistency among the different sources of input data. It has been developed with a primary task in head, which is, essentially: to be capable of simulating the same sort of data that will be released by some major campaigns of wide-field photometry conducted these years. Of primary importance in this context, are the several parts of the ESO Imaging Survey (EIS, Renzini & da Costa 1997), the Two Micron All Sky Survey (2MASS, Cutri et al. 2003), and the Sloan Digital Sky Survey (SDSS, York et al. 2000). Present and future data from HST deep fields, VIMOS, VISTA, UKIDSS, GAIA, might be considered as well. Moreover, our model should also be able to take advantage of the extraordinary constraints provided by the astrometric mission Hipparcos (Perryman et al. 1997). Of course, a program which meets these aims can be applied to any other sort of wide field data as well.
Before proceeding, let us briefly summarize our primary objectives and how these translate into technical requirements.
First of all, our primary goal is to simulate the expected star counts in several passband systems, such as those used by Hipparcos, EIS, 2MASS, SDSS, etc. For doing so, we should be able to consistently predict the stellar photometry in a lot of different photometric systems. The way out to this problem has been settled in a previous work (Girardi et al. 2002), that describes a quite general method for performing synthetic photometry and deriving bolometric corrections from an extended library of stellar spectra. Such tables are now routinely produced for any new system that we want to compare the models with.
The second requirement is of being able to simulate both
very shallow - but of excellent quality -
photometric data samples as Hipparcos (Perryman et al. 1997),
and very deep ones such as the EIS Deep Public Survey
(e.g. Paper I).
The former case implies that we include all important
evolutionary sequences, such as most of the main sequence,
and giants both in the red giant branch (RGB) and red clump,
which make the bulk of the Hipparcos colour-magnitude diagram (CMD).
In the latter case, we should also include an extended
lower main sequence, reaching down to visual absolute
magnitudes as faint as ![]() ,
which corresponds to
stellar masses of
,
which corresponds to
stellar masses of ![]() 0.1
0.1 ![]() .
Moreover, old white dwarfs start to
become frequent at such faint magnitudes as well.
Therefore, the libraries of stellar data should be extended
to the intervals of very low masses, and to very old white
dwarfs.
.
Moreover, old white dwarfs start to
become frequent at such faint magnitudes as well.
Therefore, the libraries of stellar data should be extended
to the intervals of very low masses, and to very old white
dwarfs.
It is also clear that these requirements imply, necessarily, that we opt for the population synthesis approach. In fact, there is little hope that we could collect empirical data for such a variety of stars, in the several photometric systems involved, and with good enough statistics that the intrinsic CMDs could be constructed with reliability. Theoretical data, instead, is available for all of our purposes, as will be shown in what follows. Such theoretical data is also routinely submitted to stringent tests against photometric data, such as the Hipparcos CMD, star clusters, eclipsing binaries, red giants with measured diameters, etc. In general, the errors detected in the models amount to less than a few tenths of a magnitude, and just for some particular stars and/or passbands. Certainly, the time is ripe for completely relying in theoretical data in Galaxy star count models.
The plan of this paper is as follows: Sects. 2 and 3 detail the code and its input data, respectively. Section 4 describes its initial calibration as performed for Groenewegen et al.'s (2002) work, based mostly on EIS and DMS data. Section 5 details and presents the fine-tuning of the initial calibration, including additional comparisons with 2MASS and Hipparcos data. Section 6 draws a few final comments and summarizes the main results of the present paper.
We describe here all the necessary input for
computing a Galactic Model. Normally, this means
simulating the photometric properties of stars located towards
a given direction ![]() .
This task is performed by the newly
developed code TRILEGAL, which stands for TRIdimensional
modeL of thE GALaxy
.
This task is performed by the newly
developed code TRILEGAL, which stands for TRIdimensional
modeL of thE GALaxy![]() .
.
The code is written in C language. Its core is made of a few subroutines that efficiently interpolate and search for stars of given mass, age, or metallicity, inside a database of stellar evolutionary tracks. They deal with all the intrinsic properties of stars - luminosity, effective temperature, mass, metallicity, etc. These subroutines, developed in Girardi (1997), have so far been used in a series of works dealing from the construction of theoretical isochrones (e.g. Girardi et al. 2000; Salasnich et al. 2000) to the simulations of synthetic CMDs for nearby galaxies (e.g. Girardi et al. 1998; Girardi 1999; Girardi & Salaris 2001; Marigo et al. 2003). Another set of routines, more recently developed, deal with all aspects related with synthetic photometry, i.e. the conversion between intrinsic stellar properties and observable magnitudes. They rely on the same simple formalism described in Girardi et al. (2002).
A general scheme of the code is provided in Fig.1. It makes use of 4 main elements: a library of theoretical evolutionary tracks, a library of synthetic spectra, some parameters of the detection system, and the detailed description of the Galaxy components. The libraries of evolutionary tracks and spectra can be pre-processed in the form of theoretical isochrones and tables of bolometric corrections, so as to reduce the number of redundant operations during a simulation. These are to be considered as "fixed input'', but can be easily changed so as to consider alternative sets of data.
The instrumental setup specifies, among others: (1) the set of filters+detector+telescope throughputs in which the observations are performed; any change of them implies the recalculation of the bolometric correction tables; (2) the effective sky area to be simulated; the number of simulated stars scales with this quantity.
The several Galactic components (halo, thin and thick disc, bulge, etc.) are specified by their initial distributions of stellar ages and metallicities (SFR and AMR), masses (IMF), space densities, and interstellar absorption. This is done separately for each component. The space densities are in the form of simple expressions containing a few modifiable parameters, to be specified in Sect. 3 below.
A run of TRILEGAL is formally a Monte Carlo simulation in which stars are generated according to the probability distributions already described. Equation (1) is used for predicting the number of expected stars in each bin of distance modulus. For each simulated star, the SFR, AMR and IMF are used to single out the stellar age, metallicity, and mass. Finally its absolute photometry is derived via interpolation in the grids of evolutionary tracks (or isochrones), and converted to the apparent magnitudes using the suitable values of bolometric corrections, distance modulus and extinction.
During the simulations, a lot of different stellar parameters can be kept in memory and printed out: initial and current mass, age, metallicity, surface chemical composition and gravity, luminosity, effective temperature, core mass, etc. In the case of thermally-pulsing (TP-) AGB stars, this information is also used to simulate the pulse cycle variations (see Marigo et al. 2003).
The calculation initially produces a "perfect photometric catalogue'', which perfectly reflect the input probability distributions but for the Poisson noise. This catalogue can be later degraded by using the known photometric errors, such as photon noise, saturation and incompleteness for a given instrumental setup. This second task does not belong to TRILEGAL, but is performed by separated subroutines, like for instance the ones described by Paper I.
There are essentially 5 different input datasets in TRILEGAL:
Based on our previous work on simulations of synthetic CMDs for Local Group galaxies, we have assembled a large, quite complete, and as far as possible homogeneous - in terms of their input physics - database of stellar tracks. They are illustrated in the HR diagram of Fig. 2:
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2352f2.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg60.gif) |
Figure 2: HR diagram containing all tracks assembled for the solar metallicity. Our database contains similar data for 6 other values of metallicity. In the electronic version of this paper, tracks from different sources are marked with different colours: Girardi et al. (2000, black) for most evolutionary phases of low- and intermediate-mass stars, complemented with the TP-AGB phase from Marigo et al. (2003, and in preparation, magenta), massive stars from Bertelli et al. (1994, green), very-low mass stars and brown dwarfs from Chabrier et al. (2000, red), post-AGB and PNe nuclei from Vassiliadis & Wood (1994) complemented with WD cooling sequences from Benvenuto & Althaus (1999, both in blue). |
The TP-AGB evolution included in these tracks is estimated
from a simplified synthetic evolutionary code (cf. Girardi & Bertelli
1998, case of Eqs. (17) plus (20)). Although this TP-AGB evolution
is very approximated, it provides a reasonable
initial-final mass relation (see Fig. 2 in Girardi & Bertelli 1998),
and hence reasonable masses for the white dwarfs to be considered
below. The maximum mass of WDs attained is about 1.2 ![]() for the
lowest metallicities, and 0.9 for the highest.
On 2002, we replaced these simplified TP-AGB tracks for more
detailed ones computed by Marigo et al. (2003; and in preparation),
which are based on the new formulation for molecular opacities by
Marigo (2002);
for the
lowest metallicities, and 0.9 for the highest.
On 2002, we replaced these simplified TP-AGB tracks for more
detailed ones computed by Marigo et al. (2003; and in preparation),
which are based on the new formulation for molecular opacities by
Marigo (2002);
The complete set of stellar models for solar metallicity is plotted
in the HR diagram of Fig. 2. Similar
grids of tracks are available also for metallicities
Z=0.0001, 0.0004, 0.001, 0.004, 0.008 and 0.03 (limited to
![]()
![]() in the latter case).
in the latter case).
Finally, we remark that the present stellar database corresponds
to the "basic set'' of isochrones as mentioned by
Girardi et al. (2002) and available at the web page
http://pleiadi.pd.astro.it/isoc_photsys.00.html,
but for three important improvements: the inclusion of post-AGB
and white dwarf
cooling tracks, the extension of very-low mass stars and
brown dwarfs down to 0.01 ![]() ,
and the improved
prescriptions for the TP-AGB phase.
,
and the improved
prescriptions for the TP-AGB phase.
Once a star of
![]() is selected by the code, its
bolometric luminosity
is selected by the code, its
bolometric luminosity
![]() is converted
into absolute magnitudes by means of
is converted
into absolute magnitudes by means of
![]() .
The bolometric corrections
.
The bolometric corrections
![]() are derived from a large
database of synthetic and empirical spectra, according to the synthetic
photometry procedure throughly descrived in Girardi et al. (2002).
Importantly, this allows the application to a very wide set of
photometric systems, provided that we deal with
are derived from a large
database of synthetic and empirical spectra, according to the synthetic
photometry procedure throughly descrived in Girardi et al. (2002).
Importantly, this allows the application to a very wide set of
photometric systems, provided that we deal with
In the present work we compute the
![]() ratio for a
G2V star (the Sun) subject to mild absorption (AV<0.5 mag) and
following the Cardelli et al. (1989) absorption curve with RV=3.1.
The derived
ratio for a
G2V star (the Sun) subject to mild absorption (AV<0.5 mag) and
following the Cardelli et al. (1989) absorption curve with RV=3.1.
The derived
![]() quantities
quantities![]() are then applied to stars
of all spectral types and reddening values, although, formally,
they are adequate only for low-reddening G2V stars in the case
RV=3.1. This approach is adopted just for the sake of simplicity.
In alternative, it is very easy to implement a more accurate
approach to the problem, which will be
followed in future applications.
are then applied to stars
of all spectral types and reddening values, although, formally,
they are adequate only for low-reddening G2V stars in the case
RV=3.1. This approach is adopted just for the sake of simplicity.
In alternative, it is very easy to implement a more accurate
approach to the problem, which will be
followed in future applications.
The IMF ![]() is a crucial ingredient because it determines the
relative numbers of very-low mass stars, that may dominate star
counts at visual magnitudes fainter than
is a crucial ingredient because it determines the
relative numbers of very-low mass stars, that may dominate star
counts at visual magnitudes fainter than ![]() 22.
We have introduced the IMF in a very flexible way, so that
it that can be easily changed.
In order to be able to use star formation rates in units of
22.
We have introduced the IMF in a very flexible way, so that
it that can be easily changed.
In order to be able to use star formation rates in units of ![]() /yr,
our default IMF normalization is for a total mass equal to 1, i.e.
/yr,
our default IMF normalization is for a total mass equal to 1, i.e.
![\begin{displaymath}\phi_m \propto m~\exp
\left[-\frac{(\log m - \log m_0)^2}{2\sigma^2}\right],
\end{displaymath}](/articles/aa/full/2005/24/aa2352-04/img75.gif)
Other commonly-used IMFs, like segmented power-laws (Salpeter 1955; Kroupa 2001) and Larson's (1986) exponential form, are also included in the code.
The IMF as given above refers to the mass distribution of
single stars. Additionally to them, it is very easy to
simulate non-interacting binaries in our simulations.
When so required, we adopt the same prescription as in
Barmina et al. (2002): for each primary star of
mass m1, there is a probability ![]() that it
contains a secondary, whose mass m2 is given by a flat
distribution of mass ratios comprised
in the interval
that it
contains a secondary, whose mass m2 is given by a flat
distribution of mass ratios comprised
in the interval
![]() .
This prescription is
particularly useful for simulating the binary sequences which
are often evident in CMDs of open clusters. Typical
values of
.
This prescription is
particularly useful for simulating the binary sequences which
are often evident in CMDs of open clusters. Typical
values of ![]() and
and ![]() are 0.3 and 0.7,
respectively, which we adopt as a default.
are 0.3 and 0.7,
respectively, which we adopt as a default.
Each Galaxy component is made of combination of
stellar populations of varying age and metallicity.
In our code, their distribution is completely specified by the
functions SFR, ![]() ,
and AMR, Z(t).
Both are given in a single input file containing, for each
age value,
,
and AMR, Z(t).
Both are given in a single input file containing, for each
age value,
For this paper, ![]() enhancement is taken into consideration
for the low-metallicity Galaxy components (halo and old disc).
In these cases, we can safely
convert a given [Fe/H] into Z by means of Eq. (5),
and associate to that Z the evolutionary tracks computed
with scaled-solar compositions using the relations provided
by Salaris et al. (1993). For
metallicities higher than about half solar, this approximation
is no longer valid and it is preferable to use tracks
specifically computed for
enhancement is taken into consideration
for the low-metallicity Galaxy components (halo and old disc).
In these cases, we can safely
convert a given [Fe/H] into Z by means of Eq. (5),
and associate to that Z the evolutionary tracks computed
with scaled-solar compositions using the relations provided
by Salaris et al. (1993). For
metallicities higher than about half solar, this approximation
is no longer valid and it is preferable to use tracks
specifically computed for ![]() -enhanced composition (see
Salaris & Weiss 1998; VandenBerg et al. 2000; Salasnich et al. 2000).
-enhanced composition (see
Salaris & Weiss 1998; VandenBerg et al. 2000; Salasnich et al. 2000).
The SFR can only be considered well-known for the old Galactic components. In fact, for ages close to 12 Gyr, a change of age of 1 Gyr causes just small changes in the stellar luminosity function, and hence has a minor impact on the simulated star counts. For the disc components, the SFR is less constrained. Anyway, the Galactic model is also relatively insensitive to the disc SFR, at least as long as we are not sampling regions at low Galactic latitude and/or the Solar vicinity (as will be shown later). In general, even more important than the SFR is the choice of the AMR Z(t) and its dispersion, that may change the position of simulated stars in colour-colour diagrams, and cause a significant colour dispersion.
After these considerations, it is convenient to specify what are to be considered "default'' SFR and AMR - i.e. those used in Paper I, and partially also in this work:
At this point, having described the default SFR, AMR, IMF,
and libraries of evolutionary tracks and spectra, it is useful
to open a parenthesis and illustrate the intrinsic CMDs and
LFs that we derive from these ingredients.
Notice that these intrinsic data are the only
stellar ingredients that enter in the old
"empirical ![]() approach'' mentioned in Sect. 1.
approach'' mentioned in Sect. 1.
In Fig. 3 we show, for both disc and halo,
the MV vs. ![]() diagram that follow from our choices,
together with the intrinsic distributions of MV and
diagram that follow from our choices,
together with the intrinsic distributions of MV and ![]() values.
values.
Several aspects of this figure are remarkable:
Let us also briefly comment on the general aspect of the
CMDs shown in Fig. 3: in the case of the disc population
shown in the left panel,
it is evident that the low-mass and brown dwarf models, taken
from different sources, combine in a continuous and well-behaved
way with the sequence drawn by more massive stellar models.
There is just one abrupt change in the width of this main sequence,
occurring at
![]() ,
that is caused by the fact that below
this limit we rely on solar-metallicity models, whereas
above it the metallicity dispersion is fully represented in the
models. Exactly the same problem is present
for the halo population shown in the right panel. Anyway, this seems
a minor problem because - as will be shown in the following sections -
these stars, although always present, do not make the main features
of CMDs observed up to now. Also, this seems an acceptable price to
pay for having an extremely complete intrinsic CMD.
,
that is caused by the fact that below
this limit we rely on solar-metallicity models, whereas
above it the metallicity dispersion is fully represented in the
models. Exactly the same problem is present
for the halo population shown in the right panel. Anyway, this seems
a minor problem because - as will be shown in the following sections -
these stars, although always present, do not make the main features
of CMDs observed up to now. Also, this seems an acceptable price to
pay for having an extremely complete intrinsic CMD.
Finally, we recall that star counts of dwarfs below
![]() are affected just by the particular choice of IMF, whereas above
this limit also the SFR and AMR play a major role.
are affected just by the particular choice of IMF, whereas above
this limit also the SFR and AMR play a major role.
For the sake of illustration, Fig. 4 shows
the intrinsic MK vs. ![]() diagram. This looks very
different from the former BV-diagram, and is
particularly useful for the discussion of 2MASS data
(see Sect. 5.3, and Marigo et al. 2003).
diagram. This looks very
different from the former BV-diagram, and is
particularly useful for the discussion of 2MASS data
(see Sect. 5.3, and Marigo et al. 2003).
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{2352f4.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg96.gif) |
Figure 4:
The same as Fig. 3
but limited to the disc intrinsic MK vs. |
Five are the Galaxy components presently defined in TRILEGAL: the thin and thick discs, the halo, the bulge, and the disc extinction layer. There is also the possibility of simulating additional objects of known distance.
| (6) |
The normalization constant ![]() is set so as to produce a given
"total surface density of thin disc stars ever formed in the
Solar Neighbourhood'',
is set so as to produce a given
"total surface density of thin disc stars ever formed in the
Solar Neighbourhood'',
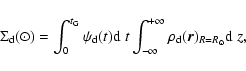
So, just the parameters
![]() ,
,
![]() ,
and
,
and
![]() ,
defined similarly to the thin disc ones,
would suffice to define the thick disc. Needless to
say, this galactic component can be incorporated in the formula for
the thin disc, by assuming suitable scale heights hzat large ages in Eq. (7).
,
defined similarly to the thin disc ones,
would suffice to define the thick disc. Needless to
say, this galactic component can be incorporated in the formula for
the thin disc, by assuming suitable scale heights hzat large ages in Eq. (7).
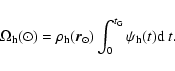
Extinction is always specified in terms of AV
(V in this case stands for the effective wavelength
of Johnson's V-band, 5550 Å).
The AV values found for individual stars
are later converted to those in the several pass-bands, ![]() ,
using the
,
using the
![]() ratios previously tabulated
(Sect. 3.2).
ratios previously tabulated
(Sect. 3.2).
This option was recently used by Marigo et al. (2003) to simulate the 2MASS data towards the Large Magellanic Cloud (LMC), and by Carraro et al. (2002) to simulate the field of the open cluster NGC 2158. Open cluster simulations in EIS fields will also be the subject of an upcoming paper (Hatziminaoglou et al., in preparation).
We also have "pointing parameters'', that specify the region of the
Galaxy sampled during a simulation. Two main modes are presently
allowed: either (1) simulations of a projected (conic) region
of the sky, that requires the specification of the central
Galactic coordinates ![]() and total sky area; or
(2) a volume-limited sample centered on the Sun and complete
up to a specified maximum distance.
and total sky area; or
(2) a volume-limited sample centered on the Sun and complete
up to a specified maximum distance.
In both of the above cases, by specifying a given limiting magnitude in any of the available filters, we avoid generating too many faint stars in the output.
Another input parameter is the resolution in magnitudes, ![]() .
It represents the largest sub-step for the numerical integration
of Eq. (1).
Any detail of the Galaxy geometry that is caused by a depth structure
(in distance modulus) smaller than this resolution, or by a LF
structure finer than it, will be lost. A resolution of
0.1 mag is adequate for the purpose of this paper.
.
It represents the largest sub-step for the numerical integration
of Eq. (1).
Any detail of the Galaxy geometry that is caused by a depth structure
(in distance modulus) smaller than this resolution, or by a LF
structure finer than it, will be lost. A resolution of
0.1 mag is adequate for the purpose of this paper.
The Sun's position with respect to the Galactic Plane is specified by the galactocentric radius and height on disc.
The initial calibration is described in Paper I. The most important points, relevant for the present paper, are repeated here. That paper describes, amongst other things, the first application of the TRILEGAL code. The initial calibration is derived from the six fields at high galactic latitude covered by the "Deep Multicolor Survey'' (DMS, Osmer et al. 1998, and references therein), and EIS data for the South Galactic Pole (SGP, Prandoni et al. 1999). Then, the code, with the parameters fixed, was applied to the EIS data in the Chandra Deep Field South (CDFS, Arnouts et al. 2001; Vandame et al. 2001).
The IMF, SFR, and AMR for the disc and halo were those already specified in Sects. 3.3 and 3.4 as being the default ones.
The disc component was described by a double-exponential in
scale height and Galactocentric distance. The model did not have
separate components representing the thin or thick disc.
Instead the scale height
for disc stars was a function of age, and was parametrized as
in Eq. (7). The parameter values in this equation were not
the same as in Rana & Basu (1992) - namely z0=95 pc, t0=0.5 Gyr
and
![]() ,
since this does not fit very well the derived scale
height of "thick'', "old'', "intermediate'' and "young''
disc components as
derived by Ng et al. (1997). Their results are described by
z0=95 pc, t0=4.4 Gyr and
,
since this does not fit very well the derived scale
height of "thick'', "old'', "intermediate'' and "young''
disc components as
derived by Ng et al. (1997). Their results are described by
z0=95 pc, t0=4.4 Gyr and
![]() ,
which was adopted in
Paper I.
,
which was adopted in
Paper I.
Since none of the six DMS fields, nor the CDFS and SGP, contains a bulge component, this population was not included.
The Sun was assumed to be 15 pc above the Galactic Plane (Cohen 1995; Ng et al. 1997; Binney et al. 1997) and the distance of the Sun to the Galactic Centre was assumed to be 8.5 kpc.
With these input ingredients fixed, the halo oblateness (and local
halo number density) was derived by fitting the number of halo stars,
defined by (in the Johnson-Cousins system)
![]() in the
range
20 < B < 22 and
in the
range
20 < B < 22 and
![]() in the range
18 < I < 20, in
these seven fields and was found to be
in the range
18 < I < 20, in
these seven fields and was found to be
![]() .
This value
was smaller than the value of
.
This value
was smaller than the value of
![]() quoted by Reid &
Majewski (1993), but Robin et al. (2000) could not exclude a spheroid
with a flattening as small as q = 0.6 and Chen et al. (2001) derived
quoted by Reid &
Majewski (1993), but Robin et al. (2000) could not exclude a spheroid
with a flattening as small as q = 0.6 and Chen et al. (2001) derived
![]() .
.
The disc radial scale length (and local disc number density) was
derived by fitting the number of disc stars, defined by
![]() in the range
20 < B < 22 and
in the range
20 < B < 22 and
![]() in the range
18
< I < 20, and was found to be
in the range
18
< I < 20, and was found to be
![]() pc. This was
in agreement with the lower limit of 2.5 kpc (Bahcall & Soneira 1984)
and the work of Zheng et al. (2001) on M-dwarfs who derived
pc. This was
in agreement with the lower limit of 2.5 kpc (Bahcall & Soneira 1984)
and the work of Zheng et al. (2001) on M-dwarfs who derived
![]() pc and Ojha (2001) who derive
pc and Ojha (2001) who derive
![]() pc for the thin disc.
pc for the thin disc.
The model with these parameters was then used to estimate the stellar counts in the CDFS field, yielding a fairly good fit of the UBVRIJK number counts, CMDs, and colour distributions. The model with these parameters was also used by Marigo et al. (2003) to successfully predict the foreground population towards the LMC in JHK.
It is very instructive to look at the characteristic
distributions of distance moduli,
![]() ,
for this model calibration. Were all
stars in a given field - even the dimmest
ones - possible to be observed, such distribution would be
proportional to the integral of the quantity
,
for this model calibration. Were all
stars in a given field - even the dimmest
ones - possible to be observed, such distribution would be
proportional to the integral of the quantity ![]() (see Eq. (1)) over small bins of distance modulus.
We show these quantities as evaluated for the line of
sight of the North Galactic Pole (NGP)
in Fig. 5. In the case of the
disc, we separate the profiles coming from different ages (i.e.
different scale heights) spaced by 1 Gyr. As can be noticed,
a simulation of the NGP - if not constrained by
any limiting magnitude - would contain increasing numbers of
disc stars as we go to older ages,
and at increasing mean distances (from
(see Eq. (1)) over small bins of distance modulus.
We show these quantities as evaluated for the line of
sight of the North Galactic Pole (NGP)
in Fig. 5. In the case of the
disc, we separate the profiles coming from different ages (i.e.
different scale heights) spaced by 1 Gyr. As can be noticed,
a simulation of the NGP - if not constrained by
any limiting magnitude - would contain increasing numbers of
disc stars as we go to older ages,
and at increasing mean distances (from
![]() to 12 as the
age goes from very young to 11 Gyr). For each age considered,
the disc distribution of
to 12 as the
age goes from very young to 11 Gyr). For each age considered,
the disc distribution of ![]() looks like an asymmetric
curve with a slow increase followed by a faster decay.
The
looks like an asymmetric
curve with a slow increase followed by a faster decay.
The ![]() distribution of halo stars, instead,
looks like a single Gaussian of mean
distribution of halo stars, instead,
looks like a single Gaussian of mean
![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2352f5.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg139.gif) |
Figure 5:
Distribution of stellar distance moduli in the
simulation corresponding to our initial calibration,
in a conic bean towards the NGP.
This is shown for 11 disc components of increasing age -
at steps of 1 Gyr, as labelled - and for the halo.
The top panel shows all the curves, whereas the
bottom one expands the vertical axis in order
to detail the profiles for ages younger than 5 Gyr.
It can be noticed that younger disc components
are found at lower mean distances (peaking from say
|
As a rule, we can conclude that halo stars dominate star counts at
very large distance moduli (
![]() ), whereas intermediate-age to
old disc stars would dominate counts at most "intermediate distances''
(
), whereas intermediate-age to
old disc stars would dominate counts at most "intermediate distances''
(
![]() from say 9 to 13). Only at very short distance moduli -
from say 9 to 13). Only at very short distance moduli -
![]() ,
i.e. in the immediate Solar Neighbourhood -
can the young disc stars make a sizeable contribution to the
star counts.
Alternatively, one has to look at lower galactic latitudes to see
a higher contribution from the young disc.
,
i.e. in the immediate Solar Neighbourhood -
can the young disc stars make a sizeable contribution to the
star counts.
Alternatively, one has to look at lower galactic latitudes to see
a higher contribution from the young disc.
Of course, the situation gets more complex as we consider the limiting magnitudes that are present in any survey, and that favour the detection of the few closest stars in spite of the many distant ones. Anyway, the present Fig. 5 shows the type of stars which make the major contribution depending on the depth of a given survey. This information is relevant for the discussion presented in the next section.
Since Paper I, we have improved many aspects of TRILEGAL, and checked the model predictions with additional datasets. This has forced some changes in the model calibration, as will be detailed in the subsections below.
First of all, we opted for a better temporal accuracy as
given by
![]() (see Sect. 3.6)
instead of the
(see Sect. 3.6)
instead of the
![]() adopted in
Paper I.
adopted in
Paper I.
![]() implies a virtually
continuous change of thin disc geometry with age, which
in itself represents a novelty in star count models.
implies a virtually
continuous change of thin disc geometry with age, which
in itself represents a novelty in star count models.
Second, we have adopted a more realistic metallicity distribution for halo stars, namely the one measured by Ryan & Norris (1991). The Sun's height above the disc was corrected to 24.2 pc (cf. Maíz-Apellániz 2001).
So far, these changes have just a minor impact in our final number counts. Major revisions instead resulted from our attempts to reproduce 2MASS and Hipparcos data, not considered in Paper I. Without entering in a detailed description of all attempts carried out to fit the models to the data, here we describe the main arguments used in establishing our final calibration. They are:
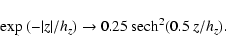 |
(8) |
Finally, in order to improve upon our final results for
2MASS and Hipparcos,
he have modified the SFR of the thin disc: we have
assumed that between 1 and 4 Gyr the SFR has been 1.5 times
larger than at other ages. This causes a moderate impact
in the distribution of stars in the MV vs. ![]() diagram,
that can only be explored by means of Hipparcos data.
In fact, such a change in the disc SFR has a negligible impact
on deep fields and just a minor impact on 2MASS counts.
diagram,
that can only be explored by means of Hipparcos data.
In fact, such a change in the disc SFR has a negligible impact
on deep fields and just a minor impact on 2MASS counts.
The normalization constants we derived imply
A main characteristic of deep photometric surveys is the rich presence of galaxies, a significant fraction of which appears as point sources and cannot be easily distinguished from real stars. Thus, object classification by means of morphological and photometric criteria is of central importance in these fields. The reader is referred to Paper I and Hatziminaoglou et al. (2002) for a discussion of these aspects.
In this paper, we deal with 3 deep catalogues which, as far as possible, have been cleaned from contamination by galaxies.
The first one is the CDFS stellar catalogue
(Paper I), which points towards a relatively
clean area centered in
![]() .
According to
Schlegel et al. (1998) maps, the reddening for background sources
amounts to
.
According to
Schlegel et al. (1998) maps, the reddening for background sources
amounts to
![]() or
AV=0.0458.
We make use of UBVRI data from the 5-passband catalogue
covering 0.263 deg2, and JK from the
7-passband catalogue covering 0.0927 deg2.
The data has been cleaned from non-stellar objects according to the
criteria and methods thoroughly discussed in Paper I.
For this field, we simulate the galactic population for a 2.63 deg2region. Figure 6 shows the results in units of number of
stars per unit deg2 and 0.5-mag intervals. As can be noticed, the
agreement between modelled and observed counts is good, their
ratio being comprised between 0.87 and 1.08 for all 7 pass-bands
considered.
or
AV=0.0458.
We make use of UBVRI data from the 5-passband catalogue
covering 0.263 deg2, and JK from the
7-passband catalogue covering 0.0927 deg2.
The data has been cleaned from non-stellar objects according to the
criteria and methods thoroughly discussed in Paper I.
For this field, we simulate the galactic population for a 2.63 deg2region. Figure 6 shows the results in units of number of
stars per unit deg2 and 0.5-mag intervals. As can be noticed, the
agreement between modelled and observed counts is good, their
ratio being comprised between 0.87 and 1.08 for all 7 pass-bands
considered.
![\begin{figure}
\mbox{\resizebox{8cm}{!}{\includegraphics[clip]{2352f7a.eps}}\hspace*{1.3cm}
\resizebox{8cm}{!}{\includegraphics[clip]{2352f7b.eps}} }
\end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg158.gif) |
Figure 7:
The same as Fig. 6,
but now limiting data and models to the "blue subsample''
with
|
Particularly interesting is the comparison between simulated and
observed number counts for stars in the interval
![]() .
This subsample, according to the models, is completely dominated
by disc stars at brighter magnitudes (
.
This subsample, according to the models, is completely dominated
by disc stars at brighter magnitudes (![]() ), and then by
halo stars at fainter magnitudes (
), and then by
halo stars at fainter magnitudes (![]() ); this is
illustrated by the comparisons between observed and
simulated CMDs shown in Paper I (see
in particular the online version of their Fig. 5).
Hence, by fitting number counts in this particular subsample we can
be sure to be correctly modelling the relative proportion
between halo and disc densities.
Moreover, a "blue subsample'' defined in this way is composed
mostly by stars in well-modelled evolutionary stages -
i.e. main sequence stars of moderately high
); this is
illustrated by the comparisons between observed and
simulated CMDs shown in Paper I (see
in particular the online version of their Fig. 5).
Hence, by fitting number counts in this particular subsample we can
be sure to be correctly modelling the relative proportion
between halo and disc densities.
Moreover, a "blue subsample'' defined in this way is composed
mostly by stars in well-modelled evolutionary stages -
i.e. main sequence stars of moderately high
![]() - and
excludes the hot white dwarfs and the reddest
very-low mass stars, for which the reliability of present-day
evolutionary and spectral models could still be questioned.
- and
excludes the hot white dwarfs and the reddest
very-low mass stars, for which the reliability of present-day
evolutionary and spectral models could still be questioned.
Such a comparison is presented in Fig. 7.
As can be noticed, the blue subsample
presents good evidence that the ratio
between halo and disc densities is well represented
for this line-of-sight. The most significant discrepancy that
appears at this point is a moderate excess of halo stars at
![]() .
As demonstrated in Paper I,
this is a magnitude interval in which
number counts become sensitive to the very low-mass IMF.
In fact, we have verified that a better agreement with
observations turns out if we artificially eliminate halo stars
with
.
As demonstrated in Paper I,
this is a magnitude interval in which
number counts become sensitive to the very low-mass IMF.
In fact, we have verified that a better agreement with
observations turns out if we artificially eliminate halo stars
with
![]()
![]() from our models. However, we prefer
not to draw any strong conclusion from this test, since
from our models. However, we prefer
not to draw any strong conclusion from this test, since
![]() is also close to both the limit for efficient
morphological classification, MAG_STAR_LIM, and the
90-percent completeness limit of CDFS data.
is also close to both the limit for efficient
morphological classification, MAG_STAR_LIM, and the
90-percent completeness limit of CDFS data.
The Deep Multicolor Survey by Hall et al. (1996) and
Osmer et al. (1998) provides deep UBVR'I75 and I86 data
for 6 different fields of
![]() .
From their catalogue, we eliminated the objects that are likely
not to correspond to stars, i.e. those marked as
"galaxy'', "noise'', "diffuse object'', or "long object''
in any of the DMS passbands.
.
From their catalogue, we eliminated the objects that are likely
not to correspond to stars, i.e. those marked as
"galaxy'', "noise'', "diffuse object'', or "long object''
in any of the DMS passbands.
![\begin{figure}
\par\resizebox{6.85cm}{!}{\includegraphics[clip]{2352f8a.eps}}\hs...
...*{12mm}
\resizebox{6.85cm}{!}{\includegraphics[clip]{2352f8f.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg164.gif) |
Figure 8:
The same as Fig. 6,
but for the several fields of the DMS (Osmer et al. 1998),
whose |
![\begin{figure}
\par\resizebox{7cm}{!}{\includegraphics[clip]{2352f9a.eps}}\hspac...
...ace*{12mm}
\resizebox{7cm}{!}{\includegraphics[clip]{2352f9f.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg166.gif) |
Figure 9:
The same as Fig. 8,
but now limiting data and models to the "blue subsample'' with
|
Figure 8 shows the UBVR results as compared to our models. As shown in the figure, if we limit the analysis to magnitudes between the DMS "upper limiting'' and the "threshold'' one - an interval almost free from saturation, incompleteness and contamination effects - there is a good overall agreement in the number counts between the data and our model. With the exception of DMS field 21, the largest discrepancies reach about 10 percent in number counts.
Again, the comparison between simulated and
observed number counts for stars in a "blue subsample'' -
now defined in the interval
![]()
![]() - are important for verifying whether we have the right
proportions between disc and halo stars. A careful examination of
Fig. 9 reveals that this is indeed the case,
but for DMS field 21, where, apparently, simulations
contain too few disc stars. Field 21 is the innermost of DMS fields,
pointing to a Galactic region for which actually our model calibration
indeed presents the largest problems (see Sect. 5.3).
- are important for verifying whether we have the right
proportions between disc and halo stars. A careful examination of
Fig. 9 reveals that this is indeed the case,
but for DMS field 21, where, apparently, simulations
contain too few disc stars. Field 21 is the innermost of DMS fields,
pointing to a Galactic region for which actually our model calibration
indeed presents the largest problems (see Sect. 5.3).
The South Galactic Pole (SGP) as observed by EIS
(Prandoni et al. 1999; Zaggia et al. 1999)
presents BVI data for an effective area of
1.21 deg2 centered at
![]() .
Figure 10 shows the comparison between the data
and our models. This time, the shape of the observed counts are,
in general, fairly well reproduced, except that the amplitude
of our model is twice as large as observed.
We did not find any obvious way of reducing
this discrepancy, without spoiling the excellent agreement we find
for the other fields considered in this paper - including 2MASS data
for the SGP itself.
Also, the lack of U-band data prevent us from analysing a blue
subsample essential in order to investigate the source
of the discrepancies.
.
Figure 10 shows the comparison between the data
and our models. This time, the shape of the observed counts are,
in general, fairly well reproduced, except that the amplitude
of our model is twice as large as observed.
We did not find any obvious way of reducing
this discrepancy, without spoiling the excellent agreement we find
for the other fields considered in this paper - including 2MASS data
for the SGP itself.
Also, the lack of U-band data prevent us from analysing a blue
subsample essential in order to investigate the source
of the discrepancies.
As seen above and also in Paper I, the deep
simulations of DMS, SGP and CDFS data are ideal for probing
the relative proportions between halo and disc components, as
well as the shape of the halo and the IMF of the disc.
For better probing the disc and its details (spiral arms, dust lanes,
warps, etc.), shallower surveys covering larger areas are better suited.
However, if one wants to avoid complications
caused by dust, we should consider only counts at the infrared.
In this context, 2MASS constitutes an invaluable dataset: it covers
the all sky in JH![]() for magnitudes as faint as
for magnitudes as faint as ![]() .
.
From the 2MASS All-Sky Data Release Point Source Catalog
we have selected the sub-sample obeying the so-called
"2MASS level 1 science requirements'' (see the User's Guide
in Cutri et al. 2003). In practice, these criteria refers to
stellar sources falling outside of tile overlap regions, and
of high photometric quality (namely
![]() and
and
![]() mag, band-by-band). For most of the
sky - excluding the most crowded low-latitude and bulge fields
- this subsample of 2MASS is essentially complete for
magnitudes brighter than about 15.
mag, band-by-band). For most of the
sky - excluding the most crowded low-latitude and bulge fields
- this subsample of 2MASS is essentially complete for
magnitudes brighter than about 15.
In the panels of Fig. 11, we show the
complete results for two 2MASS fields, one of high latitude
(the NGP at
![]() )
and one of low
(
)
and one of low
(
![]() ).
Plots for symmetric fields - namely the SGP
and the
).
Plots for symmetric fields - namely the SGP
and the
![]() ones - look very much
the same and present similar number counts.
The counts in these particular fields are very well
reproduced by the model, over a wide range of magnitudes in all
the 3 pass-bands of 2MASS. The reader can also notice that the
J, H and
ones - look very much
the same and present similar number counts.
The counts in these particular fields are very well
reproduced by the model, over a wide range of magnitudes in all
the 3 pass-bands of 2MASS. The reader can also notice that the
J, H and
![]() diagrams contain essentially the same information,
so that examining all of them may be redundant. For this reason
and for the sake of conciseness, in the next figure we prefer
to present just results for the H band.
diagrams contain essentially the same information,
so that examining all of them may be redundant. For this reason
and for the sake of conciseness, in the next figure we prefer
to present just results for the H band.
Figure 12 presents the H-band results
for a series of 2MASS fields disposed along a great circle
in the sky - the one at
![]() ,
encompassing the Galactic centre, anticentre and
polar regions. We show only the northern Galaxy fields, since
results for southern fields are essentially the same.
Moreover,
we remind the reader that the 2MASS data for CDFS fields
have already been presented in previous Fig. 6.
,
encompassing the Galactic centre, anticentre and
polar regions. We show only the northern Galaxy fields, since
results for southern fields are essentially the same.
Moreover,
we remind the reader that the 2MASS data for CDFS fields
have already been presented in previous Fig. 6.
The results are certainly encouraging. We are able to predict the
correct number counts, with errors smaller than ![]() 30 percent, for
all fields located at least 10 degrees above the Galactic Plane,
except for inner Galactic regions where the lack of a Bulge component
- presently not included in the model - becomes noticeable.
Moreover, it is not to be excluded that the present description
of the Galactic halo fails for small galactocentric distances,
hence contributing to the discrepancies we find at inner galactic
regions.
30 percent, for
all fields located at least 10 degrees above the Galactic Plane,
except for inner Galactic regions where the lack of a Bulge component
- presently not included in the model - becomes noticeable.
Moreover, it is not to be excluded that the present description
of the Galactic halo fails for small galactocentric distances,
hence contributing to the discrepancies we find at inner galactic
regions.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2352f10.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg178.gif) |
Figure 10: The same as Fig. 6, but for the EIS-deep SGP data (Prandoni et al. 1999). The limits of reliability of the data were located, somewhat arbitrarily this time, at magnitudes 16 and 21.5 for all filters. |
Remarkably, we find that for all 2MASS fields away from the Bulge
we have analysed, disc stars make the bulk of the number counts.
The halo contribution is almost negligible.
However, we recall that halo stars contribute to make
a particular feature in wide-area J vs.
![]() CMDs,
namely the central of three vertical fingers discussed by Marigo
et al. (2003), that are clearly present in 2MASS CMDs towards the
LMC. This indicates that the halo component has its importance
in analyses of 2MASS photometry.
CMDs,
namely the central of three vertical fingers discussed by Marigo
et al. (2003), that are clearly present in 2MASS CMDs towards the
LMC. This indicates that the halo component has its importance
in analyses of 2MASS photometry.
In fields too close to the Galactic Plane, instead, our model predictions fail, as demonstrated by the first panel of Fig. 12 regarding the direction of the Galactic anticentre. One of the reasons for this failure is surely the too simplistic modelling of the dust distribution along the Galactic Plane. Improving this aspect of the model, however, is beyond the scope of the present paper.
Examining the stellar counts in the immediate Solar Neighbourhood is an obvious test for any Galaxy model. In fact, present models usually check whether their results are consistent with the observed "local stellar density'', or with some similar parameter derived from Hipparcos data (see e.g. Robin et al. 2003). Of course, by using just a single density parameter as a constraint, we ignore the wealth of photometric information that is present in the data for nearby stars, that could tell us much about the distribution of stellar parameters in the disc. In order to start exploring this information, in the following we try to predict the counts of a local sample, using the Hipparcos dataset.
First of all, however, we should remind that
our model in Paper I has been effectively calibrated on
deep data (![]() ).
For such deep surveys the effective distributions of
distance moduli should approach the ones
shown in Fig. 5, i.e. the samples
are dominated by relatively far objects, at distance moduli
ranging from
).
For such deep surveys the effective distributions of
distance moduli should approach the ones
shown in Fig. 5, i.e. the samples
are dominated by relatively far objects, at distance moduli
ranging from
![]() to 14 for the disc populations,
and from
to 14 for the disc populations,
and from
![]() to 18 for the halo.
It is then obvious that our previous model
calibration has almost nothing to do with the very
local sample of stars, i.e. the one observed at distances
lower or comparable to 100 pc, and at bright magnitudes such
as
to 18 for the halo.
It is then obvious that our previous model
calibration has almost nothing to do with the very
local sample of stars, i.e. the one observed at distances
lower or comparable to 100 pc, and at bright magnitudes such
as ![]() ,
that we will define below. Deep and local samples
could even be considered, in terms of their
stellar populations, as completely independent data samples.
,
that we will define below. Deep and local samples
could even be considered, in terms of their
stellar populations, as completely independent data samples.
![\begin{figure}
\mbox{\resizebox{8cm}{!}{\includegraphics[clip]{2352f11a.eps}}\hspace*{8mm}
\resizebox{8cm}{!}{\includegraphics[clip]{2352f11b.eps}} }
\end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg186.gif) |
Figure 11:
The same as Fig. 6,
but for two sample fields of 2MASS data:
|
![\begin{figure}
\par\mbox{\resizebox{8.5cm}{!}{\includegraphics[clip]{2352f12a.ep...
...*{3mm}
\resizebox{8.5cm}{!}{\includegraphics[clip]{2352f12d.eps}} }
\end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg187.gif) |
Figure 12:
The same as Fig. 11,
but limited to the H-band and for
a series of fields disposed along the
|
The Hipparcos and Tycho catalogues (ESA 1997) have provided
parallaxes with ![]() 10 milliarcsec (mas) accuracy for several
thousands of stars, together with accurate BV photometry.
The Hipparcos input catalogue was
constructed in such a way that there are no clearcut criteria
for defining volume-limited samples out of its data.
This problem has been recognized by a number of previous authors.
Hernandez et al. (2000) and Bertelli & Nasi (2001), for instance,
find it to be extremely difficult to
define volume-limited samples containing enough
stars for studying the SFR in the solar vicinity up to the
oldest possible ages (see also Schröder & Pagel 2003).
10 milliarcsec (mas) accuracy for several
thousands of stars, together with accurate BV photometry.
The Hipparcos input catalogue was
constructed in such a way that there are no clearcut criteria
for defining volume-limited samples out of its data.
This problem has been recognized by a number of previous authors.
Hernandez et al. (2000) and Bertelli & Nasi (2001), for instance,
find it to be extremely difficult to
define volume-limited samples containing enough
stars for studying the SFR in the solar vicinity up to the
oldest possible ages (see also Schröder & Pagel 2003).
However, our aim in this paper is different from previous works. We consider a subsample of the Hipparcos catalogue to be good provided it is complete and could be simulated. Differently from the above-mentioned papers, we do not need to limit our simulations to stars being all contained in the same volume. Our sample can be selected by using a few simple criteria, based on the following realizations:
We then simulated this local sample using the TRILEGAL code.
To do so, we have generated synthetic samples up to a distance
![]() pc. This is large enough to include all stars that,
due to parallax errors, will later be scattered to apparent distances
closer than 100 pc.
pc. This is large enough to include all stars that,
due to parallax errors, will later be scattered to apparent distances
closer than 100 pc.
The simulated true physical distances r0 are first converted
in the true parallax
![]() .
The simulated parallax errors
.
The simulated parallax errors ![]() (described in the
Appendix) are then added to
(described in the
Appendix) are then added to ![]() so as to
generate the "observed'' parallaxes and distances,
so as to
generate the "observed'' parallaxes and distances, ![]() and
and
![]() .
The "observed'' absolute magnitude is then derived
by the usual formula,
.
The "observed'' absolute magnitude is then derived
by the usual formula,
![]() .
Extinction has been ignored, since its effect
inside a radius of 200 pc is negligible.
.
Extinction has been ignored, since its effect
inside a radius of 200 pc is negligible.
The results of this exercise can be seen in
Fig. 13, for the conservative
choice of
![]() and
and
![]() mas.
In the left-hand panel, we compare the simulated and observed
MV vs.
mas.
In the left-hand panel, we compare the simulated and observed
MV vs. ![]() diagram.
The agreement between simulated and observed samples is striking.
It can be noticed that models describe very well both the location
and width of the main sequence all along from
diagram.
The agreement between simulated and observed samples is striking.
It can be noticed that models describe very well both the location
and width of the main sequence all along from
![]() to -4.
Particularly good is the description of the left boundary of the
MS, very well marked because it is produced by stars in their phase of
slowest evolution, when they depart from their ZAMS to the right
in the HR diagram. Regarding the MS width,
we know from stellar models that it is affected essentially
by two factors: the assumed metallicity dispersion (or equivalently
the AMR in our models) and the efficiency of convective core
overshooting for M>1
to -4.
Particularly good is the description of the left boundary of the
MS, very well marked because it is produced by stars in their phase of
slowest evolution, when they depart from their ZAMS to the right
in the HR diagram. Regarding the MS width,
we know from stellar models that it is affected essentially
by two factors: the assumed metallicity dispersion (or equivalently
the AMR in our models) and the efficiency of convective core
overshooting for M>1 ![]() stars. The good agreement
between models and simulations seems to indicate that both these
ingredients are well described in our models. Of course,
before considering the implications that this result may have
for the disc AMR and for the theory of stellar evolution more
quantitative comparisons would have to be made. However, such a
discussion is beyond the scope of the present paper.
stars. The good agreement
between models and simulations seems to indicate that both these
ingredients are well described in our models. Of course,
before considering the implications that this result may have
for the disc AMR and for the theory of stellar evolution more
quantitative comparisons would have to be made. However, such a
discussion is beyond the scope of the present paper.
Regarding the evolved stars (subgiants and red giants), the agreement is also very good: we can notice the right width of the subgiant and lowest part of RGB; the clumping of core-He burning stars in the right location; the bifurcation of the red giants above the clump into two loose broad sequences: a vertical one made of intermediate-mass core-He burners and the inclined one, going to the red, made of genuine first-ascent RGB and early-AGB stars.
As can be seen, the simulation predicts about the same star counts as observed: the total number of objects in both panels is 4085 and 4182 for the data and models, respectively.
The right panels show the corresponding
distributions of apparent distance r and derived absolute
magnitude MV (continuous lines). The dashed lines
refer to the subsample of subgiants and giants, defined by
the stars with
![]() .
.
There, although a first look indicates a good overall level
of agreement between models and data, some discrepancies
become apparent. In the histogram of r, the most noticeable
one seems to be a modest excess of simulated stars at
![]() pc, that amounts to about 20 percent.
Since the volume sampled in the simulation is very small,
we consider that such a discrepancy is unlikely to be derived
from inhomogeneities in the local distribution of stars;
more likely, a better simulation of Hipparcos parallax errors
could improve the models in this particular range
of distances (parallaxes). There is also a modest
deficit of simulated stars in the smallest distances
(from 15 to 35 pc), amounting again to about 20 percent,
which however does not appear among the subgiants and giants.
This again might indicate a problem in the simulation of
parallax errors for the faintest stars. On the other hand,
the spike of observed star counts at r=45 pc is to be
assigned to the Hyades cluster, which was not considered in
our simulation.
pc, that amounts to about 20 percent.
Since the volume sampled in the simulation is very small,
we consider that such a discrepancy is unlikely to be derived
from inhomogeneities in the local distribution of stars;
more likely, a better simulation of Hipparcos parallax errors
could improve the models in this particular range
of distances (parallaxes). There is also a modest
deficit of simulated stars in the smallest distances
(from 15 to 35 pc), amounting again to about 20 percent,
which however does not appear among the subgiants and giants.
This again might indicate a problem in the simulation of
parallax errors for the faintest stars. On the other hand,
the spike of observed star counts at r=45 pc is to be
assigned to the Hyades cluster, which was not considered in
our simulation.
The histogram of number counts against MV indicates, once again, some modest discrepancies, that are however statistically very significant. The most important one consists on an excess of simulated bright stars accompanied by a deficit of the faintest ones. We have performed a KS-test comparison between the two MV distributions, and find that the probability of them being drawed from the same distribution would be highly increased - from its present close-to-zero value up to about 0.3 - if our models were shifted by 0.26 mag in MV. We think however that applying such a shift whould not be justified, and it could not be easily translated onto a physical interpretation (i.e. shifts in the MV distribution can be forced by using models with a corrected photometric zero-point, different IMF, different SFR, modified prescription for simulating parallax errors, or a combination of all these effects).
![\begin{figure}
\par\resizebox{12.5cm}{!}{\includegraphics[clip]{2352f14.eps}} \end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg212.gif) |
Figure 14:
The same as Fig. 13,
but for samples limited to an apparent magnitude of
|
To conclude, we remark that all the above-mentioned
discrepancies are, from the statistical point of view,
highly significant, since they refer to samples
containing large numbers of stars. They may be indicating
points where the present models can be improved.
They however do not invalidate the present model calibration,
for a series of reasons: first of all, many of the discrepancies
are suspected to result from the imperfect simulation of
parallax errors; second, when one deals with normal
star counts data, fine details (i.e. those seen at ![]() 0.25 mag
resolution) of the MV distribution become of little relevance
since stars are dispersed over a large range of
distance moduli; third, the most relevant comparison regards
the total star counts that are directly linked to the local
density of stars: in our case they are very well predicted,
to within 5 percent. Reaching such a result for the star counts
is already remarkable, whereas reaching a statistically-robust
comparison with Hipparcos, in all its details, may be still
far from reach. In this regard, the present work represents
just the first attemp.
0.25 mag
resolution) of the MV distribution become of little relevance
since stars are dispersed over a large range of
distance moduli; third, the most relevant comparison regards
the total star counts that are directly linked to the local
density of stars: in our case they are very well predicted,
to within 5 percent. Reaching such a result for the star counts
is already remarkable, whereas reaching a statistically-robust
comparison with Hipparcos, in all its details, may be still
far from reach. In this regard, the present work represents
just the first attemp.
Figure 14 presents the same as
Fig. 13, but for a slightly deeper sample,
of
![]() and
and
![]() mas.
The effect of selecting a deeper
mas.
The effect of selecting a deeper
![]() is that more stars
with
is that more stars
with
![]() are included in the sample, then increasing the
contribution of intermediate-age to old stars (in their main sequence,
subgiant branch, and initial RGB evolution) to the number counts.
In this case, the star counts are 8055 and 7640
for data and models, respectively. The discrepancies between
model and observations seem slightly increased, as expected
since we are including data for which the completeness starts
to become an issue, and for which parallax errors are slightly
larger with respect to the previous V<7 sample.
are included in the sample, then increasing the
contribution of intermediate-age to old stars (in their main sequence,
subgiant branch, and initial RGB evolution) to the number counts.
In this case, the star counts are 8055 and 7640
for data and models, respectively. The discrepancies between
model and observations seem slightly increased, as expected
since we are including data for which the completeness starts
to become an issue, and for which parallax errors are slightly
larger with respect to the previous V<7 sample.
We have presented a new code for simulating the photometry of Galaxy fields.
The code has been calibrated by predicting counts in a variety of stellar surveys, that comprehend some very deep multi-passband catalogues cleaned from galaxies (CDFS, DMS, SGP), the "intermediate-depth'' near-IR point source catalogue of 2MASS, and the very local stellar sample derived from Hipparcos catalogue.
The results are certainly satisfactory, since we have demonstrated that the predicted star counts agree well with the observed ones. The typical discrepancies are smaller than 30 percent for most of the sky, and inside the estimated magnitude limits of reliability of the observed star counts. This agreement is remarkable, when we consider the wide ranges of magnitudes, passbands (from U to K) and sky positions that were considered in this work.
The major discrepancies were found for: (1) inner Galactic fields,
located within about 30 deg from the Galactic Center, for which we
largely underestimate the number counts. Part of this discrepancy
can be attributed to the lack of a bulge component in the
present model, but probably a better modelling of the inner disc
and halo densities is also necessary. (2) Low-latitude fields,
with
![]() ,
which probably require a detailed modelling of
the distribution of dust and recent star formation along the disc.
Finally, (3) the SGP as observed by EIS, for which we predict
twice as many counts in the optical as observed. In this case,
the origin of the discrepancy could not be identified.
,
which probably require a detailed modelling of
the distribution of dust and recent star formation along the disc.
Finally, (3) the SGP as observed by EIS, for which we predict
twice as many counts in the optical as observed. In this case,
the origin of the discrepancy could not be identified.
Note that the present model calibration is not yet fully optimized
and is likely not to be unique, in the
sense that other choices for the stellar densities and
star formation histories of Galaxy components might produce
similarly good results. In fact, the question arises whether
TRILEGAL could be adapted to find, in an objective way,
a maximum-likelihood solution for
the functions ![]() ,
,
![]() ,
,
![]() ,
etc. -
using a database of few high-quality
multiband catalogues covering several regions of the sky and
with a large range in depth. The answer is likely
yes, but the way is certainly not straightforward.
Such a work would imply at least the following steps:
(a) finding a zeroth-order calibration producing
"acceptable'' results, which is actually the step performed
in this paper;
(b) establishing a robust likelihood criterium for
comparing the resulting models with the stellar data;
(c) establishing a numerical algorithm to migrate from the
zeroth-order to improved maximum-likelihood solutions
(see for instance Ng et al. 2002);
(d) exploring the problem of uniqueness of solution
by using different starting solutions.
Therefore, what is presented in this paper can be seen as the
initial step of a bigger project, that we expect to pursue
in the future.
,
etc. -
using a database of few high-quality
multiband catalogues covering several regions of the sky and
with a large range in depth. The answer is likely
yes, but the way is certainly not straightforward.
Such a work would imply at least the following steps:
(a) finding a zeroth-order calibration producing
"acceptable'' results, which is actually the step performed
in this paper;
(b) establishing a robust likelihood criterium for
comparing the resulting models with the stellar data;
(c) establishing a numerical algorithm to migrate from the
zeroth-order to improved maximum-likelihood solutions
(see for instance Ng et al. 2002);
(d) exploring the problem of uniqueness of solution
by using different starting solutions.
Therefore, what is presented in this paper can be seen as the
initial step of a bigger project, that we expect to pursue
in the future.
Aside from the good model calibration we have reached, the most important advantages of the TRILEGAL code can be identified in: (1) the fairly complete database of stellar evolutionary tracks already implemented; (2) the use of an extended spectral library to simulate many different photometric systems, and their extinction coefficients, in a self-consistent way; (3) the modular and flexible structure of the code, that allows easy changes and additions to both input functions (SFR, AMR, IMF, etc.) and geometric parameters (the density of Galaxy components, Sun's position, pointing parameters, etc.).
With respect to other population synthesis codes commonly used to simulate the photometry of Galaxy fields (e.g. Ng et al. 1995; Vallenari et al. 2000; Castellani et al. 2002; Robin et al. 2003), TRILEGAL shares the advantage of being intrinsically self-consistent in the relative numbers of stars predicted to be in different evolutionary phases (including stellar remnants such as white dwarfs). In fact, for a given Galaxy geometry, stellar number ratios are univoquely determined by the choice of SFR, AMR and IMF, and are not tunable parameters. In TRILEGAL, this self-consistency of population synthesis codes is kept as a very stringent criteria, since there are explicit checks for the continuity of all stellar quantities (including core mass, envelope mass, and surface chemical composition when applicable) in the isochrone-construction routines that make part of the code.
As already mentioned, a main positive characteristic of TRILEGAL consists in the extreme flexibility in the way input libraries (evolutionary tracks, atmospheres) and functions (geometry, IMF, SFR, AMR of Galaxy components) can be changed, tested, and added to a database for future use. Improvements in the stellar evolutionary tracks, for instance those described in Marigo et al. (2003), have been inserted in TRILEGAL in almost no time. We have so far computed test models in at least 10 different photometric systems (including UBVRIJHK, Washington, HST-based instruments like WFPC2, NICMOS and ACS, the EIS photometric system, 2MASS and SDSS), and we are confident that virtually any broadband Vega, AB or ST magnitude system can be considered as well (cf. Girardi et al. 2002). Needless to say, before the present TRILEGAL calibration has been considered as acceptable, we have made wide use of its flexibility by testing many different IMFs, AMRs, SFRs, and density functions published by different authors. Such a flexibility is of fundamental importance for facing the huge amount of wide-field photometric data that is becoming available these days, and to take immediate advantage of the next generation of improved/expanded stellar evolutionary and atmospheric models, that are now being prepared by different groups around the world.
Therefore, the TRILEGAL code is ready to use for the variety of wide-angle surveys in the optical/infrared that will become available in the coming years and will provide constraints that will help us to pin down the structure of our Galaxy.
Acknowledgements
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We acknowledge the referee for the interesting remarks, which helped to improve this paper.
In this Appendix we describe how the parallax errors in the Hipparcos
catalogue have been simulated. From the about 118 000 objects in the
Hipparcos catalogue the about 99 000 objects have been selected that
fulfill: "goodness-of-fit'' flag (H30) less than 3,
"percentage-of-rejected-data'' flag (H29) less than 10, "number of
components'' flag (H58) of 1, that have a V-band magnitude and a
parallax larger than 0.5 mas. Figure A.1 shows the
distribution of errors ![]() for these data.
From this dataset the following recipe was devised.
for these data.
From this dataset the following recipe was devised.
The median parallax error (in mas) is calculated from:
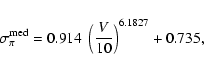 |
(A.1) |
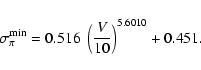 |
(A.2) |
Once a star of magnitude V and his error ![]() are simulated,
the individual measurement error
are simulated,
the individual measurement error ![]() is drawn
from the Gaussian of dispersion
is drawn
from the Gaussian of dispersion ![]() .
.
![\begin{figure}
\resizebox{8cm}{!}{\includegraphics[clip]{2352fap1.eps}}\end{figure}](/articles/aa/full/2005/24/aa2352-04/Timg221.gif) |
Figure A.1: Errors in Hipparcos parallaxes. The data is in the lower panel, our simulations in the upper one. |