A&A 435, 125-129 (2005)
DOI: 10.1051/0004-6361:20042225
Interaction of young stellar object jets with their accretion disk![[*]](/icons/foot_motif.gif) ,
,![[*]](/icons/foot_motif.gif)
N. Soker
Department of Physics, Technion-Israel Institute of
Technology, 32000 Haifa, Israel
Received 21 October 2004 / Accepted 10 January 2005
Abstract
I reexamine recent observations of velocity profiles
across jets blown by young stellar objects, and argue that the
observations do not support the earlier interpretation of jets
rotating around their symmetry axes. Instead, I propose that
interaction of the jets with a twisted-tilted (wrapped) accretion
disk can form the observed asymmetry in the jets' line of sight
velocity profiles. The proposed scenario is based on two plausible
assumptions. (1) There is an inclination between the jet and the
outer parts of the disk, such that the jet is perpendicular to the inner
part of the disk; i.e., there is a twisted-tilted (wrapped)
disk. (2) The disk-jet interaction slows the jet down as the jet
entrains mass from the disk, with larger decelaration of jet
segments closer to the tilted disk. The proposed scenario can
account for the basic properties of the observed velocity
profiles, while offering the advantage of not needing to
refer to any magnetic jet launching model, and there is no need to
invoke jet rotation with a huge amount of angular momentum.
Key words: accretion, accretion disks - ISM: jets and outflows -
stars: pre-main-sequence - stars: formation
1 Introduction
Asymmetry in the line of sight velocity across some jets ejected by
young stellar objects (YSOs) has been interpreted as caused by
a large scale rotation of the material in each jet around the jet's
symmetry axis (e.g., Bacciotti et al. 2002; Coffey et al. 2004,
hereafter B2002 and C2004).
Rotation around the jet axis is predicted by the
magneto-centrifugal models for jet launching.
In these models the magnetic fields that are anchored into the
accretion disk-star system play a dominate role in accelerating
the jet's material from the accretion disk.
Most models in YSOs are based on the operation of large scale magnetic
fields driving the flow from the disk: either via the "centrifugal wind''
mechanism, first proposed by Blandford & Payne (1982), or from a narrow
region in the magnetopause of the stellar field via an "X-wind
mechanism'' introduced by Shu et al. (1988, 1991) and, in a
somewhat different setting, by Ferreira & Pelletier (1993, 1995).
See recent reviews and papers by Königl and Pudritz (2000), Shu et al.
(2000), Ferreira (2002), and Krasnopolsky et al. (2003).
It should, however, be pointed out that there
are still open key issues (e.g. Heyvaerts et al. 1996).
One of them is the origin of the large scale
magnetic fields and the manner open field lines of sufficiently
strong magnitude persist (in the centrifugal wind models).
Another open issue is the manner by which a stellar field interacts
with the disk, allowing inflow and at the same time driving an
outflow (in the X-wind models).
In addition, it seems that thermal pressure is needed in
some of these models (e.g., Ferreira & Casse 2004).
In a recent paper, Cerqueira & de Gouveia Dal Pino (2004)
conduct magnetohydrodynamics (MHD) 3D numerical simulations
of YSO jets with rotation.
They use parameters suitable for the jet of DG Tauri, a YSO
studied by B2002, and obtain radial velocity maps in
good agreement with the observations of B2002.
In the Appendix I point out some difficulties with this
interpretation of jet rotation.
Magnetic fields might also play a role in triggering the jet's ejection
event, e.g., by causing instabilities in the disk and
in collimating the jets (e.g., Heyvaerts & Norman 1989).
The collimation issue is, however, still quite controversial, and while
magnetic collimation is certainly plausible, its exact nature is
probably quite involved and still not fully understood (see the
recent works of Bogovalov & Tsinganos 2001; Li 2002).
In some models external pressure is required to maintain collimation,
e.g., Kato et al. (2004) and the magnetic tower model
of Lynden-Bell (2003).
Although some of the arguments in these papers apply to
relativistic jets, I mention them here in my search for a unified
collimation machanism in different jets' environments.
In Sect. 2 I discuss some aspects of disk-jet interaction
in YSOs.
In some models, magnetic fields do not play a major role
in launching the jet.
These include the thermally-launched jet model (Torbett 1984;
Torbett & Gilden 1992) that was applied to YSOs
(Soker & Regev 2003) and cataclysmic variables
(Soker & Lasota 2004).
Motivated by non-magnetic models, in Sect. 3 I show that the
asymmetric radial velocity field of these YSO jets may be
interpreted in an alternative way, where the magnetic field
play no major role.
In this proposed model, instead of jet rotation, the velocity field is
attributed to interaction of the jet with the accretion disk wind
and/or corona.
A summary of the main results is found in Sect. 4.
2 Interaction of a fast outflow with the disk
I here discuss an alternative explanation for the results in
C2004, one based on the interaction of an outflow (jets), blown
at large speeds from the vicinity of the central star,
with the accretion disk, mainly via entrainment of disk
mass by the jets.
The entrainment process itself has been studied in the past.
This entrainment is likely to occur in a turbulent mixing layer
between the jet and the ambient gas (e.g., Kahn 1980;
Canto & Raga 1991).
While most studies consider entrainment of (molecular) gas
at distances of hundreds of AU from the source (e.g. Davis et al. 2004),
I consider entrainment of disk material at a distance of
several AU from the source.
Based on CO observations, Stahler (1994) build an empirical model for
entrainment in YSO jets on scales of hundreds of AU.
According to this model, the velocity of matter
inside the jet decreases with increasing distance from the jet's axis.
This velocity profile is assumed here as well.
The next step in developing the presently proposed scenario will be
to include such an effect for interaction of a jet with a wrapped
disk, but on a scale of several AU rather than hundreds of AU.
First I note that accretion disks around YSOs can be quite extended in
the vertical direction (e.g., Semenov et al. 2004; Malbet et al. 2001).
In addition, the disk may blow a slow wind from an extended region caused,
e.g., by coronal type magnetic activity on the surface of the disk.
I assume therefore that a fast wind, hereafter referred to as jets,
blown from the vicinity of the central star at a speed of
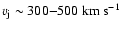 ,
interacts with the disk and/or
its wind.
The outer parts of the jets are influenced the most.
Let us first assume that the outskirts of the jet are strongly shocked
at a distance of
,
interacts with the disk and/or
its wind.
The outer parts of the jets are influenced the most.
Let us first assume that the outskirts of the jet are strongly shocked
at a distance of 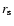 from the central star.
The density of the post-shocked gas, which is
from the central star.
The density of the post-shocked gas, which is  4 times the
pre-shocked density, is given by
4 times the
pre-shocked density, is given by
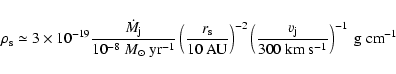 |
(1) |
where
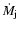 is the mass loss rate into the two jets together.
I assume above a spherically symmetric fast wind (jet);
an initial (poor) collimation means a higher jet's density.
On the other hand, higher mass loss rate near the jet axis
(e.g., Liseau et al. 2005)
means a lower density on the jet's outskirts.
The density given in Eq. (1) is lower than
the disk's surface density
is the mass loss rate into the two jets together.
I assume above a spherically symmetric fast wind (jet);
an initial (poor) collimation means a higher jet's density.
On the other hand, higher mass loss rate near the jet axis
(e.g., Liseau et al. 2005)
means a lower density on the jet's outskirts.
The density given in Eq. (1) is lower than
the disk's surface density
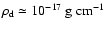 at
at
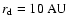 in the
model of Semenov et al. (2004) for an accretion rate of
in the
model of Semenov et al. (2004) for an accretion rate of
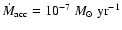 .
The gas shocked to a temperature of
.
The gas shocked to a temperature of
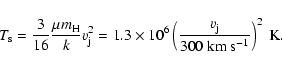 |
(2) |
For this temperature I approximate the cooling curve
(e.g., Gaetz et al. 1988) by
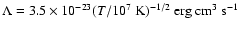 ,
for
,
for
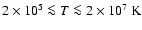 .
The cooling rate in power per unit volume is given by
.
The cooling rate in power per unit volume is given by
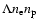 ,
where
,
where 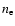 and
and 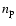 are the
electron and proton density, respectively.
I take the cooling time at a constant pressure
are the
electron and proton density, respectively.
I take the cooling time at a constant pressure
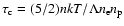 for a fully ionized post-shock gas.
For the flow time I take
for a fully ionized post-shock gas.
For the flow time I take
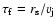 ,
which is about the time
required for the high post shock pressure to
re-accelerate the post shock gas.
Relating the shock temperature to the speed of a fully ionized solar
composition wind, and taking the density from Eq. (1),
gives
,
which is about the time
required for the high post shock pressure to
re-accelerate the post shock gas.
Relating the shock temperature to the speed of a fully ionized solar
composition wind, and taking the density from Eq. (1),
gives
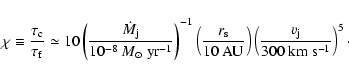 |
(3) |
The reacceleration distance is shorter than 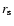 ,
and the reacceleration
time shorter than
,
and the reacceleration
time shorter than
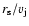 .
Also, the shock is oblique, and less of the wind kinetic energy is thermalized.
Therefore, the value given in Eq. (3) is a lower limit.
.
Also, the shock is oblique, and less of the wind kinetic energy is thermalized.
Therefore, the value given in Eq. (3) is a lower limit.
From Eqs. (1)-(3) the following conclusions can be drawn.
- (1)
- The density in the surface layer of disks around YSOs can
be higher than that in the jet, influencing its propagation.
The main modes of interaction are thereby entraining of the disk's mass
by the jets, a process that slows down the region of the jets
entraining the mass, and deflection of the jet's outskirts
via a strong shock, a process which recollimates the jet and which
may deflect somewhat the jet.
- (2)
- The shocked material is heated to soft X-ray emission temperatures
and can cool on a longer time scale than the time it is
being re-accelerated;
that is, there is an adiabatic-type flow.
Note that the fraction of the mass in the jet that is
shocked to X-ray emitting temperature is very low, as only the
outskirts of the jets are shocked.
Pressure gradient then collimates the inner regions of the jet,
and entrainment slows the jet down.
Therefore, X-ray emission from the shocked region will be weak,
which is compatible with the Chandra observations of
Getman et al. (2002), who find that the presence or absence of an outflow
does not appear to produce any difference in the X-ray properties
of YSOs.
- (3)
- The relatively small energy loss implies that the re-acclerated
gas reaches velocity close to its original speed.
- (4)
- However, because of the high disk-density in the interaction
region, even a small-volume mixing implies that substantial disk
material is entrained by the jet outskirts.
This, and some radiative cooling, will slow down the re-accelerated gas.
- (5)
- The last point implies that if a large amount of gas from the
disk is entrained by the fast jet, a slow dense jet might
be formed.
- (6)
- The inner boundary of the surface layer in the disk
model of Semenov et al. (2004) mentioned above is at a height
of
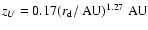 .
The outer boundary of the surface layer flares even faster.
If the surface layer redirects the outskirts of the jets, this
flaring will lead to collimation of the jet.
.
The outer boundary of the surface layer flares even faster.
If the surface layer redirects the outskirts of the jets, this
flaring will lead to collimation of the jet.
- (7)
- Cooling time is not much longer than flow time.
Because of inhomogeneities, some blobs may still cool.
I attribute differences in the velocities observed in
different lines by C2004 to such inhomogeneities, which
possibly led to thermal instabilities as well.
3 Interaction with the disk and radial velocity profiles
In the previous section I discussed the interaction of
a fast wind (2 opposite ejected jets) with the accretion disk.
This might result in jets' collimation, where the basic collimating
force is thermal pressure, with possible help from ram
pressure of a slow disk's wind.
Magnetic hoop-stress might still play a role, but not
necessarily a dominant one.
In this section I show that in principle the radial-velocity gradient
in the jets observed by B2002 and C2004 can be explained by interaction
of the jets with the accretion disk, if one assumes that the
accretion disk is tilted with respect to the jets' axis.
What C2004 attributes to rotation, I attribute to a different
degree in the slowing down process of different
segments of the jets, caused by a tilted accretion disk.
Since the jets will be blown perpendicular to the inner
disk, what is required is for the inner disk to be twisted with
respect to the further out regions of the disk.
These are the outer parts of the disk which the jets interact with.
Such a twisted (wrapped) disk can result from
(i) radiation induced warping
(Armitage & Pringle 1997; see Figs. 7 and 10 of Wijers & Pringle
1999 for the geometry of a twisted disk); (ii) from
the influence a stellar binary companion (Larwood et al. 1996);
or (iii) possibly from the influence of a massive planet.
![\begin{figure}
\par\includegraphics[width=5cm,clip]{2225fig1.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg23.gif) |
Figure 1:
Schematic drawing of the jet-disk-observer geometry in the plane defined by
the jets' symmetry (z) axis, and the line of sight. The solid
thick lines mark the boundary of the two jets. The dotted thick
line shows a cut through the twisted-tilted accretion disk. The
three points which are marked i, ii, and iii, are the three
points along each line of sight, at distance y from the jet's
axis, for which the line of sight velocity is plotted in Fig. 3. |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2225fig2.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg24.gif) |
Figure 2:
Like Fig. 1, but showing the plane perpendicular to the
jets' axis, and through the source of the jets.
The tilting and twisting of the accretion disk is monotonic,
with maximum flaring in the +z direction at an angle 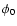 to the +x axis, and the maximum flaring in the -z direction
occurring at an angle to the +x axis, and the maximum flaring in the -z direction
occurring at an angle
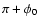 to the +x axis.
to the +x axis. |
The assumed disk structure is schematically drawn in Fig. 1.
The z axis is taken along the jet axis with the positive side
in the receding (red-shifted) jet direction.
The xz plane is taken to be the plane defined by the jet axis and
the line of sight with the positive x axis on the
observer side.
The angle between the approaching (blue-shifted) jet's axis and the
line of sight is 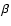 .
The observed section of the jet is assumed to be cylindrical with
radius
.
The observed section of the jet is assumed to be cylindrical with
radius 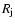 .
The y axis is perpendicular to the jet's axis and to the line of sight
(Fig. 2).
The first basic assumption is that the disk plane is inclined to the
xy plane; it has a maximum height toward the +z direction at an angle
.
The y axis is perpendicular to the jet's axis and to the line of sight
(Fig. 2).
The first basic assumption is that the disk plane is inclined to the
xy plane; it has a maximum height toward the +z direction at an angle
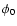 from the x axis, and a maximum height in the -z direction
at an angle of
from the x axis, and a maximum height in the -z direction
at an angle of
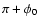 relative to the x axis.
The tilt angle is
relative to the x axis.
The tilt angle is 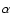 .
The second basic assumption is that the disk slows down the jet
with larger decelaration of jet segments closer to the tilted disk
and less efficient deceleration closer to the jets' axis and away
from the disk.
I also consider all regions with jets far from their origins, after the
different segments have reached their terminal speed; i.e.,
.
The second basic assumption is that the disk slows down the jet
with larger decelaration of jet segments closer to the tilted disk
and less efficient deceleration closer to the jets' axis and away
from the disk.
I also consider all regions with jets far from their origins, after the
different segments have reached their terminal speed; i.e.,
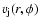 does not depend on z.
I parameterize the slowing down of the jet material by taking the
velocity at a distance r from the jet axis and at an angle
does not depend on z.
I parameterize the slowing down of the jet material by taking the
velocity at a distance r from the jet axis and at an angle 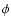 to the x axis as
to the x axis as
![\begin{displaymath}\frac {{\vec{v}}_{\rm j}(r,\phi)}{v_{\rm ja}} = k \hat z -
C_...
...s (\phi-\phi_0) ]
\left( \frac{r}{R_{\rm j}} \right)^n \hat z,
\end{displaymath}](/articles/aa/full/2005/19/aa2225-04/img30.gif) |
(4) |
where C1>0, which is a constant, and
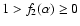 ,
which
is a monotonic function of the tilt angle
,
which
is a monotonic function of the tilt angle 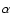 ,
depend both
on the strength of the jet-disk interaction;
,
depend both
on the strength of the jet-disk interaction;
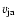 is the magnitude of
the outflow speed along the jets' axis, and
is the magnitude of
the outflow speed along the jets' axis, and
 |
|
|
(5) |
The observation at specific point across the jet includes all
jet segments along the line of sight to that point.
To get a sense of the range of the observed velocities, I draw
the component of the jet's radial velocity in Fig. 3 along the
line of sight, as a function of the distance from the jet's axis
for three locations along the line of sight for each point:
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2225fig3.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg34.gif) |
Figure 3:
The observed line of sight velocity across the jet, in units of
the real velocity along the jet's axis. y is the distance from the jet's symmetry axis, perpendicular to the line
of sight.
In each panel the upper 3 lines are for the receding jet, while the lower
3 lines are for the approaching jet.
Thick solid line is the velocity of the closest point in the jet along
the line of sight (Eq. (6); point i in Figs. 1 and 2);
Thick dashed line is the velocity of the farthest point in the jet
along the line of sight (Eq. (6) with minus sign in
front of the square root; point ii in Figs. 1 and 2);
Thin solid line is the velocity of the jet's element closest to the
jet's axis, namely, on a line from the jet's axis and perpendicular
to the line of sight (Eq. (7); point iii in Figs. 1 and 2).
In all panels the jet axis in the -z direction has an angle of
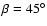 to the line of sight.
to the line of sight.
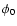 is defined in Fig. 2, while the meaning of n, C1 and
f2 can be seen in Eq. (4);
n=2 in all cases drawn.
is defined in Fig. 2, while the meaning of n, C1 and
f2 can be seen in Eq. (4);
n=2 in all cases drawn. |
- (i)
- The close (to the observer) side of the jet along
the line of sight (marked i in Figs. 1 and 2; thick solid line in Fig. 3).
In this case the point is located at
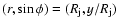 ,
with
,
with
 .
Substituting this value in Eq. (4) yields, for the
jet velocity component along the line of sight:
.
Substituting this value in Eq. (4) yields, for the
jet velocity component along the line of sight:
![\begin{displaymath}\frac {v_{\rm j}}{v_{\rm ja}} = \left[ k -
C_1 k - C_1 f_2
\...
...
+\frac{y}{R_{\rm j}} \sin \phi_0 \right) \right] \cos \beta .
\end{displaymath}](/articles/aa/full/2005/19/aa2225-04/img37.gif) |
(6) |
- (ii)
- The far side edge of the jet (marked ii in Figs. 1 and 2;
thick dashed line in Fig. 3).
In this case the point is located at
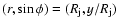 ,
with
,
with
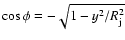 .
Substituting this value in Eq. (4) yields an expression like that
in Eq. (6) for the jet velocity component along the line of sight,
but with a minus sign in front of the square root.
.
Substituting this value in Eq. (4) yields an expression like that
in Eq. (6) for the jet velocity component along the line of sight,
but with a minus sign in front of the square root.
- (iii)
- The point closest to the jet's axis, i.e., on a line through
the jet's axis and perpendicular to the line of sight
(marked iii in Figs. 1 and 2; thin solid line in Fig. 3).
This gas element resides at distance y from the jet axis and
perpendicular to the line of sight (i.e., in the yz plane).
In Eq. (4), substituting
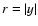 (see Fig. 2),
and
(see Fig. 2),
and
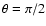 and
and
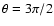 ,
for y>0 and y<0, respectively,
gives
,
for y>0 and y<0, respectively,
gives
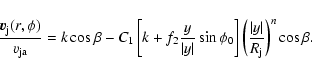 |
(7) |
The following conclusions follow from Fig. 3, regarding the proposed scenario
for jet-disk interaction.
- 1.
- This scenario explains the decline in radial velocity with
increasing distance from the jet's axis. Such behavior is clearly
observed in DG Tauri (Fig. 1 of B2002), in the red lobe of RW Aurigae
(Fig. 5 of C2004), and in LkH
 321 (Fig. 5 of C2004).
321 (Fig. 5 of C2004).
- 2.
- An inclination of the jet to the outer disk with which it
interacts (the inner disk that blows the jet
 ,
is perpendicular to the jet) can explain the velocity shift between the
two sides of each jet with the same sense of shift in the blue shifted
(approaching) and red shifted (receding) jets.
,
is perpendicular to the jet) can explain the velocity shift between the
two sides of each jet with the same sense of shift in the blue shifted
(approaching) and red shifted (receding) jets.
- 3.
- Different regions along each line of sight have different
projected velocities.
The variation increases toward the jet's symmetry axis.
If different spectral lines originate in different regions in the jet,
then there will be large variations in the projected velocities
between different spectral lines.
This might be the case, for example, if instabilities in the jet-disk
interaction region lead to formation of dense clumps, where the
emission of some spectral lines are favored over other spectral lines.
The instabilities might occur in some places, but not in others.
Large differences in velocity profiles between different spectral lines
are observed in a large fraction of the jets, e.g.,
in the red lobe of TH28 (Fig. 5 of C2004).
The data are too noisy to tell whether the variation near the jet's center
is larger.
- 4.
- Large velocity differences between the two jet's sides can be
explained without invoking a huge amount of angular momentum in the jet.
4 Summary
The goal of the present paper is to provide an interpretation
of the velocity profiles of some YSO jets without referring to
any magnetic jet-launching model.
These observations (B2002; C2004) show that the two sides of some YSO
jets have different projected velocity (line of sight velocity), and
that the sense of the velocity shift is the same in the blue
(approaching) and red (receding) jets.
B2002 and C2004 interpret the velocity profiles as rotation of the jets
around their symmetry axis, something to be expected in some magnetic
jet-launching models (Cerqueira & de Gouveia Dal Pino 2004).
In the Appendix I show that the angular momentum required to explain the
rotation is at the upper limit of what the accretion disk can supply.
In other words, to account for the required angular momentum and the
kinetic energy of the jets, the mass outflow must be smaller than
observed.
Alternatively, I propose a scenario where the velocity profile results
from the interaction of the jets with the accretion disk.
In Sect. 2 I argued that such an interaction is likely
to occur, as accretion disks around YSOs might have a
thick surface layer.
I then (Sect. 3) presented a phenomenological scenario based on two
assumptions.
(1) There is an inclination between the jet and the disk further out.
Namely, the inner disk is perpendicular to the jet, but then the disk
flares in a point-symmetric manner: one side up and the opposite
side (relative to the central star) down (Fig. 2).
(2) The disk slows the jet down, with larger decelaration of jet
segments closer to the tilted disk and less efficient deceleration
closer to the jets' axis.
The velocity of the gas inside the jet as function of distance from the
jet's symmetry axis r, and the angle relative to the direction
where the disk flares up (in the +z direction)
 ,
was parameterized in Eq. (4).
The different values appearing in that equation are defined in
Figs. 1 and 2.
The calculated projection velocity profiles for 4 cases
are plotted in Fig. 3.
,
was parameterized in Eq. (4).
The different values appearing in that equation are defined in
Figs. 1 and 2.
The calculated projection velocity profiles for 4 cases
are plotted in Fig. 3.
The conclusions drawn from Fig. 3 are summarized in the last
paragraph of Sect. 3.
In short, these are:
(1) the proposed non-magnetic scenario explains the decline in
radial velocity with increasing distance from the jet's axis.
(2) The inclined jet-disk scenario might explain the velocity shift
between the two sides of each jet with the same sense of shift
in the blue shifted (approaching) and red shifted (receding) jets.
(3) The large velocity variations between different spectral lines
can be accounted for if different lines originate in different
regions in the jets.
For example, instabilities in the jet-disk interaction leads to
formation of dense clumps where some lines are favored over
others.
(4) There is no need to depend on jet rotation with
a huge amount of angular momentum.
The interaction of the warrped-tilted disk with the jet will
cause a point-symmetric structure, and, high spatial resolution
imaging may reveal such a structure close to the star.
In Th 28, the H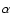 image of the two HH objects
possesses a point-symmetric structure (Krauter 1986),
which most likely comes from precessing jets.
The two jets in RW Aur are highly symmetric and show no
point-symmetry (Dougados et al. 2000).
The one jet of DG Tau, as presented in the high velocity (HV)
map by Lavalley-Fouquet et al. (2000; the upper row of their
Fig. 1), possesses some wiggling.
In any case, the predicted point-symmetry morphology is
of small degree, but still might be noticed.
image of the two HH objects
possesses a point-symmetric structure (Krauter 1986),
which most likely comes from precessing jets.
The two jets in RW Aur are highly symmetric and show no
point-symmetry (Dougados et al. 2000).
The one jet of DG Tau, as presented in the high velocity (HV)
map by Lavalley-Fouquet et al. (2000; the upper row of their
Fig. 1), possesses some wiggling.
In any case, the predicted point-symmetry morphology is
of small degree, but still might be noticed.
Another prediction of the proposed scenario is that in some cases,
where disk changes twisting (wrapping) direction in a relatively short time
period, the sense of asymmetry will change; i.e.,
the side which presently has a lower radial velocity,
might slowly, say on a time scale of 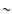
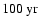 ,
change
to higher radial velocity.
However, in most disks the expected time scale is very long,
according to the different mechanisms that cause such twisting
(or titling or warping;
Armitage & Pringle 1997; Larwood et al. 1996).
,
change
to higher radial velocity.
However, in most disks the expected time scale is very long,
according to the different mechanisms that cause such twisting
(or titling or warping;
Armitage & Pringle 1997; Larwood et al. 1996).
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., &
Blandford, R. D. 2003, ApJ, 590, L107
- Anderson, J. M., Li, Z.-Y., Krasnopolsky, R., &
Blandford, R. D. 2005, ApJ, submitted [arXiv:astro-ph/0410704]
- Armitage, P. J., & Pringle, J. E. 1997, ApJ, 488, L47
- Bacciotti, F., Ray, T. P., Mundt, R., Eislöffel, J., & Solf, Jo. 2002,
ApJ, 576, 222 (B2002)
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883
- Bogovalov, S., & Tsinganos, K. 2001, MNRAS, 325, 249
- Canto, J., & Raga, A. C. 1991, ApJ, 372, 646
- Casse, F., & Ferreira, J. 2000, A&A, 361, 1178
- Cerqueira, A. H., & de Gouveia Dal Pino, E. M. 2004, A&A, 426, L25
- Coffey, D., Bacciotti, F., Woitas, J., Ray, T. P.,
& Eisloffel, J. 2004, ApJ, 604, 758 (C2004)
- Davis, C. J., Varricatt, W. P., Todd, S. P.,
& Ramsay Howat, S. K. 2004, A&A, 425, 981
- Dougados, C., Cabrit, S., Lavalley, C., & Menard, F.
2000, A&A, 357, L61
- Ferreira, J. 2002, in
Star Formation and the Physics of Young Stars - Summer school on
Stellar Physics X, EAS Vol. III, ed. J. Bouvier, & J.-P. Zahn
(Les Ulis: EDP Sciences)
- Ferreira, J., & Casse, F. 2004, ApJ, 601, L139
- Ferreira, J., & Pelletier, G. 1993, A&A, 276, 625
- Ferreira, J., & Pelletier, G. 1995, A&A, 295, 807
- Gaetz, T. J., Edgar, R. J., & Chevalier, R. A.
1988, ApJ, 329, 927
- Garcia, P. J. V., Ferreira, J., Cabrit, S.,
& Binette, L. 2001, A&A, 377, 589
- Getman, K. V., Feigelson, E. D., Townsley, L.,
et al. 2002, ApJ, 575, 354
- Heyvaerts, J., & Norman, C. 1989, ApJ, 347, 1055
- Heyvaerts, J., Priest, E. R., & Bardou, A. 1996, ApJ, 473, 403
- Kahn, F. D. 1980, A&A, 83, 303
- Kato, Y., Mineshige, S., & Shibata, K. 2004, ApJ, 605, 307
- Königl, & Pudritz, R. E.
2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, &
S. S. Russell (Tucson: Univ. of Arizona Press), 759
- Krasnopolsky, R., Li, Z.-Y., & Blandford, R. D.
2003, ApJ, 595, 631
- Krautter, J. 1986, A&A, 161, 195
- Larwood, J. D., Nelson, R. P., Papaloizou, J. C. B.,
& Terquem, C. 1996, MNRAS, 282, 597
- Lavalley-Fouquet, C., Cabrit, S., & Dougados, C.
2000, A&A, 356, L41
- Li, L.-X. 2002, ApJ, 564, 108
- Liseau, R., Fridlund, C. V. M., & B. Larsson, B.
2005 ApJ, in press [arXiv:astro-ph/0410405]
- Lynden-Bell, D. 2003, MNRAS, 341, 1360
- Malbet, F., Lachaume, R., & Monin, J.-L. 2001, A&A, 379, 515
- Pesenti, N., Dougados, C., Cabrit, S., et al. 2004, A&A, 416, L9
- Semenov, D., Wiebe, D., & Henning, Th. 2004, A&A, 417, 93
- Shu, F. H., Lizano, S., Ruden, S., &
Najita, J. 1988, ApJ, 328, L19
- Shu, F. H., Najita, J. R., Shang, H., & Li, Z.-Y.
2000, in Protostars and Planets IV, ed. V. Mannings, A. P. Boss, &
S. S. Russell (Tucson: Univ. of Arizona Press), 789
- Shu, F. H., Ruden, S. P., Lada, C. J., &
Lizano, S. 1991, ApJ, 370, L31
- Soker, N., & Lasota, J.-P. 2004, A&A, 422, 1039
- Soker, N., & Regev, O. 2003, A&A, 406, 603
- Stahler, S. W. 1994, ApJ, 422, 616
- Torbett, M. V. 1984, ApJ, 278, 318
- Torbett, M. V., & Gilden, D. L. 1992, A&A, 256, 686 (TG)
- Wijers, R. A. M. J., & Pringle, J. E. 1999, MNRAS, 308, 207
- Woitas, J., Bacciotti, F., Ray, T. P., et al. 2005, A&A, 432, 149
- Woitas, J., Ray, T. P., Bacciotti, F., Davis, C. J.,
& Eisloffel, J. 2002, ApJ, 580, 336
5 Online Material
Appendix: Differential radial velocity along YSO jets
In a recent paper for three YSOs, C2004 present observed profiles
of line-of-sight velocity as function of the distance from the
jet's symmetry axis. They interpret their observations as
indicating jet rotation, and claim that the magnetocentrifugal jet
launching model is consistent with their results.
This is problematic on both accounts.
More sophisticated and detailed MHD models for jet rotation,
though, might overcome these problems.
By examining the radial velocity figures of C2004, I note the following issues.
- (1)
- Stochastic velocity profiles.
Different lines show very different profiles, as is most
evidence from their Fig. 5.
In the red lobe of TH28, for example, the difference in velocity
between the [NII]
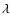 6548 and the [SII]
6548 and the [SII]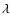 6716 is
6716 is
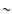
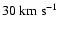 in the SW side, while the difference is
almost an order of magnitude smaller in the NE side of the
jet axis in the same lobe.
In the YSO LkH
in the SW side, while the difference is
almost an order of magnitude smaller in the NE side of the
jet axis in the same lobe.
In the YSO LkH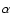 321 the difference between these two lines
in the SE side reaches a value of
321 the difference between these two lines
in the SE side reaches a value of 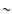
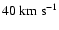 .
These differences are larger than the claimed rotational velocity
of the corresponding jets.
Later, I attribute these differences between the velocities observed in
different lines, and the difference between the two sides of the jets'
axes, to the interaction of the jet with a tilted disk (Sect. 3).
.
These differences are larger than the claimed rotational velocity
of the corresponding jets.
Later, I attribute these differences between the velocities observed in
different lines, and the difference between the two sides of the jets'
axes, to the interaction of the jet with a tilted disk (Sect. 3).
- (2)
- Angular momentum.
If the radial velocity gradient is attributed to the jet's rotation,
then the specific angular momentum of the gas at the edge of
the jets must be extremely high.
For example, in the redshifted lobe of RW Aur the toroidal velocities are
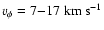 (see last paragraph of Sect. 3 in C2004),
in the range
(see last paragraph of Sect. 3 in C2004),
in the range
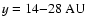 ,
where y is the
distance from the jet's axis.
The specific angular momentum is in the range
,
where y is the
distance from the jet's axis.
The specific angular momentum is in the range
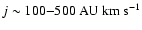 .
For an accretion disk around a central object of mass
.
For an accretion disk around a central object of mass 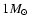 ,
this range corresponds to disk radii in the range
,
this range corresponds to disk radii in the range
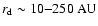 .
In the magnetocentrifugal jet launching model the magnetic stress
transports energy and angular momentum from the accreted mass to
the ejected mass.
In RW Aur the ejected mass is
.
In the magnetocentrifugal jet launching model the magnetic stress
transports energy and angular momentum from the accreted mass to
the ejected mass.
In RW Aur the ejected mass is 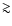
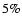 the accreted mass
(Woitas et al. 2002), namely
the accreted mass
(Woitas et al. 2002), namely
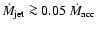 ,
and C2004 find the foot point
(where the streamline leaves the disk) of the outermost
stream line to be at
,
and C2004 find the foot point
(where the streamline leaves the disk) of the outermost
stream line to be at
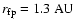 .
The inner-most foot point is at
.
The inner-most foot point is at
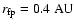 .
The specific angular momentum of Keplerian disk material
at
.
The specific angular momentum of Keplerian disk material
at
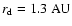 is
is  0.07 times the specific angular
momentum of matter flowing on the outer stream line.
This implies a very efficient angular momentum transfer.
The accreted mass required to give all of its angular momentum
is
0.07 times the specific angular
momentum of matter flowing on the outer stream line.
This implies a very efficient angular momentum transfer.
The accreted mass required to give all of its angular momentum
is  14 times the mass ejected in the outer parts of the jet
(for
14 times the mass ejected in the outer parts of the jet
(for
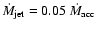 ).
For the average of the jet's specific angular momentum I take
).
For the average of the jet's specific angular momentum I take
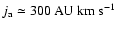 ,
which is also the
value used in the numerical simulations of
Cerqueira & de Gouveia Dal Pino (2004).
The total rate at which the jet carries angular momentum is then
,
which is also the
value used in the numerical simulations of
Cerqueira & de Gouveia Dal Pino (2004).
The total rate at which the jet carries angular momentum is then
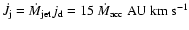 .
In an undisturbed disk, the gas losses angular momentum
as it flows from
.
In an undisturbed disk, the gas losses angular momentum
as it flows from
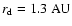 to
to
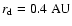 (from outer to inner foot point) at a rate of
(from outer to inner foot point) at a rate of
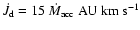 .
This implies that if C2004 interpretation of the
jets in RW Aur is correct, then according to the jet-disk models
they use, the disk must lose all of its angular
momentum already at
.
This implies that if C2004 interpretation of the
jets in RW Aur is correct, then according to the jet-disk models
they use, the disk must lose all of its angular
momentum already at
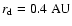 .
This is a much larger radius than that of the accreting
central star, which implies that the disk is truncated at
a very large redius, where escape speed is much below the
jet's speed.
.
This is a much larger radius than that of the accreting
central star, which implies that the disk is truncated at
a very large redius, where escape speed is much below the
jet's speed.
- (3)
- Energy.
In the analysis of Anderson et al. (2003; see also 2005), the poloidal
speeds along jets' stream lines of the YSO DG Tauri are <3 times what would be
the escape velocity at the foot points of the stream lines.
In the numerical calculations of Krasnopolsky et al. (2003) the
poloidal terminal speeds along jet's streamlines are
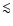 2
times the escape velocity at the foot point of the stream lines.
The velocities found by C2004 (their Table 4) are much higher than
the theoretical expectation; along most stream lines the terminal
jets' speeds found by C2004 are
2
times the escape velocity at the foot point of the stream lines.
The velocities found by C2004 (their Table 4) are much higher than
the theoretical expectation; along most stream lines the terminal
jets' speeds found by C2004 are 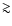 3 time the escape speeds.
In the YSO LkH
3 time the escape speeds.
In the YSO LkH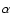 321, for example, the jet speed is
321, for example, the jet speed is
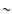 4-4.5 times the escape velocity.
The required efficiency of energy transfer from accreted to ejected
mass seems to be higher than that expected in the magneto-centrifugal
models.
Higher velocities are obtained in the numerical simulations
of Garcia et al. (2001) which includes the thermal state of the jet.
The major heating process of the jet is ambipolar diffusion.
High poloidal velocities are obtained along stream lines,
4-4.5 times the escape velocity.
The required efficiency of energy transfer from accreted to ejected
mass seems to be higher than that expected in the magneto-centrifugal
models.
Higher velocities are obtained in the numerical simulations
of Garcia et al. (2001) which includes the thermal state of the jet.
The major heating process of the jet is ambipolar diffusion.
High poloidal velocities are obtained along stream lines,
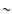 10 times the escape velocity from the footpoint of
the stream line.
However, the fraction of ejected mass (out of the accreted
mass) is
10 times the escape velocity from the footpoint of
the stream line.
However, the fraction of ejected mass (out of the accreted
mass) is 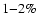 ,
much below the value of
,
much below the value of 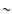
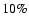 in
RW Tau (Woitas et al. 2005).
But, again, in this section I am dealing mainly with C2004
interpretation of their observations, and not with the
general MHD model.
in
RW Tau (Woitas et al. 2005).
But, again, in this section I am dealing mainly with C2004
interpretation of their observations, and not with the
general MHD model.
- (4)
- Model versus observations.
C2004 use the jet launching model as presented by Anderson et al. (2003), who use it for the YSO DG Tau.
However, in that model the toroidal velocity decreases with distance
from the jet's axis, while in the observations, both of DG Tau
(Anderson et al. 2003) and the three YSOs studied by C2004, the
toroidal velocity increases with distance from the jet's axis.
The opposite behavior is attributed by C2004 to projection
and beam smearing effects.
Still, despite these effects they compare their results with
the theoretical model.
I find this unjustified.
In a recent paper Pesenti et al. (2004) present a more detailed
MHD model based on jet rotation to account for the observation
of DG Tau (B2002).
Pesenti et al. (2004) find a good fit between their model and the
velocity map of DG Tau.
However, the model of Pesenti et al. (2004) for
DG Tau has two significant differences from that of TW Aur
(Woitas et al. 2005).
First, their derive typical toroidal velocity for stream lines
with footpoints of
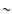
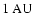 is much lower than that in TW Aur.
In TW Aur the central star mass is
is much lower than that in TW Aur.
In TW Aur the central star mass is
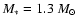 ,
and in DG Tau model of Pesenti et al. (2005) it is
,
and in DG Tau model of Pesenti et al. (2005) it is
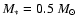 .
Velocities should be scaled like the square root of the
central mass ratio
(1.3/0.5)1/2=1.6.
Namely, the specific angular momentum in the outer jet radii in the
model of Pesenti et al. (2004), of
.
Velocities should be scaled like the square root of the
central mass ratio
(1.3/0.5)1/2=1.6.
Namely, the specific angular momentum in the outer jet radii in the
model of Pesenti et al. (2004), of 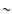
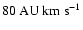 ,
is much lower than that the value of
,
is much lower than that the value of 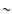
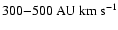 found by Woitas et al. (2005) for the jets in TW Aur.
The second difference involved the theoretical model used by
Pesenti et al. (2004).
Pesenti et al. (2004) find that only the warm jet model fit the
observations.
In this model the jet is thermally-driven (Casse & Ferreira 2002).
Both these differences, that the jets have low specific angular
momentum, and are thermally driven, are along the main
theme of the present paper, although significant differences exist
between the warm MHD model used by Pesenti et al. (2004) and
the model proposed here.
found by Woitas et al. (2005) for the jets in TW Aur.
The second difference involved the theoretical model used by
Pesenti et al. (2004).
Pesenti et al. (2004) find that only the warm jet model fit the
observations.
In this model the jet is thermally-driven (Casse & Ferreira 2002).
Both these differences, that the jets have low specific angular
momentum, and are thermally driven, are along the main
theme of the present paper, although significant differences exist
between the warm MHD model used by Pesenti et al. (2004) and
the model proposed here.
Copyright ESO 2005
![]() ,
interacts with the disk and/or
its wind.
The outer parts of the jets are influenced the most.
Let us first assume that the outskirts of the jet are strongly shocked
at a distance of
,
interacts with the disk and/or
its wind.
The outer parts of the jets are influenced the most.
Let us first assume that the outskirts of the jet are strongly shocked
at a distance of ![]() from the central star.
The density of the post-shocked gas, which is
from the central star.
The density of the post-shocked gas, which is ![]() 4 times the
pre-shocked density, is given by
4 times the
pre-shocked density, is given by
![\begin{figure}
\par\includegraphics[width=5cm,clip]{2225fig1.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2225fig2.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg24.gif)
![]() .
The observed section of the jet is assumed to be cylindrical with
radius
.
The observed section of the jet is assumed to be cylindrical with
radius ![]() .
The y axis is perpendicular to the jet's axis and to the line of sight
(Fig. 2).
The first basic assumption is that the disk plane is inclined to the
xy plane; it has a maximum height toward the +z direction at an angle
.
The y axis is perpendicular to the jet's axis and to the line of sight
(Fig. 2).
The first basic assumption is that the disk plane is inclined to the
xy plane; it has a maximum height toward the +z direction at an angle
![]() from the x axis, and a maximum height in the -z direction
at an angle of
from the x axis, and a maximum height in the -z direction
at an angle of
![]() relative to the x axis.
The tilt angle is
relative to the x axis.
The tilt angle is ![]() .
The second basic assumption is that the disk slows down the jet
with larger decelaration of jet segments closer to the tilted disk
and less efficient deceleration closer to the jets' axis and away
from the disk.
I also consider all regions with jets far from their origins, after the
different segments have reached their terminal speed; i.e.,
.
The second basic assumption is that the disk slows down the jet
with larger decelaration of jet segments closer to the tilted disk
and less efficient deceleration closer to the jets' axis and away
from the disk.
I also consider all regions with jets far from their origins, after the
different segments have reached their terminal speed; i.e.,
![]() does not depend on z.
I parameterize the slowing down of the jet material by taking the
velocity at a distance r from the jet axis and at an angle
does not depend on z.
I parameterize the slowing down of the jet material by taking the
velocity at a distance r from the jet axis and at an angle ![]() to the x axis as
to the x axis as
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2225fig3.eps} %\end{figure}](/articles/aa/full/2005/19/aa2225-04/Timg34.gif)
![]() ,
was parameterized in Eq. (4).
The different values appearing in that equation are defined in
Figs. 1 and 2.
The calculated projection velocity profiles for 4 cases
are plotted in Fig. 3.
,
was parameterized in Eq. (4).
The different values appearing in that equation are defined in
Figs. 1 and 2.
The calculated projection velocity profiles for 4 cases
are plotted in Fig. 3.
![]() image of the two HH objects
possesses a point-symmetric structure (Krauter 1986),
which most likely comes from precessing jets.
The two jets in RW Aur are highly symmetric and show no
point-symmetry (Dougados et al. 2000).
The one jet of DG Tau, as presented in the high velocity (HV)
map by Lavalley-Fouquet et al. (2000; the upper row of their
Fig. 1), possesses some wiggling.
In any case, the predicted point-symmetry morphology is
of small degree, but still might be noticed.
image of the two HH objects
possesses a point-symmetric structure (Krauter 1986),
which most likely comes from precessing jets.
The two jets in RW Aur are highly symmetric and show no
point-symmetry (Dougados et al. 2000).
The one jet of DG Tau, as presented in the high velocity (HV)
map by Lavalley-Fouquet et al. (2000; the upper row of their
Fig. 1), possesses some wiggling.
In any case, the predicted point-symmetry morphology is
of small degree, but still might be noticed.
![]()
![]() ,
change
to higher radial velocity.
However, in most disks the expected time scale is very long,
according to the different mechanisms that cause such twisting
(or titling or warping;
Armitage & Pringle 1997; Larwood et al. 1996).
,
change
to higher radial velocity.
However, in most disks the expected time scale is very long,
according to the different mechanisms that cause such twisting
(or titling or warping;
Armitage & Pringle 1997; Larwood et al. 1996).