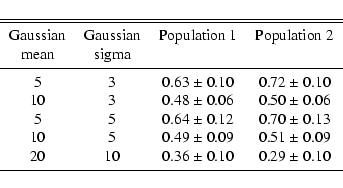
**Table 2:** Simulation of the effect of the presence of primordial binaries on a sample of dynamically formed binaries. We have simulated two distributions containing a mixture of sources that obey the linear relationship given in Eq. (2) and a random number which simulates the primordial source number. We have searched for a power law relationship within this distribution. Population 1 is a population where there is no dynamical destruction, while population 2 is a population where primordial binaries can be destroyed by dynamical interactions. The power law index is indicated in this table together with its error (errors are quoted at the 1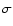 $\sigma$ level). The Gaussian parameters (in unit of sources) are the parameters of the distribution of the random number simulating the primordial binary number.
$\begin{displaymath}\begin{tabular}{cccc} \hline\hline \noalign{\smallskip } G... ...29 $\pm$ 0.10\\ \noalign{\smallskip } \hline \end{tabular} \end{displaymath}$