A&A 428, 925-934 (2004)
DOI: 10.1051/0004-6361:20040457

A photometric pilot study on Sonneberg archival patrol plates

How many "constant'' stars are in fact long-term variables?

N. Vogt^1,2 - P. Kroll ¹ - E. Splittgerber ¹

1 - Sonneberg Observatory, Sternwartestr. 32, 96515 Sonneberg, Germany
2 - Instituto de Astronomia, Universidad Catolica del Norte, Avenida Angamos 0610, Antofagasta, Chile

Receiced 16 March 2004 / Accepted 7 June 2004

Abstract
The light curves of 216 arbitrarly chosen field stars and of 23 known variables in the Aur/Tau/Ori region were derived ( $7\hbox{$.\!\!^{\rm m}$ }8 \leq B \leq 12\hbox{$.\!\!^{\rm m}$ }2$ ) from scanned, blue-sensitive archival patrol plates, covering a total of 34 years (1961-1995). We achieved a photometric accuracy of 0.07 ... 0.12 mag in spite of rather unfavourable locations of most stars near the plate borders. 17 field stars turned out to be variables, most of them with time scales of 1000-8000 days in the form of slow waves with amplitudes between 0.1 and 0.3 mag, i.e. below the threshold of traditional variable searches on photographic plates. About 50% of these new long-term variables exhibit drifts indicating periodic or erratic variability at much longer time scales than covered here. For the 23 known variables we achieved improvements in their periods and amplitudes and detected long-term variations (drifts, waves) in about 50% of them. The above fraction of low-amplitude long-term variables among field stars implies that a total of about 45 000 new variables should be detectable in the Sonneberg patrol plate archive. They will represent a new, hitherto not investigated population of variable stars with a possibly significant impact on our understanding of the stellar interior and evolution.

Key words: stars: variables: general - stars: evolution

1 Introduction

For more than a century, the photographic plate has been the most reliable light detector and data storage device available for astronomical observations. However, it is being nearly completely replaced by digital detectors like CCDs in practically all astronomical applications, even those requiring wide fields. This implies that most of the older photographic observations are becoming obsolete, unless they document variations on long time scales.

This is the case if one considers the patrol plate archive of the Sonneberg Observatory, which, following Harvard, is the second largest in size and plate number (Bräuer & Fuhrmann 1992). The Sonneberg Observatory was continuously active in sky patrol observations from the 1930ies until today in a very homogeneous manner, using the same optics and very similar plate scales, sizes and emulsions for many decades. Therefore, the Sonneberg archive which contains more than 275 000 plates and films, today represents a unique collection of sky patrol coverage of the entire northern and equatorial sky (down to declination $-33^\circ$ ), without any major gaps.

There was a considerable impact of this effort on variable star research. Hoffmeister, together with his collaborators and successors, detected, classified and investigated a total of more than 10 000 variable stars in the Milky Way, about 25% of all variables known at the time when the latest edition of the General Catalogue of Variable Stars (GCVS) was published (Kholopov et al. 1985). The technique used for this purpose: blink comparison and eye estimates of magnitudes. Obviously, only a very small fraction of all the information contained in the plate archive could be extracted this way. Now, with the advent of rapid and precise scanners, the entire plate archive can be digitized and subsequently analysed in a more general manner. As a first step in this direction we determine here the photometric variations of 216 arbitrarily chosen fields stars and, in addition, 23 known variables over a period of 34 years. Our study is restricted to rather small areas (about 74 square degrees in total) in the region of Aur/Tau/Ori. The main aim of this patrol project is to determine the photometric accuracy of scanned stellar images on patrol plates, as well as to find out what kind of information on the long-term variability of all classes of stars can be derived and expected from a comprehensive analysis of patrol plates.

2 Plate material, scanning and reduction procedure

The Sonneberg Sky Patrol (SSP), originally proposed by Paul Guthnik (1879-1947), is recording the entire accessible sky with 14 short-focus cameras simultaneously in two colours "pg'' and "pv'' (Bräuer & Fuhrmann 1992; Bräuer et al. 1999). The plate size is $13 \times 13~{\rm cm}^2$ , the scale 830''/mm resulting in a useful field size of about $26^\circ \times 26^\circ$ . The cameras are centred at declinations $-20^\circ, 0^\circ, +20^\circ, +40^\circ, +60^\circ$ and $+80^\circ$ , recording the sky every $1^{\rm h}$ in right ascension at $\delta = +40^\circ$ and south of it, and every $2^{\rm h}$ in the $60^\circ$ and $80^\circ$ zones. The limiting magnitudes are of the order of $14\hbox{$.\!\!^{\rm m}$ }5$ in pg (blue) and $13\hbox{$.\!\!^{\rm m}$ }5$ in pv (red), but the average limit achieved is about 1 mag brighter than these values.

Plate scanning was performed with the digitalization machine DIA ("Digital Image Analyser'') described by Kroll & Neugebauer (1993). DIA was able to scan an SSP plate with a resolution of $15~\mu {\rm m}$ and 8 bit data depth within 45 min. More than 5000 plates have been recorded this way between 1994 and 1999, mainly in the Taurus/Orion region for the study of T Tauri stars (Heines 1999). Each plate was subdivided into 4 quarter subsections for the scanning procedure, called 00, 01, 10 and 11 for the NE, NW, SE and SW quarter resp. of each plate.

$\begin{figure} \par\includegraphics[width=6cm,clip]{0457fg01.eps} \end{figure}$

Figure 1: Approximate locations of the sub-fields on the SSP field 5h +20 $^\circ$ (plate center).

For our pilot project we selected a total of 11 smaller sub-fields (about $2.8^\circ \times 2.8^\circ$ ) in the quarter sections 00 and 10 of the SSP field $5^{\rm h} +20^\circ$ . The 7 fields in quarter 00 are called: 00.A, 00.B, 00.C, ... 00.G, the remaining 4 in quarter 10: 10.A, 10.B, 10.C and 10.D. These sub-fields were chosen in order to include some known bright variable stars. Their positions on the sky and plate are shown in Fig. 1 in a schematic way. Most of them are rather far away from the plate centre and near the edges and/or corners of the plate. This choice was made to study the photometric accuracy under "worst case conditions''. Our study refers only to the blue pg plates.

In each of these sub-fields 20-30 field stars were selected according to the following criteria:

1.: accurate B and B-V values are available from the HIPPARCOS and TYCHO photometric catalogue (van Leeuwen et al. 1997);
2.: Single star image on the SSP plates, well separated from its neighbour, no blends;
3.: There is no strong background variation present in the surroundings of the scanned star image;
4.: The entire magnitude range of $7\hbox{$.\!\!^{\rm m}$ }8 \leq B \leq 12\hbox{$.\!\!^{\rm m}$ }2$ and colours from B-V = 0.0-1.8or more is represented in the sample.

For the measuring procedure we used the software package described by Kroll & Neugebauer (1993). The basic algorithm of this method is to perform a seven-parametric, three-dimensional Gaussian fit over the pixel grey values of a single star imprint. It was shown that the logarithm of the volume, $I = \ln V$ , of the Gaussian bell is a convenient measure of the magnitude of the star. This software, however, requires the manual selection and measurement of each star image on each of the nearly 500 SSP plates, a task which was performed by ES and NV, eliminating, this way, also contamination by emulsion faults, scratches, spots, as well as meteor, satellite and airplane tracks and other artefacts (see, e.g. Kroll 1999).

For each sub-field, the I-values were linked to the HIPPARCOS and TYCHO catalogue magnitudes, m_B and m_V, of the constant stars in order to define a transformation between I and the photographic magnitude $m_{\rm phot}$ :

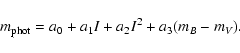
$\begin{displaymath}m_{\rm phot} = a_{0} + a_{1} I + a_{2} I^2 + a_{3} (m_{B} - m_{V}).\end{displaymath}$

By setting $m_{\rm phot} = m_{B}$ , for each sub-field and each plate, the coefficients, a₀ ... a₃, were determined with the least-square method. This fit also gives the standard deviation $\sigma$ corresponding to the differences between catalogue magnitudes and reduced magnitudes of all stars in a sub-field. In order to apply the above fit to unknown program stars one has to know their B-V colour. In a few cases in which this colour value was not known we applied a mean value of B-V = 0.6. If the colour is different from this, some zero point shift in $m_{\rm phot}$ will result. This, however, will not affect the variability discussion given here.

Originally, we had included stars between $6^{\rm m}$ and $13^{\rm m}$ in our measurement program. In the course of the reduction procedure the coverage of very bright and very faint stars in most sub-fields was too poor to get reliable photometric values. In addition, systematic variations from the above parabolic fit arise as soon as the total magnitude range exceeds about 4.5 mag. Therefore, we limited the final reduction to stars in the range $7\hbox{$.\!\!^{\rm m}$ }8 \leq m_{B} \leq 12\hbox{$.\!\!^{\rm m}$ }2$ .

The colour coefficients a₃ were determined, in a first step, for different sets of about 60 plates each taken within a three year interval. However, the coefficient did not vary significantly from epoch to epoch, so we could use a mean colour coefficient for each sub-field. Table 1 lists their values, together with the approximate mean distance of each sub-field from the plate center. Apparently, there is no correlation; however, the most distant field 00.A has the largest value of a₃.

The mean distances from the plate center and the colour coefficients for each sub-field are listed in Table 1, together with the mean standard deviations $\sigma$ from the calibration fits.

Table 1: Center distances, colour coefficients and mean scatter $\sigma$ of the sub-fields.
Sub-field Distance from Colour Mean standard deviation

plate center coefficient from calibration fit

(degrees) a₃ $\sigma$ (mag)

00.G 6.5 0.359 0.077

10.B 10.4 0.356 0.087

00.F 10.6 0.353 0.091

00.E 12.4 0.249 0.098

10.A 12.7 0.281 0.083

00.C 12.8 0.309 0.120

10.D 12.8 0.336 0.112

10.C 14.1 0.277 0.088

00.B 14.3 0.305 0.110

00.D 14.4 0.289 0.089

00.A 16.2 0.422 0.096

**Table 1:** Center distances, colour coefficients and mean scatter $\sigma$ of the sub-fields.
Sub-field	Distance from	Colour	Mean standard deviation
	plate center	coefficient	from calibration fit
	(degrees)	a₃	$\sigma$ (mag)
00.G	6.5	0.359	0.077
10.B	10.4	0.356	0.087
00.F	10.6	0.353	0.091
00.E	12.4	0.249	0.098
10.A	12.7	0.281	0.083
00.C	12.8	0.309	0.120
10.D	12.8	0.336	0.112
10.C	14.1	0.277	0.088
00.B	14.3	0.305	0.110
00.D	14.4	0.289	0.089
00.A	16.2	0.422	0.096

They range from 0.07 to 0.12 mag, and there is no close correlation with the position on the plate. However, the field nearest to the plate center (00.G) also reveals the smallest scatter, as expected. In general, we derived our photometric data with a mean error of 0.096 mag, and we expect that this value could improve to about 0.06-0.08 mag if all stars of an entire plate are measured, since most stars in our sample are located near the plate edges.

3 Constant stars and new variables

The above reduction procedure reveals light curves of a total of 239 stars, with an average of about 450 measurements distributed more or less homogeneously over 34 years (1961-1995). 23 of them are known variables that will be discussed in Sect. 4.

All light curves were analysed in various ways. We calculated seasonal means and searched for drifts, waves and erratic variability in all accessible time scales. In addition, we applied a period search routine developed by Schwarzenberg-Czerny (1989), searching for periodicities between 1 and 10 000 days. A critical comparative analysis of all light curves revealed a total of 17 new variable stars while the remaining 199 stars of our sample have to be considered as constant within the time interval and accuracy considered here. The latter are listed in Tables 2 and 3 (see online material). The scatter around their mean magnitude value is always of the order of 0.08-0.12 mag, as expected from the photometric accuracy determined in Sect. 2. Only these constant stars were used for the magnitude calibration.

The most important properties of the 17 new variable stars are given in Table 4. Eight of them were drifting, showing a linear increase or decrease in brightness over the entire 34-year time interval with a total amplitude between 0.09 and 0.25 mag (- sign refers to increasing, + sign to decreasing brightness with time). This may indicate the presence of periodic or erratic variations at much larger time scales than covered here. Five stars show periodic long-term variations with periods between 3500 and 11 000 days, and amplitudes up to 0.25 mag. In addition, in seven cases erratic variability with similar or shorter time scales (down to about 20 days) is present while in one case (S10953 = GSC 708.0904) the enhanced scatter suggests unresolved short-term variability. The amplitude of the erratic variations ranges from 0.15 to 0.5 mag. A special case is S10955 = GSC 714.0246 for which the period search routine has revealed a strictly periodic variation with 1.58625 days, displaying the typical light curve of an eclipsing binary (Fig. 4), probably of $\beta$ Lyrae type with small amplitude (0.2 mag).

**Table 4:** New variable stars.
Sonneberg	Hip or	Spec.	N	Mean	Drift	Periodic Var.		Erratic Variable		Remarks
variable	GSC No.	type		mag	ampl.	P(d)	ampl.	Time scale	ampl.
designation				B	(mag)		(mag)	(d)	(mag)
S10949	Hip 25972	A0	478	8.547	-0.15			30-8000	0.35
S10950	Hip 26162	B8e	467	8.570	-0.22			1000-4000	0.5
S10951	Hip 26669	A0	497	9.027		8000:	0.2	30-300	0.15	see Fig. 2
S10952	Hip 27699	B5e	477	9.010	+0.26	4700	0.25			see Fig. 3
S10953	0708.0904	M0	473	11.158						=NSV 2001,(1), $\sigma = 0.186$ mag
S10954	0709.0746	A5	425	9.778	+0.21
S10955	0714.0246	A0	481	9.281		1.58625	0.2			(2), see Fig. 4
S10956	0714.1144	K0	476	9.578		11000:	0.2			"wave'' see Fig. 5
S10957	1873.0775	M	468	11.026				4000-6000	0.3	=NSV 2444, Fig. 6
S10958	1875.2587	A2	474	8.182	+0.18					=NSV 2670
S10959	2403.0702	A5m	461	10.265	+0.17	8000:	0.15			see Fig. 7
S10960	2405.0168	A0	461	10.764	+0.09
S10961	2405.0203	F2	389	11.370				2000	0.25
S10962	2405.1545	B0e	409	9.716		3580	0.12			see Fig. 8
S10963	2407.0022	M3	372	11.554				20-100	0.4	=NSV 2073
S10964	2408.0661	B5	397	9.003				3000	0.2	see Fig. 9
S10965	2409.0265	A2	401	11.091	-0.16

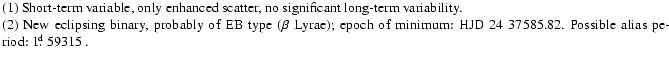
$\textstyle \parbox{16.8cm}{ $(1)$\space Short-term variable, only enhanced scat... ...m: HJD 24 37585.82. Possible alias period:~$1\hbox{$.\!\!^{\rm d}$ }59315$ .}$

The most interesting light curves of these new variables are shown in Figs. 2 to 9, together with that of a nearby constant star from the same sub-field and similar brightness.

In general, most observed amplitudes of the new variables do not exceed 0.3 mag, the typical threshold for a detection with blink comparator or similar visual inspection methods, as applied traditionally at the Sonneberg Observatory. Therefore, it is not surprising that the variables listed in Table 4 have previously not been detected. However, four of them are listed in the New Catalogue of Suspected Variables (NSV: Kukarkin et al. 1982).

The spectral type o the 17 new variable stars are distributed as follows: B(4 stars), A(8), F(1), G(0), K(1) and M(3). This could be a hint of a bimodal frequency distribution in spectral types of long-term variables with low amplitude, with maxima around types A and M, since the fraction of A type among the constant stars in our sample is only 20%, that of M stars only 1%. The maximum at A stars is surprising and would require more data for confirmation. This preliminary result suffers from the low star numbers.

4 Known variable stars

The 23 previously named variable stars included in our study are listed in Table 5; a sample of the most interesting light curves is given in Figs. 10 to 20.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg02.eps} \end{figure}$

Figure 2: Light curve of the new variable star S10951 = Hip 26669 ( lower panel) and the constant star Hip 26239.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg03.eps} \end{figure}$

Figure 3: Light curve of the new variable S10952 = Hip 27699 ( upper panel) and the constant star Hip 27686.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg04.eps} \end{figure}$

Figure 4: Light curve of the new eclipsing binary S10955 = GSC 714.0246 ( lower panel) and the constant star Hip 25814 vs. phase of the period $1\hbox{$.\!\!^{\rm d}$ }58625$ .

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg05.eps} \end{figure}$

Figure 5: Light curve of the new variable S10956 = GSC 714.1144 ( central panel) and the two constant stars Hip 26729 ( upper panel) and GSC 701.0006 ( lower panel).

**Table 5:** Known variable stars.
Name	Type	Spectr.	N	Mean	Drift	Periodic Variable		Erratic Variable		Remarks
	(GCVS)	type		mag.	ampl.	P(d)	ampl.	Time scale	ampl.
				B	(mag)		(mag)	(d)	(mag)
U Aur	M	M9	392	11.184		408.09	2.5			(4), see Fig. 10
RZ Aur	EA/SD	A	306	11.564		3.010644	?			(1), (3)
FP Aur	EA		286	11.531	+0.35	0.947236(?)				(5), see text
FU Aur	LB	CII	426	11.152				20-100	0.4	carbon star
FW Aur	EA/SD		322	11.671		2.55997	?			(1), (2), (3)
HH Aur	INSB:	G6IV	485	9.95						constant, $\sigma = 0.104^m$
V356 Aur	DSCT	F4IIIp	483	8.69		0.18916				constant, $\sigma = 0.139^m$
V362 Aur	LC	M1.5Ia	438	9.612	+0.23			1000-3000	0.4	see Fig. 11
V399 Aur	SR	S	431	11.734		8000:	0.5	30-1000	0.3	(8)
V438 Aur	GCAS	B2pshl	415	8.044				50-6000	0.5	see text and Fig. 12
BK Ori	M	M7	165	11.899		346.3	>2.5			(1), (6), see text and Fig. 13
CO Ori	INSB	G5Vpe	404	11.711	-0.50			20-1000	0.8	(1)
GW Ori	INST	K3V:e	476	10.818	+0.14
HK Ori	INSA	A4pe	426	11.608	+0.13	2400	0.25	30-1000	0.2	(8), see Figs. 14 and 15
OS Ori	EA/SD	A0	358	12.087		2.383525	>0.6			(1), (3), (10), see Fig. 16
V440 Ori	LB	M5	357	11.692	+0.13					(10), $\sigma = 0.32^m$
V451 Ori	GCAS	B9	425	9.858	-0.09			100-3000	0.1
V1374 Ori	BE	B8	481	8.082	-0.25	5685	0.5			(8), (9), see Fig. 17
V1376 Ori	LB	M5	483	9.029		see (11)	see (11)			=NSV 2258, (11)
V1409 Ori	INA	AIab:e	471	10.490		3445:	0.1:			=NSV 2041, (8)
SV Tau	EA/SD	B9	467	10.128		2.1669051	1.2			(4), (7) see Fig. 18
AB Tau	SRA	M3	456	11.649		143	0.25	10-50	0.2	(6), see text and Fig. 19
V1163 Tau	BE	B1Vne	469	8.451				20-6000	0.5	see Fig. 20

$\textstyle \parbox{17cm}{ \hspace*{1.5mm}$(1)$\space Minimum~magnitude below th... ... d}$ }82$\space and~$41\hbox{$.\!\!^{\rm d}$ }37$ ; amplitudes 0.1$-$0.15~mag.}$

These variables can be subdivided into the following classes (GCVS designations in brackets):

1.: Eclipsing binaries of Algol type (EA): 5 stars;
2.: Mira-type variables (M): 2 stars;
3.: Other red semiregular or irregular giant/supergiant late type variables (LB,LC,SR,SRA): 6 stars;
4.: Orion-type variables (INS,INA): 5 stars;
5.: Be and shell stars (BE,GCAS): 4 stars;
6.: $\delta$ Scuti variable (DSCT): 1 star.

In 4 of the 5 eclipsing binaries our data confirm or are compatible with the published ephemeris. Only for FP Aur is this not the case: The GCVS gives a period of $0\hbox{$.\!\!^{\rm d}$ }947236$ and an amplitude of only 0.3 mag. Our data give a mean brightness of $\overline{B} = 11\hbox{$.\!\!^{\rm m}$ }419$ in HJD 24 37500 to 41700 ( $\sigma = 0.15$ mag) and $\overline{B} = 11\hbox{$.\!\!^{\rm m}$ }640$ in HJD 24 42400 to 49800 ( $\sigma = 0.28$ mag), but no indication of eclipses. The enhanced scatter may be due to another kind of short-term variability.

For one Mira star, U Aur, our data give exactly the published ephemeris values. In the other case, BK Ori, the GCVS gives a period of $354\hbox{$.\!\!^{\rm d}$ }2$ , valid after HJD 24 38800, and an epoch of maximum HJD 24 40925. At earlier epochs, the period varied between 326 and 346 days. Our data fit best the element maximum = HJD 24 40908 + 346.3 E (see Fig. 13).

As expected, the third group of late type giants and supergiants demonstrate a wide range of behaviour, from unresolved short-term variability (V440 Ori), to erratic variations at all time scales from 20 to 3000 days and amplitudes up to 0.4 mag, as well as possible long-term waves with quasi-periods up to 8000 days. A special case is AB Tau: the GCVS gives an epoch HJD 24 37340 for the light maximum and a period of $142\hbox{$.\!\!^{\rm d}$ }0$ . Our data fit well to the epoch, but the period search routine reveals $143^{\rm d}$ as the best period. The enhanced scatter (see Fig. 19) implies additional short-term variability.

One of the Orion-type variables (HH Aur) turned out to be constant in our data set. The remaining variables show either erratic variations at time scales of 20 to 1000 days with amplitudes up to 0.8 mag, or waves with quasi-periods of 2400-3500 days and amplitudes up to 0.25 mag.

The group of Be stars is characterized by erratic variations in all time scales between 20 and 6000 days, with amplitudes up to 0.6 mag. The only $\delta$ Scuti star in our sample, V 356 Aur, seems to be constant with a slightly enhanced scatter. Its $0\hbox{$.\!\!^{\rm d}$ }19$ -period (amplitude 0.1 mag) reported in the literature apparently was not resolved by our data.

Due to our period search routine it was possible to discover new, hitherto unknown long-term periodicities in four cases (V399 Aur, HK Ori, V 1374 Ori and V 1409 Ori), with $2400^{\rm d} \leq P \leq 8000^{\rm d}$ and amplitudes between 0.1 and 0.5 mag. In another four cases (U Aur, BK Ori, SV Tau and AB Tau) we were able to modify and/or improve the published periods. In addition, eight stars (35% of our sample of previously known variables) show significant drift variations in the entire 34 year interval covered, with amplitudes between 0.09 and 0.5 mag. Three of them belong to the group of Orion variables, the remaining ones are more or less evenly distributed among the other variable types. All these findings support the importance of this kind of supplementary information which can be derived by a study like ours even for known variables: they all are either well known, or recently discovered by HIPPARCOS due to striking short-term variations. Their long-term behaviour has never been investigated because there is essentially no way to do this other than via sky patrol plate archives.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg06.eps} \end{figure}$

Figure 6: Light curve of the new variable S10957 = GSC 1873.0775 (NSV 2444: central panel) and the two constant stars GSC 1873.0519 ( upper panel) and GSC 1873.0489 ( lower panel).

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg07.eps} \end{figure}$

Figure 7: Light curve of the new variable S10959 = GSC 2403.0702 ( upper panel) and the constant star Hip 25512.

5 Discussion

Our sample consisted of a total of 316 field stars and 23 known variables. 17 of the field stars, i.e. 7%, are variable with amplitudes between 0.1 and 0.3 mag, below the threshold of traditional visual searches on photographic sky patrol plates. Richter (1968) estimated that 2% of the bright field stars of about $6^{\rm m}$ show variability exceeding the above threshold in amplitude while this fraction is a factor of 10 lower (0.2%) for $16^{\rm m}$ stars. He explained this difference by the fact that bright stars are mainly giants which have a much stronger tendency to vary while in the faint star sample relatively stable main sequence stars are dominating. On the other hand, Jackisch (1963) found in a photoelectric study on micro-variability that about 40% of supergiants, 26% of giants and 16% of main sequence stars show variations with amplitudes of more than 0.02 mag. Our fraction of 7% lies between these earlier findings, as is the amplitude range covered by us, which links those of Richter (1968) and Jackisch (1963).

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg08.eps} \end{figure}$

Figure 8: Light curve of the new periodic variable S10962 = GSC 2405.1545 ( lower panel) and the constant star Hip 27404 vs. phase of the period 3580 days.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg09.eps} \end{figure}$

Figure 9: Light curve of the new variable S10964 = GSC 2408.0661 ( lower panel) and the constant star Hip 26326.

This comparison, however, has to be considered with caution for two reasons. Firstly, our fraction of 7% variables is a lower limit because many "constant'' stars show drifts and/or possible waves with amplitudes between 0.05 and 0.1 mag which, however, failed the test of statistical significance with the presently available data. This problem will be solved as soon as the red plates are included in the analysis. They will provide a simultaneously observed, independent data set in a band pass whose variations should be similar to those on blue plates. Secondly, none of the above cited studies investigated the long-term behaviour. 15 of the 17 new variables show variations with time scales of the order of 1000 days or longer. This makes any comparison with published results difficult.

Similar arguments are valid if we compare our study with those made with other modern techniques. Recently, many new variable stars have been detected and investigated as a by-product of the search for gravitational microlensing effects such as MACHO and OGLE. These surveys record simultaneously millions of stars on large CCD arrays with higher photometric accuracy, lower limiting magnitude and better time resolution than provided by SSP. OGLE has detected a total of about 200 000 variables stars in the Galactic Bulge (Wozniak et al. 2002) and 68 000 variables in the Magellanic Clouds (Zebrun et al. 2001). Thus, the question arises to what extent we should study relatively bright stars on photographic sky patrol plates (with all the problems of calibration, image distortions, blends etc.) if we can get similar information from other ongoing research projects?

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg10.eps} \end{figure}$

Figure 10: Light curve of the Mira type variable U Aur vs. phase of the period $408\hbox{$.\!\!^{\rm d}$ }09$ .

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg11.eps} \end{figure}$

Figure 11: Light curve of the LC type variable V362 Aur ( upper panel) and the constant star GSC 1860.1270.

We would have to wait more than 50-100 years to be able to cover the time scales available in Harvard, Sonneberg and few similar existing plate archives. Archival studies cover mainly stars of the solar neighbourhood, i.e. a rather homogeneous population of stars whose fundamental data such as spectral type, luminosity class, radial velocity, parallax, proper motion, UV and IR spectrum etc. are known or at least will be known very soon due to scheduled survey projects and space missions. In contrast, OGLE and MACHO observe a mixture of stellar populations at far distances, consisting of very faint stars without any hope of easily obtaining the fundamental data mentioned above and required for a meaningful astrophysical discussion of their variation. Both methods, instead, could complement each other. In the near future plates will definitely be replaced by large CCDs, but the policy to observe the entire sky or at least a large fraction of it should be maintained.

The future impact of a complete analysis of all SSP plates is obvious: according to Allen (1973) there are about 29 stars per square degree brighter than $12\hbox{$.\!\!^{\rm m}$ }0$ in average. SSP has covered the entire sky down to about $-30^\circ$ declination, containing about 28 000 square degrees in total. This means that a total of roughly 800 000 stars in the magnitude range of our pilot study have been monitored in Sonneberg during the past five or more decades. These data will soon be available in digital form: about 30% of the plates have already been scanned with the new HP flat-bed scanners, and we expect to digitize the entire Sonneberg archive within the next five years. If we modify our software so that full-automatic photometric measurements are possible and if we eliminate, in a first attempt, 20% of the targets due to blends, background variability etc. we could study the long-term behaviour of about 650 000 stars just with the methods presented here. 7% of them, i.e. about 45 000 are expected to show long-term variability according to our pilot results; this number is of the same order as that of all known galactic variable stars in the GCVS. This means, on the other hand, that more than 50% of stellar variability is unknown to us because never investigated with proper methods. We will be able to determine, for the first time, the entire frequency distribution of variable stars, including its hitherto unknown tail at low amplitudes and time scales of over 1000 days. Such a study will have important consequences for our understanding of the stellar interior, evolution and variability.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg12.eps} \end{figure}$

Figure 12: Light curve of the $\gamma$ Cas type variable V438 Aur ( lower panel) and the constant star Hip 27605.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg13.eps} \end{figure}$

Figure 13: Light curve of the Mira type variable BK Ori vs. phase of the period $346\hbox{$.\!\!^{\rm d}$ }3$ .

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg14.eps} \end{figure}$

Figure 14: Light curve of the INSA type variable HK Ori ( lower panel) and the constant star GSC 709.1948.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg15.eps} \end{figure}$

Figure 15: Light curve of the INSA type variable HK Ori ( lower panel) and the constant star GSC 709.1948 vs. phase of the period 2400 days.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg16.eps} \end{figure}$

Figure 16: Light curve of the eclipsing binary OS Ori ( lower panel) and the constant star GSC 701.0006 vs. phase of the period $2\hbox{$.\!\!^{\rm d}$ }383525$ .

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg17.eps} \end{figure}$

Figure 17: Light curve of the Be type variable V1374 Ori ( upper panel) and the constant star GSC 701.0053 vs. phase of the period 5685 days.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg18.eps} \end{figure}$

Figure 18: Light curve of the eclipsing Algol type binary SV Tau vs. phase of the period $2\hbox{$.\!\!^{\rm d}$ }1669051$ .

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg19.eps} \end{figure}$

Figure 19: Light curve of the SRA type variable AB Tau ( lower panel) and the constant star GSC 1869.1671 vs. phase of the period 143 days.

$\begin{figure} \par\includegraphics[angle=270,width=8.8cm,clip]{0457fg20.eps} \end{figure}$

Figure 20: Light curve of the Be type variable V1163 Tau ( upper panel) and the constant star Hip 26845.

6 Conclusions

We can summarize the main results of our pilot study as follows:

The brightness of a single star of $8^{\rm m}{-}12^{\rm m}$ on a scanned blue-sensitive Sonneberg patrol plate can be measured with an accuracy of between 0.07 and 0.12 mag, using a two-dimensional Gaussian star image fit method and a parabolic calibration fit to HIPPARCOS and TYCHO standard stars.
This is valid even at plate positions near the edges and corners if the star image is not affected by superposition of nearby neighbours.
About 7% of the 216 field stars measured over a time interval of 34 years turned out to be variable with amplitudes of 0.1-0.3 mag, just below the threshold of traditional visual plate inspection methods for variable star research.
The time scales of most of the new variable stars exceed 1000 days, and are in many cases of the order of 5000-8000 days in the form of slow waves.
Nearly 50% of these new long-term variables exhibit slow drifts indicating periodic or erratic variability at much longer time scales than covered here.
In addition to the field stars we have monitored 23 known variables in the same manner. We achieved improvements in their periods and amplitudes and detected long-term variations (drifts, waves) in about 50% of them.
We demonstrate that other presently active projects as MACHO and OGLE which recently have detected a large number of new variable stars do not deliver the same information as our archival patrol plate approach. The methods complement each other.
We estimate that about 650 000 field stars recorded on Sonneberg patrol plates could be studied with our methods. If 7% of them, as suggested by our pilot study, will show long-term variations with low amplitude, we may, this way, double the number of known variable stars and thus add a population hitherto not investigated.

Acknowledgements

We thank 4pi Systeme - Gesellschaft für Astronomie und Informationstechnologie mbH, Sonneberg, Germany, for financial and logistic support for this project.

References

Allen, C. W. 1973, Astrophysical Quantities (London: Third edition, The Athlone Press), 243
Bräuer, H.-J., & Fuhrmann, B. 1992, Die Sterne, 68, 19
Bräuer, H.-J., Häusele, I., Löchel, K., & Polko, N. 1999, in Treasure-Hunting in Astronomical Plate Archives, ed. P. Kroll, C. La Dous, & H.-J. Bräuer (Frankfurt: H. Deutsch), 70
Heines, A. 1999, in Treasure-Hunting in Astronomical Plate Archives, ed. P. Kroll, C. La Dous, & H.-J. Bräuer (Frankfurt: H. Deutsch), 205
Jackisch, G. 1963, Veröff. Sternwarte Sonneberg, V, 5, 225
Khopolov, P. N., et al. 1985, General Catalogue of Variable Stars (Moscow: Fourth edition, Nauka Publishing House), Vol. I-IV
Kroll, P. 1999, in Treasure-Hunting in Astronomical Plate Archives, ed. P. Kroll, C. La Dous, & H.-J. Bräuer (Frankfurt: H. Deutsch), 191
Kroll, P., & Neugebauer, P. 1993, A&A, 273, 341
Kukarkin, B. V., et al. 1982, New Catalogue of Suspected Variables (Moscow: Nauka Publishing House)
Richter, G. 1968, Veröff. Sternwarte Sonneberg, VII, 3, 229
Schwarzenberg-Czerny, A. 1989, MNRAS, 241, 153
van Leeuwen, F., Evans, D. W., Grenon, M., et al. 1997, A&A, 323, L61
Wozniak, P. R., Udalski, A., Szymanski, M., et al. 2002, Acta Astron., 52, 129
Zebrun, K., Soszynski, I., Wozniak, P. R., et al. 2001, Acta Astron., 51, 317

7 Online Material

Table 2: Number of measurements, mean B magnitude and scatter $\sigma$ of the constant HIPPARCOS stars.
HIPPARCOS Number of $\overline{B}$ Standard dev. $\overline{\sigma}$ HIPPARCOS Number of $\overline{B}$ Standard dev. $\overline{\sigma}$

Number measurements from $\overline{B}$ Number measurements from $\overline{B}$

23201
268 8.758 0.049 26163 275 10.191 0.095

23209 274 9.174 0.055 26196 455 11.600 0.098

23523 389 9.310 0.057 26206 414 8.724 0.092

23570 425 10.483 0.081 26227 446 11.266 0.084

23634 427 9.537 0.065 26239 467 8.350 0.051

23721 431 10.694 0.105 26291 414 8.379 0.105

23772 430 9.839 0.068 26326 417 8.605 0.079

24035 385 10.511 0.085 26335 488 10.729 0.039

25033 420 10.049 0.094 26341 474 8.920 0.090

25077 477 8.098 0.127 26342 481 10.061 0.080

25123 480 10.879 0.092 26356 447 8.233 0.054

25157 433 8.006 0.076 26374 456 10.875 0.088

25160 408 7.927 0.067 26418 278 8.484 0.089

25185 425 9.289 0.113 26419 461 8.736 0.075

25245 466 8.152 0.066 26518 462 8.269 0.064

25286 486 9.056 0.096 26550 472 9.863 0.105

25294 480 10.135 0.077 26555 475 8.804 0.088

25297 484 8.614 0.090 26570 452 11.213 0.101

25323 484 8.489 0.091 26609 478 9.399 0.074

25326 418 10.301 0.091 26618 478 9.998 0.093

25375 484 10.365 0.096 26658 399 9.115 0.089

25433 451 7.793 0.092 26711 473 8.470 0.076

25445 481 8.526 0.083 26729 479 8.776 0.080

25481 485 9.152 0.118 26765 438 11.076 0.085

25494 446 10.183 0.086 26845 472 9.263 0.080

25512 468 10.845 0.083 26852 403 8.485 0.078

25554 449 11.055 0.091 26854 466 9.738 0.092

25609 105 9.253 0.068 26875 485 9.358 0.089

25614 466 10.849 0.086 26946 467 9.896 0.088

25666 485 8.879 0.117 26969 467 7.977 0.065

25698 434 10.276 0.111 26993 480 9.146 0.093

25711 462 10.252 0.094 27312 450 7.849 0.094

25789 454 11.365 0.117 27404 464 8.896 0.049

25794 460 7.969 0.080 27548 463 9.165 0.088

25801 449 9.818 0.122 27605 405 7.684 0.078

25814 402 8.817 0.069 27613 466 9.702 0.107

25876 412 10.947 0.110 27635 414 10.341 0.117

25904 447 10.781 0.105 27676 472 8.150 0.095

25917 420 10.227 0.120 27686 475 9.620 0.095

25948 423 8.455 0.099 27783 413 8.967 0.100

26028 479 9.356 0.075 27798 435 9.064 0.084

26044 479 9.994 0.086 27800 472 9.231 0.095

**Table 2:** Number of measurements, mean B magnitude and scatter $\sigma$ of the constant HIPPARCOS stars.
HIPPARCOS	Number of	$\overline{B}$	Standard dev. $\overline{\sigma}$	HIPPARCOS	Number of	$\overline{B}$	Standard dev. $\overline{\sigma}$
Number	measurements		from $\overline{B}$	Number	measurements		from $\overline{B}$
23201	268	8.758	0.049	26163	275	10.191	0.095
23209	274	9.174	0.055	26196	455	11.600	0.098
23523	389	9.310	0.057	26206	414	8.724	0.092
23570	425	10.483	0.081	26227	446	11.266	0.084
23634	427	9.537	0.065	26239	467	8.350	0.051
23721	431	10.694	0.105	26291	414	8.379	0.105
23772	430	9.839	0.068	26326	417	8.605	0.079
24035	385	10.511	0.085	26335	488	10.729	0.039
25033	420	10.049	0.094	26341	474	8.920	0.090
25077	477	8.098	0.127	26342	481	10.061	0.080
25123	480	10.879	0.092	26356	447	8.233	0.054
25157	433	8.006	0.076	26374	456	10.875	0.088
25160	408	7.927	0.067	26418	278	8.484	0.089
25185	425	9.289	0.113	26419	461	8.736	0.075
25245	466	8.152	0.066	26518	462	8.269	0.064
25286	486	9.056	0.096	26550	472	9.863	0.105
25294	480	10.135	0.077	26555	475	8.804	0.088
25297	484	8.614	0.090	26570	452	11.213	0.101
25323	484	8.489	0.091	26609	478	9.399	0.074
25326	418	10.301	0.091	26618	478	9.998	0.093
25375	484	10.365	0.096	26658	399	9.115	0.089
25433	451	7.793	0.092	26711	473	8.470	0.076
25445	481	8.526	0.083	26729	479	8.776	0.080
25481	485	9.152	0.118	26765	438	11.076	0.085
25494	446	10.183	0.086	26845	472	9.263	0.080
25512	468	10.845	0.083	26852	403	8.485	0.078
25554	449	11.055	0.091	26854	466	9.738	0.092
25609	105	9.253	0.068	26875	485	9.358	0.089
25614	466	10.849	0.086	26946	467	9.896	0.088
25666	485	8.879	0.117	26969	467	7.977	0.065
25698	434	10.276	0.111	26993	480	9.146	0.093
25711	462	10.252	0.094	27312	450	7.849	0.094
25789	454	11.365	0.117	27404	464	8.896	0.049
25794	460	7.969	0.080	27548	463	9.165	0.088
25801	449	9.818	0.122	27605	405	7.684	0.078
25814	402	8.817	0.069	27613	466	9.702	0.107
25876	412	10.947	0.110	27635	414	10.341	0.117
25904	447	10.781	0.105	27676	472	8.150	0.095
25917	420	10.227	0.120	27686	475	9.620	0.095
25948	423	8.455	0.099	27783	413	8.967	0.100
26028	479	9.356	0.075	27798	435	9.064	0.084
26044	479	9.994	0.086	27800	472	9.231	0.095

Table 3: Number of measurements, mean B magnitude and scatter $\sigma$ of the constant TYCHO stars.
GSC Number of $\overline{B}$ Standard dev. $\overline{\sigma}$ GSC Number of $\overline{B}$ Standard dev. $\overline{\sigma}$

Number measurements from $\overline{B}$ Number measurements from $\overline{B}$

0700.0205 466 10.852 0.106 1873.0388 479 9.840 0.069

0700.0658 271 11.757 0.090 1873.0489 399 11.717 0.085

0700.0904 439 11.210 0.103 1873.0505 470 10.980 0.087

0700.0931 485 9.178 0.077 1873.0519 484 10.316 0.103

0700.1022 473 11.055 0.110 1873.0712 452 11.625 0.104

0700.1074 453 11.186 0.094 1873.0733 417 11.777 0.093

0700.1124 391 11.863 0.099 1873.0742 435 10.620 0.096

0700.1155 462 11.360 0.124 1873.0784 461 9.809 0.085

0700.1347 484 9.961 0.097 1873.0833 438 11.808 0.091

0700.1538 397 11.513 0.101 1874.0147 193 11.881 0.092

0700.1580 465 10.995 0.104 1874.0642 468 9.744 0.091

0700.1745 480 10.942 0.108 1874.1252 385 11.643 0.081

0701.0006 423 10.297 0.072 1874.1261 349 11.783 0.092

0701.0053 482 9.151 0.082 1875.0065 461 9.278 0.104

0701.0171 477 9.327 0.079 2403.0052 454 11.548 0.111

0701.0356 280 10.290 0.106 2403.0181 446 11.454 0.128

0701.0669 477 9.838 0.082 2403.0287 440 11.319 0.097

0701.0974 277 9.453 0.085 2403.0297 472 10.666 0 084

0701.1392 472 10.828 0.107 2403.0309 457 10.661 0.100

0704.0195 484 9.780 0.117 2403.0496 467 10.780 0.089

0704.0605 483 9.932 0.090 2403.0654 469 9.939 0.109

0704.1511 465 11.197 0.121 2403.0655 458 10.177 0.093

0705.0092 313 12.160 0.066 2403.0657 456 11.212 0.109

0705.0366 391 11.714 0.079 2403.0736 426 11.676 0.113

0705.0442 102 10.397 0.081 2403.0758 325 11.271 0.105

0705.0920 479 9.853 0.100 2403.0857 443 11.248 0.103

0708.0577 485 9.727 0.090 2403.0963 414 11.630 0.120

0708.1646 479 9.867 0.087 2403.1062 452 11.656 0.124

0708.1710 453 9.206 0.094 2403.1246 384 12.100 0.111

0709.0030 422 9.664 0.102 2403.1379 407 11.391 0.117

0709.1150 400 11.607 0.069 2404.0110 464 11.067 0.091

0709.1571 375 11.555 0.071 2404.0128 427 9.851 0.107

0709.1948 431 10.904 0.078 2404.0204 369 11.680 0.086

0709.2061 455 11.232 0.093 2404.0231 192 11.640 0.098

0714.0247 477 9.327 0.079 2404.0358 449 11.131 0.093

1840.0262 317 11.725 0.038 2404.0403 420 11.625 0.112

1853.0315 429 10.949 0.111 2404.0564 454 11.098 0.094

1853.0713 428 11.007 0.095 2404.0578 467 10.518 0.095

1857.1561 431 10.954 0.095 2404.0746 214 11.832 0.075

1857.1645 431 10.112 0.081 2404.0821 446 10.809 0.096

1859.0283 252 12.122 0.067 2404.0993 439 11.591 0.101

1859.1338 403 9.775 0.094 2404.1175 455 11.268 0.105

1860.0021 423 10.666 0.099 2405.0063 420 9.421 0.074

1860.0211 130 11.414 0.078 2405.0620 429 11.579 0.071

1860.0229 240 11.105 0.091 2405.0856 458 9.982 0.110

1860.0362 443 10.249 0.090 2405.1338 384 10.861 0.075

1860.0486 198 11.549 0.081 2405.1617 409 11.478 0.100

1860.0726 310 11.106 0.099 2405.1747 403 11.217 0.086

1860.0785 300 11.421 0.081 2406.0439 456 10.937 0.103

1860.1233 436 9.663 0.093 2406.0529 352 11.812 0.053

1860.1260 427 9.452 0.079 2406.0677 458 11.155 0.108

1860.1270 432 10.668 0.093 2407.0056 378 8.963 0.099

1869.1223 468 11.341 0.087 2407.1282 412 11.130 0.116

1869.1325 481 8.619 0.093 2408.0323 364 11.651 0.127

1869.1671 475 10.041 0.074 2408.0619 336 11.617 0.085

1869.1689 474 11.278 0.098 2409.0281 409 10.692 0.116

1870.1592 129 12.089 0.095 2409.0423 392 9.991 0.094

1873.0139 468 11.299 0.098