A&A 428, 953-967 (2004)
DOI: 10.1051/0004-6361:20034442
N. Huélamo1 - M. Fernández2 - R. Neuhäuser3 - S. J. Wolk4
1 - European Southern Observatory, Alonso de Cordova 3107,
Casilla 19001, Santiago, Chile
2 - Instituto de Astrofísica de Andalucía, CSIC,
Camino Bajo de Huétor 24, 18080 Granada, Spain
3 - Astrophysikalishes Institut, Universität Jena, Schillergässchen 2-3,
07745 Jena, Germany
4 - Harvard Smithsonian Center for Astrophysics, Mail Stop 72,
Cambridge, MA02138, USA
Received 3 October 2003 / Accepted 8 August 2004
Abstract
We present a rotational study of Post-T Tauri stars (PTTSs)
in Lindroos systems, defined as binaries with early type primaries on
the main-sequence (MS) and late-type secondaries on the
pre-main-sequence (PMS) phase. The importance of this study in
comparison with previous ones is that the Lindroos sample is not X-ray
selected so we avoid a possible bias towards fast rotators. In
this preliminary study we have monitored eleven stars in the UBVRI bands during two campaigns of ten consecutive nights each.
Eight of the observed PTTSs show periodic modulations in their
lightcurves and the derived periods range from 1.9 d to 8.0 d. The
comparison of these results with theoretical rotational tracks based
on disk-star locking theory shows that star-disk decoupling times of
1-20 Myr could reproduce the rotational properties of the targets,
assuming an initial rotation period of ![]() 8 d and a mass of
1
8 d and a mass of
1 ![]() .
We have studied the rotation-activity relations of
Lindroos PTTSs and compared them with those found in other groups of
PMS and zero-age main-sequence (ZAMS)
.
We have studied the rotation-activity relations of
Lindroos PTTSs and compared them with those found in other groups of
PMS and zero-age main-sequence (ZAMS) ![]() 1
1 ![]() stars. The
Lindroos sample displays activity-rotation relations very similar to
those found in TTSs. It contains a mixture of very active stars, with
stars. The
Lindroos sample displays activity-rotation relations very similar to
those found in TTSs. It contains a mixture of very active stars, with
![]() ratios close to the saturation level of -3,
and less active (unsaturated) stars. This could be the result of
different star-disk decoupling times. Future monitoring of a larger
and unbiased sample of PTTS will be important to confirm the
significance of these results.
ratios close to the saturation level of -3,
and less active (unsaturated) stars. This could be the result of
different star-disk decoupling times. Future monitoring of a larger
and unbiased sample of PTTS will be important to confirm the
significance of these results.
Key words: stars: pre-main sequence - stars: late-type - stars: rotation - X-rays: stars - stars: binaries: visual
In the last decade a large number of works have been devoted to study
the angular momentum evolution of T Tauri stars (TTSs), that is,
late-type stars contracting towards the main-sequence (MS).
Observations of late-type pre-main sequence (PMS) stars have allowed
investigators to derive the rotational properties of TTSs in different
star forming regions (e.g. Bouvier et al. 1993; Edwards et al. 1993;
Choi & Herbst 1996; Wichmann et al. 1998; Herbst et al. 2001a; Rebull
2001; Lamm et al. 2004). The earliest studies reported the existence
of a bimodal distribution of rotational periods among TTSs in Taurus:
while accreting TTSs surrounded by disks were generally slow rotators
with periods longer than 4.4 days, non-accreting TTSs were faster
rotators showing periods that range from a few hours to 3 days. Recent
rotational studies on late-type PMS stars in Orion are more
controversial: while some works do not find a bimodal distribution
among late-type PMS stars (e.g. Stassun et al. 1999), other studies
(e.g. Herbst et al. 2001b) have shown that the bimodal distribution is
present but is mass-dependent, that is, it is only found in stars with
masses above a certain limit (
![]() ).
).
Most of the results from the rotational studies support disk-locking as the most plausible mechanism to regulate the angular momentum of late-type PMS stars (see Rebull et al. 2002). The so-called disk-locking theory (e.g. Königl 1991; Collier Cameron & Campbell 1993; Shu et al. 1994; Bouvier et al. 1997a) explains the rotational properties of late-type PMS stars as a result of magnetic coupling between the star-disk system, that prevents the star from spinning-up during the mass accretion phase. Once the disk is dissipated the couping no longer exists and the star begins to rotate faster due to on-going contraction to the MS.
The rotational properties of late-type Zero-Age Main-Sequence (ZAMS)
dwarfs in open clusters like the Pleiades or ![]() Per have been
also extensively studied in different works (e.g. Stauffer et
al. 1989; Soderblom et al. 1993; Prosser et al. 1995; Allain et al.
1996; Queloz et al. 1998; Terndrup et al. 2000). These works have
reported a large scatter in the rotational rates of these stars:
while half of the objects display projected velocities (
Per have been
also extensively studied in different works (e.g. Stauffer et
al. 1989; Soderblom et al. 1993; Prosser et al. 1995; Allain et al.
1996; Queloz et al. 1998; Terndrup et al. 2000). These works have
reported a large scatter in the rotational rates of these stars:
while half of the objects display projected velocities (![]() )
of a few km s-1, half of them are faster rotators with velocities up to
200 km s-1 (the so-called ultra fast rotators, UFR's). A decoupling
between the radiative core and the convective envelope has been
studied to explain the large spread of rotational properties among
ZAMS stars (e.g. Allain 1998). In the case of older clusters like
the Hyades (Radick et al. 1987; Stauffer et al. 1997), the rotation
rates are significantly smaller and most of the late-type stars
display projected velocities of
)
of a few km s-1, half of them are faster rotators with velocities up to
200 km s-1 (the so-called ultra fast rotators, UFR's). A decoupling
between the radiative core and the convective envelope has been
studied to explain the large spread of rotational properties among
ZAMS stars (e.g. Allain 1998). In the case of older clusters like
the Hyades (Radick et al. 1987; Stauffer et al. 1997), the rotation
rates are significantly smaller and most of the late-type stars
display projected velocities of
![]() km s-1.
km s-1.
Post-T Tauri stars (PTTSs, Herbig 1978) are intermediate between the oldest T Tauri stars and the youngest dwarfs in open clusters. As noted by Bouvier et al. (1997b), it is precisely at this evolutionary stage when the stellar interior changes from completely convective to radiative, so the internal changes may be reflected in the surface rotation properties. Two main studies have tried to derive the rotational properties of PTTSs: Bouvier et al. (1997b) and Wichmann et al. (1998) in the Taurus and Lupus star forming regions (SFR), respectively. Both works showed that most of the PTTSs under study were fast rotators. However, this conclusion could be the result of their sample selection criteria which included the X-ray detection of the sources. X-ray selected samples tend to be biased towards fast rotators: late-type stars show a connection between magnetic activity and rotation, with the strongest X-ray emitters being the fastest rotators (e.g. Bouvier 1990; Neuhäuser et al. 1995). Hence, an unbiased sample of PTTSs is required to understand the rotational properties of late-type stars at that evolutionary stage.
In this context, the so-called Lindroos sample of PTTSs (Lindroos 1986) is important because it is not X-ray selected and complements the previous samples of PTTSs. Lindroos systems are defined as visual binary systems mainly comprised of early-type primaries on the MS and late-type secondaries (Lindroos 1985). The ages of Lindroos primaries have been derived through photometric and spectroscopic observations, showing values between 107-108 yr. This age interval is comparable to the contraction time-scale of late-type stars to the MS. If the systems are physically bound, the secondaries are late-type PMS stars still contracting to the ZAMS, that is, PTTSs.
Lindroos (1985, 1986) carried out an exhaustive study of 253 visual
binary systems and found 78 binary or multiple systems likely to be
physical. A total of 45 companion candidates with spectral types later
than F0 were selected among the binary and multiple systems.
Pallavicini et al. (1992) and Martín et al. (1992) have reported
the presence of indicators of youth (Li I absorption line) and
activity (H![]() emission line) in 40% of the Lindroos late-type
secondaries. The analysis of the X-ray emission from 22 Lindroos
systems resolved by the ROSAT High Resolution Imager (HRI) has shown
that most of the Lindroos PTTSs candidates are X-ray emitters, with
X-ray luminosities comparable to those from younger late-type PMS stars (Huélamo et al. 2000).
emission line) in 40% of the Lindroos late-type
secondaries. The analysis of the X-ray emission from 22 Lindroos
systems resolved by the ROSAT High Resolution Imager (HRI) has shown
that most of the Lindroos PTTSs candidates are X-ray emitters, with
X-ray luminosities comparable to those from younger late-type PMS stars (Huélamo et al. 2000).
In this preliminary work we have analyzed the rotational properties of bona-fide PTTSs in Lindroos systems. Given that the sample is not X-ray selected, it is ideal to study the rotational properties of PMS stars in that evolutionary phase. Our main goal is twofold: first, we will compare the observed rotational properties with theoretical predictions of angular momentum evolution of late-type stars and, second, we will derive the rotation-activity relations for our sample and compare them with groups of late-type stars at different evolutionary stages. This way, we can trace the evolution of activity parameters as stars evolve and reach the MS. The Lindroos sample is described in Sect. 2. The optical observations of the sample are described in Sect. 3, while the analysis of the data is provided in Sect. 4. The main results are described in Sects. 5-7, while our preliminary conclusions are drawn in Sect. 8.
Table 1: Stellar properties of the selected sample of Lindroos PTTSs.
The Post-T Tauri stars in the sample were selected according to these criteria: their ages must be within 10-100 Myr and they must show indications of being physically bound to their primaries. The ages of the Lindroos PTTSs have been derived using four sets of evolutionary tracks (Gerbaldi et al. 2001). Different models provide different age estimations (see Table 1) but, in general, all lie within the selected interval. Most of the late-type stars in the sample show ages and/or radial velocity measurements consistent with those of the early-type primaries. Moreover, if the systems are bound the secondaries are in the PMS phase. Hence, we have also looked for indicators of youth among the sample to reinforce the evidences of being physically bound to their primaries (see Jensen 2002). All these properties are summarized in Table 7 of Huélamo et al. (2000). The final sample contains 18 stars.
The Lindroos sample is not X-ray selected implying that our rotational study should not be biased towards fast rotators. However, Lindroos PTTSs are found in binary systems and we were concerned that such binarity could introduce a different bias in our analysis. We have analyzed whether the Lindroos secondary stars studied here are representative PTTSs or, on the other hand, they are somehow "special'' PTTSs because of being members of binary systems. In the next subsections we have analyzed two binarity effects that can influence the rotational evolution of these young objects: first, we have analyzed if the separation between the members of the binary systems is small enough to produce a circularization of their orbits and, subsequently, a synchronization of both the orbital and rotation period. Secondly, we have analyzed the effect of the UV radiation field of the early-type primaries on the late-type secondaries. Given that such radiation can accelerate the dissipation of circumstellar matter around PMS stars, it could produce an earlier spin-up of the PTTSs (in the framework of the disk-star locking theory).
It is an observational fact that close binary systems with orbital periods smaller than a given critical value (called the circularization period) evolve to circularize their orbits (e = 0). In this process, a synchronization of their rotational and orbital periods is observed (e.g. Zahn 1977; Mathieu 1992; Melo et al. 2001). The mechanism that produces such circularization is still not well understood (i.e. a tidal-torque mechanism or a hydrodynamical mechanism).
The circularization is a slow process, so that the larger the
separation of the system the longer it takes to circularize the orbit.
Observations of PMS binary systems have shown that all short period
(
![]() )
binaries display circular orbits at ages of 106 yr (Melo et al. 2001). This period can be taken as a circularization
cutoff period for PMS stars. The lack of circular or near-circular
(e<0.1) orbits for PMS binaries with orbital periods longer
than the cutoff period is evident for systems with
)
binaries display circular orbits at ages of 106 yr (Melo et al. 2001). This period can be taken as a circularization
cutoff period for PMS stars. The lack of circular or near-circular
(e<0.1) orbits for PMS binaries with orbital periods longer
than the cutoff period is evident for systems with
![]() (Duquennoy & Mayor 1991; Pan et al. 1998). Taking into account the
separations and the masses of the Lindroos systems, we have derive
orbital periods larger than 1000 yr. Hence, we do not expect any
circularization process among the Lindroos sample.
(Duquennoy & Mayor 1991; Pan et al. 1998). Taking into account the
separations and the masses of the Lindroos systems, we have derive
orbital periods larger than 1000 yr. Hence, we do not expect any
circularization process among the Lindroos sample.
B-type stars mostly radiate in the far ultraviolet (FUV) range. If
FUV radiation impacts onto a circumstellar disk it can produce its
photoevaporation whenever the incident FUV flux is of the order of
10
![]() ,
being
,
being ![]() the average UV photon flux in the
local interstellar medium (Johnstone et al. 1998). As an example, such
a radiation flux is produced by O-type stars in the Orion Trapezium
which photoevaporate disks up to a distance of 1pc (Störzer &
Hollenbach 1999). In the case of the Lindroos systems, the presence of
a B-type star close to a late-type companion could produce the same
effect.
the average UV photon flux in the
local interstellar medium (Johnstone et al. 1998). As an example, such
a radiation flux is produced by O-type stars in the Orion Trapezium
which photoevaporate disks up to a distance of 1pc (Störzer &
Hollenbach 1999). In the case of the Lindroos systems, the presence of
a B-type star close to a late-type companion could produce the same
effect.
As shown in Table 1, the spectral types of the Lindroos
primaries range between B2 and A0. As discussed by Bouvier & Corporon
(2001), the distance up to which these stars produce the minimum flux
required to photoevaporate disks is of the order of 104 AU for a
B3 star and about 500 AU for a A0 star. Most of the Lindroos
primaries are late B-type stars and the separations of the systems
range between 600 AU and 9000 AU (with a mean value of ![]() 3000 AU). Hence, we do not expect any effect of the UV radiation
field from the primaries into the secondaries. There are two
exceptions, HD 113703 B and HD 113791 B, with early B-type
primaries (B4 and B2) and separations smaller than 3500 AU. These two
stars will be discussed in Sect. 6.
3000 AU). Hence, we do not expect any effect of the UV radiation
field from the primaries into the secondaries. There are two
exceptions, HD 113703 B and HD 113791 B, with early B-type
primaries (B4 and B2) and separations smaller than 3500 AU. These two
stars will be discussed in Sect. 6.
Lindroos PTTSs are spread over different regions in the Northern and Southern hemisphere. In order to monitor the stars in the northern hemisphere, four weeks were allocated at the 1.5 m Spanish telescope and the 1.23 m telescope at the Calar Alto Observatory (CAHA). Unfortunately, we could not obtain good quality data due to poor weather conditions.
We observed the southern sources in two campaigns in different observatories: seven sources were observed at the 0.9 m CTIO telescope at the beginning of January 2001, while a second campaign at the 1.5 m Danish telescope in La Silla Observatory in February 2001 allowed us to observe the rest of the targets. In both campaigns (CTIO and La Silla) we monitored the sources during 10 consecutive nights each. The stellar data of the observed sample is summarized in Table 1. Note that two of the stars in the sample could not be monitored: HD 108767 B was too bright and saturated the detector, while HD 109573 B, the only M-type star of the sample, is too faint and too close to the early-type primary.
The observations at the 0.9 m CTIO telescope were carried out during
ten consecutive nights in January 2001 (from the 4![]() to the
13
to the
13![]() ). The detector used was an ARCON
). The detector used was an ARCON
![]() pixels CCD camera, which is a multi-readout camera
with four different amplifiers. The plate-scale of the camera is
0.396''/pixel, providing a total field of view of
pixels CCD camera, which is a multi-readout camera
with four different amplifiers. The plate-scale of the camera is
0.396''/pixel, providing a total field of view of
![]() .
We made use of the UBV(RI)C filter set.
.
We made use of the UBV(RI)C filter set.
We observed the Lindroos secondary stars during ten nights with random spacing times to avoid as much as possible false periodicities. Most of the stars were observed at least twice during the same night to be sensitive to periods shorter than one day. The exposure times of the scientific images ranged between 0.5 s and 10 s. The shortest exposure times were necessary to avoid the light of the primary star in those binaries with smaller separations. In these cases, several consecutive exposures were taken in each filter in order to average them and to increase the signal to noise ratio (SNR) of the final images.
The data were reduced using the QUADPROC/CCRED package into IRAF
(Image Reduction and Analysis Facility![]() ),
specially designed to reduce multi-readout data. All the images were
bias subtracted and flatfield corrected. The shutter delay of the
camera is not negligible, so we have applied a shutter correction to
the images to compensate the inhomogeneous illumination of the
detector at short exposure times. In order to do this we created
shutter masks at different exposures times. After their
normalization, we corrected the scientific images multiplying by the
corresponding shutter mask. The correction must be applied to images
with exposures times shorter than 10 s.
),
specially designed to reduce multi-readout data. All the images were
bias subtracted and flatfield corrected. The shutter delay of the
camera is not negligible, so we have applied a shutter correction to
the images to compensate the inhomogeneous illumination of the
detector at short exposure times. In order to do this we created
shutter masks at different exposures times. After their
normalization, we corrected the scientific images multiplying by the
corresponding shutter mask. The correction must be applied to images
with exposures times shorter than 10 s.
We carried out aperture photometry on the sources. For the closest
pairs (separations < 10
![]() )
with a very bright primary
(V-
)
with a very bright primary
(V-![]() mag), the emission from the late-type secondary could be
contaminated with the light from the early-type star. In these cases
we have applied multi-aperture photometry on the secondaries
correcting the magnitudes with field stars. We have measured the
brightness of the objects in both the individual and the averaged
images to check the reliability of the combined image. In general,
there is a good agreement between the magnitudes derived in this two
ways. We have assumed that the uncertainties in the final magnitudes
are given by the ratio of the standard deviation of the mean of the
individual magnitudes to the square root of the number of individual
observations.
mag), the emission from the late-type secondary could be
contaminated with the light from the early-type star. In these cases
we have applied multi-aperture photometry on the secondaries
correcting the magnitudes with field stars. We have measured the
brightness of the objects in both the individual and the averaged
images to check the reliability of the combined image. In general,
there is a good agreement between the magnitudes derived in this two
ways. We have assumed that the uncertainties in the final magnitudes
are given by the ratio of the standard deviation of the mean of the
individual magnitudes to the square root of the number of individual
observations.
Apart from the Lindroos objects we have also selected objects in the field of view as comparison stars. We have used these stars to carry out differential photometry on the Lindroos secondaries.
The data from the 1.5 m telescope were collected from the 29![]() January to the 8
January to the 8![]() February 2001. The telescope is equipped
with DFOSC, a
February 2001. The telescope is equipped
with DFOSC, a
![]() pixels CCD camera with a plate-scale of
0.39
pixels CCD camera with a plate-scale of
0.39
![]() /pixel. The total field of view is
/pixel. The total field of view is
![]() .
We used the UBVRi filter set.
.
We used the UBVRi filter set.
The data reduction was carried out using the CCDRED package within IRAF. The images were bias and flat-field corrected. DFOSC is equipped with a fast shutter (the shutter delay is of the order of milliseconds), so in this case it was not necessary to apply a shutter correction to the data. For those binaries with smaller separations we took several short exposures in each filter. The final images are the result of combining all individual frames.
The optical magnitudes have been measured following the same procedure
described for the CTIO data: we carried out aperture photometry on the
sources; for the closest pairs (separation < 5
![]() )
we carried
out multi-aperture photometry correcting with field stars. Finally,
we carried out differential photometry of all the targets using
comparison stars which were monitored during the ten nights.
)
we carried
out multi-aperture photometry correcting with field stars. Finally,
we carried out differential photometry of all the targets using
comparison stars which were monitored during the ten nights.
![\begin{figure}
\par\resizebox{15.5cm}{!}{\includegraphics[clip]{0442fg1a.ps}} \end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg24.gif) |
Figure 1: BVR lightcurves of the observed Lindroos PTTSs. The differences in magnitudes between the target and the "artificial comparison'' star (see text) are displayed versus Julian Date at different filters for the variable stars. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{15.5cm}{!}{\includegraphics[clip]{0442fg1b.ps}} \end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg25.gif) |
Figure 1: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{15.5cm}{!}{\includegraphics[clip]{0442fg1c.ps}} \end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg26.gif) |
Figure 1: continued. |
| Open with DEXTER | |
The optical lightcurves of the sample in the BVR-bands are
displayed in Fig. 1. We have constructed them
subtracting the magnitudes of the targets from the magnitudes of an
"artificial comparison'' star. The "artificial'' stars have been
derived in the following way: for each observation we have analyzed
the lightcurves of several field stars in order to select those that
are not varying over the ten nights. From these stars we have
rejected those displaying instrumental magnitudes and colors very
different from that of the targets. We have finally weighted the
selected stars according to their observational errors (the weight is
taken as the inverse of the square of the magnitude error,
![]() )
and computed their averaged magnitude. The
lightcurve of the corresponding "artificial'' star is shown in the panel
below the lightcurve of each target in Fig. 1.
)
and computed their averaged magnitude. The
lightcurve of the corresponding "artificial'' star is shown in the panel
below the lightcurve of each target in Fig. 1.
In order to detect variability in the stellar light of the Lindroos
stars, we have adopted the following criteria: we consider the
Lindroos stars to be variable when the standard deviation of their
mean magnitude over the ten nights is three times larger than the
standard deviation of the mean magnitude of the artificial star, that
is,
![]() .
.
We have analyzed the lightcurves of each target in the five filters. In general, the U-band data show a lower SNR when compared to the BVRI filters given that the targets (and the comparison stars) are fainter at that wavelength. However, the amplitudes in this band are larger, so in most of the cases we can use the U-band to report significant variability of the targets.
The rotation periods have been computed from the photometric data applying two different methods: the string-length (SL) method proposed by Dworetsky (1983) and the Scargle periodogram (SP, Scargle 1982).
The string length method works in the phase space and it is well suited for samples with a small number of unevenly spaced data points (Dworetski 1983). This method seems not to be well-suited for large and clumped datasets (Scholz & Eislöffel 2004). In this method, a rotational period is assumed and the phase-folded lightcurve is constructed. Afterward, the length of the string that joins consecutive points in the folded diagram is computed. The string-length algorithm is then applied to a set of trial periods and the one showing the shortest string length is chosen as the best period. We have applied the algorithm to all the targets in the different filters.
In order to check the significance level of the derived periods, we have performed several tests. Firstly, we have generated 10 000 synthetic lightcurves using a Monte-Carlo method. The 10 000 aleatory samples have the same temporal sampling as our data (that is, we have preserved the Julian Dates) but aleatory photometric values within the amplitudes of the observational data. We have applied the string length method to the 10 000 synthetic lightcurves. Each data set provides a minimum value of the string length that corresponds to the best period. The percentage of samples showing a string length larger than the string length of the observational data provides the confidence level of the period determination. We assignee a 99% confidence level to a case in which all the randomized data show a string length larger than that obtained with the observational data, because we consider that we cannot discriminate between 99% and 100%. Whenever more than one period is found to be statistically significant, the visual inspection of the data and the quality of the phase-folded lightcurve has helped us to choose the most probable one. The main disadvantage of this test is that if the random magnitudes can adopt any value within the given amplitude, the probability of having a string value larger than the one found in the real data can be high. This translates into a high significance of the derived period that may be overestimated.
As a second test, we have generated 10 000 aleatory samples preserving the Julian Date and randomly distributing the real magnitude values. We have applied the SL method to the 10 000 samples and kept the minimum SL for each of them. The confidence level is given the fraction of samples with SL values smaller than the one obtained with the real data. The results obtained with this method are similar to the ones obtained with the first test.
As a final test, we have generated 10 000 pseudo-aleatory samples
retaining the Julian Dates of the observations and generating
randomized magnitudes within a given interval. The magnitudes are not
completely random in the sense that they can only adopt values
following this expression:
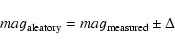 |
(1) |
Table 2: Photometric amplitudes in the UBVRI and rotational periods of PTTSs in Lindroos systems.
We have also analyzed the periodicity of our lightcurves using the
Scargle method, which works in the frequency domain. We have used
Interactive Data Language (IDL) routines to derive the periodogram of
the sources within a period interval of
![]() days to
days to
![]() days. In the case of HD 60102, we have considered a
days. In the case of HD 60102, we have considered a
![]() days given the better temporal sampling of the data.
We have also derived the SP of the "artificial'' comparison stars and
we have checked that the periods obtained for the Lindroos sample are
not present in their periodograms.
days given the better temporal sampling of the data.
We have also derived the SP of the "artificial'' comparison stars and
we have checked that the periods obtained for the Lindroos sample are
not present in their periodograms.
Given that most of the lightcurves show unevenly distributed datapoints, we have not applied Horne & Baliunas (1986) to derive the false alarm probability (fap). Instead, we have generated 10 000 aleatory samples preserving the Julian Date and randomly distributing the magnitude values (as in the case of the SL method). We have derived the Scargle periodogram for each sample and retained the power of the highest peak. The significance level is given by the fraction of samples with power values smaller than the one obtained with the real data.
As an extra test, we have averaged the data points taken during a single night and repeated the period search applying both the SL and the SP methods. In the latter case we have derived the fap following Horne & Baliunas (1986). As a result, the derived periods are similar to the ones derived previously. The faps are larger than those derived with our significance method for some of the stars. We think this result is related with the small number of data points used to derive the periodogram.
The results provided by the two methods, SP and SL, are shown in Table 2. We can consider as more secure (or probable) periods those that fulfilled the conditions: (i) the periods are similar in both the V- and B-band. We have chosen these two bands because they provide the best combination of amplitude and signal to noise ratio. Whenever possible, we have also used the R-band and/or the U-band and/or the I-band data to confirm the periodicity; (ii) such periodicity is not found in the comparison stars; and (iii) the confidence level is higher than 95%. We have classified as less secure (or possible) those periods that only have data in one optical filter but fulfilled statements (ii) and (iii) and those periods that fulfilled (i) and (ii) but show confidence levels between 90-95%.
The results for each star are discussed in detail in the next section.
![\begin{figure}
\par\resizebox{15.7cm}{!}{\includegraphics[clip]{0442fig2.ps}} \end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg39.gif) |
Figure 2: V-band phase-folded lightcurves of the Lindroos PTTSs for which we have found a rotational modulation. The difference in magnitude between the target and the "artificial'' star (see text) is displayed against the Julian Date. The phases have been computed using the rotation periods shown in Table 2. |
| Open with DEXTER | |
The phase-folded lightcurves of the targets have been plotted using the periods provided in Table 2. They are shown in Fig. 2. The amplitudes derived in the BV bands are very similar to those derived by Wichmann et al. (1998) and Bouvier et al. (1997b) in their samples of PTTSs. We have analyzed the individual stars separately:
HD 33802 B: It is a variable star according to its BVR lightcurves (Fig. 1). The data in the three filters are in phase and they display a significant variation in comparison with the artificial star. The derived period is 2.8 days for the BV data, and a period of 3.0 days for the R-data. According to the lightcurves, a period of 2.8 days fits better the observed variation. We have obtained the same result with the two methods, with a confidence level of 99%.
HD 38622 C: This PTTSs could not be monitored during the ten consecutive nights given its proximity to the moon path. We have plotted the obtained data points in Fig. 1. The star is variable in the BVR filters but we cannot report any periodicity due to the scarcity of data.
HD 40494 B: We have recorded a clear modulation of the light in the BVRI filters. The string-length method provides two periods to fit the data: 6.4 days (VB-bands) and 5.6 (R-band). The minimum value of the string-length is obtained for 6.4 days with a significance of 99%. Moreover, the visual inspection of the data suggests that a period larger than six days fits better the observed modulation. The SP method provides a period of 6.4 d for the V-band and 6.1 d for the B-band. We have constructed the phase-folded lightcurve using a value of 6.4 d (see Fig. 2).
HD 53191 B: The UBVRI lightcurves of HD 53191 B show a clear modulation over the ten nights of observations. The minimum and maximum values of the brightness are observed at the same Julian dates in the five filters. We have found a large number of comparison stars in the field of view of HD 53191 B whose relative brightness is constant over the ten nights. The derived period is 4.4 days with the two methods, with a significance level of 99%.
HD 60102 B: This source shows clear variability in all lightcurves although it is difficult to see a periodic modulation in the data. We observed the star three times during one of the nights and we could see that the object is varying significantly in a short timescale (see Fig. 1). We have derived a period of 1.9 days (UVR-bands) that provides a smooth phase-folded lightcurve. The B-band provides a very close period of 1.8 d. We obtain the same result with the two methods with a significance level of 99%.
If we averaged the data points, the SP method provides a period of
2.3 days with a lower significance level (![]() 96% in VR and
smaller in the UB-bands). The phase-folded lightcurve is not
well fitted with such period in any of the optical bands, so we have
rejected this period.
96% in VR and
smaller in the UB-bands). The phase-folded lightcurve is not
well fitted with such period in any of the optical bands, so we have
rejected this period.
HD 86388 B shows variations in the V-band lightcurve, but we cannot study this variation in the BRI filters due the lack of non-variable comparison stars.
We have applied the string-length method to the V-band data obtaining a period of 5.7 days with a confidence level smaller than 90%. When using the Scargle periodogram we derived a photometric period of 5.3 days and a confidence level of 85%. The visual inspection of the V-band lightcurve shows a clear modulation. However, given that (i) there is only one band to derive the period; and (ii) the significance level is very low, we conclude that more data is needed to validate the periodicity of this object.
HD 90972 B: In the case of HD 90972, the U-band data
are noisy and the artificial star shows a large scatter, so we have
only used the BVRI data to study the variability and periodicity
of the object. The target shows a significant variability in these
four filters over the ten observing nights. The errors associated to
the data points are larger than in other stars because the separation
of this Lindroos system is small (11
![]() )
and the primary star is
very bright (V-mag = 5.6 mag). As a result, the multi-aperture
photometry is less accurate than in other targets.
)
and the primary star is
very bright (V-mag = 5.6 mag). As a result, the multi-aperture
photometry is less accurate than in other targets.
The SL provides a period of ![]() 3.3 d in BVR-bands with a
confidence level of 93%. The SP provides a period of 3.2 d (in
BVR-bands) with a 91% confidence level. The observational
data are well fitted with a period of 3.3 d, as shown in the phase-folded
lightcurve (Fig. 2). However, we have classified
this period as "possible'' given its relatively low significance level.
3.3 d in BVR-bands with a
confidence level of 93%. The SP provides a period of 3.2 d (in
BVR-bands) with a 91% confidence level. The observational
data are well fitted with a period of 3.3 d, as shown in the phase-folded
lightcurve (Fig. 2). However, we have classified
this period as "possible'' given its relatively low significance level.
![\begin{figure}
\par\resizebox{12.8cm}{!}{\includegraphics[clip]{0442fig3.ps}}\end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg41.gif) |
Figure 3:
Rotational evolution of a 1 |
| Open with DEXTER | |
HD 113703 B: The PTTSs HD 113703 B was observed with the 1.5 m Danish telescope on La Silla. We obtained lightcurves in the BVI filters. We have not considered the R-band data of this object, given that it is too bright and it was saturated in some of the exposures. In the U-band there were no suitable reference stars.
The BV-band lightcurves show a clear modulation and we have found two significant periods: 7.6 days (obtained with the V-band data and 8.0 days (obtained with the B- and I-band data). We have also derived a shorter period of 0.9 days that fits the observed data. We have found that this period is an alias of 8 days. Unfortunately, our time sampling is not short enough to confirm a short period of 0.9 days. The visual inspection of the lightcurves suggests that a period of 8.0 days is the one that better reproduces the observed modulation, so we have adopted this value as the most probable. Given this discrepancy in the V and B-data and the possibility of having a shorter period, we have classified the derived period as "possible''. The phase-folded lightcurve is shown in Fig. 2.
HD 113791 B could only be monitored in the U-filter given that it is too bright at longer wavelengths, saturating the detector. The U-band lightcurve of HD 113791 B is displayed in Fig. 1. It shows a clear variability in its brightness displaying a U-band amplitude 0.08 mag. We have derived a possible period of 3.8 days with a confidence level of 98%. A very similar result is obtained with the SP method. As seen in Fig. 2, this rotation period fits the modulation observed in the U-band data. Due to the lack of data in a different optical filter, we have classified the period as "possible''.
HD 129791 B: This K-type star seems to be a variable source
according to its U-band lightcurve. The standard deviation of
the data is exactly 3 times that of the artificial star. The
amplitude in this band is 0.07 mag, which is one of the smallest among
the sample. In the BVRI-bands the amplitudes are ![]() 0.03 mag, with the artificial star varying at the same level, so
these bands do not provide further information.
0.03 mag, with the artificial star varying at the same level, so
these bands do not provide further information.
There is no obvious modulation in the U-band lightcurve of HD 129791 B. The star was observed twice during three different nights, so we have studied if it could be a short-period variable. After applying the SL and SP methods we do not find any significant period. Hence, we can only conclude that HD 129791 B seems to be a variable star without an obvious periodicity within ten days of monitoring.
HD 143939 B: We have found non-variable comparison stars only in the R- and I-band. Using the R-band data we have derived a period of 3.0 d which provides the phase-folded lightcurves displayed in Fig. 2. The confidence level is of 97%. We obtain the same result with both the SL and the SP methods. In the case of the I-band we obtain a periodicity of 3.2 d with a confidence level of 97% when using the SL method. The SP method provides a similar period value but a lower significance (85%). Hence, we have classified this period as "possible''.
In order to examine the rotational properties of Lindroos PTTSs, we
have represented the sample with probable and possible periods (groups
a and b in Table 2) in an age-rotation diagram
(Fig. 3). The rotational evolution of late-type PMS
stars is mass-dependent. The estimated masses of the Lindroos PTTSs
with measured rotation periods range between 0.9-1.2 ![]() (see
Table 1), so we have focused our study on this mass range.
(see
Table 1), so we have focused our study on this mass range.
As shown in Fig. 3, the Lindroos PTTSs populate the central part of the diagram with ages that range from 10-100 Myr and periods larger than 1.9 d. We have represented the ages derived by Palla & Stahler (1999, PS99 hereafter) which results on a mixture of PMS and ZAMS stars among the Lindroos sample. If we consider the ages provided by D'Antona & Mazzitelli (1998, DM98), the Lindroos sample populate a narrower age interval (10-35 Myr) of the diagram (see Table 1) and all the stars can be classified as PMS stars.
We have overplotted the PTTSs samples studied by Bouvier et
al. (1997b) and Wichmann et al. (1998). In both cases we have only
considered stars with masses between 0.9 and 1.2 ![]() .
The
comparison of the three samples of PTTSs shows that they are
complementary: while most of the Lindroos PTTSs display periods longer
than 3 d, the other two samples contain faster rotators that populate
the lower part of the diagram. This result is probably related with
the different criteria used to select the samples: X-ray selected
samples mostly contains fast rotators, while non X-ray selected
samples can contain both slow and fast rotators. Our study has not
revealed the presence of very slow rotators among the Lindroos PTTSs,
that is, the slowest rotators among the Lindroos sample show rotation
periods comparable to the largest periods reported in Lupus and Taurus
PTTSs samples.
.
The
comparison of the three samples of PTTSs shows that they are
complementary: while most of the Lindroos PTTSs display periods longer
than 3 d, the other two samples contain faster rotators that populate
the lower part of the diagram. This result is probably related with
the different criteria used to select the samples: X-ray selected
samples mostly contains fast rotators, while non X-ray selected
samples can contain both slow and fast rotators. Our study has not
revealed the presence of very slow rotators among the Lindroos PTTSs,
that is, the slowest rotators among the Lindroos sample show rotation
periods comparable to the largest periods reported in Lupus and Taurus
PTTSs samples.
The rotational properties of the Lindroos systems can be compared with
the predictions of the disk-locking theory. In order to do this we
have used the rotational tracks by Bouvier et al. (1997a).
Figure 3 shows the theoretical age-rotation diagram for
1 ![]() star (suitable to study the Lindroos PTTSs with masses
between 0.9-1.2
star (suitable to study the Lindroos PTTSs with masses
between 0.9-1.2 ![]() )
and an initial rotation period of
P0=7.8 d for CTTSs. This value is based on the period distribution
of CTTSs in the Taurus SFR (Bouvier et al. 1993). Younger late-type
stars presumably undergoing a mass accretion process (with masses >0.25
)
and an initial rotation period of
P0=7.8 d for CTTSs. This value is based on the period distribution
of CTTSs in the Taurus SFR (Bouvier et al. 1993). Younger late-type
stars presumably undergoing a mass accretion process (with masses >0.25 ![]() )
in the Orion Nebula Cluster (ONC) show a broader
range of rotation periods but they also display a peak at 8 d in
their period distribution. Only a 5% of the sample of periodic
variables display periods longer than 12 d (e.g. Attridge & Herbst
1992; Eaton et al. 1995; Choi & Herbst 1996; Stassun et al. 1999;
Herbst et al. 2002). Hence, we have kept the value of 8 days as the
initial rotation period in the model. The solid and dotted lines
represent the rotational tracks for different star-disk decoupling
times, which range between
)
in the Orion Nebula Cluster (ONC) show a broader
range of rotation periods but they also display a peak at 8 d in
their period distribution. Only a 5% of the sample of periodic
variables display periods longer than 12 d (e.g. Attridge & Herbst
1992; Eaton et al. 1995; Choi & Herbst 1996; Stassun et al. 1999;
Herbst et al. 2002). Hence, we have kept the value of 8 days as the
initial rotation period in the model. The solid and dotted lines
represent the rotational tracks for different star-disk decoupling
times, which range between
![]() .
.
![\begin{figure}
\par\resizebox{13.5cm}{!}
{\includegraphics[clip]{0442fig4.ps}} \end{figure}](/articles/aa/full/2004/48/aa0442-03/Timg44.gif) |
Figure 4:
Activity-rotation relations for late-type PMS and ZAMS
stars with masses between 0.9-1.2 |
| Open with DEXTER | |
The Lindroos PTTSs lie in different regions within the diagram (Fig. 3) which suggests different decoupling times for the star-disk system. Their rotational properties can be explained assuming decoupling times between 1-20 Myr. Note that HD 113703 B and HD 113791 B, the two PTTS close to its early B-type primary, show relatively long rotation periods with estimated decoupling times of 10 and 20 Myr, respectively. Both, the long periods and the estimated decoupling times, suggest that the UV radiation field of the early-type primaries have not played an important role in the early dissipation of their disks. When adopting the ages provided by DM98 instead of PS99, we find a similar decoupling time interval (10-20 Myr) for the Lindroos sample. However, three stars displaying younger ages (HD 33802 B, HD 40494 B and HD 53191 B) show different properties: although they remain almost on the same rotational tracks, they lie at the end of the spin-up phase, while PS99 ages suggest that the three of them are spinning down.
All our conclusions are model-dependent, given the uncertainties in the initial rotation periods of the Lindroos sample. If we assume a longer initial rotation period (15 d) in the theoretical model, the absolute values of the star-disk decoupling times are different for the individual Lindroos PTTS. However, their rotational properties can still be explained with decoupling times between 1-20 Myr. In the case of shorter initial periods (e.g. 4.4 d), all the decoupling times are longer than 5 Myr while the stars with longer periods are not well-fitted by the model.
If we include the other two samples of PTTSs (Taurus and Lupus) in
our analysis, a slightly different range of decoupling times is
necessary to explain their rotational properties (![]() 0.5-10 Myr).
And, finally, if we consider other samples of late-type stars
at different evolutionary stages (TTS, PTTS and ZAMS stars) a broader
range of decoupling times (0.5-20 Myr) is required to explain their
position in the age-rotation diagram (see Fig. 3).
0.5-10 Myr).
And, finally, if we consider other samples of late-type stars
at different evolutionary stages (TTS, PTTS and ZAMS stars) a broader
range of decoupling times (0.5-20 Myr) is required to explain their
position in the age-rotation diagram (see Fig. 3).
The decoupling times are related to the lifetime of optically thick
circumstellar disks. According to Fig. 3, the
existence of both short and long-lived disks is required to explain
the different rotational properties of Lindroos, Taurus and Lupus PTTS stars. Infrared studies of young stellar clusters have shown that the
mean lifetime of protoplanetary disks is ![]() 6 Myr (Haisch et
al. 2001). This disk lifetime can explain the rotational properties
of most of the TTSs and part of the PTTSs and ZAMS stars represented
in Fig. 3. However, it cannot explain the presence
of slow rotators among the PTTSs and Pleiades samples.
6 Myr (Haisch et
al. 2001). This disk lifetime can explain the rotational properties
of most of the TTSs and part of the PTTSs and ZAMS stars represented
in Fig. 3. However, it cannot explain the presence
of slow rotators among the PTTSs and Pleiades samples.
The existence of long-lived optically thick disks has been studied by
Strom (1995) who showed that 30% of 10 Myr old late-type PMS stars
in the L 1641 cloud display infrared excesses. More recently, Lyo et
al. (2003) have reported the presence of circumstellar disks around
60% of 10 Myr old late-type stars in the young cluster ![]() Chamaleontis. One important result from their study is that 30% of
the stars with infrared excesses also show on-going accretion
processes. This result supports the possibility of having decoupling
times of
Chamaleontis. One important result from their study is that 30% of
the stars with infrared excesses also show on-going accretion
processes. This result supports the possibility of having decoupling
times of ![]() 10 Myr among late-type PMS stars and could explain
the presence of 10-100 Myr old slow rotators in the age-rotation
diagram. The Lindroos stars located in this part of the diagram have
already decoupled from their disks which have presumably dissipated at
earlier stages in their evolution. Hence, we do not expect these
PTTSs to show IR excesses at near-IR wavelengths but maybe at longer
wavelengths as a result of grain growth during disk evolution
(Brandner et al. 2000). In fact, some Lindroos PTTS were observed by
the Infrared Space Observatory (ISO) at 6.5 and 15
10 Myr among late-type PMS stars and could explain
the presence of 10-100 Myr old slow rotators in the age-rotation
diagram. The Lindroos stars located in this part of the diagram have
already decoupled from their disks which have presumably dissipated at
earlier stages in their evolution. Hence, we do not expect these
PTTSs to show IR excesses at near-IR wavelengths but maybe at longer
wavelengths as a result of grain growth during disk evolution
(Brandner et al. 2000). In fact, some Lindroos PTTS were observed by
the Infrared Space Observatory (ISO) at 6.5 and 15 ![]() m and display
mid-IR excesses. This result is interpreted as evidence of remnant
circumstellar matter (Moneti et al. 1998).
m and display
mid-IR excesses. This result is interpreted as evidence of remnant
circumstellar matter (Moneti et al. 1998).
The connection between coronal activity and rotation in late-type PMS
stars has been extensively studied in different works
(e.g. Pallavicini et al. 1981; Bouvier 1990; Stauffer et al. 1994;
Neuhäuser et al. 1995; Flaccomio et al. 2003). These studies have
revealed that most 1 ![]() late-type PMS stars with ages less
than 10 Myr display a high level of magnetic activity. Stelzer &
Neuhäuser (2001) have studied the rotation-age-activity relation for
TTSs in Taurus (with ages between 105-107 yr) in comparison to
dwarf stars in the Pleiades (age
late-type PMS stars with ages less
than 10 Myr display a high level of magnetic activity. Stelzer &
Neuhäuser (2001) have studied the rotation-age-activity relation for
TTSs in Taurus (with ages between 105-107 yr) in comparison to
dwarf stars in the Pleiades (age ![]() 108 yr; Meynet et al. 1993)
and the Hyades (
108 yr; Meynet et al. 1993)
and the Hyades (
![]() Myr; Perryman et al. 1998).
They have reported a tight connection between coronal activity and
rotation for all three groups.
Myr; Perryman et al. 1998).
They have reported a tight connection between coronal activity and
rotation for all three groups.
Lindroos PTTSs are intermediate between TTSs and Pleiades, so we have studied the rotation-activity relations for our sample and compared it with other groups of younger and older late-type stars.
We have started our study comparing the rotation period and the X-ray luminosity of the Lindroos PTTSs. As seen in the upper panel of Fig. 4, Lindroos PTTS show a clear anti-correlation between rotation and X-ray emission being the strongest X-ray emitters are the fastest rotators. The other two samples of PTTS contain faster rotators. They show a flatter relation with a larger spread in rotation periods for a given X-ray luminosity.
In order to analyze the evolution of the
![]() -period
relation with age, we have also included in Fig. 4
three samples of late-type stars at different evolutionary stages:
TTSs in Taurus, Pleiades and Hyades dwarf stars. The observational
data for these three samples have been taken from Stelzer &
Neuhäuser (2001) and references therein. As in the previous
section, our study is focused on late-type stars with masses between
0.9-1.2
-period
relation with age, we have also included in Fig. 4
three samples of late-type stars at different evolutionary stages:
TTSs in Taurus, Pleiades and Hyades dwarf stars. The observational
data for these three samples have been taken from Stelzer &
Neuhäuser (2001) and references therein. As in the previous
section, our study is focused on late-type stars with masses between
0.9-1.2 ![]() .
.
PTTSs and TTSs show a very similar X-ray luminosity-period relation:
the strongest X-ray emitters display a broad range of rotation periods
(from 0.3 d-10 d) and show no correlation between X-ray luminosity and
rotation period. On the other hand, the less active stars show
periods longer than ![]() 4 d and display a steep relation between
X-ray luminosity and rotation with the strongest X-ray emitters being
the fastest rotators.
4 d and display a steep relation between
X-ray luminosity and rotation with the strongest X-ray emitters being
the fastest rotators.
Five Lindroos PTTSs occupy the same region of the diagram as WTTSs, displaying the strongest X-ray luminosity of the whole sample. Their X-ray emission is not correlated with the rotation period. On the other hand, two Lindroos systems (HD 40494 B, HD 53191) display lower activity levels. These are the oldest stars in the sample. According to PS99, HD 40494 and HD 53191 B show ages of 80 Myr and 100 Myr respectively, so they could be considered as ZAMS stars. In that case, their position in the diagram could reflect an age effect, that is, they show lower levels of X-ray emission due to their older ages. However, if we consider DM98 tracks, these stars are significantly younger (35 Myr and 30 Myr, respectively) and an age effect is not longer able to explain their position in the diagram. In this case, they could be considered the less active PTTSs among the sample.
According to Fig. 4, the most active late-type PMS
stars (
![]() erg/s) do not show a correlation
between activity and rotation: for a given X-ray luminosity we found a
wide range of rotation periods. On the other hand, the weakest X-ray
PMS emitters
erg/s) do not show a correlation
between activity and rotation: for a given X-ray luminosity we found a
wide range of rotation periods. On the other hand, the weakest X-ray
PMS emitters
![]() erg/s) display a correlation between
the X-ray luminosity and rotation period. At the age of the Pleiades,
all stars display X-ray luminosities
erg/s) display a correlation between
the X-ray luminosity and rotation period. At the age of the Pleiades,
all stars display X-ray luminosities
![]() erg/s and show a connection between activity and rotation.
erg/s and show a connection between activity and rotation.
The comparison of PTTS with Pleiades and Hyades stars shows a
connection between activity-rotation with age. ZAMS stars do not
display a
![]() -period relation as steep as that found for
less active late-type PMS stars. Moreover, the fastest rotators in the
Pleiades exhibit lower X-ray luminosities than those from PTTSs and
TTSs samples. The decrease in the magnetic activity is more evident
in the Hyades, where the mean X-ray luminosity is one order of
magnitude smaller than that from the other three samples.
-period relation as steep as that found for
less active late-type PMS stars. Moreover, the fastest rotators in the
Pleiades exhibit lower X-ray luminosities than those from PTTSs and
TTSs samples. The decrease in the magnetic activity is more evident
in the Hyades, where the mean X-ray luminosity is one order of
magnitude smaller than that from the other three samples.
The X-ray luminosity depends, among other factors, on the stellar
radius. We have taken into account this effect studying normalized
activity parameters like the ratio between the X-ray and the
bolometric luminosity,
![]() ,
and the X-ray surface
flux,
,
and the X-ray surface
flux,
![]() ,
of the Lindroos PTTSs. We have computed these
parameters adopting the bolometric luminosities and effective
temperatures listed in Gerbaldi et al. (2001).
,
of the Lindroos PTTSs. We have computed these
parameters adopting the bolometric luminosities and effective
temperatures listed in Gerbaldi et al. (2001).
The
![]() ratio has been derived for a large
number of late-type star samples. In general, the most active stars
show ratios close to the saturation value of
ratio has been derived for a large
number of late-type star samples. In general, the most active stars
show ratios close to the saturation value of
![]() (e.g. Fleming et al. 1989; Feigelson et al. 1993; Micela et
al. 1999): late-type stars displaying that ratio have reached the
highest level of X-ray activity, e.g. by coverage of the whole
surface with magnetic spots. The middle panel of
Fig. 4 shows the relation between the
(e.g. Fleming et al. 1989; Feigelson et al. 1993; Micela et
al. 1999): late-type stars displaying that ratio have reached the
highest level of X-ray activity, e.g. by coverage of the whole
surface with magnetic spots. The middle panel of
Fig. 4 shows the relation between the
![]() ratio and the rotation period for TTSs, PTTSs,
Pleiades and Hyades stars. In the case of the Lindroos PTTSs, the
relation is very steep and includes both saturated and unsaturated
stars. Three of the stars display ratios close to the saturation
value of -3 and short rotation periods.
ratio and the rotation period for TTSs, PTTSs,
Pleiades and Hyades stars. In the case of the Lindroos PTTSs, the
relation is very steep and includes both saturated and unsaturated
stars. Three of the stars display ratios close to the saturation
value of -3 and short rotation periods.
The Lindroos sample display a
![]() -period
relation very similar to that found in TTSs, containing the two
samples very active stars with both short and long rotation
periods. The most active PTTSs show a relation very similar to that of
WTTSs while the less active Lindroos PTTSs occupy the same region in
the diagram as CTTSs. In both groups, TTSs and PTTSs, we find stars
with periods between 1-8 days and with
-period
relation very similar to that found in TTSs, containing the two
samples very active stars with both short and long rotation
periods. The most active PTTSs show a relation very similar to that of
WTTSs while the less active Lindroos PTTSs occupy the same region in
the diagram as CTTSs. In both groups, TTSs and PTTSs, we find stars
with periods between 1-8 days and with
![]() ratios close to the saturation value of -3, indicating that during
the PMS phase the saturation level is reached with different
rotational properties. ZAMS and MS stars show flatter
activity-rotation relations, with all of them displaying
ratios close to the saturation value of -3, indicating that during
the PMS phase the saturation level is reached with different
rotational properties. ZAMS and MS stars show flatter
activity-rotation relations, with all of them displaying
![]() ratios lower than the saturation value of -3. In the
case of the Hyades, most of the targets exhibit
ratios lower than the saturation value of -3. In the
case of the Hyades, most of the targets exhibit
![]() ratios close to the value of -4.5 and long periods.
ratios close to the value of -4.5 and long periods.
Flaccomio et al. (2003) have shown that at ages between 1-7 Myr most
of the 1 ![]() late-type PMS stars are saturated and their
X-ray and rotational properties are not correlated. They report a
decrease in the magnetic activity at the age of the Pleiades
(
late-type PMS stars are saturated and their
X-ray and rotational properties are not correlated. They report a
decrease in the magnetic activity at the age of the Pleiades
(![]() 100 Myr) suggesting that this decrease must take place at ages
older than 10 Myr. We find a mixture of saturated and non-saturated
stars among the Lindroos sample. This result suggests high activity
levels at ages of 10 Myr and a decrease in coronal activity at longer
ages.
100 Myr) suggesting that this decrease must take place at ages
older than 10 Myr. We find a mixture of saturated and non-saturated
stars among the Lindroos sample. This result suggests high activity
levels at ages of 10 Myr and a decrease in coronal activity at longer
ages.
Finally, we have studied the relation between the rotation period and
the X-ray surface flux for PTTSs, TTSs, Pleiades and Hyades stars
(lower panel in Fig. 4). The X-ray surface flux is
implicitly related to the fraction of stellar surface covered with
active regions. As seen in Fig. 4, there is a clear
variation in the steepness of the relation from the younger stars to
the older ones. As in the case of the
![]() ratio, TTS and PTTS display very similar relations although the most
active stars among the PTTSs sample show larger X-ray surface fluxes
than the most active TTSs. These could be related to the fact that
TTSs are still contracting to the MS, displaying larger surface areas
than PTTSs. The latest have finished their contraction and approach
the MS following the radiative part of the evolutionary tracks. The
ratio, TTS and PTTS display very similar relations although the most
active stars among the PTTSs sample show larger X-ray surface fluxes
than the most active TTSs. These could be related to the fact that
TTSs are still contracting to the MS, displaying larger surface areas
than PTTSs. The latest have finished their contraction and approach
the MS following the radiative part of the evolutionary tracks. The
![]() -period relation becomes flatter for stars in the
Pleiades and the Hyades.
-period relation becomes flatter for stars in the
Pleiades and the Hyades.
In this preliminary study, we have analyzed the rotational properties of a sample of PTTSs in Lindroos systems. We have derived their rotation periods after an optical monitoring of the targets during two campaigns of 10 nights each. We have compared the derived periods with theoretical PMS rotational tracks. Finally, we have studied the activity-rotation relation for PTTSs and compared it with samples of younger and older stars. The main results of this study can be summarized as follows:
We have compared the rotation periods of Lindroos PTTS with
theoretical models by Bouvier et al. (1997a). The largest scatter in
rotation periods corresponds to the PTTSs phase, and it can be
explained as a result of the different decoupling times between the
star-disk system during the PMS phase. The rotational properties of
the Lindroos PTTSs can be explained assuming different star-disk
decoupling times, between ![]() 1-20 Myr, for an initial period of
8 d. If we consider other samples of PTTSs, the range of decoupling
times is broader (0.5-20 Myr). This range of times is directly
related to the lifetime of circumstellar disks. IR studies of young
stellar clusters have shown that disks can survive up to 10 Myr. The
reason why disks could dissipate at such different timescales is still
an open question, although the initial star formation conditions (dust
and gas content in the initial cloud) and the environment in which
disks evolve (close to early-type stars) could certainly have an
influence in their lifetimes.
1-20 Myr, for an initial period of
8 d. If we consider other samples of PTTSs, the range of decoupling
times is broader (0.5-20 Myr). This range of times is directly
related to the lifetime of circumstellar disks. IR studies of young
stellar clusters have shown that disks can survive up to 10 Myr. The
reason why disks could dissipate at such different timescales is still
an open question, although the initial star formation conditions (dust
and gas content in the initial cloud) and the environment in which
disks evolve (close to early-type stars) could certainly have an
influence in their lifetimes.
Acknowledgements
We thank the referee, W. Herbst, for useful comments that improved the manuscript. We thank CTIO and La Silla staff, in special E. Cosgrove and F. Selman, for their support during the observations. N.H. thanks B. Stelzer and A. Scholz for useful comments on the manuscript and M. Billeres for her assistance. M.F. was partially supported by the Spanish grant AYA2001-1696. N.H. and R.N. did most of this work at MPE Garching, where RN was supported by the BMBF Verbundforschung ROSAT.