- ... Center
![[*]](/icons/foot_motif.gif)
- See http://www.asdc.asi.it/bepposax
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... galaxies
![[*]](/icons/foot_motif.gif)
- Part of the measured thermal emission may also come from
OB stars, which are expected to be abundant in SB regions and
whose thermal emission is characterized by
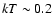 keV,
keV,
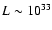 erg s-1 (see PR02).
erg s-1 (see PR02).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2003)
![[*]](/icons/foot_motif.gif)
- The two quoted limits correspond to
Eddington luminosities for, respectively, a
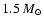 neutron star and a
neutron star and a
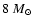 black hole (BH) which is the limiting
BH mass obtainable via ordinary stellar evolution.
ULXs are called "super-Eddington sources''.
black hole (BH) which is the limiting
BH mass obtainable via ordinary stellar evolution.
ULXs are called "super-Eddington sources''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... HMXBs
![[*]](/icons/foot_motif.gif)
- In a few cases the optical counterparts
of ULX have been identified as O stars (Liu et al.
2002; Roberts et al. 2002), thus suggesting a
relation between ULXs and HMXBs, which of course
are young objects that trace the current SFR.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... BH
![[*]](/icons/foot_motif.gif)
- Qualitatively, the inverse correlation between
L2-10 and
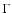 (i.e., flatter spectra for higher luminosities)
can be understood within the standard accretion model devised to
explain the high
(i.e., flatter spectra for higher luminosities)
can be understood within the standard accretion model devised to
explain the high 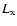 of interacting binaries. The increase
in
of interacting binaries. The increase
in 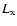 is driven by an increase of
is driven by an increase of 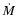 ,
which in turn
means a piling up of material around the emission region that leads
to a higher Compton scattering optical depth, and hence to a flatter
spectrum. E.g., according to Sunyaev & Titarchuk (1980) and Shapiro
et al. (1976), if a source of photons is embedded in a plasma cloud
of optical depth
,
which in turn
means a piling up of material around the emission region that leads
to a higher Compton scattering optical depth, and hence to a flatter
spectrum. E.g., according to Sunyaev & Titarchuk (1980) and Shapiro
et al. (1976), if a source of photons is embedded in a plasma cloud
of optical depth 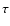 and temperature T, the escaping radiation
has a high-energy photon index
and temperature T, the escaping radiation
has a high-energy photon index
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![\begin{displaymath}\Gamma ~=~ \biggl[ {9 \over 4} ~+~ {\pi^2 m_{\rm e} c^2 \over
3 ~ (\tau + 2/3)^2 ~ kT} \biggr]^{1/2} ~-~ {1 \over 2} \cdot
\end{displaymath}](/articles/aa/full/2004/43/aa1128/img128.gif)