A&A 426, 729-736 (2004)
DOI: 10.1051/0004-6361:20040201
All-sky imaging at high angular resolution:
An overview using lossy compression
C. Dollet - A. Bijaoui - F. Mignard
CERGA, UMR 6527, CNRS, Observatoire de la Côte d'Azur, BP 4229,
Le Mont-Gros, 06304 Nice Cedex 4, France
Received 5 February 2004 / Accepted 30 June 2004
Abstract
We examine a possible extension of the Gaia mission in the form of a high-spatial resolution all-sky survey in the visible based on a scanning
satellite and show that the main limitation is the amount of collected data to be transmitted. We then investigate the kind of image compression that would make it possible to carry out a complete cartography at a resolution of
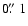 ,
which would constitute a major advance in sky mapping. The most significant
information is projected into wavelet space after the subtraction of the brighter objects that are mapped independently with the instrument point spread function and transmitted separately. The study is based on a Gaia-like instrument using a
rectangular pupil and one-dimensional high resolution along scan. The difference of resolution across- and along-scan is compensated by the combination of all the observations at the end of the mission in Fourier space. A gain of 2-3 mag compared with the magnitude limit of the on-board detection could be achieved with the features of the Astro Sky Mapper of the Gaia mission.
,
which would constitute a major advance in sky mapping. The most significant
information is projected into wavelet space after the subtraction of the brighter objects that are mapped independently with the instrument point spread function and transmitted separately. The study is based on a Gaia-like instrument using a
rectangular pupil and one-dimensional high resolution along scan. The difference of resolution across- and along-scan is compensated by the combination of all the observations at the end of the mission in Fourier space. A gain of 2-3 mag compared with the magnitude limit of the on-board detection could be achieved with the features of the Astro Sky Mapper of the Gaia mission.
Key words: surveys - instrumentation: high angular resolution - astrometry - methods: data analysis - stars: imaging - galaxies: structure
A few decades after the invention of photography (incidentally it was
so named by two astronomers: J. H. Mädler and J. Herschel) and
its successful use in astronomical research, the idea came very
naturally (around 1880) to map the entire sky with this new
technique, once the problem of long exposure times, or
equivalently that of accurately clock-driven mounted telescopes,
was mastered. Although quickly effective for nebulous objects, it
took more time before the technique could take over direct
observation at the eyepiece in positional astronomy, like double
star measurements or parallax determination. Moreover the mapping
of the deep sky (at the time objects fainter than
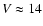 )
was hampered by the lack of sensitivity of photographic plates,
although this situation improved quickly after 1860.
)
was hampered by the lack of sensitivity of photographic plates,
although this situation improved quickly after 1860.
It was in this context that Admiral Mouchez, the then Director
of Paris Observatory, launched in 1887 (with Sir David Gill and
Otto Struve) an international undertaking aiming to make a
complete photographic map of the sky down to the 15th mag.
It was the beginning of a worldwide collaboration, the so-called
Carte du Ciel project which lasted until about 1950 and even
very recently, new reductions of the plates were made in
a consistent way and put into the Hipparcos system
(Urban et al. 1998, 2001). The stars were mapped up to magnitude 14-15 thanks to a set of similar astrographs
distributed around the world (Weimer 1987) and to a division
of the sky into non-overlapping zones. Later, in the mid-1950s, a
new sky survey was started with the 48-inch Palomar Schmidt
telescope
with the northern hemisphere covered at
two different epochs and later digitised (Djorgovski et al. 1998).
Then observations with SERC and the ESO Schmidt telescopes, and a
second epoch with the upgraded Palomar Schmidt, completed this mapping of the whole sky in  1980.
1980.
These surveys were somewhat heterogeneous, this being more
pronounced for the Carte du Ciel, despite the efforts to use the
same technique on similar refractors. The image quality varied
with the site, the observation epoch, the plate and the location
in the image. The resulting analyses took as much as possible of
these variations into account but the remaining biases due to this
heterogeneity are often not well known. For the POSS I (Palomar Observatory Sky Survey) the limiting magnitude is around 19-20, and 21-22 for
POSS II with an angular resolution of typically around 2 arcsec
for the latter survey, with a scatter within each plate and from
plate to plate.
Many astrophysical problems will benefit from surveys reaching
fainter stars in several colours and with a sub-arcsec angular
resolution. For example, the separation between faint galaxies and
field stars is very sensitive to the resolution and to the
ability to detect the extendedness of the galaxies. The galaxy counts
would be much improved if these observational parameters were
better defined (Yasuda et al. 2001). Similarly, QSO identification and
the understanding of these sources will be improved with the
detection of the host galaxy, so difficult to achieve at the
moment because of the weak surface luminosity. This detection is sensitive
to the inhomogeneity and the dearth of data (Myers et al. 2003).
Systematic studies of weak lensing need both deep imaging and high
resolution images (Mellier & Van Waerbeke 2002), and repeated
observations are mandatory for monitoring the varying sky. Many other
topics require systematic searches in the form of surveys like the
determination of the geometry of the universe, the distribution
and properties of dark matter, the distant quasars, the monitoring
of SNe I, the properties of galaxy clustering at high redshift,
the relation(s) between dark and luminous matter, proper motions
of stars in the Galaxy or, closer to us, the trans-Neptunian objects
in the Solar System.
Given this wide range of scientific interest and the expected
output, several ground-based and space projects at different
wavelengths have been designed to map the sky. They are very
deep in general, but limited to small patches of the sky (e.g. the
Canada-France-Hawaii Telescope Legacy Survey (CFHTLS)). From the ground, unless adaptive optics is used, the
image resolution is never better than  1 arcsec, and
at present there is no possibility to reach at the same time a
high-resolution with adaptive optics and a large field of view. One must then
accept to reserve the use of telescopes fitted with adaptive
optics to very well selected objects of great astrophysical
interest. The Hubble Space Telescope outside the atmosphere could
theoretically reach the goal, but has not been designed to carry
out extended surveys covering a significant fraction of the sky.
1 arcsec, and
at present there is no possibility to reach at the same time a
high-resolution with adaptive optics and a large field of view. One must then
accept to reserve the use of telescopes fitted with adaptive
optics to very well selected objects of great astrophysical
interest. The Hubble Space Telescope outside the atmosphere could
theoretically reach the goal, but has not been designed to carry
out extended surveys covering a significant fraction of the sky.
Therefore future all-sky mappings, genuine successors of the Carte
du Ciel or of the Palomar Sky Surveys, at a resolution of, or
better than,
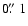 will only be possible with a
dedicated space mission, scanning the sky in a systematic way for
several years and imaging large fields on electronic detectors.
Today imaging missions are considered only for specific purposes
such as the SNAP project (The Supernova Acceleration Probe, Kim
et al. 2002, at present known as the Joint Dark Energy Mission) dedicated to the detection and the follow-up of distant supernovae around the north and south ecliptic poles over fields limited to a twenty-square-degree region with repeated observations separated by short intervals of time.
will only be possible with a
dedicated space mission, scanning the sky in a systematic way for
several years and imaging large fields on electronic detectors.
Today imaging missions are considered only for specific purposes
such as the SNAP project (The Supernova Acceleration Probe, Kim
et al. 2002, at present known as the Joint Dark Energy Mission) dedicated to the detection and the follow-up of distant supernovae around the north and south ecliptic poles over fields limited to a twenty-square-degree region with repeated observations separated by short intervals of time.
Full sky coverage, repeated observations every few days and high
spatial resolution are conflicting requirements with the available
technology. Restricting ourselves to the goal, which aims at a spatial
resolution at the level of
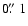 ,
we realise that a
single full coverage of the sky will need the reading out and
storage of
,
we realise that a
single full coverage of the sky will need the reading out and
storage of
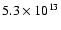 pixels. The transmission capability
appears the most stringent limitation and image
compression must be investigated thoroughly. In this paper we
discuss several of these constraints facing the realizers of
such a survey. In the first section, the optical design and the
focal environment are discussed with the Gaia instrument
as an example for a possible design. In the second
section we discuss a compression strategy while simulations of
typical celestial fields are presented in the next section. The
compression results are then examined and discussed. As each
field is observed about one hundred times during the mission, a
final image can be restored taken into account all the exposures.
In the final section, the method is described and examples of
restoration are given. In the conclusion, we discuss the astrophysical interest of this type of space mission.
pixels. The transmission capability
appears the most stringent limitation and image
compression must be investigated thoroughly. In this paper we
discuss several of these constraints facing the realizers of
such a survey. In the first section, the optical design and the
focal environment are discussed with the Gaia instrument
as an example for a possible design. In the second
section we discuss a compression strategy while simulations of
typical celestial fields are presented in the next section. The
compression results are then examined and discussed. As each
field is observed about one hundred times during the mission, a
final image can be restored taken into account all the exposures.
In the final section, the method is described and examples of
restoration are given. In the conclusion, we discuss the astrophysical interest of this type of space mission.
In this section we examine the constraints set by an all-sky
imaging survey with special emphasis on the ESA approved mission
Gaia, to show how this could meet the science requirements,
provided a higher telemetry rate could be made available. Even
with the current design, a selection strategy of small fields
(a few seconds of arc wide) will make it possible to retrieve images around
dedicated objects compatible with the telemetry rate.
Let us consider as a base of this investigation a full-sky
mapping at 0.1 arcsec in the visible using CCD detectors with a
maximum sensitivity between 0.6 and 0.8 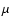 m. Then, the nominal
resolution is achieved with a telescope having an aperture of at
least 1.2 m. To reduce the cost and the mechanical constraints it
will be sufficient to use a rectangular pupil with one dimension much smaller than the other, and even a slit telescope
would make it possible to obtain the nominal resolution in one dimension.
Eventually the full resolution in all directions will be
obtained by giving the telescope different orientations (Martin et al. 1986)
in the course of the mission.
m. Then, the nominal
resolution is achieved with a telescope having an aperture of at
least 1.2 m. To reduce the cost and the mechanical constraints it
will be sufficient to use a rectangular pupil with one dimension much smaller than the other, and even a slit telescope
would make it possible to obtain the nominal resolution in one dimension.
Eventually the full resolution in all directions will be
obtained by giving the telescope different orientations (Martin et al. 1986)
in the course of the mission.
This solution has been retained for the ESA Gaia mission (Perryman
et al. 2001), which, while not primarily designed to map the
sky in its entirety, rests heavily on this combination: high
resolution in one direction combined with repeated scans in
different orientations. As successor of the Hipparcos mission,
this project is a cornerstone of ESA's science programme with a
payload consisting of three telescopes. Two of them are dedicated
to the astrometric measurements, while the third should
provide photometric and radial velocity data. The Gaia satellite
is foreseen to be launched no later that 2012 and to be put in the
Sun-Earth Lagrange point L2.
The two astrometric telescopes have rectangular primary mirrors
of
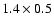 m2. Therefore the resolution is not
identical in the two directions, parallel or orthogonal to the
mirror major axis. The optical design is based on a three-mirror
combination which makes it possible at the same time to have a large FOV
(Field of View) and keep the optical distortion at a very low
level, compatible with the requirements of a nominal astrometric
accuracy of 10 micro-arcseconds (
m2. Therefore the resolution is not
identical in the two directions, parallel or orthogonal to the
mirror major axis. The optical design is based on a three-mirror
combination which makes it possible at the same time to have a large FOV
(Field of View) and keep the optical distortion at a very low
level, compatible with the requirements of a nominal astrometric
accuracy of 10 micro-arcseconds (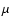 as) at the end of the mission.
The field height
as) at the end of the mission.
The field height
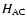 is 0.65 degree and the field width
is 0.65 degree and the field width
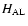 is 0.80 degree. The 0.52 square degree field of view is
covered by 153 CCDs detectors fitted in the focal plane. The pixel
size is about 10
is 0.80 degree. The 0.52 square degree field of view is
covered by 153 CCDs detectors fitted in the focal plane. The pixel
size is about 10 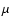 m along the scan and 30
m along the scan and 30 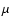 m across
it, amounting to an area of
m across
it, amounting to an area of
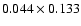 arcsec2 on the sky.
arcsec2 on the sky.
Each astrometric field is composed of an astrometric sky mapper (ASM), the astrometric field proper and a broad-band photometer
along the scan direction. The object detection and their selection
for further observations are carried out by the two ASMs. For each
ASM, there is a strip of 9 CCDs, each having
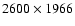 pixels. Due
to an electronic
pixels. Due
to an electronic 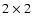 binning on-board the actual image
samples have a resolution of 0.088 arcsec along the scan and
0.266 arcsec across. So the transmission of all of these samples
would lead to a telemetry rate of
binning on-board the actual image
samples have a resolution of 0.088 arcsec along the scan and
0.266 arcsec across. So the transmission of all of these samples
would lead to a telemetry rate of  100 Mbits/s per ASM field with
a coding over 16 bits and an integration time of 1.9 s per CCD (meaning that each CCD line must be read out every 1.9 s). For comparison, the actual radio
link of Gaia with the ground station allows a sustained
transmission rate of
100 Mbits/s per ASM field with
a coding over 16 bits and an integration time of 1.9 s per CCD (meaning that each CCD line must be read out every 1.9 s). For comparison, the actual radio
link of Gaia with the ground station allows a sustained
transmission rate of  4 Mbits/s, during the period of
visibility. The actual rate averaged out over one day is about
4 Mbits/s, during the period of
visibility. The actual rate averaged out over one day is about
 1.3 Mbits/s for a visibility of 8 h per day.
The design (Jordi et al. 2003) so described refers to the version of Gaia
after it was rescoped in Spring 2002 and is in no way frozen.
However no major changes are expected for the astrometric
instrument during the final definition phase extending to early 2005.
1.3 Mbits/s for a visibility of 8 h per day.
The design (Jordi et al. 2003) so described refers to the version of Gaia
after it was rescoped in Spring 2002 and is in no way frozen.
However no major changes are expected for the astrometric
instrument during the final definition phase extending to early 2005.
Sky imaging at high angular resolution has not been the main
driver in the design of the mission, which is primarily an
astrometry mission supplemented by photometry and spectroscopy.
The main purpose lies in
the detection of all the star-like objects up to magnitude 20
and in the determination of their coordinates, parallaxes and
proper motions with the highest accuracy, and specific procedures
are defined for optimising the exploitation of the focal data to
ensure the best science return in agreement with the scientific
objectives of the mission. Consequently, full or partial sky
mapping is considered only as a secondary objective, to be
included only if it is achievable at a moderate cost and without
having an impact on the main mission.
A specific project for a cartography of the sky will certainly be
designed somewhat differently from what Gaia is today, but its main
features already make it possible to point out its strengths and weaknesses
in achieving a full-sky imaging and the changes required to reach this goal.
![\begin{figure}
\par\includegraphics*[width=7cm,clip]{0201fig1.eps} \end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg15.gif) |
Figure 1:
A schematic design of the focal plane assembly of a scanning satellite designed to map the sky in four colours. |
| Open with DEXTER |
Let us start from a system having an entrance pupil and a focal
plane with size similar to Gaia but with square pixels of
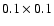 arcsec2, that is to say a smaller resolution than Gaia's, at
least in the direction of the scan motion. Four spectral bands
(Fig. 1) are spread out in this plane:
U, B, V, I in
contrast with the situation of Gaia with its single G band in the
ASM CCDs. The pixels across the scan direction are distributed over 10 CCDs for
calibration purposes and to keep the actual size of the CCDs
acceptable from a technological point of view. Assuming a mission
of five years, two configurations can be compared according to the
scan rate. First, the same scan rate as Gaia is used:
arcsec2, that is to say a smaller resolution than Gaia's, at
least in the direction of the scan motion. Four spectral bands
(Fig. 1) are spread out in this plane:
U, B, V, I in
contrast with the situation of Gaia with its single G band in the
ASM CCDs. The pixels across the scan direction are distributed over 10 CCDs for
calibration purposes and to keep the actual size of the CCDs
acceptable from a technological point of view. Assuming a mission
of five years, two configurations can be compared according to the
scan rate. First, the same scan rate as Gaia is used:
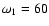 arcsec/s (one revolution about the spin axis every
six hours). Then we consider a spin rate two times larger.
arcsec/s (one revolution about the spin axis every
six hours). Then we consider a spin rate two times larger.
The field exposure mode with dedicated pointing at different areas
of the sky used in previous surveys was very expensive both in money and
in time and is not appropriate for a space mission. The
continuous scanning by Hipparcos or Gaia based on a regular rotation
of the spacecraft and a controlled motion of the spin axis is much
less expensive and the best way to map the same region of the
sky at different epochs. With the scanning mode and a
mission of 5 years the same celestial region is seen about one
hundred times at different epochs with different orientations of
the instantaneous motion of the field of view.
Table 1 gives the main parameters for two possible
projects evolved from Gaia. The total integration time
in a given region of the sky is identical in the two cases; however,
the distribution of the observations over the five years is not
the same, as indicated by the total number of observations. With a
slower scan rate, every field crossing lasts 24 s, meaning a
better instantaneous signal-to-noise ratio at the expense of a
lower recurrence of observations (21 instead of 42 with the faster
scan rate). Without binning and with a 16 bit coding, the
telemetry for each band is about one or two hundreds Mbits/s. A
compression rate of about a hundred would reduce the telemetry to 4
or 8 Mbits/s for the two scan rates, a goal technically achievable
within the coming ten years.
A great advantage of these designs over Gaia is the increase of
the limiting magnitude per observation (Lindegren 1998). The
Gaia mission is designed for the detection of stellar objects up
to magnitude 20, and this must be achieved with an integration
of only 1.9 s. With the lower rotation of the satellite, the
limiting magnitude becomes 23.9 for the band G, 22.3 for U, 23.4
for B, 22.7 for V and 22.1 for I. For the same scan rate as Gaia
the magnitude limit decreases by 1.1 mag in each band.
Table 1:
Main parameters for the two virtual space missions dedicated to a full sky cartography with a pixel size of
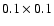 arcsec2.
arcsec2.
The comparison between the three surveys gives an evident
advantage to a dedicated mission for achieving the best sky mapping:
faintest limiting magnitude, multiband photometric capability and a
realistic compression rate. In the following, we describe the main
features of a possible compression algorithm and evaluate its
performance in the case of Gaia, for images based on the sky
mapper observations. This methodology can be considered as a test
for a more specialised mission.
For the ASM (Gaia sky mapper detector), to limit the
telemetry rate (Hoeg et al. 2003), an area of about 100 pixels (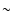
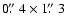 )
around each detected
object (this is called a window in Gaia terminology) is
planned to be transmitted to the ground. For an average star density of
25 000 per square degree at magnitude 20, a raw data rate of
250 kbits/s is estimated for each ASM (without compression),
instead of the 97 Mbits/s that would be required for all the ASM pixels and 16 bit coding. We show in the subsequent sections
how a clever compression scheme could relax this constraint, and
without allowing full mapping, could help increase the size
of the downlinked patch around each detected object.
)
around each detected
object (this is called a window in Gaia terminology) is
planned to be transmitted to the ground. For an average star density of
25 000 per square degree at magnitude 20, a raw data rate of
250 kbits/s is estimated for each ASM (without compression),
instead of the 97 Mbits/s that would be required for all the ASM pixels and 16 bit coding. We show in the subsequent sections
how a clever compression scheme could relax this constraint, and
without allowing full mapping, could help increase the size
of the downlinked patch around each detected object.
A lossless compression could not meet the goals of reducing the data rate to few Mbits per second. It was thus essential to examine a process with information selection. As has been largely demonstrated (Richter et al. 1991; White et al. 1992; Louys et al. 1999), astronomical images can be represented with few significant wavelet coefficients leading to a considerable compression rate and a reduced information loss. The whole cycle from the data to the final images goes through several steps. The overall scheme of the proposed on-board compression method is featured in Fig. 2. More details concerning the technical aspects of this method will be given in an article submitted at the same time (Dollet et al. in IJIST).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0201fig2.ps}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg19.gif) |
Figure 2:
Schematic chart showing the successive steps used for the
compression and decompression of an ASM Gaia image. |
| Open with DEXTER |
Before the transformation of the ASM values into wavelet coefficients, a Generalised Anscombe transform (GAT, Murtagh et al. 1994) is applied to each pixel. It allows a stabilisation of the noise variance. This step is necessary for the statistical selection and the quantisation because the ASM noise is a combination of a Poisson process on the photons and that of read-out noise that can be taken as Gaussian.
A wavelet transform corresponds to a projection on a mathematical basis generated from the dilation and translation of a single function (Mallat 1999; Starck et al. 1998). One applies first the Haar wavelet (Richter 1991). As the
compression rate is rather high for astronomical images, this
wavelet transform was used in particular for the on-line
transmission of the Digital Sky Survey (White et al. 1992). However,
comparisons were made with a bi-orthogonal 9/7 filter (Daubechies et al. 1998). With both
techniques, a high compression rate (such as several hundred)
implies the generation of artefacts in the restored image.
It would be possible to carry out directly this coding procedure
but preliminary simulations showed us that the compression rate
was not sufficient (see Parnaudeau 1999; Massart 2000). To increase it drastically, we also considered the possibility of
using information already transmitted to the ground with another
instrument of the same mission or already available from existing
surveys. The basic idea is to generate a simulated image for all
the point sources brighter than a certain limiting magnitude, e.g. 20, and to remove this information from the observed image by subtraction. Thus, at the end only the new objects remain in the
resulting image and are transmitted to the ground.
The simulation of a pseudo-image for all these sources, equivalent to what would be observed if no other sources were present, is carried out on-board. In the following, to avoid confusion with the observed image, we will
call this reference image the map. The Anscombe and wavelet
transforms are applied to the map before determining the difference between the two
images. Obviously when the catalogue of the brightest
point sources is also created on board with an auxiliary detector
it must be transmitted, but the amount of data is much smaller
than for a full image.
The wavelet coefficients of the difference between the GAT image
and the GAT map are set to zero at a certain threshold, below which it is
assumed that the wavelets carry only noise. A multiple k of the standard deviation of the equivalent Gaussian noise determined with the values of the generalised Anscombe transform is considered as threshold. In this way we keep only the significant information.
The next step is the coding in order to store the residual information. A 4-bit coding (Huang 1991; Huang & Bijaoui 1991) is used and is sufficient in the present context. This step is reversible and the coding algorithm is fast.
For the image restoration, each step of the processing is inversed. The map is regenerated from the catalogue of the detected objects. As was done on board, a
generalised Anscombe transform and a wavelet transform are applied to this map before its addition to the restored wavelet coefficients.
The application of an inverse wavelet transform and a reverse generalised Anscombe transform to these new coefficients gives the restored image. However, in the decompressed image the threshold generates artefacts, known as block effects. Methods called regularized inversion were proposed for reducing these (White et al. 1992; Richter 1991; Bobichon 1997; Bobichon & Bijaoui 1997). But the studies were carried out for limited compression rates. The distortion in the restored images was less significant than it is here.
During a space mission covering the whole sky, the number of
objects observed in a particular direction is a strong function of
the galactic latitude for stellar sources while it is more or less
uniform for galaxies or quasars. To assess the average compression
rate, tests must be carried out with simulations of sufficiently large fields (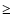 0.015 square degree) with a star
density close to the sky average and significantly fainter than
the instantaneous (one transit) detection capability, so that one
can test the improvement when stacking several images. Extended
objects with low surface brightness must also be included in the
simulated fields. In the following these fields are referred to as
reference fields.
0.015 square degree) with a star
density close to the sky average and significantly fainter than
the instantaneous (one transit) detection capability, so that one
can test the improvement when stacking several images. Extended
objects with low surface brightness must also be included in the
simulated fields. In the following these fields are referred to as
reference fields.
Two programs, STUFF and SKYMAKER (Bertin & Arnouts 1996; Erben et al. 2001), were used to generate fields meeting the above
criteria. STUFF is able to generate a data catalogue of galaxies
used by SKYMAKER to simulate large fields with these galaxies and with stars.
The program was adapted to allow for the non-axisymmetric Gaia point spread function and for the detector having rectangular pixels.
For the galaxies, two profiles were combined. The disk component
was simulated by an exponential profile and the bulge by a de
Vaucouleurs profile. Several types of galaxies were defined by
changing the distribution of the total flux over these two
profiles. The distributions of the scale radii for the bulge and the disk are
fixed by an empirical relation for the former and a semi-analytical model for the latter linking these quantities to the absolute
magnitudes (de Jong & Lacey 1999). The galaxies are allotted a random inclination of the disk and a position angle which define the apparent ellipticity of the objects. For the distribution with
magnitude, the number of galaxies is determined from a Poisson distribution assuming a non-evolving Schechter luminosity function.
Stellar objects are generated with the help of the point spread function of the instrument. Their number density down to a limiting apparent brightness can be
specified as input parameter. Objects much fainter than the detection limit obviously have to be included as it should be possible to retrieve them when the repeated observations are combined. For the simulation of the map associated to each image of the sky, only a selection of the objects from the input catalogue was required, in this simulation those brighter than 20 mag.
In this section, numerical results based on the compression method developed
earlier are shown, emphasising the use of a map for the brightest sources to achieve full sky imaging in space with a resolution of at least 0.1 arcsec. Simulated large fields will make it possible to define the telemetry rate according to the densities of relevant astronomical sources. Finally we estimate the gain in magnitude from the objects detected on board to those obtained in the restored image on the ground from the combination of the repeated observation of similar fields.
A set of five fields was generated with a density of
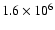 stars per square degree up to magnitude 26 (This is just an extrapolation of the mean density of 25 000 stars per square
degree at G=20). Fifteen galaxies were distributed on a surface
of 0.015 square degree. These large fields fill
stars per square degree up to magnitude 26 (This is just an extrapolation of the mean density of 25 000 stars per square
degree at G=20). Fifteen galaxies were distributed on a surface
of 0.015 square degree. These large fields fill
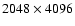 samples on the CCDs. This density can be considered as
representative of an average area of sky at mid galactic
latitude. Thus the results should be a good estimate of the
information to be transmitted every second during the mission. For
the stars we find a compression rate close to 700 for a
threshold at
samples on the CCDs. This density can be considered as
representative of an average area of sky at mid galactic
latitude. Thus the results should be a good estimate of the
information to be transmitted every second during the mission. For
the stars we find a compression rate close to 700 for a
threshold at 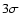 .
One must note at this point that our images are coded in floating numbers over 32 bits. For such a floating coding, the transmission of all the pixels of one Astro Sky Mapper corresponds to a reference data rate of
.
One must note at this point that our images are coded in floating numbers over 32 bits. For such a floating coding, the transmission of all the pixels of one Astro Sky Mapper corresponds to a reference data rate of 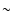 200 Mbits/s (see the rate of
200 Mbits/s (see the rate of 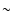 100 Mbits/s indicated in Sect. 2.1 concerning a 16 bits coding). Consequently, a compression rate close to 700 leads to an average telemetry rate of 290 kbits/s to transmit all the pixels of one Astro Sky Mapper. This compression rate increases quickly to several thousands for higher thresholds, at the expense of the information
available on the ground.
100 Mbits/s indicated in Sect. 2.1 concerning a 16 bits coding). Consequently, a compression rate close to 700 leads to an average telemetry rate of 290 kbits/s to transmit all the pixels of one Astro Sky Mapper. This compression rate increases quickly to several thousands for higher thresholds, at the expense of the information
available on the ground.
Table 2 shows the evolution of the
compression rate as the threshold gets more severe. The numbers
are an average for the five independent stellar fields. For the
highest thresholds, our use of a map (for the subtraction of the stars
brighter than limiting magnitude 20 in the observed image)
proves very useful for increasing the compression rate. With a
threshold at 3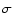 one has a 40 percent increase in the
compression efficiency when the brightest stars are transmitted
separately.
one has a 40 percent increase in the
compression efficiency when the brightest stars are transmitted
separately.
Table 2:
Compression rates for different thresholds with or without map.
In order to increase the signal to noise ratio, and consequently
the detection limit, we also used the correlation between the
observed image and the map constructed with a mean Gaia point
spread function. This makes it possible to retain higher spatial information
particularly for the extended objects. For an identical threshold
the compression rate is smaller when the correlation is taken into account. Nevertheless
a threshold at 4.5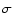 provides a compression rate close to 450, yielding a telemetry rate of 430 kbits/s.
provides a compression rate close to 450, yielding a telemetry rate of 430 kbits/s.
The accuracy of the position (about 0.1 pixel) and the magnitude
of the objects detected on board will be high enough to
achieve this result and a slight bias does not affect
the compression rate significantly. With a random shift of
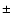 0.5 pixel across the scan,
0.5 pixel across the scan, 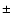 0.5 pixel in the direction of the scan and
0.5 pixel in the direction of the scan and 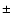 0.1 mag for each object we found that the value of the
compression rate is 530 (that is to say a telemetry of 365 kbits/s)
instead of 710.
0.1 mag for each object we found that the value of the
compression rate is 530 (that is to say a telemetry of 365 kbits/s)
instead of 710.
These compression rates refer to an average situation and will change
with the actual star density. For high density regions, like 47 Tuc, we have found a compression of about 100 instead of 670 and
on the opposite, in the sparsely populated regions (say
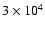 stars per square degree at G=26), the compression factor
rises to 710.
stars per square degree at G=26), the compression factor
rises to 710.
5.2 Discussion
The lossy compression determined by the trimming of the wavelet
coefficients leads to the appearance of zones with a homogeneous
intensity during the image restoration. This would complicate
the estimation of the detection limit for the astronomical objects
if we had a single restored image per field. However, the same
field of the sky will be observed about a hundred times during the
5 years of a scanning mission like Gaia. These images can be
stacked at the end of the mission to increase the signal to noise
ratio of the final restored image, provided that there is not too
much variability in the sources.
In this section we restrict ourselves to the addition of the images of the
same area of the sky in a very simple manner, assuming that the
geometry of the observations remains constant during the repeated
scans. A more realistic situation will be considered later in this
paper. To generate the equivalent of a long exposure image, the wavelet coefficients of the 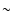 100 observations distributed over the five years are added.Then one includes the coefficients of the map of the brightest point sources. Finally the two inverse transforms are applied: the Haar transform for
the wavelets and the Anscombe transform for the dynamics.
100 observations distributed over the five years are added.Then one includes the coefficients of the map of the brightest point sources. Finally the two inverse transforms are applied: the Haar transform for
the wavelets and the Anscombe transform for the dynamics.
The analysis of the restored image with the help of an isotropic wavelet
has permitted the estimation of a detection limit close to 22 mag for the stars. For the galaxies, this detection limit is around magnitude 20. If a correlation with a mean point spread function is carried out before the on-board compression, a gain of one magnitude is still possible. The detection limit for stars is near magnitude 23 and that of the galaxies is about 21.5 for a
threshold of 4.5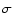 .
.
As the resolution of the Gaia Sky Mapper is three times higher along the scan than across the scan, and as observations of the same zone of the sky with different scan directions are available, special processing is needed to
recover the highest possible resolution in the final restored
images when all the individual images are stacked. Instead of
interpolating each sample directly (Vaccari 2000), these scans
(about one hundred) can be combined by taking
into account their specific orientations in Fourier space
using the invariance property of the Fourier transform. So the
exact knowledge of the orientation of the satellite scan makes it possible to make an inverse rotation of each observation in the frequency
space. This space can be recovered gradually thanks to all these
observations. A single inverse Fourier transform gives a final
image with a resolution close to the best resolution of the
sample. As this stage we have not considered the slight
variation of position of the stars or their photometric
variability, which would add some complexities in the procedure.
If fully neglected, this would essentially spread out the resulting image of a point source. This approximate superimposition of each stellar observation decreases the flux per square arcsec. It is then possible that the faintest stars will not be detectable above the noise. The cosmic rays would also be a source of spurious images,
but the vast majority of these events will be eliminated with the
use of a repeated detection during a transit.
The Fourier transform of an image with a rotation of an angle 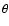 is equal to the rotation of
is equal to the rotation of 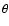 of the Fourier transform of the image without rotation. As is well known the sampling theorem leads to periodic sampling in the spectral domain. Conversely, the Fourier transform sampling also leads to a periodicity in direct space. Two images with different rotations do not have the same periodicity grid in direct space. After the inverse rotations, the resulting grids cannot be superimposed (Stone et al. 2000). To prevent the generation of artefacts at the time of the reconstruction, the differences between these fields must be limited and the presence of discontinuities must be avoided.
of the Fourier transform of the image without rotation. As is well known the sampling theorem leads to periodic sampling in the spectral domain. Conversely, the Fourier transform sampling also leads to a periodicity in direct space. Two images with different rotations do not have the same periodicity grid in direct space. After the inverse rotations, the resulting grids cannot be superimposed (Stone et al. 2000). To prevent the generation of artefacts at the time of the reconstruction, the differences between these fields must be limited and the presence of discontinuities must be avoided.
First, so as to respect the Shannon theorem, the difference of
resolution in the along- and across-scan directions must be compensated with
the same difference in the dimensions of the initial image. The
use of large fields makes it possible to limit the influence of the corners
of each observation. To reduced the artefacts resulting from the
sampling variation, a mask is applied to all the observed images.
In the central region, delimited by a circle with a diameter equal
to half the size of the field, the value is equal to one. Between
this circle and another of diameter 3/4 the size of the
field, the value of the mask decreases smoothly (a sine function
has been used here). Outside this circle the mask is equal to zero.
The rotation in Fourier space is performed with a two-dimensional interpolation like a pseudo-spline of degree 3. Once multiplied by a Von Hann window to smooth out the frequency space, the FFT of the whole set of images are added together. The final weighted mean of the observations in Fourier space is multiplied by the sum of the FFT of the PSFs with the correct orientations. As this PSF is symmetric, this multiplication in Fourier space is equivalent to a correlation in direct space. Consequently, taking into account the point spread function in this procedure improves the final signal to noise ratio. From the weighted mean of the FFTs, an inverse Fourier transform generates a field at highest resolution.
This algorithm was implemented first with a field of mean density
(
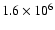 stars per square degree up to magnitude 26)
corresponding to 0.0014 deg2 (
stars per square degree up to magnitude 26)
corresponding to 0.0014 deg2 (
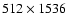 samples). There is a
single galaxy at the centre whose size and shape are determined by
STUFF. The objects are included by SKYMAKER. Figure 3
shows the deterministic simulated field.
samples). There is a
single galaxy at the centre whose size and shape are determined by
STUFF. The objects are included by SKYMAKER. Figure 3
shows the deterministic simulated field.
![\begin{figure}
\par\resizebox{7.3cm}{7.3cm}{\includegraphics[clip]{0201fig3.eps}}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg28.gif) |
Figure 3:
Simulation of a field with
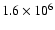 stars per square
degree up to magnitude 26 without noise and including one
galaxy at its centre.
stars per square
degree up to magnitude 26 without noise and including one
galaxy at its centre. |
| Open with DEXTER |
The restored image based on a single observation is shown in
Fig. 4 for a threshold of
3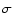 and a decomposition on 6 scales for both types of
transformation. The block effects are visible for the Haar
transform (compression rate of 660 or a telemetry of 294 kbits/s). The elliptical shape of the galaxy in the middle is not
properly recovered at this stage. For the biorthogonal 9/7 filter,
the image is smoother but for such a high compression, false
small structures appear everywhere (compression rate of 590 or a
telemetry of 329 kbits/s). Only the six stars included in the
transmitted catalogue are well identifiable.
and a decomposition on 6 scales for both types of
transformation. The block effects are visible for the Haar
transform (compression rate of 660 or a telemetry of 294 kbits/s). The elliptical shape of the galaxy in the middle is not
properly recovered at this stage. For the biorthogonal 9/7 filter,
the image is smoother but for such a high compression, false
small structures appear everywhere (compression rate of 590 or a
telemetry of 329 kbits/s). Only the six stars included in the
transmitted catalogue are well identifiable.
![\begin{figure}
\par\includegraphics[width=7.2cm,height=7.2cm,clip]{0201f4a.eps}\par\includegraphics[width=7.2cm,height=7.2cm,clip]{0201f4b.eps}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg29.gif) |
Figure 4:
Dilation of the restored image (single observation) with
the biorthogonal 9/7 filter ( top) and the Haar wavelet ( bottom). |
| Open with DEXTER |
When 100 observations are available, they are stacked and rotated
in the Fourier space as explained earlier. The result is shown in
Fig. 5 where the effect of the mask
appears conspicuously. This must be compared with Fig. 6 resulting from the simulated images (Fig. 3) when all sources fainter than 22 mag have been removed. One sees clearly that the restoration of point
sources down to magnitude 22 is achieved with this procedure despite the very high and lossy compression rate applied. Consequently, there is a gain of two magnitudes compared to the on-board limiting magnitude.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics*[clip]{0201fig5.eps}}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg30.gif) |
Figure 5:
Restored image in the Fourier space from 100observations with different orientations for the biorthogonal 9/7 filter. The masking from centre to borders can be noted. |
| Open with DEXTER |
 |
Figure 6:
Field without noise and identical to Fig 3 with only the objects brighter than magnitude 22. |
| Open with DEXTER |
An all-sky imaging survey from space at high resolution will
benefit many areas of astronomical research but is technically
very difficult to achieve because of the volume of data to be
transmitted to the ground. In this paper we have first
investigated the existing gap between the required data rate to
carry out such a survey and the state of the art in terms of
data
transmission. Then we have considered several kinds of data
compression and image restoration which would decrease very
significantly the amount of data to be sent to the ground station,
without degrading too much the image quality and the spatial
resolution. We have shown that the association of a catalogue of
stars to each observed field also makes it possible to decrease the
transmitted information by a factor of several hundreds. The
image stacking in Fourier space for fields observed in very
different scan directions makes it possible to improve the detection level on
the ground by two magnitudes and justifies by itself the interest
of keeping all the pixels around brighter detected objects to
locate nearby faint contaminants. Another magnitude can be gained
just by also using a correlation with a mean point spread function of each
observation.
The Gaia design has been used as an example for the simulation and the
assessment of the compression rates and we show where the effort
should be directed with the current design to improve its imaging
capabilities. However a genuine full-sky mapping could only be
really achieved with a dedicated system as sketched in this
paper. With a field of view similar to that of Gaia, a lower scan
rate gives a higher integration time at each observation and a
fainter limiting magnitude. Eventually the higher resolution and
the use of several spectral bands will be useful for the
identification of faint sources and the discovery of new classes
of objects. The catalogue extracted after such a mission will be
used as a reference for the selection of targets for future
missions limited to specific types of objects in small fields or
for ground based follow-up.
In this paper we have only considered the overall principles that
should be put in place to ensure that the imaging of faint sources
is achievable. Many practical questions have not been answered, in
particular the size of the computation and data processing on
the ground and the level of automation it will require. This can only
be done within a more accurate definition of the design, and belongs
to the preliminary study phase of a survey mission.
- Bertin, E., &
Arnouts, S. 1996, A&AS, 117, 393 (In the text)
- Bobichon, Y.
1997, Ph.D. Thesis
(In the text)
- Bobichon, Y.,
& Bijaoui, A. 1997, Proc. SPIE, 36
(In the text)
- Daubechies,
I., & Sweldens, W. 1998, J. Fourier Anal. Appl., 4, 247 [NASA ADS] (In the text)
- Djorgovski,
S. C., de Carvalho, R. R., Gal, R. R., et al. 1998, New Horizons
from Multi-Wavelength Sky Surveys, IAU Symp., 179, 424
(In the text)
- Dollet, C.,
Bijaoui, A., & Mignard, F. 2004, IJIST, submitted
- Erben, T., Van
Waerbeke, L., Bertin, E., et al. 2001, A&A, 366, 717 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Hoeg, E., Arenou, F.,
Mignot, S., et al. 2003, Scientific requirements for the on-board
processing, Technical report GAIA-CUO-117
(In the text)
- Huang, L. 1991,
Ph.D. Thesis
(In the text)
- Huang, L., &
Bijaoui, A. 1991, Exp. Astron., 311
(In the text)
- de Jong, R. S., &
Lacey C. 1999, ASP Conf. Ser., 170, 52 [NASA ADS] (In the text)
- Jordi, C., Babusiaux,
C., Katz, D., et al. 2003, GAIA: satellite and instrument
parameters, Technical report UB-SWG-012
(In the text)
- Kim, A. G., Akerlof, C.
W., Aldering, G., et al. 2002, Proc. SPIE, 4836, 53 [NASA ADS] (In the text)
- Lindegren, L.
1998, Astrometric precision of GAIA (2), Technical report
SAG-LL-017
(In the text)
- Louys, M., Starck, J.
L., Mei, S., et al. 1999, A&AS, 136, 579 [NASA ADS] (In the text)
- Mallat, S. 1999, A
wavelet tour of the signal processing (New York: Academic
Press)
(In the text)
- Martin, F.,
Bijaoui, A., Touma, H., et al. 1986, Proc. SPIE, 189
(In the text)
- Massart, B. 2000,
Compression et restauration d'images pour la mission GAIA, Rapport
de stage, OCA
(In the text)
- Mellier, Y.,
& Van Waerbeke, L. 2002, Class. Quantum Grav., 19, 3505 [NASA ADS] [CrossRef] (In the text)
- Myers, A. D., Outram,
P. J., Shanks, T., et al. 2003, MNRAS, 342, 467 [NASA ADS] [CrossRef] (In the text)
- Murtagh, F.,
Starck, J. L., & Bijaoui, A. 1994, A&AS, 112, 179 [NASA ADS] (In the text)
- Parnaudeau,
J. 1999, Étude de la compression d'images pour la mission
spatiale GAIA, Rapport de fin d'étude, OCA/ISIMA
(In the text)
- Perryman, M. A.
C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369,
339 [EDP Sciences] [NASA ADS] (In the text)
- Richter, G. M.
1991, 3th ESO/ST-ECF Data Analysis workshop, 37
(In the text)
- Starck, J. L.,
Murtagh, F., & Bijaoui, A. 1998, Image processing and data
analysis. The multiscale approach (Cambridge University Press)
(In the text)
- Stone, H. S., Tao,
B., & McGuire, M. 2000, Analysis of image registration noise
due to rotationally dependent aliasing, submitted Visual
Communication and Image Representation
(In the text)
- Urban, S. E, Corbin,
T. E., Wycoff, G. L., et al. 1998, AJ, 115, 1212 [NASA ADS] [CrossRef] (In the text)
- Urban, S. E, Corbin,
T. E., Wycoff, G. L., et al. 2001, BAAS, 33(4), 1494
(In the text)
- Vaccari, M. 2000,
GAIA Galaxy Survey, simulated observation of galaxies with ESA GAIA
satellite, Master Thesis
(In the text)
- Weimer, T. 1987,
Mapping the sky, past heritage and future directions, IAU Symp.,
133, 29
(In the text)
- White, R., Postman,
M., & Lattanzi, M. 1992, in Digitized Optical Sky Surveys
(Kluwer), 167
(In the text)
- Yasuda, N.,
Fukugita, M., Narayanan, V. K., et al. 2001, AJ, 122, 1104 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics*[width=7cm,clip]{0201fig1.eps} \end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg15.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0201fig2.ps}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg19.gif)
![\begin{figure}
\par\resizebox{7.3cm}{7.3cm}{\includegraphics[clip]{0201fig3.eps}}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,height=7.2cm,clip]{0201f4a.eps}\par\includegraphics[width=7.2cm,height=7.2cm,clip]{0201f4b.eps}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg29.gif)
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics*[clip]{0201fig5.eps}}\end{figure}](/articles/aa/full/2004/41/aa0201-04/Timg30.gif)
