A&A 426, 279-296 (2004)
DOI: 10.1051/0004-6361:20041098
G. Perrin 1 - S. T. Ridgway 1,2 - B. Mennesson 3 - W. D. Cotton 4 - J. Woillez 1,5 - T. Verhoelst 1,6 - P. Schuller 7 - V. Coudé du Foresto 1 - W. A. Traub 7 - R. Millan-Gabet 8 - M. G. Lacasse 7
1 - Observatoire de Paris, LESIA, UMR 8109, 92190 Meudon, France
2 -
National Optical Astronomy Observatories, Tucson, AZ 85726-6732, USA![]()
3 - Jet Propulsion Laboratory, California Institute of Technology, MS 306-388, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
4 - National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903-2475, USA
5 - Keck Observatory, 65-1120 Mamalahoa Highway, Kamuela,
HI 96743, USA
6 - Sterrenkunde Leuven, Leuven, Belgium
7 - Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA
8 - Caltech/Michelson Science Center, Pasadena, CA 91125, USA
Received 15 April 2004 / Accepted 15 June 2004
Abstract
We have observed Mira stars with the FLUOR beamcombiner on the IOTA interferometer in narrow bands around ![]() m wavelength. We find systematically larger diameters in bands contaminated by water vapor and CO. The visibility measurements can be interpreted with a model comprising a photosphere surrounded by a thin spherical molecular layer. The high quality of the fits we obtain demonstrates that this simple model accounts for most of the star's spatial structure. For each star and each period we were able to derive the radius and temperature of the star and of the molecular layer as well as the optical depth of the layer in absorption and continuum bands. The typical radius of the molecular layer is
m wavelength. We find systematically larger diameters in bands contaminated by water vapor and CO. The visibility measurements can be interpreted with a model comprising a photosphere surrounded by a thin spherical molecular layer. The high quality of the fits we obtain demonstrates that this simple model accounts for most of the star's spatial structure. For each star and each period we were able to derive the radius and temperature of the star and of the molecular layer as well as the optical depth of the layer in absorption and continuum bands. The typical radius of the molecular layer is
![]() with a temperature ranging between 1500 and 2100 K. The photospheric temperatures we find are in agreement with spectral types of Mira stars. Our photospheric diameters are found smaller than in previous studies by several tens of percent. We believe previous diameters were biased by the use of unsuited geometrical models to explain visibilities. The conclusions of this work are various. First, we offer a consistent view of Mira stars over a wide range of wavelengths. Second, the parameters of the molecular layer we find are consistent with spectroscopic studies. Third, from our diameter measurements we deduce that all Mira stars are fundamental mode pulsators and that previous studies leading to the conclusion of the first-overtone mode were biased by too large diameter estimates.
with a temperature ranging between 1500 and 2100 K. The photospheric temperatures we find are in agreement with spectral types of Mira stars. Our photospheric diameters are found smaller than in previous studies by several tens of percent. We believe previous diameters were biased by the use of unsuited geometrical models to explain visibilities. The conclusions of this work are various. First, we offer a consistent view of Mira stars over a wide range of wavelengths. Second, the parameters of the molecular layer we find are consistent with spectroscopic studies. Third, from our diameter measurements we deduce that all Mira stars are fundamental mode pulsators and that previous studies leading to the conclusion of the first-overtone mode were biased by too large diameter estimates.
Key words: techniques: interferometric - stars: AGB and post-AGB - stars: fundamental parameters - stars: mass-loss - infrared: stars
Depending on their initial mass on the Main Sequence, stars will evolve differently. Following a similar giant branch evolution, the evolutionary tracks split - stars with masses lower than 5 to 8 ![]() ,
depending on evolution models, ascend the more luminous Asymptotic Giant Branch (AGB) and become unstable to hydrodynamic pulsations. AGB stars with large and regular V magnitude variability (100-1000 day periods and greater than 2.5 mag amplitudes) are classified as Mira stars of which the prototype is Mira itself. Mira stars are molecule and dust factories. Mass loss has become far more efficient (up to a few
,
depending on evolution models, ascend the more luminous Asymptotic Giant Branch (AGB) and become unstable to hydrodynamic pulsations. AGB stars with large and regular V magnitude variability (100-1000 day periods and greater than 2.5 mag amplitudes) are classified as Mira stars of which the prototype is Mira itself. Mira stars are molecule and dust factories. Mass loss has become far more efficient (up to a few
![]() /yr) compared to, for example, solar type stars on the Main Sequence (
/yr) compared to, for example, solar type stars on the Main Sequence (
![]() /yr). Circumstellar shells are ubiquitous around AGB stars, becoming dense in Mira stars and extremely dense (to the point that the star may be completely hidden by the dust shell) in the related OH/IR and extreme carbon stars (van Loon et al. 1998). As a consequence the environment of Mira stars is very complex. The next stage of their evolution is a protoplanetary nebula, in which some of the products of mass-loss are illuminated by the now-hot star's ionizing radiation. AGB stars contribute more than 75% of the mass loss in the galaxy with an estimated galactic rate of
/yr). Circumstellar shells are ubiquitous around AGB stars, becoming dense in Mira stars and extremely dense (to the point that the star may be completely hidden by the dust shell) in the related OH/IR and extreme carbon stars (van Loon et al. 1998). As a consequence the environment of Mira stars is very complex. The next stage of their evolution is a protoplanetary nebula, in which some of the products of mass-loss are illuminated by the now-hot star's ionizing radiation. AGB stars contribute more than 75% of the mass loss in the galaxy with an estimated galactic rate of
![]() yr. These stars are thus fundamental to the evolution of galactic abundances, and supply the heavier elements required for the formation of earth-like planets and an interesting terrestrial biology. The reader is referred to the more detailed review of mass loss in AGB stars by Willson (2000).
yr. These stars are thus fundamental to the evolution of galactic abundances, and supply the heavier elements required for the formation of earth-like planets and an interesting terrestrial biology. The reader is referred to the more detailed review of mass loss in AGB stars by Willson (2000).
The field of cool evolved stars is therefore very rich and is addressed with many different techniques which share many goals. Although Mira stars have been modeled, their inner structure at the interface between the photosphere and the near environment has not been clearly disclosed yet by modern observing techniques. Radio and millimetric observations are sensitive to the molecular environment, primarily at tens to thousands of stellar radii. Dust is imaged in the thermal infrared as close as a few stellar radii. The high mass loss rates are suggestive of a dense, extended atmosphere, but high angular resolution measurements in the visible-near IR, which offer ample angular resolution to measure the sizes of nearby AGB stars, have yielded inconclusive and even confusing results for Mira stars.
Apparent Mira sizes are large in the blue-visible, smaller in the near-IR, and then large again in the thermal IR. Although this trend might appear consistent with the trend of opacity (and a continuous opacity minimum at 1.6 microns between H- bound-free and free-free absorptions) the obvious prominence of strong molecular bands in the Mira spectra, and the sheer scale of the size differences, suggests that the observations are revealing something more complex.
Several measurements show that the light distributions of Mira stars are not well represented as simple limb-darkened disks. The shortest wavelength measurements are more compatible with Gaussian intensity distributions (Young et al. 2000; Hofmann et al. 2000, 2001; Tuthill et al. 1999). Measurements in the K band on R Leo (Perrin et al. 1999) depart from both Gaussian and limb-darkened disk geometries. In particular, the displacement of the first zero of the K-band visibility to higher spatial frequency suggested that the stellar diameter was significantly smaller than would be estimated from the mid-spatial frequency visibilities alone and that a molecular environment could account for the shape of the visibility curve. The smaller stellar diameter favored a fundamental mode pulsation model. However, the nature of the stellar light distribution and the relation of the K-band to visible and thermal IR diameters remained mysterious. While numerical dynamical models capture some of the character of the observed visibilities, they do not yet offer a consistent interpretation of the measurements. More recent observations of Mira with VINCI in the K band (October 22 and 23, 2001) have confirmed the departure from classical geometries (Woodruff et al. 2004).
Mennesson et al. (2002) found a strong diameter increase from K to L band in Mira stars, but not in other AGB stars, and proposed and explored a simple empirical model in which a central stellar disk (the "star'') was surrounded by a somewhat larger (25-100% depending on the case), partially opaque shell. In this model, the varying appearance of the star with wavelength could be understood as due in first order to the varying transparency of the shell and the wavelength dependence of the Planck function. More recently, Perrin et al. (2004) have shown that this model adapts gracefully to account for the diameter wavelength trends in the supergiant, ![]() Ori. Although not an AGB star,
Ori. Although not an AGB star, ![]() Ori has a low-density and extended atmosphere which appears as an intermediate case, less extended and less dense than the Miras.
Ori has a low-density and extended atmosphere which appears as an intermediate case, less extended and less dense than the Miras.
According to this interpretation of the angular measurements, Mira stars are hotter than thought and have smaller diameters than previously measured. Confirmation of this effect would shift the center of gravity of the debate on pulsation modes of Mira stars strongly towards the fundamental mode thus reconciling theory and observations on this point.
In order to go further in this interpretation we have decided to observe the largest and brightest Mira stars in narrow bands near 2 microns wavelength corresponding to strong CO and H2O molecular bands, with adjacent "continuum'' bands. Preliminary versions of this study have been presented in conferences (e.g. Perrin 2003c). The interpretation of these observations is the subject of this paper. After describing observations (Sect. 2) and the procedure to get photometric data contemporaneous with our observations (Sect. 3), we describe the model used in this paper in Sect. 4. Interpretation of our visibilities with this model is detailed in Sect. 5. We show in Sect. 6 that our interpretation is compatible with other independent observations. The issue of pulsation modes is discussed in Sect. 7 and the general consequences of our study are presented in Sect. 8.
The stars in our sample are among the brightest and largest (in apparent diameter) Mira variables seen from the Northern hemisphere. They have been observed in October 2000, November 2001 and May 2002 at the IOTA (Infrared-Optical Telescope Array) interferometer located at the Smithsonian Institution's Whipple Observatory on Mount Hopkins, Arizona (Traub 1998). Several baselines of IOTA have been used to sample visibilities at different spatial frequencies. The data have been acquired with FLUOR (Fiber Linked Unit for Optical Recombination) in the version described by Coudé du Foresto et al. (1998). FLUOR is the precursor of the now well-known VLTI/VINCI (Kervella et al. 2000). Beam combination is achieved by a single-mode fluoride glass triple coupler optimized for the K band. The fibers spatially filter the wavefronts corrugated by the atmospheric turbulence. The phase fluctuations are traded against photometric fluctuations which are monitored for each beam to correct for them a posteriori. The accuracy on visibility estimates measured by FLUOR is usually on the order of 1% for most sources and can be as good as 0.2% (Perrin et al. 2004). The triple coupler has four outputs (two interferometric and two photometric) which were focused on a NICMOS3 array developed by Millan-Gabet et al. (1999) and operated with frame rates ranging from 500 up to 2000 Hz.
| Filter |
|
FWHM | R | T |
| ( |
( |
|||
| K203 | 2.03 | 0.10 | 0.67 | 0.33 |
| K215 | 2.15 | 0.10 | 0.53 | 0.47 |
| K222 | 2.22 | 0.10 | 0.56 | 0.44 |
| K239 | 2.39 | 0.10 | 0.78 | 0.22 |
Observations were carried out in narrow bands with filters specially designed for this project. We have used four filters whose characteristics are defined in Table 1 and transmissions are plotted in Fig. 1. They are named K203, K215, K222 and K239 where the three digits characterize the central wavelength. The two continuum filters K215 and K222 sample the maximum transmission region of the K band. The K203 (H2O bands) and K239 (H2O and CO bands) sample the edges of the K band where stellar flux is attenuated by the poorer transmission of the earth'satmosphere due to the absorption by water. It is to be noted that the splitting ratios of the couplers are well balanced in the center of the band and poorly balanced (though still fully calibrated) at the edges (see Table 1). For these reasons, the interferometric sensitivity is always better in the continuum bands compared to the molecular bands. The stellar flux is reduced even further for Mira stars with their own strong molecular absorption. This is the reason why the accuracy on visibilities is usually better in the K215 and K222 filters when the dominant noise is detector noise.
Observations of sources have most often been bracketed by observations of calibrators. The characteristics of calibrators are listed in Table 2. They are mostly bright giant and supergiant stars with spectral types as late as M5 III. The diameter of ![]() CMi was recently measured interferometrically by Kervella et al. (2004). Their value (
CMi was recently measured interferometrically by Kervella et al. (2004). Their value (
![]() mas) is compatible with our photometric estimate. The estimates of transfer functions established with the smallest and the largest calibrators are consistent thus justifying the use of sources with diameters as large as 14 mas. None of the calibrators is a large amplitude variable and it is legitimate to assume that band-to-band diameter variations are far smaller than in Miras. Consequently, we are confident that the strong effects reported in this paper cannot be attributed to calibrators.
mas) is compatible with our photometric estimate. The estimates of transfer functions established with the smallest and the largest calibrators are consistent thus justifying the use of sources with diameters as large as 14 mas. None of the calibrators is a large amplitude variable and it is legitimate to assume that band-to-band diameter variations are far smaller than in Miras. Consequently, we are confident that the strong effects reported in this paper cannot be attributed to calibrators.
| HD number | Source | Spectral type | Uniform disk |
| name | diameter (mas) | ||
| HD 6860 | |
M 0 III |
|
| HD 9927 | 51 And | K3 III |
|
| HD 18884 | |
M 1.5 III |
|
| HD 42995 | |
M 3 III |
|
| HD 44478 | |
M 3 III |
|
| HD 48329 | |
G8 Ib |
|
| HD 61421 | |
F5 IV |
|
| HD 62509 | |
K0 IIIb |
|
| HD 81797 | |
K3 II-III |
|
| HD 130144 | HR 5512 | M 5 III |
|
| HD 140573* | |
K2 IIIb |
|
| HD 146051* | |
M 0.5 III |
|
| HD 183439* | |
M 0 III |
|
| HD 187076* | |
M 2 II |
|
| HD 197989 | |
K0 III |
|
| HD 213310 | 5 Lac | M 0 II |
|
|
The log of the observations is given in Table 3.
The phases have been derived from the visual magnitudes of the AFOEV![]() . In general all narrow bands have been observed. The spatial frequency vector is given in polar coordinates comprising the azimuth and the modulus listed under Spatial Frequency. Fringe contrasts have been derived with the procedure explained in Coudé du Foresto et al. (1997). The bias in visibility estimates due to photon noise has been removed following Perrin (2003a). The expected visibility of the calibrators is computed at the time they were observed. The instrumental visibility is then interpolated at the time when the science targets have been observed. Division of the fringe contrast of the science targets by the interpolated instrumental visibility provides the final visibility estimate. Correlations in fringe contrast and transfer function estimates are taken into account in the computation of error bars. The whole calibration procedure has been published in Perrin (2003b).
. In general all narrow bands have been observed. The spatial frequency vector is given in polar coordinates comprising the azimuth and the modulus listed under Spatial Frequency. Fringe contrasts have been derived with the procedure explained in Coudé du Foresto et al. (1997). The bias in visibility estimates due to photon noise has been removed following Perrin (2003a). The expected visibility of the calibrators is computed at the time they were observed. The instrumental visibility is then interpolated at the time when the science targets have been observed. Division of the fringe contrast of the science targets by the interpolated instrumental visibility provides the final visibility estimate. Correlations in fringe contrast and transfer function estimates are taken into account in the computation of error bars. The whole calibration procedure has been published in Perrin (2003b).
| Star | Phase | J | H | K | L |
| Mira | 0.01 |
|
|
|
|
| 0.20 |
|
|
|
|
|
| R Leo | 0.80 |
|
|
|
|
| 0.76 |
|
|
|
|
|
| 0.24 |
|
|
|
|
|
| U Ori | 0.83 |
|
|
|
|
| 0.91 |
|
|
|
|
|
| T Cep | 0.67 |
|
|
|
Photometry in J, H, K and L has been established from the measurements of Whitelock et al. (2000a). We directly used the published magnitudes when they were measured at the same time as our own visibility measurements. We have otherwise sampled the periodic magnitude curves at the phase when the source was observed. Photometric measurements have generally been taken at different cycles which allows to derive an estimate of the uncertainty of the magnitude. In the case of ![]() Cyg where photometric data are too sparse to yield a reliable estimate we have used the average uncertainties measured on R Leo and Mira. No photometric data were available in Whitelock et al. (2000a) for T Cep. We have used the photometric data of Smith et al. (2002) measured at the same phase and also applied the Mira and R Leo uncertainties. The magnitudes we have used in this paper are listed in Table 4. We have used the SAAO filter transmissions published in Glass (1973) to compute synthetic magnitudes in Sect. 4.2.
Cyg where photometric data are too sparse to yield a reliable estimate we have used the average uncertainties measured on R Leo and Mira. No photometric data were available in Whitelock et al. (2000a) for T Cep. We have used the photometric data of Smith et al. (2002) measured at the same phase and also applied the Mira and R Leo uncertainties. The magnitudes we have used in this paper are listed in Table 4. We have used the SAAO filter transmissions published in Glass (1973) to compute synthetic magnitudes in Sect. 4.2.
As will be illustrated in the following, the observations clearly require a wavelength dependence of apparent diameter. Further, the visibility data are not compatible with classical limb-darkened disk models. We have already measured chromatic diameters between the K and the L bands (Mennesson et al. 2002; Chagnon et al. 2002). It was possible to account for those observations with a model in which a photosphere was surrounded by an emissive and absorbing layer a few radii above the stellar surface. The nature of the layer was assumed to be
![]() as this molecule had also been detected spectroscopically. The narrow band observations reported here will allow us to identify some of the sources of opacity. Because of the large number of parameters and data we have chosen a simpler model than the one used in Mennesson et al. (2002). This model has an analytical solution for the radiative transfer calculations which makes the parameter search quicker and the computation of error bars possible. The model is spherically symmetric. Although some asymmetries have been found on Mira stars (Quirrenbach et al. 1992; Lopez et al. 1997; Hofmann et al. 2000) they have been measured at wavelengths outside of the maximum of flux emission where sensitivity to the star environment is larger (TiO bands and dust). Besides, it is clear in our case, as will be demonstrated, that the chromaticity of visibility curves can be explained by the physical properties of the object rather than by a particular symmetry. This is why we have privileged spherical symmetry. We have also preferred to use an ad-hoc geometrical model rather than a model derived from hydrodynamical calculations in order to provide physical parameters that are then useful to hydrodynamical calculations. Other types of models will be discussed in Sect. 8.
as this molecule had also been detected spectroscopically. The narrow band observations reported here will allow us to identify some of the sources of opacity. Because of the large number of parameters and data we have chosen a simpler model than the one used in Mennesson et al. (2002). This model has an analytical solution for the radiative transfer calculations which makes the parameter search quicker and the computation of error bars possible. The model is spherically symmetric. Although some asymmetries have been found on Mira stars (Quirrenbach et al. 1992; Lopez et al. 1997; Hofmann et al. 2000) they have been measured at wavelengths outside of the maximum of flux emission where sensitivity to the star environment is larger (TiO bands and dust). Besides, it is clear in our case, as will be demonstrated, that the chromaticity of visibility curves can be explained by the physical properties of the object rather than by a particular symmetry. This is why we have privileged spherical symmetry. We have also preferred to use an ad-hoc geometrical model rather than a model derived from hydrodynamical calculations in order to provide physical parameters that are then useful to hydrodynamical calculations. Other types of models will be discussed in Sect. 8.
The model we have chosen is close to the one used in Mennesson et al. (2002). Instead of having an extended layer around the star, the layer is compact. The star is modeled by a stellar surface of diameter
![]() which emits as a blackbody of temperature
which emits as a blackbody of temperature ![]() .
It is surrounded by a spherical layer of diameter
.
It is surrounded by a spherical layer of diameter
![]() with no geometrical thickness. The layer is characterized by its temperature
with no geometrical thickness. The layer is characterized by its temperature
![]() and its optical depth
and its optical depth
![]() .
The layer absorbs the radiation emitted by the star and re-emits like a blackbody. Scattering is neglected for our range of wavelengths. The space between the layer and the stellar photosphere is empty. Figure 2 gives a sketch of the star+layer model. Limb darkening of the central star is neglected, but the composite model has interesting brightness variations, more complex than classical limb darkening.
.
The layer absorbs the radiation emitted by the star and re-emits like a blackbody. Scattering is neglected for our range of wavelengths. The space between the layer and the stellar photosphere is empty. Figure 2 gives a sketch of the star+layer model. Limb darkening of the central star is neglected, but the composite model has interesting brightness variations, more complex than classical limb darkening.
![\begin{figure}
\par\includegraphics[angle=90,width=7cm,clip]{1098f2.eps} \end{figure}](/articles/aa/full/2004/40/aa1098/Timg82.gif) |
Figure 2:
Model of the star surrounded by a thin molecular layer. |
The analytical expression of the model is given by the equations below:
| |
= | (1) | |
![\begin{displaymath}I(\lambda,\theta)=B(\lambda,T_{{\rm layer}})\left[1-\exp(-2\tau(\lambda)/\cos(\theta))\right]\end{displaymath}](/articles/aa/full/2004/40/aa1098/img87.gif) |
(2) |
![\begin{displaymath}\chi^{2}=\sum_{i=1}^{N}\left[\frac{V_{i}^{2}-M(\O_{\star}, \O...
...m layer}}, \tau_{\lambda_{i}} ;S_{i})}{\sigma_{i}}\right]^{2}
\end{displaymath}](/articles/aa/full/2004/40/aa1098/img90.gif) |
(3) |
The hyper-surface defined by the ![]() is not convex in the parameter space and many local minima occur. Also, the minimum might be badly defined and may be very sensitive to individual measurements.
is not convex in the parameter space and many local minima occur. Also, the minimum might be badly defined and may be very sensitive to individual measurements.
We have used the following strategy to find the best parameter estimates. We first have noticed that for a given set of diameter and temperature values the hyper-surface is close to convex leading to a fast convergence of the Levenberg-Marquardt algorithm towards the optimum optical depths. On the other hand, the temperatures are not well constrained by just the interferometric data. The simple reason for this is that the visibilities are not absolute flux measurements but are relative to the zero spatial frequency. The visibility data do not therefore constrain the total flux of the model. In our case they are just sensitive to the relative flux of the star and of the layer. As a consequence, the locus for the optimum set of temperatures is not a single low point but a trough. The temperatures of the star and of the layer are coupled and inaccurate. We therefore first have constrained the diameters of the photosphere and of the layer by computing a 2D grid of ![]() values. Each
values. Each ![]() is the result of the minimization with the parameters left, temperatures and optical depths, using a Levenberg-Marquardt algorithm. The first guess temperatures are 2000 and 3000 K for the layer and photosphere respectively. The first guess optical depths are 0.1, 0.5, 0.5 and 0.1 for the K203, K215, K222 and K239 filters respectively. The first solution found for the diameters is generally very well defined as the
is the result of the minimization with the parameters left, temperatures and optical depths, using a Levenberg-Marquardt algorithm. The first guess temperatures are 2000 and 3000 K for the layer and photosphere respectively. The first guess optical depths are 0.1, 0.5, 0.5 and 0.1 for the K203, K215, K222 and K239 filters respectively. The first solution found for the diameters is generally very well defined as the ![]() is locally convex.
is locally convex.
In a second step, the diameters are set to the values found by this procedure. A 2D grid of ![]() values is built in temperature space, the optimum optical depths being computed with the Levenberg-Marquardt algorithm. As mentioned, the locus of best parameters is a trough if the number of visibilities is larger than the number of free parameters and if the visibility function is adequately sampled. The optimum set of temperatures is determined by applying a photometric constraint. A synthetic K magnitude is computed from the model parameters and solutions which are not compatible with the measured photometry (to within its uncertainty, see Sect. 3) are excluded. L band photometry is also used to set the photometric constraint when L band visibility data are available. The intersection of the temperature trough (defined as the area to within the range
values is built in temperature space, the optimum optical depths being computed with the Levenberg-Marquardt algorithm. As mentioned, the locus of best parameters is a trough if the number of visibilities is larger than the number of free parameters and if the visibility function is adequately sampled. The optimum set of temperatures is determined by applying a photometric constraint. A synthetic K magnitude is computed from the model parameters and solutions which are not compatible with the measured photometry (to within its uncertainty, see Sect. 3) are excluded. L band photometry is also used to set the photometric constraint when L band visibility data are available. The intersection of the temperature trough (defined as the area to within the range
![]() to
to
![]() with respect to the bottom of the trough) and of the photometry-compliant area yields the best set of temperatures and their uncertainties. Eventually the best solution is computed by doing a global fit with the parameters found in the two previous steps as first guess parameters.
with respect to the bottom of the trough) and of the photometry-compliant area yields the best set of temperatures and their uncertainties. Eventually the best solution is computed by doing a global fit with the parameters found in the two previous steps as first guess parameters.
This procedure has proved to converge for all the cases studied here.
The visibilities we have obtained for all Miras are clearly wavelength dependent. The general shapes of the visibility functions are in agreement with what we have measured in 1997 on R Leo (Perrin et al. 1999). They are very different from a simple limb-darkened disk visibility model and are not Gaussian as is often the case at shorter wavelengths, especially in the visible. We generally find a characteristic plateau or slowly decreasing function around 20% visibility. As shown in Mennesson et al. (2002) this effect can be accounted for by a spherical layer around the star and above the photosphere.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{1098f3.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg94.gif) |
Figure 3: Fit of the 1997 K band (triangles) and 2000 L band (circles) data of R Leo. |
| Model | Mennesson et al. (2002) | This paper |
|
|
10 | 10.5 |
|
|
15-27 | 23.65 |
| 2700 | 2700 | |
|
|
<1730 | 1300 |
|
|
|
1.04 |
|
|
|
0.81 |
| Year | 2001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Year | 2000 | 2001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Year | 2002 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Year | 2000 | 2001 |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Year | 2001 | 2002 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{1098f4a.eps}\hspace*{4mm}
\includegraphics[angle=-90,width=7.7cm,clip]{1098f4b.eps} \end{figure}](/articles/aa/full/2004/40/aa1098/Timg166.gif) |
Figure 4: Fit and synthetic spectrum based on the November 2001 narrow band and November 2000 L band data of R Leo. Photometric data are from Whitelock et al. (2000a). An average layer optical depth of 1 has been used to compute the synthetic spectrum. |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1098f5a.eps}\hsp...
...ce*{3mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1098f5d.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg167.gif) |
Figure 5: Fit and synthetic spectrum based on the October 2000 narrow band and November 2000 L band data of Mira ( top). Fit and synthetic spectrum based on the November 2001 narrow band data of Mira ( bottom). Photometric data are from Whitelock et al. (2000a). Average layer optical depths of 0.10 and 0.40 have been used to compute the synthetic spectra for the 2000 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{1098f6a.eps}\hspace*{3mm}
\includegraphics[angle=-90,width=7.8cm,clip]{1098f6b.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg168.gif) |
Figure 6: Fit and synthetic spectrum based on the May 2002 narrow band data of T Cep. Photometric data are from Smith et al. (2002). An average layer optical depth of 0.20 has been used to compute the synthetic spectrum. |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{1098f7a.eps}\hsp...
...ce*{4mm}
\includegraphics[angle=-90,width=7.7cm,clip]{1098f7d.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg169.gif) |
Figure 7: Fit and synthetic spectrum based on the October 2000 narrow band and November 2000 L' band data of U Ori ( top). Fit and synthetic spectrum based on the November 2001 narrow band data of U Ori ( bottom). Photometric data are from Whitelock et al. (2000a). Average layer optical depths of 0.85 and 0.95 have been used to compute the synthetic spectra for the 2000 and 2001 data, respectively. |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{1098f8a.eps}\hspac...
...pace*{3mm}
\includegraphics[angle=-90,width=8cm,clip]{1098f8d.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg170.gif) |
Figure 8:
Fit and synthetic spectrum based on the November 2001 ( top) and May 2002 ( bottom) narrow band data of |
For each observed filter, the observed spatial frequencies constrain the visiblity and its first and second derivatives, but for each filter the model has only one added parameter - the layer opacity in that filter. The goodness of fit of the multi-filter data to the complex family of visibility model curves strongly suggests that the model captures the essential geometric and temperature dependence (through the Planck function) of the brightness distribution.
We note that the model visibilities come to a null which is characteristic of a hard-edged light distribution, thus giving a quantitative idea of the ratio between the apparent diameter and the diameter of the photosphere, up to a factor of 2 in K239 and L'. The larger optical depths measured in the molecular bands where the apparent diameter of the star is larger confirms the gaseous nature of the layer which very certainly contains water vapor and CO (as confirmed spectroscopically - Hinkle et al. 1984). Generally (except for U Ori in October 2000), the similar visibility values obtained in the K region molecular bands and in L' confirm the gaseous nature of the layer detected in L' for R Leo as suggested by Mennesson et al. (2002). The optical depths fitted in K203 and K239 are larger than in the continuum and usually close and the difference in apparent size of the star in these two filters is due to the decreasing contrast between the Planck functions of the photosphere and of the layer as a function of wavelength.
The radii and temperatures found for the stars are very interesting. Firstly, the photospheric diameter estimates are the smallest ever reported for these stars at any wavelength as previous simplistic interpretation of the raw visibilities led to larger estimates. Our modeling shows that the classical interpretation of apparent diameters results in a strong bias for Mira stars. This confirms our earlier hypothesis of Perrin et al. (1999). Secondly, the high temperatures we have obtained are consistent with the spectral types of the stars: M0 to M7 (Ridgway et al. 1980; Perrin et al. 1998, but see the discussion of back-warming, below), and are much higher than the temperatures used so far to model their photospheres. Temperatures are consistent with excitation temperatures observed spectroscopically for R Leo, Mira, T Cep and ![]() Cyg (Hinkle et al. 1984).
Cyg (Hinkle et al. 1984).
For each star we have compared photometric data to a synthetic spectrum computed from the parameters fitted to the interferometric data and extrapolated from the UV to the mid-infrared. Neither dust nor spectral features are modeled here - the underlying flux distribution is Planckian. The dashed line is the stellar flux attenuated by the absorbing layer. The short dashed line is the flux emitted by the layer and the continuous line is the total flux. We have used the same optical depth for all wavelengths to simulate the whole spectrum - that is, no wavelength dependence of the layer - surely a gross simplification. There is a general clear consistency in our approach between the photometric and visibility data in the K and L bands (except for some cases, see below). The simple photometric model apparently reproduces quite satisfactorily the J band photometry but fails to account for the H band data. We note that more sophisticated atmospheric models have a similar difficulty (Lobel et al. 2000). The agreement with J may come from the right range found for the photosphere temperature at a wavelength where the layer radiation tends to be very small and which is free of strong absorber bands like TiO and therefore a near "continuum''. The excess of predicted flux at H may point to some extra absorbers or to a different opacity in this region. The H band is weakly contaminated by H2O compared to K but is exactly centered on the CO second overtone bands whereas CO and H2O absorptions are attenuated by the edge of the
K band filter. The H gap could therefore be explained if absorption was mainly due to CO. The CO layer could have different characteristics such as being closer to the photosphere hence hotter and optically thicker, a closer layer being less diluted. CO can form at larger temperatures than H2O and can therefore be found closer. This would be compatible with the systematically larger ![]() in K239, a mean of the H2O and CO optical depths. A similar interferometric study in the H band would readily test this suggestion.
in K239, a mean of the H2O and CO optical depths. A similar interferometric study in the H band would readily test this suggestion.
The discussion of the nature of the layer is still speculative but the observed and model visibilities and photometry indicate a layer opacity which is stronger in K and L than in H, and which is stronger in prominent H2O and CO bands. As in most of the model results, the temperature derived for the layer is significantly below the grey body equilibrium temperature at the corresponding radial distance. This appears qualitatively consistent with a composition for which mid-IR opacity is much higher than near-IR opacity, providing a surface cooling effect. Such an effect would depend on the relative importance of radiative and collisional heating and possible non-LTE effects, hence would be strongly density dependent and could vary from star to star and phase to phase - as it appears to do.
In the discussion below, we point out a number of discrepancies in the model fits. These may arise from the extreme simplicity of the model. Most could be resolved with a few additional model parameters, such as separate layers or temperatures for different bands - however, as the fits show, these are probably second order effects and we have preferred the clarity of discussing only the single thin shell, with consistent treatment of all stars.
The K band data were acquired in November 2001 at phase 0.80. The L band data were acquired a cycle earlier at phase 0.63. The two phases are close and we make the assumption that the star characteristics are the same for these two phases although at two different cycles. The quality of the fit is very satisfying with a reduced ![]() of 12.73 (bias detection probability of
of 12.73 (bias detection probability of ![]() ).The best quality is obtained in the continuum bands whereas the highest frequency point in the K203 filter lies a few sigma below the model visibility.
We have used an average optical depth of 1 to simulate the whole spectrum.
The analysis performed with the layer model confirms our earlier hypothesis of Perrin et al. (1999) and our diameter for the photosphere confirms what was then a hypothetical value.
).The best quality is obtained in the continuum bands whereas the highest frequency point in the K203 filter lies a few sigma below the model visibility.
We have used an average optical depth of 1 to simulate the whole spectrum.
The analysis performed with the layer model confirms our earlier hypothesis of Perrin et al. (1999) and our diameter for the photosphere confirms what was then a hypothetical value.
We have observed Mira twice in narrow bands in October 2000 (phase 0.01) and in November 2001 (phase 0.20). The set of October 2000 data is complemented by L band measurements of November 2000 at phase 0.09. Unfortunately, only one baseline was measured in October 2000. The quality of fits is very satisfying with reduced ![]() of 1.56 and 6.68 for the 2000 and 2001 data respectively yielding bias detection probabilities of 18.4 and 75.4%. The poor
of 1.56 and 6.68 for the 2000 and 2001 data respectively yielding bias detection probabilities of 18.4 and 75.4%. The poor ![]() for
the 2001 data is due to one of the K203 visibilities.
for
the 2001 data is due to one of the K203 visibilities.
The synthetic spectra have been computed with average optical depths of 0.10 and 0.40 for the 2000 and 2001 data respectively. It is very encouraging that the L band flux can be so well predicted in 2001 although no interferometric data were available possibly showing that the molecular layer is well determined with the K band measurements and that the major contributors are water vapor and possibly carbon monoxide.
The Mira data are still more interesting than the R Leo data because they were obtained a year apart and at slightly different phases. Fitting these data with a classical uniform disk model would yield an increase of the apparent diameter of 20% between phase 0.01 and phase 0.20. We find a much smaller photospheric diameter increase of 3% which is not statistically significant and a contraction of the layer by 7.3% whereas its optical depth in the K203 and K239 filters has significantly increased. Instead of an apparent diameter increase between the two phases we believe that the layer opacity has increased thus mimicking the effect. This shows the necessity of a realistic model of the star to study its pulsation interferometrically. It casts into doubt previous reports of Mira star diameter variations, including our own (Perrin et al. 1999).
T Cep was observed once in May 2002 at phase 0.67. Measurements were taken at two spatial frequencies in the first lobe. T Cep is a case for which there are as many parameters for the model as data points, which must be recognized when considering the small ![]() of 1.52. Contrary to R Leo and Mira for which data were taken at larger spatial frequencies there are no inconsistent data with respect to the model. Because of the relatively small number of data points and limit to low spatial frequencies, the
of 1.52. Contrary to R Leo and Mira for which data were taken at larger spatial frequencies there are no inconsistent data with respect to the model. Because of the relatively small number of data points and limit to low spatial frequencies, the ![]() surface is chaotic making it difficult to compute errors. Our errors are therefore rough estimates. Temperatures are poorly constrained if only the
K magnitude is used. As studies of Mira and R Leo have shown the consistency of our modeling in K and L, we have included as a complement the L magnitude from Smith et al. (2002) in order to provide better constraints. The results are consistent with both Mira and R Leo. The layer is found at 1 photospheric radius above the photosphere. The optical depths we find are moderate. The synthetic spectrum was computed using an average optical depth of 0.20. No H band data is available. The agreement with the J and L band fluxes is not as good as it was for R Leo and Mira.
It is nevertheless relatively good in reproducing the general shape of the spectrum.
surface is chaotic making it difficult to compute errors. Our errors are therefore rough estimates. Temperatures are poorly constrained if only the
K magnitude is used. As studies of Mira and R Leo have shown the consistency of our modeling in K and L, we have included as a complement the L magnitude from Smith et al. (2002) in order to provide better constraints. The results are consistent with both Mira and R Leo. The layer is found at 1 photospheric radius above the photosphere. The optical depths we find are moderate. The synthetic spectrum was computed using an average optical depth of 0.20. No H band data is available. The agreement with the J and L band fluxes is not as good as it was for R Leo and Mira.
It is nevertheless relatively good in reproducing the general shape of the spectrum.
U Ori was measured at phase 0.83 in October 2000 and at phase 0.91 in November 2001. The October K band data were complemented with the November 2000 L' data of Chagnon et al. (2002) taken at phase 0.97. The 2000 data are quite sparse. Only one point is available in the K239 filter. Although very noisy, this visibility point is clearly inconsistent with the L' data. The same holds for the K203 data. This is reflected in the opacity differences in the model. The paucity of data for U Ori in 2000 has not allowed us to correctly determine error bars for the model parameters. The large optical depth we measure in the L' band is questionable.
Fortunately the visibility function was better sampled in 2001. The large reduced ![]() of 5.56 is indicative of the weakness of the model to exactly reproduce the apparent large curvature of the visibility function in the 40-60 cycles/arcsec range.
The differential behaviors between bands are clearly established and are more consistent with the findings on the stars previously studied here. It is remarkable that the parameters derived from the fit are globally consistent with those of the 2000 data fit except for optical depths which are systematically much lower even though at relatively close phase.
of 5.56 is indicative of the weakness of the model to exactly reproduce the apparent large curvature of the visibility function in the 40-60 cycles/arcsec range.
The differential behaviors between bands are clearly established and are more consistent with the findings on the stars previously studied here. It is remarkable that the parameters derived from the fit are globally consistent with those of the 2000 data fit except for optical depths which are systematically much lower even though at relatively close phase.
The synthetic spectral energy distribution based on the 2000 model parameters clearly fails to account for the photometric flux. The fit has not picked-up the right parameters. A larger photosphere temperature would have better fit the J band flux. However, we refrained from optimizing the visibility-driven model to match the photometry. Although computed with an average optical depth of 0.85 our predicted L band flux is very close to the measured one. The 2001 SED computed with an average optical depth of 0.95 agrees much better with the flux data.
U Ori is the only oxygen-rich Mira studied in this paper for which the use of a single layer to consistently explain both K and L' band data may be questionable. It is beyond the scope of this paper to address this issue. Yet, a hint may be found in the literature. Several authors have studied the masers around U Ori and found extended structures possibly arranged in a torus or with a bipolar symmetry as listed in Chapman et al. (1991). Reid & Menten (1997) and Cotton et al. (2004) have found radio sizes consistent with the near-infrared molecular layer sizes (see Sect. 9) and the extra structures identified in the radio domain in the case of U Ori may be the source of discrepancy with our model. The high L-band optical depth found for the layer in 2000 (3.28) is suggestive of a more extreme shell than in other stars observed, likely leading to greater discrepancies with the first-order model. As the 2001 data show, our model is successful in explaining the narrow band data in K.
![]() Cyg is the only S-type star studied in this program. We have observed it at phase 0.76 in November 2001 and at phase 0.24 in May 2002. The November 2001 observations were difficult because
Cyg is the only S-type star studied in this program. We have observed it at phase 0.76 in November 2001 and at phase 0.24 in May 2002. The November 2001 observations were difficult because ![]() Cyg was only observable for a few tens of minutes, a challenge for interferometers. Only a few visibility points are available. Yet, it is obvious from Fig. 8 that the visibilities have different properties than for oxygen-rich Miras. The optical depths in the two continuum bands are the same as Table 10 shows. The optical depth in the K203 band is close to the continuum bands, as might be expected since H2O, which dominates this filter in O-rich Miras, is not expected or observed to be abundant in the S-star atmosphere. The optical depth is much greater in the K239 band in which the star appears bigger. This is as expected, since the K239 filter catches the CO first overtone bands which are unusually strong in S Miras. If compared to oxygen-rich stars, the error in deriving diameters from wide-band visibilities is smaller. The visibility curve in all filters except K239 is relatively close to a uniform or limb-darkened disk. This is especially true for the May 2002 data. The diameter is still biased towards large values but the error is reduced to 20%.
Cyg was only observable for a few tens of minutes, a challenge for interferometers. Only a few visibility points are available. Yet, it is obvious from Fig. 8 that the visibilities have different properties than for oxygen-rich Miras. The optical depths in the two continuum bands are the same as Table 10 shows. The optical depth in the K203 band is close to the continuum bands, as might be expected since H2O, which dominates this filter in O-rich Miras, is not expected or observed to be abundant in the S-star atmosphere. The optical depth is much greater in the K239 band in which the star appears bigger. This is as expected, since the K239 filter catches the CO first overtone bands which are unusually strong in S Miras. If compared to oxygen-rich stars, the error in deriving diameters from wide-band visibilities is smaller. The visibility curve in all filters except K239 is relatively close to a uniform or limb-darkened disk. This is especially true for the May 2002 data. The diameter is still biased towards large values but the error is reduced to 20%.
It is remarkable that the optical depths in the continuum and "water vapor''-only bands are stable from phase 0.76 to phase 0.24. In the meantime, the optical depth in K239 (CO) has decreased. Also, the temperatures of the layer and of the photosphere have not significantly varied.
The somewhat simpler visibility curves, with likely well-defined zeroes, permit a more confident distinction between geometric pulsation and variable layer opacity. As opposed to the case of Mira in Sect. 5.3.2 it is clear here that the pulsation of the star and of the layer is measured and is not confused with an optical depth effect. By the way, the layer has turned less opaque during the expansion - this may result simply from geometric dilution, since the CO molecule is very stable in this temperature range.
Another difference with oxygen-rich Miras is the altitude of the layer which is 0.8 and 0.9 stellar radii above the photosphere.
Although the star looks simpler than the previous stars in K, the compact layer model fails to reproduce the SED in J and H and underestimates the L band magnitude. The spectra have been synthesized using the average optical depth of 0.20. This discrepancy with the oxygen-rich Mira case clearly indicates very different opacities, and it would be plausible to associate this with the dramatically different chemical equilibrium in the S-star. The discovery that Mira stars of different chemical composition have different wavelength dependence of size clearly shows the diagnostic value of angular measurements in validating models.
The differences we have noted in the case of ![]() Cyg compared to oxygen-rich Miras lead to the following speculations for the latter types. i) The larger optical depth systematically measured in K215 relative to K222 for oxygen-rich Miras may be due to a contamination by water vapor of the K215 band. ii) The systematically larger optical depth in K239 is likely due to the presence of CO vapor in the layer.
Cyg compared to oxygen-rich Miras lead to the following speculations for the latter types. i) The larger optical depth systematically measured in K215 relative to K222 for oxygen-rich Miras may be due to a contamination by water vapor of the K215 band. ii) The systematically larger optical depth in K239 is likely due to the presence of CO vapor in the layer.
Woodruff et al. (2004) have compared center-to-limb variation models of Mira to data collected with VINCI in the K band at different phases. Most of the visibilities were obtained at a single spatial frequency except at phase 0.13. These data can easily be compared to our November 2001 data as they were collected less than a month apart. More precisely, the full K band data can be compared to the K215 and K222 data. The absorption by water and CO is so large that the contribution of the edges of the K band to the visibility can be neglected. The VINCI visibilities decrease from 40 to 20% in the 25-35 cycles/arcsec range in perfect agreement with our model (see Fig. 5). Yet, our modeling leads to a photospheric diameter 14% smaller than their Rosseland diameter. Two reasons can explain this difference.
First, their model does not exactly reproduce the slope of the measured visibilities, perhaps biasing the result. Second, and perhaps sufficiently, the diameter which we provide gives the geometrical diameter of a compact photosphere, which would be most nearly comparable in opacity to continuum optical depth unity, whereas the Rosseland optical depth is a mean including wavelength regions of extremely strong absorption, and which would be expected to select a level well above continuum optical depth unity.
IOTA gives access to baselines up to 38 m which in K translates into an angular resolution of 12 mas. We have therefore studied the largest Miras which are well resolved on these baselines. We have observed R Tri, a much smaller source than the Miras studied in this paper, but which was fortunately also observed by the Palomar Testbed Interferometer (PTI) at a much longer baseline. Our observations took place on October 16 and 18, 2000 at phase 0.84. We have selected the PTI observations published in Thompson et al. (2002) and taken almost simultaneously on October 21, 2000. The PTI observations, over a small range in position angles, revealed a departure of the visibilities from the uniform disk model.
The FLUOR K' band data are well complemented by the PTI data as the full set covers both high and low visibilities. We have tried our model on these wide-band data following the analysis procedure described in Sect. 5.1 on the R Leo data. The modeling has been done without the outlier visibility at 172 cycles/arcsec which would have otherwise biased the result. The search for the optimum parameters is quite difficult as we have only one color. Based on findings on other stars, and noticing that the visibility curve shape is close to that of U Ori, we first imposed
![]() K and
K and
![]() K to explore the
K to explore the ![]() ,
,
![]() parameter space. The exploration yields a trough of minima. We have chosen a solution which looks realistic with respect to the results found on the other stars and we imposed a ratio
parameter space. The exploration yields a trough of minima. We have chosen a solution which looks realistic with respect to the results found on the other stars and we imposed a ratio
![]() as close as possible to 2. We then have searched for the best couple possible with respect to the K magnitude of
as close as possible to 2. We then have searched for the best couple possible with respect to the K magnitude of
![]() deduced from the photometry of Whitelock et al. (2000a) at phase 0.84. The result is displayed in Fig. 9. The full data set can be almost perfectly reproduced using the star+layer model with parameters of Table 11.
deduced from the photometry of Whitelock et al. (2000a) at phase 0.84. The result is displayed in Fig. 9. The full data set can be almost perfectly reproduced using the star+layer model with parameters of Table 11.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{1098f9.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg177.gif) |
Figure 9: Fit of the FLUOR and PTI K' band R Tri data. The discrepant datum at 172 arcsec-1 is the outlier mentioned in the text. |
|
|
|
|
|
|
| (mas) | (mas) | (K) | (K) | |
| 1.75 | 4.11 | 3500 | 2388 | 0.09 |
The resulting reduced ![]() is 3.91. This solution is only indicative. Better physical parameters would require multicolor data. This is why we do not indicate error bars. But still the conclusion is that our model also works for these data and offers an alternative explanation to the one provided in Thompson et al. (2002). The star would have a smaller diameter of 3.50 mas with the temperature of an M4 star (Ridgway et al. 1980) surrounded by a layer of molecular material of radius 2.3
is 3.91. This solution is only indicative. Better physical parameters would require multicolor data. This is why we do not indicate error bars. But still the conclusion is that our model also works for these data and offers an alternative explanation to the one provided in Thompson et al. (2002). The star would have a smaller diameter of 3.50 mas with the temperature of an M4 star (Ridgway et al. 1980) surrounded by a layer of molecular material of radius 2.3 ![]() and temperature 2388 K. The variation of the visibility with baseline of the PTI data was interpreted by Thompson et al. (2002) as a result of changing apparent diameter with position angle (as the PA was changing with baseline in the super-synthesis effect). Fit of the PTI data by an asymmetric model led to a
and temperature 2388 K. The variation of the visibility with baseline of the PTI data was interpreted by Thompson et al. (2002) as a result of changing apparent diameter with position angle (as the PA was changing with baseline in the super-synthesis effect). Fit of the PTI data by an asymmetric model led to a ![]() of 1.49. If, however, our data are added to the PTI data set, the
of 1.49. If, however, our data are added to the PTI data set, the ![]() for the asymmetric model increases to 11.89 which is much larger than 3.91. Our model, while crudely applied in this case, shows that conclusions should probably not be drawn about azimuthal stellar symmetry without preliminary measurement of the radial visibility function. The possible asymmetry of the star cannot be absolutely excluded, but is not required by the star-layer model.
for the asymmetric model increases to 11.89 which is much larger than 3.91. Our model, while crudely applied in this case, shows that conclusions should probably not be drawn about azimuthal stellar symmetry without preliminary measurement of the radial visibility function. The possible asymmetry of the star cannot be absolutely excluded, but is not required by the star-layer model.
Measurements at wavelengths close to 11 ![]() m of Mira stars with the ISI interferometer (Weiner et al. 2003a,b) show a visibility curve very similar to that expected of a photosphere with a diameter in general twice as large as the diameter we find in this paper for Mira, R Leo and
m of Mira stars with the ISI interferometer (Weiner et al. 2003a,b) show a visibility curve very similar to that expected of a photosphere with a diameter in general twice as large as the diameter we find in this paper for Mira, R Leo and ![]() Cyg. The ISI radii and the FLUOR layer radii observed at the same dates to within a few days (except in the case of
Cyg. The ISI radii and the FLUOR layer radii observed at the same dates to within a few days (except in the case of ![]() Cyg for which the difference is
3 months) are compared in the table below:
Cyg for which the difference is
3 months) are compared in the table below:
| Star | |
FLUOR | ISI | ISI |
| layer |
|
|
||
| Mira | 0.01 |
|
|
|
| Mira | 0.20 |
|
|
|
| R Leo | 0.80 |
|
|
|
| 0.76 |
|
|
Two different possibilities are invoked to explain the ISI results. The first one (Weiner et al. 2003a,b) is that the limb-darkening might be very strong at shorter wavelengths mimicking a much smaller apparent diameter. However, we find that the concept of a darkened disk does not fit the near-IR visibilities.
An alternative explanation can be based on our measurements in the narrow bands and in L. The layer we hypothesize is warm enough to contribute strongly to, and even dominate, the total flux at the ISI wavelengths. The diameters found by ISI are indeed comparable to the diameters we find for the layer. The ISI measurements are made inside and outside water vapor lines. The concentration of water vapor is likely to be low at photospheric temperatures, but high at the temperature of the high layer (Decin 2000). High altitude water vapor can form lines in either absorption or emission or a combination. We therefore suggest that ISI sees a relatively continuous opacity, perhaps in a pseudo-continuum of blended weak lines, generated by water vapor or other molecules such as SiO, instead of seeing the photosphere directly.
Yet, the radii derived with ISI are usually larger than the FLUOR layer radii. In our model, the geometric thickness of the layer is zero and is characteristic of the weighted brightness of a more physical layer modeled by Mennesson et al. (2002). It is not surprising that we do not accurately agree with the results of ISI as the weights certainly vary in the layer between the near-infrared and 11 ![]() m because of the dependence of brightness and optical depth on wavelength. The important conclusion is that the characteristic size of the layer which is mandatory to explain our data and the characteristic ISI sizes are similar.
m because of the dependence of brightness and optical depth on wavelength. The important conclusion is that the characteristic size of the layer which is mandatory to explain our data and the characteristic ISI sizes are similar.
The October 2000 data on Mira for which the FLUOR radius is larger than the ISI radius offer the possibility to compare our model extrapolated to
![]() m to the data (Fig. 10). We have used the original ISI data kindly provided by J. Weiner. In their work, the visibilities are modeled by a uniform disk visibility function times a constant A smaller than 1 to take into account the low spatial frequency energy of the dusty environment:
m to the data (Fig. 10). We have used the original ISI data kindly provided by J. Weiner. In their work, the visibilities are modeled by a uniform disk visibility function times a constant A smaller than 1 to take into account the low spatial frequency energy of the dusty environment:
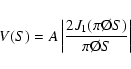 |
(4) |
Weiner (2004) has carried out a similar work to show that Mira's diameter variations from the near-infrared to the mid-infrared could be explained with the presence of a water vapor layer using part of the Mira data presented in the present paper.
Inspired by the success of the model for Mira stars, we carried out a similar analysis of the M supergiant Betelgeuse, including ISI data, and could consistently explain the K, L and 11.15![]() m interferometry (Perrin et al. 2004).
m interferometry (Perrin et al. 2004).
| Star | Phase |
|
|
| Mira | 0.01 | 2.2 | 2100 |
| Mira | 0.20 | 2.0 | 2000 |
| T Cep | 0.67 | 2.2 | 1700 |
| R Leo | 0.80 | 2.3 | 1600 |
| U Ori | 0.83 | 2.4 | 1500 |
| U Ori | 0.91 | 2.5 | 1900 |
| 0.24 | 1.8 | 1700 | |
| 0.76 | 1.9 | 1700 |
Evidence for a layer structure in Miras may be a novelty for optical interferometry, but it has been suggested by spectroscopic data for a few years. ISO, with its combination of broad spectral coverage and spectral resolution, has offered a rich repository of information. This data is somewhat difficult of access over broad bandwidths, owing to issues of deglitching, fringing, calibration and joining of sub-bands, but clearly supports a molecular layer structure for Mira atmospheres.
In a study of the H2O bands with ISO, Matsuura et al. (2002) deduced that oxygen-rich Miras are surrounded by hot and cool water-vapor layers. In their model, a hot layer has an estimated temperature of 2000 K and is located near the photosphere at minimum phase and at 2 ![]() at maximum. A cool layer has a temperature in the range 1000-1400 K and lies between 2.5 and 4 stellar radii. The radius variations are believed due to the propagation of a shock created by the pulsation of the star that heats the molecules.The parameters we derive for our layer are fairly consistent with those of Matsuura et al. (2002) and we probably observe the same structure that they detected by spectroscopy. The cool layer being in general more resolved and a minor contributor to the total flux in the near-infrared, our visibilities are less sensitive to it. It may corrupt our optical depth estimates in the K203 and K239 filters but the bias is all the smaller as the layer is at large distance since
at maximum. A cool layer has a temperature in the range 1000-1400 K and lies between 2.5 and 4 stellar radii. The radius variations are believed due to the propagation of a shock created by the pulsation of the star that heats the molecules.The parameters we derive for our layer are fairly consistent with those of Matsuura et al. (2002) and we probably observe the same structure that they detected by spectroscopy. The cool layer being in general more resolved and a minor contributor to the total flux in the near-infrared, our visibilities are less sensitive to it. It may corrupt our optical depth estimates in the K203 and K239 filters but the bias is all the smaller as the layer is at large distance since
![]() . This may explain why a single layer seems sufficient to model our visibilities. Nevertheless we always find a radius around 2
. This may explain why a single layer seems sufficient to model our visibilities. Nevertheless we always find a radius around 2 ![]() for the layer and no smaller radii even for the phases close to minimum as in the case of T Cep. Our temperatures are however larger as the phase is closer to maximum. Oxygen-rich Mira observations are ordered by increasing phase in the table above. (
for the layer and no smaller radii even for the phases close to minimum as in the case of T Cep. Our temperatures are however larger as the phase is closer to maximum. Oxygen-rich Mira observations are ordered by increasing phase in the table above. (![]() Cyg being an S star is listed separately). Trends seem to show-up such as a decrease of temperature with phase and an increase of radius which could be the trace of a shock propagating in the stellar atmosphere. But since this is not based on the observation of a single object it is speculative to propose a systematic effect rather than a coincidence. Also, it is impossible to compare this trend with the Matsuura et al. (2002) results as their hot layer temperature of 2000 K was a relatively unconstrained estimate owing to lack of spectral resolution of ISO. More phase coverage and high resolution spectroscopy (possible from the ground) could greatly improve the comparison of the H2O excitation and the interferometric model.
Cyg being an S star is listed separately). Trends seem to show-up such as a decrease of temperature with phase and an increase of radius which could be the trace of a shock propagating in the stellar atmosphere. But since this is not based on the observation of a single object it is speculative to propose a systematic effect rather than a coincidence. Also, it is impossible to compare this trend with the Matsuura et al. (2002) results as their hot layer temperature of 2000 K was a relatively unconstrained estimate owing to lack of spectral resolution of ISO. More phase coverage and high resolution spectroscopy (possible from the ground) could greatly improve the comparison of the H2O excitation and the interferometric model.
In a plane-parallel approximation, van Malderen (2003) has extensively compared ISO spectra with models very similar in structure to our empirical model, choosing a classical photosphere with one or more layers above it. His Fig. 4.2 in particular nicely illustrates the ubiquity and importance of H2O opacity in a Mira spectrum, appearing in emission and/or absorption throughout the infrared, in many regions as a pseudo-continuum. He carried out a thorough study of T Cep, observed with ISO at multiple phases. For the closest phase to our observations, van Malderen (2003) found the following parameters for the star-H2O layer model - the current model results, from Table 8, are shown in parentheses: Phase = 0.74 (0.67);
![]() (3158);
(3158);
![]() (2.2);
(2.2);
![]() (1700). We interpret this as highly specific confirmation of the empirical model in this particular case in which the most detailed comparison is possible.
(1700). We interpret this as highly specific confirmation of the empirical model in this particular case in which the most detailed comparison is possible.
| Star | Phase | |
Phase (spectroscopy) |
|
| R Leo | 0.80 | 3856 | 0.73 | 3200 |
| Mira | 0.01 | 3260 | 0.02 | 3000 |
| Mira | 0.20 | 3600 | 0.24 | 3600 |
| T Cep | 0.67 | 3158 | 0.69 | 2900 |
| U Ori | 0.83 | 3053 | 0.85 | 3000 |
| U Ori | 0.91 | 3106 | 0.97 | 2700 |
| chi Cyg | 0.24 | 3316 | 0.24 | 3100 |
Extensive high resolution infrared spectroscopy of Miras does offer a point of comparison with our model. Time series spectroscopy has been used by Hinkle et al. (1984, 1997) to monitor multiple absorption components of the CO molecule, separated in wavelength by differential depth dependent pulsational expansion velocity. The excitation temperatures of these components have been monitored as a function of phase. Aside from shock excitation effects, these components would be expected to show an excitation temperature similar to or somewhat lower than the ![]() temperatures of the buried photosphere against which they are seen. Table 12 compares the model and observed temperatures at similar phases. Although there is considerable scatter, the excitation temperatures are similar to or less than the
temperatures of the buried photosphere against which they are seen. Table 12 compares the model and observed temperatures at similar phases. Although there is considerable scatter, the excitation temperatures are similar to or less than the ![]() in every case, with a reasonable average temperature difference of 240 K. (Note that for Mira at phase 0.02, U Ori at phase 0.97 and T Cep at phase 0.67, the spectroscopic data showed an additional CO absorption component at rotational excitational temperature higher than
in every case, with a reasonable average temperature difference of 240 K. (Note that for Mira at phase 0.02, U Ori at phase 0.97 and T Cep at phase 0.67, the spectroscopic data showed an additional CO absorption component at rotational excitational temperature higher than ![]() .
The authors suggested that this component was shock heated, possibly explaining the temperature excess above the stellar photospheric temperature.)
.
The authors suggested that this component was shock heated, possibly explaining the temperature excess above the stellar photospheric temperature.)
| Star |
|
|
|
| (mas) | (mas) | ||
| R Leo | 25.00 | 30.6 | 1.22 |
| Mira | 24.95 | 37.8 | 1.52 |
| U Ori | 12.00 | 14.4 | 1.20 |
SiO masers are commonly observed in the atmospheres of oxygen rich Miras. These masers are believed (Reid & Menten 1997) to arise in the outer portion of the molecular envelope just interior to the region where the SiO condenses into dust grains. The masers are generally observed in a ring as the long paths of constant radial velocity needed for the development of the maser gain are tangent to the shell of masing gas. If our conjecture about the presence of an extended molecular layer are true then the radii of the SiO maser rings should be related to our derived radii of the layer component fitted to the data presented here.
Cotton et al. (2004) report the sizes of the maser rings in R Leo, Mira and U Ori in November 2001, close to one of the epochs reported for these stars in the present work. Table 13 shows the comparison between our derived layer radii and the average radii of the SiO maser rings. While the number of cases compared is small, the consistency is quite encouraging and further supports our interpretation of the interferometric data as being due to the stellar photosphere and a molecular envelope.
The proximity of the maser region to the top of the NIR atmosphere at
![]() suggests an additional constraint on the stellar size. The NIR interferometric results require a large gas column density at high altitude. But the typical densities required for efficient masing are in the range
109 - 1010 cm-3. This is at least 103 to 104 smaller than the number densities required in the molecular layer to produce the observed optical depth. The strong density gradient above
suggests an additional constraint on the stellar size. The NIR interferometric results require a large gas column density at high altitude. But the typical densities required for efficient masing are in the range
109 - 1010 cm-3. This is at least 103 to 104 smaller than the number densities required in the molecular layer to produce the observed optical depth. The strong density gradient above
![]() confirms the correctness of identifying this level as a fiducial indicator of the top of the atmosphere.
This constraint on the density profile deserves careful study as it must be intimately related to the mass-loss process.
confirms the correctness of identifying this level as a fiducial indicator of the top of the atmosphere.
This constraint on the density profile deserves careful study as it must be intimately related to the mass-loss process.
| Star | P (days) | |
|
|
|
| R Leo | 312 |
|
|
2980 | 4000 |
| Mira | 333 |
|
|
2865-3210 | 7250-12 000 |
| 406 |
|
|
3210-3320 | 2380-3580 | |
| T Cep | 398 |
|
|
2900 | 7900 |
| U Ori | 368 |
|
|
2770-3085 | 7010-8750 |
| R Tri | 266 |
|
|
3450 | 11 200 |
Effective temperature is defined in terms of a hypothetical stellar surface and bolometric luminosity.
The bolometric flux is relatively unambiguous, determined by integrating over the stellar brightness. In the extended Mira atmosphere the most characteristic reference level seems to be near optical depth unity in the near-IR continuum at ![]() .
A temperature can be formally calculated from the model star radius and the total stellar flux, according to
.
A temperature can be formally calculated from the model star radius and the total stellar flux, according to
![]() ,
where we designate the quantity
,
where we designate the quantity
![]() a pseudo effective temperature because it does not satisfy the formal definition of effective temperature. It would appropriately describe the stellar effective temperature with the extended atmosphere removed, and thus might be of interest in quantitatively relating Mira stars to semi-regular AGB stars, and it is certainly a useful quantity to give an intuitive understanding of the character of the underlying star.
a pseudo effective temperature because it does not satisfy the formal definition of effective temperature. It would appropriately describe the stellar effective temperature with the extended atmosphere removed, and thus might be of interest in quantitatively relating Mira stars to semi-regular AGB stars, and it is certainly a useful quantity to give an intuitive understanding of the character of the underlying star.
![]() of Table 14 has been calculated with
of Table 14 has been calculated with ![]() measured in this paper. The table also shows observed luminosities based on an integration of the total observed flux from the photometry presented above, augmented with photometry from Simbad for other wavelengths. The error estimate on
measured in this paper. The table also shows observed luminosities based on an integration of the total observed flux from the photometry presented above, augmented with photometry from Simbad for other wavelengths. The error estimate on
![]() is also based on the dispersion of bolometric fluxes deduced from the scattered flux measurements. The temperatures depend on only the 4th root of the flux, so the errors associated with photometry, variability and integration of the discrete bands correspond to a temperature uncertainty of only about 200 K, and is negligible in the following discussion. The tabulated pseudo-effective temperatures are indicative of spectral types M6-M8 based on semi-regular variable stars observations (Perrin et al. 1998). The uncertainties in observed luminosity associated with the photometry are typically 200
is also based on the dispersion of bolometric fluxes deduced from the scattered flux measurements. The temperatures depend on only the 4th root of the flux, so the errors associated with photometry, variability and integration of the discrete bands correspond to a temperature uncertainty of only about 200 K, and is negligible in the following discussion. The tabulated pseudo-effective temperatures are indicative of spectral types M6-M8 based on semi-regular variable stars observations (Perrin et al. 1998). The uncertainties in observed luminosity associated with the photometry are typically 200 ![]() .
.
The
![]() is not expected to equal the observed model temperature
is not expected to equal the observed model temperature ![]() .
.
![]() should be significantly enhanced over
should be significantly enhanced over
![]() due to backwarming from the molecular layer. General arguments indicate that a layer opacity of order 0.5-1.0 should produce a backwarming temperature increase of about 6-8%. The observed enhancement of
due to backwarming from the molecular layer. General arguments indicate that a layer opacity of order 0.5-1.0 should produce a backwarming temperature increase of about 6-8%. The observed enhancement of ![]() over
over
![]() is somewhat larger, but follows the expected trend that the larger enhancements correspond to the larger layer optical depths (R Leo being the most extreme example).
is somewhat larger, but follows the expected trend that the larger enhancements correspond to the larger layer optical depths (R Leo being the most extreme example).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{1098f11.eps}
\end{figure}](/articles/aa/full/2004/40/aa1098/Timg216.gif) |
Figure 11: Linear radii deduced from the present interferometric measurements vs. pulsation periods. Continuous and dotted lines are expectations for respectively fundamental mode and first overtone pulsators from Wood (1989). Comparison of this figure with a similar figure in Feast (1996) dramatically illustrates the impact of the revised interpretation of Mira brightness distributions. |
Some conclude that Mira stars should be first overtone pulsators (e.g. Tuthill et al. 1994; Feast 1996; Whitelock et al. 2000b). Others conclude that the two types of pulsators can be found in Mira stars (e.g. Fox & Wood 1982; Ostlie & Cox 1986). Rather recently, Wood (2000) has shown evidence that period-luminosity relations for Mira stars comply with the fundamental pulsation mode hypothesis. It turns out that studies leading to the first overtone conclusion are based on diameter measurements. As shown in this paper, high angular resolution diameters are very dependent upon the model used to interpret them. It is therefore interesting to look at the pulsation issue in detail with our new photospheric diameters that are systematically smaller than found in previous studies.
Theoretical studies of pulsation lead to relations (PMR relations) linking the period, the mass and the radius of the pulsator. We have plotted our linear radii as a function of pulsation period in Fig. 11. We have also plotted the relations of Wood (1989) for fundamental mode and first overtone pulsators of probable mass range 1 to 2 ![]() .
There is a clear tendency that our diameters are consistent with the fundamental mode hypothesis. The case of Mira itself may look marginal as it could be compatible with both a low mass first overtone and a high mass fundamental mode pulsator. This conclusion is strongly dependent upon the parallax used to derive the linear radius. As underlined in Whitelock et al. (2000b), parallaxes for Mira stars are smaller than the star diameters and are measured in the visible where Miras are known to have spotty surfaces. This may add dispersion to the parallax estimates. There is a priori no reason why Mira should pulsate in a different mode than other Miras (its characteristics are for example very close to that of R Leo) and we conclude that Mira stars are more likely to pulsate in the fundamental mode. A stronger conclusion could be reached with pulsation models built on the new parameters found in our study - most published models make use of lower temperatures for the star.
.
There is a clear tendency that our diameters are consistent with the fundamental mode hypothesis. The case of Mira itself may look marginal as it could be compatible with both a low mass first overtone and a high mass fundamental mode pulsator. This conclusion is strongly dependent upon the parallax used to derive the linear radius. As underlined in Whitelock et al. (2000b), parallaxes for Mira stars are smaller than the star diameters and are measured in the visible where Miras are known to have spotty surfaces. This may add dispersion to the parallax estimates. There is a priori no reason why Mira should pulsate in a different mode than other Miras (its characteristics are for example very close to that of R Leo) and we conclude that Mira stars are more likely to pulsate in the fundamental mode. A stronger conclusion could be reached with pulsation models built on the new parameters found in our study - most published models make use of lower temperatures for the star.
We can summarize our conclusion by first quoting Wood (2000), "This then raises the question of why the directly observed radii of Miras ... are so large'', and responding with a clear new answer - they are not so large, but only appear to be large because of a high opacity layer.
Under these circumstances, the use of simple empirical models is justified in an attempt to capture with a minimum of complexity the geometrical and radiometric character of the source. This has led us to a very simple model consisting of a star with a thin molecular shell of variable but low opacity. Of course this is not a complete representation of the physical situation. We assume that the atmosphere is probably continuous between the star and shell - but of sufficiently low opacity in the relevant bandpasses that it can be neglected to first approximation. Observations at another wavelength, of course, might lead to somewhat different conclusions about the dominant layers and their characteristics - as for example with the ISO and ISI studies described above.
With such a complex situation, it may be wondered why we have chosen to designate the deepest layer in our model as the "star''. This is at least a convenient and graphic terminology, but it may also be a fairly accurate physical description. If we seek the physical parameter which bests localizes the photosphere of a star, it is of course the optical depth "unity'' in the dominant wavelengths of radiation transport. The energy of these cool stars is overwhelmingly transported in the spectral region near 2 microns (in the model described here, this is true both for Planckian emission at ![]() and for the integrated stellar spectrum). It is precisely at the near-IR wavelengths around
2 microns where the apparent Mira size is smallest - furthermore, our model analysis indicates that the actual optical depth unity is even somewhat deeper, once the shell contribution to the visibility has been compensated. Clearly stellar interior models intended to describe the stellar luminosity and pulsations are dominated by the material interior to
and for the integrated stellar spectrum). It is precisely at the near-IR wavelengths around
2 microns where the apparent Mira size is smallest - furthermore, our model analysis indicates that the actual optical depth unity is even somewhat deeper, once the shell contribution to the visibility has been compensated. Clearly stellar interior models intended to describe the stellar luminosity and pulsations are dominated by the material interior to ![]() .
The region above
.
The region above ![]() ,
of very low density, with small infrared opacity, extending over a very large (many AU) region, constitutes an observationally important part of the atmosphere, but most likely not a structurally important part of the star.
,
of very low density, with small infrared opacity, extending over a very large (many AU) region, constitutes an observationally important part of the atmosphere, but most likely not a structurally important part of the star.
The empirical dissection of the Mira stars into star+layer offers now, perhaps for the first time, an observational basis for critically testing the structural predictions of the Mira atmosphere dynamical models. A number of additional measurements can now be expected with existing optical interferometers. The visibility distributions can be mapped more completely at multiple wavelengths - currently, near IR and thermal IR are available at several facilities, though not the interesting cross-over regions at 4 and 5 microns. The evidence for or against circularity of Mira stars (probably relevant just to the upper layers), obtained from multiple position angle measurements, can be examined in the light of the new understanding that the visibility distributions are complex and probably different for each star and probably phase dependent. The evidence for observed variation in the radii of Miras must be examined in light of the structured atmosphere, in order to distinguish photospheric motions and structural changes from opacity and temperature changes of the upper layer(s). The characteristics of the observed Mira "core'' stars can be compared to non-Mira AGB stars. The similarity of the Mira TPE and the semi-regular variable stars effective temperature ranges already suggests that the Mira and semi-regular variable stars may be quite similar, differing mainly in the resonant amplification of ubiquitous pulsations.
The remarkable discovery of warm H2O in the spectra of late K and early M giants (Tsuji 2001), though at a column-density much lower than in Miras, offers an intriguing possible link between models of Mira stars and hotter stars with less extended atmospheres.
Optical interferometry at multiple wavelengths has offered a key insight into the Mira atmospheres - in the six cases studied, at least, they can be approximated by a central star with an extremely thin and nearly transparent envelope whose opacity in the infrared is dominated by a single high layer. This model has a close analog in the models required to understand certain infrared spectra of Mira stars. Either the spectroscopy-inspired models or the interferometry-inspired models might ideally stand alone in demonstrating the Mira structure. Since both lead to similar conclusions from quite different observational information (molecular microphysics on the one hand and global radiometry on the other) the Mira model appears to be solidly established as a useful and important approximation, capturing the chief essentials of the radial structure and the radiometric state.
While an extreme simplification, this model already reconciles in a natural way seemingly discrepant sizes observed at different wavelengths. It strongly confirms suspicions of a smaller stellar diameter for Mira stars, removing a long-standing puzzle in the interpretation of the pulsational physics. The galactic Mira period-radius relation is indicative of fundamental mode vibration, consistent with the conclusion for Miras in the LMC. The empirical model offers a new observation-based approach to analysis of Mira atmospheres, and until dynamical models come into better agreement with the observations, this empirical approach must be considered a serious and even preferred option.
Nearby Miras are bright and easily observed with small interferometric baselines. However, thorough characterization of time varying visibilities at multiple wavelengths and position angles for a number of stars requires major, long-term efforts. In view of the effort, it may be wise to coordinate such campaigns with contemporaneous photometric and spectroscopic studies. The parallel investigation of hydrodynamic models can serve to identify the most critical issues and measurements.
Acknowledgements
The authors wish to thank the Association Française des Observateurs d'Étoiles Variables whose database was used to compute the phases of the stars and Centre de Données Astronomiques de Strasbourg whose database provided photometric data, as well as J. Weiner for providing the ISI data. The authors are also grateful to the anonymous referee for fruitful interactions that help improving the manuscript and to J. Aufdenberg for his valuable comments.
| Source | UT date | JD | Phase | Filter | Sp. Freq. | Azimuth | V2 | Calibrator 1 | Calibrator 2 |
| -2 450 000 | (arcsec-1) | (
|
(HD number) | (HD number) | |||||
|
|
17/11/2001 | 2230 | 0.75 | K203 | 49.45 | 116.65 | 0.0591 |
HD 6860 | HD 6860 |
| 17/11/2001 | 2230 | 0.75 | K215 | 46.59 | 117.03 | 0.0979 |
HD 6860 | HD 6860 | |
| 17/11/2001 | 2230 | 0.75 | K222 | 45.14 | 117.34 | 0.1117 |
HD 6860 | HD 6860 | |
| 17/11/2001 | 2230 | 0.75 | K239 | 41.91 | 117.94 | 0.0290 |
HD 6860 | HD 6860 | |
| 22/11/2001 | 2235 | 0.76 | K203 | 71.09 | 97.50 | 0.0032 |
HD 197989 | HD 61421 | |
| 22/11/2001 | 2235 | 0.76 | K215 | 67.11 | 99.95 | 0.0062 |
HD 197989 | HD 197989 | |
| 22/11/2001 | 2235 | 0.76 | K222 | 65.13 | 100.63 | 0.0117 |
HD 197989 | HD 197989 | |
| 30/05/2002 | 2424 | 0.23 | K203 | 50.59 | 95.72 | 0.0043 |
HD 183439 | HD 183439 | |
| 30/05/2002 | 2424 | 0.23 | K215 | 47.71 | 99.71 | 0.0151 |
HD 183439 | HD 183439 | |
| 02/06/2002 | 2427 | 0.24 | K215 | 35.57 | 120.95 | 0.1321 |
HD 140573 | ||
| 02/06/2002 | 2427 | 0.24 | K222 | 34.50 | 121.79 | 0.1535 |
HD 197989 | ||
| 04/06/2002 | 2429 | 0.24 | K203 | 37.55 | 110.45 | 0.0947 |
HD 197989 | HD 197989 | |
| 04/06/2002 | 2429 | 0.24 | K215 | 35.46 | 111.43 | 0.1334 |
HD 197989 | HD 197989 | |
| 04/06/2002 | 2429 | 0.24 | K222 | 34.43 | 112.50 | 0.1511 |
HD 197989 | HD 197989 | |
| 04/06/2002 | 2429 | 0.24 | K239 | 32.06 | 113.22 | 0.0940 |
HD 197989 | HD 197989 | |
| 05/06/2002 | 2430 | 0.25 | K203 | 26.65 | 102.13 | 0.3067 |
HD 146051 | HD 187076 | |
| 05/06/2002 | 2430 | 0.25 | K215 | 25.15 | 102.70 | 0.3440 |
HD 146051 | HD 187076 | |
| 05/06/2002 | 2430 | 0.25 | K222 | 24.40 | 103.25 | 0.3713 |
HD 146051 | HD 187076 | |
| 05/06/2002 | 2430 | 0.25 | K239 | 22.72 | 104.24 | 0.2713 |
HD 146051 | HD 187076 | |
| 06/06/2002 | 2431 | 0.25 | K203 | 37.52 | 109.38 | 0.0937 |
HD 130144 | HD 187076 | |
| 06/06/2002 | 2431 | 0.25 | K215 | 35.44 | 110.67 | 0.1511 |
HD 130144 | HD 187076 | |
| 06/06/2002 | 2431 | 0.25 | K222 | 34.40 | 111.26 | 0.1706 |
HD 130144 | HD 187076 | |
| 06/06/2002 | 2431 | 0.25 | K239 | 32.04 | 112.04 | 0.1075 |
HD 130144 | HD 187076 | |
| U Ori | 17/10/2000 | 1834 | 0.83 | K203 | 89.00 | 75.29 | 0.0125 |
HD 61421 | |
| 17/10/2000 | 1834 | 0.83 | K215 | 83.03 | 84.17 | 0.0318 |
HD 61421 | HD 9927 | |
| 17/10/2000 | 1834 | 0.83 | K222 | 81.88 | 72.52 | 0.0433 |
HD 61421 | HD 213310 | |
| 19/10/2000 | 1836 | 0.83 | K203 | 49.55 | 90.62 | 0.0865 |
HD 42995 | HD 42995 | |
| 19/10/2000 | 1836 | 0.83 | K215 | 46.91 | 97.88 | 0.1887 |
HD 42995 | HD 42995 | |
| 19/10/2000 | 1836 | 0.83 | K222 | 45.62 | 100.44 | 0.2304 |
HD 42995 | HD 42995 | |
| 19/10/2000 | 1836 | 0.83 | K239 | 42.35 | 82.47 | 0.1875 |
HD 42995 | HD 42995 | |
| 15/11/2001 | 2228 | 0.90 | K203 | 49.66 | 96.52 | 0.0791 |
HD 42995 | HD 42995 | |
| 15/11/2001 | 2228 | 0.90 | K215 | 46.99 | 99.80 | 0.2159 |
HD 42995 | HD 42995 | |
| 15/11/2001 | 2228 | 0.90 | K222 | 45.73 | 102.52 | 0.2696 |
HD 42995 | HD 42995 | |
| 15/11/2001 | 2228 | 0.90 | K239 | 42.81 | 107.18 | 0.1790 |
HD 42995 | HD 42995 | |
| 16/11/2001 | 2229 | 0.90 | K203 | 50.04 | 104.05 | 0.1080 |
HD 42995 | HD 42995 | |
| 16/11/2001 | 2229 | 0.90 | K215 | 47.16 | 103.11 | 0.2272 |
HD 42995 | HD 42995 | |
| 17/11/2001 | 2230 | 0.90 | K222 | 45.65 | 78.86 | 0.2879 |
HD 42995 | HD 44478 | |
| 17/11/2001 | 2230 | 0.90 | 8:45 | 42.46 | 79.61 | 0.1568 |
HD 42995 | HD 44478 | |
| 18/11/2001 | 2231 | 0.91 | K215 | 34.71 | 117.91 | 0.4624 |
HD 42995 | HD 44478 | |
| 18/11/2001 | 2231 | 0.91 | K203 | 36.69 | 117.08 | 0.3138 |
HD 42995 | HD 44478 | |
| 18/11/2001 | 2231 | 0.91 | K222 | 33.74 | 118.50 | 0.5124 |
HD 42995 | HD 44478 | |
| 18/11/2001 | 2231 | 0.91 | K239 | 31.47 | 119.09 | 0.3926 |
HD 42995 | HD 44478 | |
| 20/11/2001 | 2233 | 0.91 | K203 | 26.31 | 113.99 | 0.5628 |
HD 62509 | HD 62509 | |
| 20/11/2001 | 2233 | 0.91 | K215 | 24.85 | 114.53 | 0.6629 |
HD 62509 | HD 62509 | |
| 20/11/2001 | 2233 | 0.91 | K222 | 24.15 | 115.12 | 0.6997 |
HD 18884 | HD 62509 | |
| 20/11/2001 | 2233 | 0.91 | K239 | 22.50 | 115.67 | 0.5406 |
HD 62509 | HD 62509 | |
| 21/11/2001 | 2234 | 0.92 | K203 | 70.24 | 66.81 | 0.0421 |
HD 62509 | ||
| 21/11/2001 | 2234 | 0.92 | K215 | 66.15 | 67.60 | 0.0989 |
HD 62509 | ||
| 21/11/2001 | 2234 | 0.92 | K222 | 64.10 | 68.18 | 0.1305 |
HD 62509 | ||
| 22/11/2001 | 2235 | 0.92 | K203 | 68.10 | 85.03 | 0.0436 |
HD 61421 | HD 48329 | |
| 22/11/2001 | 2235 | 0.92 | K215 | 64.23 | 85.63 | 0.1235 |
HD 61421 | HD 48329 | |
| 22/11/2001 | 2235 | 0.92 | K222 | 62.30 | 86.18 | 0.1598 |
HD 61421 | HD 48329 | |
| 22/11/2001 | 2235 | 0.92 | K239 | 57.97 | 86.90 | 0.0578 |
HD 61421 | HD 48329 | |
| Mira | 19/10/2000 | 1836 | 0.01 | K203 | 42.00 | 98.43 | 0.0114 |
HD 18884 | HD 18884 |
| 19/10/2000 | 1836 | 0.01 | K215 | 40.28 | 102.99 | 0.0287 |
HD 18884 | HD 18884 | |
| 19/10/2000 | 1836 | 0.01 | K222 | 39.40 | 104.71 | 0.0368 |
HD 18884 | HD 18884 | |
| 19/10/2000 | 1836 | 0.01 | K222 | 39.48 | 105.08 | 0.0343 |
HD 18884 | HD 18884 | |
| 19/10/2000 | 1836 | 0.01 | K239 | 37.15 | 107.08 | 0.0105 |
HD 18884 | HD 18884 | |
| 15/11/2001 | 2228 | 0.19 | K203 | 42.90 | 104.01 | 0.0013 |
HD 18884 | HD 18884 | |
| 16/11/2001 | 2229 | 0.19 | K203 | 44.04 | 108.67 | 0.0016 |
HD 18884 | HD 18884 | |
| 16/11/2001 | 2229 | 0.19 | K215 | 40.23 | 102.68 | 0.0112 |
HD 18884 | HD 18884 | |
| 16/11/2001 | 2229 | 0.19 | K222 | 39.57 | 105.51 | 0.0161 |
HD 18884 | HD 18884 | |
| 16/11/2001 | 2229 | 0.19 | K239 | 38.14 | 111.01 | 0.0006 |
HD 18884 | HD 18884 | |
| 18/11/2001 | 2231 | 0.20 | K203 | 35.97 | 131.10 | 0.0095 |
HD 18884 | HD 18884 | |
| 18/11/2001 | 2231 | 0.20 | K215 | 34.11 | 131.34 | 0.0352 |
HD 18884 | HD 18884 | |
| 18/11/2001 | 2231 | 0.20 | K222 | 33.22 | 131.53 | 0.0558 |
HD 18884 | HD 18884 | |
| 18/11/2001 | 2231 | 0.20 | K239 | 31.12 | 131.84 | 0.0024 |
HD 18884 | ||
| 20/11/2001 | 2233 | 0.21 | K203 | 22.18 | 114.02 | 0.1028 |
HD 18884 | HD 18884 | |
| 20/11/2001 | 2233 | 0.21 | K215 | 21.15 | 115.21 | 0.2290 |
HD 18884 | HD 18884 | |
| 20/11/2001 | 2233 | 0.21 | K222 | 20.99 | 117.61 | 0.2686 |
HD 18884 | HD 18884 | |
| 20/11/2001 | 2233 | 0.21 | K239 | 19.66 | 118.21 | 0.1285 |
HD 18884 | HD 18884 | |
| R Leo | 15/11/2001 | 2228 | 0.79 | K215 | 44.82 | 94.71 | 0.0108 |
HD 61421 | |
| 16/11/2001 | 2229 | 0.79 | K203 | 47.60 | 83.51 | 0.0055 |
HD 61421 | HD 61421 | |
| 16/11/2001 | 2229 | 0.79 | K215 | 44.88 | 84.11 | 0.0196 |
HD 61421 | HD 61421 | |
| 16/11/2001 | 2229 | 0.79 | K222 | 43.52 | 84.75 | 0.0316 |
HD 61421 | HD 61421 | |
| 18/11/2001 | 2231 | 0.80 | K203 | 34.66 | 115.73 | 0.0181 |
HD 61421 | HD 81797 | |
| 18/11/2001 | 2231 | 0.80 | K215 | 32.84 | 116.48 | 0.0712 |
HD 61421 | HD 81797 | |
| 18/11/2001 | 2231 | 0.80 | K222 | 31.96 | 117.04 | 0.1030 |
HD 61421 | HD 81797 | |
| 18/11/2001 | 2231 | 0.80 | K239 | 29.85 | 117.65 | 0.0129 |
HD 61421 | HD 81797 | |
| 20/11/2001 | 2233 | 0.80 | K203 | 24.20 | 101.64 | 0.1062 |
HD 61421 | HD 81797 | |
| 20/11/2001 | 2233 | 0.80 | K215 | 22.88 | 102.51 | 0.2267 |
HD 61421 | HD 81797 | |
| 20/11/2001 | 2233 | 0.80 | K222 | 22.25 | 103.30 | 0.2789 |
HD 61421 | HD 81797 | |
| 20/11/2001 | 2233 | 0.80 | K239 | 20.76 | 104.08 | 0.1067 |
HD 61421 | HD 81797 | |
| T Cep | 5/06/02 | 2399 | 0.67 | K203 | 22.61 | 109.67 | 0.5466 |
HD 187076 | |
| 05/06/2002 | 2399 | 0.67 | K215 | 21.31 | 110.29 | 0.6814 |
HD 187076 | ||
| 05/06/2002 | 2399 | 0.67 | K222 | 20.65 | 110.90 | 0.7070 |
HD 187076 | ||
| 05/06/2002 | 2399 | 0.67 | K239 | 19.18 | 111.87 | 0.5732 |
HD 187076 | ||
| 07/06/2002 | 2401 | 0.67 | K203 | 40.64 | 90.94 | 0.1761 |
HD 187076 | ||
| 07/06/2002 | 2401 | 0.67 | K215 | 38.34 | 91.66 | 0.2967 |
HD 187076 | ||
| 07/06/2002 | 2401 | 0.67 | K222 | 37.20 | 92.12 | 0.3333 |
HD 187076 | ||
| 07/06/2002 | 2401 | 0.67 | K239 | 34.61 | 92.91 | 0.1566 |
HD 187076 |