Contents

A&A 425, 849-869 (2004)
DOI: 10.1051/0004-6361:20034522

Oxygen and nitrogen abundances in nearby galaxies[*]

Correlations between oxygen abundance and macroscopic properties

L. S. Pilyugin 1,2 - J. M. Vílchez 2 - T. Contini 3


1 - Main Astronomical Observatory of National Academy of Sciences of Ukraine, 27 Zabolotnogo str., 03680 Kiev, Ukraine
2 - Instituto de Astrofísica de Andalucía, CSIC, Apdo, 3004, 18080 Granada, Spain
3 - Laboratoire d'Astrophysique de l'Observatoire Midi-Pyrénées - UMR 5572, 14 avenue E. Belin, 31400 Toulouse, France

Received 26 May 2003 / Accepted 16 June 2004

Abstract
We performed a compilation of more than 1000 published spectra of H  II regions in spiral galaxies. The oxygen and nitrogen abundances in each H  II region were recomputed in a homogeneous way, using the P-method. The radial distributions of oxygen and nitrogen abundances were derived. The correlations between oxygen abundance and macroscopic properties are examined. We found that the oxygen abundance in spiral galaxies correlates with its luminosity, rotation velocity, and morphological type: the correlation with the rotation velocity may be slightly tighter. There is a significant difference between the luminosity-metallicity relationship obtained here and that based on the oxygen abundances determined through the $R_{\rm 23}$-calibrations. The oxygen abundance of NGC 5457 recently determined using direct measurements of $T_{\rm e}$ (Kennicutt et al. 2003) agrees with the luminosity-metallicity relationship derived in this paper, but is in conflict with the luminosity-metallicity relationship derived with the $R_{\rm 23}$-based oxygen abundances. The obtained luminosity-metallicity relation for spiral galaxies is compared to that for irregular galaxies. Our sample of galaxies shows evidence that the slope of the ${\rm O/H} - M_B$ relationship for spirals ( $-0.079 \pm 0.018$) is slightly more shallow than that for irregular galaxies ( $-0.139 \pm 0.011$). The effective oxygen yields were estimated for spiral and irregular galaxies. The effective oxygen yield increases with increasing luminosity from  $M_{B} \sim -11$to $M_{B} \sim -18$ (or with increasing rotation velocity from  $V_{\rm rot} \sim 10$ km s-1 to $V_{\rm rot} \sim 100$ km s-1) and then remains approximately constant. Irregular galaxies from our sample have effective oxygen yields lowered by a factor of 3 at maximum, i.e. irregular galaxies usually keep at least 1/3 of the oxygen they manufactured during their evolution.

Key words: galaxies: abundances - galaxies: ISM - galaxies: spiral - galaxies: evolution

1 Introduction

Investigating the macroscopic properties of galaxies that could drive their chemical evolution is very important in understanding their global evolution, which has been the goal of many studies over the past twenty years. It has been found, for example, that the properties of H  II regions in late-type galaxies are linked to macroscopic characteristics of galaxies such as luminosity or Hubble type. Smith (1975) concluded that excitation differences among the H  II regions of Sbc-Scd-Irr galaxies can be best understood in terms of an abundance sequence which progresses from higher to lower heavy-element enrichment as one progresses from earlier to later type galaxies. He also noted that his results show no apparent correlation between the average heavy-element abundance and galaxy mass. The correlation between oxygen abundance and the morphological type of galaxy was later confirmed by Vila-Costas & Edmunds (1992) and Zaritsky et al. (1994).

Lequeux et al. (1979) revealed that the oxygen abundance correlates with total galaxy mass for irregular galaxies, in the sense that the higher the total mass, the higher the heavy element content. Since the galaxy mass is a poorly known parameter, the metallicity-luminosity relation instead of the mass-metallicity relation is usually considered (Skillman et al. 1989; Richer & McCall 1995; Hunter & Hoffman 2000; Pilyugin 2001c; Melbourne & Salzer 2002, among others). Garnett & Shields (1987) found that spiral disk abundance also correlates very well with galaxy luminosity. They concluded that the metallicity of galaxies correlates better with galaxy luminosity than with morphological type. Zaritsky et al. (1994) found that the characteristic gas-phase abundances and luminosities of spiral galaxies are strongly correlated, and this relationship maps almost directly onto the luminosity-metallicity relationship of irregular galaxies.

The origin of this correlation is open to debate. It is widely suggested that there are two mechanisms which can be responsible for a luminosity-metallicity relation for spirals and irregulars: higher astration level and decreasing efficiency of heavy-element loss with increasing luminosity. The mass exchange between a galaxy and its environment can alter the relation between oxygen abundance and gas mass fraction; it mimics the variation in the oxygen yield. To investigate the possibility of a varying yield, Edmunds (1990) and Vila-Costa & Edmunds (1992) have suggested to use the "effective'' oxygen yield, $y_{\rm eff}$, as the yield that would be deduced if a system was assumed to behave as in the simplest model of chemical evolution. The variation of the value of the effective oxygen yield from galaxy to galaxy can be considered as indicative of the efficiency of mass exchange between galaxies and their environments. A similar approach, the concept of the oxygen abundance deficiency in the galaxy which is introduced as a deficiency of the oxygen abundance observed in the galaxy in comparison with the oxygen abundance predicted by the closed-box model for the same gas mass fraction, has been used by Pilyugin & Ferrini (1998; 2000a,b). The effective oxygen yields for a set of spiral and irregular galaxies were derived recently by Garnett (2002). He found that the value of effective oxygen yield is approximately constant, $y_{\rm eff} = 0.0112$, for $V_{\rm rot} > 150$ km s-1. The effective oxygen yield decreases by a factor of 10-20 from $V_{\rm rot} \sim 300$ km s-1 to 5. This means that low-mass galaxies have lost the bulk of their manufactured oxygen, up to 90-95%.

Accurate abundance determinations are mandatory for such investigations. In H  II regions, they can be derived from measurements of temperature-sensitive line ratios, such as [OIII] $\lambda \lambda$4959,5007/[OIII]$\lambda$4363. Unfortunately, in oxygen-rich H  II regions, the temperature-sensitive lines such as [OIII]$\lambda$4363 are often too weak to be detected. For such H  II regions, abundance indicators based on more readily observable lines were suggested (Pagel et al. 1979; Alloin et al. 1979). The oxygen abundance indicator $R_{\rm 23} = ($[OII] $\lambda \lambda3727,3729 + [$OIII] $\lambda \lambda$4959,5007)/H$_{\beta}$, suggested by Pagel et al. (1979), has found widespread acceptance and use for the oxygen abundance determination in H  II regions where the temperature-sensitive lines are undetectable. Grids of photoionization models are often used to establish the relation between strong oxygen line intensities and oxygen abundances (Edmunds & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; Kobulnicky et al. 1999; Kewley & Dopita 2002, among others). Radial distributions of oxygen abundance determined with theoretical (or model) calibrations have been obtained for large samples of spiral galaxies by Vila-Costas & Edmunds (1992), Zaritsky et al. (1994), van Zee et al. (1998), Considère et al. (2000), among others.

The early calibrations were one-dimensional (Edmunds & Pagel 1984; McCall et al. 1985; Dopita & Evans 1986; Zaritsky et al. 1994), i.e. a relation of the type ${\rm O/H} = f(R_{\rm 23})$ was used. It has been shown (Pilyugin 2000; 2001a,b) that the error in the oxygen abundance derived with the one-dimensional calibrations involves a systematic error. The origin of this systematic error is evident. In a general case, the intensity of oxygen emission lines in spectra of H  II regions depends not only on the oxygen abundance but also on the physical conditions (hardness of the ionizing radiation and geometrical factors) in the ionized gas. Thus, when one estimates the oxygen abundance from emission line intensities, the physical conditions in H  II regions should be taken into account. In the $T_{\rm e}$-method this is done via the electron temperature $T_{\rm e}$. In one-dimensional calibrations the physical conditions in H  II regions are ignored. Starting from the idea of McGaugh (1991) that the strong oxygen lines contain the necessary information for determinining accurate abundances in (low-metallicity) H  II regions, it has been shown (Pilyugin 2000, 2001a,b) that the physical conditions in H  II regions can be estimated and taken into account via the excitation parameter P. A two-dimensional or parametric calibration (the so-called "P-method'') has been suggested. A more general relation of the type ${\rm O/H} = f(P, R_{\rm 23})$ is used in the P-method, compared with the relation of the type ${\rm O/H} = f(R_{\rm 23})$ used in one-dimensional calibrations. Thus, the one-dimensial  $R_{\rm 23}$-calibration provides more or less realistic oxygen abundances in high-excitation H  II regions, but yields overestimated oxygen abundances in low-excitation H  II regions. This is in agreement with the results of Kinkel & Rosa (1994), Castellanos et al. (2002), Kennicutt et al. (2003), Garnett et al. (2004), who found that the $R_{\rm 23}$-method yields overestimated oxygen abundances in high-metallicity H  II regions.

It should be stressed that "strong lines-oxygen abundance'' calibrations do not form an uniform family. The calibrations of the first type are the empirical calibrations, established on the basis of H  II regions in which the oxygen abundances are determined through the $T_{\rm e}$-method. Two-dimensional empirical calibrations both at low and high metallicities were recently derived by Pilyugin (2000, 2001a,c). The calibrations of the second type are the theoretical (or model) calibrations, established on the basis of the grids of photoionization models of H  II regions. The two-dimensional theoretical calibrations were recently proposed by Kobulnicky et al. (1999) and Kewley & Dopita (2002). It has been shown (Pilyugin 2003b) that there is a discrepancy between the oxygen abundances in high-metallicity H  II regions determined with the $T_{\rm e}$-method (and/or with the corresponding "strong lines-oxygen abundance'' calibration) and that determined with the model fitting (and/or with the corresponding "strong lines-oxygen abundance'' calibration). Thus, so far, there actually exist two scales of oxygen abundances in H  II regions. The first (empirical) scale corresponds to the oxygen abundances derived with the $T_{\rm e}$- ${\rm method}$ or with empirical calibrations (the P-method). The second (theoretical or model) scale corresponds to the oxygen abundances derived through model fitting or with theoretical (model) calibrations.

Pilyugin (2003b) suggested to use the interstellar oxygen abundance in the solar vicinity, derived with very high precision from the high-resolution observations of the weak interstellar OI$\lambda$1356 absorption line towards the stars, as a "Rosetta Stone'' to make a choice between "theoretical'' and "empirical'' scales of oxygen abundances in high-metallicity H  II regions. The agreement between the value of the oxygen abundance at the solar galactocentric distance traced by the abundances derived in H  II regions through the $T_{\rm e}$-method and that derived from the interstellar absorption lines towards the stars is strong evidence that the classical $T_{\rm e}$-method provides accurate oxygen abundances in H  II regions, i.e. the "empirical'' scale of oxygen abundances in high-metallicity H  II regions is correct. Therefore, at high metallicities the "strong lines-oxygen abundance'' calibrations must be based on the H  II regions with the oxygen abundances derived through the $T_{\rm e}$-method but not on the existing grids of models for H  II regions.

The usual quantities: the oxygen and nitrogen abundance distributions in galaxies (Sect. 2), the correlations between oxygen abundance and macroscopic properties of galaxies (Sects. 3 and 4), and the estimation of effective oxygen yields and their variations among galaxies (Sect. 5) will be considered in this paper.

What is the novelty of our study? All previous investigations of these problems were carried out with the $R_{\rm 23}$-based oxygen abundances. Let us refer to the recent analysis and conclusion of Pagel who is the foundator of the $R_{\rm 23}$-calibrations: "starting from around 1980, the notorious $R_{\rm 23}$ method has been the most widely used method for the oxygen abundance determination. Investigations since then have shown that our calibrations have overestimated oxygen abundances near solar. There is some promise in newly developed strong-line indices and especially in refinements of the $R_{\rm 23}$ method (P-calibration). Until more of these refinements have been applied, abundances near and above solar have to be taken with a grain of salt'' (Pagel 2003). For the present study, the oxygen and nitrogen abundances for a large sample of H  II regions in late-type galaxies will be derived using a homogeneous method: the two-dimensional calibration (P-method). In Sect. 6, the oxygen abundances obtained here will be compared with the recently derived $T_{\rm e}$-based oxygen abundances in the disk of the galaxy NGC 5457 (Kennicutt et al. 2003). The ${\rm O/H} - M_B$ relationship obtained here with the P-based oxygen abundances will be compared with the ${\rm O/H} - M_B$ relathionship obtained recently by Garnett (2002) on the basis of oxygen abundances derived through the $R_{\rm 23}$-calibrations. The comparison between P-based, $T_{\rm e}$-based, and $R_{\rm 23}$-based data provides an additional check of the P-based abundances and shows the difference between the P-based and $R_{\rm 23}$-based data.

2 The chemical abundances

2.1 The algorithm for oxygen and nitrogen abundances determination

The oxygen and nitrogen abundances in H  II regions are derived in the following way. We adopt a two-zone model for the temperature structure within H  II regions.

As the first step, the (O/H)P oxygen abundance in H  II regions is determined with the expression suggested in Pilyugin (2001a)

 \begin{displaymath}12+\log~({\rm O/H})_{P} = \frac{R_{23} + 54.2 + 59.45 P + 7.31 P^{2}} {6.07 + 6.71 P + 0.37 P^{2} + 0.243 R_{23}} , \end{displaymath} (1)

where $R_{\rm 23} =R_{2}$ + R3, $R_{\rm 2} = I_{[\rm OII] \lambda 3727+ \lambda 3729} /I_{\rm H\beta }$, $R_{\rm 3} = I_{[\rm OIII] \lambda 4959+ \lambda 5007} /I_{\rm H\beta }$, and  $P = R_{\rm 3}$/ $R_{\rm 23}$.

Then, the electron temperatures within the [OIII] and [OII] zones are derived. For this purpose the expressions for the oxygen abundance determination from Pagel et al. (1992) and the $T_{\rm e}($[OII] $) - T_{\rm e}$([OIII]) relation from Garnett (1992) are used,

 \begin{displaymath}\frac{\rm O}{\rm H} = \frac{\rm O^+}{\rm H^+} + \frac{\rm O^{++}}{\rm H^+}, \end{displaymath} (2)


 
  $\displaystyle 12+ \log~ ({\rm O}^{++}/{\rm H}^+)$ = $\displaystyle \log \frac{I_{[{\rm OIII}] \lambda 4959 + \lambda 5007}} {I_{{\rm H}_{\beta}}}$  
    $\displaystyle +6.174 + \frac{1.251}{t_3} - 0.55 \log t_3 ,$ (3)


 
      $\displaystyle 12+ \log~ ({\rm O}^{+}/{\rm H}^+)$ = $\displaystyle \log \frac{I_{[{\rm OII}] \lambda 3726 + \lambda 3729}} {I_{{\rm H]}_{\beta}}} + 5.890$  
  + $\displaystyle \frac{1.676}{t_2} - 0.40 \log t_2+\log~ (1+1.35x) ,$ (4)


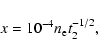\begin{displaymath}x= 10^{-4} n_{\rm e} t_2^{-1/2}, \end{displaymath} (5)

where $n_{\rm e}$ is the electron density in cm-3 (we assume a constant value of $n_{\rm e} = 100$ cm-3), $t_3 = t_{[\rm OIII]}$is the electron temperature within the [OIII] zone in units of 104 K, $t_2 = t_{[\rm OII]}$ is the electron temperature within the [OII] zone in units of 104 K. The t2 value is determined from the equation (Garnett 1992)

 
t2 = 0.7   t3 + 0.3 . (6)

Using the value of O/H derived from Eq. (1) and the measured emission line ratios, Eqs. (2)-(6) can be solved for  $t_{[\rm OII]}$ and  $t_{[\rm OIII]}$.

Assuming $t_2=t_{[\rm NII]}=t_{[\rm OII]}$, the N/O abundance ratio in H  II regions is determined from the expression (Pagel et al. 1992)

 
$\displaystyle \log~({\rm N/O}) = \log~({\rm N^+/O^+})$ = $\displaystyle \log \frac{I_{[\rm NII] \lambda 6548 + \lambda 6584}} {I_{[\rm OII] \lambda 3726 + \lambda 3729}}$  
    $\displaystyle +0.307 - \frac{0.726}{t_2} - 0.02 \log t_2 .$ (7)

Alternatively, the value of t3 can be derived from the following expression for tP = t3 (Pilyugin 2001a)

 \begin{displaymath}t_{P} = \frac{R_{23} + 3.09 + 7.05 P + 2.87 P^{2}} {9.90 + 11.86 P + 7.05 P^{2} - 0.583 R_{23}}\cdot \end{displaymath} (8)

Then the oxygen (and nitrogen) abundances (O/H)tP can be determined from Eqs. (2)-(7) with t3 =tP. The oxygen abundance (O/H)tP is in good agreement with the value of (O/H)P (the differences between (O/H)tP and (O/H)P are usually less than 0.03 dex, see Fig. 12 in Pilyugin 2001a). However, for H  II regions in which most of the oxygen is in the O+ stage, the value of (O/H)tP is less reliable than the value of (O/H)P.

2.2 Central abundances and radial gradients

A compilation of published spectra of H  II regions in late-type galaxies has been carried out. Our list contains more than 1000 individual spectra of H  II regions in 54 late-type galaxies. We performed an extensive compilation of spectra of H  II regions from the literature but our collection does not pretend to be exhaustive. Only the galaxies with available spectra for at least four H  II regions were taken into consideration. Using these spectrophotometric data and the algorithm described in the previous section, the oxygen and nitrogen abundances were derived for our sample of H  II regions.

In investigations of the relationships between the oxygen abundances and the macroscopic properties of spiral galaxies, the concept of the characteristic oxygen abundance has been introduced: it is defined as the oxygen abundance in the disk at a predetermined galactocentric distance. Due to the presence of radial abundance gradients in the disks of spiral galaxies, the choice of the characteristic (or representative) value of the oxygen abundance in a galaxy is not trivial. The value of the oxygen abundance at the B-band effective (half-light) radius of the disk (Garnett & Shields 1987; Garnett 2002), the value of the central oxygen abundance extrapolated to zero radius from the radial abundance gradient (Vila-Costas & Edmunds 1992), the value of the oxygen abundance at $r=0.4R_{\rm 25}$, where $R_{\rm 25}$ is the isophotal (or photometric, or Holmberg) radius, (Zaritsky et al. 1994), and the value of the oxygen abundance at one disk scale length from the nucleus (Garnett et al. 1997), have been used as the characteristic oxygen abundance in a galaxy. To estimate the characteristic oxygen abundance in spiral galaxies, the radial distribution of oxygen abundances within the galaxies should be established.

The radial oxygen abundance distribution in every galaxy is well fitted by the following equation:

 \begin{displaymath}12+\log~({\rm O/H}) = 12+\log~({\rm O/H})_0 + C_{{\rm O/H}} \times (R/R_{25}) , \end{displaymath} (9)

where 12 + log (O/H)0 is the extrapolated central oxygen abundance, $C_{\rm O/H}$ is the slope of the oxygen abundance gradient expressed in terms of dex/ $R_{\rm 25}$, and R/ $R_{\rm 25}$ is the fractional radius (the galactocentric distance normalized to the disk isophotal radius).

The derived parameters of the oxygen abundance distributions are presented in Table 1. The name of the galaxy is listed in Col. 1. The isophotal radius $R_{\rm 25}$ (in arcmin) taken from the Third Reference Catalog of Bright Galaxies (de Vaucouleurs et al. 1991) is given in Col. 2. The extrapolated central $12 + \log~($O/H)0 oxygen abundance and the gradient (the coefficient  $C_{\rm O/H}$ in Eq. (9)) expressed in terms of dex/ $R_{\rm 25}$ are listed in Cols. 3 and 4. The scatter of oxygen abundances around the general radial oxygen abundance trend is reported in Col. 5. The number of available individual spectra of H  II regions in the galaxy is listed in Col. 6. The source(s) for the emission line flux measurements in the H  II regions is(are) reported in Col. 7. The list of references to Table 1 is given in Table 2.

The derived radial distributions of the oxygen abundance in galaxies are presented in Figs. 1 to 5. The oxygen abundances for individual H  II regions are shown by the filled circles. The linear best fits (derived via the least squares method) to these points are presented by solid lines. The galactocentric distances are normalized to the isophotal radius.

 

 
Table 1: The adopted and derived parameters of the radial oxygen abundance distributions in galaxies.
galaxy $R_{\rm 25}$ 12+log (O/H)0 Gradient $\Delta$log (O/H) Number of References
  arcmin    dex/R25  dex H  II regions  
NGC 0224 102.07 8.76 -0.52 0.09 22 BKC82, BKG99, DK81
NGC 0253 14.09 8.71 -0.54 0.10 9 WS83
NGC 0300 11.19 8.49 -0.40 0.13 45 CPG97, DCL88, dORW83,
            EP84, PEB79, WS83
NGC 0598 37.06 8.57 -0.20 0.08 41 BKG99, DTP87, GOS92, KA81,
            MRS85, P70, S71, S75, VPD98
NGC 0628 5.36 8.68 -0.45 0.08 37 BKG99, FGW98, MRS85, vZSH98
NGC 0753 1.32 8.82 -0.21 0.08 12 HBC96
NGC 0925 5.48 8.51 -0.48 0.10 20 vZSH98, ZKH94
NGC 1058 1.62 8.71 -0.32 0.04 6 FGW98
NGC 1068 3.54 8.83 -0.26 0.03 9 OK93, vZSH98
NGC 1232 3.71 8.73 -0.58 0.09 15 vZSH98
NGC 1365 5.61 8.74 -0.70 0.14 53 AEL81, PEB79, RW97
NGC 1637 2.04 8.67 0.02 0.11 14 vZSH98
NGC 2403 11.45 8.52 -0.35 0.11 56 BKG99, GSP99, GSS97, FTP86,
            MRS85, S75, vZSH98
NGC 2442 3.23 8.70 -0.17 0.05 8 R95
NGC 2541 3.30 8.23 0.14 0.14 19 ZKH94
NGC 2805 3.30 8.44 -0.26 0.11 17 vZSH98
NGC 2835 3.62 8.31 -0.07 0.12 17 R95
NGC 2841 4.06 9.12 -0.78 0.01 5 BKG99, OK93
NGC 2903 6.29 8.94 -0.71 0.09 31 MRS85, vZSH98, ZKH94
NGC 2997 5.00 8.66 -0.39 0.08 6 EP84, MRS85
NGC 3031 13.77 8.69 -0.43 0.09 36 BKG99, GS87, OK93, SB84
NGC 3184 3.71 8.97 -0.63 0.06 30 MRS85, vZSH98, ZKH94
NGC 3198 4.26 8.69 -0.64 0.07 14 ZKH94
NGC 3344 3.54 8.63 -0.48 0.09 15 MRS85, VEP88, ZKH94
NGC 3351 3.79 8.90 -0.26 0.05 19 BK02, BKG99, MRS85, OK93
NGC 3521 5.48 8.86 -0.93 0.06 9 ZKH94
NGC 3621 6.74 8.55 -0.44 0.12 26 R95, ZKH94
NGC 4254 2.81 8.94 -0.65 0.06 19 HPC94, MRS85, SSK91
NGC 4258 9.31 8.57 -0.20 0.08 33 BKG99, C00, OK93, ZKH94
NGC 4303 3.23 8.84 -0.72 0.10 22 HPL92, SSK91
NGC 4321 3.79 8.86 -0.37 0.06 10 MRS85, SSK91
NGC 4395 6.59 8.27 -0.02 0.08 16 MRS85, vZSH98
NGC 4501 3.54 8.99 -0.52 0.07 5 SKS96
NGC 4559 5.48 8.48 -0.38 0.13 20 ZKH94
NGC 4571 1.86 8.90 -0.20 0.04 4 SKS96, SSK91
NGC 4651 2.04 8.72 -0.64 0.06 6 SKS96
NGC 4654 2.45 8.85 -0.77 0.06 7 SKS96
NGC 4689 2.18 8.89 -0.41 0.08 5 SKS96, SSK91
NGC 4713 1.35 8.71 -0.73 0.05 4 SKS96
NGC 4725 5.34 9.01 -0.88 0.13 8 ZKH94
NGC 4736 5.61 8.60 -0.26 0.05 16 BKG99, MRS85, OK93
NGC 5033 5.36 9.06 -1.78 0.06 5 ZKH94
NGC 5055 6.29 9.01 -0.83 0.07 5 MRS85
NGC 5068 3.88 8.32 +0.08 0.12 23 MRS85, R95
NGC 5194 5.61 8.92 -0.40 0.06 21 BKG99, DTV91, MRS85
NGC 5236 6.59 8.79 -0.28 0.07 27 BK02, DTJ80, WS83
NGC 5457 14.42 8.80 -0.88 0.09 65 GSP99, KG96, KR94, MRS85, RPT82,
            S71, S75, SS78, TPF89, vZSH98
NGC 6384 3.38 8.90 -0.62 0.05 16 BK02, BKG99, OK93
NGC 6744 10.21 9.00 -0.89 0.04 16 R95
NGC 6946 8.30 8.70 -0.41 0.06 9 FGW98, MRS85
NGC 7331 5.74 8.68 -0.48 0.04 12 BKG99, OK93, ZKH94
NGC 7793 4.78 8.54 -0.50 0.07 22 EP84, MRS85, WS83
IC 0342 22.33 8.85 -0.90 0.12 5 MRS85
IC 5201 4.26 8.27 +0.09 0.14 11 R95



  \begin{figure} \par\includegraphics[width=17.5cm,clip]{a522f01.eps} \end{figure} Figure 1: Oxygen and nitrogen abundances, and nitrogen-to-oxygen abundance ratios versus galactocentric distance for late-type galaxies. The oxygen abundances are shown by filled circles, the linear least-squares fits to these data are presented by solid lines. The nitrogen abundances are shown by open squares, the linear least-squares fits to these data are presented by dashed lines. The nitrogen-to-oxygen abundance ratios are shown by open circles, the linear least-squares fits to these data are presented by solid lines. The galactocentric distances are normalized to the isophotal radius.


   
Table 3: The derived parameters of the radial distributions of the nitrogen abundance and nitrogen-to-oxygen abundance ratios for our sample of galaxies.

Galaxy		 12+log (N/H)0 Gradient $\Delta$log (N/H) Number of log (N/O)0 Gradient $\Delta$log (N/O)
     dex/ $R_{\rm 25}$  dex H  II regions    dex/ $R_{\rm 25}$  

NGC 0224		 8.17 -1.24 0.15 22 -0.59 -0.71 0.09
NGC 0253 7.81 -0.79 0.17 9 -0.90 -0.26 0.09
NGC 0300 7.29 -0.72 0.19 15 -1.17 -0.37 0.12
NGC 0598 7.48 -0.74 0.11 29 -1.08 -0.53 0.10
NGC 0628 7.92 -0.95 0.13 36 -0.77 -0.51 0.09
NGC 0753 8.14 -0.48 0.18 11 -0.66 -0.30 0.14
NGC 0925 7.50 -1.27 0.10 17 -1.00 -0.74 0.04
NGC 1058 7.89 -0.68 0.12 6 -0.81 -0.36 0.08
NGC 1068              
NGC 1232 8.09 -1.22 0.12 15 -0.64 -0.64 0.06
NGC 1365 8.05 -1.20 0.19 53 -0.69 -0.50 0.08
NGC 1637 8.04 -0.18 0.21 14 -0.63 -0.18 0.12
NGC 2403 7.48 -1.01 0.14 50 -1.04 -0.69 0.11
NGC 2442 7.95 -0.26 0.08 8 -0.75 -0.09 0.06
NGC 2541              
NGC 2805 7.44 -0.75 0.12 17 -1.00 -0.49 0.06
NGC 2835 7.38 -0.50 0.16 17 -0.93 -0.43 0.09
NGC 2841 8.80 -1.50 0.05 4 -0.30 -0.75 0.04
NGC 2903 8.62 -1.52 0.14 11 -0.38 -0.76 0.06
NGC 2997 7.94 -0.80 0.17 5 -0.71 -0.39 0.08
NGC 3031 7.96 -0.70 0.17 33 -0.75 -0.23 0.10
NGC 3184 8.60 -1.35 0.08 20 -0.42 -0.69 0.05
NGC 3198              
NGC 3344              
NGC 3351 8.57 -0.75 0.08 13 -0.33 -0.47 0.06
NGC 3521              
NGC 3621 7.74 -0.98 0.17 19 -0.76 -0.65 0.07
NGC 4254 8.19 -0.97 0.11 18 -0.75 -0.33 0.08
NGC 4258 7.70 -0.41 0.07 13 -0.87 -0.18 0.04
NGC 4303 8.21 -1.37 0.23 22 -0.62 -0.66 0.15
NGC 4321 8.12 -0.51 0.10 10 -0.73 -0.14 0.04
NGC 4395 7.18 -0.73 0.17 16 -1.09 -0.72 0.15
NGC 4501 8.75 -1.52 0.18 5 -0.24 -1.00 0.12
NGC 4559              
NGC 4571 8.38 -0.62 0.12 4 -0.52 -0.41 0.09
NGC 4651 8.04 -1.28 0.14 6 -0.67 -0.64 0.08
NGC 4654 8.29 -1.66 0.14 7 -0.56 -0.89 0.11
NGC 4689 8.32 -0.93 0.08 4 -0.57 -0.66 0.08
NGC 4713 7.84 -1.70 0.14 4 -0.88 -0.95 0.12
NGC 4725              
NGC 4736              
NGC 5033              
NGC 5055 8.38 -1.29 0.10 4 -0.60 -0.50 0.03
NGC 5068 7.48 -0.49 0.18 19 -0.03 -0.57 0.10
NGC 5194 8.26 -0.31 0.15 19 -0.61 -0.04 0.10
NGC 5236 8.32 -0.82 0.15 27 -0.46 -0.54 0.09
NGC 5457 8.23 -2.32 0.22 63 -0.56 -1.44 0.16
NGC 6384 8.44 -1.40 0.10 9 -0.47 -0.73 0.05
NGC 6744 8.61 -1.90 0.06 16 -0.38 -1.01 0.04
NGC 6946 8.15 -1.32 0.11 9 -0.54 -0.92 0.07
NGC 7331 7.97 -0.82 0.02 4 -0.74 -0.27 0.02
NGC 7793 7.53 -1.15 0.10 20 -1.02 -0.60 0.08
IC 0342 8.39 -2.38 0.21 5 -0.46 -1.46 0.11
IC 5201 6.99 -0.05 0.25 8 -1.30 -0.09 0.22

As in the case of the oxygen abundance, the radial nitrogen abundance distribution in every galaxy is well fitted by the following equation:

 \begin{displaymath}12+\log~({\rm N/H}) = 12+\log~({\rm N/H})_0 + C_{{\rm N/H}} \times (R/R_{25}) , \end{displaymath} (10)

and the radial distribution of the nitrogen to oxygen abundance ratios is well fitted by the single equation of the type:

 \begin{displaymath}\log~({\rm N/O}) = \log~({\rm N/O})_0 + C_{{\rm N/O}} \times (R/R_{25}) . \end{displaymath} (11)

The derived parameters of the nitrogen abundance distributions are presented in Table 3. The name of the galaxy is listed in Col. 1. The extrapolated central $12 + \log~($N/H)0 nitrogen abundance and the gradient (the coefficient $C_{\rm N/H}$ in Eq. (10)) expressed in terms of dex/ $R_{\rm 25}$ are listed in Cols. 2 and 3. The scatter of nitrogen abundances around the general radial nitrogen abundance trend is reported in Col. 4. The number of available individual spectra of H  II regions in the galaxy with measured nitrogen emission line fluxes is listed in Col. 5. The extrapolated central value of the nitrogen-to-oxygen ratio log (N/O)0 is listed in Col. 6. The radial gradient of the nitrogen-to-oxygen abundance ratio (the coefficient $C_{\rm N/O}$ in Eq. (11)) expressed in terms of dex/ $R_{\rm 25}$ is reported in Col. 7. The scatter of log (N/O) values around the general radial trend is presented in Col. 8. The nitrogen emission line fluxes in the H  II regions were taken from the same sources as the oxygen emission line fluxes (see references in Table 1).

The derived radial distributions of the nitrogen abundances and nitrogen-to-oxygen abundance ratios in galaxies are shown in Figs. 1 to 5. The nitrogen abundances for individual H  II regions are shown by the open squares. The linear best fits to these points are presented by dashed lines. The nitrogen-to-oxygen abundance ratios for individual H  II regions are shown by the open circles. The linear best fits to these points are presented by solid lines.

For the majority of galaxies, all the H  II regions with available oxygen and nitrogen emission line measurements were used in the analysis of the abundance gradients. For a few galaxies, however, some H  II regions were rejected for the following reason. The relationship between oxygen abundance and strong line intensities is double-valued with two distincts parts usually known as the "lower'' and "upper'' branches of the $R_{\rm 23}$-O/H relationship. Thus, one has to know a priori on which of the two branches the H  II region lies. The above expression for the oxygen abundance determination in H  II regions, Eq. (1), is valid only for H  II regions which belong to the upper branch, with $12 + \log~($O/H) higher than $\sim$8.2. It has been known for a long time (Searle 1971; Smith 1975) that disks of spiral galaxies show radial oxygen abundance gradients, in the sense that the oxygen abundance is higher in the central part of the disk and decreases with galactocentric distance. We thus start from the H  II regions in the central part of disks and move outward until the radius R* where the oxygen abundance decreases to $12 + \log~($O/H $) \sim 8.2$. It should be noted that it is difficult to establish the exact value of R* due to the scatter in oxygen abundance values at any fixed radius. An unjustified use of Eq. (1) in the determination of the oxygen abundance in low-metallicity H  II regions beyond R* would result in overestimated oxygen abundances, and would produce a false bend in the slope of abundance gradients (Pilyugin 2003a). Therefore, H  II regions with galactocentric distances larger than R*, those with $12 + \log~($O/H) less than 8.2 were rejected. The list of such galaxies is given in Table 4.

The credibility of the radial oxygen abundance gradients (as well as gradients of the nitrogen abundance and gradients of the nitrogen-to-oxygen abundance ratios) is defined not only by the large number of H  II regions and their small dispersion but also by the distribution of these H  II regions along the galactic radius. For example, the six H  II regions in the galaxy NGC 4651 (Fig. 3) give a much more reliable value of abundance gradients than the 8 H  II regions in the galaxy NGC 4725 (Fig. 4). The estimated values of the radial oxygen abundance gradient in galaxies NGC 1068, NGC 1637, NGC 2841, NGC 3521, NGC 4571, NGC 4713, NGC 4725, NGC 5033, and NGC 5055 are not beyond question.

3 Characteristic oxygen abundance in spirals as a function of ${M}_{\rm B}$, $V_{\rm rot}$, and Hubble type


 

 
Table 4: Galaxies with the observed H  II regions which are expected to not belong to the upper branch of the $R_{\rm 23}- {\rm O/H}$ diagram and the radius R* where the oxygen abundance decreases to around $12 + \log~($O/H) = 8.2.
Galaxy R*/ $R_{\rm 25}$ Galaxy R*/ $R_{\rm 25}$
NGC 300 0.8 NGC 4651 0.8

NGC 925

 0.5 NGC 5033 0.5

NGC 1365

 0.7 NGC 5457 0.6

NGC 2805

 0.9 NGC 7793 0.6

NGC 3198

 0.8 IC 342 0.7


As was noted above, in investigations of the relationships between the oxygen abundances and the macroscopic properties of spiral galaxies, the concept of the characteristic oxygen abundance has been introduced: it is defined as the oxygen abundance in the disk at a predetermined galactocentric distance. Following Zaritsky et al. (1994), the value of the oxygen abundance at $r=0.4R_{\rm 25}$ will be used here as the characteristic oxygen abundance in a galaxy. To derive a reliable galaxy luminosity the accurate value of the distance is necessary. The compilation of the up-to-date distance measurements for our sample of galaxies is discussed in the Appendix.

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f06.eps} \end{figure} Figure 6: The characteristic oxygen abundance as a function of absolute blue magnitude MB for our sample of spiral galaxies. The solid line is the ${\rm O/H} - M_B$ relationship (best fit derived through the least squares method). The dashed lines correspond to the lines shifted by -0.2 dex and +0.2 dex along the vertical axes relatively to the derived ${\rm O/H} - M_B$ relationship. The dotted line is the ${\rm O/H} - M_B$ relationship for our sample of irregular galaxies extrapolated to the luminosity range of spiral galaxies. The line presented by the plus signs is the extrapolated ${\rm O/H} - M_B$ relationship for irregular galaxies derived by Richer & McCall (1995).

The characteristic oxygen abundance in spiral galaxies as a function of absolute blue magnitude MB is shown in Fig. 6. The solid line is the characteristic oxygen abundance-luminosity relationship (linear best fit derived through the least squares method):

 \begin{displaymath}12+\log~({\rm O/H}) = 6.93~ (\pm 0.37) - 0.079~(\pm 0.018)~ M_{B} . \end{displaymath} (12)

The dashed lines correspond to this relation shifted by -0.2 dex and +0.2 dex. Figure 6 clearly demonstrates that there is a correlation between the characteristic oxygen abundance of a galaxy and its blue luminosity. The bulk of the galaxies lies within the band defined by the dashed lines ($\pm$0.2 dex around the best fit). The dotted line in Fig. 6 is the luminosity-metallicity relathionship for irregular galaxies (see below) extrapolated to the luminosity range of spiral galaxies. The line presented in Fig. 6 by the plus signs is the extrapolated O/H - MB relationship for irregular galaxies derived by Richer & McCall (1995). Inspection of Fig. 6 shows that the slope of the derived luminosity-metallicity relationship for spiral galaxies is lower than the one for irregular galaxies.

We have carried out a search in the literature for measurements of rotation velocities for our sample of spiral galaxies. Unfortunately, a measurement of the rotation velocity is not available for 7 galaxies of our sample. On the contrary, there are two or more measurements of rotation velocities for a number of galaxies. The more recent value (or a mean value if the measurements are close to each other) is taken for these galaxies. The adopted values of the rotation velocity for the galaxies and corresponding reference(s) are listed in Tables 5 and 6.

 

 
Table 5: The characteristic oxygen abundance (at $r=0.4R_{\rm 25}$), gas (atomic and molecular) mass fraction $\mu $, atomic and molecular hydrogen contents, and rotation velocity for spiral galaxies from our sample. The oxygen abundance is given as 12+log (O/H).

Galaxy		 O/H $\mu $ $M_{\rm H_I}/L_B$ $M_{\rm H_2}$/LB $V_{\rm rot}$ References
NGC     $M_{\odot}$/$L_{\odot}$ $M_{\odot}$/$L_{\odot}$ km s-1 ( $M_{\rm H_I}$; $M_{\rm H_2}$; $V_{\rm rot}$)

224		 8.55 0.09 0.15 0.004 269 DD, HR; KDI; H
253 8.50 0.12 0.15 0.057 215 SD, HR, HS; YXT, SNK; PCG, H
300 8.33 0.38 0.93 .... 95 RCC, HR; -; PCB, H, RCC
598 8.49 0.24 0.46 0.004 116 DD, HR; YXT; H, CS
628 8.51 0.35 0.76 0.052 153 WKA, R, SD, DD; NN, YXT, S, HTR; NNK
753 8.73 0.18 0.33 .... 215 Sh, BSC; -; RFT, AMB
925 8.32 0.28 0.58 0.013 127 WKA, R, DD, HHG; S; KS
1058 8.58 0.35 0.79 0.017 .... SD, vKS; S; -
1068 8.73 0.10 0.04 0.117 220 HS, HBS; YXT; HB
1232 8.50 0.19 0.35 .... 229 SD, RMG, ZB, BMR; -; ZB, BMR
1365 8.46 0.21 0.27 0.130 285 OH, RMG, JM; SJL; OH
2403 8.39 0.31 0.67 0.004 135 WKA, R, HR; YXT, S; H, BBS
2442 8.64 0.11 0.18 0.013 .... BM, RMG, RKS; BWR; -
2541 8.29 0.43 1.16 .... .... R, BR, HS, HHM; -; -
2805 8.33 0.29 0.63 .... 78 Sh, Re, BCH; -; Re
2835 8.28 0.19 0.35 .... 120 SD, RMG, BMR; -; BMR
2841 8.81 0.16 0.23 0.052 318 R, B, HS; YXT; BBS, B
2903 8.66 0.15 0.22 0.043 223 WKA, HR, HS, HHG, HHM; NN, YXT, S, HTR; NNK, BBS
2997 8.51 0.13 0.22 .... 195 SD, RMG; -; P, MM
3031 8.52 0.10 0.16 0.004 240 ADS, HR; S; H, Ro
3184 8.72 0.21 0.34 0.052 .... Sh, HS; NN, YXT, S; -
3198 8.43 0.28 0.57 .... 154 WKA, R, SD; -; ABB, HRG, BBS
3344 8.43 0.29 0.60 0.030 .... R, HHG; YXT, S; -
3351 8.80 0.10 0.14 0.035 236 Sc, HS; YXT, S, HTR; Bu
3521 8.49 0.22 0.33 0.091 235 R; NN, YXT, S, HTR; NNK, CG
3621 8.38 0.34 0.78 .... 163 RMG, HR, BMR; -; BMR
4254 8.68 0.18 0.20 0.126 264 SD, Wb, HRb; YXT, SKB, SEC, KY; NNK, GGK, Wb
4258 8.49 0.14 0.23 0.022 200 WKA, R, HS; YXT, HTR, CD; AS
4303 8.55 0.17 0.20 0.104 178 Sh, Wb, HS, HRb; YXT, SKB, HTR, KY; NNK, GGK, Wb
4321 8.71 0.15 0.12 0.139 236 Sh, Wa, HRb; YXT, SKB, HTR, KY; GGK, Wa
4395 8.26 0.43 1.07 0.083 83 WKA, R, HR, HS, HHM; SEC; BB
4501 8.78 0.09 0.07 0.083 295 Wa, HRb; YXT, SKB, KY; NNK, GGK, Wa, KS
4559 8.33 0.27 0.54 0.017 129 BR, Sh, HS; S; KS
4571 8.82 0.12 0.14 0.078 165 Wb, HR, HRb; YXT, KY; Wb
4651 8.46 0.19 0.33 0.035 250 Wa, HHG, HRb; YXT, SKB, KY; Wa
4654 8.54 0.15 0.20 0.070 195 Sh, Wb, HRb; YXT, SKB, KY; GGK, Wb
4689 8.72 0.10 0.05 0.104 182 Wb, HRb; YXT, SKB, SEC, KY; GGK, Wb
4713 8.42 0.29 0.58 0.017 137 Sh, Wb, HRb, HHM; YXT, KY; Wb
4725 8.66 0.14 0.18 0.065 249 WKA, GDH, WAD; YXT -; Bu, WAD
4736 8.50 0.05 0.05 0.022 198 R,BHS, HR; NN, YXT, S, HTR; NNK, Bu, BHS
5033 8.35 0.28 0.50 0.096 228 WKA, R, SD, B; YXT, SEC, HTR; NNK, HAS, B
5055 8.68 0.24 0.42 0.061 210 WKA, R, B; YXT, S, HTR; TM, B
5068 8.35 0.18 0.34 .... .... RMG, HR; -; -
5194 8.75 0.14 0.14 0.109 242 WG, DD; YXT, S, HTR; KN, WG
5236 8.68 0.31 0.57 0.104 205 SD, HR, DD; YXT; VPD
5457 8.44 0.32 0.69 0.026 180 R, DD, HR; S, HTR; GW
6384 8.65 0.19 0.29 0.070 200 Sh, HHM; YXT; SCR
6744 8.64 0.31 0.67 .... .... RMG; -; -
6946 8.53 0.15 0.22 0.048 179 R, DD, HR; YXT, S, HTR; NNK, H, CCB
7331 8.48 0.18 0.24 0.078 262 R, Sh, B; NN, YXT, HTR, HHM; NNK, BBS, B, KS
7793 8.34 0.18 0.31 0.013 117 CP, RMG, HR, BMR; SEC; CP, BMR
IC 0342 8.49 0.16 0.26 0.026 192 R, HR; YXT, S; H
IC 5201 8.31 0.36 0.86 .... 97 BM, RMG, BMR; -; BMR


The characteristic oxygen abundance in spiral galaxies as a function of rotation velocity  $V_{\rm rot}$ is shown in Fig. 7. The solid line is the oxygen abundance-rotation velocity relationship (linear best fit)

 \begin{displaymath}12+\log~({\rm O/H}) = 8.18~(\pm 0.06) + 0.00179~(\pm0.00031)~ V_{\rm rot} . \end{displaymath} (13)

The dotted lines correspond to this relation shifted by -0.2 dex and +0.2 dex. Figure 7 shows that the characteristic oxygen abundance of a galaxy correlates with its rotation velocity. The deviation of an individual galaxy from the general trend is usually less than 0.2 dex. The mean value of the scatter in the characteristic oxygen abundances at a given rotation velocity is 0.12 dex for 46 points.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f07.eps} \end{figure} Figure 7: The characteristic oxygen abundance as a function of rotation velocity for our sample of spiral galaxies. The solid line is the ${\rm O/H} -V_{\rm rot}$ relationship (best fit derived through the least squares method). The dashed lines correspond to the lines shifted by -0.2 dex and +0.2 dex relatively to the derived ${\rm O/H} -V_{\rm rot}$ relationship.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f08.eps} \end{figure} Figure 8: The characteristic oxygen abundance as a function of Hubble type, expressed in the terms of T-type, for our sample of spiral galaxies. The solid line is the O/H-T relationship derived through the least squares method. The dashed lines correspond to the lines shifted by -0.2 dex and +0.2 dex relatively to the derived O/H-T relationship.

The characteristic oxygen abundance in spiral galaxies as a function of morphological type, expressed in terms of T-type, is shown in Fig. 8. The solid line is the characteristic oxygen abundance-T relationship (best fit)

 \begin{displaymath}12+\log~({\rm O/H}) = 8.81~(\pm 0.06) - 0.059~(\pm 0.011)~ T . \end{displaymath} (14)

The dotted lines correspond to this relation shifted by -0.2 dex and +0.2 dex. Figure 8 shows that the characteristic oxygen abundance of a galaxy correlates with its morphological type. The deviation of an individual galaxy from the general trend usually does not exceed the value $\pm$0.2 dex, as in the cases of the O/H - MB and the O/H -  $V_{\rm rot}$ diagrams. The mean value of the scatter in the characteristic oxygen abundances at a given morphological type is 0.13 dex for 53 points.

One can see that the characteristic oxygen abundance correlates well with both the absolute blue luminosity, the rotational velocity, and the morphological type; the correlation with the rotation velocity perhaps being slightly tighter.

4 Comparison between O/H- ${M}_{\rm B}$ relationship for spiral and irregular galaxies

Zaritsky et al. (1994) found that the characteristic gas-phase oxygen abundance-luminosity relation of spiral galaxies extends almost directly to the luminosity-metallicity relationship of irregular galaxies. Melbourne & Salzer (2002) and Lamareille et al. (2004) found that the slope of the oxygen abundance-luminosity relationship for high-luminosity galaxies is steeper than when dwarf galaxies are considered alone and may be evidence that the relationship is not linear over the full luminosity range. Garnett (2002) concluded that the metallicity-luminosity correlation shows a roughly uniform growth in the average present-day O/H abundance over 11 mag in absolute blue magnitude MB. Let us compare the derived metallicity-luminosity relationship for spiral galaxies with that for irregular galaxies.

The irregular galaxies were selected from the samples of Richer & McCall (1995) and Pilyugin (2001c). The luminosities and oxygen abundances for irregular galaxies are taken from these studies and are listed in Cols. 3 and 4 of Table 7. The values of the gas mass fraction in the irregular galaxies were estimated taking into account the atomic hydrogen mass only since the molecular hydrogen in dwarf irregular galaxies is only a small fraction of the total gas mass. The H  I fluxes were taken mainly from Karachentsev et al. (1999). The derived values of gas mass fraction $\mu $ in irregular galaxies are reported in Col. 5 of Table 7. The rotation velocities for irregular galaxies taken from the literature, the values of the rotation velocity and corresponding references to the sources are listed in Cols. 6 and 7 of Table 7.


 

 
Table 7: Data for irregular galaxies. References - (a) Lee et al. (2003); (b) Pilyugin (2001c); (c) Karachentsev et al. (1999); (d) Skillman et al. (1988); (e) Hoffman et al. (1996); (f) Côté et al. (2000); (g) Kinman & Davidson (1981); (h) Richer & McCall (1995); (i) Wilcots & Miller (1998); (j) Alves & Nelson (2000).
galaxy T-type MB 12+logO/H $\mu $ $V_{\rm rot}$ References
          km s-1 (MB, O/H, $\mu $, $V_{\rm rot}$)
Sextans B 10 -14.02 7.86 0.43 24 a, b, c, c
Sextans A 10 -14.04 7.71 0.60 37 a, b, c, d
GR 8 10 -12.19 7.60 0.54 13 a, b, c, e
WLM 10 -13.92 7.78 0.44 31 a, b, c, c
UGC 4483 10 -12.80 7.47 0.68 22 b, b, c, c
UGC 5423 10 -12.90 7.81 0.36 27 b, b, c, c
UGC 6456 10 -13.24 7.71 0.68 24 b, b, c, c
Leo A 10 -11.53 7.27 0.58 16 a, b, c, c
UGCA 292 10 -11.43 7.22 0.83 12 b, b, c, c
DDO 167 10 -13.30 7.81 0.50 17 b, b, c, c
SagDIG 10 -12.10 7.48 0.51 19 b, b, c, f
A1116+51 10 -14.99 7.76 0.69 - b, b, g, -
A1228+12 10 -14.57 7.79 0.46 - b, b, g, -
A2228-00 10 -14.57 7.79 0.65 - b, b, g, -
ESO 245-G05 10 -15.50 7.94 0.66 48 b, b, c, i
DDO 53 10 -13.35 7.75 0.75 - b, b, c, -
DDO 190 10 -15.10 7.74 0.51 - b, b, c, -
Holmberg II 10 -15.98 7.92 0.57 34 a, h, c, c
IC 10 10 -15.82 8.22 0.22 30 a, h, c, i
IC 1613 10 -14.53 7.71 0.46 21 a, h, c, e
IC 2574 9 -16.85 8.08 0.50 50 h, h, c, c
IC 4662 10 -15.64 8.09 0.30 48 h, h, c, c
LMC 9 -17.73 8.35 0.20 72 h, h, c, j
NGC 1560 7 -16.17 8.02 0.27 59 h, h, c, c
NGC 2366 10 -16.28 7.92 0.48 44 a, h, c, c
NGC 3109 9 -15.30 8.06 0.47 49 a, h, c, c
NGC 4214 10 -17.82 8.23 0.37 - h, h, c, -
NGC 5408 10 -15.60 8.01 0.35 38 h, h, c, c
NGC 55 9 -18.07 8.34 0.20 71 h, h, c, c
SMC 9 -16.35 8.03 0.49 21 h, h, c, c


The oxygen abundances in spiral and irregular galaxies are plotted versus absolute blue magnitude MBin Fig. 9. The filled circles in Fig. 9 are spiral galaxies, and the solid line is the O/H - MBrelationship for spiral galaxies, Eq. (12). The open squares in Fig. 9 are irregular galaxies from Table 7. The dashed line is the O/H - MB relationship (best fit) for irregular galaxies

 \begin{displaymath}12+\log~({\rm O/H}) = 5.80~(\pm 0.17) - 0.139~(\pm 0.011)~ M_{B}. \end{displaymath} (15)

The dotted line is the O/H - MB relationship for irregular galaxies

 \begin{displaymath}12+\log~({\rm O/H}) = 5.59~(\pm 0.54) - 0.153~(\pm 0.025)~ M_{B} \end{displaymath} (16)

derived by Lee et al. (2003). The O/H - MB relationship for irregular galaxies

 \begin{displaymath}12+\log~({\rm O/H}) = 5.67~(\pm 0.48) - 0.147~(\pm 0.029)~ M_{B} \end{displaymath} (17)

derived by Richer & McCall (1995) is presented by the plus signs. Inspection of Fig. 9 (as well as the comparison between Eqs. (15)-(17)) shows that the O/H - MB relationship for our sample of irregular galaxies agrees, within the uncertainties, with that from Lee et al. (2003) and from Richer & McCall (1995). Figure 9 shows a familiar oxygen abundance-luminosity correlation for late-type galaxies, an increase in metallicity with luminosity over the full range of absolute blue magnitude, MBfrom $\sim$-22 to $\sim$-11. Comparison between Eqs. (12) and (15) shows that the O/H - MB relationships for spiral and irregular galaxies have slightly different slopes.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f09.eps} \end{figure} Figure 9: The characteristic oxygen abundance as a function of absolute blue magnitude MB for our sample of spiral galaxies (the filled circles). The solid line is the best (linear least-squares) fit to these data. The open squares are oxygen abundances in irregular galaxies, the dashed line is the metallicity-luminosity relationship for our sample of irregular galaxies. The dotted line is the O/H - MB relationship for irregular galaxies derived by Lee et al. (2003). The O/H - MB relationship for irregular galaxies derived by Richer & McCall (1995) is presented by the plus signs.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f10.eps} \end{figure} Figure 10: The characteristic oxygen abundance as a function of rotation velocity $V_{\rm rot}$ for our sample of spiral galaxies (the filled circles). The solid line is the best (linear least-squares) fit to these data. The open squares are oxygen abundances in irregular galaxies, the dashed line is the linear least-squares fit to these data.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f11.eps} \end{figure} Figure 11: The absolute blue magnitude MB as a function of the rotation velocity. The filled circles are spiral galaxies, the open squares are irregular galaxies.

Figure 10 shows the oxygen abundance in spiral (filled circles) and irregular (open squares) galaxies as a function of rotation velocity  $V_{\rm rot}$. The most prominent feature is the bend in the O/H - $V_{\rm rot}$relation. Garnett (2002) also found that the correlation between O/H and  $V_{\rm rot}$ does not increase steadily but rather turns over for rotation speeds greater than 125 km s-1. It is worth noting that the presence of the bend in the O/H - $V_{\rm rot}$ relation does not necessary imply the existence of a bend in the O/H - MB trend. Figure 11 shows the absolute blue magnitude MBas a function of the rotation velocity  $V_{\rm rot}$ for spiral (filled circles) and irregular (open squares) galaxies. Inspection of Fig. 11 shows that the correlation between MB and $V_{\rm rot}$ is not linear but rather shows a bend. This bend in the O/H - $V_{\rm rot}$ trend would thus occur even if the increase in oxygen abundance with luminosity can be described by a single linear function over the full magnitude range.

5 The effective oxygen yields

The observed oxygen abundance in a galaxy is defined not only by the astration level but also by the mass exchange between a galaxy and its environment. The latter can alter the relation between oxygen abundance and gas mass fraction; it mimics the variation in the oxygen yield. To investigate the possibility of a varying yield, it is useful to define the "effective'' oxygen yield, $y_{\rm eff}$, as the yield that would be deduced if a system was assumed to behave as in the simplest model of chemical evolution (Edmunds 1990; Vila-Costa & Edmunds 1992)

 \begin{displaymath}y_{\rm eff} = \frac{z_{\rm O}}{\ln (\frac{1}{\mu})} \cdot \end{displaymath} (18)

Since we used the oxygen abundances given by number relative to hydrogen, while the value of z$_{\rm O}$ in Eq. (18) is given in units of mass fraction, the conversion for oxygen from Garnett et al. (1997) and Garnett (2002)

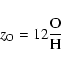\begin{displaymath}z_{\rm O} = 12 \frac{\rm O}{\rm H} \end{displaymath} (19)

was adopted.

5.1 The gas mass fractions

The gas fraction $\mu $ in a galaxy is estimated using the following standard relation:

 \begin{displaymath}\mu = \frac{M_{\rm H_I} + M_{\rm H_2}}{M_{\rm H_I} + M_{\rm H_2} + k~L_B} , \end{displaymath} (20)

where $M_{\rm H_I}$ is the mass of atomic hydrogen in the galaxy, $M_{\rm H_2}$ is the mass of molecular hydrogen in the galaxy (both  $M_{\rm H_I}$ and  $M_{\rm H_2}$ are corrected for the helium and heavy element contribution), LB is the blue luminosity of the galaxy, and k is the mass-to-luminosity ratio. The mass of atomic hydrogen is derived in a standard way using the measured H  I flux taken from literature and the adopted distance (Table A.1). If the mass of atomic hydrogen instead of the H  I flux measurement is reported in literature, this value is rescaled to the adopted distance. The atomic hydrogen masses expressed in terms of  $M_{\rm H_I}$/LB and corresponding references to the H  I flux measurements are listed in Tables 5 and 6.

The mass of molecular hydrogen can only be estimated with indirect methods. The commonly accepted method is the use of the CO line flux and X conversion factor between the flux in the CO line and the amount of molecular hydrogen. The conversion factor X = N(H2)/I(CO) strongly depends on the physical properties of the interstellar medium which are known to vary from galaxy to galaxy. The best-estimated values of the conversion factor for a sample of well-studied nearby galaxies span the range $0.6 \leq X \leq 10 \times 10^{20}$ mol cm-2 (K km s-1)-1 (Boselli et al. 2002). The high values of the conversion factor correspond to low-luminosity irregular galaxies, and the low values of the conversion factor are found in spiral galaxies. Then the value of $X = 1 \times 10^{20}$ mol cm-2 (K km s-1)-1 (including helium and heavy elements contribution) is adopted here for spiral galaxies. The molecular gas content is derived with this conversion factor using the measured CO flux from literature and distance (Table A.1). If the mass of molecular hydrogen instead of the CO flux measurement is reported in the literature, this value is rescaled to the adopted distance and adopted conversion factor. The molecular hydrogen masses expressed in terms of  $M_{\rm H_2}$/LB and corresponding references to the CO flux measurements are given in Tables 5 and 6.

The mass of the stellar component of the galaxy is estimated by converting the measured luminosity to mass via the mass-to-luminosity ratio. It is difficult to get a reliable estimation of the mass-to-luminosity ratio for individual galaxies. The $\mu $ and $\mu $-dependent values will be used here only for examination of the general trends of these values with luminosity and rotation velocity but not for examination of individual galaxies. A similar investigation was carried out by Garnett (2002). He considered the impact of the choice of the mass-to-luminosity ratio on the trends by comparing the trends derived with the color-based mass-to-luminosity ratio and constant mass-to-luminosity ratio. Garnett (2002) has found that the trends are fairly robust against the choice of mass-to-luminosity ratio. Based on this conclusion, a constant value of the mass-to-luminosity ratio k=1.5 is adopted here for all spiral galaxies, and k=1 is adopted for all irregular galaxies.

The derived values of the gas mass fraction in galaxies $\mu $ are listed in Table 5 (Col. 3). Unfortunately, for several spiral galaxies on our list no measurement of the CO flux is available. For these galaxies, the gas mass fraction is based on the atomic hydrogen mass only and is a lower limit. Taking into account that the average value is $M_{\rm H_2}$/ $M_{\rm H_I} = 0.14$(Boselli et al. 2002), one can hope that the use of a lower limit instead of the estimated value of gas fraction for several galaxies is quite acceptable.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f12.eps} \end{figure} Figure 12: Gas mass fraction as a function of the absolute blue magnitude MB. The filled circles are spiral galaxies, the open squares are irregular galaxies. The solid line is the $\mu - M_B$ relationship for spiral galaxies, the dashed line is the $\mu - M_B$ relationship for irregular galaxies.

The gas mass fraction in spiral galaxies as a function of absolute blue magnitude MB is shown by the filled circles in Fig. 12. The solid line is the gas mass fraction-luminosity relationship (best fit determined via the least squares method) for spiral galaxies

 \begin{displaymath}\mu = 1.264~(\pm 0.220) + 0.0522~(\pm 0.0109)~ M_{B} . \end{displaymath} (21)

The open squares in Fig. 12 are irregular galaxies. The dashed line is the gas fraction-luminosity relationship (best fit) for irregular galaxies

 \begin{displaymath}\mu = 1.289~(\pm 0.198) + 0.0542~(\pm 0.0134)~ M_{B} . \end{displaymath} (22)

Comparison between Eqs. (21) and (22) shows that the $\mu - M_B$ relationship for spiral galaxies coincides remarkably well with the $\mu - M_B$ relationship for irregular galaxies. It can also be seen in Fig. 12 that the gas mass fraction-luminosity relation for spiral galaxies is a direct continuation of the gas mass fraction-luminosity relationship for irregular galaxies.

5.2 The effective oxygen yields

The derived effective oxygen yields are presented as a function of absolute blue magnitude MB in Fig. 13a and as a function of rotation velocity  $V_{\rm rot}$ in Fig. 13b.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f13.eps} \end{figure} Figure 13: a) Effective oxygen yield as a function of the absolute blue magnitude MB. The filled circles are spiral galaxies, the open circles are irregular galaxies. The solid line is the $y_{\rm eff} - M_{B}$ relation for spiral galaxies (best fit). The dashed line corresponds to the mean $y_{\rm eff} = 0.00268$ for spiral galaxies. b) Effective oxygen yield as a function of the rotation velocity. Symbols are the same as in panel  a).

Inspection of Figs. 13a,b shows that there is only a hint of trends of the effective oxygen yield with luminosity and rotation velocity. The formal best fit to the log ( $y_{\rm eff}$) - MB relation (solid line in Fig. 13a) is

 \begin{displaymath}\log y_{\rm eff} = -2.834~(\pm 0.371) - 0.0120~(\pm 0.0183)~ M_{B} . \end{displaymath} (23)

The mean value of the deviation of individual galaxies from the general trend is 0.13 dex. The formal best fit (least squares method) to data for spiral galaxies, the log ( $y_{\rm eff}$) - $V_{\rm rot}$ relation (solid line in Fig. 13b) is

 \begin{displaymath}\log y_{\rm eff} = -2.698~(\pm 0.065) + 0.000496~(\pm 0.000321)~ V_{\rm rot} . \end{displaymath} (24)

The mean value of the deviation of individual galaxies from the general trend is 0.12 dex. The mean value of the effective oxygen yield in spiral galaxies is $y_{\rm eff} = 0.00268$. The dashed line in Figs. 13a,b corresponds to the mean value of  $y_{\rm eff}$. Taking into account the large scatter of points in the log ( $y_{\rm eff}$) - MB and the log ( $y_{\rm eff}$) - $V_{\rm rot}$ diagrams, it is difficult to establish firmly how real are the trends of the effective oxygen yield in spiral galaxies with luminosity and rotation velocity. More accurate data are needed to confirm or reject these trends. Here we can only conclude that the effective oxygen yield in spiral galaxies remains approximatively constant.

It is widely accepted that the mass exchange (gas infall and/or galactic wind) between a galaxy and its environment plays a major role in the evolution of galaxies. Gas infall and galactic winds produce a shift of the position of a galaxy in the $\mu - {\rm O/H}$ diagram towards lower oxygen abundances compared to the predictions of the closed-box models (see e.g. Mouhcine & Contini 2002). The location of spiral and irregular galaxies in the $\mu $-O/H diagram together with the predictions of the closed-box model

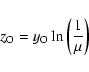\begin{displaymath}z_{\rm O} = y_{\rm O} \ln \left(\frac{1}{\mu}\right) \end{displaymath} (25)

are presented in Fig. 14a.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f14.eps} \end{figure} Figure 14: a) The positions of spiral (filled circles) and irregular (open squares) galaxies in the $\mu $ - O/H diagram together with the predictions of the closed-box models. The solid curve is the prediction of the closed-box model with oxygen yield y0 = 0.00268(the mean value of the effective oxygen yields derived for spiral galaxies). The dashed curves correspond to the predictions of the closed-box models with oxygen yields $y=1.5\times y_0$ and y=y0/1.5. The dotted curve is the prediction of the closed-box models with oxygen yields y=y0/4. b) The oxygen abundances extrapolated to zero radius (open triangles) and extrapolated to the isophotal radius  $R_{\rm 25}$ (filled triangles) in spiral galaxies with well defined radial oxygen abundance gradients together with the $\mu - {\rm O/H}$ track predicted by the closed-box model with oxygen yield y0 = 0.00268. The large plus sign is the position of the solar vicinity region.

The solid line in Fig. 14a is the prediction of the closed-box model for the evolution of galaxies with oxygen yield $y_0 = y_{\rm eff} = 0.00268$. As can be seen in Fig. 14a, the positions of spiral galaxies in the $\mu $ - O/H diagram are close to the track predicted by the closed-box model. The mean value of the O/H deviation of the individual galaxies from the closed-box model is 0.13 dex. The dashed lines in Fig. 14a correspond to the predictions of the closed-box models with oxygen yields $y=1.5\times y_0$ and y=y0/1.5. The majority of spiral galaxies is located within the band defined by dashed lines.

It is well known that the closed-box model predicts many more low-metallicity stars than are observed in the solar neighbourhood, the so called "G-dwarf'' paradox. Various versions of the infall model, in which an infall of gas onto the disk takes place for a long time, have been suggested (Tosi 1988a,b; Pagel & Tautvaisiene 1995; Pilyugin & Edmunds 1996a,b; Chiappini et al. 2001, among many others) to explain the observed metallicity function. An infall model has also been applied to other spiral galaxies (Díaz & Tosi 1986; Mollá et al. 1996, 1997; Pilyugin et al. 2002; Mouhcine & Contini 2002; Chiappini et al. 2003). It is thus generally accepted that gas infall can play an important role in the chemical evolution of disks of spiral galaxies. Therefore, the fact that the positions of spiral galaxies are close to the position of the track of the closed-box model may appear surprising. It has been shown (Pilyugin & Ferrini 1998) that the present-day position of a system in the $\mu - {\rm O/H}$ diagram is governed by its evolution in the recent past and is, in fact, independent of its evolution on long timescales. Therefore, the fact that the present-day position of spiral galaxies is close to the position of the closed-box model is not in conflict with the model, in which an infall of gas onto disk takes place for a long time (which is necessary to satisfy the observed abundance distribution function and the age-metallicity relation in the solar neighbourhood) since these observational data reflect the evolution of a system in the distant past. Of course, the simple model of chemical evolution of galaxies can be used only as the first-order approximation. To establish a more accurate relation between the present-day values of oxygen abundance and gas mass fraction in a galaxy, an appropriate model of chemical evolution should be developed (e.g. Pagel & Tautvaisiene 1995).

Inspection of Figs. 13a,b shows that the values of the effective oxygen yield in irregular galaxies are lower than that in spiral galaxies. The effective oxygen yield in irregular galaxies shows a clear trend with luminosity and rotation velocity. The positions of irregular galaxies in the $\mu $ - O/H diagram are systematically shifted towards lower oxygen abundances compared to the predictions of the closed-box model with oxygen yield y0typical for spiral galaxies. This suggests that the mass exchange between a galaxy and its environment (galactic winds) plays an important role in the chemical evolution of irregular galaxies. The dotted line in Fig. 14a corresponds to the closed-box models with oxygen yield y=y0/4. Only two irregular galaxies from our sample are located below the dotted line. This implies that irregular galaxies lose only a moderate part of their manufactured heavy elements. Two facts are important: i) the smooth variation in gas mass fraction in spiral and irregular galaxies with luminosity over the full luminosity range; ii) the growth of effective oxygen yield with increasing luminosity from $M_{B} \sim -11$ to -18 which remains approximately constant for more luminous galaxies. These two facts taken together allow us to suggest that the difference in the slopes of the O/H - MB relationships for spiral and irregular galaxies is real and that the variation of the effective oxygen yield with luminosity is responsible for the bend in the luminosity-metallicity relationship.

How realistic is the value of the mean oxygen yield derived here for spiral galaxies? Figure 14b shows the oxygen abundances extrapolated to zero radius in spiral galaxies together with the $\mu - {\rm O/H}$ track predicted by the closed-box model with the derived oxygen yield. One can expect that the central oxygen abundances in the most evolved spiral galaxies correspond to the oxygen abundance when the system had exhausted the gas. As can be seen in Fig. 14b, the upper limit of the central oxygen abundances in spiral galaxies is close to the oxygen abundances predicted by the model with derived oxygen yield when the gas mass fraction is close to zero. The present-day oxygen abundance at the solar galactocentric distance in our Galaxy is about $12 + \log~($O/H) = 8.50 as traced by H  II regions (Rodríguez 1999; Caplan et al. 2000; Deharveng et al. 2000; Pilyugin et al. 2003) and derived from the interstellar absorption lines towards the stars (Meyer et al. 1998; Sofia & Meyer 2001), and for the present-day gas mass fraction, 0.15-0.20 appears to be a reasonable value (Malinie et al. 1993). As shown in Fig. 14b, the position of the solar vicinity (large plus sign) is close to the $\mu - {\rm O/H}$ track predicted by the closed-box model with derived oxygen yield. Thus, the data in Fig. 14b imply that the value of the oxygen abundance derived here is quite realistic.

It should be noted that the value of the oxygen yield is derived here on the basis of gas-phase oxygen abundances. Some fraction of the oxygen is locked into dust grains in H  II regions. Meyer et al. (1998) obtained a limit to the dust-phase oxygen abundance in the interstellar medium in the vicinity of the Sun. Assuming various mixtures of oxygen-bearing grain compounds, they found that it is difficult to increase the oxygen dust fraction beyond $\sim$0.14 dex, simply because the requisite metals are far less abundant than oxygen. Esteban et al. (1998) found that the fraction of the dust-phase oxygen abundance in the Orion nebula is about 0.1 dex. Thus, the true value of the oxygen yield is slightly higher than the value obtained here and is around y = 0.003.

6 Comparison with previous studies

How reliable are the results obtained here? How significant is the difference between the P-based and the $R_{\rm 23}$-based ${\rm O/H} - M_B$ relationships? The validity of the oxygen abundances obtained here can be tested by a comparison with the $T_{\rm e}$-based oxygen abundances determined recently in the disk of the galaxy NGC 5457 by Kennicutt et al. (2003). It is worth noting that the comparison of oxygen abundances derived through the P-method and through the $T_{\rm e}$-method has already been made for the galaxy NGC 5457 (Pilyugin 2001b), as well as for the Milky Way (Pilyugin et al. 2003), and for a sample of star-forming emission-line galaxies from the KPNO International Spectroscopic Survey (KISS) (Melbourne et al. 2004). A good agreement has been found in all cases. Recently Kennicutt et al. (2003) obtained new spectra for a number of H  II regions in the disk of the galaxy NGC 5457 and determined the $T_{\rm e}$-based abundances. They compared their temperature-based abundances with those derived for the same H  II regions using different calibrations. According to their Fig. 14, the validity of the P-based abundances is questionable. The data from Kennicutt et al. (2003) have been used here to test the validity of the P-calibration as well as other popular calibrations. To enlarge the comparison we have also included direct abundance measurements of H  II regions in this galaxy from the literature (the compilation of the spectral data was performed by Pilyugin 2001b) as well as direct abundance measurements of H  II regions in other galaxies (compilation from Pilyugin 2001a).

  \begin{figure} \par\includegraphics[width=8cm,clip]{a522f15.eps} % \end{figure} Figure 15: Comparison of temperature-based oxygen abundances O/H $_{T_{\rm e}}$ with those derived with different calibrations for high-metallicity H  II regions. a) The O/HP - O/H $_{T_{\rm e}}$ diagram. The filled circles represent the O/H $_{T_{\rm e}}$ abundances for H  II regions in the galaxy NGC 5457 from Kennicutt et al. (2003), the filled triangles are the O/H $_{T_{\rm e}}$ abundances for H  II regions in this galaxy from other authors. The open squares are the O/H $_{T_{\rm e}}$ abundances for H  II regions in other galaxies. The O/HP abundances are derived through the high-metallicity P-calibration. The solid line is the equal-value line, the dashed lines are shifted by +0.15 dex and -0.15 dex. b) The O/H $_{\rm ZKH}$ - O/H $_{T_{\rm e}}$ diagram for the same H  II regions. The O/H $_{\rm ZKH}$ abundances are derived using the high-metallicity calibration from Zaritsky et al. (1994). c) The O/H $_{\rm KKP}$ - O/H $_{T_{\rm e}}$ diagram for the same H  II regions. The O/H $_{\rm KKP}$ abundances are derived using the high-metallicity calibration from Kobulnicky et al. (1999).

Figure 15a shows the O/HP - O/H $_{T_{\rm e}}$ diagram (the analog of Fig. 14 from Kennicutt et al. 2003). The filled circles are direct abundance measurements of H  II regions in the galaxy NGC 5457 with $12+\log{\rm O/H}_{T_{\rm e}}> 8.2$ from Kennicutt et al. (2003). The filled triangles are direct abundance measurements of H  II regions in this galaxy from other authors (compilation from Pilyugin 2001b) The open squares are direct abundance measurements of H  II regions in other galaxies (compilation from Pilyugin 2001a). Figure 15a shows that there is a satisfactory agreement between O/H $_{T_{\rm e}}$ and O/HPabundances. The origin of the disagreement between Kennicutt et al's and our conclusions is evident. The relationship between oxygen abundance and strong oxygen line intensities is double-valued with two distincts parts usually known as the "lower'' and "upper'' branches of the $R_{\rm 23}- {\rm O/H}$ relationship. The high-metallicity P-calibration is valid only for H  II regions which belong to the upper branch, i.e. with $12 + \log~($O/H) higher than $\sim$8.2. The unjustified use of the high-metallicity P-calibration in the determination of the oxygen abundance in low-metallicity H  II regions results in overestimated P-based oxygen abundances (Pilyugin 2003a). Our O/H $_{P} - {\rm O/H}_{T_{\rm e}}$ diagram (Fig. 15a) shows only the high-metallicity H  II regions with $12+\log{\rm O/H}_{T_{\rm e}}> 8.2$. On the contrary, Fig. 14 of Kennicutt et al. (2003) also includes low-metallicity H  II regions, with $12 + \log~($O/H) lower than $\sim$8.2. They do not belong to the upper branch, and, as a consequence, the high-metallicity P-calibration cannot be used in the determination of the oxygen abundance in these H  II regions. This is the reason why the low-metallicity H  II regions in the galaxy NGC 5457 are not presented in our Fig. 15a and are excluded from the analysis above (see Sect. 2).

Figure 15b shows the O/H $_{\rm ZKH}$ versus (O/H) $_{T_{\rm e}}$ diagram for the same sample of H  II regions as in Fig. 15a. The O/H $_{\rm ZKH}$ abundances are derived using the high-metallicity calibration from Zaritsky et al. (1994). Zaritsky et al.'s calibration is an average of the three calibrations by Edmunds & Pagel (1994), McCall et al. (1985), and Dopita & Evans (1986), hence this calibration can be considered as "representative'' for one-dimensional calibrations. Figure 15c shows the O/H $_{\rm KKP}$ versus (O/H) $_{T_{\rm e}}$ diagram for the same sample of H  II regions as in Fig. 15a. The O/H $_{\rm KKP}$ abundances are derived using the two-dimensional high-metallicity calibration from Kobulnicky et al. (1999). Figure 15a-c shows that the O/HP abundances agree significantly better with the O/H $_{T_{\rm e}}$ abundances than do the (O/H) $_{\rm ZKH}$ and (O/H) $_{\rm KKP}$ abundances.

We assume that the temperature-based abundance is the "true'' abundance and that the difference between, e.g. the P-based abundance and the $T_{\rm e}$-based abundance is due only to the error attached to the P-based abundance. However, the O/H $_{T_{\rm e}}$ abundances determined by Kennicutt et al. (2003) in H  II regions of the galaxy NGC 5457 with close galactocentric distances ( $0.55R_{\rm 25} \leq R_{\rm g} \leq 0.57R_{\rm 25}$) show a large scatter, from $12 + \log~($O/H $) _{T_{\rm e}} = 8.05$ for H  II region H71 to $12 + \log~($O/H $) _{T_{\rm e}} = 8.45$ for H  II region H128. This may be evidence for large uncertainty in O/H $_{T_{\rm e}}$ abundances. If this is the case, the uncertainty in the O/H $_{T_{\rm e}}$ abundances can make an appreciable contribution to the disagreement between the P-based and the $T_{\rm e}$-based abundances.

It is worth noting that the direct comparison of temperature-based oxygen abundances O/H $_{T_{\rm e}}$ with those derived with different calibrations is affected by the selection criteria. Indeed, in the high metallicity range, the weak temperature-sensitive line O[III]$\lambda$4363 is usually measured in high-excitation H  II regions. It is known that the disagreement between temperature-based abundances and those derived with one-dimensional $R_{\rm 23}$ calibrations is lowest for high-excitation H  II regions and is larger for low-excitation H  II regions, while the P-based abundances agree with the $T_{\rm e}$-based abundances both for high- and low-excitation H  II regions. Since the two-dimensional calibration of Kobulnicky et al. (1999) converts, in fact, into one-dimensional calibration at high metallicities, one can expect that the mean value of the disagreement between O/H $_{\rm KKP}$ and (O/H) $_{T_{\rm e}}$ abundances is larger than for the sample of high-excitation H  II regions in Fig. 15c. This statement can be checked through comparing the radial gradients traced by oxygen abundances derived using different methods. This also provides additional verification of the validity of oxygen abundances derived through different methods.

  \begin{figure} \par\includegraphics[width=8cm,clip]{a522f16.eps} \end{figure} Figure 16: The oxygen abundance versus galactocentric distance for the galaxy NGC 5457. a) The filled circles are temperature-based abundances from Kennicutt et al. (2003). The solid line is the least squares fit to these data. The open circles are temperature-based abundances from other authors (compilation from Pilyugin 2001b). The dashed line is the least squares fit to all the temperature-based abundances. b) The filled circles are oxygen abundances derived through the high-metallicity P-calibration for a large sample of H  II regions with $R_{\rm g} < 0.60 R_{\rm 25}$. The best fit to these data is presented by the dashed line. The solid line is the same as in  a). c) The filled circles are abundances derived using the calibration from Kobulnicky et al. (1999) for the same H  II regions. The least squares fit to these data is presented by the dashed line.

The O/H $_{T_{\rm e}}$ abundances versus galactocentric distance for the galaxy NGC 5457 are shown in Fig. 16a. The small filled circles are the data from Kennicutt et al. (2003). The best fit to these data

 
$\displaystyle 12+\log~({\rm O/H})_{T_{\rm e, KBG}} = 8.76~(\pm 0.06) - 0.90~(\pm 0.08) \times (R/R_{25})$     (26)

is shown by the solid line. The open circles are O/H $_{T_{\rm e}}$ abundances from other authors (compilation from Pilyugin 2001b). The best fit to all data
 
$\displaystyle 12+\log~({\rm O/H})_{T_{\rm e, all}} = 8.79~(\pm 0.04) - 0.90~(\pm 0.06) \times (R/R_{25})$     (27)

is shown by the dashed line. Figure 16a, as well as the comparison between Eqs. (26) and (27), shows that the O/H $_{T_{\rm e}}$ abundances from Kennicutt et al. (2003) are slightly shifted towards lower abundances compared to those from other authors.

Figure 16b shows the oxygen abundances derived here using the P-calibration for a large (65) sample of H  II regions with $R_{\rm g} > 0.6R_{\rm 25}$. The least squares fit to these data

 
$\displaystyle 12+\log~({\rm O/H})_{P} = 8.79~(\pm 0.03) - 0.88~(\pm 0.08) \times (R/R_{25})$     (28)

is shown in Fig. 16b by the dashed line. The O/H $_{T_{\rm e}} - R_{\rm g}$relationship of Kennicutt et al. (2003) is shown by the solid line. Figure 16b, as well as the comparison between Eqs. (26)-(28), shows that there is a very good agreement, both in the zero point and slope, between the radial O/H $_{T_{\rm e}}$ abundance gradient and the O/HP abundance gradient in the disk of the galaxy NGC 5457.

Figure 16c shows the radial distribution of the O/H $_{\rm KKP}$ abundances, derived using the high-metallicity calibration from Kobulnicky et al. (1999), for the sample of H  II regions from Fig. 16b. The least squares fit to these data

 
$\displaystyle 12+\log~({\rm O/H})_{\rm KKP} = 9.12~(\pm 0.03) - 1.08~(\pm 0.07) \times (R/R_{25})$     (29)

is shown in Fig. 16c by the dashed line. The O/H $_{T_{\rm e}} - R_{\rm g}$ relationship of Kennicutt et al. (2003) is shown by the solid line. Figure 16c, as well as the comparison between Eqs. (26), (27) and (29), clearly shows that the central oxygen abundance in NGC 5457, derived using the calibration from Kobulnicky et al. (1999), is overestimated (by a factor $\sim$2) in comparison with the one derived with the $T_{\rm e}$ and P-methods. The slopes of the (O/H) $_{T_{\rm e}}$-based and the (O/H)R23-based gradients are significantly different.

According to Garnett et al. (1997), the radial oxygen abundance gradient within the disk of NGC 5457 with oxygen abundances derived through the $R_{\rm 23}$-calibration is

 \begin{displaymath}12+\log~({\rm O/H})_{R_{23}} = 9.13 - 1.36 \times (R/R_{25}) . \end{displaymath} (30)

Comparison between Eqs. (26), (27) and (30) clearly shows that the central oxygen abundance in NGC 5457, derived using the $R_{\rm 23}$ calibration, is overestimated (by a factor $\sim$2) in comparison with the one derived with the $T_{\rm e}$ and P-methods. The slopes of the (O/H) $_{T_{\rm e}}$-based and the (O/H)R23-based gradients are significantly different.

There is thus a very good agreement, both in the zero point and slope, between the radial O/H $_{T_{\rm e}}$ abundance gradient and the O/HP abundance gradient within the disk of the galaxy NGC 5457. For radial distributions of abundances derived with other calibrations, both the central oxygen abundances and the slopes do not agree with (O/H) $_{T_{\rm e}}$-based values. This strongly supports our claim that the O/HP abundances are significantly more realistic than abundances derived with other calibrations.


  \begin{figure} \par\includegraphics[width=8.8cm,clip]{a522f17.eps} \end{figure} Figure 17: The characteristic oxygen abundance as a function of absolute blue magnitude MB for our sample of spiral galaxies (the filled circles). The solid line is the O/H - MB relationship (best fit derived through the least squares method). The dashed lines correspond to the lines shifted by -0.2 dex and +0.2 dex along the vertical axes relatively to the derived ${\rm O/H} - M_B$ relationship. The oxygen abundances in the galaxy NGC 5457 are presented by the open circle (O/H at $R=0.4R_{\rm 25}$) and open square (O/H at the disk half-light radius). The ${\rm O/H} - M_B$ relationship from Garnett (2002) is shown by plus signs.

The temperature-based characteristic oxygen abundance in the galaxy NGC 5457 can also be used as the "Rosetta Stone'' to test the validity of the ${\rm O/H} - M_B$ relationship obtained here. The characteristic oxygen abundance as a function of absolute blue magnitude MB for our sample of spiral galaxies is presented in Fig. 17. The positions of individual galaxies (points) and the ${\rm O/H} - M_B$ relationship (solid line) are the same as in Fig. 6. The dashed lines correspond to the lines shifted by -0.2 dex and +0.2 dex along the vertical axes relatively to the derived ${\rm O/H} - M_B$ relationship. The oxygen abundances in the galaxy NGC 5457 are presented by the open circle (O/H at $R=0.4R_{\rm 25}$) and open square (O/H at the disk half-light radius). The line shown by plus signs in Fig. 17 is the luminosity-metallicity relathionship for spiral galaxies obtained by Garnett (2002). Figure 17 shows that there is a large difference between the luminosity-metallicity relationship derived here and that from Garnett (2002). The main reason of this discrepancy is due to the fact that our luminosity-metallicity relationship is based on the oxygen abundances derived through the P-calibration while Garnett has used oxygen abundances derived through the $R_{\rm 23}$-calibrations. The recent results on the oxygen abundance determination in the disk of the well-studied spiral galaxy NGC 5457 (M 101) provide a possibility to check the credibility of these relationships. Kennicutt et al. (2003) derived the radial distribution of the oxygen abundance in the disk of NGC 5457, traced by the H  II regions with oxygen abundances derived with the classical $T_{\rm e}$-method. The characteristic oxygen abundance (as adopted here the oxygen abundance at $R=0.4R_{\rm 25}$) in the galaxy NGC 5457 is presented by the open circle in Fig. 17. It is evident that the $T_{\rm e}$-based characteristic oxygen abundances in the galaxy NGC 5457 are in conflict with Garnett's luminosity-metallicity relationship but agree with our luminosity-metallicity relationship. It is not suprising since it was shown above that there is a very good agreement, both in the zero point and slope, between our P-based oxygen abundance distribution, Eq. (28), and the $T_{\rm e}$-based oxygen abundance distribution, Eq. (26), of Kennicutt et al. (2003), while the $R_{\rm 23}$-based oxygen abundance distribution, Eq. (30), of Garnett et al. (1997) is quite different. It should be noted that Garnett (2002) used the oxygen abundances at the disk half-light radius to built the luminosity-metallicity relationship. Can this make a significant contribution to the deviation of the characteristic oxygen abundance in the galaxy NGC 5457 from the luminosity-metallicity relationships based on oxygen abundances at the disk half-light radius? Based on Garnett's conclusion: "for comparison, I include results based on using the value of O/H at one disk scale length; this change has little effect on the overall results'', one can expect that the difference in the choice of the "characteristic'' radius plays a minor role. For verification and illustration, the $T_{\rm e}$-based oxygen abundance in the galaxy NGC 5457 at the disk half-light radius (equal to 1.685 times the exponential scale length) is obtained and presented in Fig. 17 by the open square. Figure 17 shows that using the characteristic oxygen abundance at $R=0.4_{\rm 25}$ in the galaxy NGC 5457 instead of the value of O/H at the disk half-light radius has little effect on the overall result. Thus, the $T_{\rm e}$-based characteristic oxygen abundances in the galaxy NGC 5457 are in conflict with the luminosity-metallicity relationship derived by Garnett (2002) with the $R_{\rm 23}$-based oxygen abundances, but agree with our luminosity-metallicity relationship derived with the P-based oxygen abundances.

7 Conclusions

We performed a compilation of more than 1000 published spectra of H  II regions in 54 spiral galaxies. The oxygen and nitrogen abundances in each H  II region were recomputed in a homogeneous way, using the P-method. The radial distributions of the oxygen abundances, nitrogen abundances, and nitrogen-to-oxygen abundance ratios were derived. The parameters of the radial distributions (the extrapolated central intersect value and the gradient) are listed.

The correlations between oxygen abundance and macroscopic properties of galaxies are examined. The oxygen abundance in the disk of a galaxy at $r=0.4R_{\rm 25}$, where $R_{\rm 25}$ is the isophotal radius, is used as a characteristic (or representative) oxygen abundance for spiral galaxies. We found that the oxygen abundance in spiral galaxies correlates with its luminosity, rotation velocity, and morphological type: the correlation with the rotation velocity may be slightly tighter.

There is a significant difference between the luminosity-metallicity relationship derived here and that based on the oxygen abundances derived through the $R_{\rm 23}$-calibrations. The $T_{\rm e}$-based characteristic oxygen abundances in the galaxy NGC 5457 (Kennicutt et al. 2003) agree with our luminosity-metallicity relationship derived with the P-based oxygen abundances but is in conflict with the luminosity-metallicity relationship derived by Garnett (2002) with the $R_{\rm 23}$-based oxygen abundances.

The derived luminosity-metallicity relation for spiral galaxies is compared to that for irregular galaxies. We found that the slope of the oxygen abundance-luminosity relationship for spirals is slightly more shallow than the one for irregular galaxies.

The effective oxygen yields were derived for spiral and irregular galaxies. We found that the effective oxygen yield increases with increasing luminosity from $M_{B} \sim -11$ to  $M_{B} \sim -18$ (or with increasing rotation velocity from  $V_{\rm rot} \sim 10$ km s-1 to $V_{\rm rot} \sim 100$ km s-1) and then remains approximately constant. Irregular galaxies from our sample have effective oxygen yields lowered by a factor of 3 at maximum, i.e. irregular galaxies usually retain at least 1/3 of the oxygen they manufactured during their evolution. From the comparison between the effective oxygen yields for spiral and irregular galaxies (with $R_{\rm 23}$-based oxygen abundances in spiral galaxies), Garnett (2002) found however that an irregular galaxy can lose up to $90\% \div 95\%$ of the oxygen manufactured.

Acknowledgements
We thank Prof. B. E. J. Pagel for a careful reading of the manuscript and useful comments and suggestions which helped to improve the paper. We thank the anonymous referee for helpful comments. This study was supported by the sabbatical grant SAB2001-0165 of the Spanish Ministerio de Educación, Cultura y Deporte (L.S.P.) and by the Ukrainian Fund of Fundamental Investigation, grant No 02.07/00132 (L.S.P.).

References

 

  
8 Online Material


 

 
Table 2: List of references to Table 1.
Abrrev. Source
AEL81 Alloin et al. (1981)
BK02 Bresolin & Kennicutt (2002)
BKC82 Blair et al. (1982)
BKG99 Bresolin et al. (1999)
C00 Castellanos (2000)
CPG97 Christensen et al (1997)
DCL88 Deharveng et al. (1988)
DK81 Dennefeld & Kunth (1981)
dORW83 d'Odorico et al. (1983)
DTJ80 Dufour et al. (1980)
DTP87 Diaz et al. (1987)
DTV91 Diaz et al. (1991)
EP84 Edmunds & Pagel (1984)
FGW98 Ferguson et al. (1998)
FTP86 Fierro et al. (1986)
GOS92 Garnett et al. (1992)
GS87 Garnett & Shields (1987)
GSP99 Garnett et al. (1999)
GSS97 Garnett et al. (1997)
HBC96 Henry et al. (1996)
HPC94 Henry et al. (1994)
HPL92 Henry et al. (1992)
KA81 Kwitter & Aller (1981)
KG96 Kennicutt & Garnett (1996)
KR94 Kinkel & Rosa (1994)
MRS85 McCall et al. (1985)
OK93 Oey & Kennicutt (1993)
P70 Peimbert (1970)
PEB79 Pagel et al. (1979)
R95 Ryder (1995)
RPT82 Rayo et al. (1982)
RW97 Roy & Walsh (1997)
S71 Searle (1971)
S75 Smith (1975)
SB84 Stauffer & Bothun (1984)
SKS96 Skillman et al. (1996)
SS78 Shields & Searle (1978)
SSK91 Shields (1991)
TPF89 Torres-Peimbert (1989)
VEP88 Vílchez et al. (1988)
VPD88 Vílchez et al. (1988)
vZSH98 van Zee et al. (1998)
WS83 Webster & Smith (1983)
ZKH94 Zaritsky et al. (1994)



 

 
Table 6: List of references to Table 5.
Abbr. Reference Abbr Reference
ABB van Albada et al. (1985) KN Kuno & Nakai (1997)
ADS Appleton et al. (1981) KS Krumm & Salpeter (1979)
AMB Amram et al. (1994) KY Kenney & Young (1988)
AS van Albada & Shane (1975) MM Milliard & Marcelin (1981)
B Bosma (1981) NN Nishiyama & Nakai (2001)
Bu Buta (1988) NNK Nishiyama et al. (2001)
BB de Blok & Bosma (2002) OH Ondrechen & van der Hulst (1989)
BBS Begeman et al. (1991) P Peterson (1978)
BCH Bosma et al. (1980) PCB Puche et al. (1990)
BHS Bosma et al. (1977) PCG Puche et al. (1991)
BM Bajaja & Martin (1985) R Rots (1980)
BMR Becker et al. (1988) RCC Rogstad et al. (1979)
BR Broeils & Rhee (1997) Re Reakes (1979)
BSC Bravo-Alfaro et al. (1997) Ro Rots (1975)
BWR Bajaja et al. (1995) RFT Rubin et al. (1980)
CCB Carignan et al. (1990) RKS Ryder et al. (2001)
CD Cox & Downes (1996) RMG Reif et al. (1982)
CG Casertano & van Gorkom (1991) S Sage (1993)
CS Corbelli & Salucci (2000) Sc Schneider (1989)
DD Dean & Davies (1975) SCR Sperandio et al. (1995)
GDH García-Barreto et al. (1994) Sh Shostak (1978)
GGK Guhathakurta et al. (1988) SD Staveley-Smith & Davies (1988)
GW Guélin & Weliachew (1970) SEC Stark et al. (1987)
H Huchtmeier (1975) SJL Sandqvist et al. (1995)
HAS Hoekstra et al. (2001) SKB Stark et al. (1986)
HB Helfer & Blitz (1995) SNK Sorai et al. (2000)
HBS Heckman et al. (1978) TM Thornley & Mundy (1997)
HHG Hewitt et al. (1983) vKS van der Kruit & Shostak (1984)
HHM Haynes et al. (1998) VPD de Vaucouleurs et al. (1983)
HR Huchtmeier & Richter (1986a) Wa Warmels (1988a)
HRb Huchtmeier & Richter (1986b) Wb Warmels (1988b)
HRG Hunter et al. (1986) WAD Wevers et al. (1984)
HS Huchtmeier & Seiradakis (1985) WG Weliachew & Gottesman (1973)
HTR Helfer et al. (2003) WKA Wevers et al. (1986)
JM Jörsäter & van Moorsel (1995) YXT Young (1995)
KDI Koper et al. (1991) ZB van Zee & Bryant (1999



  \begin{figure} \par\includegraphics[width=17.5cm,clip]{a522f02.eps} \end{figure} Figure 2: Oxygen and nitrogen abundances and nitrogen-to-oxygen abundance ratio versus galactocentric distance for late-type galaxies. The oxygen abundances are shown by filled circles, the linear least-squares fits to these data are presented by solid lines. The nitrogen abundances are shown by open squares, the linear least-squares fits to these data are presented by dashed lines. The nitrogen-to-oxygen abundance ratios are shown by open circles, the linear least-squares fits to these data are presented by solid lines. The galactocentric distances are normalized to the isophotal radius. The H  II regions with depleted oxygen abundances in NGC 2903 are shown by pluses.


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{a522f03.eps} \end{figure} Figure 3: Oxygen and nitrogen abundances and nitrogen-to-oxygen abundance ratio versus galactocentric distance for late-type galaxies. The oxygen abundances are shown by filled circles, the linear least-squares fits to these data are presented by solid lines. The nitrogen abundances are shown by open squares, the linear least-squares fits to these data are presented by dashed lines. The nitrogen-to-oxygen abundance ratios are shown by open circles, the linear least-squares fits to these data are presented by solid lines. The galactocentric distances are normalized to the isophotal radius.


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{a522f04.eps} \end{figure} Figure 4: Oxygen and nitrogen abundances and nitrogen-to-oxygen abundance ratio versus galactocentric distance for late-type galaxies. The oxygen abundances are shown by filled circles, the linear least-squares fits to these data are presented by solid lines. The nitrogen abundances are shown by open squares, the linear least-squares fits to these data are presented by dashed lines. The nitrogen-to-oxygen abundance ratios are shown by open circles, the linear least-squares fits to these data are presented by solid lines. The galactocentric distances are normalized to the isophotal radius.


  \begin{figure} \par\includegraphics[width=17.5cm,clip]{a522f05.eps} \end{figure} Figure 5: Oxygen and nitrogen abundances and nitrogen-to-oxygen abundance ratio versus galactocentric distance for late-type galaxies. The oxygen abundances are shown by filled circles, the linear least-squares fits to these data are presented by solid lines. The nitrogen abundances are shown by open squares, the linear least-squares fits to these data are presented by dashed lines. The nitrogen-to-oxygen abundance ratios are shown by open circles, the linear least-squares fits to these data are presented by solid lines. The galactocentric distances are normalized to the isophotal radius.

Appendix A: Distances and luminosities


 

 
Table A.1: The general properties of spiral galaxies from our sample.

Galaxy		 T-type Morphology BT0 log LB Distance References for
        ($L_{\odot}$)  Mpc distance values

NGC 224 = M 31		 3.0 SA(s)b 3.36 10.63 0.78 FMG01, JPN03, MK86, JTB03, TDB01, SS94
NGC 253 5.0 SAB(s)c 7.09 10.55 3.94 KSD03, TS00
NGC 300 7.0 SA(s)d 8.49 9.40 2.00 FMG01, SMJ96
NGC 598 = M 33 6.0 SA(s)cd 5.75 9.74 0.84 FMG01, TS00, MCM00, LKS02, KKL02
NGC 628 = M 74 5.0 SA(s)c 9.76 10.01 7.28 SD96, SKT96, HFS97
NGC 753 4.0 SAB(rs)bc 12.35 10.64 49.30 R02
NGC 925 7.0 SAB(s)d 9.97 10.13 9.16 FMG01, SD98, TPE02
NGC 1058 5.0 SA(rs)c 11.55 9.62 10.60 SKE94, TPE02
NGC 1068 = M 77 3.0 (R)SA(rs)b 9.47 10.77 15.30 SS94, TS00, HFS97
NGC 1232 5.0 SAB(rs)c 10.38 10.55 17.90 R02, TPE02
NGC 1365 3.0 (R)SBb(s)c 9.93 10.73 17.95 FMG01, SS94
NGC 2403 6.0 SAB(s)cd 8.43 9.84 3.22 FMG01, CFJ02
NGC 2442 3.7 SAB(s)bc 10.36 10.72 21.58 RKS01, TDB01
NGC 2541 6.0 SA(s)cd 11.57 9.66 11.22 FMG01, FHS97
NGC 2805 7.0 SAB(rs)d 11.17 9.70 9.77 TDB01
NGC 2835 5.0 SAB(rs)c 10.31 10.05 9.80 R02, TDB01
NGC 2841 3.0 SA(r)b 9.58 10.66 14.06 MSB01, HFS97
NGC 2903 4.0 SB(s)d 9.11 10.44 8.87 DK00, TPE02, TS00
NGC 2997 5.0 SA(s)c 9.34 10.46 10.05 R02, SPU94, T88, V79
NGC 3031 = M 81 2.0 SA(s)ab 7.39 10.36 3.63 FMG01, JCB89, JTB03, TDB01, TPE02
NGC 3184 6.0 SAB(rs)cd 10.34 10.15 11.10 HFS97, LFL02, V79
NGC 3198 5.0 SB(rs)c 10.21 10.39 13.80 FMG01, TPE02
NGC 3344 4.0 (R)SAB(r)bc 10.50 9.67 6.90 VBA00
NGC 3351 = M 95 3.0 SB(r)b 10.26 10.09 10.00 CFJ02, FMG01, TPE02
NGC 3521 4.0 SAB(rs)bc 9.29 10.49 10.21 HFS97, RST00, TS00
NGC 3621 7.0 SA(s)d 9.20 10.16 6.64 FMG01, TPE02
NGC 4254 = M 99 5.0 SA(s)c 10.10 10.57 16.14 R02, SS97, SSS02
NGC 4258 = M 106 4.0 SAB(s)bc 8.53 10.58 7.98 CFJ02, CMM02, FMG01, HMG99, NFS01
NGC 4303 = M 61 4.0 SAB(rs)bc 10.12 10.10 9.55 SPU94, SS97, TS00
NGC 4321 = M 100 4.0 SAB(s)bc 9.98 10.56 15.21 FMG01, R02, SKE94, SSS02, TPE02, TS00
NGC 4395 9.0 SA(s)m 10.57 9.29 4.61 HFS97, KMS03, KD98
NGC 4501 = M 88 3.0 SA(rs)b 9.86 10.74 17.58 R02, SS97, SSS02
NGC 4559 6.0 SAB(rs)cd 9.76 9.90 6.40 HFS97, RST00
NGC 4571 6.5 SA(r)d 11.73 9.97 17.22 PMR92, SS97, SSS02, TGD00
NGC 4651 5.0 SA(rs)c 11.04 10.47 22.28 SS97, SSS02, TPE02
NGC 4654 6.0 SAB(rs)cd 10.75 10.17 13.74 SS97, SSS02
NGC 4689 4.0 SA(rs)bc 11.39 9.99 15.00 SS97, SSS02
NGC 4713 7.0 SAB(rs)d 11.85 9.72 13.61 SSS02
NGC 4725 2.0 SAB(r)ab 9.78 10.46 12.36 JTB03, FMG01, TDB01, TPE02
NGC 4736 = M 94 2.0 (R)SA(r)ab 8.75 10.08 4.93 KMS03, SS94, TDB01, TPE02, TS00
NGC 5033 5.0 SA(s)c 10.21 10.51 15.82 RST00, SFE01, TPE02
NGC 5055 = M 63 4.0 SA(rs)bc 9.03 10.47 8.81 RST00, TPE02, TS00
NGC 5068 6.0 SB(s)d 10.09 9.70 5.90 SFE01
NGC 5194 = M 51 4.0 SA(s)bc 8.67 10.49 7.64 CFJ02, FCJ97, SS94, TDB01, TS00
NGC 5236 = M 83 5.0 SAB(s)c 7.98 10.30 4.49 ESK96, SKE94, TTS03
NGC 5457 = M 101 6.0 SAB(rs)cd 8.21 10.56 6.70 DK00, FCJ97, FMG01, JPJ00, SKE94
NGC 6384 4.0 SAB(r)bc 10.60 10.79 26.14 P94, PSS00, S97, TPE02
NGC 6744 4.0 SAB(r)bc 8.82 10.60 9.33 SFE01, TPE02
NGC 6946 6.0 SAB(rs)cd 7.78 10.59 5.70 ESK96, SKE94, SKT97, SS94, TPE02, TS00
NGC 7331 3.0 SA(s)b 9.38 10.78 14.72 FMG01, JTB03, SKE94, TDB01, TPE02
NGC 7793 7.0 SA(s)d 9.37 9.63 3.91 KSD03, D98
IC 342 6.0 SAB(rs)cd 6.04 10.81 3.28 KT93, SCH02, SS94, TS00
IC 5201 6.0 SB(s)cd 11.00 9.87 11.00 T88


To derive a reliable galaxy luminosity, an accurate value of the distance is necessary. Over the past decade, great progress has been made in accurate distance measurements for galaxies using many different methods. Therefore, we have performed a thorough literature search for distance information to determine the most reliable, up-to-date distances for our sample.

The Cepheid period-luminosity relation remains the most useful method for estimating the distance of galaxies. Another efficient tool is the luminosity of the tip of the red giant branch (TRGB) stars. One of the most promising distance indicators is believed to be the peak brightness of type Ia supernovae (SNe Ia). The supernovae of type II (SNe II) are also reliable distance indicators; the method of distance determination is based on models of the expanding photospheres of SNe II (EPM). The planetary nebula luminosity function (PNLF) is a reliable distance indicator for galaxies potentially as far away as $\sim$25 Mpc. Surface brightness fluctuations (SBF) have emerged as a reliable distance indicator. The classic method of distance measurements via the luminosity of the brighest blue and red supergiants (BBSG and BRSG) has been widely used over last decade. The Tully-Fisher (TF) relation, or "luminosity-rotation velocity'' relation, is the most commonly applied distance indicator for spiral galaxies at the present time. There are different versions of the TF relation: the luminosity in different bands can be used in the TF relation, and the CO linewidth instead of the H  I linewidth can be used as the tracer of rotation velocity.

The important point is that the TRGB, SNIa, PNLF, SBF, BRSG, and TF methods request a calibration. The Hubble Space Telescope Key Project on the Extragalactic Distance Scale has provided Cepheid distances to more than 20 galaxies, in addition to the existing ground-based Cepheid distances to about 10 galaxies. This data set constitutes a solid basis for calibrating other distance indicators (Ferrarese et al. 2000). It should be noted, however, that some uncertainty in the Cepheid distances still remains, due to uncertainties in the slope and zero point of the Cepheid period-luminosity relation (see discussion in Ferrarese et al. 2000; Freedman et al. 2001, among others). Therefore, the slightly different values of the Cepheid distance to a given galaxy have been derived by different authors using the same observational data. As a result, there is some disagreement in the literature on the magnitudes of other standard candles. For example, two recent calibrations of the peak absolute magnitude of SNe Ia, based on the SNe Ia events in galaxies with known Cepheid distances result in slightly different magnitudes: MB = -19.56 (Parodi et al. 2000) and MB = -19.32(Gibson & Stetson 2001). The method based on modeling the expanding photospheres of SNe II is a "physical method'' and is hence completely independent of the calibration of the local distance scale. The EPM distances agree with the Cepheid distances within around 10% (Eastman et al. 1996; Leonard et al. 2002a). Since systematic uncertainty clearly remains at the 10% level for Cepheid and at the 10-20% level for EPM, it is not clear whether the observed discrepancy is significant (Leonard et al. 2002a).

The most important point to take into account when comparing different methods of distance determination is their accuracy. The relative Cepheid distances are determined to $\sim$$\pm$5% (Freedman et al. 2001). A typical accuracy of the TRGB distances is $\sim$12% (Karachentsev et al. 2003a,b). According to Parodi et al. (2000), the SNe Ia are the best standard candles known so far, with a luminosity scatter of less than 0.25 mag. The EPM distances agree with the Cepheid distances within $\sim$10% (Eastman et al. 1996; Leonard et al. 2002a). There is also a good agreement between PNLF and Cepheid distances over two orders of magnitude in the derived distances (Feldmeier et al. 1997). The SBF distance measurements rely on the empirical calibration of absolute fluctuation amplitudes. A relative accuracy of $\sim$10% in extragalactic SBF distances can be reached, provided that the galaxy color is well known (Jensen et al. 2003). Distance moduli derived with the BBSG and BRSG method have typical errors of 0.4-0.5 mag (Drozdovsky & Karachentsev 2000). Solanes et al. (2002) have examined the TF distance moduli of spiral galaxies in the region of the Virgo cluster taken from eight published datasets and have found a dispersion of 0.41 mag. Tutui & Sofue (1997, 1999) have analysed H  I and CO TF methods. They concluded that the errors in the H  I TF distances can be especially large in the case of interacting galaxies since the H  I linewidth may be strongly disturbed by galaxy-galaxy interaction and may not reflect correctly the rotation velocity of the galaxy. The method of "sosie galaxies'' (look-alike galaxies) is a particular application of the TF method which avoids some practical problems (Paturel 1984; Terry et al. 2002). The distances derived with the "sosie galaxies'' method appear to be more reliable than those obtained with the direct TF relation.


 

 
Table A.2: List of references to Table A.1.
Abbreviation Reference Method
CFJ02 Ciardullo et al. (2002) PNLF
CMM02 Caputo et al. (2002) Cepheid
D98 Davidge (1998) BRSG
DK00 Drozdovsky & Karachentsev (2000) TRGB
ESK96 Eastman et al. (1996) EPM
FCJ97 Feldmeier et al. (1997) PNLF
FMG01 Freedman et al. (2001) Cepheid
HFS97 Ho et al. (1997) H0
HMG99 Herrnstein et al. (1999) geometric
JCB89 Jacoby et al. (1989) PNLF
JPJ00 Jurcevic et al. (2000) RSGV
JPN03 Joshi et al. (2003) RSGV
JTB03 Jensen et al. (2003) SBF
KD98 Karachentsev & Drozdovsky (1998) BBSG
KKL02 Kim et al. (2002) TRGB
KMS03 Karachentsev et al. (2003a) TRGB
KSD03 Karachentsev et al. (2003b) TRGB
KT93 Karachentsev & Tikhonov (1993) BRGB
LFL02 Leonard et al. (2002b) EPM
LKS02 Lee et al. (2002) Cepheid
MCM00 Magrini et al. (2000) PNLF
MK86 Mould & Kristian (1986) TRGB
MSB01 Macri et al. (2001) Cepheid
NFS01 Newman et al. (2001) Cepheid
P94 Pierce (1994) SNIa
PMR92 Pierce et al. (1992) BRSG
PSS00 Parodi et al. (2000) SNIa
R02 Russel (2002) TF
RKS01 Ryder et al. (2001) H0
RST00 Rothberg et al. (2000) H0
S97 Shanks (1997) SNIa
SCH02 Saha et al. (2002) Cepheid
SD96 Sohn & Davidge (1996) BRSG
SD98 Sohn & Davidge (1998) BRSG
SFE01 Shapley et al. (2001) H0
SKE94 Schmidt et al. (1994) EPM
SKT96 Sharina et al. (1996) BBSG
SKT97 Sharina et al. (1997) BBSG
SMJ96 Soffner et al. (1996) BBSG
SPU94 Saikia et al. (1994) H0
SS94 Schöniger & Sofue (1994) TF
SS97 Schöniger & Sofue (1997) TF
SSS02 Solanes et al. (2002) TF
T88 Tully (1988) H0
TDB01 Tonry et al. (2001) SBF
TGD00 Tikhonov et al. (2000) BSG
TPE02 Terry et al. (2002) sosie(TF)
TS00 Takamiya & Sofue (2000) TF
TTS03 Thim et al. (2003) TF
V79 de Vaucouleurs (1979) tertiary
VBA00 Verdes-Montenegro et al. (2000) H0


Typically, two or more distance estimations for a galaxy from our sample are available in the literature. Examination of available distances confirms that the Cepheid, EPM, SBF, SNIa, PNLF, and TRGB methods provide accurate distance determinations. Estimations of distances with two or more of these methods exist for 14 galaxies from our sample. The deviation of individual distance estimations from the mean value is usually less than 10%. These methods will be refered to as "high-precision'' methods below. The agreement between the TF (and BBSG, BRSG) distances and distances derived with the high-precision methods is appreciably worse. Moreover, the TF distances derived by different authors for the same galaxy can show a significant scatter. Taking these facts into account, the adopted value of the distance for a galaxy is chosen in the following way. If the distance derived with the "high-precision'' method(s) is available, this distance is adopted. If only the TF and/or BBSG, BRSG distances are available, the mean value is adopted. If a galaxy is a member of compact group, the information on the distances to other members of the group is used to check the distance. We have to adopt the redshift (H0) distances for three galaxies (NGC 3344, NGC 5068, and IC 5201) from our sample due to the lack of other reliable distance estimations.

Here are some comments on individual galaxies.

NGC 628. - There is no distance to NGC 628 determined with one of the "high-precision'' methods. However, the available distances to NGC 628 derived with the method of brightest stars seem to be quite reliable. Firstly, the distances derived from two different investigations are in agreement: 7.24 Mpc (Sohn & Davidge 1996) compared to 7.32 Mpc (Sharina et al. 1996). Secondly, the distance moduli estimated by Sharina et al. (1996) for four galaxies in the group of NGC 628 have a mean value of 7.80 Mpc with a small scatter. As noted by Sharina et al. (1996), if a group contains a sufficient number of irregular galaxies, the "brightness stars'' method makes it possible to measure the distance to the group with almost the same accuracy as with the Cepheid method.

NGC 753. - The galaxy NGC 753 belongs to the Pisces filament. The TF distances of several dozens of galaxies of this filament lie between $\sim$50 Mpc and $\sim$80 Mpc (Tully & Pierce 2000). The TF distance (49.30 Mpc) of NGC 753 from Russel (2002) is adopted here.

NGC 1068. - Two values of TF distances to NGC 1068 show an appreciable discrepancy: 12.45 Mpc (Schöniger & Sofue 1994) compared with 18.10 Mpc (Takamiya & Sofue 2000). The galaxy NGC 1068 is a member of the LGG 73 group (Garcia 1993). A distance of 16.07 Mpc to the galaxy NGC 1055 (also a member of LGG 73 group) was estimated by Paturel et al. (1998) using the method of "sosies galaxies''. The mean TF distance of 15.30 Mpc is confirmed by the Paturel et al.'s data and is adopted here.

NGC 2442. - There is no reliable distance determination for NGC 2442. This galaxy is a member of the LGG 147 group (Garcia 1993). The distance to another member (NGC 2434) of this group has been determined with the SBF method and is equal to 21.58 Mpc (Tonry et al. 2001). This value is adopted as distance to NGC 2442.

NGC 2805. - There is no reliable distance determination for NGC 2805. This galaxy is a member of the LGG 173 group (Garcia 1993). The distance to another member (NGC 2880) of this group has been determined with the SBF method and is equal to 9.77 Mpc (Tonry et al. 2001). This value is adopted as distance to NGC 2805.

NGC 2835. - Different distance values to NGC 2835 were used recently: 10.76 Mpc (Elmegreen & Salzer 1999) and 6.03 Mpc (Larsen & Richtler 2000). The TF distance to NGC 2835 is 9.80 Mpc (Russel 2002). The galaxy NGC 2835 is a member of the LGG 172 group (Garcia 1993). The distance to NGC 2784 (a member of the LGG 172 group) has been determined with the SBF method and is equal to 9.82 Mpc (Tonry et al. 2001). This value is adopted as distance to NGC 2835.

Virgo galaxies. - We chose individual distance estimations to Virgo galaxies in the same way as in the case of field galaxies. If the distance estimation with one of the "high-precision'' methods is available, this distance is adopted. Otherwise the distance is derived by averaging the available TF distances. The distances of Virgo galaxies NGC 4254, NGC 4501, NGC 4571, NGC 4651, NGC 4654, NGC 4689, and NGC 4713 were taken from Solanes et al. (2002). These distances were obtained by averaging distance moduli based upon the TF relationship taken from eight published datasets (Ekholm et al. 2000; Fouqué et al. 1990; Federspiel et al. 1998; Gavazzi et al. 1999; Kraan-Korteweg, et al. 1988; Mould et al. 1980; Pierce & Tully 1988; Yasuda 1997). The distances from these works have been previously homogenized. It seems quite impossible to check the distance of individual Virgo cluster galaxies by comparing their value with the "group'' distance. Indeed, the galaxies NGC 4321, NGC 4651, and NGC 4689 belong to the LGG 289 group (Garcia 1993). Their TF distances range from 15.00 Mpc for NGC 4689 to 22.28 Mpc for NGC 4651. The distances for nine galaxies of the LGG 289 group have been determined with the SBF method (Tonry et al. 2001), these distances lie between 15.00 Mpc (NGC 4564) and 22.42 Mpc (NGC 4365). Thus, both the TF distances and the SBF distances of galaxies of LGG 289 group are spread over more than 7 Mpc. There are two estimations of the distance to the Virgo cluster galaxy NGC 4571 with the "brightest supergiant stars'' method. The mean BRSG distance value of 17.15 Mpc is in agreement with Solanes et al.'s TF distance of 17.22 Mpc.

The adopted values of distance and the corresponding references to sources of data are presented in Table A.1 (Cols. 6 and 7). The list of references to Table A.1 is given in Table A.2. Using the adopted distances and the total face-on blue magnitudes corrected for galactic and internal absorption  $B_{\rm T}^0$, the luminosities of galaxies were determined. The $B_{\rm T}^0$ values are taken from the Third Reference Catalog of bright Galaxies (de Vaucouleurs et al. 1991, RC3) and are listed in Col. 4 of Table A.1, the derived luminosities are given in Col. 5 of Table A.1.

Copyright ESO 2004