W. J. Chaplin1 - Y. Elsworth1 - G. R. Isaak1 - B. A. Miller1 - R. New2 - D. Salabert1
1 - School of Physics and Astronomy, University of Birmingham, Edgbaston,
Birmingham B15 2TT, UK
2 -
School of Science and Mathematics, Sheffield Hallam University, Sheffield S1 1WB, UK
Received 2 March 2004 / Accepted 21 May 2004
Abstract
We investigate the impact of a multi-site, ground-based
observational window function on the extraction of estimates of
the frequencies of low-angular-degree (low-![]() )
solar p
modes from decade-long datasets. To effect this study
we have made use of some
)
solar p
modes from decade-long datasets. To effect this study
we have made use of some ![]()
![]() of full-disc,
"Sun-as-a-star'' Doppler velocity data
collected by the Birmingham-Solar Oscillations Network (BiSON). A
coherent combination of observations made by all six BiSON sites
provided the principal time series of data. This set was then
modulated by a whole series of different window functions and the
resulting sets analyzed. The windows were made from different
combinations and numbers of BiSON stations. We find that for the
majority of low-
of full-disc,
"Sun-as-a-star'' Doppler velocity data
collected by the Birmingham-Solar Oscillations Network (BiSON). A
coherent combination of observations made by all six BiSON sites
provided the principal time series of data. This set was then
modulated by a whole series of different window functions and the
resulting sets analyzed. The windows were made from different
combinations and numbers of BiSON stations. We find that for the
majority of low-![]() modes the bias in the frequencies given by
the effects of the window function is not significant. However,
for modes above
modes the bias in the frequencies given by
the effects of the window function is not significant. However,
for modes above ![]()
![]() ,
and some
,
and some ![]() modes near
modes near ![]()
![]() ,
the bias is important when
the frequencies are extracted from long datasets.
,
the bias is important when
the frequencies are extracted from long datasets.
Key words: methods: data analysis - Sun: helioseismology
Studies of periodic and quasi-periodic astronomical phenomena can often benefit greatly from the availability of continuous observations, an obvious category being the study of various types of stellar oscillations. Here, we concentrate upon the demands offered by a single - but conspicuous - object, this being the Sun and its resonant p-mode oscillations. We do so for a ground-based observing strategy. Continuous, multi-decadal coverage of the Sun is desirable in order to investigate the 11-yr Schwabe activity cycle and to allow the accurate measurement of the frequencies and splittings of weak, but very long-lived, low-frequency modes. These serve to provide a stern test of stellar evolution theory.
If observations are made of the Sun from a single, mid-latitude, terrestrial site they will have long interruptions from the diurnal, day-night cycle. Quasi-random drop-outs in coverage will also arise from poor weather and occasional technical problems. Both effects serve to complicate analyses performed on the data in the frequency domain: quasi-random gaps increase the background level of "noise'' across a range of frequencies; while the diurnal breaks create periodic structures, or sidebands, in the power spectrum.
One strategy for attempting to remove these effects is to observe from one of the terrestrial poles. However, this can present major logistical difficulties and regardless: continuity of coverage is limited at each pole to a maximum of approximately six months; and there is no redundancy to cope with poor weather at the observing site.
A more practical, long-term approach that offers the potential for multi-year continuity and the added advantage of some redundancy (through overlaps in coverage) is to deploy a network of observatories distributed widely in longitude. Two current examples that observe globally coherent solar eigenmodes are the Birmingham Solar-Oscillations Network (BiSON; Chaplin et al. 1996) and the Global Oscillations Network Group (GONG; Harvey et al. 1996). Even though each comprises six, well-separated sites, this is insufficient to give complete, 100-% coverage all year round. Recent annual duty cycles of useful data for both networks have typically been in the 70 to mid-80% range. While the artefacts are suppressed at these high levels of coverage, they nevertheless persist in the frequency domain at a level that cannot be ignored. Furthermore, an extended database of BiSON observations is available stretching back to the mid 1970s, but with somewhat reduced temporal coverage (i.e., because of limited single- or double-site summer campaigns, or latterly fewer permanent stations prior to the complete roll-out of the network). Here, the artefacts are rather more severe.
Our aim in this paper is to present a detailed study of the impact of
a wide range of ground-based observational window functions on
estimates of low-angular-degree (low-![]() )
solar p-mode
eigenfrequencies. We do so for data collected by Doppler velocity or
intensity observations of the unresolved Sun, i.e., the "full-disc'' or
Sun-as-a-star BiSON data. Previous work in this area has concentrated
on studies of the precision of the solar p-mode parameters (Toutain &
Appourchaux 1994; Fierry-Fraillon et al. 1998), and on the evolution
for different timescales of the measurement precision of the
frequencies (Chaplin et al. 2002). Lazrek & Hill (1993) presented a
first attempt to simulate the effects of the gaps on the measurement
of oscillation parameters, but no one has investigated in detail the
effects of temporal windows with different fractional fills on the
measurement of p-mode frequencies.
)
solar p-mode
eigenfrequencies. We do so for data collected by Doppler velocity or
intensity observations of the unresolved Sun, i.e., the "full-disc'' or
Sun-as-a-star BiSON data. Previous work in this area has concentrated
on studies of the precision of the solar p-mode parameters (Toutain &
Appourchaux 1994; Fierry-Fraillon et al. 1998), and on the evolution
for different timescales of the measurement precision of the
frequencies (Chaplin et al. 2002). Lazrek & Hill (1993) presented a
first attempt to simulate the effects of the gaps on the measurement
of oscillation parameters, but no one has investigated in detail the
effects of temporal windows with different fractional fills on the
measurement of p-mode frequencies.
A study of this type is important for several reasons. Ground-based
networks making Sun-as-a-star observations - such as BiSON - have
provided invaluable low-![]() "core penetrating'' mode data since the
inception of the field, and will continue to underpin observations in
this area over the coming solar cycle. As noted above, an historical
low-
"core penetrating'' mode data since the
inception of the field, and will continue to underpin observations in
this area over the coming solar cycle. As noted above, an historical
low-![]() database is available thanks to BiSON, but with reduced
temporal coverage in its earlier years. We are currently in the process of
recalibrating these older data by taking advantage of improvements in
data preparation that have been made in recent years. Our intention
will then be to study in detail the behaviour of the low-
database is available thanks to BiSON, but with reduced
temporal coverage in its earlier years. We are currently in the process of
recalibrating these older data by taking advantage of improvements in
data preparation that have been made in recent years. Our intention
will then be to study in detail the behaviour of the low-![]() modes
over an extended period of more than 25 yr, spanning Schwabe activity
cycles 21 through 23. However, proper allowance will need to be made
for the impact of reduced temporal fill (i.e., lower duty cycles) on
the extraction of the mode parameters. Here, we investigate the effect
of window functions with fractional fills that, while well below those
encountered in post-1990 BiSON time series, will be typical of an
extended 25-yr or pre-1990 set. While some gap-filling techniques
appropriate to helioseismic data (i.e., many modes closely spaced in
frequency) may prove useful (Fossat et al. 1999; Fierry Fraillon &
Appourchaux 2001) we remain cautious regarding any advantage they may
offer under conditions of very modest fill (e.g., less than 50 per cent). We leave a discussion of the impact of this to another paper.
modes
over an extended period of more than 25 yr, spanning Schwabe activity
cycles 21 through 23. However, proper allowance will need to be made
for the impact of reduced temporal fill (i.e., lower duty cycles) on
the extraction of the mode parameters. Here, we investigate the effect
of window functions with fractional fills that, while well below those
encountered in post-1990 BiSON time series, will be typical of an
extended 25-yr or pre-1990 set. While some gap-filling techniques
appropriate to helioseismic data (i.e., many modes closely spaced in
frequency) may prove useful (Fossat et al. 1999; Fierry Fraillon &
Appourchaux 2001) we remain cautious regarding any advantage they may
offer under conditions of very modest fill (e.g., less than 50 per cent). We leave a discussion of the impact of this to another paper.
A study of this type is also important in a stellar context. First,
ground-based observations are sure to play an important rôle in
observations of low-![]() p modes on solar-like stars (Bedding &
Kjeldson 2003), and as such similar analysis problems and issues will
have to be confronted once extended time series of asteroseismic
observations are commonplace. Second, having an accurate means of
assessing the impact of different window functions on the precision
with which the eigenfrequencies can be determined has important
implications for studies of the diagnostic potential of the low-
p modes on solar-like stars (Bedding &
Kjeldson 2003), and as such similar analysis problems and issues will
have to be confronted once extended time series of asteroseismic
observations are commonplace. Second, having an accurate means of
assessing the impact of different window functions on the precision
with which the eigenfrequencies can be determined has important
implications for studies of the diagnostic potential of the low-![]() modes, e.g., for inversions of low-
modes, e.g., for inversions of low-![]() only data (Roxburgh &
Vorontsov 2002; Basu 2003), or determining the near-surface properties
of a star (Roxburgh & Vorontsov 2001; Verner et al. 2004).
only data (Roxburgh &
Vorontsov 2002; Basu 2003), or determining the near-surface properties
of a star (Roxburgh & Vorontsov 2001; Verner et al. 2004).
Our study takes as its basis the analysis of data collected by the six-station, ground-based Birmingham Solar-Oscillations Network (BiSON) over the 3660-d period beginning 1991 January 1. This extensive epoch spans the declining phase of solar activity cycle 22, and the rising phase of cycle 23.
The instruments at each BiSON site make Sun-as-a-star observations of
the Doppler shift of the potassium Fraunhofer line at 770 nm (e.g.,
Chaplin et al. 1996). Raw data were first processed in the manner
described by Elsworth et al. (1995) to yield daily calibrated velocity
residuals. We then combined coherently the resulting ![]() 2
2 ![]() 104 individual daily sets from all six stations to yield the principal
104 individual daily sets from all six stations to yield the principal ![]() 10-yr time series of residuals,
v(t). The duty cycle (fractional fill) of this combined set was
10-yr time series of residuals,
v(t). The duty cycle (fractional fill) of this combined set was
![]() 74 per cent, with breaks in coverage largely the result of inclement weather.
74 per cent, with breaks in coverage largely the result of inclement weather.
In order to study the impact on the analysis of duty cycles lower than this, the principal series was modulated by a selection of window functions which were made from different numbers of stations.
To do this, we used time series constructed from coherent
combinations of data collected by six (i.e., the principal series),
five, four and three stations having duty cycles of 74, 68, 62 and
50-per-cent respectively, taking proper account of the
longitudinal distribution of the stations. The strategy applied
here for the window-function construction is very similar to that used
by Chaplin et al. (2003a) to measure bias in the p-mode linewidths and
heights caused by a ground-based window. Each set was first
converted into a two-state format, w(t), i.e.,
The main aim of our study is to assess the impact of these window
functions on extracted estimates of the mode frequencies. Since we
make use of real, and not artificial, observations we must be sure
that frequency shifts introduced by the solar activity cycle do not
bias the results. Some of the lowest-fill sets could, in principle, be
preferentially weighted to different parts of the cycle and therefore
different frequency levels. To check this we made five full sets of
two-hundred and eighty 3660-d window functions. (The data used in the
paper are from a single, 280-window set.) The 10.7-cm solar radio
flux![]() was used as a proxy of the global
level of activity, and we computed an average of this over the period
of each window when non-zero data were present.
was used as a proxy of the global
level of activity, and we computed an average of this over the period
of each window when non-zero data were present.
Figure 2 shows the mean flux value over all five
series of window functions, plotted against the corresponding
fractional fill, D. The average value, represented by the solid
line, is slightly higher than 121 radio flux units. As can be seen,
the trend is flat with no significant evidence for the introduction of
any bias. The scatter on the average flux level does increase at lower D, reflecting the larger variance expected from fewer non-zero data. However, the full spread, of at most 5 flux units, would give rise to a frequency shift of only ![]()
![]() for a mode
at
for a mode
at ![]()
![]() .
This is somewhat smaller than the frequency uncertainty associated with modes in this part of the spectrum. The same is true for the other frequencies fitted in our
study. We conclude, therefore, that our results should not be biased by any cycle-dependent contribution and that any additional scatter introduced in the fitted frequencies will be modest.
.
This is somewhat smaller than the frequency uncertainty associated with modes in this part of the spectrum. The same is true for the other frequencies fitted in our
study. We conclude, therefore, that our results should not be biased by any cycle-dependent contribution and that any additional scatter introduced in the fitted frequencies will be modest.
The power spectrum of each time series, v'i(t), was fitted to yield
estimates of the mode parameters over the range
![]() for each of the different duty cycles. Because of
their close proximity in frequency the modes were fitted in pairs
(i.e.,
for each of the different duty cycles. Because of
their close proximity in frequency the modes were fitted in pairs
(i.e., ![]() /0 and 3/1) - following the basic prescription of
Chaplin et al. (1999) - to a model where all resonant components were
represented explicitly in the form of the asymmetric function of Nigam
& Kosovichev (1998). An additional offset was also included to
describe the background in the fitting window. We used a
multidimensional direction-set minimization algorithm (Press et al. 1992) to perform the fitting, maximizing an appropriate log-likelihood function. The natural logarithm of the height, width
and background terms were varied - not the parameter values
themselves - in order to give quasi-normal fitting distributions. Formal uncertainties on the fitted values were then derived from the Hessian matrix of each fit in the usual manner.
/0 and 3/1) - following the basic prescription of
Chaplin et al. (1999) - to a model where all resonant components were
represented explicitly in the form of the asymmetric function of Nigam
& Kosovichev (1998). An additional offset was also included to
describe the background in the fitting window. We used a
multidimensional direction-set minimization algorithm (Press et al. 1992) to perform the fitting, maximizing an appropriate log-likelihood function. The natural logarithm of the height, width
and background terms were varied - not the parameter values
themselves - in order to give quasi-normal fitting distributions. Formal uncertainties on the fitted values were then derived from the Hessian matrix of each fit in the usual manner.
In what follows we have chosen to investigate the variation of the
fitted frequencies as a function of the fractional fill, D. As
alternative independent variables we could have instead chosen to use
the fitted first sideband height, which reflects the impact of the
diurnal content of the window function, or the fitted background in
the vicinity of the modes, which reflects the remaining, quasi-random
content. Both do however show a clear functional dependence on the
fill (albeit with some realization scatter), and as such we have
settled on using D only. As an example of this dependence,
Fig. 3 shows the fitted first fractional sideband
height (left-hand panel) and background (right-hand panel) as a
function of D for each of the 280 spectra at ![]() ,
n=18.
,
n=18.
Figure 4 shows the fitted ![]() frequencies at n=18and 25. They are plotted as a function of the fractional duty cycle,
D, of each of the 280 sets. The single, representative error bar
corresponds in each case to the mean formal uncertainty returned by
the mode-fitting procedure.
frequencies at n=18and 25. They are plotted as a function of the fractional duty cycle,
D, of each of the 280 sets. The single, representative error bar
corresponds in each case to the mean formal uncertainty returned by
the mode-fitting procedure.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0372fig7.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{0372fig8.eps}\end{figure}](/articles/aa/full/2004/34/aa0372-04/Timg35.gif) |
Figure 5:
Change in fitted frequency, |
The plots reveal that there is some systematic bias, i.e., a change in
fitted frequency with fill. Interestingly, the sign of this is
reversed for some radial orders (e.g., for the two modes shown
here). A series of ![]() tests for different polynomial orders
indicated that in all cases a simple linear model provides an adequate
description of any uncovered trend. The solid line in each panel shows
such a straight-line fit.
tests for different polynomial orders
indicated that in all cases a simple linear model provides an adequate
description of any uncovered trend. The solid line in each panel shows
such a straight-line fit.
In order to quantify the extent to which the
frequencies are "pulled'' we fitted the frequency estimates
extracted at each (![]() )
to the linear model:
)
to the linear model:
Figure 5 plots the fitted sensitivities, ![]() ,
for
the complete range of modes covered by the analysis. The data have
been paired off according to the
,
for
the complete range of modes covered by the analysis. The data have
been paired off according to the ![]() with which they were fitted,
i.e.,
with which they were fitted,
i.e., ![]() with 2 (left-hand panel) and
with 2 (left-hand panel) and ![]() with 3
(right-hand panel). The sensitivity (ordinate) has been scaled in both
panels to show the frequency change expected for each 10-per-cent
decrease in fill, i.e., we show:
with 3
(right-hand panel). The sensitivity (ordinate) has been scaled in both
panels to show the frequency change expected for each 10-per-cent
decrease in fill, i.e., we show:
Some of the systematic changes uncovered at ![]() - in particular
those at n=16 (
- in particular
those at n=16 (![]()
![]() )
and 17 (
)
and 17 (![]()
![]() ) - are well out of line with the rest of the data (larger in magnitude than their neighbouring points). In order to seek a possible explanation we have checked both the quality of the
estimated frequencies used to generate these coefficients, and any
obvious spacings in frequency that might account for them, e.g., the
influence of the first diurnal sideband of the nearby
) - are well out of line with the rest of the data (larger in magnitude than their neighbouring points). In order to seek a possible explanation we have checked both the quality of the
estimated frequencies used to generate these coefficients, and any
obvious spacings in frequency that might account for them, e.g., the
influence of the first diurnal sideband of the nearby ![]() .
(The second sidebands lie too far from the principle peaks to affect
the splitting.) In this part of the spectrum, the first
sideband lies "over'' one of the outer components of the
.
(The second sidebands lie too far from the principle peaks to affect
the splitting.) In this part of the spectrum, the first
sideband lies "over'' one of the outer components of the ![]() .
In
spite of this we found that the fitting procedure is still able to
extract robust estimates of the height of the sidebands, and that as a
result the
.
In
spite of this we found that the fitting procedure is still able to
extract robust estimates of the height of the sidebands, and that as a
result the ![]() frequencies are not "pulled'' by an inadequate
modelling of them. There were also no clear outliers in the fitted
frequencies at n=16 and 17.
frequencies are not "pulled'' by an inadequate
modelling of them. There were also no clear outliers in the fitted
frequencies at n=16 and 17.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0372fig9.eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{0372fig10.eps}\end{figure}](/articles/aa/full/2004/34/aa0372-04/Timg44.gif) |
Figure 6:
Left-hand panel - fitted background-to-signal ratio,
|
Whilst we are therefore at somewhat of a loss for an explanation of
the out-of-line coefficients, it is perhaps worth noting two
points. First, we fitted the ![]() modes assuming a symmetric
arrangement of the components within each multiplet. One would expect
the observed m to be unevenly distributed in frequency on account of
the influence of the inhomogeneous distribution of magnetic activity
over the surface of the Sun. However, this effect should be very small
for most of the modes present in these 10-yr data (Chaplin et al. 2003b, 2004). Therefore, even though the fitting model used does not account for this, the effect is most likely not a cause for
concern. Second, the linewidths of the modes have a local maximum
(point of inflexion) at
modes assuming a symmetric
arrangement of the components within each multiplet. One would expect
the observed m to be unevenly distributed in frequency on account of
the influence of the inhomogeneous distribution of magnetic activity
over the surface of the Sun. However, this effect should be very small
for most of the modes present in these 10-yr data (Chaplin et al. 2003b, 2004). Therefore, even though the fitting model used does not account for this, the effect is most likely not a cause for
concern. Second, the linewidths of the modes have a local maximum
(point of inflexion) at ![]()
![]() ,
and it is over the
central part of the spectrum that a clear tendency is revealed for the
fitted widths to be overestimated in lower fill data (see Chaplin et al. 2003a). However, it is unclear why the
,
and it is over the
central part of the spectrum that a clear tendency is revealed for the
fitted widths to be overestimated in lower fill data (see Chaplin et al. 2003a). However, it is unclear why the ![]() modes might be affected whilst at the same time the other
modes might be affected whilst at the same time the other ![]() are not.
are not.
At frequencies above ![]()
![]() there is a clear increase
observed in the size of the
there is a clear increase
observed in the size of the ![]() .
This corresponds to that
part of the spectrum where the linewidths of the resonant peaks begin
to increase markedly, thereby giving rise to a total blending of
adjacent azimuthal orders, m, within a given multiplet and blending
between adjacent
.
This corresponds to that
part of the spectrum where the linewidths of the resonant peaks begin
to increase markedly, thereby giving rise to a total blending of
adjacent azimuthal orders, m, within a given multiplet and blending
between adjacent ![]() .
The
.
The ![]() and 0 modes are both very
prominent and therefore have a strong influence upon one another,
giving rise to the large increase in magnitude at the highest
frequencies (left-hand panel of Fig. 5). In contrast, the
weaker
and 0 modes are both very
prominent and therefore have a strong influence upon one another,
giving rise to the large increase in magnitude at the highest
frequencies (left-hand panel of Fig. 5). In contrast, the
weaker ![]() modes have a less pronounced impact on their
modes have a less pronounced impact on their ![]() neighbours and so the dipole frequencies are not pulled as strongly. The
neighbours and so the dipole frequencies are not pulled as strongly. The ![]() modes become difficult to fit above
modes become difficult to fit above ![]()
![]() in low-fill data and so we have not analyzed these
data at frequencies high enough to see the strong influence of the nearby
in low-fill data and so we have not analyzed these
data at frequencies high enough to see the strong influence of the nearby ![]() (right-hand panel of figure).
(right-hand panel of figure).
In order to place the sensitivities from Fig. 5 in full context they need to be compared to the typical precision with which the frequencies can be determined. If the fill-dependent frequency changes are found to be larger than the mode-frequency uncertainties the effect of this bias cannot then be ignored. As such, we look next at the behaviour of the errors.
In the absence of any source of background noise, the precision with
which the frequency of a mode can be determined is dependent upon its
lifetime,
![]() ,
and the length of time for which the
resonance has been observed, T. If
,
and the length of time for which the
resonance has been observed, T. If
![]() is the linewidth
of the resonance in the frequency domain, we define the lifetime
according to:
is the linewidth
of the resonance in the frequency domain, we define the lifetime
according to:
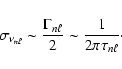 |
(6) |
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0372fig11.eps}\hspace*{2mm}
\includegraphics[width=8.85cm,clip]{0372fig12.eps}\end{figure}](/articles/aa/full/2004/34/aa0372-04/Timg59.gif) |
Figure 7:
Frequency uncertainties,
|
Chaplin et al. (2002) have shown that the background-to-signal ratio
can be modelled as a monotonic function of the fractional duty cycle,
D, according to:
The left-hand panel of Fig. 6 shows how the fitted
![]() varies at
varies at ![]() ,
n=18 (scattered points). The
observed increase with decreasing fill is representative of the trend
uncovered for all modes. The solid line is the best fit of the Chaplin
et al. (2002) model in Eq. (11) and can be used, together with
the fitted linewidth, to predict
,
n=18 (scattered points). The
observed increase with decreasing fill is representative of the trend
uncovered for all modes. The solid line is the best fit of the Chaplin
et al. (2002) model in Eq. (11) and can be used, together with
the fitted linewidth, to predict
![]() for different D (assuming
for different D (assuming
![]() ).
).
The two panels of Fig. 7 show the formal ![]() frequency uncertainties,
frequency uncertainties,
![]() (scattered points),
compared to those predicted using Eqs. (9) and (11)
(dashed line). The predictions were made using the fitted linewidths
from the principal, 74-%-fill dataset. The radial orders chosen are
the same as in Fig. 4. Again, the trend uncovered is
typical of all
(scattered points),
compared to those predicted using Eqs. (9) and (11)
(dashed line). The predictions were made using the fitted linewidths
from the principal, 74-%-fill dataset. The radial orders chosen are
the same as in Fig. 4. Again, the trend uncovered is
typical of all ![]() and n we study: a decrease in precision at
lower fill which is largely the result of the increase in the
background-to-signal ratio.
and n we study: a decrease in precision at
lower fill which is largely the result of the increase in the
background-to-signal ratio.
Except at lower radial orders, where the match is good, the prediction
is seen to underestimate the observed uncertainty at n=18 and
above. This discrepancy can be explained partly by the fact that no
account has been taken in the above of the impact of the window
function on the fitted linewidth
![]() .
Chaplin et al. (2003a) performed an in-depth study of this and found a clear tendency for the linewidth to be overestimated in data with low fill. This is illustrated clearly in the right-hand panel of
Fig. 6, where we plot the fitted linewidths for the
.
Chaplin et al. (2003a) performed an in-depth study of this and found a clear tendency for the linewidth to be overestimated in data with low fill. This is illustrated clearly in the right-hand panel of
Fig. 6, where we plot the fitted linewidths for the
![]() ,
n=18 mode. The solid line shows the best linear fit to
these data (which, given the observed uncertainties in the width,
provides an adequate description of the uncovered trend). When
corresponding linear fits are used to parameterize the fitted
,
n=18 mode. The solid line shows the best linear fit to
these data (which, given the observed uncertainties in the width,
provides an adequate description of the uncovered trend). When
corresponding linear fits are used to parameterize the fitted
![]() at each n in Eq. (9), the solid-line
predictions of the uncertainties in Fig. 7 are given.
These are seen to reduce the discrepancy between the formal and
modelled errors. That which remains is strongly dependent upon mode
frequency, with the size of the formal errors increasingly exceeding
the model at higher n (higher frequency). This can be explained by
the sharp increase in linewidth in this part of the p-mode
spectrum which gives rise to peak blending and the introduction
of effects over and above those modelled in Eq. (9).
The influence, and eventual blending, of components adjacent
in frequency then makes it harder to constrain reliably the location
of the mode peaks. This gives rise to a corresponding increase in the
uncertainty (recall that the model assumes a peak in complete
isolation).
at each n in Eq. (9), the solid-line
predictions of the uncertainties in Fig. 7 are given.
These are seen to reduce the discrepancy between the formal and
modelled errors. That which remains is strongly dependent upon mode
frequency, with the size of the formal errors increasingly exceeding
the model at higher n (higher frequency). This can be explained by
the sharp increase in linewidth in this part of the p-mode
spectrum which gives rise to peak blending and the introduction
of effects over and above those modelled in Eq. (9).
The influence, and eventual blending, of components adjacent
in frequency then makes it harder to constrain reliably the location
of the mode peaks. This gives rise to a corresponding increase in the
uncertainty (recall that the model assumes a peak in complete
isolation).
The dotted line in the left-hand panel of Fig. 7 (n=18)
is the prediction based upon the formula of Gelly et al. (1997) and
Fierry-Fraillon et al. (1998), who modified the factor of T-1/2in Eq. (9) to
(TD)-1/2. This is seen to result in a
large overestimation of the fitted uncertainty, and indicates that the
effect of the window function is adequately represented in the basic
equation by the fitted
![]() and
and
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{0372fig13.eps}\hspace*{2mm...
...m}\includegraphics[width=9.1cm,clip]{0372fig15.eps}\hspace*{4.7cm}}
\end{figure}](/articles/aa/full/2004/34/aa0372-04/Timg65.gif) |
Figure 8:
Frequency uncertainties
|
We are now in a position to assess the significance of the frequency
bias present at each (![]() ). Figure 8 plots the
magnitude of the bias, together with the fitted frequency
uncertainties, as a function of fill D for the same
). Figure 8 plots the
magnitude of the bias, together with the fitted frequency
uncertainties, as a function of fill D for the same ![]() modes
as in Figs. 4 and 7. We have chosen to
display the absolute values of the bias so that they can be
overlayed directly on the frequency uncertainties. (Note that the bias
lines appear curved because of the logarithmic scaling on each
ordinate.) We also show results for an additional
modes
as in Figs. 4 and 7. We have chosen to
display the absolute values of the bias so that they can be
overlayed directly on the frequency uncertainties. (Note that the bias
lines appear curved because of the logarithmic scaling on each
ordinate.) We also show results for an additional ![]() mode
(n=16). This is of interest since it shows an anomalously large bias
(left-hand panel Fig. 5).
mode
(n=16). This is of interest since it shows an anomalously large bias
(left-hand panel Fig. 5).
The magnitude of frequency bias in each case comes from the product
![]() (cf. Eq. (4)). Even though the
(cf. Eq. (4)). Even though the
![]() were extracted from analyses covering
were extracted from analyses covering
![]() only, we have assumed they are also valid outside this
range. Tests with artificial data indicate this is a robust assumption.
only, we have assumed they are also valid outside this
range. Tests with artificial data indicate this is a robust assumption.
The fitted uncertainties are plotted as points, with the bold line
marked "3660 days'' corresponding to the uncertainty predicted with
Eq. (9) (for which we used the mean fitted linewidth and
background-to-signal ratio for the mode in question, and
![]() ). The equation must be modified for the multi-peak
). The equation must be modified for the multi-peak
![]() mode, and we used Eq. (A.1) to generate the required
predicted uncertainties (see full discussion of errors at
mode, and we used Eq. (A.1) to generate the required
predicted uncertainties (see full discussion of errors at
![]() in Appendix A).
in Appendix A).
We have also plotted predicted uncertainties for three other dataset
lengths. These were determined by scaling the 3660-d values according
to the square root of ratio of the lengths![]() . The chosen values correspond to:
. The chosen values correspond to:
In our previous discussion in Sect. 3.1 we noted the
larger bias at higher frequencies. Here, the n=25 panel demonstrates
that the bias does indeed exceed the uncertainty,
![]() ,
for some combinations of T and D (when
,
for some combinations of T and D (when
![]() ,
it does so for all D). Only at
,
it does so for all D). Only at
![]() is the
bias smaller in size than the observed uncertainty.
is the
bias smaller in size than the observed uncertainty.
The ![]() data shown (lower panel of Fig. 8) are for
one of the modes whose extracted bias was much larger than, and
therefore out of line with, its neighbouring points. Here, we again
see that the bias is for some D significantly larger than
data shown (lower panel of Fig. 8) are for
one of the modes whose extracted bias was much larger than, and
therefore out of line with, its neighbouring points. Here, we again
see that the bias is for some D significantly larger than
![]() ,
but again only in the longer datasets.
,
but again only in the longer datasets.
Our results demonstrate that for the majority of low-![]() modes the
bias in the frequencies given by the effects of the window is not
significant. However, for modes above
modes the
bias in the frequencies given by the effects of the window is not
significant. However, for modes above ![]()
![]() ,
and
some
,
and
some ![]() modes near
modes near ![]()
![]() ,
they become
important when the frequencies are extracted from long datasets. As
such allowance then needs to be made to avoid misinterpreting any
results.
,
they become
important when the frequencies are extracted from long datasets. As
such allowance then needs to be made to avoid misinterpreting any
results.
Acknowledgements
We would like to take this opportunity to acknowledge the significant technical contribution made over many years to BiSON by our recently deceased colleague, H. K. Williams. We are indebted to J. Allison, R. Bryan and B. Jackson for their technical and analysis support in Birmingham and to former colleagues, in particular C. P. McLeod, J. Litherland and R. Lines. We also thank P. Fourie at SAAO; the Carnegie Institution of Washington; the Australia Telescope National Facility (CSIRO); E. J. Rhodes (Mt.Wilson, California); and members (past and present) of the IAC, Tenerife. BiSON is funded by the UK Particle Physics and Astronomy Research Council.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0372fig16.eps}\hspace*{2mm...
....eps}\hspace*{2mm}
\includegraphics[width=8.8cm,clip]{0372fig19.eps}\end{figure}](/articles/aa/full/2004/34/aa0372-04/Timg70.gif) |
Figure A.1:
Mean formal frequency uncertainties (as returned by the
mode-fitting procedure) for |
The analysis of the frequency uncertainties presented in
Sect. 3.2 must be extended when
![]() .
This is to
allow for the fact that these multiplets contain more than one peak.
.
This is to
allow for the fact that these multiplets contain more than one peak.
The various panels of Fig. A.1 show the mean formal
frequency uncertainties returned at ![]() ,
1, 2 and 3 by the
mode-fitting procedure (symbols joined by unbroken line). The dashed
line is in each case the single-peak prediction of Eq. (9)
and is meant to serve as an eye guide. These predictions were made
using the average fitted linewidth and background-to-signal ratio for
each mode. That there is a mis-match between the single-peak-modelled
and fitted errors is not surprising. This then begs the question of
how Eq. (9) needs to be modified when
,
1, 2 and 3 by the
mode-fitting procedure (symbols joined by unbroken line). The dashed
line is in each case the single-peak prediction of Eq. (9)
and is meant to serve as an eye guide. These predictions were made
using the average fitted linewidth and background-to-signal ratio for
each mode. That there is a mis-match between the single-peak-modelled
and fitted errors is not surprising. This then begs the question of
how Eq. (9) needs to be modified when
![]() .
.
The nature of any modification depends upon the number of peaks that
are observed, and the separation in frequency between them. When
Sun-as-a-star observations are made in or close to the ecliptic plane
(e.g., for BiSON and GOLF) only those components for which l+m is
even are clearly visible. Furthermore, the outer
![]() peaks
are by far the most prominent. Provided the separation of the outer
components is much larger than their inherent linewidth the mode can
to first order be modelled as two independent peaks.
peaks
are by far the most prominent. Provided the separation of the outer
components is much larger than their inherent linewidth the mode can
to first order be modelled as two independent peaks.
If
![]() is the splitting between adjacent m, this
demands that the "reduced splitting'',
is the splitting between adjacent m, this
demands that the "reduced splitting'',
![]() ,
be much greater in size than unity. Provided this
condition is met the frequency uncertainty will to good order be given
by:
,
be much greater in size than unity. Provided this
condition is met the frequency uncertainty will to good order be given
by:
We have estimated ![]() for each mode at
for each mode at
![]() using
the fitted data. Rearrangement of Eq. (A.1) gives:
using
the fitted data. Rearrangement of Eq. (A.1) gives:
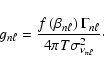 |
(13) |