J. R. Shi1,2 - T. Gehren2 - G. Zhao 1,2
1 - National Astronomical Observatories, Chinese Academy of Sciences,
Beijing 100012, PR China
2 - Institut für Astronomie und Astrophysik der
Universität München, Scheinerstrasse 1, 81679 München, Germany
Received 5 February 2004 / Accepted 4 May 2004
Abstract
We present sodium abundances for a sample of nearby stars. All results
have been derived from NLTE statistical equilibrium calculations. The influence
of collisional interactions with electrons and hydrogen atoms is evaluated by
comparison of the solar spectrum with very precise fits to the Na I
line cores. The NLTE effects are more pronounced in metal-poor stars since the
statistical equilibrium is dominated by collisions of which at least the
electronic component is substantially reduced. The resulting influence on the
determination of sodium abundances is in a direction opposite to that found
previously for Mg and Al. The NLTE corrections are about -0.1 in thick-disk
stars with
![]() .
Our [Na/Fe] abundance ratios are about solar for
thick- and thin-disk stars. The increase in [Na/Fe] as a function of [Fe/H] for
metal-rich stars found by Edvardsson et al. (1993) is confirmed. Our
results suggest that sodium yields increase with the metallicity, and quite
large amounts of sodium may be produced by AGB stars. We find that [Na/Fe]
ratios, together with either [Mg/Fe] ratio, kinematic data or stellar
evolutionary ages, make possible the individual discrimination between thin- and
thick-disk membership.
.
Our [Na/Fe] abundance ratios are about solar for
thick- and thin-disk stars. The increase in [Na/Fe] as a function of [Fe/H] for
metal-rich stars found by Edvardsson et al. (1993) is confirmed. Our
results suggest that sodium yields increase with the metallicity, and quite
large amounts of sodium may be produced by AGB stars. We find that [Na/Fe]
ratios, together with either [Mg/Fe] ratio, kinematic data or stellar
evolutionary ages, make possible the individual discrimination between thin- and
thick-disk membership.
Key words: line: formation - line: profiles - stars: abundances - stars: late-type - Galaxy: evolution
The 23Na nucleus contains an extra neutron that makes its synthesis deviate
from that of the ![]() -nuclei such as 24Mg. So the abundance ratios [Na/Fe] and/or [Na/Mg] in stars are a potential source of information concerning
the history of Galactic nucleosynthesis.
-nuclei such as 24Mg. So the abundance ratios [Na/Fe] and/or [Na/Mg] in stars are a potential source of information concerning
the history of Galactic nucleosynthesis.
It is expected that sodium is made during carbon and neon burning in massive stars, and it would therefore be ejected by Type II supernova (SN II). Type Ia supernova, on the other hand, produce little sodium (Tsujimoto et al. 1995). However, 23Na can be synthesized as a primary or secondary element. In the first case 23Na would be produced directly in the carbon burning process, and the production rate would be independent of the metal content of the proceeding stellar generation. In the second process, where 23Na is produced by an excess of neutrons, the production rate would depend on that neutron excess which in turn would be determined by the pre-existing metal abundance. In the latter case 23Na would be expected to display an underabundance compared with Fe or Mg in the most metal-poor stars. Although significant progress has been made in nucleosynthesis calculations, theoretical SN yields of sodium have not yet converged to consistency among models from different authors (Woosley & Weaver 1995; Limongi et al. 1998; Umeda et al. 2000). Also some synthesis of sodium in intermediate-mass stars can occur in the hydrogen-burning shell through the neon-sodium cycle (Denissenkov & Denissenkova 1990; Mowlavi 1999).
The observational picture for this element is complicated. The early studies
report that sodium scales with iron at all metallicities (e.g. the review of
Timmes et al. 1995; Goswami & Prantzos 2000). However, new
studies do not support this classical picture. For metal-poor stars, Pilachowski
et al. (1996) analyzed a sample of 60 halo subgiants, giants and
horizontal branch stars in the interval
![]() ,
and found a
small [Na/Fe] deficiency of -0.17 dex in the mean and that bright field halo
giants do not show the excess of sodium found in their globular cluster
counterparts. Baumüller et al. (1998) performed a NLTE analysis of
sodium and reported a clear trend of decreasing [Na/Fe] with decreasing
metallicity. Similarly, Stephens (1999) found that [Na/Fe] decreases as
one goes from
,
and found a
small [Na/Fe] deficiency of -0.17 dex in the mean and that bright field halo
giants do not show the excess of sodium found in their globular cluster
counterparts. Baumüller et al. (1998) performed a NLTE analysis of
sodium and reported a clear trend of decreasing [Na/Fe] with decreasing
metallicity. Similarly, Stephens (1999) found that [Na/Fe] decreases as
one goes from
![]() to
to
![]() ,
and thus shows the theoretically
expected behaviour of odd-Z elements. Carretta et al. (2000) and Gratton
et al. (2003) also found that sodium is overdeficient in stars with
,
and thus shows the theoretically
expected behaviour of odd-Z elements. Carretta et al. (2000) and Gratton
et al. (2003) also found that sodium is overdeficient in stars with
![]() ;
this result was confirmed by very recent work of Gehren et al.
(2004).
;
this result was confirmed by very recent work of Gehren et al.
(2004).
For disk stars, Edvardsson et al. (1993) used high-resolution, low-noise spectra to determine sodium abundance in 189 F and G stars. Their LTE analysis suggested that the [Na/Fe] ratio is solar and varies very little with metallicity, which was confirmed by Chen et al. (2000). Based on 5682/5688 and 6154/6160 lines, Prochaska et al. (2000) measured sodium abundance in their thick-disk stars and found that all the stars show mildly enhanced [Na/Fe] and there is a mild trend with metallicity (see also Gehren et al. 2004).
Concerning the most metal-rich stars in the galactic disk, the
study by Edvardsson et al. (1993) raised a number of new
questions. They found sodium relative to iron versus [Fe/H] shows
an increase for
![]() (see also Feltzing & Gustafsson
1998, their Fig. 8). Is the "upturn'' real? Large
star-to-star scatter was encountered. Could this scatter to be
reduced by using better abundance criteria?
(see also Feltzing & Gustafsson
1998, their Fig. 8). Is the "upturn'' real? Large
star-to-star scatter was encountered. Could this scatter to be
reduced by using better abundance criteria?
It is known that [Fe/H] distributions of the halo, thick- and thin-disk stars reveal considerable overlap, so it can not allow unequivocal classification for many stars without reference to other criteria such as age or kinematics. Fuhrmann (1998, 2002) suggested that the thick-disk stars represent the principal population for the early Galactic evolution, while the stellar halo contributes by only minute amounts (see also Ryan & Smith 2003). Considering the general kinematics, there may be a significant overlap of all populations (Gehren et al. 2004). Gratton et al. (1996, 2000, 2003) have shown that thick-disk stars are more [Mg/Fe] enhanced than the thin-disk stars at the same [Fe/H] value. This trend has also been reported by Fuhrmann (1998; see also Prochaska et al. 2000; Reddy et al. 2003). Finally, Mashonkina et al. (2003) have given evidence that [Eu/Mg] ratio allows the individual discrimination of halo stars from thick-disk stars, and similar behaviour is found for the [Al/Mg] ratio by Gehren et al. (2004).
The present work is based on a sample of nearby stars and aims at exploring their [Na/Fe] abundance ratios applying full spectrum synthesis based on level populations calculated from the statistical equilibrium equations. In Sect. 2 we present the observational techniques, while the atmospheric models and stellar parameters are discussed in Sect. 3. NLTE line formation is discussed in Sect. 4. The discussion is presented in Sect. 5, and the conclusions are found in the last section.
Our approach towards a representative abundance investigation is
aimed at analyzing a volume-complete sample of the F, G and early K dwarfs in the disk population, north of declination
![]() and within 25 pc of the Sun (see Fuhrmann 2004,
for details). The spectra of our samples were obtained through the years 1995 to 2000 by Klaus Fuhrmann with the fiber-coupled
Cassegrain échelle spectrograph FOCES (Pfeiffer et al.
1998) mounted at the 2.2 m telescope of the Calar Alto
Observatory. Only few of them were exposed to a 10242 24
and within 25 pc of the Sun (see Fuhrmann 2004,
for details). The spectra of our samples were obtained through the years 1995 to 2000 by Klaus Fuhrmann with the fiber-coupled
Cassegrain échelle spectrograph FOCES (Pfeiffer et al.
1998) mounted at the 2.2 m telescope of the Calar Alto
Observatory. Only few of them were exposed to a 10242 24 ![]() CCD with
CCD with
![]() ,
and their
wavelength ranges are limited to 4000-7000 Å, whereas the
standard configuration was a 20482 15
,
and their
wavelength ranges are limited to 4000-7000 Å, whereas the
standard configuration was a 20482 15 ![]() CCD that covered
4000-9000 Å with
CCD that covered
4000-9000 Å with
![]() .
All stars
were observed at least twice with a signal-to-noise ratio of at
least
.
All stars
were observed at least twice with a signal-to-noise ratio of at
least
![]() up to
up to
![]() (see Fuhrmann
1998, 2000, for details).
(see Fuhrmann
1998, 2000, for details).
For most of the stars we adopt the stellar parameters determined
by Fuhrmann (1998, 2000), where the effective
temperatures are derived from the wings of the Balmer lines;
surface gravities are taken from the strong line wings of the
Mg Ib triplet and compared with values obtained from
Hipparcos parallaxes. Iron abundances are based on Fe II
lines, and the microturbulence velocities are estimated by
requesting that the iron abundance derived from Fe II
lines should not depend on equivalent width. The uncertainties for
the temperature, surface gravity, metal abundance and
microturbulence velocities are generally assumed to be ![]() 80 K,
0.1 dex, 0.2 km s-1 and 0.07 dex respectively (see Fuhrmann
1998, 2000, for details). For Procyon the parameters
were taken from Korn et al. (2003), where the temperatures
are again from the wings of Balmer lines; surface gravities are
based on the HIPPARCOS parallaxes, and iron abundances are taken
from NLTE calculations.
80 K,
0.1 dex, 0.2 km s-1 and 0.07 dex respectively (see Fuhrmann
1998, 2000, for details). For Procyon the parameters
were taken from Korn et al. (2003), where the temperatures
are again from the wings of Balmer lines; surface gravities are
based on the HIPPARCOS parallaxes, and iron abundances are taken
from NLTE calculations.
Following Fuhrmann's work, we employ the macroturbulence parameters ![]() in
the radial-tangential form and adopt values as described in Gray (1984).
The projected rotational velocity is obtained as the residual to the observed
line profiles, after having removed the known instrumental profile obtained from
the Moon spectra.
in
the radial-tangential form and adopt values as described in Gray (1984).
The projected rotational velocity is obtained as the residual to the observed
line profiles, after having removed the known instrumental profile obtained from
the Moon spectra.
To establish the influence of deviations from LTE on the ionization equilibrium
of sodium, we have chosen the reference stars of Korn et al. (2003). The
full analysis of the solar spectrum (Kurucz et al. 1984) and those of
the reference stars allows a reasonable choice of the hydrogen collision
enhancement factor resulting in
![]() for Na , found by iteration
together with all basic stellar paraeters. This number is the same as in the
previous work of Baumüller et al. (1998).
for Na , found by iteration
together with all basic stellar paraeters. This number is the same as in the
previous work of Baumüller et al. (1998).
All calculations have been carried out with a revised version of the DETAIL program (Butler & Giddings 1985) using accelerated lambda iteration (see Gehren et al. 2001, 2004, for details).
Collisional broadening through van der Waals interaction with hydrogen atoms is
important for strong Na D lines. As already pointed out by Gehren et al.
(2001, 2004) the resulting values of the van der Waals damping
constants are mostly near those calculated according to Anstee & O'Mara's
(1991, 1995) tables. Fitting the solar profiles with a common Na
abundance then shows that our damping constants for the resonance lines are
roughly a factor of 2 below those calculated. The adopted line data (gf values
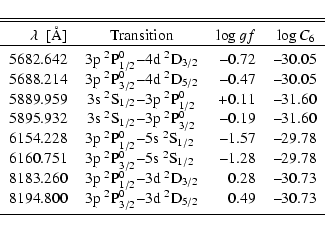
and van der Waals damping constants) are given in Table 1.
|
Baumüller et al. (1998)
Baumüller et al. (1998) performed a full NLTE line formation for a
sample of metal-poor stars. We have four stars in common with theirs. Our NLTE
results are very much in agreement with theirs, as shown in Fig. 1. The average
differences between our [Na/Fe] and theirs are
![]() .
We note that the
considerable scatter is mostly due to the different stellar parameters adopted.
.
We note that the
considerable scatter is mostly due to the different stellar parameters adopted.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0203fig1.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg39.gif) |
Figure 1:
Comparison of derived [Na/Fe] for stars in
common with other studies. Filled circles ( |
Feltzing & Gustafsson (1998)
In this study of 47 G and K metal-rich stars, they confirmed the
increase of [Na/Fe] as a function of [Fe/H] found previously by
Edvardsson et al. (1993). Their results were determined
from 6154/6160 lines, the gf values adopted in this study are
slightly lower than ours, the differences are -0.02/-0.05,
respectively. The sodium abundance determined by this study is in
good agreement with ours. For three stars in common, the average
difference is
![]() .
.
Carretta et al. (2000)
This work reanalysed the data of Edvardsson et al. (1993) including a
NLTE correction. They found no large differences from the LTE results of
Edvardsson et al., which is shown in their Fig. 9. The gf values of the
6154/6160 lines adopted by Edvardsson et al. (1993) are slightly lower
than ours, the differences are -0.04 and -0.03, respectively. The results of
Carretta et al. (2000) are very much in agreement with ours. For the 46 common stars from Edvardsson et al. (1993), the average difference
between ours and theirs is
![]() .
.
This analysis deals with a large number of metal-poor stars, of
which five stars are in common with our sample. As pointed out by
Gehren et al. (2004), there are large differences in
stellar parameters; on average, the typical difference in
temperatures for the individual star is about 150 K, and there are
a few stars for which differences may be much larger. Fulbright's
abundances are slightly larger than ours (see Fig. 1). For the
five stars in common with our list we obtain
![]() .
We find that the largest difference
(
.
We find that the largest difference
(![]() 0.4 dex) comes from warm metal-poor stars such as
HD 284248. We note that considerable discrepancies remain even
after correcting for the difference in effective temperatures. As
these stars are metal-poor, they may suffer from relatively large NLTE effects (see Sect. 5.1).
0.4 dex) comes from warm metal-poor stars such as
HD 284248. We note that considerable discrepancies remain even
after correcting for the difference in effective temperatures. As
these stars are metal-poor, they may suffer from relatively large NLTE effects (see Sect. 5.1).
Gratton et al. (2003)
The authors considered NLTE corrections and reported the sodium abundances for 150 field subdwarfs and subgiants. Our results are mostly in agreement with
theirs. For the six stars in common, the average difference is
![]() .
.
Takeda et al. (2003)
Very recently, Takeda et al. (2003) performed a NLTE analysis of sodium
abundances for disk and halo stars. They reanalysed the data from Chen et al.
(2000). Their results vary from line to line (see their Tables 4 and 5).
The results for the 6154/6160 lines show no large differences from those of Chen
et al. (see their Fig. 5c). Our [Na/Fe] values are in agreement with theirs for
the lines of 6154/6160 Å for the three stars in common; the average
difference is
![]() .
As already pointed out by Takeda et al., this line
pair is not very sensitive to the NLTE effects.
.
As already pointed out by Takeda et al., this line
pair is not very sensitive to the NLTE effects.
Reddy et al. (2003)
This sample consists of 187 F and G dwarfs. The sodium abundances
were based on 6154/6160 lines, the gf values adopted in their
work are nearly same as those we adopted. A very close star by
star agreement between the [Na/Fe] ratios derived here and those
measured by Reddy et al., no difference exceeds 0.20 dex. For the
six stars in common, we obtain
![]() .
The large scatter is due to
HD 218470 (0.16 dex). This is a high
.
The large scatter is due to
HD 218470 (0.16 dex). This is a high ![]() (13.1 km s-1), high temperature (
(13.1 km s-1), high temperature (
![]() )
and low gravity
(log g=4.02) star. For this star their temperature is about 70 K
higher than ours.
)
and low gravity
(log g=4.02) star. For this star their temperature is about 70 K
higher than ours.
The abundance analyses of sodium clearly show the NLTE effect.
There is a tendency that the NLTE effect is large for warm
metal-poor subgiant stars, as would be expected. Baumüller et al. (1998) show in their Fig. 11 that the NLTE line cores
for the Na D lines are much deeper than in LTE in metal-deficient
stars. In LTE abundance analyses this is compensated by simply
increasing the sodium abundance until the observed equivalent
width is reproduced. Such results are displayed in Table 3 of
Baumüller et al. (see also their Table 2). The results
confirm, starting from the solar abundance towards the lower
metallicity, that the NLTE abundance effect resulting from the Na D lines increases reaching a maximum near
![]() .
LTE
abundances can be significantly different from their NLTE
counterparts, with differences reaching more than 0.6 dex in
extreme cases. In Table 3 it is evident that the NLTE effects are
systematically stronger for the hotter models, which is in
agreement with the statistical equilibrium of both aluminium and
magnesium (Baumüller et al. 1997; Zhao & Gehren
2000). As expected, the strongest departures from LTE are
found for models with high temperature and low metallicity. The
reduction of surface gravity results in a decreased efficiency of
collisions with electrons and hydrogen atoms, which again leads to
stronger NLTE effects. In Fig. 2, the differences between LTE and NLTE analyses for our program stars are plotted as a function of
metal abundance, temperature and luminosity.
.
LTE
abundances can be significantly different from their NLTE
counterparts, with differences reaching more than 0.6 dex in
extreme cases. In Table 3 it is evident that the NLTE effects are
systematically stronger for the hotter models, which is in
agreement with the statistical equilibrium of both aluminium and
magnesium (Baumüller et al. 1997; Zhao & Gehren
2000). As expected, the strongest departures from LTE are
found for models with high temperature and low metallicity. The
reduction of surface gravity results in a decreased efficiency of
collisions with electrons and hydrogen atoms, which again leads to
stronger NLTE effects. In Fig. 2, the differences between LTE and NLTE analyses for our program stars are plotted as a function of
metal abundance, temperature and luminosity.
It should be noted that the NLTE effects differ from line to line, reflecting
their individual properties. For example, the 8183/8194 lines show relatively
large NLTE effects compared to the other lines at similar line-strength. From
Table 3, we can see the importance of the NLTE effect on different lines in
sodium abundance determination:
A warning is appropriate that Table 3 should not be used for LTE abundance corrections if precise Na abundances are aimed at. The data may vary considerably whenever the microturbulence velocity deviates from 1 km s-1, and any simple correction may result in an increased scatter. The reference to [Na/Fe] = 0 may also be a bad approximation, particularly in metal-poor stars.
The variation of [Na/Fe] with the stellar metal abundance [Fe/H]
contains information about the chemical evolution of the Galaxy.
Figure 3 displays the run of [Na/Fe] ratio (calculated in NLTE) with
the overall metal abundance for all stars considered in this
paper. One important feature that can be seen from Fig. 3 is that
the bulk of the sodium abundances scale approximately as iron in
thin-disk stars, with a small overabundance for the thick-disk
stars. The "upturn'' in [Na/Fe] versus [Fe/H] for metal-rich disk
stars, as observed by Edvardsson et al. (1993), is also
reproduced![]() .
.
Using magnesium instead of iron as the reference can remove Type
Ia SNe from consideration, because nearly all the sodium and
magnesium are produced in massive stars (Timmes et al.
1995). Calculations of nucleosynthsis for SNe Ia show that
they should produce only very little amounts of sodium (Nomoto et al. 1997). The odd-even effects will be enhanced using
magnesium as the basis of comparison. The overall behaviour of [Na/Mg] ratios versus [Mg/H] is therefore shown in Fig. 4 where
the Mg abundances are taken from Fuhrmann (1998,
2000). We confirm Arnett's (1971) prediction that [Na/Mg] ratios decline with decreasing metallicity. This suggests
that sodium abundances may be more closely coupled to chemical
evolution history, with a gradual enrichment of [Na/Mg] from thick
to thin disk.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0203fig3.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg51.gif) |
Figure 3: Abundance ratios [Na/Fe] for NLTE analyses. The meaning of the symbols is the same as in Fig. 2. |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0203fig4.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg52.gif) |
Figure 4: [Na/Mg] abundances ratios for NLTE analysis as a function of [Mg/H]. Symbols are the same as in Fig. 2. |
Presently, the source of sodium remains to be confirmed. Thus it
is difficult to use sodium as a probe of Galactic chemical
evolution until the effects of individual stars can be quantified.
Theoretical sodium yields of SN II have not yet converged to
consistency among models of different authors (Woosley & Weaver
1995; Umeda et al. 2000). Umeda et al.
(2000) show the yields of sodium are much less for Z=0compared to the Z=0.02 for a 20 ![]() model, while Woosley
& Weaver (1995) predict that for a 22
model, while Woosley
& Weaver (1995) predict that for a 22 ![]() SN model
the amount of sodium decreases with increasing metallicity in the
range of Z=0 to
SN model
the amount of sodium decreases with increasing metallicity in the
range of Z=0 to ![]() .
Also, AGB stars are potential
sites for the production of primary sodium (Mowlavi
1999). In this scenario synthesis of sodium can occur in
hydrogen-burning shells during ON-cycling (Denissenkov & Tout
2000). This process is supported by observations of red
giant stars in globular clusters that appear to be sodium-rich
(Kraft et al. 1997; Gratton et al. 2001).
.
Also, AGB stars are potential
sites for the production of primary sodium (Mowlavi
1999). In this scenario synthesis of sodium can occur in
hydrogen-burning shells during ON-cycling (Denissenkov & Tout
2000). This process is supported by observations of red
giant stars in globular clusters that appear to be sodium-rich
(Kraft et al. 1997; Gratton et al. 2001).
Detailed modelling of the Galactic chemical evolution has been
attempted by many authors (e.g., Timmes et al. 1995;
Goswami & Prantzos 2000). Based on Woosley & Weaver's
(1995) metallicity-dependent yields, the first authors
calculate the behaviour of [Na/Fe] as a function of metallicity.
Their results predict that [Na/Fe] decreases from
![]() to
to ![]() -1.5, while it increases from
-1.5, while it increases from
![]() to
to ![]() -0.5 (see their Fig. 17). However using the same yields
with an iron yield reduced by a factor of 2, Goswami & Prantzos'
calculation explains the decline of [Na/Fe] from
-0.5 (see their Fig. 17). However using the same yields
with an iron yield reduced by a factor of 2, Goswami & Prantzos'
calculation explains the decline of [Na/Fe] from
![]() to
to
![]() reasonably well. Their prediction suggests an
ever-decreasing [Na/Fe] toward the lower metallicity regime. They
used a different initial mass function (IMF), and a different halo
model.
reasonably well. Their prediction suggests an
ever-decreasing [Na/Fe] toward the lower metallicity regime. They
used a different initial mass function (IMF), and a different halo
model.
Our observational results provide some implications for the
nuclesynthesis of sodium. We note that in halo stars sodium is
significantly underabundant relative to iron, and [Na/Fe] (or
[Na/Mg]) increases with metallicity (Fig. 5). In the region of
overlapping metal abundances [Na/Fe] shows a clear distinction
between halo and thick-disk stars. The linear relationship
indicates that sodium production is connected to the metallicity
of the progenitor SN as suggested by Nissen & Schuster
(1997). This result agrees with nucleosynthesis
calculations of massive stars by Umeda et al. (2000), but
it is at variance with the calculations by Woosley & Weaver
(1995). We note that there are no extremely metal-poor
stars in the sample of Gehren et al. (2004), whereas
McWilliam et al. (1995) find that, for stars with
![]() ,
[Na/Fe] rises with decreasing metal abundance. Based on
this result Tsujimoto et al. (2002) argued that sodium
yields decrease with increasing Z for the very metal-poor stars.
However, nearly all the stars are giants and the abundances were
derived from the Na D (5890/5896) lines, which are very sensitive
to NLTE effects (see Sect. 5.1; Takeda et al. 2003). There
are two possibilities to explain the high [Na/Fe] values of
McWilliam et al.,
,
[Na/Fe] rises with decreasing metal abundance. Based on
this result Tsujimoto et al. (2002) argued that sodium
yields decrease with increasing Z for the very metal-poor stars.
However, nearly all the stars are giants and the abundances were
derived from the Na D (5890/5896) lines, which are very sensitive
to NLTE effects (see Sect. 5.1; Takeda et al. 2003). There
are two possibilities to explain the high [Na/Fe] values of
McWilliam et al.,
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0203fg5a.eps}\vspace*{3mm}
\includegraphics[width=7.6cm,clip]{0203fg5b.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg60.gif) |
Figure 5: Top: abundance ratios [Na/Fe] for NLTE analysis as a function of [Fe/H]. Bottom: abundance ratios [Na/Mg] for NLTE analysis as a function of [Mg/H]. Filled and open circles refer to the thin- and thick-disk stars in this paper, respectively. Asterisks refer to the stars from Gehren et al. (2004). |
Based on [Eu/Ba] ratios, Mashonkina et al. (2003) suggested that during the active phase of the thick disk formation evolved low mass stars may enrich the interstellar gas. Our observational results show that [Na/Fe] values are about solar, possibly being slightly overabundant in the thick-disk stars, which would confirm the suggestion that AGB stars may contribute some additional sodium. However, metallicity-dependent SN yields of sodium can not be excluded.
While the origin of the "upturn'' for the metal-rich stars is still unclear, Feltzing & Gustafsson (1998) argued that metallicity-dependent SN yields may play a role. Though a rather insufficient fraction of stars supersolar metal abundances prevents us from making any definitive argument, we suggest that quite large amounts of Na may be produced by proton capture on 22Ne nuclei for AGB stars (Denissenkov & Denissenkova 1990).
It is important to distinguish the individual membership of stars
in our sample. We are aware that such a discussion requires more
than the interpretation of abundance ratios alone. Following
Fuhrmann's (1998, 2000) work we use
![]() as
a first step to discriminate between thin- and thick-disk stars.
as
a first step to discriminate between thin- and thick-disk stars.
We show the distribution of [Na/Fe] versus [Mg/Fe] for the two
populations of thick- and thin-disk stars in Fig. 6. Even
comparing abundance alone, Fig. 6 suggests differences among the
two populations: the thin-disk stars are well separated on the
left side.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0203fig6.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg62.gif) |
Figure 6: [Na/Fe] abundance ratios for NLTE analyses as a function of [Mg/Fe]. The meaning of symbols is the same as in Fig. 2. |
Fuhrmann (2000) has discussed in more detail the kinematical aspects of our sample. The basic data are available in a number of catalogues which are electronically accessible (e.g. via http://www.ari.uni-heidelberg.de/aricns). The correction for the basic solar motion is that of Dehnen & Binney (1998), namely, U0/V0/W0 = 10.00/5.25/7.17 km s-1. Whenever these data are not provided, we have calculated the space velocities following the model described by Chen et al. (2000).
The first inspection of Fig. 7 shows that the V velocities of
thin-disk stars tend to be significantly larger than those of the
other populations, although there is some overlap between thin-
and thick-disk stars. The two most exceptional cases are the
thin-disk star HD 52711 (V=-98 km s-1) and the transition
star HD 90508 (V=-89 km s-1), and we will come back to
them later. The correlation between low [Na/Mg] ratios and low Vor high peculiar space velocities (
![]() )
is also instructive
(Fig. 8). The kinematic status in the Toomre diagram of our sample
was shown by Fuhrmann (2000, in his Fig. 17).
)
is also instructive
(Fig. 8). The kinematic status in the Toomre diagram of our sample
was shown by Fuhrmann (2000, in his Fig. 17).
We now come back to the transition stars HD 90508 (U/V/W
=31/-89/30 km s-1) and thin-disk object HD 52711 (
U/V/W
=-17/-98/-13 km s-1): Fuhrmann (2000) argues that
although HD 90508 shows thick-disk kinematics, its chemistry and
age are more like thin-disk stars. HD 52711 is thought to be a
thick-disk star based on its kinematics (e.g., Ibukiyama &
Arimoto 2002), however, it is very young (6.8 Gyr) and [Mg/Fe] is about solar (0.04), therefore it is also more like a
thin-disk star.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0203fg7a.eps}\vspace*{3mm}
\includegraphics[width=7.8cm,clip]{0203fg7b.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg64.gif) |
Figure 7: Correlation between Na abundance ratios and orbital V velocity components. Symbols are as in Fig. 2. |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0203fg8a.eps}\vspace*{3mm}
\includegraphics[width=7.6cm,clip]{0203fg8b.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg65.gif) |
Figure 8:
Correlation between [Na/Fe] abundance ratios
and peculiar space velocities
|
Using the stellar effective temperatures together with the
absolute magnitudes based on Hipparcos parallaxes, masses and
approximate ages can be interpolated according to [Fe/H] and [![]() /Fe] from adequate tracks of stellar evolution. Such calculations have recently become available through the work of
VandenBerg et al. (2000, 2002) and Yi et al.
(2003). In this paper we adopt the Yonsei-Yale isochrones
(Yi et al. 2003) since the evolutionary tracks of
VandenBerg contain only metal-poor (
/Fe] from adequate tracks of stellar evolution. Such calculations have recently become available through the work of
VandenBerg et al. (2000, 2002) and Yi et al.
(2003). In this paper we adopt the Yonsei-Yale isochrones
(Yi et al. 2003) since the evolutionary tracks of
VandenBerg contain only metal-poor (
![]() )
and low
mass stars (
)
and low
mass stars (
![]() ). The Yonsei-Yale isochrones are
calculated with new OPAL opacities and Kurucz model atmospheres
for a set of metallicities
Z = 0.00001, 0.0001, 0.0004, 0.001,
0.004, 0.007, 0.01, 0.02, 0.04, 0.06, 0.08, and
). The Yonsei-Yale isochrones are
calculated with new OPAL opacities and Kurucz model atmospheres
for a set of metallicities
Z = 0.00001, 0.0001, 0.0004, 0.001,
0.004, 0.007, 0.01, 0.02, 0.04, 0.06, 0.08, and
![]() ,
0.3, 0.6. The mixing length and helium enrichment rate were
fixed to
,
0.3, 0.6. The mixing length and helium enrichment rate were
fixed to
![]() and
and ![]() Y/
Y/
![]() ,
respectively. The full set of stellar models and a FORTRAN
package that works for mass, metallicity and
,
respectively. The full set of stellar models and a FORTRAN
package that works for mass, metallicity and ![]() -enhancement
interpolation are available from the authors.
-enhancement
interpolation are available from the authors.
The ages derived here are based on the assumption that
![]() .
From Fig. 9 we can
see that all the thin-disk stars do not exceed
.
From Fig. 9 we can
see that all the thin-disk stars do not exceed ![]() 9 Gyr, whereas with the exclusion
of HD 165401 all thick-disk stars are older than
9 Gyr, whereas with the exclusion
of HD 165401 all thick-disk stars are older than ![]() 9 Gyr. Fuhrmann (1998)
identified this star as a thick-disk member with an age of about 10 Gyr, but in his Paper II (Fuhrmann 2000) he noted that it is a chromospherically active, high-velocity
star, so it was excluded from his later analysis.
9 Gyr. Fuhrmann (1998)
identified this star as a thick-disk member with an age of about 10 Gyr, but in his Paper II (Fuhrmann 2000) he noted that it is a chromospherically active, high-velocity
star, so it was excluded from his later analysis.
As already pointed out by VandenBerg et al. (2002) and iterated by
Gehren et al. (2004), a significantly higher [Mg/Fe] ratio could reduce
the ages of thick-disk and halo stars by as much as 3 Gyr. For comparison, we
also calculated the ages for these stars without ![]() -enhancement. Then our
result is fairly in agreement with Fuhrmann's, namely that all the thick-disk
(excluding HD 165401) and halo stars are older than 12 Gyr, while all the
thin-disk stars are younger than 9.5 Gyr except the three transition stars
(HD 90508, HD 143761 and HD 187923). Therefore Fuhrmann's result that
the key feature to identify thick- and thin-disk stars individually is
provided by the stellar ages still holds. However, the 3 Gyr long star
formation gap between thin- and thick-disk is not confirmed here.
-enhancement. Then our
result is fairly in agreement with Fuhrmann's, namely that all the thick-disk
(excluding HD 165401) and halo stars are older than 12 Gyr, while all the
thin-disk stars are younger than 9.5 Gyr except the three transition stars
(HD 90508, HD 143761 and HD 187923). Therefore Fuhrmann's result that
the key feature to identify thick- and thin-disk stars individually is
provided by the stellar ages still holds. However, the 3 Gyr long star
formation gap between thin- and thick-disk is not confirmed here.
The three transition stars (HD 90508, HD 143761 and HD 187923) have ages
about 8.8 Gyr, thus they are as old as the oldest thin-disk stars. They would be
about 10.5 Gyr old if no ![]() -enhancement were considered.
-enhancement were considered.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0203fg9a.eps}\vspace*{3mm}
\includegraphics[width=7.7cm,clip]{0203fg9b.eps}
\end{figure}](/articles/aa/full/2004/32/aa0203-04/Timg73.gif) |
Figure 9: [Na/Fe] ratios vs. stellar ages ( top), and [Na/Mg] abundance ratios vs. stellar ages ( bottom). Ages are in Gyr. Symbols have the same meaning as in Fig. 2. |
We also note that the age of the thick-disk star HD 6582 seems to be very high (>15 Gyr); Gehren et al. (2004) have discussed this in detail.
Acknowledgements
S.J.R. thanks the Institute of Astronomy and Astrophysics of Munich University for warm hospitality during a productive stay in 2002. The authors thank Klaus Fuhrmann for his kind permission to use the reduced FOCES spectra of the stars investigated in this paper. This research was supported by the Deutsche Forschungsgemeinschaft under contract Ge 490/26-1 and by the National Natural Science Foundation of China under grants No.10173014, No.10173028 and NKBRSF 1999075406.
| HD |
|
[Fe/H] | [Na/Fe] | [Na/Fe] | ||
| LTE | NLTE | |||||
| 400 | 6149 | 4.06 | -0.25 | 1.31 | 0.11 | 0.03 |
| 3079 | 6050 | 4.17 | -0.14 | 1.42 | 0.09 | 0.02 |
| 4614 | 5939 | 4.33 | -0.30 | 1.06 | 0.09 | 0.04 |
| 5015 | 6045 | 3.90 | -0.02 | 1.39 | 0.12 | 0.04 |
| 6582 | 5387 | 4.45 | -0.83 | 0.89 | 0.14 | 0.07 |
| 6920 | 5838 | 3.48 | -0.05 | 1.35 | 0.08 | 0.02 |
| 9407 | 5663 | 4.42 | 0.03 | 0.87 | 0.09 | 0.05 |
| 9826 | 6107 | 4.01 | 0.09 | 1.40 | 0.13 | 0.04 |
| 10 697 | 5614 | 3.96 | 0.10 | 1.04 | 0.11 | 0.04 |
| 16 141 | 5737 | 3.92 | 0.02 | 1.24 | 0.14 | 0.06 |
| 16 895 | 6248 | 4.20 | -0.01 | 1.42 | 0.08 | 0.00 |
| 18 757 | 5714 | 4.34 | -0.28 | 0.95 | 0.13 | 0.06 |
| 18 803 | 5657 | 4.39 | 0.14 | 0.87 | 0.12 | 0.05 |
| 19 373 | 5966 | 4.15 | 0.03 | 1.23 | 0.24 | 0.16 |
| 19 994 | 6087 | 3.97 | 0.14 | 1.19 | 0.20 | 0.12 |
| 20 619 | 5706 | 4.48 | -0.20 | 0.90 | 0.02 | -0.04 |
| 22 879 | 5867 | 4.26 | -0.84 | 1.21 | 0.06 | 0.00 |
| 25 457 | 6246 | 4.32 | 0.06 | 1.25 | 0.10 | 0.03 |
| 30 649 | 5816 | 4.28 | -0.47 | 1.18 | 0.06 | 0.00 |
| 30 743 | 6298 | 4.03 | -0.45 | 1.64 | 0.15 | 0.04 |
| 34 411 | 5875 | 4.18 | 0.03 | 1.08 | 0.13 | 0.07 |
| 37 124 | 5610 | 4.44 | -0.44 | 0.89 | 0.17 | 0.11 |
| 43 042 | 6444 | 4.23 | 0.04 | 1.52 | 0.01 | -0.06 |
| 43 386 | 6480 | 4.27 | -0.06 | 1.56 | 0.26 | 0.16 |
| 52 711 | 5887 | 4.31 | -0.16 | 1.04 | 0.10 | 0.04 |
| 58 855 | 6309 | 4.16 | -0.32 | 1.38 | 0.14 | 0.04 |
| 61 421 | 6600 | 3.96 | -0.03 | 1.83 | 0.19 | 0.11 |
| 62 301 | 5938 | 4.06 | -0.69 | 1.28 | 0.11 | 0.04 |
| 67 228 | 5847 | 3.93 | 0.12 | 1.18 | 0.22 | 0.14 |
| 69 611 | 5821 | 4.18 | -0.60 | 1.22 | 0.14 | 0.07 |
| 75 732 | 5336 | 4.47 | 0.40 | 0.76 | 0.28 | 0.25 |
| 90 508 | 5802 | 4.35 | -0.33 | 1.02 | 0.03 | -0.02 |
| 95 128 | 5892 | 4.27 | 0.00 | 1.01 | 0.12 | 0.06 |
| 102 158 | 5758 | 4.24 | -0.46 | 1.13 | 0.14 | 0.08 |
| 102 870 | 6085 | 4.04 | 0.14 | 1.38 | 0.08 | 0.00 |
| 109 358 | 5863 | 4.36 | -0.21 | 1.12 | 0.03 | -0.02 |
| 114 710 | 6006 | 4.30 | -0.03 | 1.12 | 0.08 | 0.03 |
| 114 762 | 5934 | 4.11 | -0.71 | 1.14 | 0.13 | 0.07 |
| 117 176 | 5483 | 3.82 | -0.09 | 1.02 | 0.04 | -0.03 |
| 120 136 | 6360 | 4.17 | 0.27 | 1.56 | 0.07 | 0.00 |
| 121 370 | 6023 | 3.76 | 0.28 | 1.40 | 0.35 | 0.25 |
| 121 560 | 6144 | 4.27 | -0.43 | 1.26 | 0.14 | 0.07 |
| 122 742 | 5537 | 4.43 | -0.01 | 0.78 | 0.12 | 0.07 |
| 124 850 | 6112 | 3.78 | -0.06 | 1.48 | 0.10 | -0.03 |
| 126 053 | 5691 | 4.45 | -0.35 | 0.96 | 0.03 | -0.02 |
| 127 334 | 5691 | 4.22 | 0.21 | 0.97 | 0.18 | 0.12 |
| 130 322 | 5394 | 4.55 | 0.04 | 0.79 | 0.05 | 0.01 |
| 130 819 | 6598 | 4.18 | -0.10 | 1.76 | 0.06 | -0.02 |
| 132 254 | 6220 | 4.15 | -0.03 | 1.46 | 0.10 | 0.03 |
| 134 987 | 5740 | 4.25 | 0.25 | 1.02 | 0.24 | 0.17 |
| 136 064 | 6116 | 3.86 | -0.05 | 1.41 | 0.18 | 0.11 |
| 136 202 | 6104 | 3.80 | -0.09 | 1.45 | 0.21 | 0.12 |
| 137 052 | 6283 | 3.94 | -0.03 | 1.89 | -0.02 | -0.09 |
| 141 004 | 5864 | 4.09 | -0.03 | 1.05 | 0.08 | 0.01 |
| 142 373 | 5841 | 3.84 | -0.57 | 1.24 | 0.13 | 0.05 |
| 142 860 | 6254 | 4.02 | -0.19 | 1.36 | 0.10 | 0.02 |
| 143 761 | 5821 | 4.12 | -0.24 | 1.10 | 0.05 | -0.02 |
| 145 675 | 5334 | 4.51 | 0.45 | 0.81 | 0.23 | 0.18 |
| 146 233 | 5786 | 4.36 | 0.01 | 0.98 | 0.09 | 0.03 |
| 150 680 | 5814 | 3.72 | -0.03 | 1.38 | 0.25 | 0.16 |
| 153 597 | 6275 | 4.36 | -0.11 | 1.48 | -0.01 | -0.07 |
| 154 345 | 5507 | 4.57 | -0.03 | 0.70 | 0.00 | -0.04 |
| 157 214 | 5735 | 4.24 | -0.34 | 1.00 | 0.12 | 0.06 |
| 157 347 | 5643 | 4.31 | -0.01 | 0.90 | 0.08 | 0.02 |
| 159 222 | 5845 | 4.28 | 0.09 | 1.05 | 0.15 | 0.09 |
| 161 797 | 5596 | 3.93 | 0.23 | 1.17 | 0.23 | 0.16 |
| 162 003 | 6423 | 4.06 | -0.07 | 1.67 | 0.17 | 0.05 |
| 162 004 | 6203 | 4.24 | -0.06 | 1.29 | 0.11 | 0.04 |
| 163 989 | 6116 | 3.62 | -0.14 | 1.61 | 0.13 | 0.03 |
| 165 401 | 5811 | 4.41 | -0.39 | 1.10 | 0.10 | 0.04 |
| 165 908 | 5994 | 4.01 | -0.61 | 1.25 | 0.17 | 0.09 |
| 168 009 | 5785 | 4.23 | -0.03 | 1.03 | 0.13 | 0.06 |
| 168 151 | 6357 | 4.02 | -0.33 | 1.68 | 0.05 | -0.02 |
| 173 667 | 6305 | 3.99 | 0.03 | 1.60 | 0.09 | -0.04 |
| 176 377 | 5860 | 4.43 | -0.27 | 0.91 | 0.04 | 0.00 |
| 178 428 | 5673 | 4.23 | 0.12 | 0.96 | 0.10 | 0.04 |
| 182 572 | 5610 | 4.19 | 0.37 | 1.01 | 0.19 | 0.12 |
| 184 499 | 5828 | 4.13 | -0.51 | 1.17 | 0.14 | 0.05 |
| 186 408 | 5805 | 4.26 | 0.06 | 1.03 | 0.14 | 0.08 |
| 186 427 | 5766 | 4.29 | 0.05 | 0.89 | 0.14 | 0.08 |
| 187 013 | 6312 | 4.09 | -0.05 | 1.46 | 0.02 | -0.08 |
| 187 691 | 6088 | 4.07 | 0.07 | 1.35 | 0.13 | 0.04 |
| 187 923 | 5713 | 3.97 | -0.20 | 1.19 | 0.16 | 0.08 |
| 190 360 | 5588 | 4.27 | 0.24 | 0.98 | 0.15 | 0.09 |
| 190 406 | 5937 | 4.35 | -0.01 | 1.10 | 0.10 | 0.05 |
| 204 155 | 5829 | 4.12 | -0.63 | 1.18 | 0.12 | 0.03 |
| 207 978 | 6313 | 3.94 | -0.52 | 1.57 | 0.20 | 0.10 |
| 209 458 | 6082 | 4.33 | -0.06 | 1.15 | 0.05 | 0.00 |
| 210 277 | 5541 | 4.42 | 0.26 | 0.73 | 0.07 | 0.02 |
| 210 855 | 6176 | 3.81 | 0.21 | 1.61 | 0.11 | 0.02 |
| 215 648 | 6110 | 3.85 | -0.37 | 1.69 | 0.21 | 0.10 |
| 216 385 | 6212 | 3.85 | -0.26 | 1.54 | 0.15 | 0.05 |
| 217 014 | 5793 | 4.33 | 0.20 | 0.95 | 0.19 | 0.12 |
| 218 470 | 6407 | 4.07 | -0.12 | 1.85 | 0.05 | -0.08 |
| 219 623 | 6140 | 4.23 | 0.01 | 1.30 | 0.11 | 0.05 |
| 221 830 | 5749 | 4.19 | -0.36 | 1.14 | 0.02 | -0.04 |
| 222 368 | 6157 | 3.95 | -0.19 | 1.51 | 0.15 | 0.06 |
| G78-1 | 5895 | 4.11 | -0.88 | 1.14 | 0.17 | 0.07 |
|
|
[Fe/H] | 5682 | 5688 | 5890 | 5896 | 6154 | 6160 | 8183 | 8194 |
|
|
| 5200 | 4.50 | 0.0 | -0.08 | -0.07 | -0.04 | -0.04 | -0.04 | -0.05 | -0.15 | -0.15 | -0.08 |
| 5200 | 4.50 | -1.0 | -0.06 | -0.06 | -0.07 | -0.08 | -0.04 | -0.04 | -0.24 | -0.24 | -0.10 |
| 5200 | 4.50 | -2.0 | -0.14 | -0.17 | -0.15 |
||||||
| 5200 | 4.50 | -3.0 | -0.17 | -0.17 | -0.17 |
||||||
| 5200 | 3.50 | 0.0 | -0.14 | -0.14 | -0.04 | -0.06 | -0.06 | -0.06 | -0.31 | -0.31 | -0.14 |
| 5200 | 3.50 | -1.0 | -0.14 | -0.16 | -0.42 | -0.46 | -0.29 |
||||
| 5200 | 3.50 | -2.0 | -0.31 | -0.34 | -0.32 |
||||||
| 5200 | 3.50 | -3.0 | -0.36 | -0.28 | -0.32 |
||||||
| 5780 | 4.50 | 0.0 | -0.08 | -0.08 | -0.05 | -0.06 | -0.04 | -0.05 | -0.20 | -0.21 | -0.10 |
| 5780 | 4.50 | -1.0 | -0.06 | -0.07 | -0.16 | -0.18 | -0.05 | -0.05 | -0.27 | -0.29 | -0.14 |
| 5780 | 4.50 | -2.0 | -0.05 | -0.05 | -0.34 | -0.32 | -0.05 | -0.05 | -0.10 | -0.12 | -0.13 |
| 5780 | 4.50 | -3.0 | -0.23 | -0.16 | -0.19 |
||||||
| 5780 | 3.50 | 0.0 | -0.17 | -0.18 | -0.10 | -0.10 | -0.06 | -0.08 | -0.43 | -0.43 | -0.19 |
| 5780 | 3.50 | -1.0 | -0.11 | -0.11 | -0.33 | -0.35 | -0.39 | -0.43 | -0.29 |
||
| 5780 | 3.50 | -2.0 | -0.56 | -0.52 | -0.54 |
||||||
| 5780 | 3.50 | -3.0 | -0.27 | -0.17 | -0.22 |
||||||
| 6500 | 4.50 | 0.0 | -0.07 | -0.09 | -0.11 | -0.15 | -0.03 | -0.04 | -0.28 | -0.30 | -0.13 |
| 6500 | 4.50 | -1.0 | -0.38 | -0.41 | -0.25 | -0.30 | -0.33 |
||||
| 6500 | 4.50 | -2.0 | -0.45 | -0.38 | -0.41 |
||||||
| 6500 | 4.50 | -3.0 | -0.13 | -0.10 | -0.11 |
||||||
| 6500 | 3.50 | 0.0 | -0.12 | -0.13 | -0.22 | -0.31 | -0.05 | -0.06 | -0.47 | -0.52 | -0.23 |
| 6500 | 3.50 | -1.0 | -0.64 | -0.61 | -0.32 | -0.40 | -0.49 |
||||
| 6500 | 3.50 | -2.0 | -0.54 | -0.43 | -0.49 |
||||||
| 6500 | 3.50 | -3.0 | -0.13 | -0.09 | -0.11 |