All Figures

$\begin{figure} \par\includegraphics[width=8cm,clip]{0295f1.ps} \end{figure}$ Figure 1: Values for which $\omega _{{\rm w}}$ , $k_{{\rm w}}$ and $\gamma$ give rise to radio emission between $100\ \mbox{MHz}$ (lower solid line) and $10\ \mbox{GHz}$ (upper) according to the resonance condition (7) with K = 10. On the vertical axis is plotted $k_{{\rm w}} v - \omega _{{\rm w}}$ , because we assume the particle's velocity to be larger than the wiggler's phase velocity.
Open with DEXTER

In the text

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{0295f2a.ps} \includegraphics[width=7.8cm,clip]{0295f2b.ps} \end{figure}$ Figure 2: Wavefronts (dotted lines) and level curves at e^-n of the maximum amplitude of the Gaussian mode (solid lines, n = 1, 2, ...); top: near-field, bottom: far-field. z is in units of z₀ and $r_\perp$ in units of w₀.
Open with DEXTER

In the text

$\begin{figure}% latex2html id marker 792\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 3a: Run 1: (z, x)-behaviour of the particles during their passage in the cavity (from left to rigth; from top to bottom). On the horizontal axis is plotted the z-coordinate of all particles, subsequently for z = 2, 4, 6, 8 and 10 km. Except for $t = 3.34 \times 10^{-5}\:\mbox{s}$ , the horizontal spacing between the long ticks is 0.02 m (e.g. $\Delta z \approx 0.08 \:\mbox{m}$ for $t = 0\:\mbox{s}$ ). In the last plot, the spacing between the long ticks is 0.05 m. Bunching clearly occurs at $t = 1.33\times 10^{-5}\;\mbox{s}$ , "de-bunching'' at $t = 2.0 \times 10^{-5}\:\mbox{s}$ and "re-bunching'' at $t = 2.67 \times 10^{-5}\:\mbox{s}$ .

In the text

$\begin{figure}% latex2html id marker 807\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 3b: Run 1: Power of the pulse at the end of the simulation $t = 3.3 \times 10^{-5}\:\mbox{s}$ ( top: number of macroparticles N=200; bottom: N=2). On the horizontal axis is also plotted t, this is not the simulation time, but the duration of the pulse as a distant observer would measure. Negative t corresponds to earlier arrival. The maximum power for N=2 ( bottom) is $P_{2,{\rm max}} = 9.75 \times 10^{9}\:\mbox{W}$ . Since $P_{200} \propto N^2 P_{2}$ , this implies the radiation pulse at the top is coherent.

In the text

$\begin{figure}% latex2html id marker 824\par\includegraphics[width=8.4cm,clip]... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 3c: Run 1: spectrum at $t = 3.3 \times 10^{-5}\:\mbox{s}$ . The central frequency is at $\nu = 11\:\mbox{GHz}$ , with FWHM of $\Delta \nu = 2.42\:\mbox{GHz}$ . The peak on the right, centered on $\nu_{{\rm res}} = 11.9\:\mbox{GHz}$ , is caused by the first bunching at $t = 1.33 \times 10^{-5}\:\mbox{s}$ . And the peak on the left corresponds to the second buching, where $\gamma$ dropped $5\%$ , resulting in a lower $\nu _{{\rm res}}$ .

In the text

$\begin{figure}% latex2html id marker 838\par\includegraphics[width=8.4cm,clip]... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamed} \end{figure}$ Figure 3d: Run 1: time development of average Lorentz factor (i.e. per macro-particle) in two simulations, one with N=2 ( top) and the other with N=200 ( bottom). The N=2 case reflects the behaviour of particles radiating incoherently, with constant energy loss over time as compared with the bunching case, where there is a steep drop in energy ( $\Delta \bar{\gamma} = 50$ ) of the beam particles between 1.0 and $1.8 \times 10^{-3}\:\mbox{s}$ . Between $2.4 \times 10^{-5}\:\mbox{s}$ and $2.8 \times 10^{-5}\:\mbox{s}$ another drop in beam energy occurs, which corresponds to a second bunching of the particles. This time, the beam energy loss is less than for the first time, and the duration is much shorter. The pulse power (Fig. 3b) reflects these characterics where the first pulse is more powerful and has a longer duration than the second pulse.

In the text

$\begin{figure}% latex2html id marker 853\par\includegraphics[width=8cm,clip]{0... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 4a: Spectra for Run 2 plotted over each other; we have K = 5 (solid), 10 (dotted), 15 (short-dashed) and 20 (long-dashed). The resonance frequency shifts according to Eq. (7). The bandwidth increases with increasing $\nu _{{\rm res}}$ .

In the text

$\begin{figure}% latex2html id marker 860\par\includegraphics[width=8cm,clip]{0... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 4b: Pulse power for run 2 plotted for different K. The maximum scales roughly as K^-2.

In the text

$\begin{figure}% latex2html id marker 866\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 4c: Run 2: ( $\bar{\gamma}$ , t)-plot for K = 5, 10, 15, 20 (labelling as in Fig. 4a). Obviously, for all K, the beam particles bunch twice (also, see Fig. 4b). Corresponding to the maximum power, the beam energy loss is largest here for K = 5.

In the text

$\begin{figure}% latex2html id marker 923\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 5a: Run 3: spectrum at the end of the simulation for different $\lambda _{{\rm w}} = 100$ m (solid), 50 m (dotted), 40 m (short-dashed), 25 m (long-dashed). Spectral broadening is due to more bunchings occuring during the simulation.

In the text

$\begin{figure}% latex2html id marker 929\par\includegraphics[width=8cm,clip]{0... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 5b: Pulse power for Run 3 plotted for different $\lambda _{{\rm w}}$ values. Maximum powers are of about the same order of magnitude. Only the number of pulses differs for each run, due to number of bunching times.

In the text

$\begin{figure}% latex2html id marker 935\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 5c: Run 3: the average Lorentz factor of the macro-particles during their passage in the cavity for $\lambda _{{\rm w}} = 100$ , 50, 40, 25 m (labelling as in Fig. 5a). The starting time of the first bunching for each run is about $10 \:t_{{\rm eff}}$ (6). The energy beam loss after the first bunching is about $5\%$ .

In the text

$\begin{figure}% latex2html id marker 984\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 6a: Run 4: spectrum for $\beta _{{\rm w}} = 0.2$ (solid), 0.5 (dotted), 0.8 (short-dashed), 0.9 (long-dashed).

In the text

$\begin{figure}% latex2html id marker 990\par\includegraphics[width=8cm,clip]{0... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 6b: Pulse power for run 4 plotted for different $\beta _{{\rm w}}$ .

In the text

$\begin{figure}% latex2html id marker 996\par\includegraphics[width=8cm,clip]{0... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 6c: Run 4: the average Lorentz factor versus the average distance z of the particles in simulations with changing $\beta _{{\rm w}} = 0.2$ , 0.5, 0.8, 0.9 (labelling same as Fig. 6a). The starting time of the first bunching is $10 \:t_{{\rm eff}}$ .

In the text

$\begin{figure}% latex2html id marker 1029\par\includegraphics[width=8cm,clip]{... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 7a: Run 5: spectra for (from top to bottom along the left vertical axis) B₀ = 10^-3 T (solid), 10^-2 T (dotted), 0.0025 T (short-dashed), 0.050 T (long-dashed). For $B_0 = 10^{-3}\:\mbox{T}$ , the spectrum shows the same properties (central frequency and bandwidth) as in the case where the background magnetic field is absent. For $B_0 = 10^{-2}\:\mbox{T}$ , the central frequency shifts to $2\:\mbox{GHz}$ , whereas the bandwidth drops to $0.61\:\mbox{GHz}$ .

In the text

$\begin{figure}% latex2html id marker 1042\par\includegraphics[width=8cm,clip]{... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 7b: Pulse power (logarithmic) for Run 5. The power of the radiation becomes smaller for B₀ = 0.025 and 0.05 T.

In the text

$\begin{figure}% latex2html id marker 1047\par\includegraphics[width=8cm,clip]{... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 7c: Run 5: the average Lorentz factor versus the average distance z of the particles in simulations with background magnetic field for $B_0 = 10^{-3}, 10^{-2}, 2.5 \times 10^{-2}, 5.0 \times 10^{-2}\:\mbox{T}$ (labelling as in Fig. 7a). The last case coincides practically with the horizontal line $\bar{\gamma} = 1000$ . Only for $B_0 = 10^{-3}\:\mbox{T}$ and $B_0 = 10^{-2}\:\mbox{T}$ the beam particles show FEL action.

In the text

$\begin{figure}% latex2html id marker 1063\par\includegraphics[width=8cm,clip]{... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 8a: Run 6: spectrum (from top to bottom) for $n/n_{{\rm GJ}\ast } = 0.1$ (solid), 0.2 (dotted), 0.3 (short-dashed) and 0.4 (long-dashed). The spectrum broadens as the number density increases, as expected from Fig. 8c, which shows single bunching for $n/n_{{\rm GJ}} = 0.1$ , but multiple bunching for $n/n_{{\rm GJ}} > 0.1$ .

In the text

$\begin{figure}% latex2html id marker 1072\par\includegraphics[width=8cm,clip]{... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 8b: Pulse power for Run 6 plotted for different number densities relative to $n_{{\rm GJ}\ast }$ . As expected, the maximum power scales as n².

In the text

$\begin{figure}% latex2html id marker 1078\par\includegraphics[width=8cm,clip]{... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 8c: Run 6: from top to bottom: Average Lorentz factor per particle, for number density of the bunch n = 0.1, 0.2, 0.3, $0.4\:n_{{\rm GJ}\ast}$ (labelling as in Fig. 8a). Clearly, a small beam number density results in negligible losses, and therefore, no coherent emission.

In the text

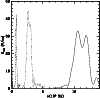$\begin{figure}% latex2html id marker 1085\par\includegraphics[width=8.6cm,clip... ...entlabel {\csname p@figure\endcsname \csname thefigure\endcsnamea} \end{figure}$ Figure 9a: Run 7: spectrum for initial Lorentz factor of the beam particles $\gamma = 1000$ (solid), 500 (dotted0), 250 (short-dashed), 100 (long-dashed). The central frequency shift as $\gamma ^2$ .

In the text

$\begin{figure}% latex2html id marker 1090\includegraphics[width=8.6cm,clip]{0... ...rentlabel {\csname p@figure\endcsname \csname thefigure\endcsnameb} \end{figure}$ Figure 9b: Pulse power for run 7 plotted.

In the text

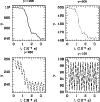$\begin{figure}% latex2html id marker 1096\par\includegraphics[width=8.6cm,clip... ...ntlabel {\csname p@figure\endcsname \csname thefigure\endcsnamec} \end{figure}$ Figure 9c: Run 7: the average Lorentz factor versus the average distance z of the particles in simulations with changing Lorentz factor.

In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{0295f1.ps} \end{figure}$	Figure 1: Values for which $\omega _{{\rm w}}$ , $k_{{\rm w}}$ and $\gamma$ give rise to radio emission between $100\ \mbox{MHz}$ (lower solid line) and $10\ \mbox{GHz}$ (upper) according to the resonance condition (7) with K = 10. On the vertical axis is plotted $k_{{\rm w}} v - \omega _{{\rm w}}$ , because we assume the particle's velocity to be larger than the wiggler's phase velocity.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{0295f2a.ps} \includegraphics[width=7.8cm,clip]{0295f2b.ps} \end{figure}$	Figure 2: Wavefronts (dotted lines) and level curves at e^-n of the maximum amplitude of the Gaussian mode (solid lines, n = 1, 2, ...); top: near-field, bottom: far-field. z is in units of z₀ and $r_\perp$ in units of w₀.
Open with DEXTER